The Effective Coverage of Homogeneous Teams with Radial Attenuation Models
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
2. Coverage of an -Node Team in Regular Polygon Formation
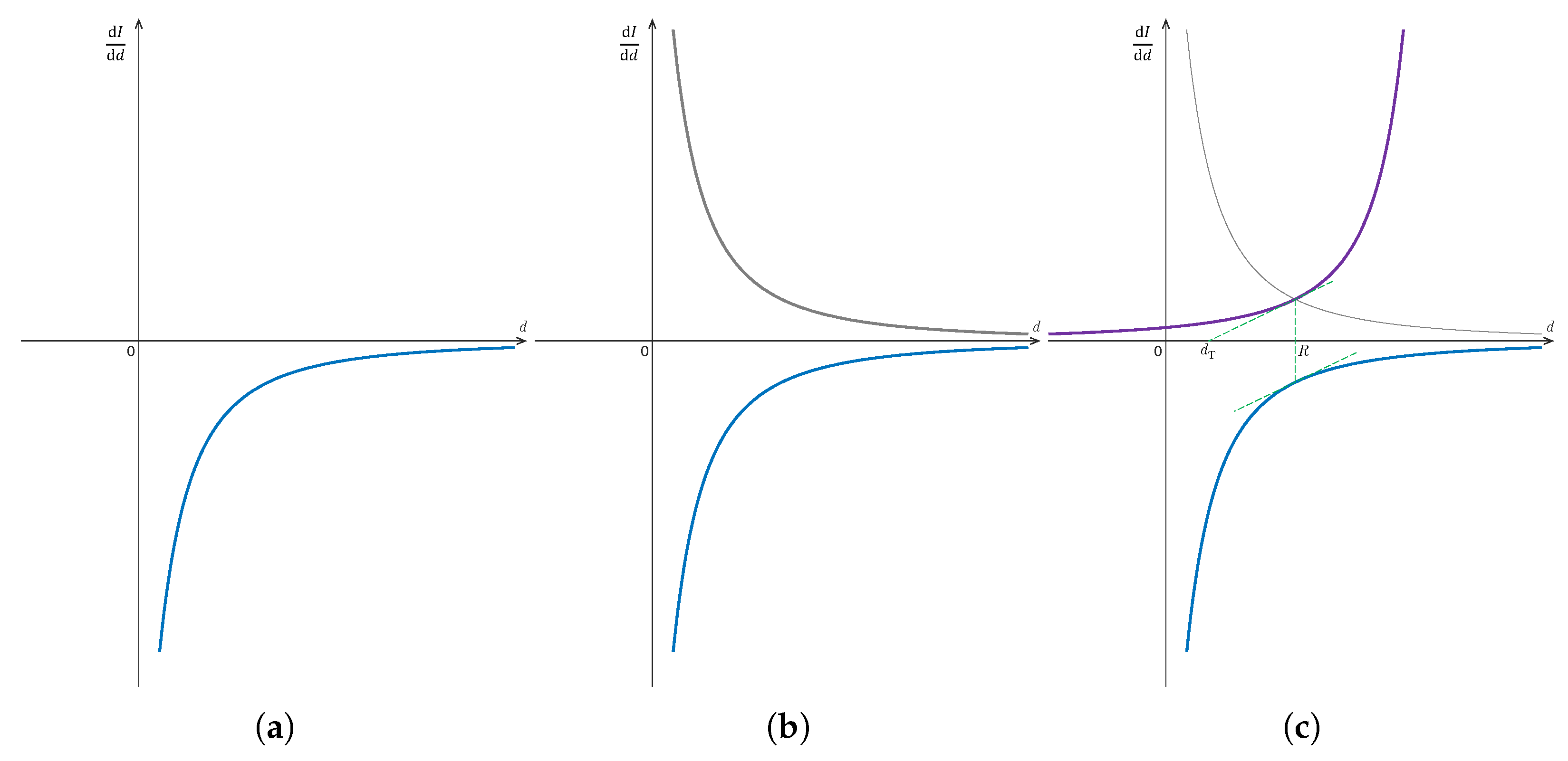
- “Max distance”, which yields the maximum team’s effective coverage.
- “Last-connection distance”. Any separation D greater than this distance will make the team’s effectively covered region disconnect into more than one part.
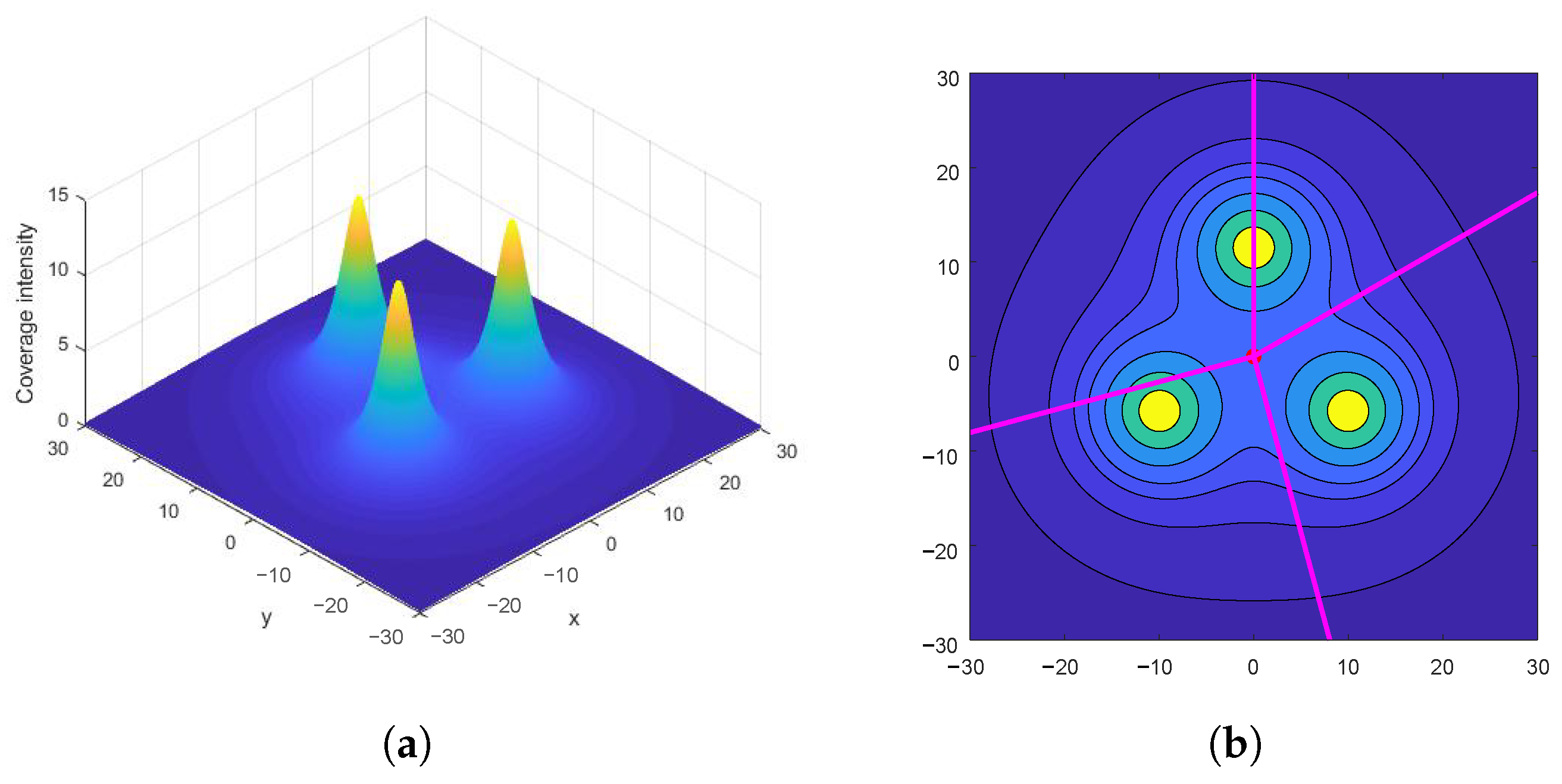
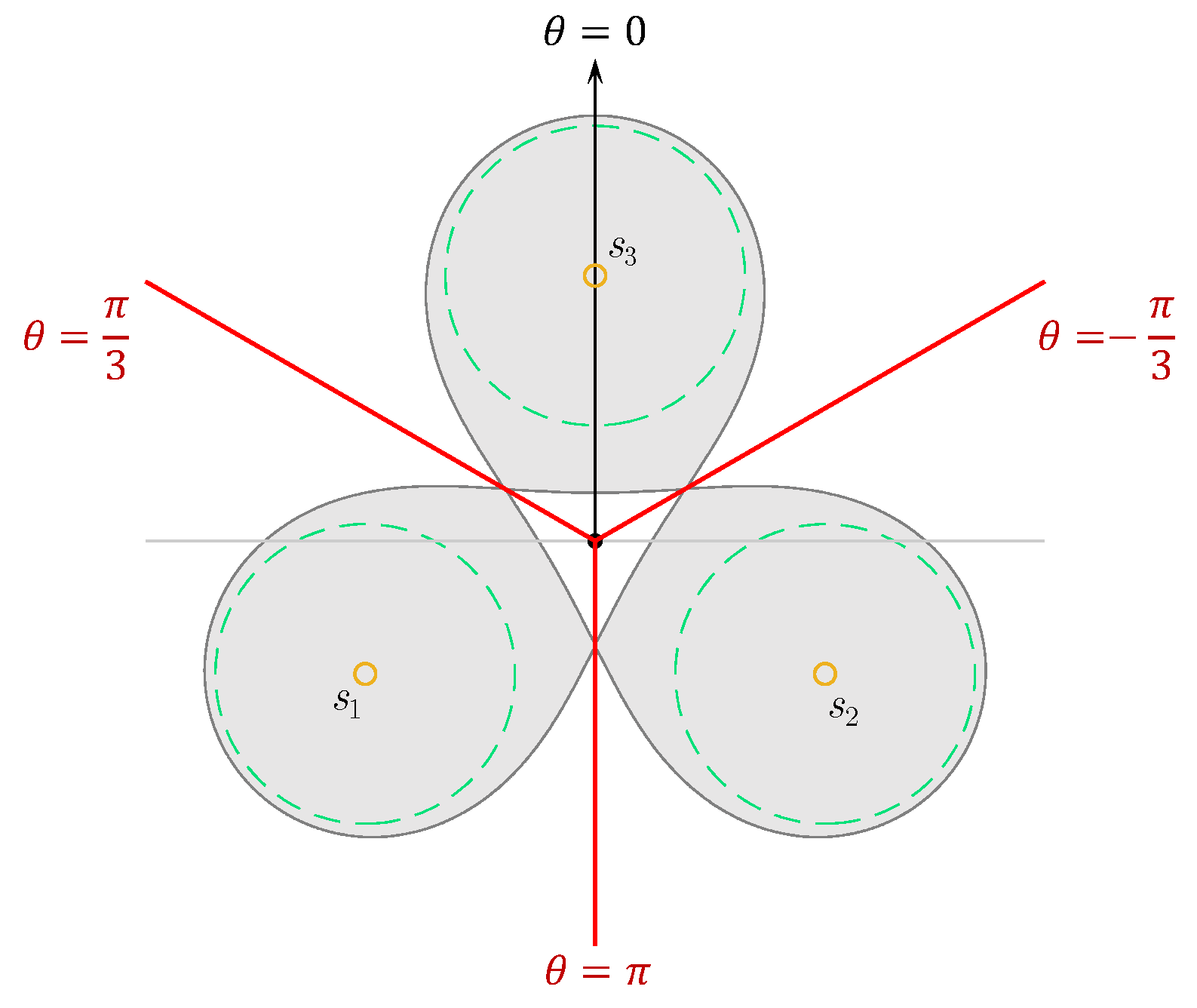
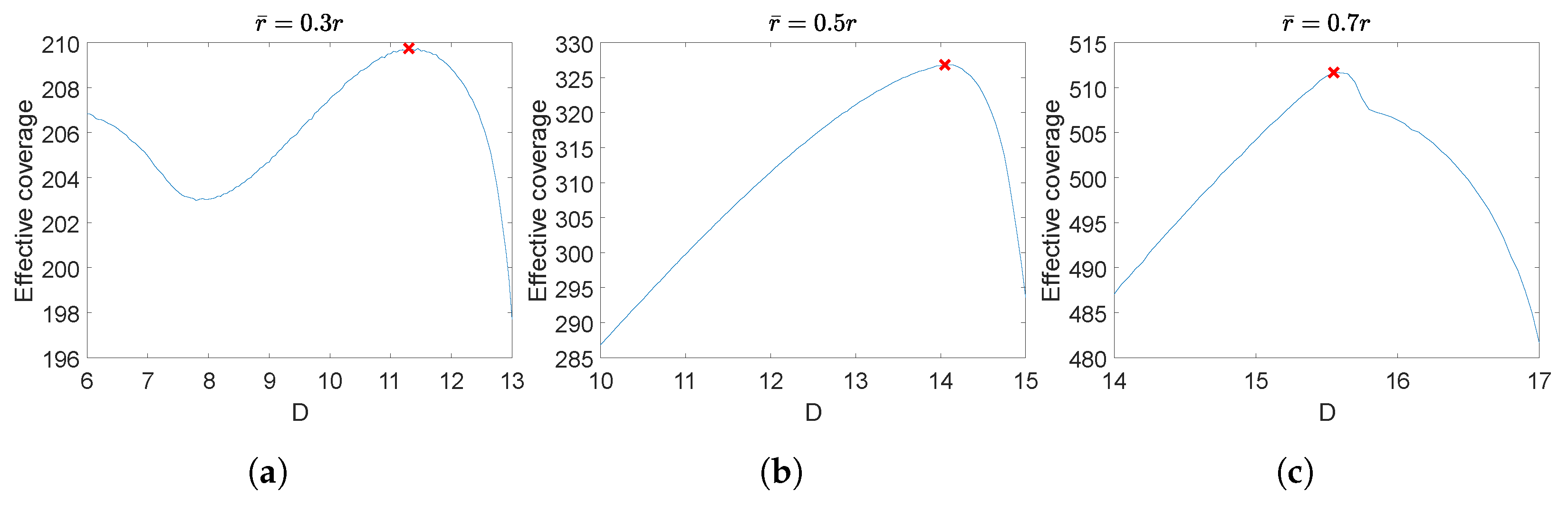
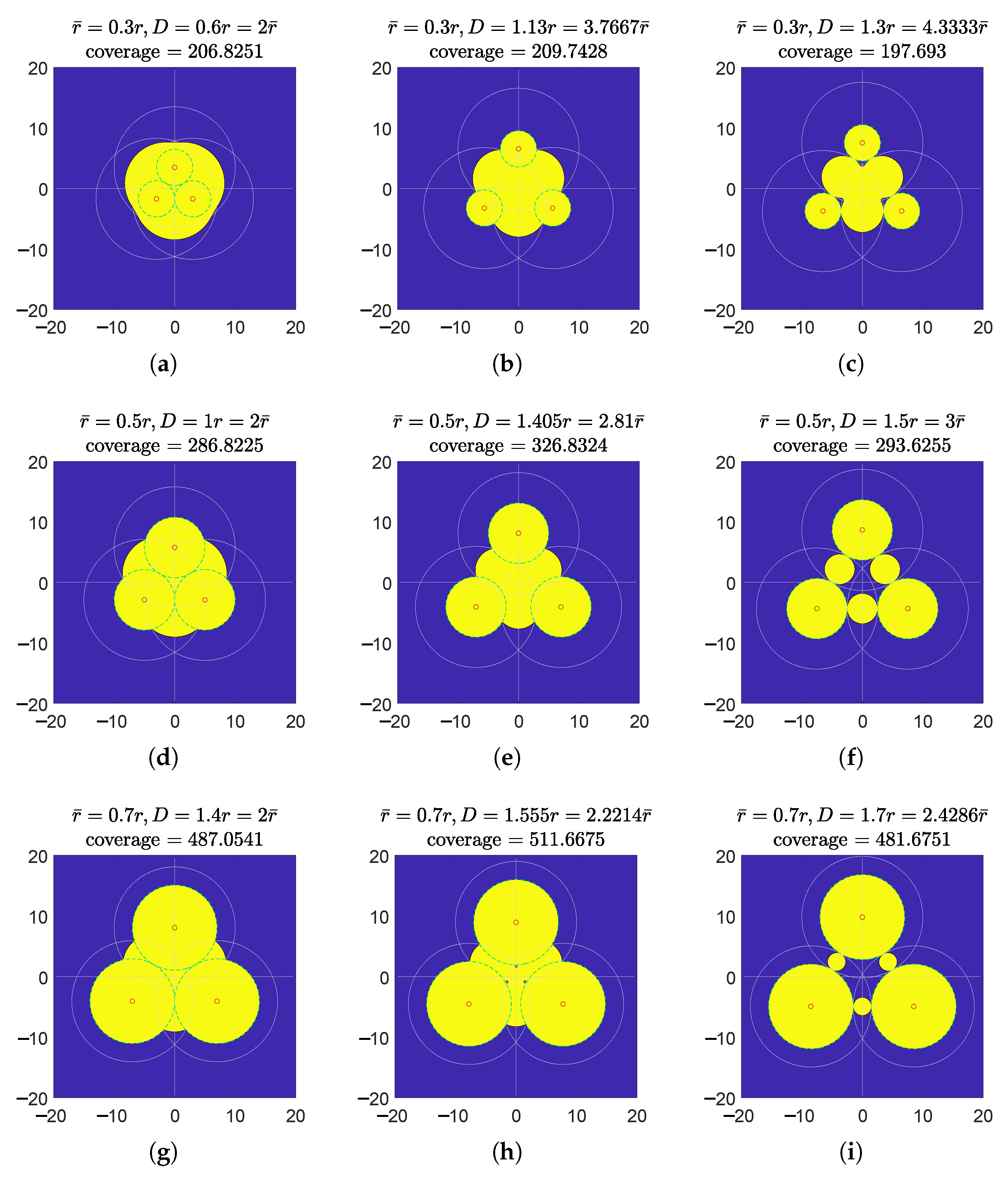
2.1. Three-Node Teams
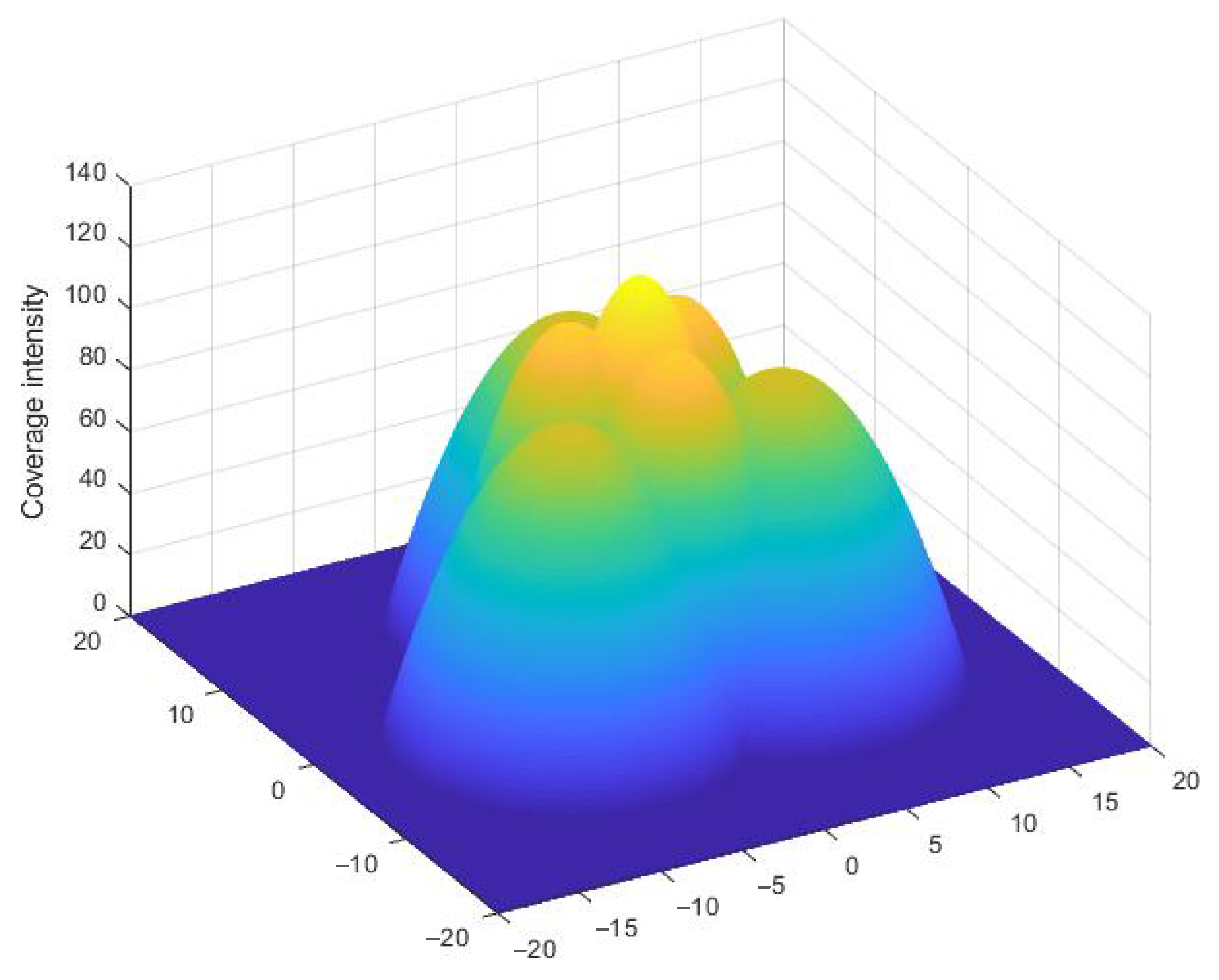
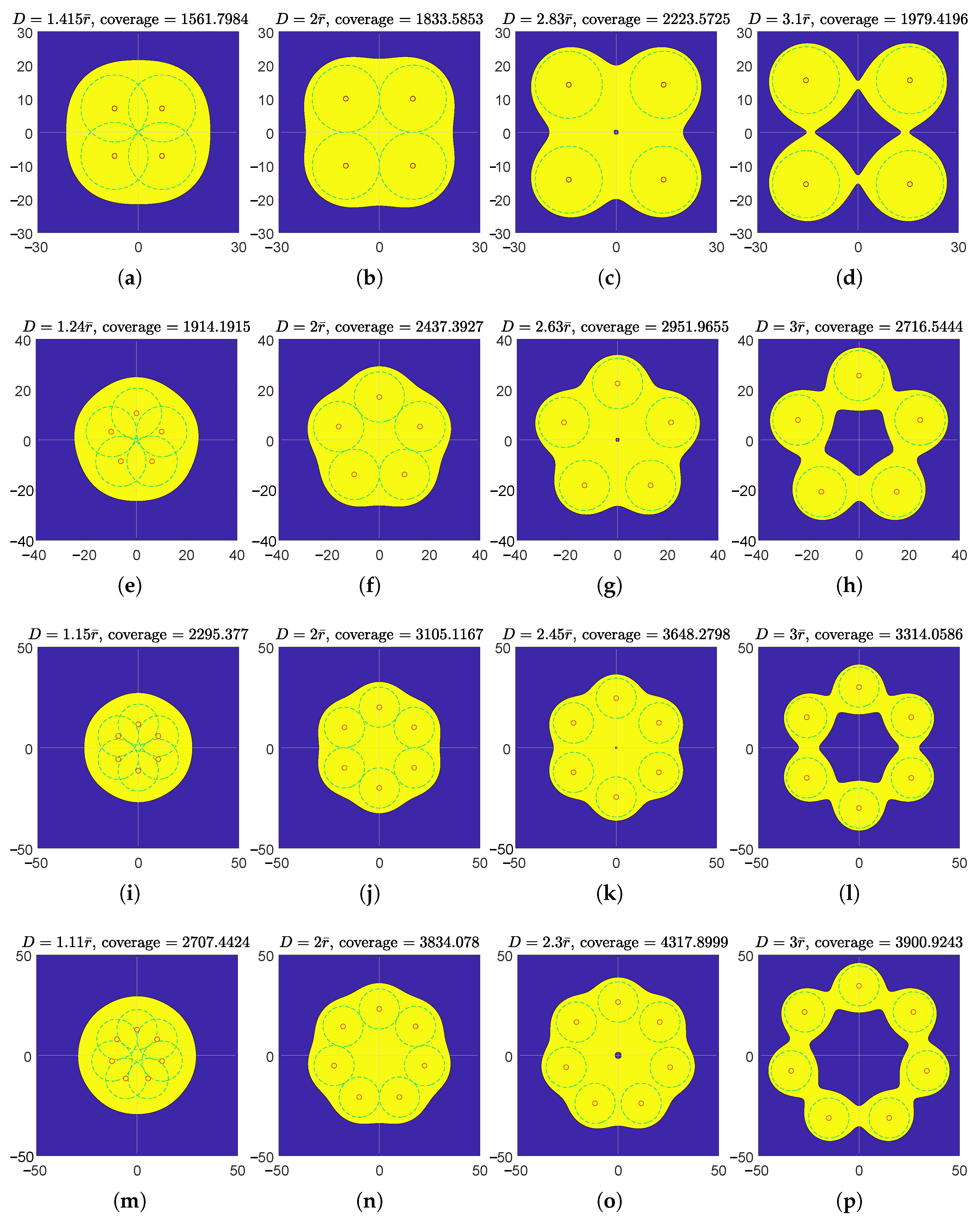
2.2. General n-Node Team
- For an n-node team in the formation of an n-sided regular polygon where each node is equipped with a convex model of coverage and , its circumcenter O is effectively covered if and only if the entire effectively covered region is simply connected.
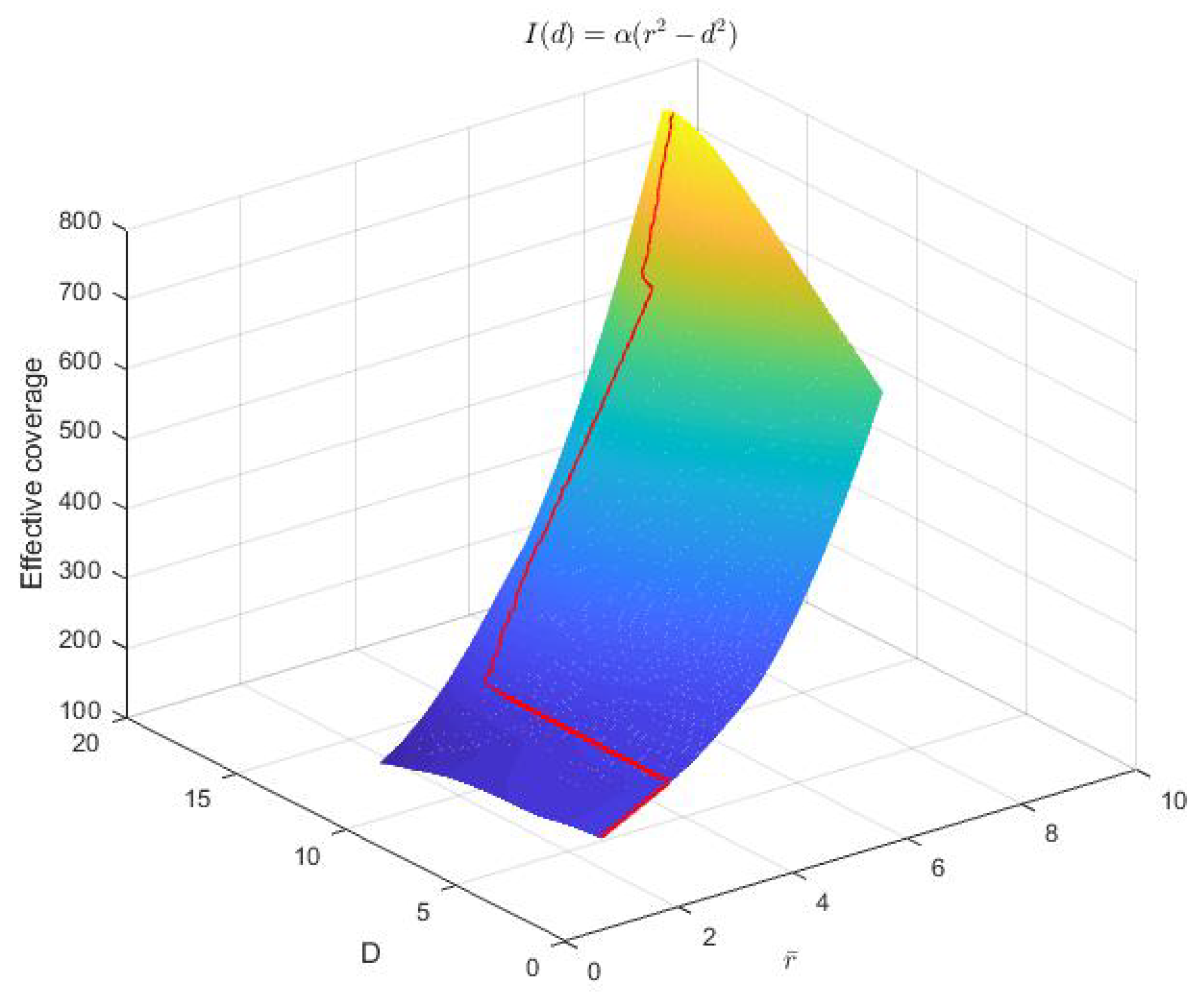
3. Simulations
3.1. Unbounded Convex Model for a 3-Node Team in Equilateral Triangle Formation
3.2. Concave Model for a 3-Node Team in Equilateral Triangle Formation
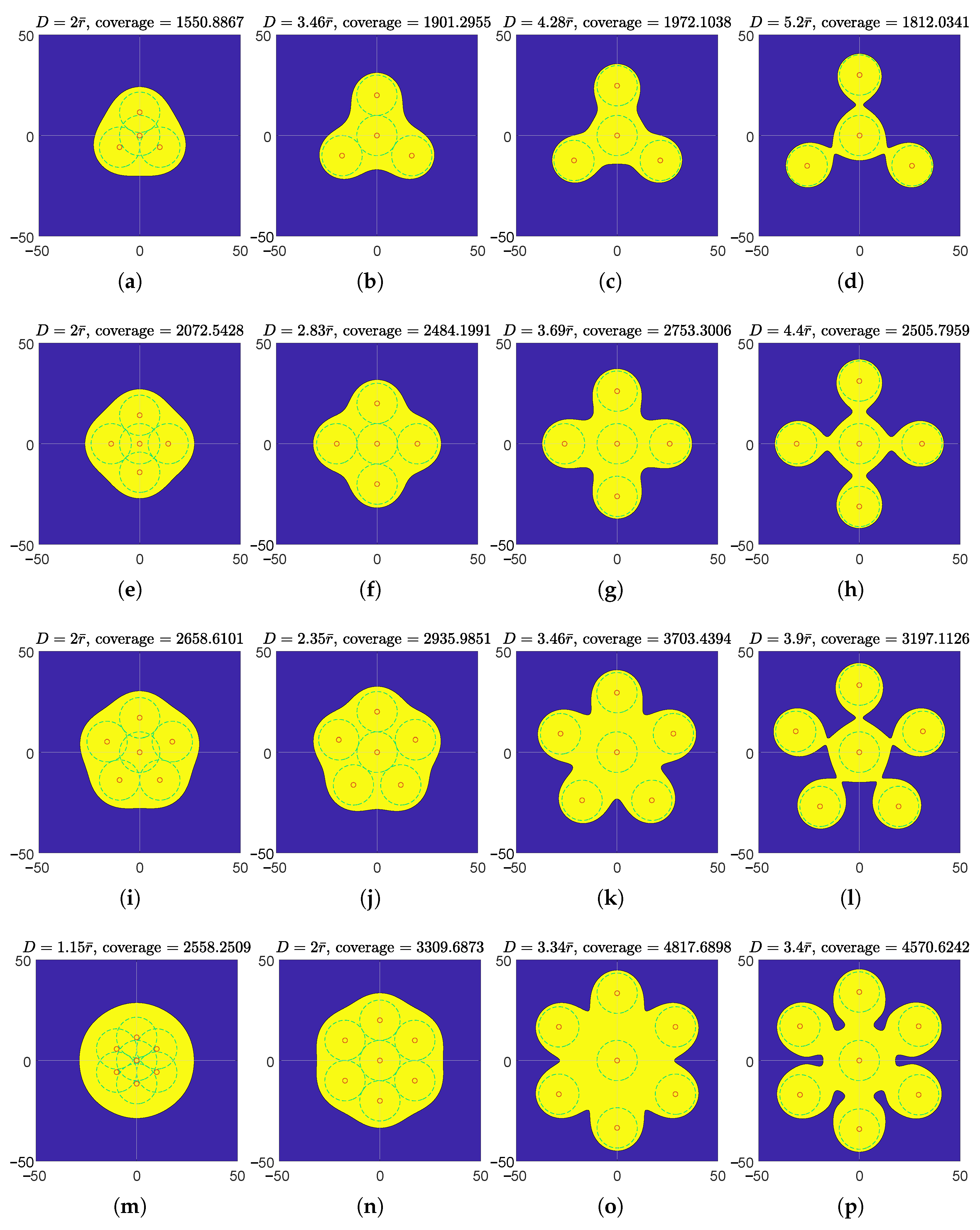
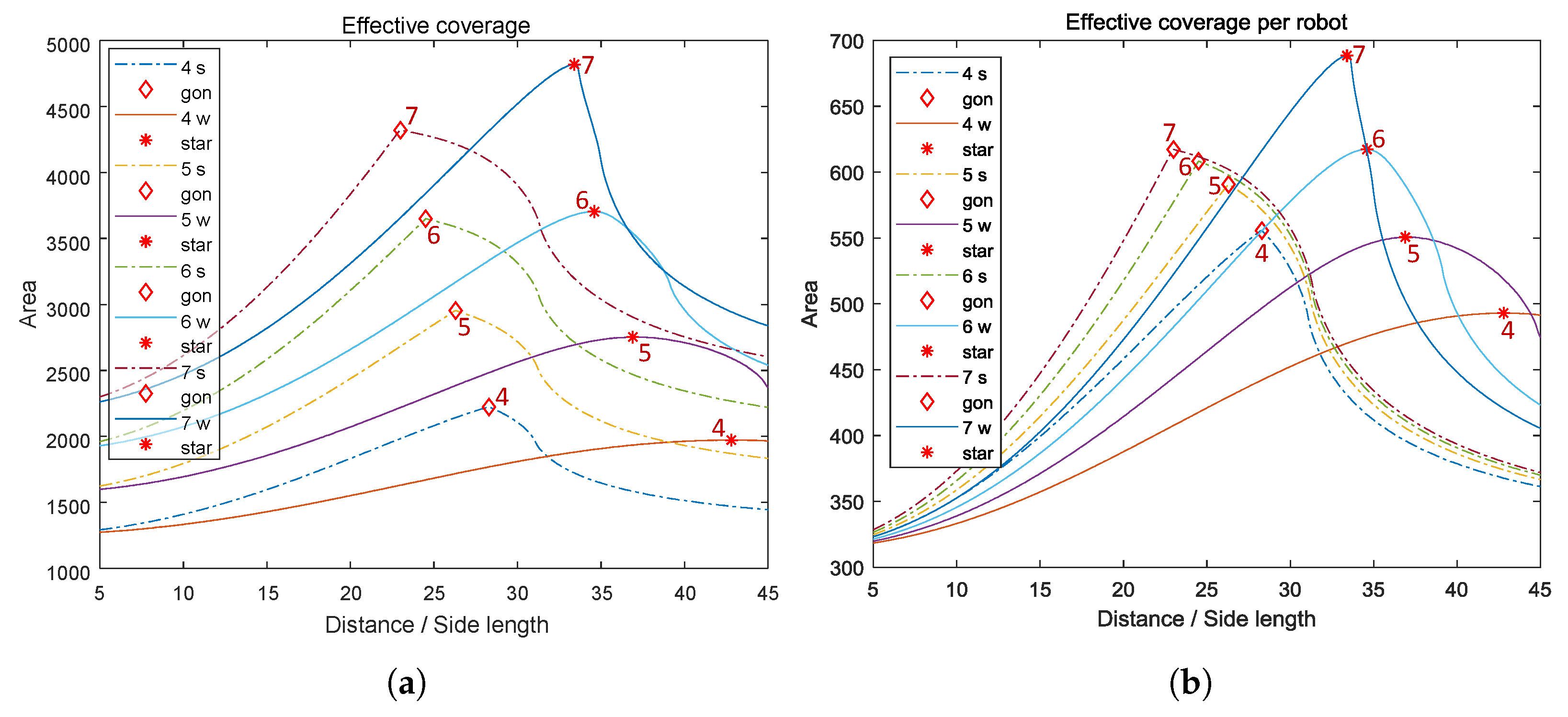
3.3. n Nodes in Regular Polygon and Regular Star Formations
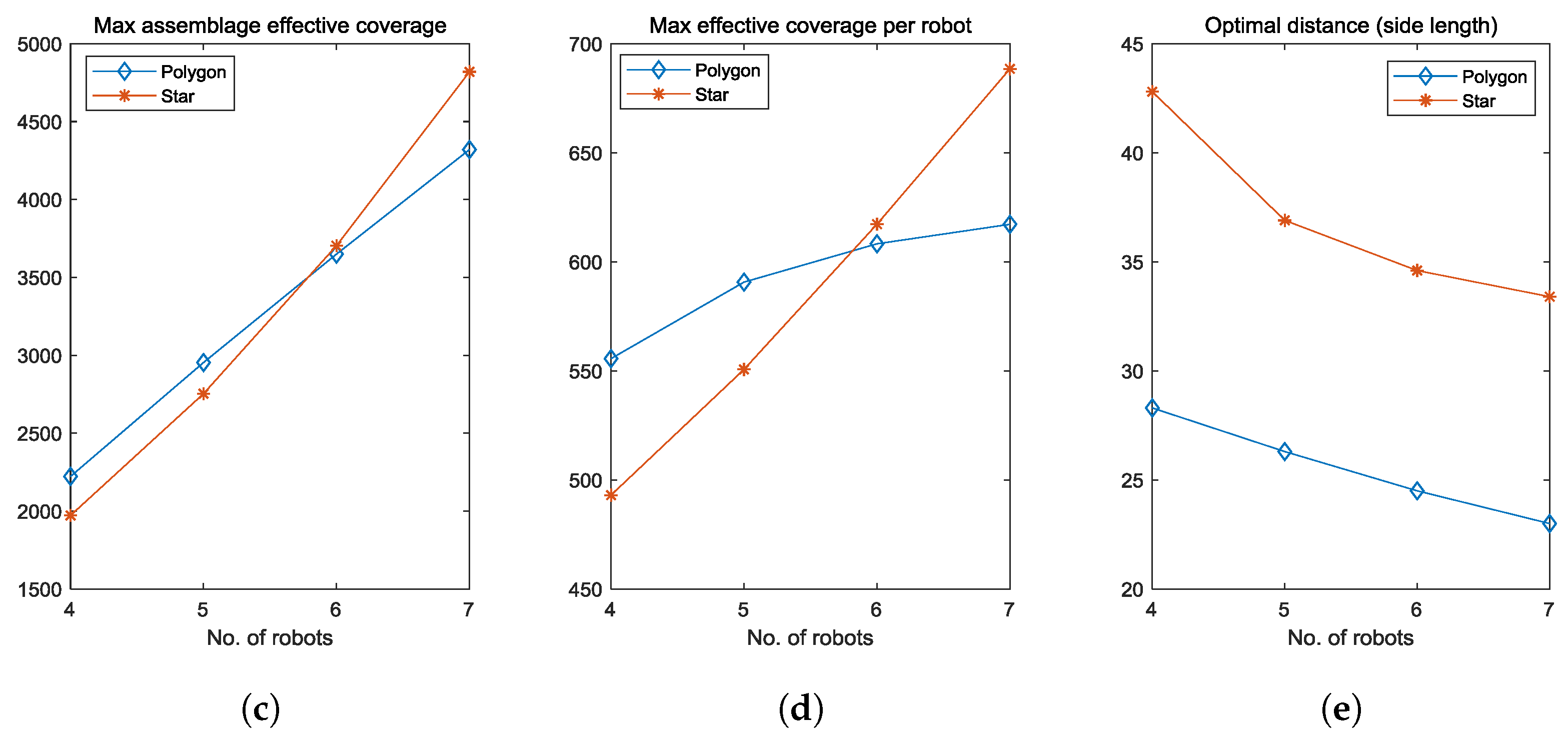
3.4. Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
Appendix A. Sum of a Sine Function with Equidistant Phases
Appendix A.1. Proof by Contradiction Using a Vector Rotation Approach
Appendix A.2. Vieta’s Formula Approach
Appendix A.3. Eular’s Formula Approach
Appendix B. Relation between First- and Second-Order Derivatives of a Convex Decreasing Function
- on
- on
- on
References
- Yáng, Y.R.; Chen, P.C. Effective Coverage of Two-Node Team with Radial Attenuation Models. J. Intell. Robot. Syst. 2021, 103, 1–13. [Google Scholar] [CrossRef]
- Gupta, H.P.; Tyagi, P.K.; Singh, M.P. Regular Node Deployment for k-Coverage in m-Connected Wireless Networks. IEEE Sens. J. 2015, 15, 7126–7134. [Google Scholar] [CrossRef]
- Sakai, K.; Sun, M.T.; Ku, W.S.; Lai, T.H.; Vasilakos, A.V. A Framework for the Optimal k-Coverage Deployment Patterns of Wireless Sensors. IEEE Sens. J. 2015, 15, 7273–7283. [Google Scholar] [CrossRef]
- Wang, B.; Deng, X.; Liu, W.; Yang, L.T.; Chao, H. Confident information coverage in sensor networks for field reconstruction. IEEE Wirel. Commun. 2013, 20, 74–81. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, B. The optimal placement pattern for confident information coverage in wireless sensor networks. IEEE Trans. Mob. Comput. 2016, 15, 1022–1032. [Google Scholar] [CrossRef]
- Yen, L.H.; Yu, C.W.; Cheng, Y.M. Expected k-coverage in wireless sensor networks. Ad Hoc Netw. 2006, 4, 636–650. [Google Scholar] [CrossRef]
- Wang, B. Coverage problems in sensor networks: A survey. ACM Comput. Surv. 2011, 43, 1–53. [Google Scholar] [CrossRef]
- Yáng, Y.R.; Chen, P.C.Y. Navigation of Robot-Formation via Overlap-Induced Equilibrium Points in Uncertain Environments. IEEE Trans. Autom. Sci. Eng. 2022, 1–12. [Google Scholar] [CrossRef]
- Bai, X.; Yun, Z.; Xuan, D.; Lai, T.H.; Jia, W. Optimal patterns for four-connectivity and full coverage in wireless sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 435–448. [Google Scholar]
- Yun, Z.; Bai, X.; Xuan, D.; Lai, T.H.; Jia, W. Optimal deployment patterns for full coverage and k-Connectivity (k ≤ 6) wireless sensor networks. IEEE/ACM Trans. Netw. 2010, 18, 934–947. [Google Scholar]
- Zhang, C.; Bai, X.; Teng, J.; Xuan, D.; Jia, W. Constructing low-connectivity and full-coverage three dimensional sensor networks. IEEE J. Sel. Areas Commun. 2010, 28, 984–993. [Google Scholar] [CrossRef]
- Ranieri, J.; Chebira, A.; Vetterli, M. Near-Optimal Sensor Placement for Linear Inverse Problems. IEEE Trans. Signal Process. 2014, 62, 1135–1146. [Google Scholar] [CrossRef]
- Lin, F.; Chiu, P. A near-optimal sensor placement algorithm to achieve complete coverage-discrimination in sensor networks. IEEE Commun. Lett. 2005, 9, 43–45. [Google Scholar] [CrossRef]
- Wang, B.; Xu, H.; Liu, W.; Yang, L.T. The Optimal Node Placement for Long Belt Coverage in Wireless Networks. IEEE Trans. Comput. 2015, 64, 587–592. [Google Scholar] [CrossRef]
- Li, L.; Chen, H. UAV Enhanced Target-Barrier Coverage Algorithm for Wireless Sensor Networks Based on Reinforcement Learning. Sensors 2022, 22, 6381. [Google Scholar] [CrossRef] [PubMed]
- Akram, J.; Munawar, H.S.; Kouzani, A.Z.; Ma mud, M.A.P. Using Adaptive Sensors for Optimised Target Coverage in Wireless Senso Networks. Sensors 2022, 22, 1083. [Google Scholar] [CrossRef] [PubMed]
- Tirandazi, P.; Rahiminasab, A.; Ebadi, M. An efficient coverage and connectivity algorithm based on mobile robots for wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2022, 1–23. [Google Scholar] [CrossRef]
- Wang, B.; Wang, W.; Srinivasan, V.; Chua, K.C. Information coverage for wireless sensor networks. IEEE Commun. Lett. 2005, 9, 967–969. [Google Scholar] [CrossRef]
- Deng, X.; Tang, Z.; Yang, L.T.; Lin, M.; Wang, B. Confident Information Coverage Hole Healing in Hybrid Industrial Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2018, 14, 2220–2229. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yang, L.T.; Deng, X.; Yi, L. A Nature-Inspired Node Deployment Strategy for Connected Confident Information Coverage in Industrial Internet of Things. IEEE Internet Things J. 2019, 6, 9217–9225. [Google Scholar] [CrossRef]
- Meng, S.; Kan, Z. Deep Reinforcement Learning-Based Effective Coverage Control With Connectivity Constraints. IEEE Control Syst. Lett. 2022, 6, 283–288. [Google Scholar] [CrossRef]
- Radermacher, R. Robotic Personal Conditioning Device. University of Maryland. 2018. Available online: https://arpa-e.energy.gov/technologies/projects/robotic-personal-conditioning-device (accessed on 20 July 2020).



| Ground Truth | Our Convex Model | Binary Model | Infinite Plane Model (e.g., [5]) | |
|---|---|---|---|---|
| 1 | , | , | , | , |
| 3 | , | , | , | , |
| 5 | , | , | , | , |
| 7 | , | , | , | , |
| 10 | , | , | , | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.-R.; Kang, Q.; She, R. The Effective Coverage of Homogeneous Teams with Radial Attenuation Models. Sensors 2023, 23, 350. https://doi.org/10.3390/s23010350
Yang Y-R, Kang Q, She R. The Effective Coverage of Homogeneous Teams with Radial Attenuation Models. Sensors. 2023; 23(1):350. https://doi.org/10.3390/s23010350
Chicago/Turabian StyleYang, Yuan-Rui, Qiyu Kang, and Rui She. 2023. "The Effective Coverage of Homogeneous Teams with Radial Attenuation Models" Sensors 23, no. 1: 350. https://doi.org/10.3390/s23010350
APA StyleYang, Y.-R., Kang, Q., & She, R. (2023). The Effective Coverage of Homogeneous Teams with Radial Attenuation Models. Sensors, 23(1), 350. https://doi.org/10.3390/s23010350






