Semantic Segmentation of Terrestrial Laser Scans of Railway Catenary Arches: A Use Case Perspective
Abstract
1. Introduction
2. Related Work
3. Catenary Arch Dataset
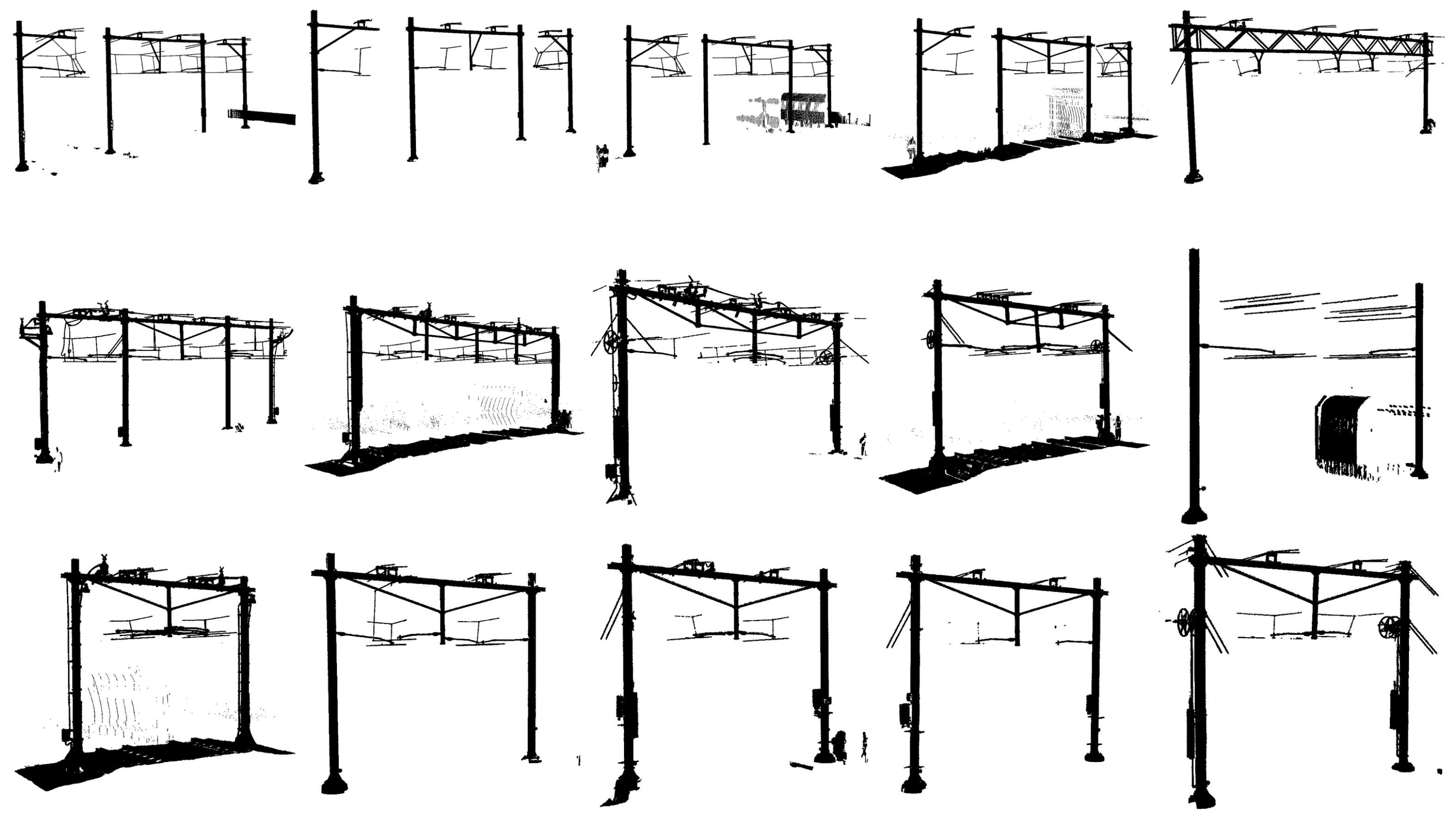
3.1. Acquisition
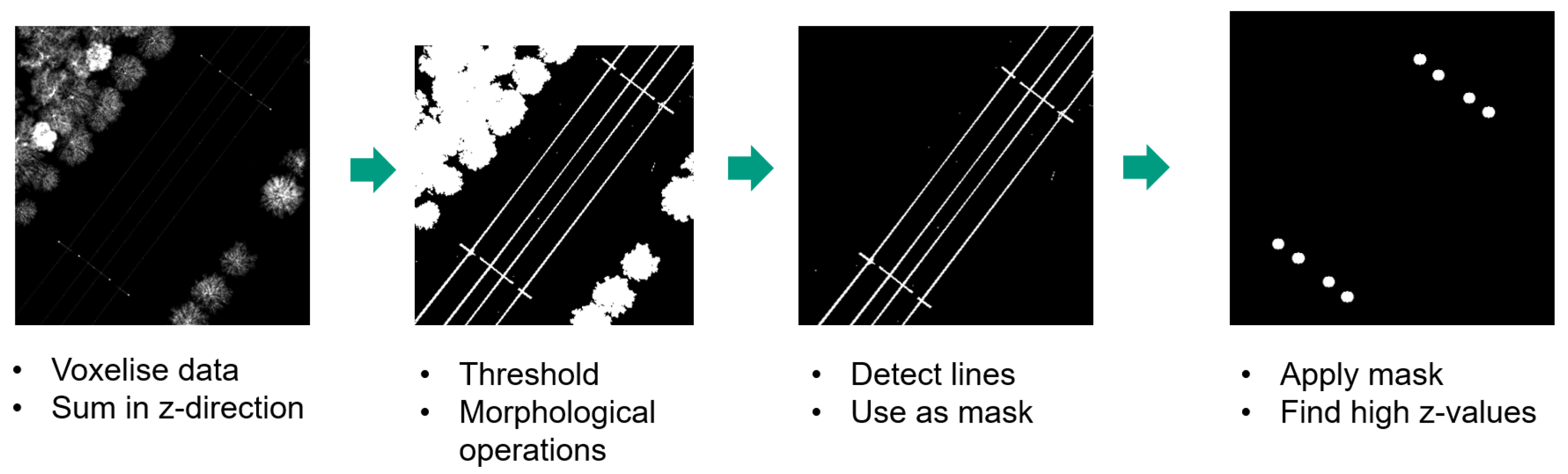
3.2. Arch Localisation
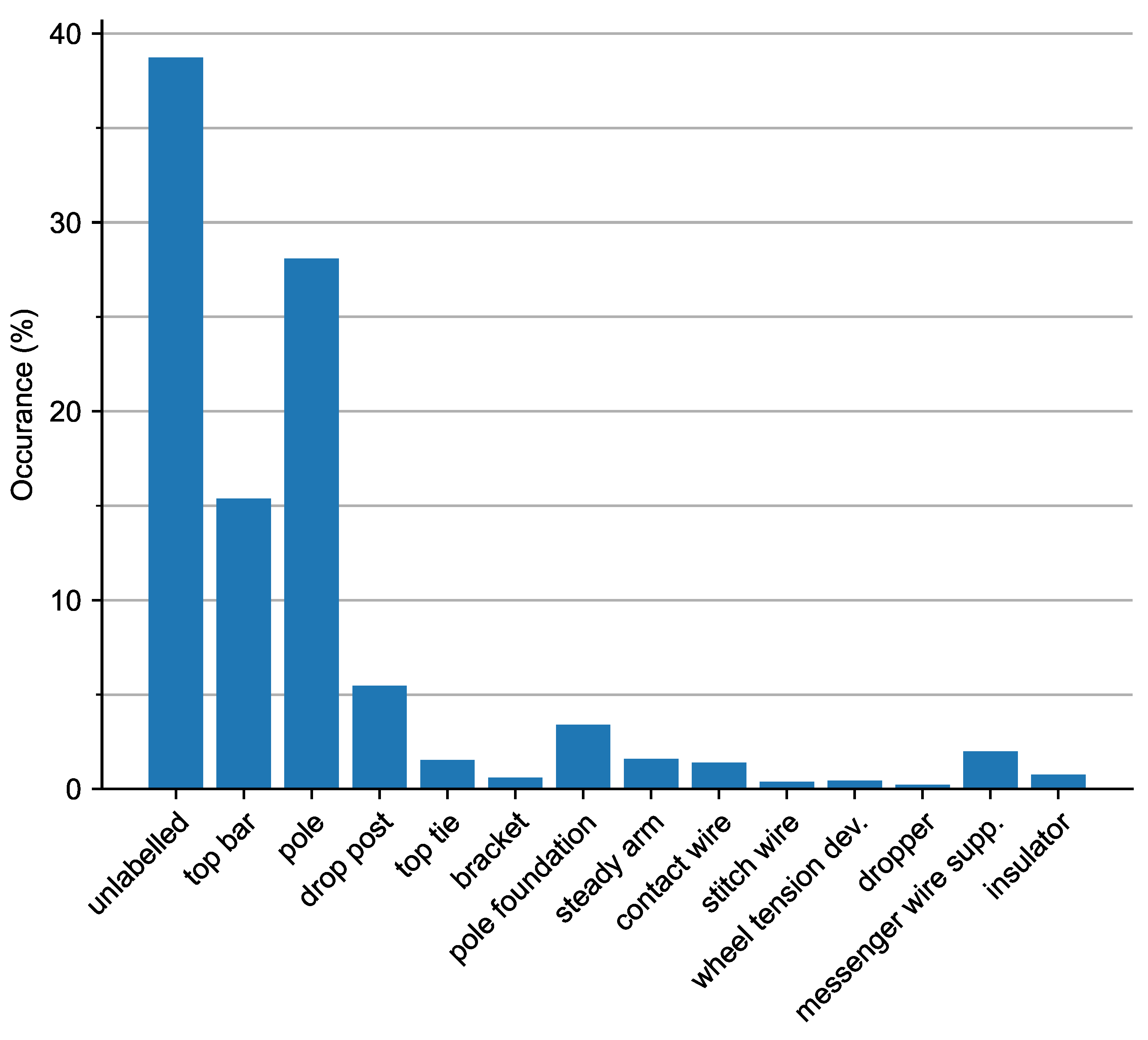
3.3. Data Summary
4. Methodology
4.1. General Pre-Processing
- Uniform random rotation between −180° and 180° of the points around the z-axis;
- Uniform random translation of the point coordinates between −1 m and 1 m in all directions;
- Adding random noise to the points. The random noise is selected from a truncated normal distribution with a mean of zero, a standard deviation of 2 cm, and truncated at ±5 cm.
4.2. PointNet++
4.3. SuperPoint Graph
4.4. Point Transformer
5. Results and Discussion
6. Conclusions
Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uddin, W.; Hudson, W.R.; Haas, R. Public Infrastructure Asset Management; McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Kalvoda, P.; Nosek, J.; Kuruc, M.; Volarik, T. Accuracy Evaluation and Comparison of Mobile Laser Scanning and Mobile Photogrammetry Data Accuracy Evaluation and Comparison of Mobile Laser Scanning and Mobile Photogrammetry Data. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5105–5114. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 16259–16268. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces Supplementary Material. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Wang, Q.; Kim, M.k. Applications of 3D point cloud data in the construction industry: A fifteen-year review from 2004 to 2018. Adv. Eng. Inform. 2019, 39, 306–319. [Google Scholar] [CrossRef]
- Callahan, M.A.; LeBlanc, B.; Vreeland, R.; Bretting, G. Close-Range Photogrammetry with Laser Scan Point Clouds; Technical Report; SAE Technical Paper: Warrendale, PA, USA, 2012. [Google Scholar]
- Valero, E.; Bosché, F.; Forster, A. Automatic segmentation of 3D point clouds of rubble masonry walls, and its application to building surveying, repair and maintenance. Autom. Constr. 2018, 96, 29–39. [Google Scholar] [CrossRef]
- Mahler, J.; Matl, M.; Satish, V.; Danielczuk, M.; DeRose, B.; McKinley, S.; Goldberg, K. Learning ambidextrous robot grasping policies. Sci. Robot. 2019, 4, eaau4984. [Google Scholar] [CrossRef] [PubMed]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on 3D Point Clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Burume, D.M.; Du, S. Deep Learning Methods Applied to 3D Point Clouds Based Instance Segmentation: A Review. Preprints 2021, 2021110228. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3D point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef]
- Liu, W.; Sun, J.; Li, W.; Hu, T.; Wang, P. Deep Learning on Point Clouds and Its Application: A Survey. Sensors 2019, 19, 4188. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, M.; Kadam, P.; Kuo, C.C.J. Deep Learning-Based Point Cloud Analysis. In 3D Point Cloud Analysis; Springer: Berlin/Heidelberg, Germany, 2021; pp. 53–86. [Google Scholar]
- Zhang, J.; Zhao, X.; Chen, Z.; Lu, Z. A review of deep learning-based semantic segmentation for point cloud. IEEE Access 2019, 7, 179118–179133. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Zeng, W.; Gevers, T. 3DContextNet: K-d tree guided hierarchical learning of point clouds using local and global contextual cues. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Arastounia, M. Automated Recognition of Railroad Infrastructure in Rural Areas from LiDAR Data. Remote Sens. 2015, 7, 14916–14938. [Google Scholar] [CrossRef]
- Chen, L.; Jung, J.; Sohn, G. Multi-Scale HierarchicalCRF for Railway Electrification Asset Classification From Mobile Laser Scanning Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3131–3148. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6410–6419. [Google Scholar] [CrossRef]
- Soilán, M.; Sánchez-Rodríguez, A.; del Río-Barral, P.; Perez-Collazo, C.; Arias, P.; Riveiro, B. Review of Laser Scanning Technologies and Their Applications for Road and Railway Infrastructure Monitoring. Infrastructures 2019, 4, 58. [Google Scholar] [CrossRef]
- Chen, L.; Xu, C.; Lin, S.; Li, S.; Tu, X. A Deep Learning-Based Method for Overhead Contact System Component Recognition Using Mobile 2D LiDAR. Sensors 2020, 20, 2224. [Google Scholar] [CrossRef]
- Lin, S.; Xu, C.; Chen, L.; Li, S.; Tu, X. LiDAR Point Cloud Recognition of Overhead Catenary System with Deep Learning. Sensors 2020, 20, 2212. [Google Scholar] [CrossRef]
- Bruijne, A.d.; Buren, J.V.; Marel, H.V.D. Geodetic Reference Frames in the Netherlands; NCG, Nederlandse Commissie voor Geodesie, Netherlands Geodetic Commission: Delft, The Netherlands, 2005; pp. 1–117. [Google Scholar]
- Zhu, L.; Hyyppa, J. The Use of Airborne and Mobile Laser Scanning for Modeling Railway Environments in 3D. Remote Sens. 2014, 6, 3075–3100. [Google Scholar] [CrossRef]
- Corongiu, M.; Masiero, A.; Tucci, G. Classification of Railway Assets in Mobile Mapping Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B1-2, 219–225. [Google Scholar] [CrossRef]
- American Society for Photogrammetry and Remote Sensing. In LAS Specification Version 1.4-R13; Technical Report; ASPRS: Bethesda, MD, USA, 2013.
- Zhan, K.; Chen, S.; Whitman, D.; Shyu, M.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning—JMLR.org, ICML’15, Lille, France, 7–9 July 2015; Volume 37, pp. 448–456. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT, Minneapolis, MN, USA, 2–7 June 2019; Burstein, J., Doran, C., Solorio, T., Eds.; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; IEEE Computer Society: Los Alamitos, CA, USA, 2018; pp. 7794–7803. [Google Scholar] [CrossRef]
- Samek, W.; Müller, K.R. Towards Explainable Artificial Intelligence. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Samek, W., Montavon, G., Vedaldi, A., Hansen, L.K., Müller, K.R., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 5–22. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A review of machine learning interpretability methods. Entropy 2021, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Wang, Z.; Zhan, W.; Tomizuka, M. Towards Better Performance and More Explainable Uncertainty for 3D Object Detection of Autonomous Vehicles. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Zhang, M.; You, H.; Kadam, P.; Liu, S.; Kuo, C.C.J. PointHop: An Explainable Machine Learning Method for Point Cloud Classification. IEEE Trans. Multimed. 2020, 22, 1744–1755. [Google Scholar] [CrossRef]
- Matrone, F.; Paolanti, M.; Felicetti, A.; Martini, M.; Pierdicca, R. BubblEX: An Explainable Deep Learning Framework for Point-Cloud Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6571–6587. [Google Scholar] [CrossRef]
- Verburg, F.M. Exploring Explainability and Robustness of Point Cloud Segmentation Deep Learning Model by Visualization. Bachelor’s Thesis, University of Twente, Enschede, The Netherlands, 2022. [Google Scholar]
- Burton, T.; Heuckelbach, D. Fugro vegetation control: A remote solution for lineside vegetation management. Perm. Way Inst. 2020, 138, 34–37. [Google Scholar]
- Gutiérrez-Fernández, A.; Fernández-Llamas, C.; Matellán-Olivera, V.; Suárez-González, A. Automatic extraction of power cables location in railways using surface lidar systems. Sensors 2020, 20, 6222. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Shen, Y.; Liang, J.; Chen, Y.; Chen, L.; Zhou, M. A Deep Learning Based Method for Railway Overhead Wire Reconstruction from Airborne LiDAR Data. Remote Sens. 2022, 14, 5272. [Google Scholar] [CrossRef]
- Marwati, A.; Wang, C.K. Automatic retrieval of railway masts tilt angle from Mobile Laser Scanning data. In Proceedings of the 42nd Asian Conference on Remote Sensing, ACRS 2021, Can Tho City, Vietnam, 22–24 November 2021; Asian Association on Remote Sensing (AARS): Can Tho, Vietnam, 2021. [Google Scholar]
- Vock, R.; Dieckmann, A.; Ochmann, S.; Klein, R. Fast template matching and pose estimation in 3D point clouds. Comput. Graph. 2019, 79, 36–45. [Google Scholar] [CrossRef]
- Vieth, Z.J. Point Cloud Classification and Segmentation of Catenary Systems. Bachelor’s Thesis, University of Twente, Enschede, The Netherlands, 2022. [Google Scholar]
- Sayin, B.; Krivosheev, E.; Yang, J.; Passerini, A.; Casati, F. A review and experimental analysis of active learning over crowd sourced data. Artif. Intell. Rev. 2021, 54, 5283–5305. [Google Scholar] [CrossRef]
- Budd, S.; Robinson, E.C.; Kainz, B. A survey on active learning and human-in-the-loop deep learning for medical image analysis. Med. Image Anal. 2021, 71, 102062. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, W.; Zhou, T.; Shen, J.; Jia, Y.; Van Gool, L. Towards a weakly supervised framework for 3D point cloud object detection and annotation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4454–4468. [Google Scholar] [CrossRef]
- Strukton, R.; Ton, B. High resolution labelled point cloud dataset of catenary arches in the Netherlands. 4TU.ResearchData, 2021. [Google Scholar] [CrossRef]


| Arch | Name | Points | Classes (out of 14) |
|---|---|---|---|
| 0 | 01_01 | 1,586,927 | 13 |
| 1 | 01_02 | 2,147,546 | 13 |
| 2 | 01_03 | 2,664,907 | 13 |
| 3 | 02_01 | 11,112,574 | 13 |
| 4 | 02_02 | 2,415,930 | 11 |
| 5 | 02_03 | 4,362,055 | 11 |
| 6 | 02_04 | 5,257,501 | 11 |
| 7 | 03_01 | 2,787,253 | 12 |
| 8 | 03_02 | 6,782,568 | 10 |
| 9 | 03_03 | 1,973,730 | 6 |
| 10 | 03_04 | 6,582,344 | 11 |
| 11 | 04_01 | 2,271,179 | 11 |
| 12 | 04_02 | 1,673,804 | 11 |
| 13 | 04_03 | 1,598,090 | 11 |
| 14 | 04_04 | 2,183,600 | 12 |
| Class | PointNet++ | Point Transformer | ||||
|---|---|---|---|---|---|---|
| Vanilla | Modified | Vanilla | ||||
| nw | iw | nw | iw | nw | iw | |
| unlabelled | 0.63 | 0.63 | 0.69 | 0.67 | 0.73 | 0.43 |
| top bar | 0.73 | 0.73 | 0.80 | 0.78 | 0.78 | 0.70 |
| pole | 0.81 | 0.81 | 0.83 | 0.82 | 0.89 | 0.76 |
| drop post | 0.77 | 0.77 | 0.81 | 0.79 | 0.80 | 0.64 |
| top tie | 0.42 | 0.59 | 0.83 | 0.79 | 0.32 | 0.20 |
| bracket | 0.59 | 0.74 | 0.88 | 0.82 | 0.33 | 0.26 |
| pole foundation | 0.60 | 0.60 | 0.67 | 0.66 | 0.74 | 0.48 |
| steady arm | 0.54 | 0.54 | 0.58 | 0.58 | 0.70 | 0.63 |
| contact wire | 0.65 | 0.65 | 0.69 | 0.68 | 0.71 | 0.69 |
| stitch wire | 0.60 | 0.67 | 0.71 | 0.68 | 0.58 | 0.60 |
| wheel tension device | 0.52 | 0.44 | 0.70 | 0.76 | 0.07 | 0.09 |
| dropper | 0.31 | 0.31 | 0.51 | 0.46 | 0.54 | 0.39 |
| messenger wire supp. | 0.45 | 0.52 | 0.69 | 0.64 | 0.73 | 0.50 |
| insulator | 0.33 | 0.38 | 0.48 | 0.46 | 0.76 | 0.58 |
| class mean | 0.57 | 0.60 | 0.71 | 0.69 | 0.62 | 0.50 |
| (0.15) | (0.14) | (0.12) | (0.12) | (0.22) | (0.20) | |
| sample mean | 0.58 | 0.60 | 0.68 | 0.66 | 0.65 | 0.50 |
| (0.10) | (0.10) | (0.12) | (0.11) | (0.15) | (0.11) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ton, B.; Ahmed, F.; Linssen, J. Semantic Segmentation of Terrestrial Laser Scans of Railway Catenary Arches: A Use Case Perspective. Sensors 2023, 23, 222. https://doi.org/10.3390/s23010222
Ton B, Ahmed F, Linssen J. Semantic Segmentation of Terrestrial Laser Scans of Railway Catenary Arches: A Use Case Perspective. Sensors. 2023; 23(1):222. https://doi.org/10.3390/s23010222
Chicago/Turabian StyleTon, Bram, Faizan Ahmed, and Jeroen Linssen. 2023. "Semantic Segmentation of Terrestrial Laser Scans of Railway Catenary Arches: A Use Case Perspective" Sensors 23, no. 1: 222. https://doi.org/10.3390/s23010222
APA StyleTon, B., Ahmed, F., & Linssen, J. (2023). Semantic Segmentation of Terrestrial Laser Scans of Railway Catenary Arches: A Use Case Perspective. Sensors, 23(1), 222. https://doi.org/10.3390/s23010222









