High-Frequency Vibration Analysis of Piezoelectric Array Sensor under Lateral-Field-Excitation Based on Crystals with 3 m Point Group
Abstract
:1. Introduction
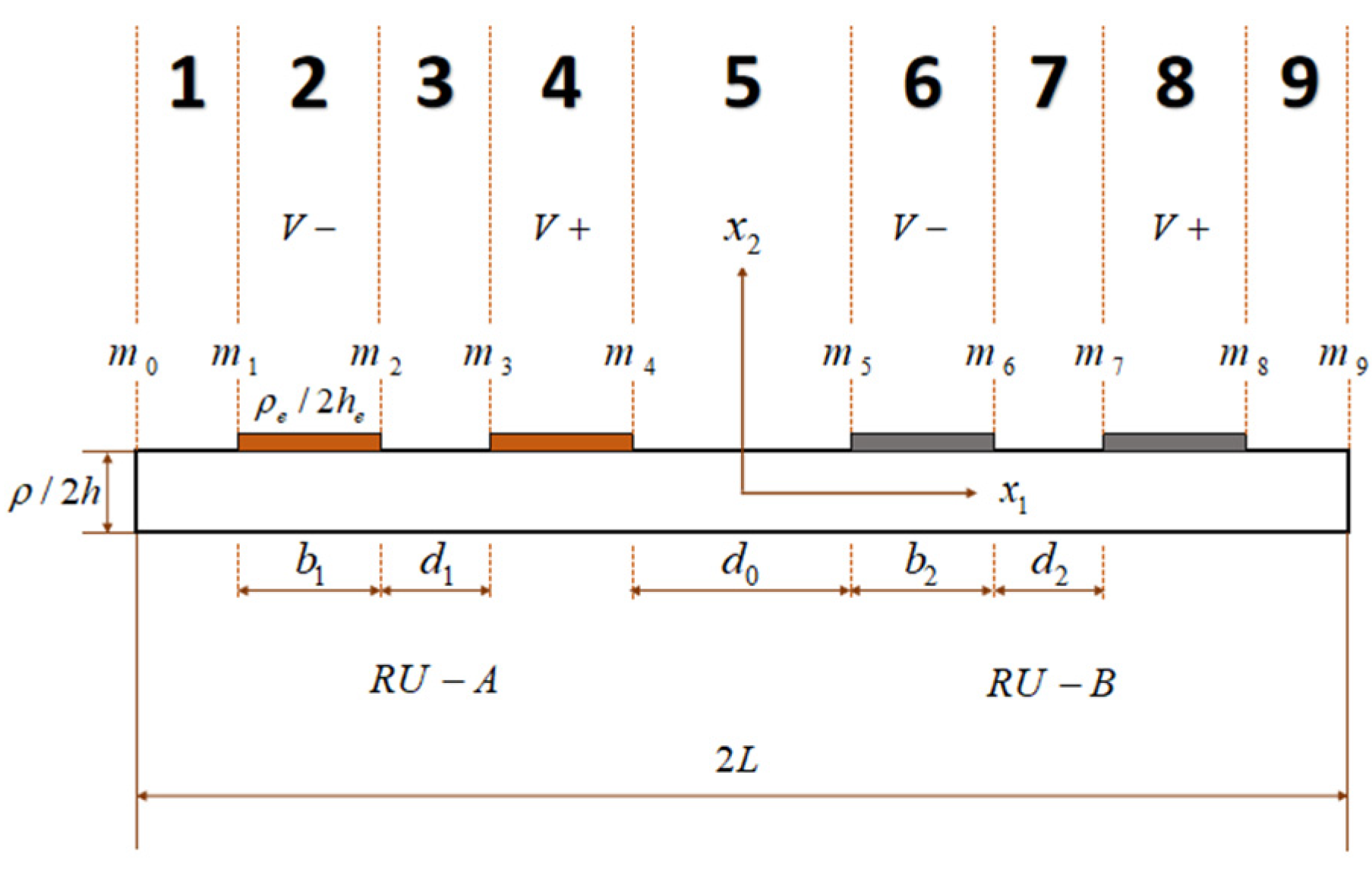
2. Frequency Spectrum Calculation
3. Electrically Forced Vibration
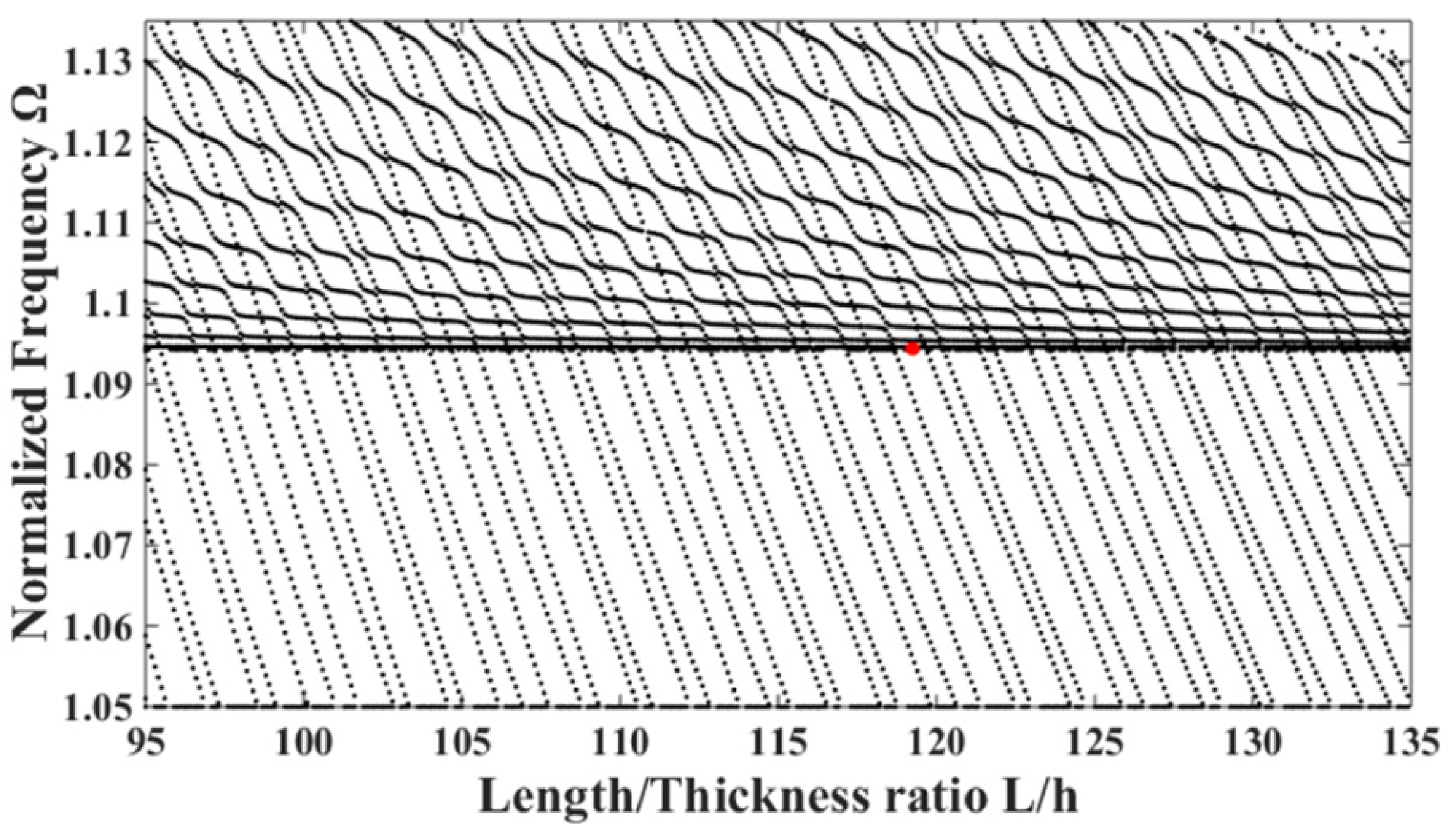
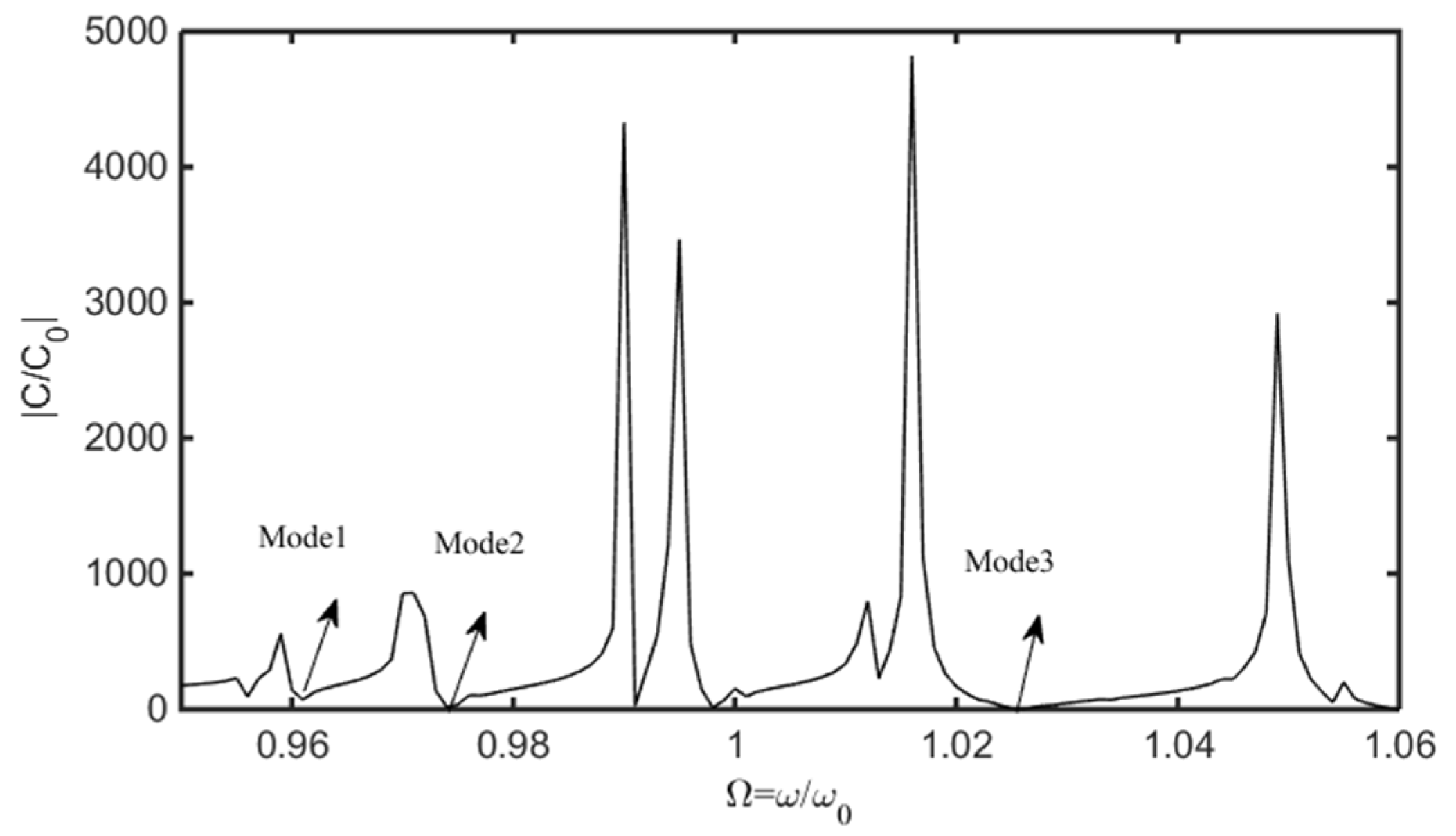
4. Results and Discussion
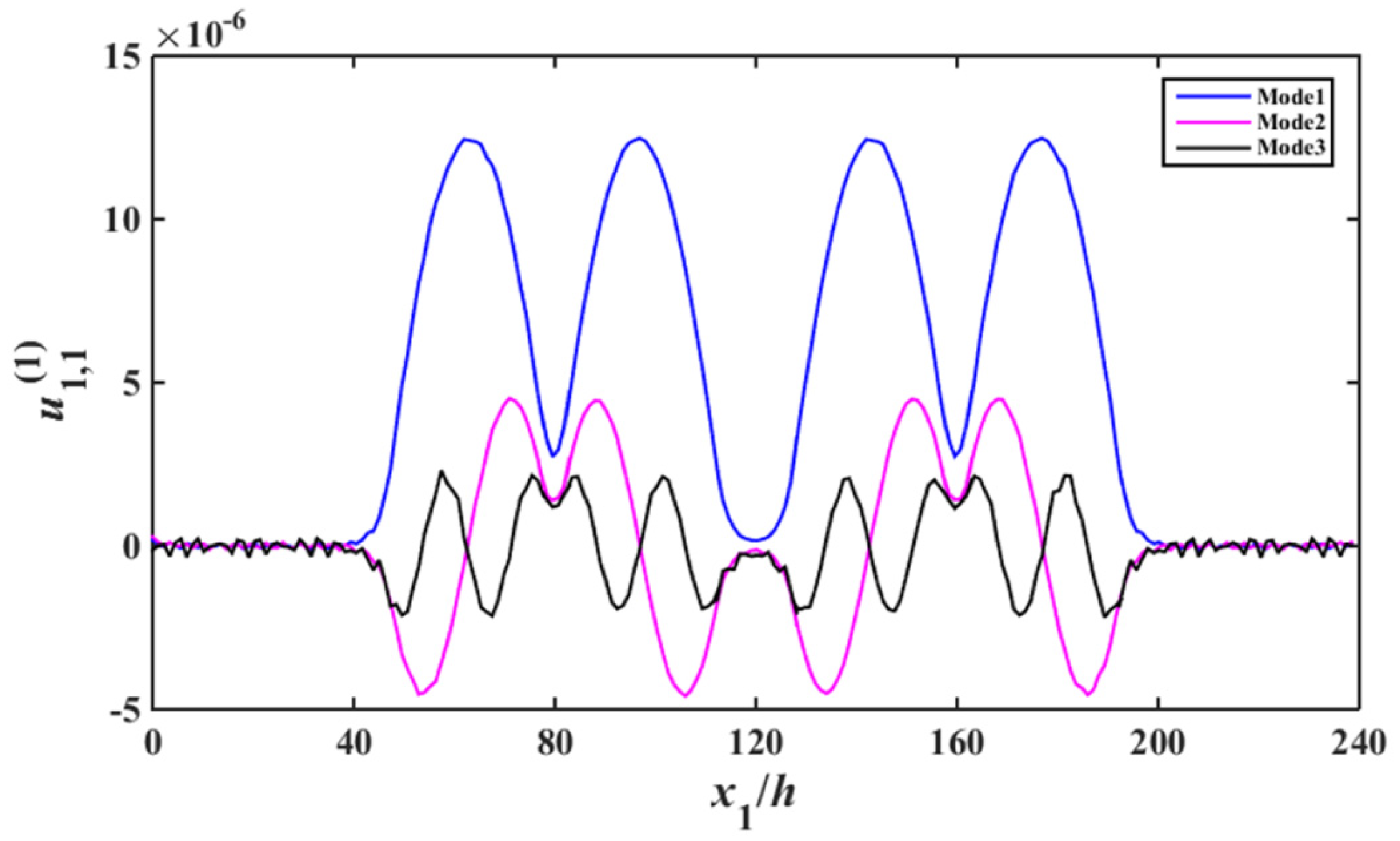
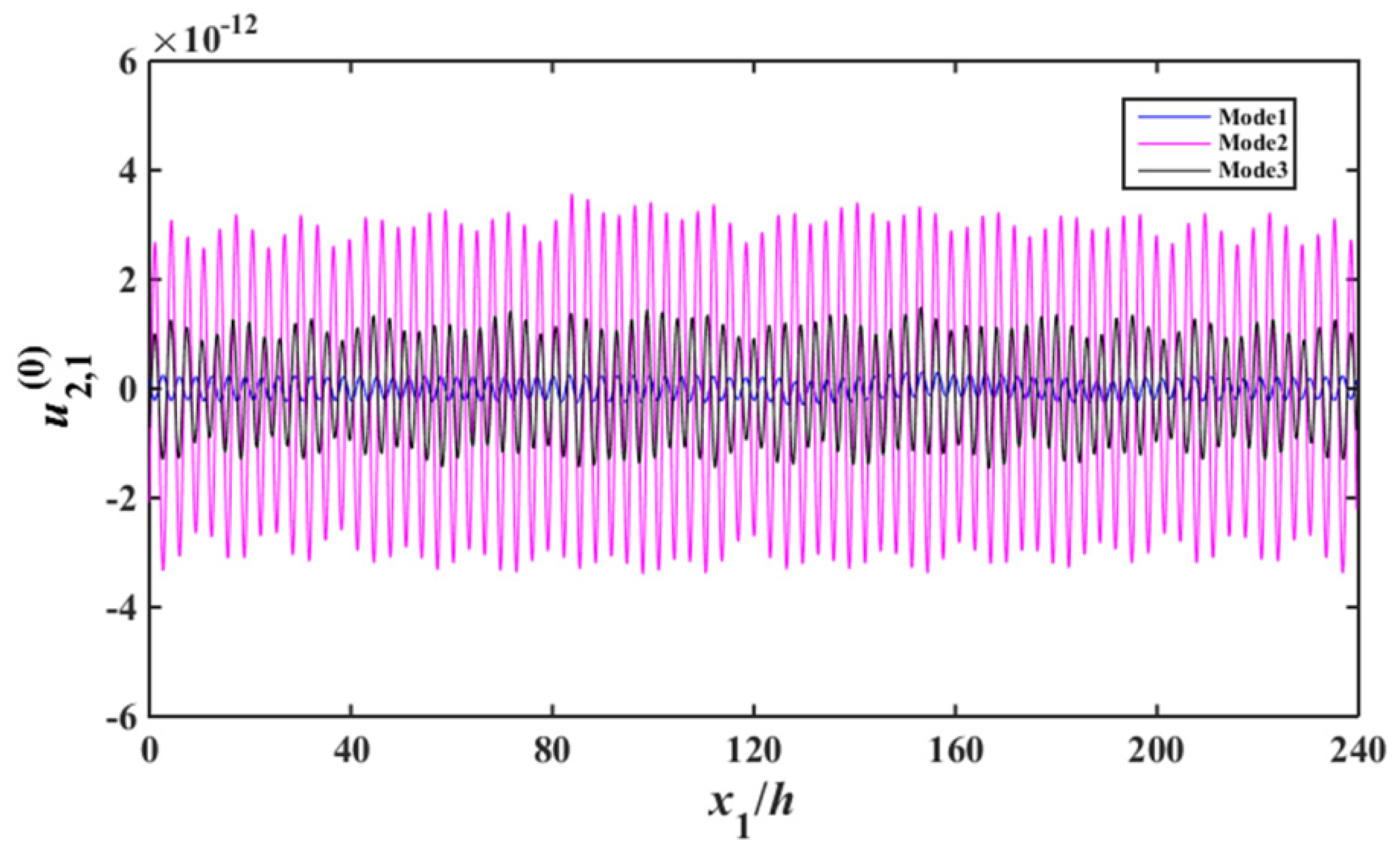
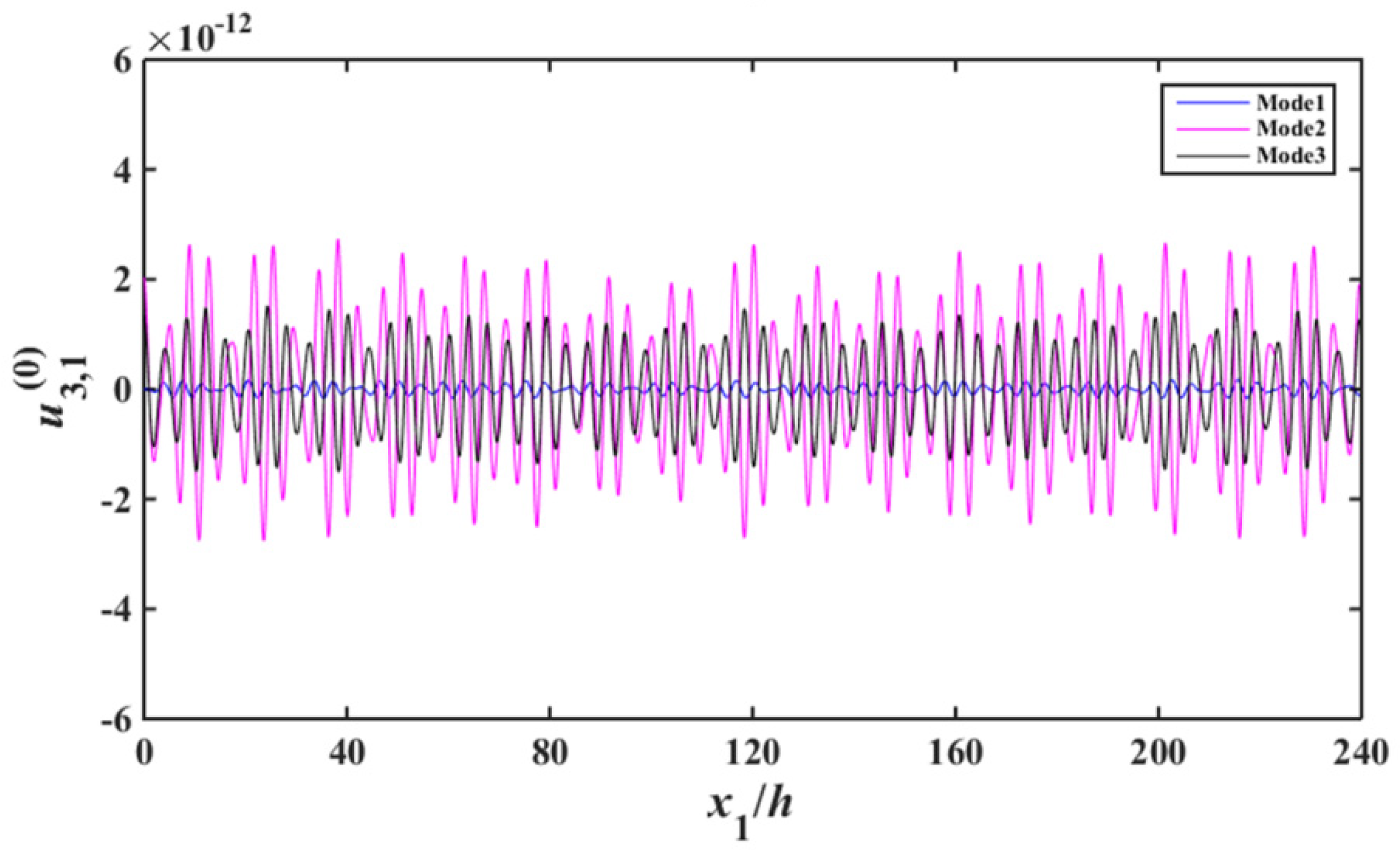
4.1. Resonance Modes
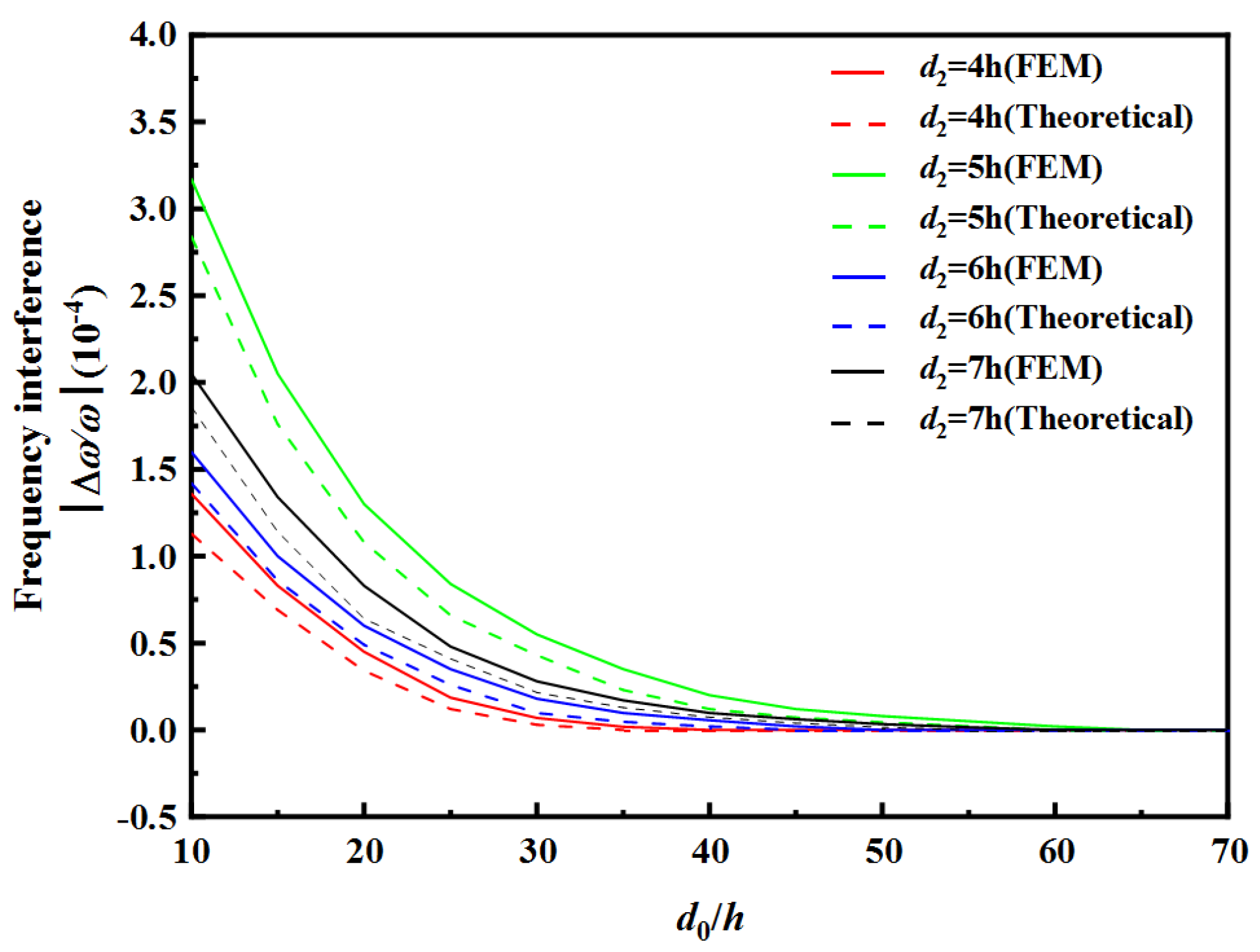
4.2. Frequency Interferences between Two Resonator Units
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, S.Y.; Kao, Y.H.; Su, Y.O.; Perng, T.P. In situ monitoring of hydrogen absorption-desorption in Pd and Pd77Ag23 films by an electrochemical quartz crystal microbalance. J. Alloys Compd. 1999, 293, 468–471. [Google Scholar] [CrossRef]
- Shen, D.Z.; Zhang, H.T.; Kang, Q.; Zhang, H.J.; Yuan, D.R. Oscillating frequency response of a langasite crystal microbalance in liquid phases. Sens. Actuators B 2006, 119, 99–104. [Google Scholar] [CrossRef]
- Lu, F.; Lee, H.P.; Lim, S.P. Energy-trapping analysis for the bi-stepped mesa quartz crystal microbalance using the finite element method. Smart Mater. Struct. 2005, 14, 272. [Google Scholar] [CrossRef]
- Liu, N.; Yang, J.S.; Jin, F. Transient thickness-shear vibration of a piezoelectric plate of monoclinic crystals. Int. J. Appl. Electrom. 2012, 38, 27–37. [Google Scholar] [CrossRef]
- Hu, Y.T.; Yang, J.S.; Zeng, Y.; Jiang, Q.A. High-sensitivity, dual-plate, thickness-shear mode pressure sensor. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2006, 53, 2193–2197. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Shen, C.Y.; Lin, Y.M.; Lin, J.C. Piezoelecreic sensor for sensitive determination of metal ions based on the phosphate-modified dendrimer. Smart Mater. Struct. 2016, 25, 085018. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, Q.; Xie, H.M.; Yang, J.S. Energy trapping in high-frequency vibrations of piezoelectric plates with partial mass layers under lateral electric field excitation. Ultrasonics 2011, 51, 376–381. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.H.; Freench, L.A.; Radecsky, K.; Da Cunha, M.P.; Millard, P.; Vetelino, J.F. A lateral field excited liquid acoustic wave sensor. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2004, 51, 1373–1380. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.S. The Mechanics of Piezoelectric Structures; World Scientific: Singapore, 2006. [Google Scholar]
- Hempel, U.; Lucklum, R.L.; Hauptmann, P.; EerNisse, E.P.; Puccio, D.; Diaz, R.F.; Vives, A.A. Lateral field excited quartz crystal resonators sensors for determination of acoustic and electrical properties of liquids. In Proceedings of the IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; pp. 705–710. [Google Scholar]
- Wang, W.Y.; Zhang, C.; Zhang, Z.T.; Liu, Y.; Feng, G.P. Three operation modes of lateral-field-excited piezoelectric devices. Appl. Phys. Lett. 2008, 93, 242906. [Google Scholar] [CrossRef]
- Borodina, I.A.; Zaitsev, B.D.; Teplykh, A.A.; Shikhabudinov, A.M.; Kuznetsova, I.E. Array of piezoelectric lateral electric field excited resonators. Ultrasonics 2015, 62, 200–202. [Google Scholar] [CrossRef] [PubMed]
- Latif, U.; Rohrer, A.; Lieberzeit, P.A.; Dickert, F.L. QCM gas phase detection with ceramic materials-VOCs and oil vapors. Anal. Bioanal. Chem. 2011, 400, 2457–2462. [Google Scholar] [CrossRef] [PubMed]
- Itoh, A.; Ichihashi, M. Separate measurement of the density and viscosity of a liquid using a quartz crystal microbalance based on admittance analysis (QCM-A). Meas. Sci. Technol. 2011, 22, 015402. [Google Scholar] [CrossRef]
- Kalchenko, V.I.; Koshets, I.A.; Matsas, E.P.; Kopylov, O.N.; Solovyov, A.; Kazantseva, Z.I.; Shirshov, Y.M. Calixarene-based QCM sensors array and its response to volatile organic vapours. Mater. Sci. Pol. 2002, 20, 73–88. [Google Scholar]
- Sayin, S.; Ozbek, C.; Okur, S.; Yilmaz, M. Perparation of the ferrocene-substituted 1,3-distal p-tert-butylcalix[4]arene based QCM sensors array and utilization of its gas-sensing affinities. J. Org. Chem. 2014, 771, 9–13. [Google Scholar] [CrossRef] [Green Version]
- Winters, S.; Bernhardt, G.; Vetelino, J.F. A dual lateral-field-excited bulk acoustic wave sensor array. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 573–578. [Google Scholar] [CrossRef] [PubMed]
- Vetelino, J.F. A lateral field excited acoustic wave sensor platform. In Proceedings of the IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; pp. 924–934. [Google Scholar]
- Warner, A.W.; Onoe, M.; Coquin, G.A. Determination of elastic and piezoelectric constants for crystals in class (3 m). J. Acoust. Soc. Am. 1967, 42, 1223–1231. [Google Scholar] [CrossRef]
- Ma, T.F.; Zhang, C.; Zhang, Z.T.; Wang, W.Y.; Feng, G.P. Investigation of lateral-field-excitation on LiTaO3 single crystal. In Proceedings of the 2010 IEEE International Frequency Control Symposium, Newport Beach, CA, USA, 1–4 June 2010; pp. 489–492. [Google Scholar]




| Parameter | Value | Description |
|---|---|---|
| 10 MHz | Fundamental frequency | |
| 2 h | 0.01755 mm | Thickness of the crystal plate |
| L | 239.6 h | Length of the crystal plate |
| 2 w | 119.8 h | Width of the crystal plate |
| R | 0.05 | Mass ratio (Electrode/crystal) |
| b | 30 h | Width of the electrode |
| d | 5 h | Space of the two electrodes |
| d0 | 15 h | Space of the two resonator units |
| 20 h | 25 h | 30 h | 35 h | |||||
|---|---|---|---|---|---|---|---|---|
| Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | |
| 45 h | 50 h | 40 h | 45 h | 60 h | 65 h | 35 h | 40 h | |
| 20 h | 25 h | 30 h | 35 h | |||||
|---|---|---|---|---|---|---|---|---|
| Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | |
| 35 h | 40 h | 40 h | 45 h | 60 h | 65 h | 45 h | 50 h | |
| 4 h | 5 h | 6 h | 7 h | |||||
|---|---|---|---|---|---|---|---|---|
| Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | |
| 55 h | 60 h | 60 h | 65 h | 45 h | 50 h | 35 h | 40 h | |
| 4 h | 5 h | 6 h | 7 h | |||||
|---|---|---|---|---|---|---|---|---|
| Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | Theoretical | FEM | |
| 35 h | 40 h | 60 h | 65 h | 45 h | 50 h | 55 h | 60 h | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Shi, H.; Sun, F.; Tang, Z.; Li, S.; Chen, D.; Ma, T.; Kuznetsova, I.; Nedospasov, I.; Zhang, C. High-Frequency Vibration Analysis of Piezoelectric Array Sensor under Lateral-Field-Excitation Based on Crystals with 3 m Point Group. Sensors 2022, 22, 3596. https://doi.org/10.3390/s22093596
Xu J, Shi H, Sun F, Tang Z, Li S, Chen D, Ma T, Kuznetsova I, Nedospasov I, Zhang C. High-Frequency Vibration Analysis of Piezoelectric Array Sensor under Lateral-Field-Excitation Based on Crystals with 3 m Point Group. Sensors. 2022; 22(9):3596. https://doi.org/10.3390/s22093596
Chicago/Turabian StyleXu, Jiachao, Hao Shi, Fei Sun, Zehuan Tang, Shuanghuizhi Li, Dudu Chen, Tingfeng Ma, Iren Kuznetsova, Ilya Nedospasov, and Chao Zhang. 2022. "High-Frequency Vibration Analysis of Piezoelectric Array Sensor under Lateral-Field-Excitation Based on Crystals with 3 m Point Group" Sensors 22, no. 9: 3596. https://doi.org/10.3390/s22093596
APA StyleXu, J., Shi, H., Sun, F., Tang, Z., Li, S., Chen, D., Ma, T., Kuznetsova, I., Nedospasov, I., & Zhang, C. (2022). High-Frequency Vibration Analysis of Piezoelectric Array Sensor under Lateral-Field-Excitation Based on Crystals with 3 m Point Group. Sensors, 22(9), 3596. https://doi.org/10.3390/s22093596







