Investigating a Dual-Channel Network in a Sustainable Closed-Loop Supply Chain Considering Energy Sources and Consumption Tax
Abstract
:1. Introduction
- ➢
- Considering the energy sources are rarely observed in the ASC optimization models, in this paper, a sustainable double-channel CLSC network for rice product considering energy sources and tax on energy consumption is designed. Then, a new MILP model is formulated for optimizing the total costs, the quantity of pollutants, and the job opportunities created in the rice CLSC in a fuzzy environment.
- ➢
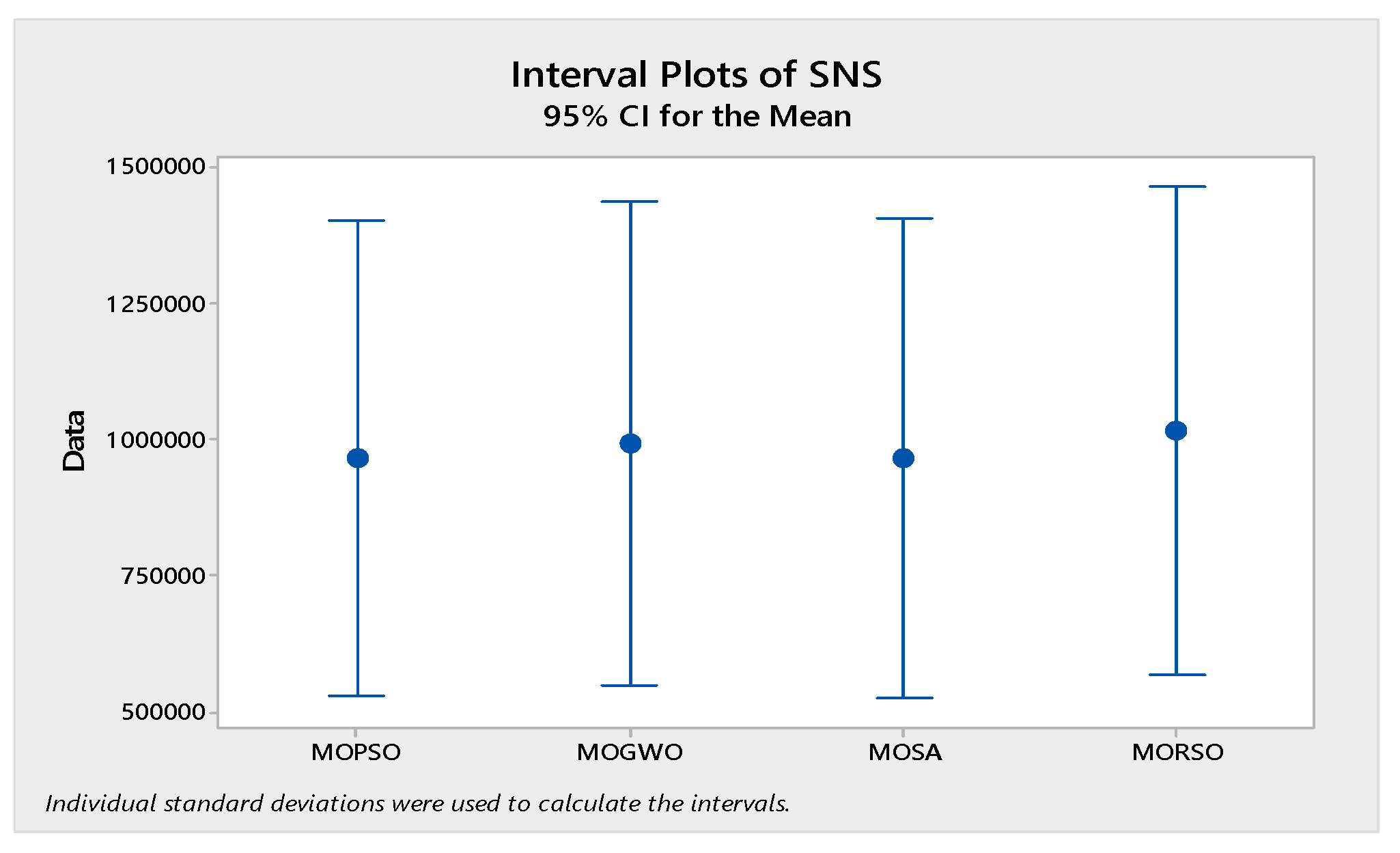
- After that, to solve the model and find the Pareto solutions, a new multi-objective version of the recently released algorithm termed Multi-Objective Reptile Search Optimizer (MORSO) is employed to solve the proposed model in high dimensions. Next, its results and performance are compared to MOSA, MOGWO, and MOPSO based on criteria such as MS, SNS, MID, and CPU time.
2. Literature Review
2.1. ASC Optimization
2.2. ASC Sustainability
2.3. Research Gap and Motivation for Research
3. Problem Statement
- Transportation costs between the network facilities are consistent with the distance.
- Processing centers have limited storage capacity.
- Deficiency cost has not been considered.
- Rice production capacity in factories is also limited.
- Excess electrical energy should be connected to the mains (grid) electricity.
3.1. Problem’s Model
3.2. Uncertainty Model
4. Solution Approach
4.1. Encoding and Decoding
4.2. Reptile Search Algorithm
4.2.1. Encircling Phase
4.2.2. Hunting Simulation
4.3. Multi-Objective Reptile Search Optimization Algorithm
4.3.1. Archive and Grid Approach
4.3.2. Selecting a Leader
4.4. Evaluation Indices of Algorithms’ Performance
4.4.1. Number of Pareto Solutions (NPS)
4.4.2. Mean Ideal Distance (MID)
4.4.3. Maximum Spread (MS)
4.4.4. Spread of Non-Dominance Solutions (SNS)
4.4.5. Computational Time Index (CPU Time)
5. Validation and Analysis of Results
5.1. Case Study
5.2. Results Analysis
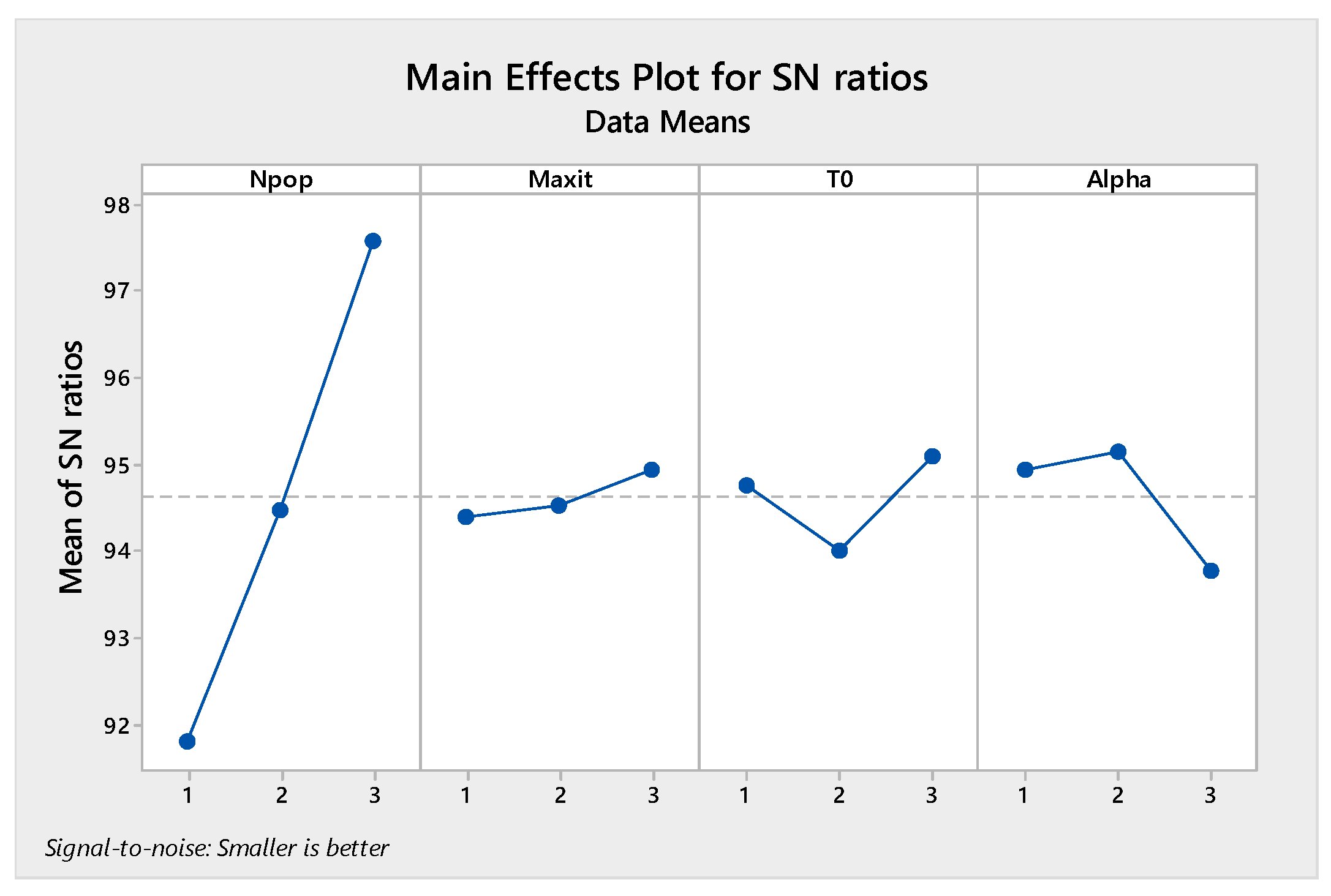
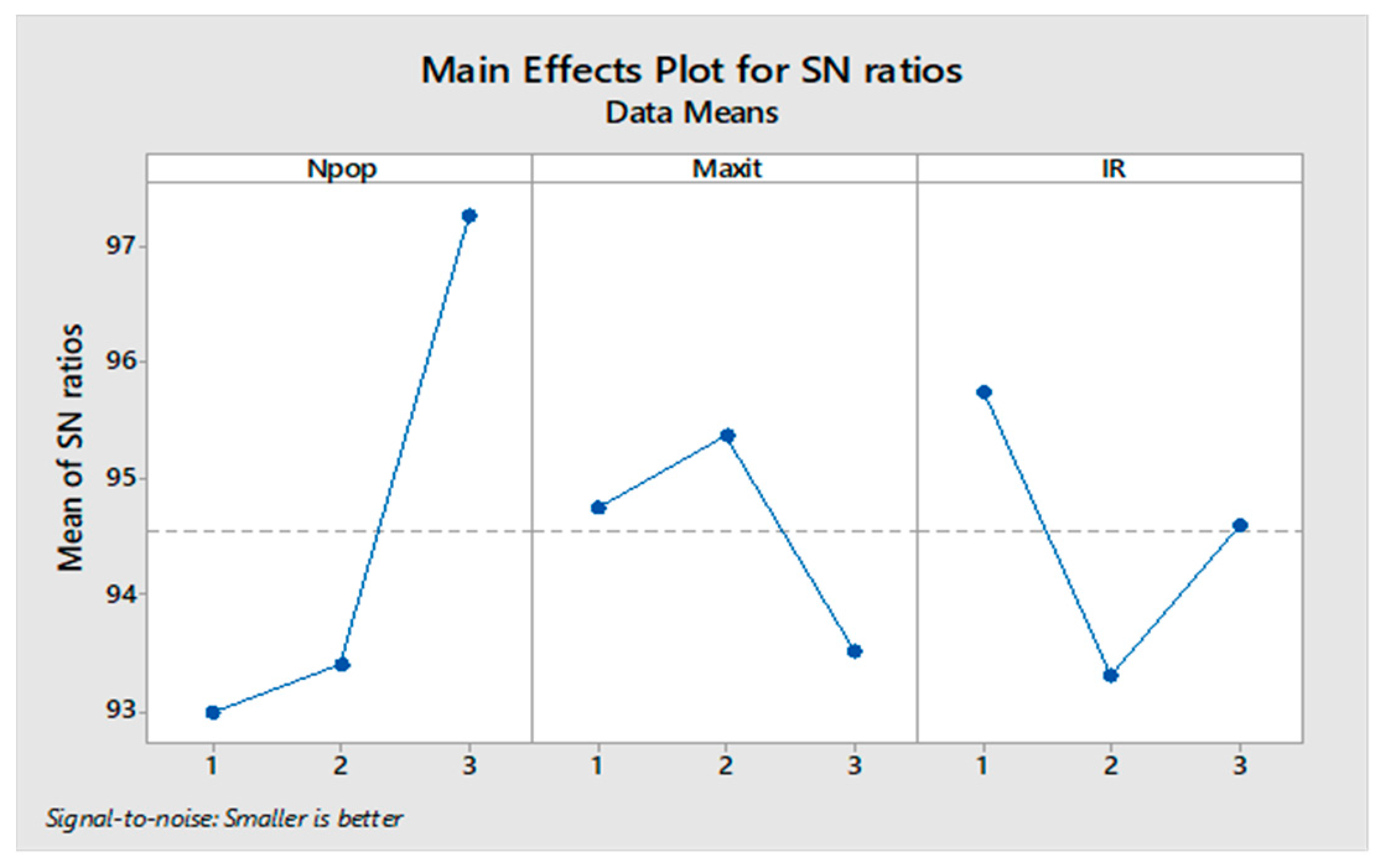
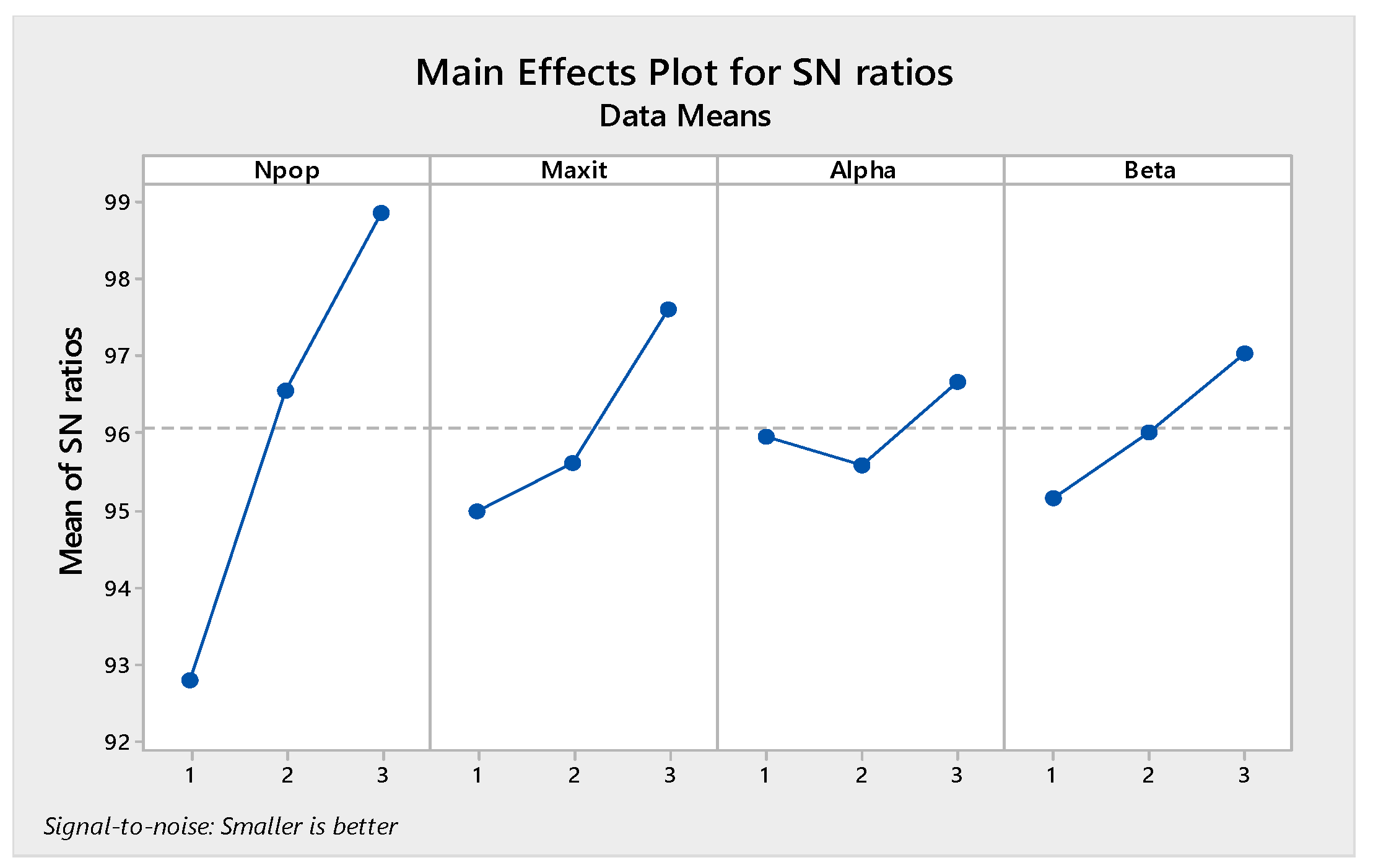
5.3. The Tune of the Algorithm’s Parameters
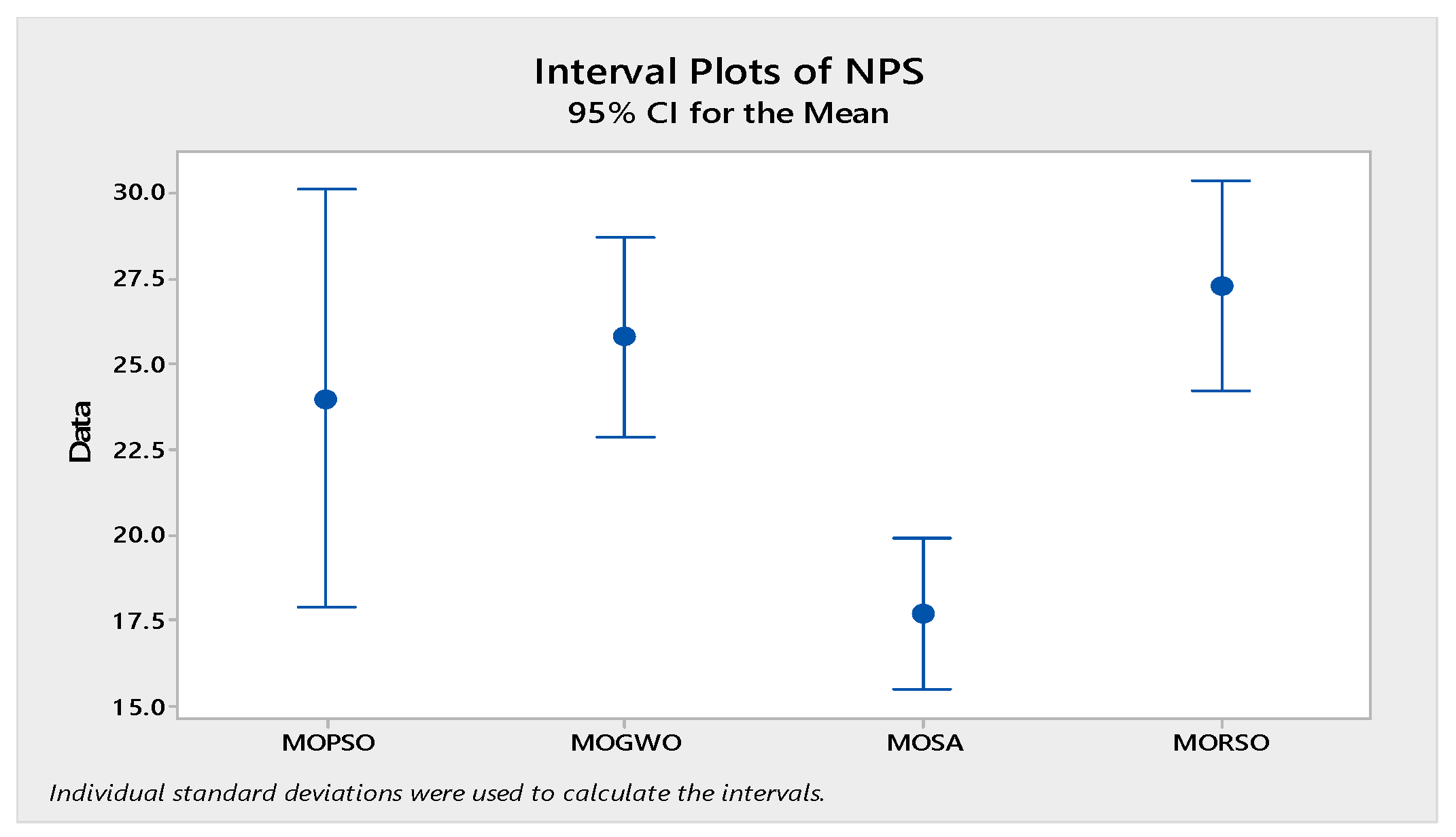
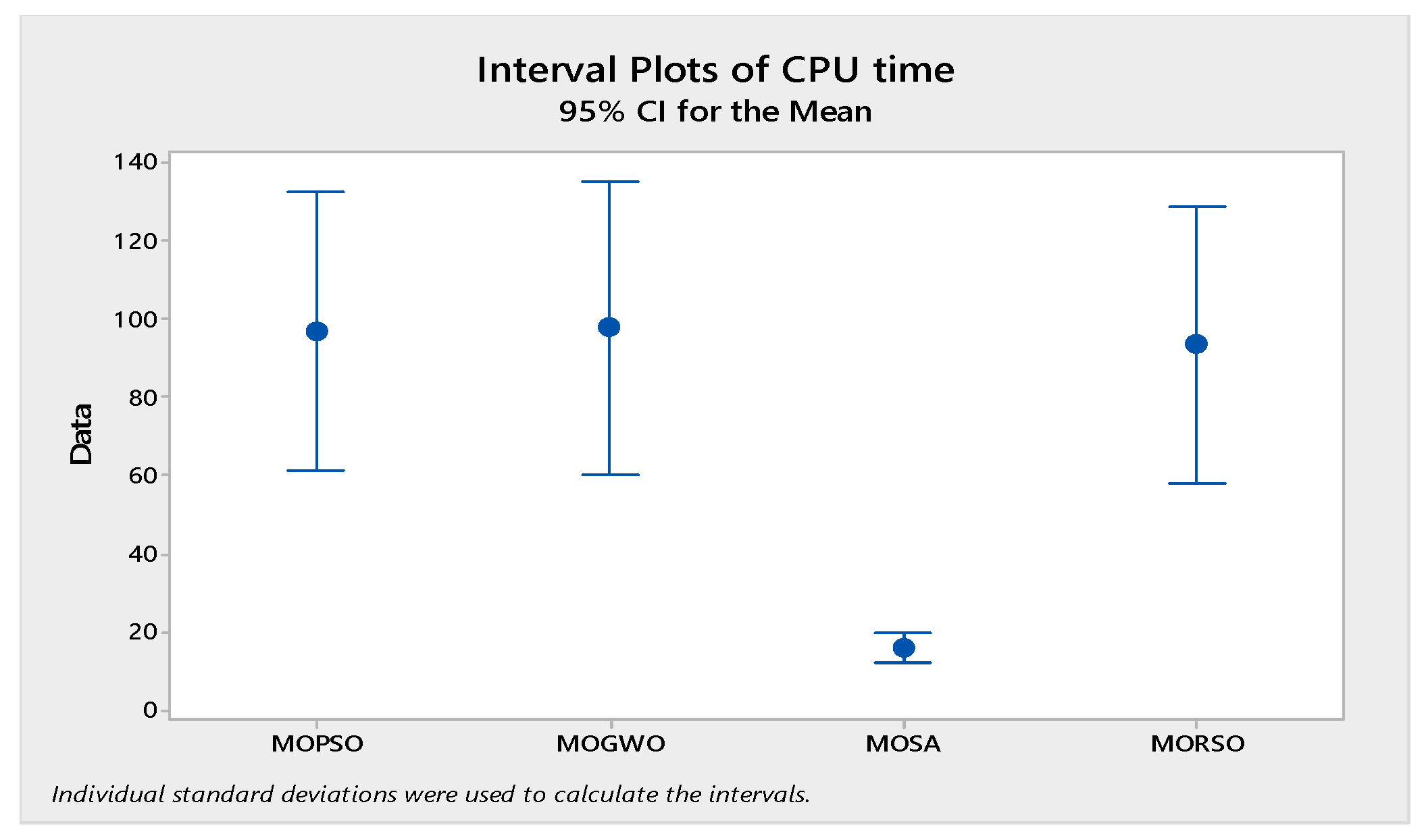
5.4. Analysis of Results
5.5. Sensitivity Analysis
5.5.1. Sensitivity Analysis on Energy Source Capacity Parameter
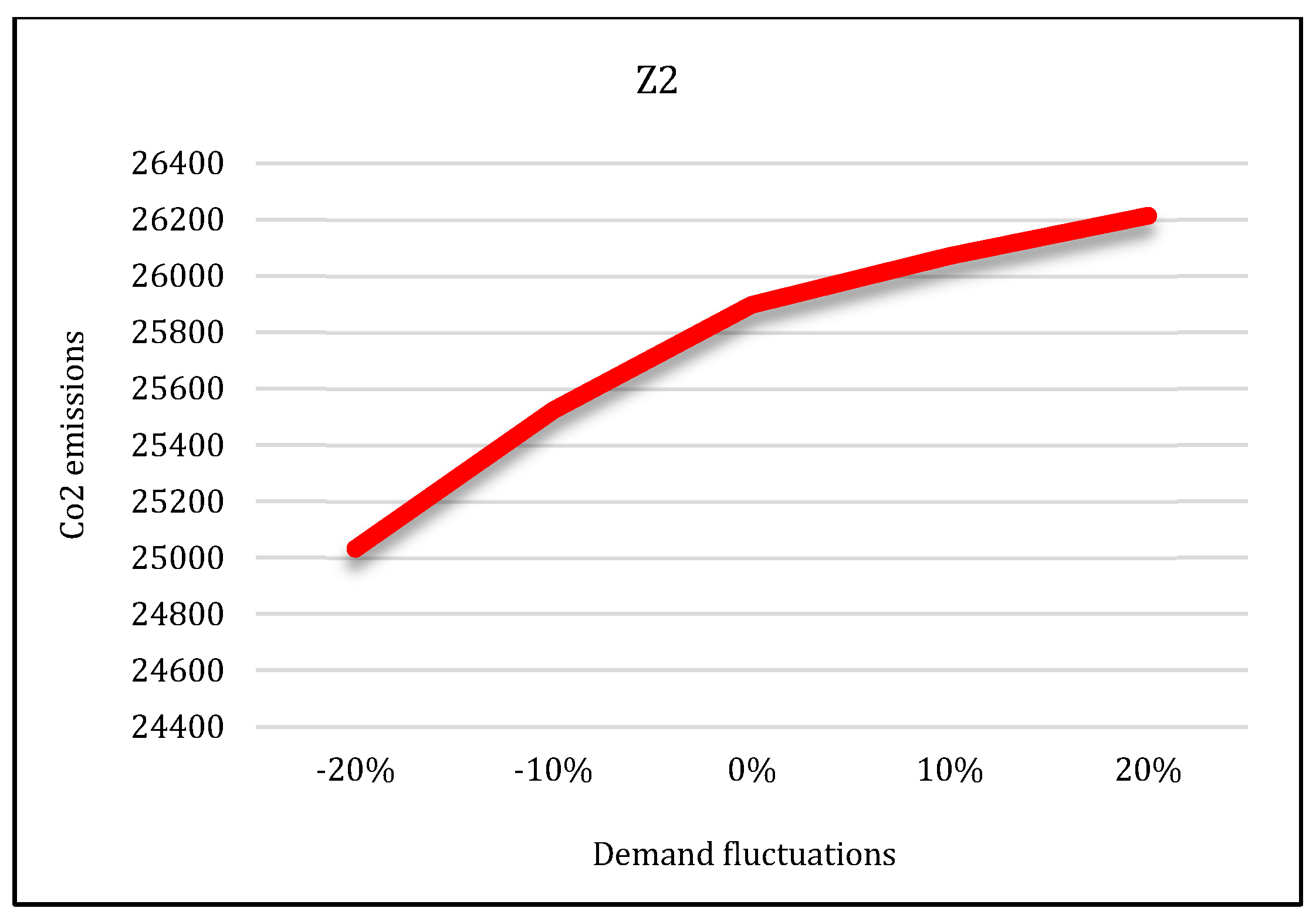
5.5.2. Sensitivity Analysis on Demand
6. Conclusions, Managerial Insight, and Future Works
- Job opportunity: Agricultural growth has led to increasing the productivity and income of small and marginal farmers and raising the employment and wages of workers. Consequently, it is critical to consider this dimension of sustainability in supply chain optimization. The proposed model pursues the goal of raising job opportunities and its results revealed that increasing rice production could boost the intended goal.
- Clean energy consumption: Using solar energy as a source of clean energy has gained importance considering the non-renewable nature of fossil sources such as oil and gas. Solar energy and biomass are viewed as a source of clean energy and the cost of generating electricity by them is less than that generated by fossil fuels. Moreover, they emit less pollution and fewer greenhouse gases. Regarding how rice straw and husk have the potential to generate energy, the current research has dealt with this matter and a mathematical model has been formulated to make strategic decisions about the construction of solar panel sites and bio-refineries and optimally using rice waste for energy generation.
Limitations of the Current Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Sets and Indicators: | |
| I | Set of producers |
| J1 | Set of existing distribution centers |
| Set of new distribution centers | |
| J | ⋃ |
| V | Set of pharmaceutical industries |
| F | Set of rice factories |
| K | Set of toiletries industries |
| M | |
| O1 | |
| O2 | |
| O | Set of all recycling centers o ∈ O = O1 ⋃ O2 |
| C | Set of customers c ∈ C |
| T′ | |
| U | Set of solar panel sites u ∈ U |
| B | Set of bio-refineries sites b ∈ B |
| X | Indicator for processed rice |
| Y | Indicator for rice bran |
| P | |
| G | Indicator for mains electricity |
| R | ={ mains electricity, solarpanel, bio-refinery} |
| Parameters: | |
| Fixed cost for launching new distribution center j2 | |
| Fixed cost for launching recycling distribution center o2 | |
| Fixed cost for launching bio-refinery b | |
| Cost of purchasing each kg of p-type product from market m (traditional purchase) during period t | |
| Cost of purchasing each kg of p-type product from factory f (online shopping) during period t | |
| Production capacity of p-type product in factory f during period t | |
| Cost of production per kg of rice plant for farmer i | |
| Tax on consumption per unit of electricity supplied from source r | |
| Production cost per kg of p-type product in factory f, whose electricity is supplied from source r | |
| Cost of per kg unprocessed rice maintenance at distribution center j during period t | |
| Cost of transporting by vehicle per kilometer | |
| Distance between producer i and distribution center j | |
| Distance between distribution center j and rice factory f | |
| Distance between rice factory f and pharmaceutical industry v | |
| Distance between rice factory f and toiletries industry k | |
| Distance between rice factory f and market m | |
| Distance between rice factory f and customer c | |
| Distance between market m and customer c | |
| Distance between producer i and recycling center o | |
| Distance between recycling center o and producer i | |
| Distance between producer i and bio-refinery b | |
| Distance between rice factory f and bio-refinery b | |
| Product’s production capacity by producer i during period t′ | |
| Max energy level supplied from source r during period t | |
| Demand for p-type product by consumer c in traditional purchase during period t | |
| Demand for p-type product by consumer c in online shopping during period t | |
| Demand for compost by farm i during period t | |
| Demand for rice bran by pharmaceutical industry v during period t | |
| Demand for rice bran by toiletries industry k during period t | |
| Electrical energy required to process per kg of rice | |
| M | A very large positive number |
| Paddy to husk conversion rate | |
| Rice husk to electrical energy conversion rate in bio-refineries | |
| Straw to electrical energy conversion rate in bio-refineries | |
| Straw to compost conversion rate | |
| Cost of production per kg of compost at recycling center o | |
| CO2 quantity released from constructing recycling center o | |
| CO2 quantity released from constructing solar panel s | |
| CO2 quantity released from constructing bio-refinery b | |
| RF | Fuel required for vehicle per travel per k |
| Capacity of vehicle | |
| Rice plant to paddy conversion rate | |
| Rice plant to straw conversion rate | |
| Paddy to product of type-p conversion rate | |
| Number of fixed job opportunities created by constructing new distribution centers j2 | |
| Number of variable job opportunities created by producing per kg of product on farm i | |
| Number of fixed job opportunities created by producing per kg of product p in factory f | |
| Decision Variables | |
| Amount of electrical energy that should be supplied from source r during period t | |
| Quantity of paddy rice stored in the distribution center j during period t | |
| Quantity of rice plant transferred from producer i to distribution center j during period t′ | |
| Quantity of paddy rice transferred from distribution center j to rice factory f during period t | |
| Quantity of rice bran transferred from rice factory f to pharmaceutical industry v during period t | |
| Quantity of rice bran transferred from rice factory f to toiletries industry k during period t | |
| Quantity of type-p product transferred from rice factory f to market m during period t | |
| Quantity of type-p product transferred from rice factory f to customer c during period t | |
| Quantity of type-p product transferred from market r to customer c during period t | |
| Quantity of compost transferred from producer i to recycling center o during period t′ | |
| Quantity of compost transferred from recycling center o to producer i during period t | |
| Quantity of rice straw transferred from farm i to bio-refinery b during period t | |
| Quantity of rice bran transferred from rice factory f to bio-refinery b during period t | |
| Amount of rice plant produced by producer i during period t′ | |
| Quantity of type-p product produced from rice factory f using source r during period t | |
| Quantity of electrical energy that should be supplied from source r during period t | |
| Variables Zero and One: | |
| Wj | if distribution center j is established, 1 |
| Vs | if solar panel site s is established, 1 |
| Zb | if bio-refinery b is established, 1 |
| Qo | if recycling center o is established, 1 |
Appendix A
| For t = 1 to T Inputs J = set of distribution centers |
| F = set of rice factories |
| = capacity of rice factories f in period t |
| capacity of distribution center j in period t |
| V(J + F) = encode solution of period t |
| distance between nodes |
| -------------------------------------------------------------------------------------- |
| Outputs: |
| = amount of shipments between node j and f in period t |
| amount of CO2 emission caused by transferring quantity |
| by vehicle between nodes |
| = amount of remained goods in distribution center j at period t |
| ------------------------------------------- |
| while ∑iCa(j,t) > 0 or ∑iD(f,t) > 0 |
| : select the value of first column of first sub-segment J for j index) |
| select the value of first column of first sub-segment F for f index |
| Update demands and capacities |
| if |
| End while |
End for |
| Fort = 1: T |
| Inputs: F = set of rice factories P = set of product |
| L = set of all customers |
| = Production capacity of rice factory f for product p in period t |
| demand of customer l in period t |
| = Encode solution of period t |
| : distance between nodes ------------------------------------------------------------------------------------------------------- Outputs: |
| amount of CO2 emission caused by transferring quantity |
| by vehicle between nodes |
| = number of created job opportunities thorough production of product p in factory f in period t -------------------------------------------------------------------------------------------------------- |
| step2: |
| Update demands and capacities |
| End while |
| End for |
| Initialize RSA parameters α, β, etc. |
| Initialize the solutions’ positions randomly. |
| While do |
| Calculate the Fitness Function for the candidate solutions |
| Find the Best solution so far. |
| Update the ES using Equation (51). |
| For do |
| For do |
| Update the η and values using Equations (49), (50) and (52), respectively. |
| If ) then |
| = |
| Else if ( ) then |
| = |
| Else if (then |
| = |
| Else |
| = |
| End if |
| End for |
| End for |
| t = t + 1 |
| End while |
| Behshahr | Neka | Sari | Juybar | Qaemshahr | Pol Sefid | Savadkooh | Babolsar | Babol | Mahmood Abad | |
|---|---|---|---|---|---|---|---|---|---|---|
| Behshahr | - | 23 | 46 | 66 | 62 | 116 | 110 | 106 | 82 | 135 |
| Neka | - | - | 23 | 37 | 43 | 93 | 90 | 83 | 63 | 112 |
| Sari | - | - | - | 20 | 20 | 70 | 65 | 60 | 40 | 89 |
| Juybar | - | - | - | - | 20 | 70 | 65 | 34 | 43 | 75 |
| Qaemshahr | - | - | - | - | - | 50 | 45 | 40 | 20 | 69 |
| Pol Sefid | - | - | - | - | - | - | 10 | 90 | 70 | 119 |
| Savadkooh | - | - | - | - | - | - | - | 86 | 65 | 110 |
| Babolsar | - | - | - | - | - | - | - | - | 20 | 41 |
| Babol | - | - | - | - | - | - | - | - | - | 49 |
| Mahmoudabad | - | - | - | - | - | - | - | - | - | - |
| Parameters | Values | Units | Parameters | Values | Unit |
|---|---|---|---|---|---|
| capait | Uniform (7000,8000) | Kilogram | capff | Uniform (70,80) | Ton |
| chjt | Uniform (70,80) | Dollar per Ton | pbb | Uniform (300,350) | Kilogram |
| cpai | Uniform (600,650) | Dollar per Ton | cpjj | Uniform (55,65) | Dollar per Ton |
| dctp1ct | Uniform (400,500) | Kilogram | dctp2ct | Uniform (30,35) | Ton |
| dcop1ct | Uniform (350,400) | Kilogram | dcop2ct | Uniform (25,30) | Ton |
| dkkt | Uniform (30,40) | Kilogram | cpoo | Uniform (200,300) | Dollar per Ton |
| duut | Uniform (20,30) | Kilogram | diit | Uniform (200,300) | Kilogram |
| dmmt | Uniform (20,30) | Kilogram | capjj | Uniform (20,30) | Ton |
| pcappft | Uniform (90,100) | Ton | πss | Uniform (200,220) | Kilogram |
| caprrt | Uniform (20,100) | Megawatt hour | πoo | Uniform (200,220) | Kilogram |
| ctaxr | Uniform (15,20) | Dollar per Megawatt hour | vii | Uniform (15,20) | Person per ton |
| prmpmt | Uniform (2,5) | Dollar per Kg | fcjj2 | Uniform (3,4) | Person |
| prfpft | Uniform (1.5,4.5) | Dollar per Kg | fcss | Uniform (70,000,80,000) | Dollar |
| πbb | Uniform (200,220) | Kilogram | fjoo2 | Uniform (5000,6000) | Dollar |
| cpoot | Uniform (200,220) | Dollar per ton | fcbb | Uniform (500,000,600,000) | Dollar |
| poo2 | Uniform (400,450) | Kilogram | fjbb | Uniform (4,5) | Person |
| pss | Uniform (100,150) | Kilogram | VJQpf | Uniform (10,12) | Person per ton |
| Run | Npop | Maxit | T0 | Alpha | Response |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 2.49 × 10−5 |
| 2 | 1 | 2 | 2 | 2 | 2.62 × 10−5 |
| 3 | 1 | 3 | 3 | 3 | 2.58 × 10−5 |
| 4 | 2 | 1 | 2 | 3 | 2.53 × 10−5 |
| 5 | 2 | 2 | 3 | 1 | 1.74 × 10−5 |
| 6 | 2 | 3 | 1 | 2 | 1.68 × 10−5 |
| 7 | 3 | 1 | 3 | 2 | 1.21 × 10−5 |
| 8 | 3 | 2 | 1 | 3 | 1.45 × 10−5 |
| 9 | 3 | 3 | 2 | 1 | 1.32 × 10−5 |
| Run | Npop | Maxit | Phi1 | Phi2 | Response |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1.54 × 10−5 |
| 2 | 1 | 2 | 2 | 2 | 1.36 × 10−5 |
| 3 | 1 | 3 | 3 | 3 | 1.33 × 10−5 |
| 4 | 2 | 1 | 2 | 3 | 1.73 × 10−5 |
| 5 | 2 | 2 | 3 | 1 | 1.28 × 10−5 |
| 6 | 2 | 3 | 1 | 2 | 1.09 × 10−5 |
| 7 | 3 | 1 | 3 | 2 | 1.03 × 10−5 |
| 8 | 3 | 2 | 1 | 3 | 1.3 × 10−5 |
| 9 | 3 | 3 | 2 | 1 | 1.22 × 10−5 |
| Run | Npop | Maxit | IR | Response |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1.75 × 10−5 |
| 2 | 1 | 2 | 2 | 2.11 × 10−5 |
| 3 | 1 | 3 | 3 | 3.06 × 10−5 |
| 4 | 2 | 1 | 2 | 2.94 × 10−5 |
| 5 | 2 | 2 | 3 | 1.77 × 10−5 |
| 6 | 2 | 3 | 1 | 1.88 × 10−5 |
| 7 | 3 | 1 | 3 | 1.19 × 10−5 |
| 8 | 3 | 2 | 1 | 1.32 × 10−5 |
| 9 | 3 | 3 | 2 | 1.63 × 10−5 |
| Run | Npop | Maxit | Alpha | Beta | Response |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 2.92 × 10−5 |
| 2 | 1 | 2 | 2 | 2 | 2.57 × 10−5 |
| 3 | 1 | 3 | 3 | 3 | 1.67 × 10−5 |
| 4 | 2 | 1 | 2 | 3 | 1.59 × 10−5 |
| 5 | 2 | 2 | 3 | 1 | 1.63 × 10−5 |
| 6 | 2 | 3 | 1 | 2 | 1.27 × 10−5 |
| 7 | 3 | 1 | 3 | 2 | 1.21 × 10−5 |
| 8 | 3 | 2 | 1 | 3 | 1.09 × 10−5 |
| 9 | 3 | 3 | 2 | 1 | 1.12 × 10−5 |
References
- Kamariotou, M.; Kitsios, F.; Charatsari, C.; Lioutas, E.D.; Talias, M.A. Digital strategy decision support systems: Agrifood supply chain management in smes. Sensors 2022, 22, 274. [Google Scholar] [CrossRef] [PubMed]
- Roghanian, E.; Cheraghalipour, A. Addressing a set of meta-heuristics to solve a multi-objective model for closed-loop citrus supply chain considering CO2 emissions. J. Clean. Prod. 2019, 239, 118081. [Google Scholar] [CrossRef]
- Santos, R.B.D.; Torrisi, N.M.; Pantoni, R.P. Third party certification of agri-food supply chain using smart contracts and blockchain tokens. Sensors 2021, 21, 5307. [Google Scholar] [CrossRef] [PubMed]
- Rockström, J.; Williams, J.; Daily, G.; Noble, A.; Matthews, N.; Gordon, L.; Wetterstrand, H.; DeClerck, F.; Shah, M.; Steduto, P.; et al. Sustainable intensification of agriculture for human prosperity and global sustainability. Ambio 2017, 46, 4–17. [Google Scholar] [CrossRef] [Green Version]
- Alkhateeb, A.; Catal, C.; Kar, G.; Mishra, A. Hybrid blockchain platforms for the internet of things (IoT): A systematic literature review. Sensors 2022, 22, 1304. [Google Scholar] [CrossRef]
- Angarita-Zapata, J.S.; Alonso-Vicario, A.; Masegosa, A.D.; Legarda, J. A taxonomy of food supply chain problems from a computational intelligence perspective. Sensors 2021, 21, 6910. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Dulebenets, M.A.; Hajiaghaei–Keshteli, M.; Tavakkoli-Moghaddam, R.; Safaeian, M.; Mirzahosseinian, H. Two hybrid meta-heuristic algorithms for a dual-channel closed-loop supply chain network design problem in the tire industry under uncertainty. Adv. Eng. Inform. 2021, 50, 101418. [Google Scholar] [CrossRef]
- Abraham, A.; Mathew, A.K.; Sindhu, R.; Pandey, A.; Binod, P. Potential of rice straw for bio-refining: An overview. Bioresour. Technol. 2016, 215, 29–36. [Google Scholar] [CrossRef]
- Ali, G.; Bashir, M.K.; Ali, H.; Bashir, M.H. Utilization of rice husk and poultry wastes for renewable energy potential in Pakistan: An economic perspective. Renew. Sustain. Energy Rev. 2016, 61, 25–29. [Google Scholar] [CrossRef]
- Firouzi, S.; Alizadeh, M.R.; Haghtalab, D. Energy consumption and rice milling quality upon drying paddy with a newly-designed horizontal rotary dryer. Energy 2017, 119, 629–636. [Google Scholar] [CrossRef]
- Palma-Heredia, D.; Verdaguer, M.; Puig-Cayuela, V.; Poch, M.; Cugueró-Escofet, M.À. Comparison of optimisation algorithms for centralised anaerobic co-digestion in a real river basin case study in Catalonia. Sensors 2022, 22, 1857. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J.R. Application of planning models in the agri-food supply chain: A review. Eur. J. Oper. Res. 2009, 196, 1–20. [Google Scholar] [CrossRef]
- Amorim, P.; Günther, H.O.; Almada-Lobo, B. Multi-objective integrated production and distribution planning of perishable products. Int. J. Prod. Econ. 2012, 138, 89–101. [Google Scholar] [CrossRef]
- Velychko, O. Integrated modeling of solutions in the system of distributing logistics of a fruit and vegetable cooperative. Bus. Theory Pract. 2014, 15, 362–370. [Google Scholar] [CrossRef]
- Nadal-Roig, E.; Plà-Aragonés, L.M. Optimal transport planning for the supply to a fruit logistic centre. Int. Ser. Oper. Res. Manag. Sci. 2015, 224, 163–177. [Google Scholar] [CrossRef]
- Soto-Silva, W.E.; González-Araya, M.C.; Oliva-Fernández, M.A.; Plà-Aragonés, L.M. Optimizing fresh food logistics for processing: Application for a large Chilean apple supply chain. Comput. Electron. Agric. 2017, 136, 42–57. [Google Scholar] [CrossRef]
- Mogale, D.G.; Kumar, M.; Krishna, S.; Kumar, M. Grain silo location-allocation problem with dwell time for optimization of food grain supply chain network. Transp. Res. Part E 2018, 111, 40–69. [Google Scholar] [CrossRef]
- Cheraghalipour, A.; Paydar, M.M.; Hajiaghaei-Keshteli, M. A bi-objective optimization for citrus closed-loop supply chain using Pareto-based algorithms. Appl. Soft Comput. J. 2018, 69, 33–59. [Google Scholar] [CrossRef]
- Hosseini-Motlagh, S.M.; Samani, M.R.G.; Saadi, F.A. Strategic Optimization of Wheat Supply Chain Network Under Uncertainty: A Real Case Study; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Sahebjamnia, N.; Goodarzian, F.; Hajiaghaei-Keshteli, M. Optimization of multi-period three-echelon citrus supply chain problem. J. Optim. Ind. Eng. 2020, 13, 39–53. [Google Scholar] [CrossRef]
- Cheraghalipour, A.; Mahdi, M.; Hajiaghaei-Keshteli, M. Designing and solving a bi-level model for rice supply chain using the evolutionary algorithms. Comput. Electron. Agric. 2019, 162, 651–668. [Google Scholar] [CrossRef]
- Salehi-Amiri, A.; Zahedi, A.; Akbapour, N.; Hajiaghaei-Keshteli, M. Designing a sustainable closed-loop supply chain network for walnut industry. Renew. Sustain. Energy Rev. 2021, 141, 110821. [Google Scholar] [CrossRef]
- Salehi-Amiri, A.; Zahedi, A.; Calvo, E.Z.R.; Hajiaghaei-Keshteli, M. Designing a Closed-loop Supply Chain Network Considering Social Factors; A Case Study on Avocado Industry. Appl. Math. Model. 2021, 101, 600–631. [Google Scholar] [CrossRef]
- Chouhan, V.K.; Khan, S.H.; Hajiaghaei-Keshteli, M. Metaheuristic approaches to design and address multi-echelon sugarcane closed-loop supply chain network. Soft Comput. 2021, 25, 11377–11404. [Google Scholar] [CrossRef]
- Catalá, L.P.; Moreno, M.S.; Blanco, A.M.; Bandoni, J.A. A bi-objective optimization model for tactical planning in the pome fruit industry supply chain. Comput. Electron. Agric. 2016, 130, 128–141. [Google Scholar] [CrossRef]
- Banasik, A.; Kanellopoulos, A.; Claassen, G.D.H.; Bloemhof-Ruwaard, J.M.; Van Der Vorst, J.G.A.J. Closing loops in agricultural supply chains using multi-objective optimization: A case study of an industrial mushroom supply chain. Int. J. Prod. Econ. 2017, 183, 409–420. [Google Scholar] [CrossRef]
- Gholamian, M.R.; Taghanzadeh, A.H. Integrated network design of wheat supply chain: A real case of Iran. Comput. Electron. Agric. 2017, 140, 139–147. [Google Scholar] [CrossRef]
- Galán-Martín, Á.; Vaskan, P.; Antón, A.; Esteller, L.J.; Guillén-Gosálbez, G. Multi-objective optimization of rainfed and irrigated agricultural areas considering production and environmental criteria: A case study of wheat production in Spain. J. Clean. Prod. 2017, 140, 816–830. [Google Scholar] [CrossRef]
- Allaoui, H.; Guo, Y.; Choudhary, A.; Bloemhof, J. Sustainable agro-food supply chain design using two-stage hybrid multi-objective decision-making approach. Comput. Oper. Res. 2018, 89, 369–384. [Google Scholar] [CrossRef] [Green Version]
- Sazvar, Z.; Rahmani, M.; Govindan, K. A sustainable supply chain for organic, conventional agro-food products: The role of demand substitution, climate change and public health. J. Clean. Prod. 2018, 194, 564–583. [Google Scholar] [CrossRef]
- Paam, P.; Berretta, R.; Heydar, M.; García-Flores, R. The impact of inventory management on economic and environmental sustainability in the apple industry. Comput. Electron. Agric. 2019, 163, 104848. [Google Scholar] [CrossRef]
- Motevalli-Taher, F.; Paydar, M.M.; Emami, S. Wheat sustainable supply chain network design with forecasted demand by simulation. Comput. Electron. Agric. 2020, 178, 105763. [Google Scholar] [CrossRef]
- Gilani, H.; Sahebi, H. Optimal Design and Operation of the green pistachio supply network: A robust possibilistic programming model. J. Clean. Prod. 2021, 282, 125212. [Google Scholar] [CrossRef]
- Naderi, B.; Govindan, K.; Soleimani, H. A Benders decomposition approach for a real case supply chain network design with capacity acquisition and transporter planning: Wheat distribution network. Ann. Oper. Res. 2020, 291, 685–705. [Google Scholar] [CrossRef]
- Hajimirzajan, A.; Vahdat, M.; Sadegheih, A.; Shadkam, E.; El Bilali, H. An integrated strategic framework for large-scale crop planning: Sustainable climate-smart crop planning and agri-food supply chain management. Sustain. Prod. Consum. 2021, 26, 709–732. [Google Scholar] [CrossRef]
- Ming, L.; GuoHua, Z.; Wei, W. Study of the game model of e-commerce information sharing in an agricultural product supply chain based on fuzzy big data and LSGDM. Technol. Forecast. Soc. Chang. 2021, 172, 121017. [Google Scholar] [CrossRef]
- Jiménez, M.; Arenas, M.; Bilbao, A.; Rodríguez, M.V. Linear programming with fuzzy parameters: An interactive method resolution. Eur. J. Oper. Res. 2007, 177, 1599–1609. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Gen, M.; Altiparmak, F.; Lin, L. A genetic algorithm for two-stage transportation problem using priority-based encoding. OR Spectr. 2006, 28, 337–354. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Sahebjamnia, N.; Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M. Sustainable tire closed-loop supply chain network design: Hybrid metaheuristic algorithms for large-scale networks. J. Clean. Prod. 2018, 196, 273–296. [Google Scholar] [CrossRef]
- Goodarzian, F.; Hosseini-Nasab, H.; Muñuzuri, J.; Fakhrzad, M.B. A multi-objective pharmaceutical supply chain network based on a robust fuzzy model: A comparison of meta-heuristics. Appl. Soft Comput. J. 2020, 92, 106331. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef] [PubMed]




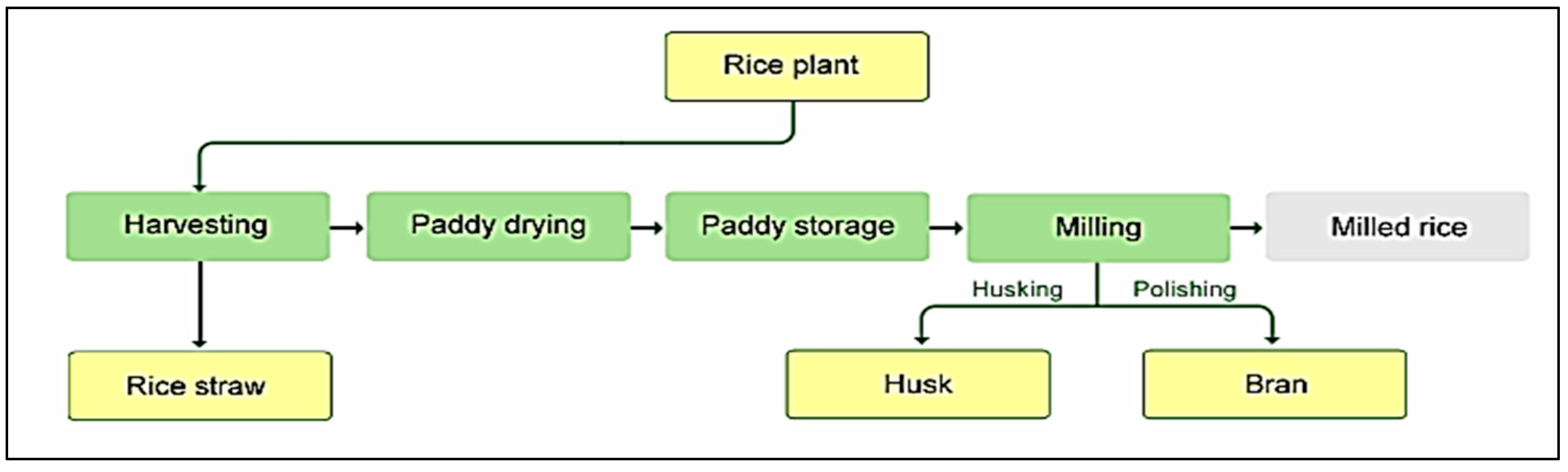


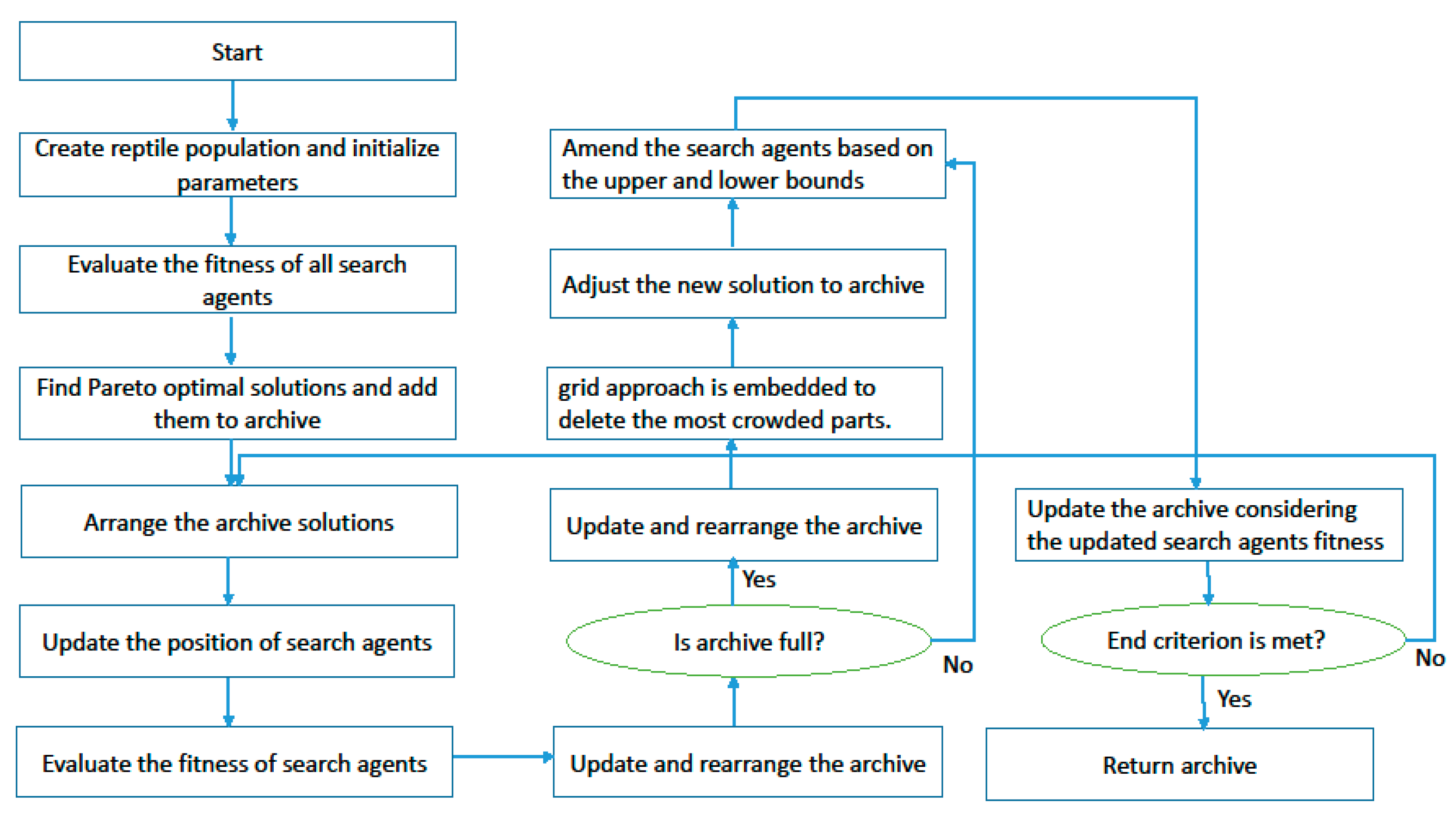
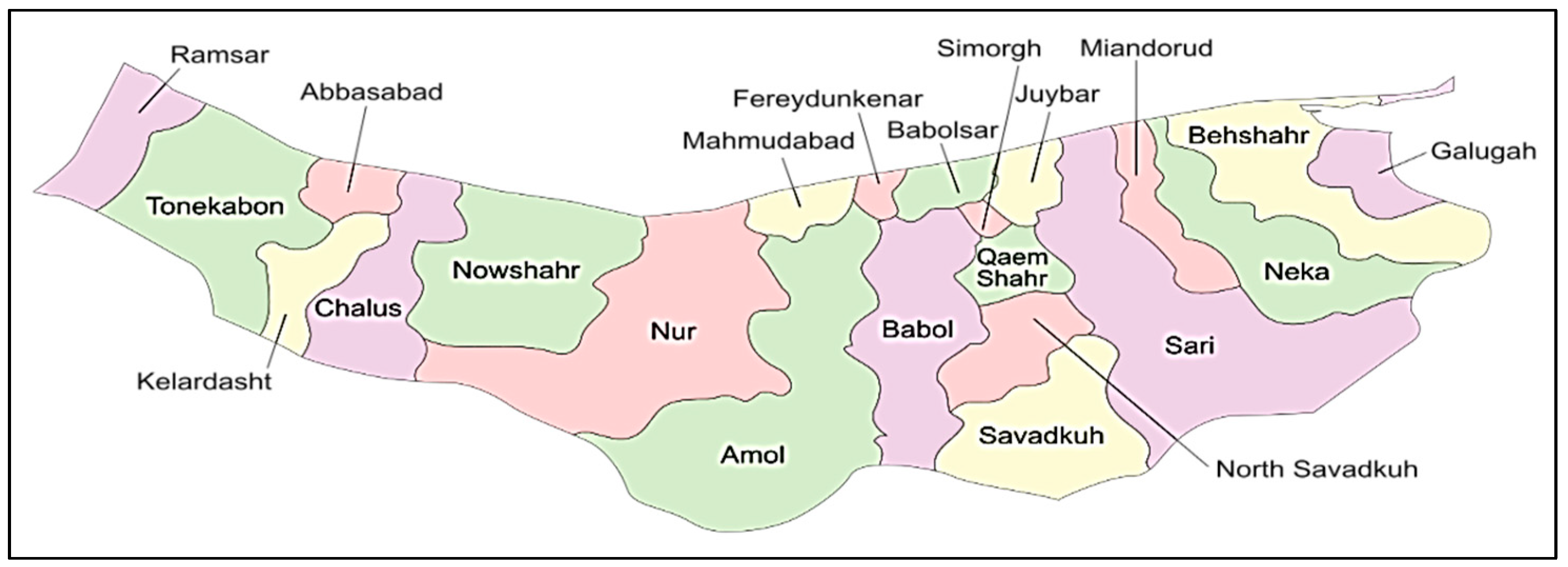



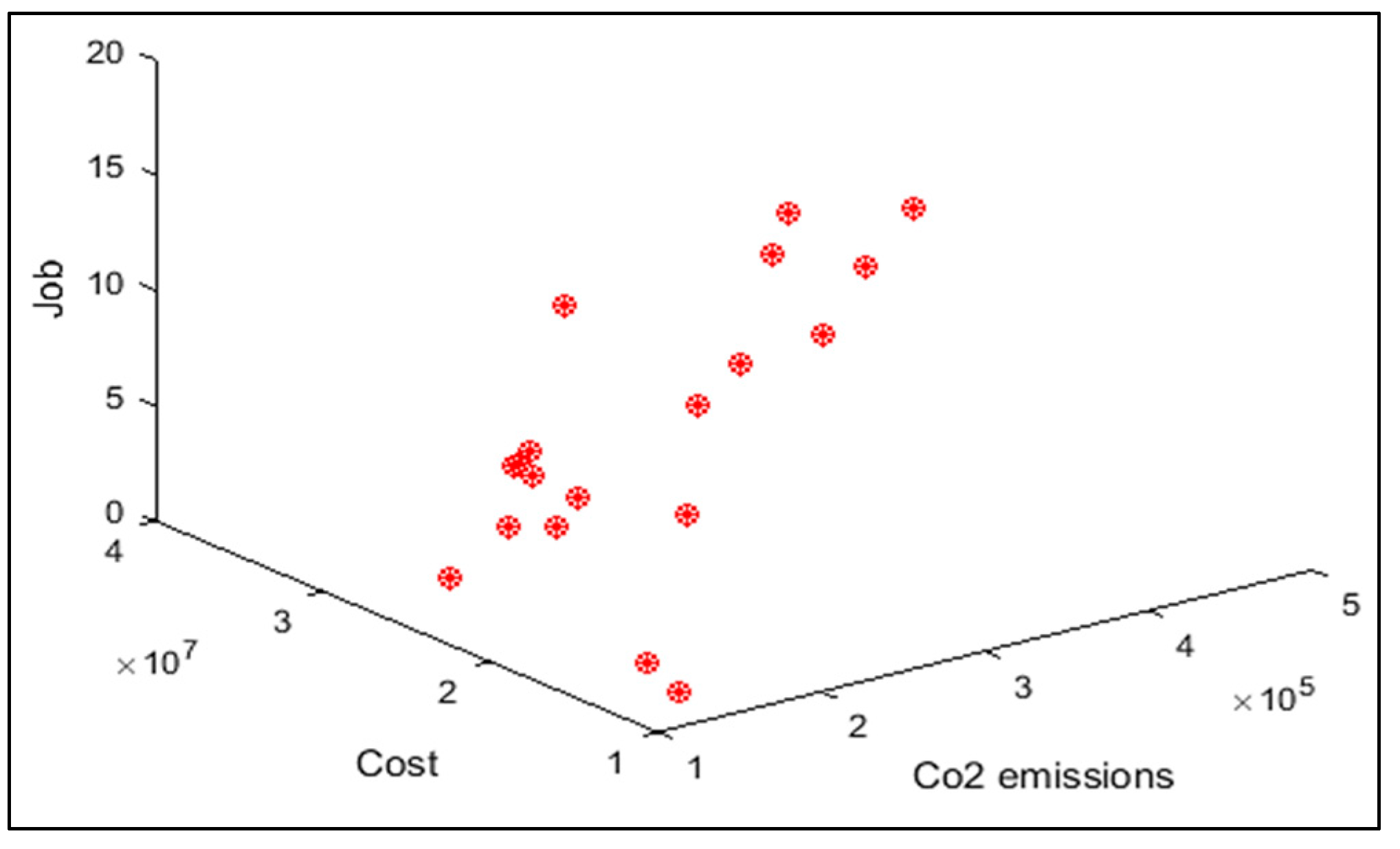

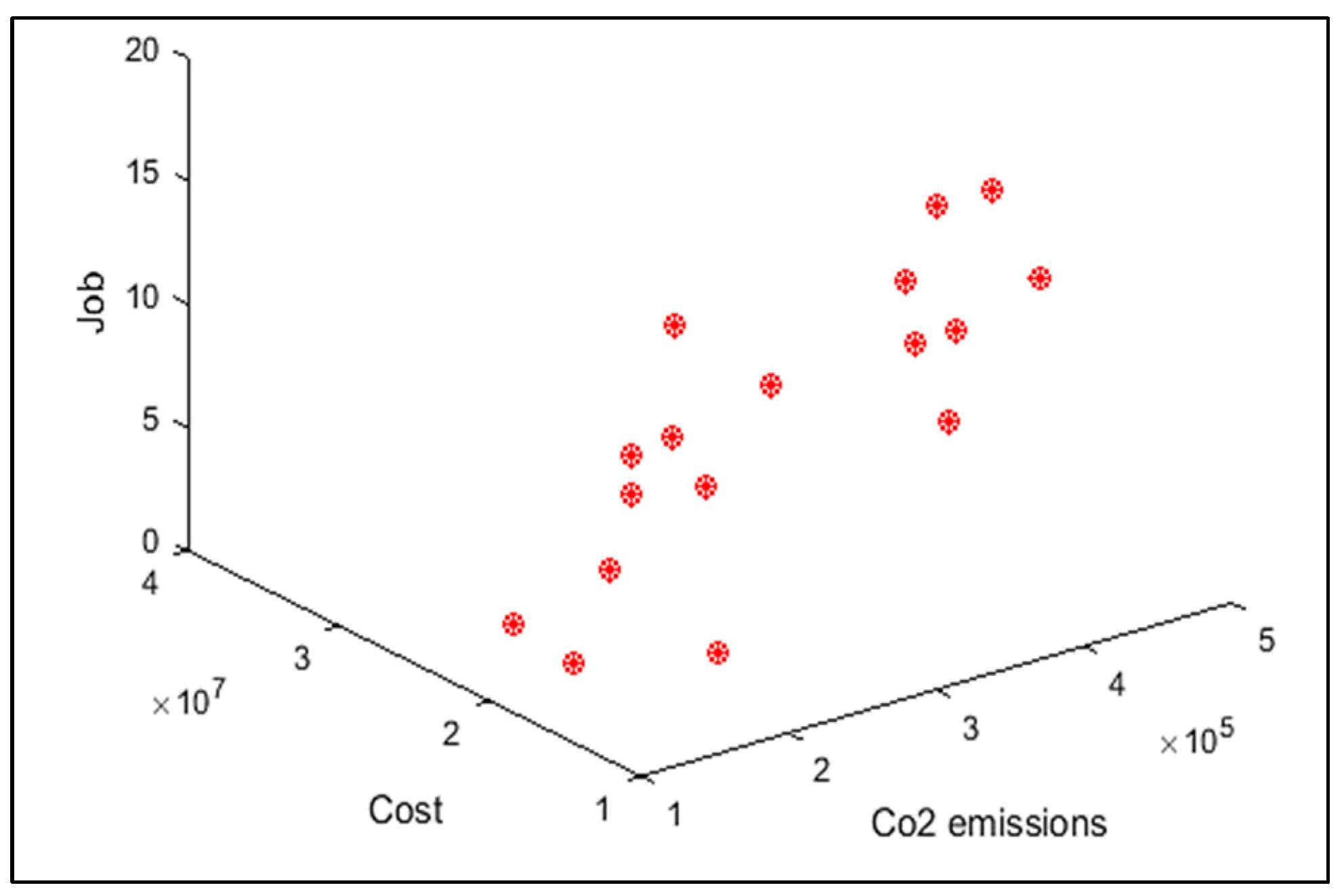
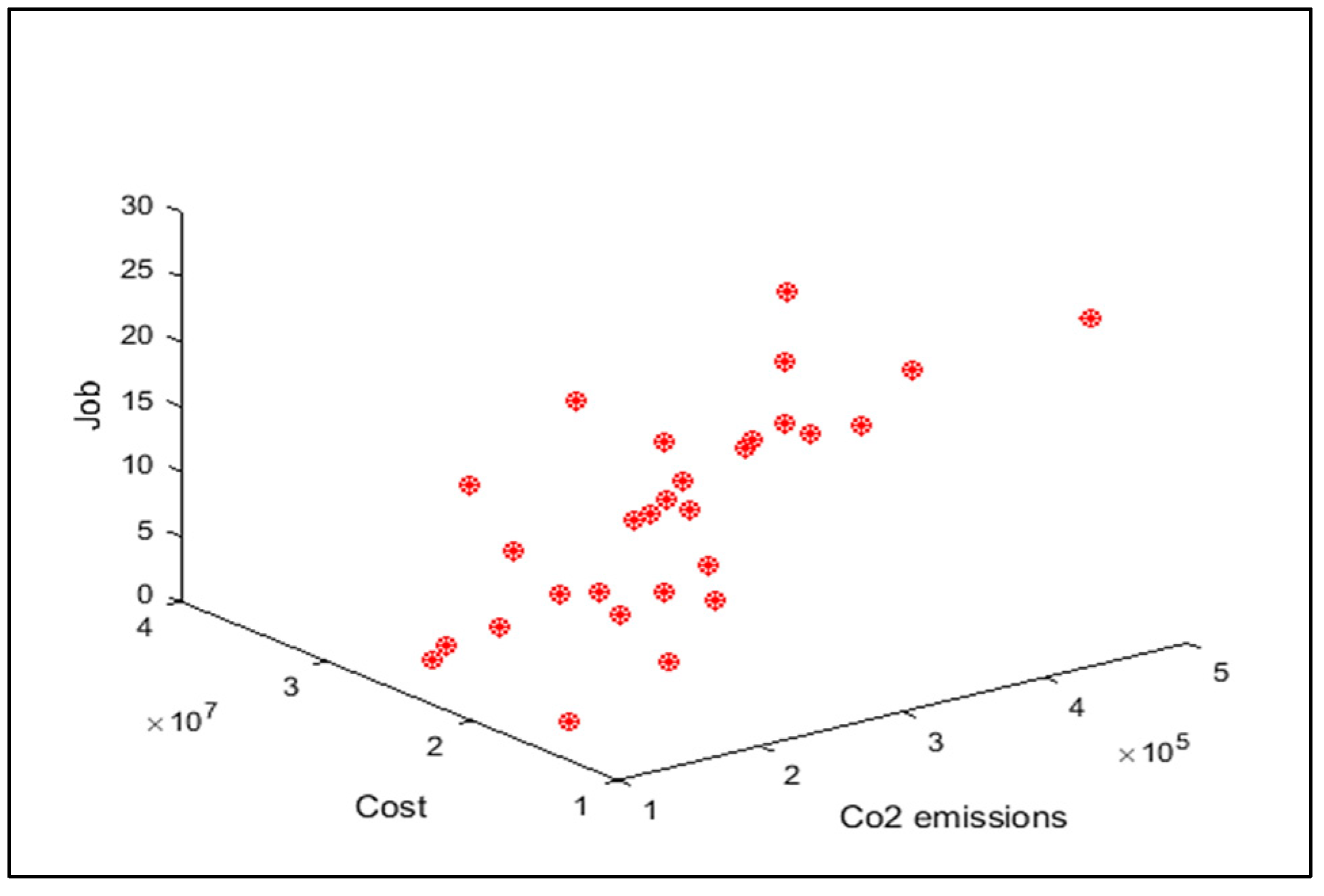


| Authors | Model | Objectives | Uncertainty | Period | Online Purchase | Energy Source | Case Study | Solution Method | |
|---|---|---|---|---|---|---|---|---|---|
| Single | Multi | ||||||||
| [15] | LP | Minimizing the transportation costs | * | Fruit | Exact | ||||
| [29] | LP | Minimizing costs Minimizing water consumption, CO2 emissions, and destructed jobs | * | An agro-food company | AHP | ||||
| [18] | MILP | Minimizing total cost Maximizing demand responsiveness | * | Citrus | Meta-heuristics | ||||
| [21] | MILP | Minimizing total cost | * | Rice | Meta-heuristics | ||||
| [19] | MILP | Minimizing total cost | Robust | * | Wheat | Exact | |||
| [2] | MILP | Minimizing CO2 emissions Minimizing total cost Maximizing demand responsiveness | * | Citrus | Meta-heuristics | ||||
| [34] | MILP | Minimizing total cost | * | Wheat | Benders decomposition | ||||
| [32] | MILP | Minimizing total cost Minimizing water consumption | Simulation | * | Wheat | Goal programming | |||
| [34] | MILP | Minimizing total cost | * | Wheat | Benders decomposition | ||||
| [33] | MILP | Maximizing total profit Minimizing CO2 emissions | Roust fuzzy | * | Pistachio | Epsilon constraint | |||
| [35] | MILP | Minimizing total cost | * | Crops | Lingo | ||||
| [22] | MILP | Minimizing total cost | * | Walnut | Meta-heuristics | ||||
| [24] | MILP | Minimizing total cost | * | Sugarcane | Meta-heuristics | ||||
| [23] | MILP | Minimizing total cost Maximizing the created jobs | * | Avocado | Meta-heuristics and Exact | ||||
| The present study | MILP | Minimizing total cost Maximizing the created jobs Minimizing CO2 emissions | Fuzzy | * | * | * | Rice | Meta-heuristics and Exact | |
| Fort = 1:T |
| Inputs: I = set of producers J = set of distribution centers |
| = production capacity of producer in period t |
| = Distance between nodes |
| Outputs: |
| and in period t |
| = binary variable shows the distribution centers j is opened |
| Step3 = |
| Update demands and capacities |
| Step4 = |
| End while Step5 = |
If |
| End if End for End for |
| Input: Reptile population and parameters |
| Output: Archive of non-dominated optimal solutions |
| Calculate the fitness value of each search agent, |
| Determine the non-dominated reptiles and add them to archive |
| While ( ) do |
| For each search agent do |
| Update the position of current search agent based on RSO mechanism |
| End for |
| Compute the fitness of all search agents |
| Find the non-dominated optimal solutions from updated search agents |
| Update the obtained non-dominated reptiles to archive |
| If archive becomes full then |
| Check if any search agent goes beyond the search space and then adjust it |
| Compute the objective function values of each search agent |
| t = t + 1 |
| End while |
| Return archive |
| Test | I | J1 | J2 | F | M | K | O1 | O2 | V | B | U |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2 | 1 | 2 | 2 | 1 | 3 | 1 | 2 | 1 | 2 |
| 2 | 13 | 4 | 2 | 4 | 3 | 2 | 5 | 2 | 4 | 3 | 3 |
| 3 | 22 | 7 | 3 | 8 | 8 | 2 | 7 | 4 | 6 | 6 | 8 |
| 4 | 30 | 9 | 5 | 9 | 6 | 3 | 9 | 7 | 9 | 8 | 11 |
| 5 | 40 | 15 | 7 | 14 | 9 | 5 | 14 | 11 | 11 | 12 | 14 |
| 6 | 55 | 20 | 8 | 20 | 14 | 9 | 23 | 13 | 18 | 17 | 17 |
| 7 | 65 | 24 | 11 | 24 | 16 | 12 | 28 | 15 | 25 | 24 | 22 |
| 8 | 72 | 30 | 14 | 28 | 20 | 15 | 35 | 16 | 31 | 30 | 26 |
| 9 | 80 | 34 | 17 | 32 | 24 | 19 | 42 | 18 | 37 | 39 | 34 |
| 10 | 82 | 38 | 20 | 36 | 28 | 21 | 49 | 20 | 42 | 40 | 39 |
| Algorithm | Parameter | Parameter Level | Best Level | ||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |||
| MOSA | Maximum iteration (Maxiter) | 50 | 100 | 150 | 150 |
| Population size (Npop) | 40 | 50 | 60 | 60 | |
| T | 30 | 40 | 50 | 50 | |
| Alpha | 0.9 | 0.95 | 0.99 | 0.95 | |
| MOGWO | Maximum iteration (Maxiter) | 50 | 100 | 150 | 150 |
| Population size (Npop) | 40 | 50 | 60 | 50 | |
| Initialization ratio (IR) | 0.5 | 0.6 | 0.7 | 0.5 | |
| MOPSO | Maximum iteration (Maxiter) | 50 | 100 | 150 | 150 |
| Population size (Npop) | 40 | 50 | 60 | 50 | |
| C1 | 1.9 | 2 | 2.1 | 2.1 | |
| C2 | 2 | 2.1 | 2.2 | 2.1 | |
| MORSO | Maximum iteration (Maxiter) | 50 | 100 | 150 | 150 |
| Population size (Npop) | 40 | 50 | 60 | 60 | |
| Alpha | 0.1 | 0.12 | 0.14 | 0.1 | |
| Beta | 0.1 | 0.12 | 0.14 | 0.12 | |
| Problem | NPS | CPU Time (Second) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MOPSO | MOGWO | MOSA | MORSO | LP-Metric | MOPSO | MOGWO | MOSA | MORSO | LP-Metric | |
| 1 | 22 | 24 | 16 | 25 | 11 | 29 | 28 | 4.1 | 25 | 1223 |
| 2 | 13 | 22 | 14 | 24 | 11 | 44 | 40 | 3.3 | 37 | 1757 |
| 3 | 23 | 24 | 15 | 24 | 12 | 57 | 54 | 3.6 | 53 | 2598 |
| 4 | 36 | 35 | 17 | 37 | 11 | 67 | 71 | 4 | 68 | 3150 |
| 5 | 26 | 24 | 23 | 28 | 13 | 83 | 88 | 4.2 | 85 | 5294 |
| 6 | 28 | 30 | 16 | 32 | NA | 98 | 101 | 4.5 | 96 | NA |
| 7 | 17 | 21 | 15 | 23 | NA | 116 | 125 | 4.8 | 112 | NA |
| 8 | 32 | 27 | 20 | 27 | NA | 137 | 139 | 5.1 | 132 | NA |
| 9 | 29 | 25 | 21 | 27 | NA | 155 | 163 | 5.4 | 151 | NA |
| 10 | 27 | 26 | 20 | 29 | NA | 179 | 197 | 5.6 | 173 | NA |
| Problem | MS | SNS | ||||||||
| MOPSO | MOGWO | MOSA | MORSO | LP-Metric | MOPSO | MOGWO | MOSA | MORSO | LP-Metric | |
| 1 | 76,996 | 78,902 | 80,928 | 81,616 | 813,421 | 97,270 | 76,686 | 62,796 | 98,209 | 96,036 |
| 2 | 179,312 | 191,723 | 329,516 | 258,032 | 293,404 | 322,501 | 303,975 | 300,817 | 331,716 | 339,023 |
| 3 | 362,921 | 402,387 | 334,579 | 410,477 | 425,328 | 476,055 | 493,922 | 475,192 | 498,241 | 500,445 |
| 4 | 483,448 | 512,464 | 415,642 | 517,116 | 505,373 | 637,523 | 682,038 | 598,916 | 672,870 | 675,803 |
| 5 | 495,925 | 472,086 | 426,705 | 522,802 | 480,042 | 773,715 | 876,200 | 834,830 | 881,936 | 852,516 |
| 6 | 514,229 | 503,311 | 350,392 | 530,459 | NA | 1021,995 | 1031,169 | 1087,758 | 1105,495 | NA |
| 7 | 668,699 | 613,566 | 597,331 | 608,137 | NA | 1241,442 | 1262,644 | 1241,226 | 1293,651 | NA |
| 8 | 348,317 | 563,723 | 552,739 | 583,602 | NA | 1489,544 | 1549,389 | 1438,068 | 1567,032 | NA |
| 9 | 737,518 | 794,779 | 649,699 | 774,415 | NA | 1664,923 | 1723,552 | 1732,838 | 1743,955 | NA |
| 10 | 835,031 | 887,315 | 587,273 | 906,189 | NA | 1947,220 | 1931,833 | 1895,988 | 1963,370 | NA |
| Problem | MS | |||||||||
| MOPSO | MOGWO | MOSA | MORSO | LP-Metric | ||||||
| 1 | 1.56 | 1.3 | 1.5 | 1.2 | 1.3 | |||||
| 2 | 4 | 2.5 | 3.7 | 3.1 | 2.2 | |||||
| 3 | 3.5 | 3.2 | 2.5 | 2.3 | 2.46 | |||||
| 4 | 4.2 | 3.7 | 5.4 | 3.5 | 3.1 | |||||
| 5 | 4.7 | 6.1 | 5.2 | 4.4 | 4.2 | |||||
| 6 | 4.8 | 4.6 | 6.5 | 4.3 | NA | |||||
| 7 | 5.4 | 6.9 | 8.8 | 5.5 | NA | |||||
| 8 | 7.1 | 4.9 | 8.6 | 4.7 | NA | |||||
| 9 | 5.4 | 7.7 | 8 | 5.9 | NA | |||||
| 10 | 5.9 | 7.9 | 7.8 | 6.1 | NA | |||||
| Caprrt | Xsert | |||||
|---|---|---|---|---|---|---|
| Condition | Bio-Refinery | Solar Panels | Mains Electricity | Bio-Refinery | Solar Panels | Mains Electricity |
| 1 | 0 | 0 | +19% | −100% | −100% | - |
| 2 | +7% | 13% | −7% | +30% | +30% | −30% |
| 3 | 8% | 16% | −9% | +50% | +50% | −40% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharye Mirzaei, M.; Goodarzian, F.; Maddah, S.; Abraham, A.; Abdelkareim Gabralla, L. Investigating a Dual-Channel Network in a Sustainable Closed-Loop Supply Chain Considering Energy Sources and Consumption Tax. Sensors 2022, 22, 3547. https://doi.org/10.3390/s22093547
Gharye Mirzaei M, Goodarzian F, Maddah S, Abraham A, Abdelkareim Gabralla L. Investigating a Dual-Channel Network in a Sustainable Closed-Loop Supply Chain Considering Energy Sources and Consumption Tax. Sensors. 2022; 22(9):3547. https://doi.org/10.3390/s22093547
Chicago/Turabian StyleGharye Mirzaei, Mehran, Fariba Goodarzian, Saeid Maddah, Ajith Abraham, and Lubna Abdelkareim Gabralla. 2022. "Investigating a Dual-Channel Network in a Sustainable Closed-Loop Supply Chain Considering Energy Sources and Consumption Tax" Sensors 22, no. 9: 3547. https://doi.org/10.3390/s22093547
APA StyleGharye Mirzaei, M., Goodarzian, F., Maddah, S., Abraham, A., & Abdelkareim Gabralla, L. (2022). Investigating a Dual-Channel Network in a Sustainable Closed-Loop Supply Chain Considering Energy Sources and Consumption Tax. Sensors, 22(9), 3547. https://doi.org/10.3390/s22093547







