Study of Model Uncertainties Influence on the Impact Point Dispersion for a Gasodynamicaly Controlled Projectile
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.1.1. Assumptions
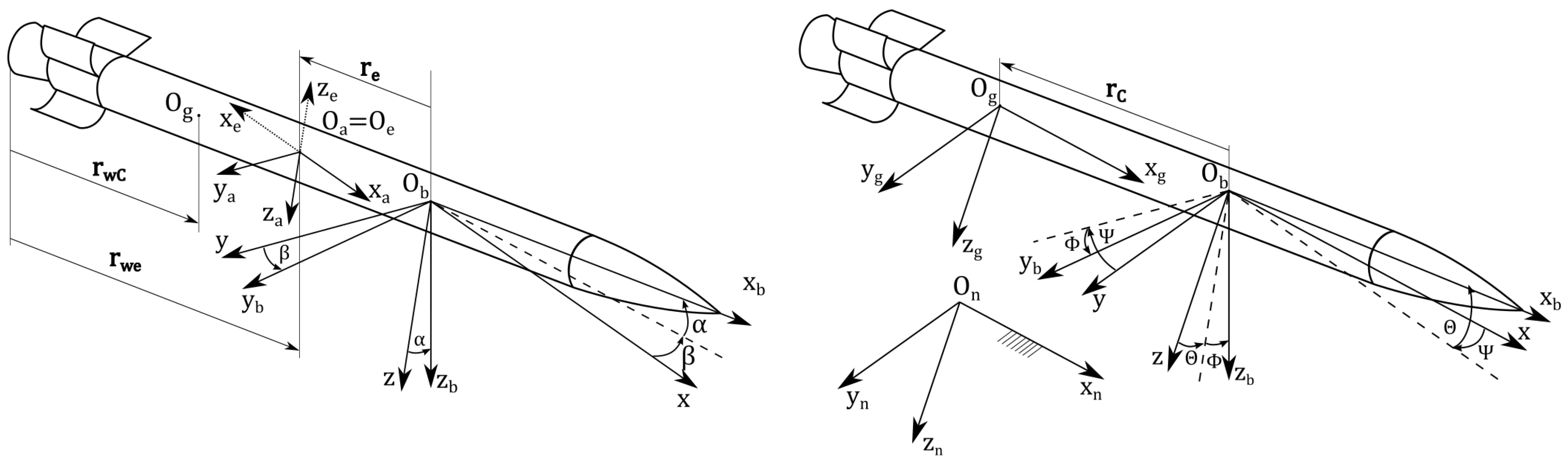
2.1.2. Coordinate Systems
- The navigational coordinate system is a right-handed, Cartesian coordinate system fixed to earth. Its origin is located at any point and the plane is tangent to the surface of the earth. The axis points in the direction of a launch rail, axis in the direction of the gravitational acceleration and axis completes the right-handed coordinate system.
- The gravitational coordinate system is a right-handed, Cartesian moving coordinate system fixed with the rocket. Its origin is located at the center of mass of the rocket and the whole system remains parallel to the navigational system during the whole flight of the rocket.
- The body coordinate system is a right-handed Cartesian coordinate system. Its origin is located at any point of the rocket. The axis is parallel to the rockets longitudinal axis and points forward, axis points at the right wing and axis completes the right-handed coordinate system. Orientation of the body coordinate system with respect to the gravitational coordinate system is described by the Euler angles of yaw , pitch and roll .
- The measuring coordinate system is a right-handed, Cartesian coordinate system fixed with the airflow. Its origin is located at any point of the symmetry plane and the position of that point with respect to the coordinate system is defined by the vector . The axis lies in the direction of the airflow, axis points upwards and the axis points to the right.
- The aerodynamic coordinate system is the right-handed Cartesian coordinate system fixed with the airflow. The axis points in the opposite direction that the airflow, axis points downwards and the completes the right-handed coordinate system.
2.1.3. Dynamic Equations of Motion
2.1.4. Orientation
2.1.5. External Loads
2.1.6. Aerodynamics
2.1.7. Gravity
2.1.8. Thrust
2.1.9. Correction Thrusters
2.1.10. Inertial Parameters
2.1.11. Atmosphere Model
2.1.12. Inertial Measurement Unit Model
Gyroscopes Model
2.1.13. Control Algorithms
- Correction thruster was not used already (solid motor thrusters are single-use motors)
- The time between the last thruster ignition is greater than some limit value
- The correction thruster must be ignited so that the resultant thrust force was in the direction of the desired lateral displacement [35,36], which means that the absolute value of the difference between the error phase and thruster azimuth angle diminished by the control prediction times and multiplied by the roll angular velocity was lower than some limit value .
- The rocket’s pitch angle must be lower or equal the threshold value and the time of flight must be at least equal to the threshold value
- The distance between the rocket’s center of mass and the reference trajectory , measured perpendicular, is greater than some limit value
- the norm of the commanded value of the lateral acceleration must be greater than the threshold value
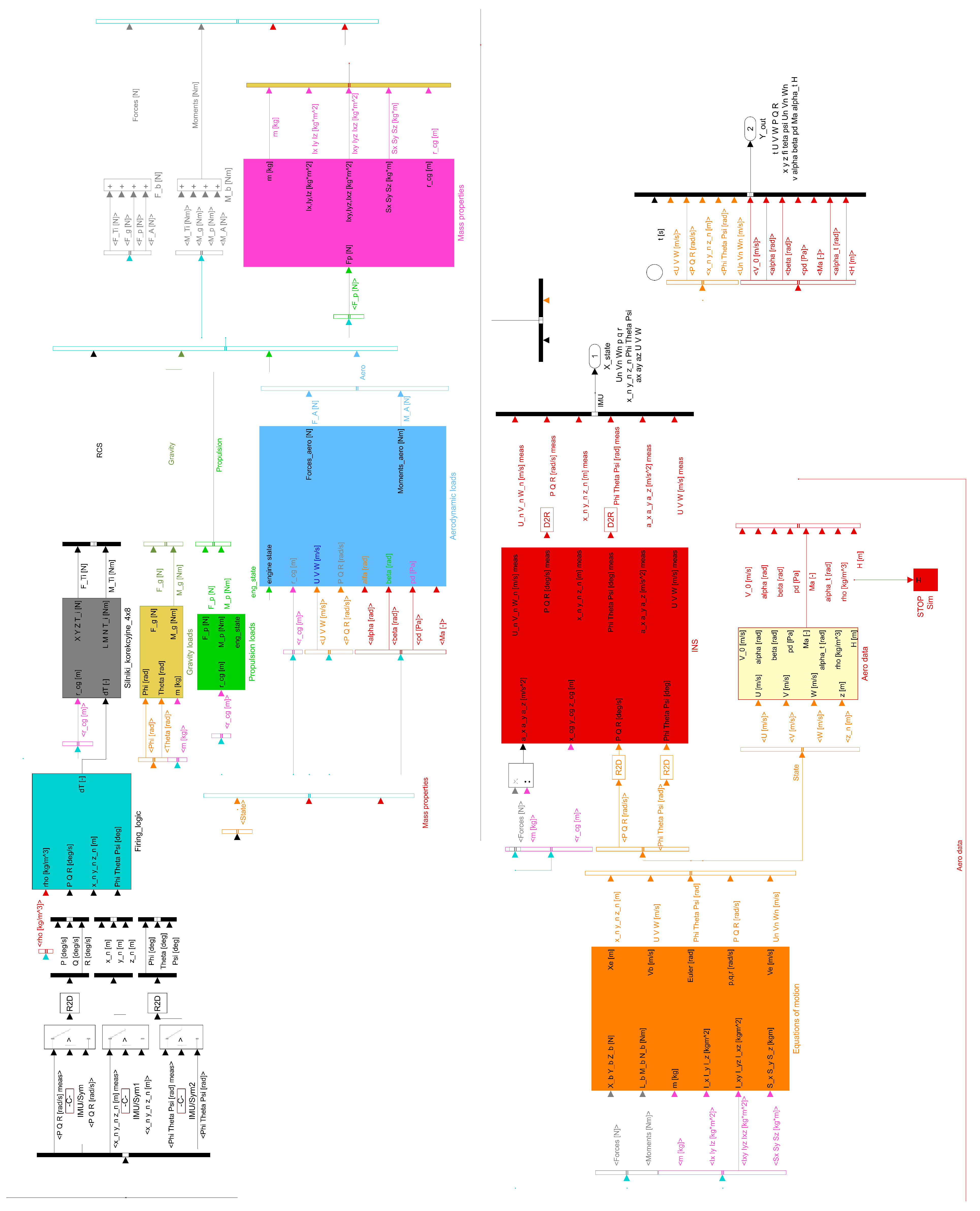
2.2. Simulation Model
3. Results and Discussion
3.1. Input Data for the Simulation Study
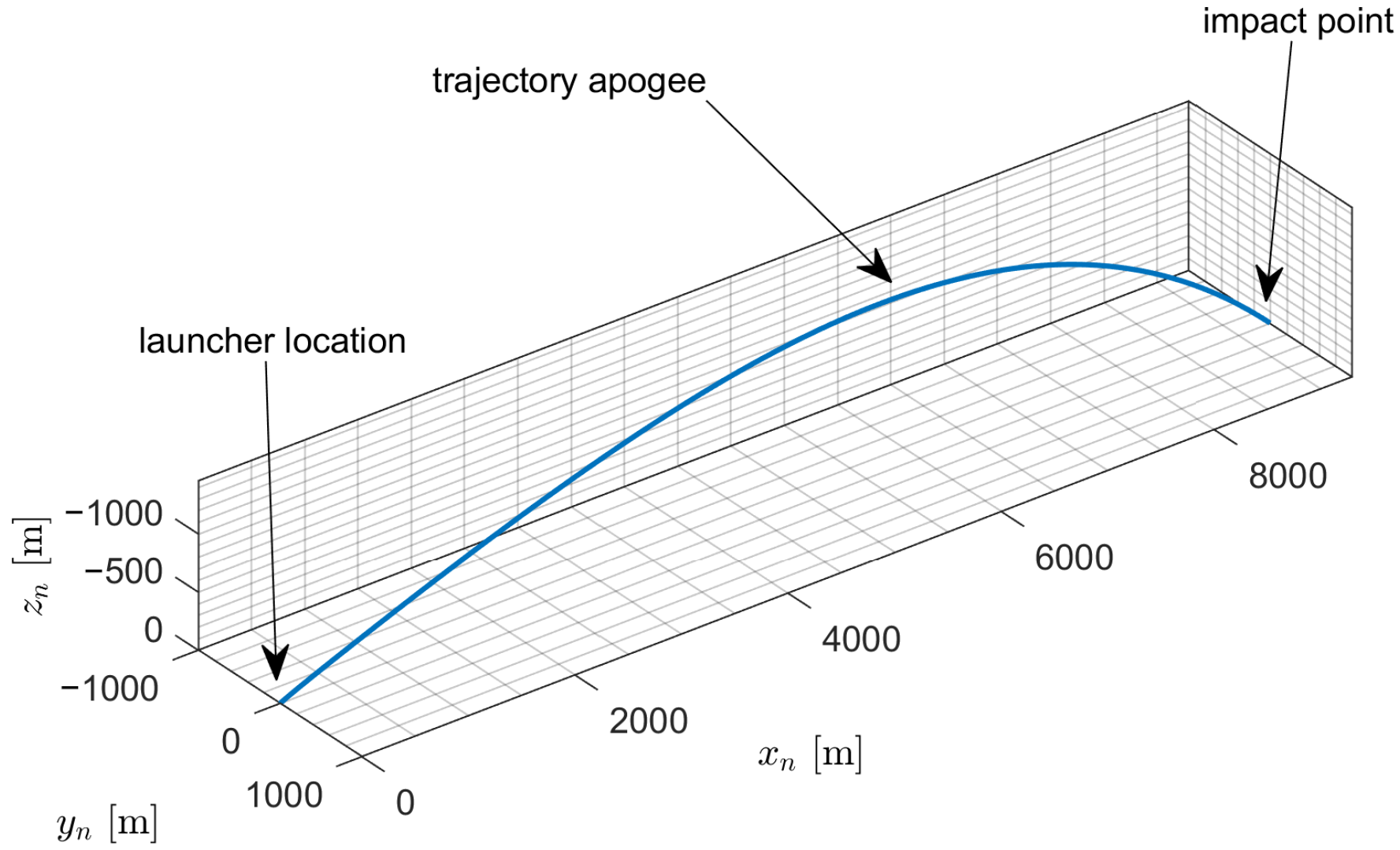
3.2. Initial Verification of Control Algorithms
3.3. Monte-Carlo Simulations
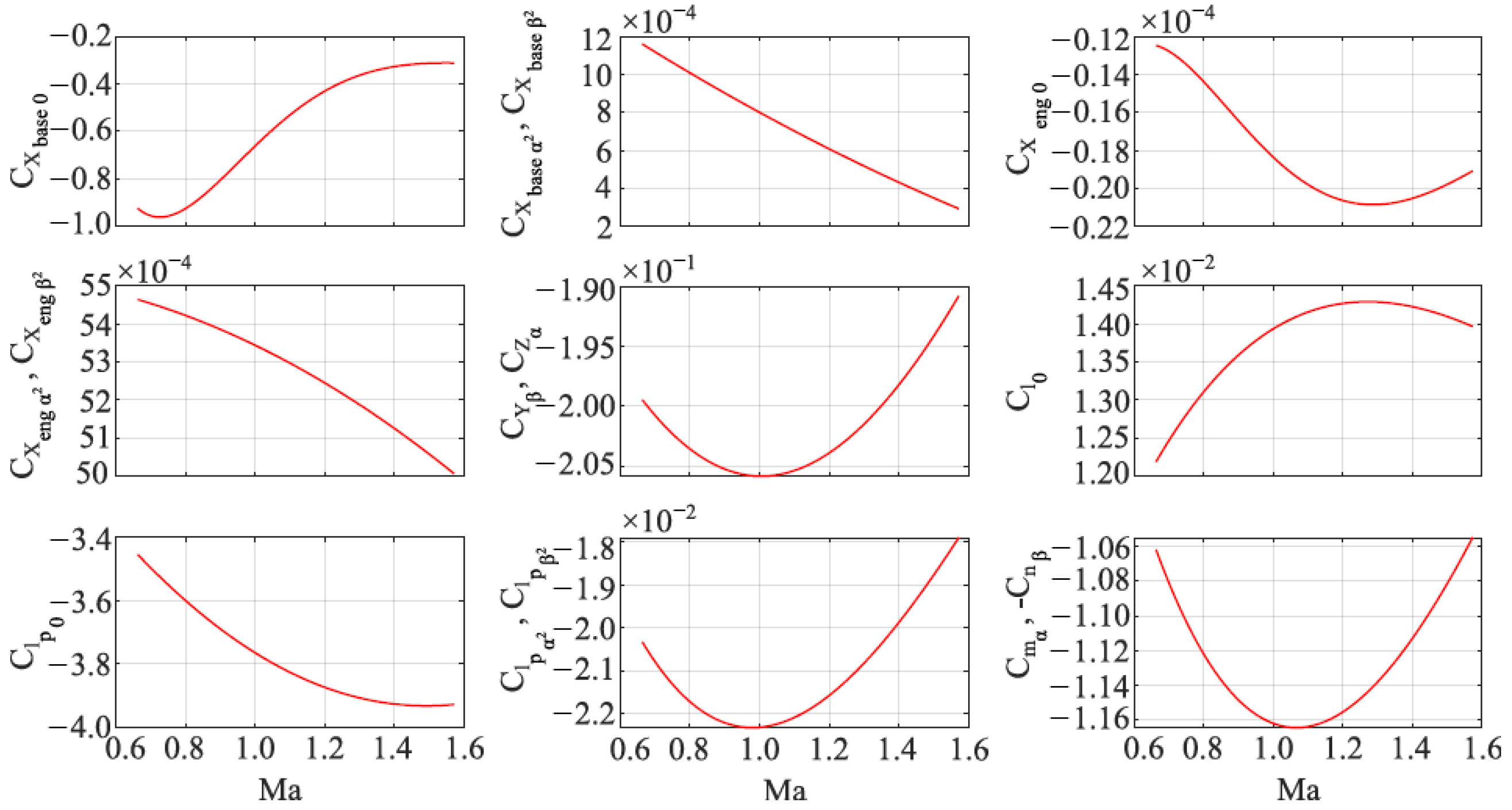
3.3.1. Aerodynamic Parameters Uncertainties
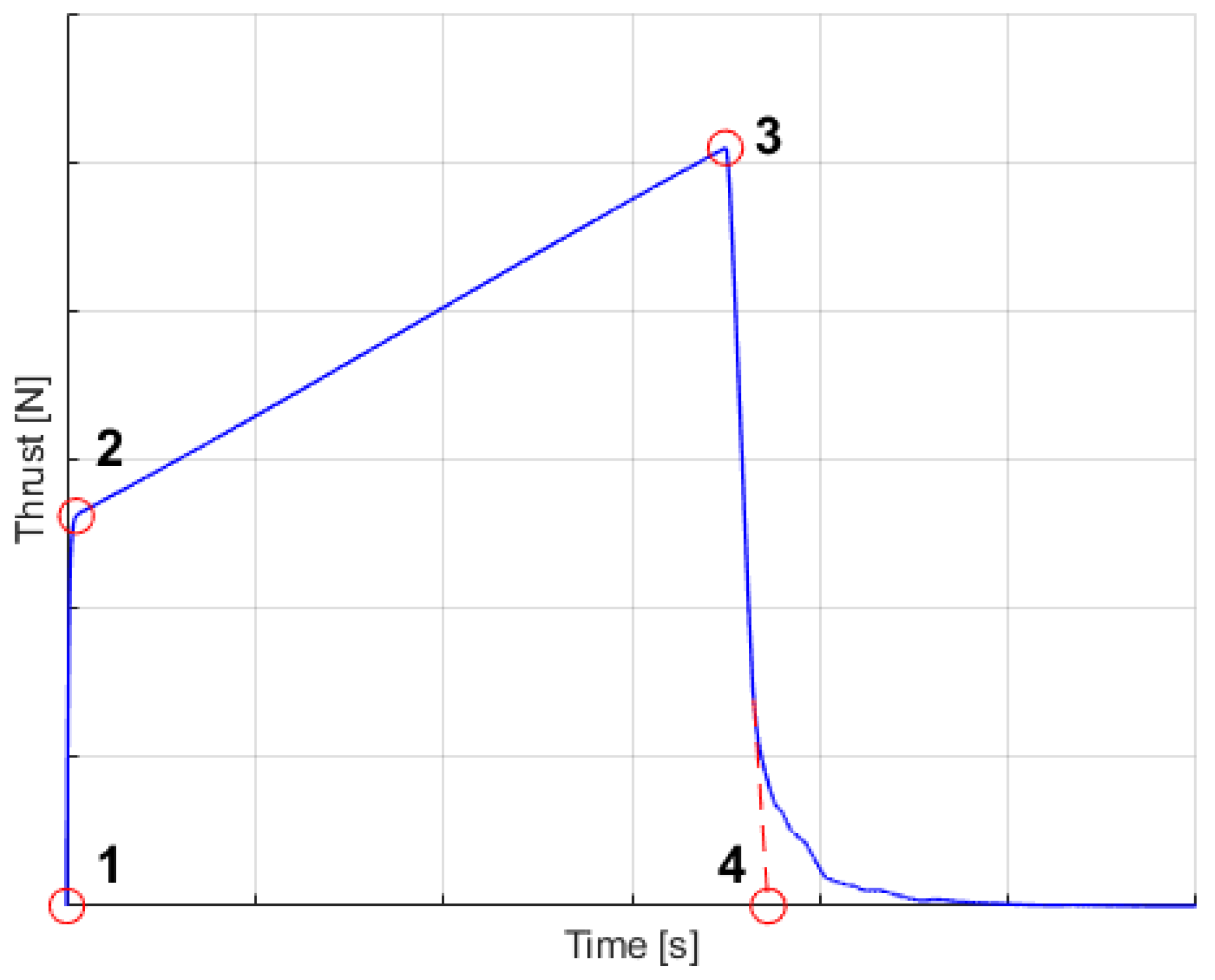
3.3.2. Thrust Curve Uncertainties
3.3.3. Initial Condition Uncertainties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.J.; Shen, Y. Three-Dimension H∞ Guidance Law and Capture Region Analysis. Trans. Aerosp. Electron. Syst. 2012, 48, 419–429. [Google Scholar]
- Budiyono, A.; Rachman, H. Proportional Guidance and CDM Control Sythesis for a Short-Range Homing Surface-to-Air Missile. J. Aerosp. Eng. 2012, 25, 168–177. [Google Scholar] [CrossRef]
- Guo, Y.; Li, X.; Zhang, H.; Cai, M.; He, F. Data-Driven Method for Impact Time Control Based on Proportional Navigation Guidance. J. Guid. Control. Dyn. 2020, 43, 955–966. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Optimal Control Based Guidance Law to Control Both Impact Time and Impact Angle. Aerosp. Sci. Technol. 2018, 84, 454–463. [Google Scholar] [CrossRef]
- He, S.; Lee, C.H. Gravity-Turn-Assisted Optimal Guidance Law. J. Guid. Control. Dyn. 2018, 41, 171–183. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Shin, H.S.; Tsourdos, A.; Lee, C.H. Energy-Optimal Waypoint-Following Guidance Considering Autopilot Dynamics. Trans. Aerosp. Electron. Syst. 2020, 56, 2701–2717. [Google Scholar] [CrossRef] [Green Version]
- Guelman, M.; Shinar, J. Optimal Guidance Law in the Plane. J. Guid. 1984, 7, 471–476. [Google Scholar] [CrossRef]
- Burchett, B.; Costello, M. Model Predictive Lateral Pulse Jet Control of an Atmospheric Rocket. J. Guid. Control. Dyn. 2002, 25, 860–867. [Google Scholar] [CrossRef]
- Gupta, S.K.; Saxena, S.; Singhal, A.; Ghosh, A.K. Trajectory Correction Flight Control System using Pulsejet on an Artillery Rocket. Def. Sci. J. 2008, 58, 15–33. [Google Scholar] [CrossRef] [Green Version]
- Głębocki, R. Guidance Impulse Algorithms for Air Bomb Control. Bull. Pol. Acad. Sci. 2012, 60, 825–833. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, Y.; Yang, S. Firing Control Optimization of Impulse Thrusters for Trajectory Correction Projectiles. Int. J. Aerosp. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Jitpraphai, T.; Costello, M. Dispersion Reduction of a Direct Fire Rocket Using Lateral Pulse Jets. J. Spacecr. Rocket. 2001, 38, 929–936. [Google Scholar] [CrossRef] [Green Version]
- Trzun, Z.; Vrdoljak, M.; Cajner, H. Statistical Analysis of Missile’s Trajectory Deviation Due to Production Errors. Proc. Appl. Math. Mech. 2020, 20, e202000059. [Google Scholar] [CrossRef]
- Trzun, Z.; Vrdoljak, M. Monte Carlo Simulation of Missile Trajectories Dispersion Due to Imperfectly Manufactured Warhead. In Proceedings of the 31st DAAAM International Symposium, Vienna, Austria, 21–24 October 2020; Katalinic, B., Ed.; DAAAM International: Vienna, Austria, 2020. [Google Scholar]
- Mingireanu, F. Trajectory Modelling of GRAD Rocket with Low-Cost Terminal Guidance Upgrade Coupled to Range Increase Through Step-Like Thrust-Curves. In Proceedings of the Aerospace Sciences & Aviation Technology, Cairo, Egypt, 28–30 May 2013. [Google Scholar]
- Głębocki, R.; Jacewicz, M. Parametric Study of Guidance of a 160-mm Projectile Steered with Lateral Thrusters. Aerospace 2020, 7, 61. [Google Scholar] [CrossRef]
- Głębocki, R.; Jacewicz, M. Sensitivity Analysis and Flight Tests Results for a Vertical Cold Launch Missile System. Aerospace 2020, 7, 168. [Google Scholar] [CrossRef]
- Figueroa-Gonzales, A.; Cacciatore, F.; Haya-Ramos, R. Landing Guidance Strategy of Space Rider. J. Spacecr. Rocket. 2021, 54, 1220–1231. [Google Scholar] [CrossRef]
- Mandić, S. Dispersion Reduction of Artillery Rocket Guided by Flight Path Steering Method. Aeronaut. J. 2016, 120, 435–456. [Google Scholar] [CrossRef]
- De Celis, R.; Cadarso, L.; Sánchez, J. Guidance and Control for High Dynamic Rotating Artillery Rockets. Aerosp. Sci. Technol. 2017, 64, 204–212. [Google Scholar] [CrossRef]
- Chen, S.Y.; Xia, Q.L. A Multicontrained Ascent Guidance Method for Solid Rocket-Powered Launch Vehicles. Int. J. Aerosp. Eng. 2016, 2016, 6346742. [Google Scholar] [CrossRef]
- Saghafi, F.; Khalilidelshad, M. A Monte Carlo Dispersion Analysis of a Rocket Flight Simulation Software. In Proceedings of the 17th European Simulation Multiconference, Nottingham, UK, 9–11 June 2003. [Google Scholar]
- Le, V.D.T.; Nguyen, A.T.; Nguyen, L.H.; Dang, N.T.; Tran, N.D. Effectiveness Analysis of Spin Motion in Reducing Dispersion of Sounding Rocket Flight due to Thrust Misalignment. Int. J. Aeronaut. Space Sci. 2021, 22, 1194–1208. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. U.S. Standard Atmosphere; Technical Report; Government Printing Office: Washington, DC, USA, 1976.
- National Imagery and Mapping Agency. Department of Defense World Geodetic System 1984: Its Definition, and Relationship with Local Geodetic Systems, TR8350.2; Technical Report; Department of Defense: Washington, DC, USA, 2000.
- Nizioł, J.; Radziszewski, B. Dynamika ukłAdów Mechanicznych; Komitet Mechaniki PAN: Warsaw, Poland, 2005. [Google Scholar]
- Etkin, B. Dynamics of Atmospheric Flight; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Rogers, R.M. Applied Mathematics in Integrated Navigation Systems; AIAA: Reston, VA, USA, 2000. [Google Scholar]
- Zipfel, P.H. Modeling and Simulation of Aerospace Vehicle Dynamics; AIAA: Reston, VA, USA, 2007. [Google Scholar]
- Allerton, D. Principles of Flight Simulation; John Wiley & Sons: Wiltshire, UK, 2009. [Google Scholar]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation. Dynamics, Controls Design, and Autonomous System; John Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- Winchenbach, G.L. Aerodynamic Testing in a Free-Flight Spark Range; Weapon Flight Mechanics Division: Valparaiso, FL, USA, 1997. [Google Scholar]
- Ozog, R.; Głębocki, R.; Jacewicz, M. Modified Trajectory Tracking Guidance for Artillery Rocket. J. Theor. Appl. Mech. 2020, 3, 611–622. [Google Scholar] [CrossRef]
- Zarchan, P. Tactical and Strategic Missile Guidance, 6th ed.; AIAA: Washington, DC, USA, 2012. [Google Scholar]
- Xiaobing, C.; Yicen, X.; Changying, R.; Zhengya, S. Simulation of Trajectory Correction for an Impulse Control Mortar Projectile with a Strapdown Laser Seeker. Appl. Mech. Mater. 2013, 367, 377–381. [Google Scholar]
- Lichota, P.; Jacewicz, M.; Szulczyk, J. Spinning Gasodynamic Projectile System Identification Experiment Design. Aircr. Eng. Aerosp. Technol. 2020, 92, 452–459. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef] [Green Version]

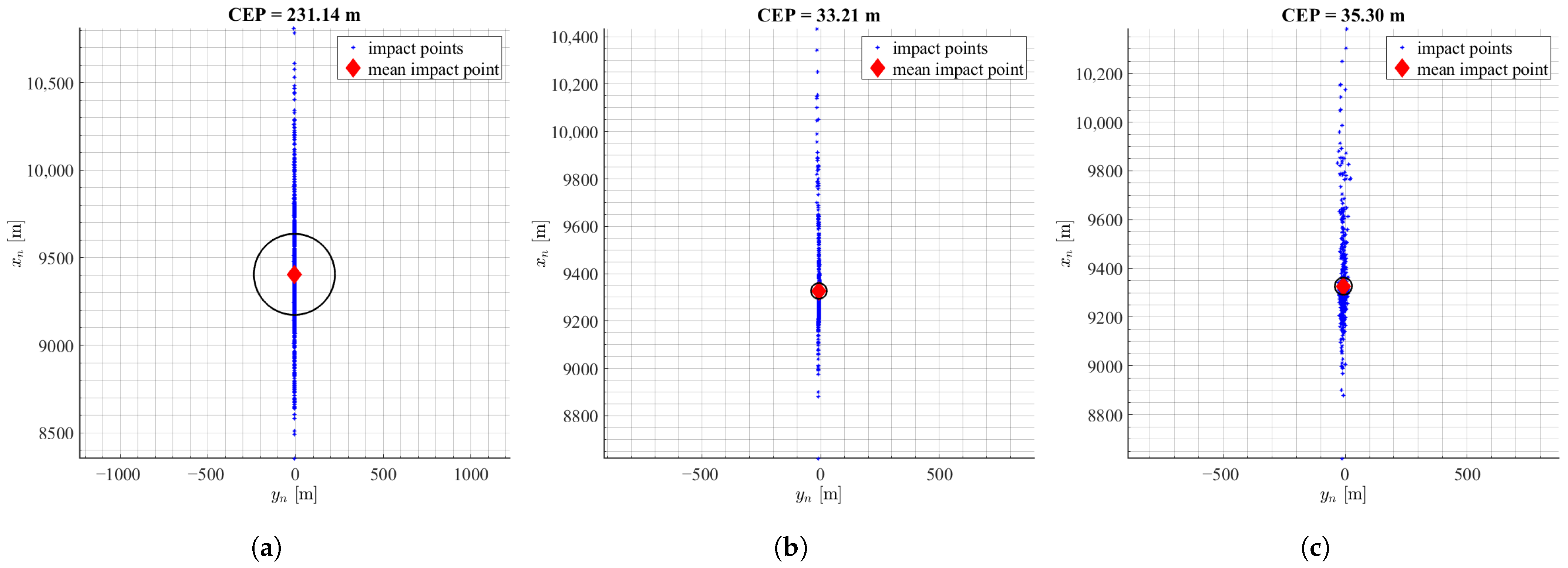
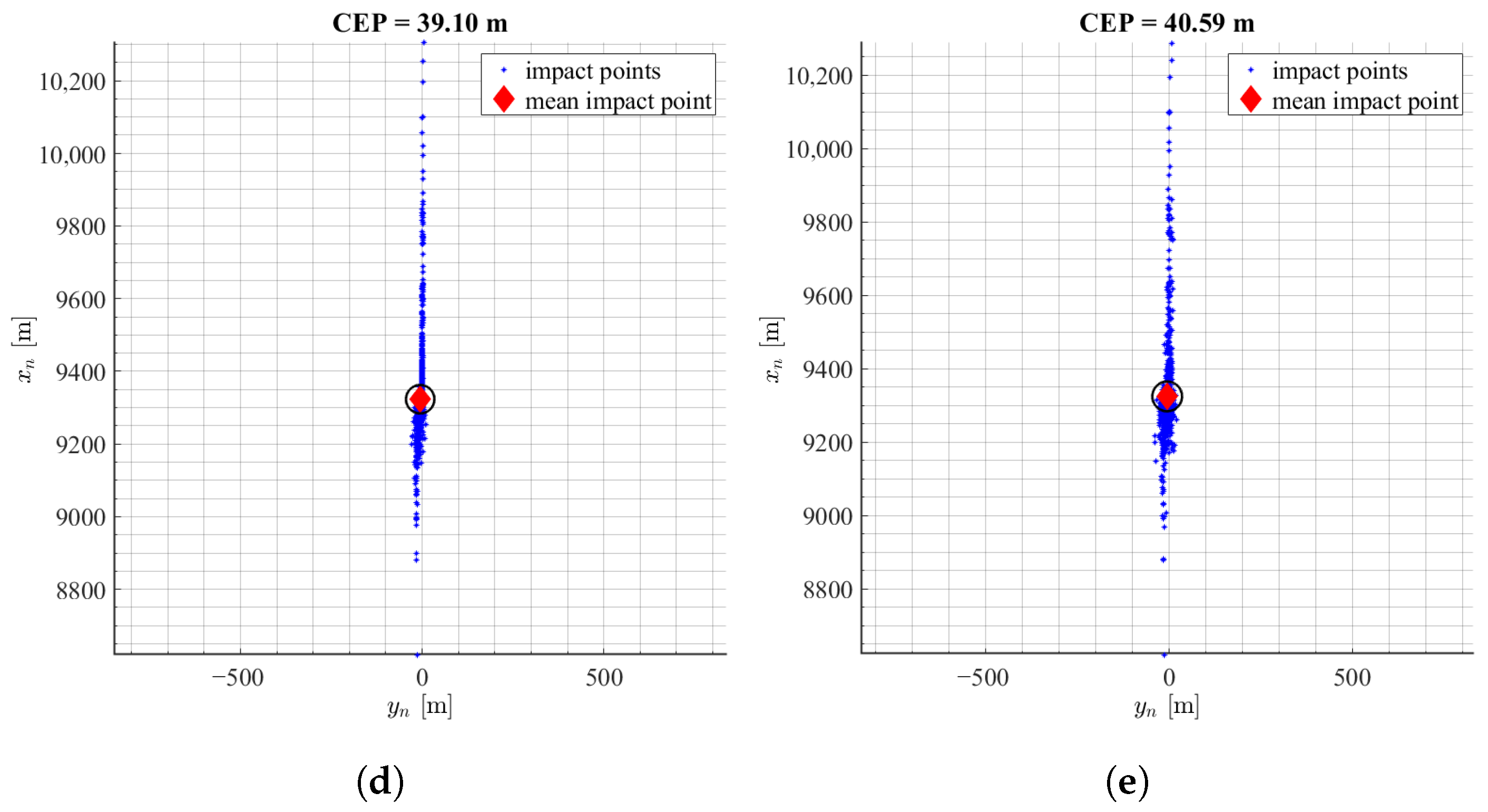


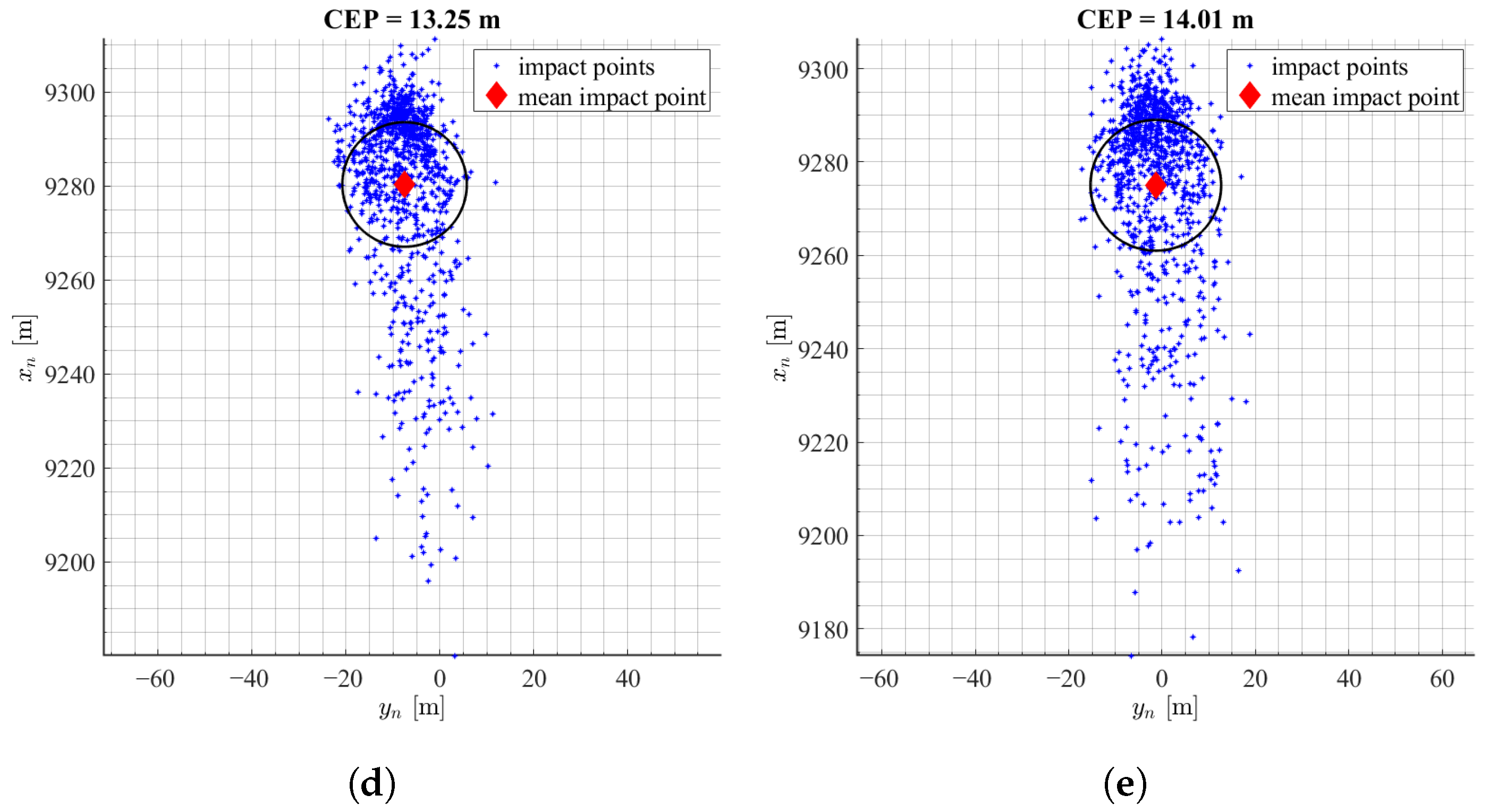
| Parameter | Value | Unit |
|---|---|---|
| diameter | 122 | mm |
| length | m | |
| initial mass | kg | |
| propellant mass | kg | |
| initial moment of inertia | kg·m | |
| final moment of inertia | kg·m | |
| initial moment of inertia | kg·m | |
| final moment of inertia | kg·m | |
| initial moment of inertia | kg·m | |
| final moment of inertia | kg·m | |
| maximum thrust | N | |
| average thrust | N | |
| burn time | s | |
| total impulse | 13,529 | N |
| correction thruster’s thrust | 200 | N |
| correction thruster’s burn time | s | |
| number of correction thrusters per layer | 8 | - |
| number of correction thrusters’ layers | 4 | - |
| Algorithm | [m] | [m] | [m] |
|---|---|---|---|
| None | |||
| mPNG | |||
| mPNG + IMU | |||
| MCCA | |||
| MCCA + IMU |
| Point | Value | Time t [s] | Thrust T [N] |
|---|---|---|---|
| 1 | min | 0 | 0 |
| 1 | max | 0 | 0 |
| 2 | min | 0 | 3600 |
| 2 | max | 4400 | |
| 3 | min | 6900 | |
| 3 | max | 8700 | |
| 4 | min | 0 | |
| 4 | max | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacewicz, M.; Lichota, P.; Miedziński, D.; Głębocki, R. Study of Model Uncertainties Influence on the Impact Point Dispersion for a Gasodynamicaly Controlled Projectile. Sensors 2022, 22, 3257. https://doi.org/10.3390/s22093257
Jacewicz M, Lichota P, Miedziński D, Głębocki R. Study of Model Uncertainties Influence on the Impact Point Dispersion for a Gasodynamicaly Controlled Projectile. Sensors. 2022; 22(9):3257. https://doi.org/10.3390/s22093257
Chicago/Turabian StyleJacewicz, Mariusz, Piotr Lichota, Dariusz Miedziński, and Robert Głębocki. 2022. "Study of Model Uncertainties Influence on the Impact Point Dispersion for a Gasodynamicaly Controlled Projectile" Sensors 22, no. 9: 3257. https://doi.org/10.3390/s22093257
APA StyleJacewicz, M., Lichota, P., Miedziński, D., & Głębocki, R. (2022). Study of Model Uncertainties Influence on the Impact Point Dispersion for a Gasodynamicaly Controlled Projectile. Sensors, 22(9), 3257. https://doi.org/10.3390/s22093257







