Predicting Soil Properties and Interpreting Vis-NIR Models from across Continental United States
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset Description and Extraction
2.2. Data Screening and Processing
2.3. Chemometric Modeling
3. Results and Discussion
3.1. Data Summary and Statistics
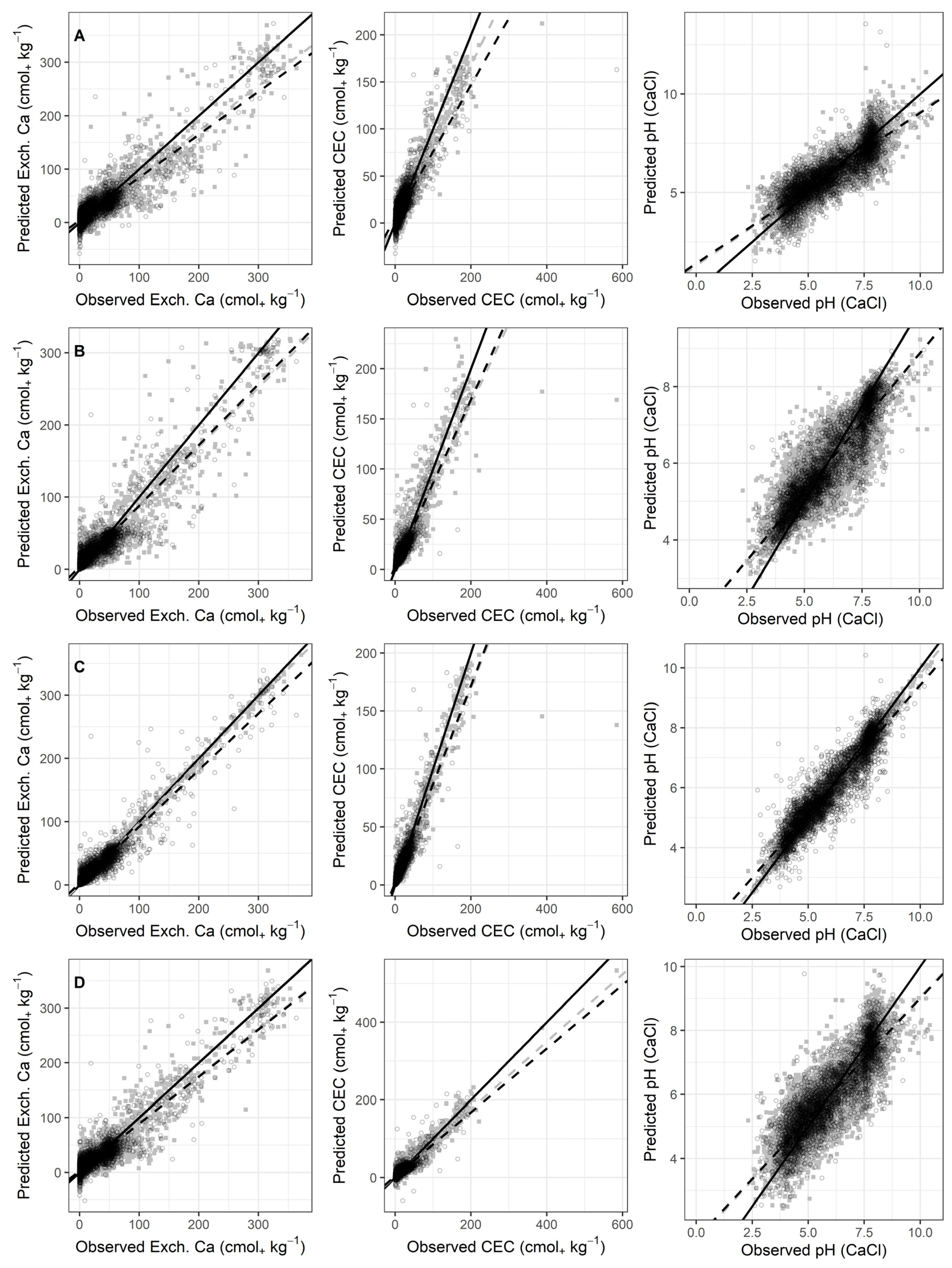
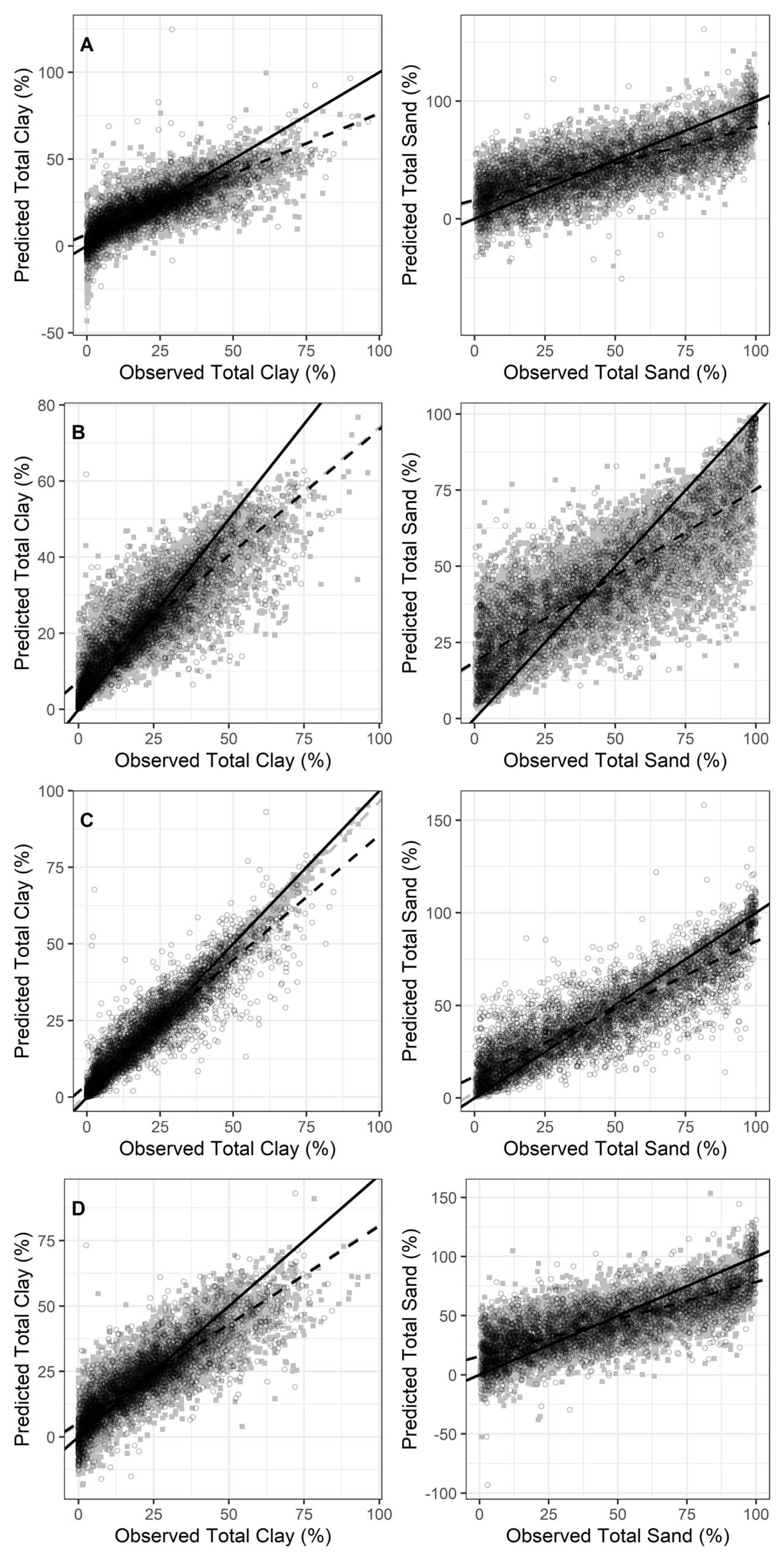
3.2. Prediction Results
3.3. Model Comparisons
3.4. Model Interpretations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shepherd, K.D.; Walsh, M.G. Infrared Spectroscopy—Enabling an Evidence-Based Diagnostic Surveillance Approach to Agricultural and Environmental Management in Developing Countries. J. Near Infrared Spectrosc. 2007, 15, 1–19. [Google Scholar] [CrossRef]
- Rossel, R.V.; McBratney, A.B. Diffuse Reflectance Spectroscopy as a Tool for Digital Soil Mapping. In Digital Soil Mapping with Limited Data; Springer: Berlin/Heidelberg, Germany, 2008; pp. 165–172. [Google Scholar]
- Du, C.; Zhou, J. Evaluation of Soil Fertility Using Infrared Spectroscopy: A Review. Environ. Chem. Lett. 2009, 7, 97–113. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; McBratney, A. Near-Infrared (NIR) and Mid-Infrared (MIR) Spectroscopic Techniques for Assessing the Amount of Carbon Stock in Soils—Critical Review and Research Perspectives. Soil Biol. Biochem. 2011, 43, 1398–1410. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; van Wesemael, B.; Aitkenhead, M.; Bachmann, M.; Barthès, B.; Ben Dor, E.; Brown, D.J.; Clairotte, M.; Csorba, A.; et al. Soil Spectroscopy: An Alternative to Wet Chemistry for Soil Monitoring. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2015; Volume 132, pp. 139–159. ISBN 978-0-12-802135-4. [Google Scholar]
- Dalal, R.C.; Henry, R.J. Simultaneous Determination of Moisture, Organic Carbon, and Total Nitrogen by near Infrared Reflectance Spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Banin, A. Near-Infrared Analysis as a Rapid Method to Simultaneously Evaluate Several Soil Properties. Soil Sci. Soc. Am. J. 1995, 59, 364–372. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-Infrared Reflectance Spectroscopy–Principal Components Regression Analyses of Soil Properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Bertrand, I.; Janik, L.J.; Holloway, R.E.; Armstrong, R.D.; McLaughlin, M.J. The Rapid Assessment of Concentrations and Solid Phase Associations of Macro and Micronutrients in Alkaline Soils by Mid-Infrared Diffuse Reflectance Spectroscopy. Aust. J. Soil Res. 2002, 40, 1339–1356. [Google Scholar] [CrossRef]
- Islam, K.; Singh, B.; McBratney, A. Simultaneous Estimation of Several Soil Properties by Ultra-Violet, Visible, and near-Infrared Reflectance Spectroscopy. Aust. J. Soil Res. 2003, 41, 1101–1114. [Google Scholar] [CrossRef]
- Bogrekci, I.; Lee, W.S. Spectral Soil Signatures and Sensing Phosphorus. Biosyst. Eng. 2005, 92, 527–533. [Google Scholar] [CrossRef]
- Brown, D.J.; Bricklemyer, R.S.; Miller, P.R. Validation Requirements for Diffuse Reflectance Soil Characterization Models with a Case Study of VNIR Soil C Prediction in Montana. Geoderma 2005, 129, 251–267. [Google Scholar] [CrossRef]
- Reeves, J.B.; Smith, D.B. The Potential of Mid- and near-Infrared Diffuse Reflectance Spectroscopy for Determining Major- and Trace-Element Concentrations in Soils from a Geochemical Survey of North America. Appl. Geochem. 2009, 24, 1472–1481. [Google Scholar] [CrossRef]
- Vašát, R.; Kodešová, R.; Borůvka, L.; Klement, A.; Jakšík, O.; Gholizadeh, A. Consideration of Peak Parameters Derived from Continuum-Removed Spectra to Predict Extractable Nutrients in Soils with Visible and near-Infrared Diffuse Reflectance Spectroscopy (VNIR-DRS). Geoderma 2014, 232–234, 208–218. [Google Scholar] [CrossRef]
- Bellino, A.; Colombo, C.; Iovieno, P.; Alfani, A.; Palumbo, G.; Baldantoni, D. Chemometric Technique Performances in Predicting Forest Soil Chemical and Biological Properties from UV-Vis-NIR Reflectance Spectra with Small, High Dimensional Datasets. Iforest-Biogeosci. For. 2016, 9, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Waruru, B.K.; Shepherd, K.D.; Ndegwa, G.M.; Kamoni, P.T.; Sila, A.M. Rapid Estimation of Soil Engineering Properties Using Diffuse Reflectance near Infrared Spectroscopy. Biosyst. Eng. 2014, 121, 177–185. [Google Scholar] [CrossRef] [Green Version]
- Awiti, A.O.; Walsh, M.G.; Shepherd, K.D.; Kinyamario, J. Soil Condition Classification Using Infrared Spectroscopy: A Proposition for Assessment of Soil Condition along a Tropical Forest-Cropland Chronosequence. Geoderma 2008, 143, 73–84. [Google Scholar] [CrossRef]
- Bikindou, F.D.A.; Gomat, H.Y.; Deleporte, P.; Bouillet, J.-P.; Moukini, R.; Mbedi, Y.; Ngouaka, E.; Brunet, D.; Sita, S.; Diazenza, J.-B.; et al. Are NIR Spectra Useful for Predicting Site Indices in Sandy Soils under Eucalyptus Stands in Republic of Congo? For. Ecol. Manag. 2012, 266, 126–137. [Google Scholar] [CrossRef]
- Camacho-Tamayo, J.H.; Rubiano, S.; Hurtado, S.; del Pilar, M. Near-Infrared (NIR) Diffuse Reflectance Spectroscopy for the Prediction of Carbon and Nitrogen in an Oxisol. Agron. Colomb. 2014, 32, 86–94. [Google Scholar] [CrossRef]
- Clingensmith, C.M.; Grunwald, S.; Wani, S.P. Evaluation of Calibration Subsetting and New Chemometric Methods on the Spectral Prediction of Key Soil Properties in a Data-Limited Environment: Evaluation of Subsetting and New Chemometric Methods. Eur. J. Soil Sci. 2019, 70, 107–126. [Google Scholar] [CrossRef] [Green Version]
- Cozzolino, D.; Morón, A. The Potential of Near-Infrared Reflectance Spectroscopy to Analyse Soil Chemical and Physical Characteristics. J. Agric. Sci. 2003, 140, 65–71. [Google Scholar] [CrossRef]
- Daniel, K.W.; Tripathi, N.K.; Honda, K. Artificial Neural Network Analysis of Laboratory and in Situ Spectra for the Estimation of Macronutrients in Soils of Lop Buri (Thailand). Aust. J. Soil Res. 2003, 41, 47–59. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the Soil Clay Content and Organic Matter by Means of Different Calibration Methods of Vis-NIR Diffuse Reflectance Spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef] [Green Version]
- Shepherd, K.D.; Walsh, M.G. Development of Reflectance Spectral Libraries for Characterization of Soil Properties. Soil Sci. Soc. Am. J. 2002, 66, 988–998. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Ben-Dor, E.; Theocharis, J.; Zalidis, G. A Memory-Based Learning Approach Utilizing Combined Spectral Sources and Geographical Proximity for Improved VIS-NIR-SWIR Soil Properties Estimation. Geoderma 2019, 340, 11–24. [Google Scholar] [CrossRef]
- Volkan Bilgili, A.; van Es, H.M.; Akbas, F.; Durak, A.; Hively, W.D. Visible-near Infrared Reflectance Spectroscopy for Assessment of Soil Properties in a Semi-Arid Area of Turkey. J. Arid Environ. 2010, 74, 229–238. [Google Scholar] [CrossRef]
- Grunwald, S.; Yu, C.; Xiong, X. Transferability and Scalability of Soil Total Carbon Prediction Models in Florida, USA. Pedosphere 2018, 28, 856–872. [Google Scholar] [CrossRef]
- Brown, D.J.; Shepherd, K.D.; Walsh, M.G.; Dewayne Mays, M.; Reinsch, T.G. Global Soil Characterization with VNIR Diffuse Reflectance Spectroscopy. Geoderma 2006, 132, 273–290. [Google Scholar] [CrossRef]
- Gogé, F.; Joffre, R.; Jolivet, C.; Ross, I.; Ranjard, L. Optimization Criteria in Sample Selection Step of Local Regression for Quantitative Analysis of Large Soil NIRS Database. Chemom. Intell. Lab. Syst. 2012, 110, 168–176. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Webster, R. Predicting Soil Properties from the Australian Soil Visible–near Infrared Spectroscopic Database. Eur. J. Soil Sci. 2012, 63, 848–860. [Google Scholar] [CrossRef]
- Castaldi, F.; Chabrillat, S.; Chartin, C.; Genot, V.; Jones, A.R.; van Wesemael, B. Estimation of Soil Organic Carbon in Arable Soil in Belgium and Luxembourg with the LUCAS Topsoil Database: Estimation of SOC with the LUCAS Topsoil Database. Eur. J. Soil Sci. 2018, 69, 592–603. [Google Scholar] [CrossRef]
- Guerrero, C.; Wetterlind, J.; Stenberg, B.; Mouazen, A.M.; Gabarrón-Galeote, M.A.; Ruiz-Sinoga, J.D.; Zornoza, R.; Viscarra Rossel, R.A. Do We Really Need Large Spectral Libraries for Local Scale SOC Assessment with NIR Spectroscopy? Soil Tillage Res. 2015, 155, 501–509. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, Q.; Wang, X.; Wu, Y.; Yang, X.; Liu, F. Estimation of Soil Organic Carbon and Total Nitrogen in Different Soil Layers Using VNIR Spectroscopy: Effects of Spiking on Model Applicability. Geoderma 2017, 293, 54–63. [Google Scholar] [CrossRef]
- Lacerda, M.; Demattê, J.; Sato, M.; Fongaro, C.; Gallo, B.; Souza, A. Tropical Texture Determination by Proximal Sensing Using a Regional Spectral Library and Its Relationship with Soil Classification. Remote Sens. 2016, 8, 701. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Shen, H.; Chen, S.; Zhao, X.; Biswas, A.; Jia, X.; Shi, Z.; Fang, J. Estimating Forest Soil Organic Carbon Content Using Vis-NIR Spectroscopy: Implications for Large-Scale Soil Carbon Spectroscopic Assessment. Geoderma 2019, 348, 37–44. [Google Scholar] [CrossRef]
- Moura-Bueno, J.M.; Dalmolin, R.S.D.; ten Caten, A.; Dotto, A.C.; Demattê, J.A.M. Stratification of a Local VIS-NIR-SWIR Spectral Library by Homogeneity Criteria Yields More Accurate Soil Organic Carbon Predictions. Geoderma 2019, 337, 565–581. [Google Scholar] [CrossRef]
- Ogen, Y.; Zaluda, J.; Francos, N.; Goldshleger, N.; Ben-Dor, E. Cluster-Based Spectral Models for a Robust Assessment of Soil Properties. Geoderma 2019, 340, 175–184. [Google Scholar] [CrossRef]
- Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of Soil Organic Carbon at the European Scale by Visible and near Infrared Reflectance Spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar] [CrossRef] [PubMed]
- Tsakiridis, N.L.; Tziolas, N.V.; Theocharis, J.B.; Zalidis, G.C. A Genetic Algorithm-based Stacking Algorithm for Predicting Soil Organic Matter from Vis–NIR Spectral Data. Eur. J. Soil Sci. 2019, 70, 578–590. [Google Scholar] [CrossRef]
- Tsakiridis, N.L.; Keramaris, K.D.; Theocharis, J.B.; Zalidis, G.C. Simultaneous Prediction of Soil Properties from VNIR-SWIR Spectra Using a Localized Multi-Channel 1-D Convolutional Neural Network. Geoderma 2020, 367, 114208. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Wang, R.; Wang, H. Combination of Convolutional Neural Networks and Recurrent Neural Networks for Predicting Soil Properties Using Vis–NIR Spectroscopy. Geoderma 2020, 380, 114616. [Google Scholar] [CrossRef]
- Demattê, J.A.M.; Dotto, A.C.; Paiva, A.F.S.; Sato, M.V.; Dalmolin, R.S.D.; de Araújo, M.d.S.B.; da Silva, E.B.; Nanni, M.R.; ten Caten, A.; Noronha, N.C.; et al. The Brazilian Soil Spectral Library (BSSL): A General View, Application and Challenges. Geoderma 2019, 354, 113793. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V. A Global Spectral Library to Characterize the World’s Soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef] [Green Version]
- Dangal, S.; Sanderman, J.; Wills, S.; Ramirez-Lopez, L. Accurate and Precise Prediction of Soil Properties from a Large Mid-Infrared Spectral Library. Soil Syst. 2019, 3, 11. [Google Scholar] [CrossRef] [Green Version]
- Ng, W.; Minasny, B.; Montazerolghaem, M.; Padarian, J.; Ferguson, R.; Bailey, S.; McBratney, A.B. Convolutional Neural Network for Simultaneous Prediction of Several Soil Properties Using Visible/near-Infrared, Mid-Infrared, and Their Combined Spectra. Geoderma 2019, 352, 251–267. [Google Scholar] [CrossRef]
- Sanderman, J.; Savage, K.; Dangal, S.R.S. Mid-infrared Spectroscopy for Prediction of Soil Health Indicators in the United States. Soil Sci. Soc. Am. J. 2020, 84, 251–261. [Google Scholar] [CrossRef] [Green Version]
- Seybold, C.A.; Ferguson, R.; Wysocki, D.; Bailey, S.; Anderson, J.; Nester, B.; Schoeneberger, P.; Wills, S.; Libohova, Z.; Hoover, D.; et al. Application of Mid-Infrared Spectroscopy in Soil Survey. Soil Sci. Soc. Am. J. 2019, 83, 1746–1759. [Google Scholar] [CrossRef]
- Wijewardane, N.K.; Ge, Y.; Sanderman, J.; Ferguson, R. Fine Grinding Is Needed to Maintain the High Accuracy of Mid-infrared Diffuse Reflectance Spectroscopy for Soil Property Estimation. Soil Sci. Soc. Am. J. 2021, 85, 263–272. [Google Scholar] [CrossRef]
- Sequeira, C.H.; Wills, S.A.; Grunwald, S.; Ferguson, R.R.; Benham, E.C.; West, L.T. Development and Update Process of VNIR-Based Models Built to Predict Soil Organic Carbon. Soil Sci. Soc. Am. J. 2014, 78, 903–913. [Google Scholar] [CrossRef] [Green Version]
- Wijewardane, N.K.; Ge, Y.; Wills, S.; Loecke, T. Prediction of Soil Carbon in the Conterminous United States: Visible and near Infrared Reflectance Spectroscopy Analysis of the Rapid Carbon Assessment Project. Soil Sci. Soc. Am. J. 2016, 80, 973–982. [Google Scholar] [CrossRef] [Green Version]
- Coutinho, M.A.; Alari, F.D.O.; Ferreira, M.M.; do Amaral, L.R. Influence of Soil Sample Preparation on the Quantification of NPK Content via Spectroscopy. Geoderma 2019, 338, 401–409. [Google Scholar] [CrossRef]
- McDowell, M.L.; Bruland, G.L.; Deenik, J.L.; Grunwald, S.; Knox, N.M. Soil Total Carbon Analysis in Hawaiian Soils with Visible, near-Infrared and Mid-Infrared Diffuse Reflectance Spectroscopy. Geoderma 2012, 189–190, 312–320. [Google Scholar] [CrossRef]
- Shao, Y.; He, Y. Nitrogen, Phosphorus, and Potassium Prediction in Soils, Using Infrared Spectroscopy. Soil Res. 2011, 49, 166–172. [Google Scholar] [CrossRef]
- Van Groenigen, J.W.; Mutters, C.S.; Horwath, W.R.; Van Kessel, C. NIR and DRIFT-MIR Spectrometry of Soils for Predicting Soil and Crop Parameters in a Flooded Field. Plant Soil 2003, 250, 155–165. [Google Scholar] [CrossRef]
- Xie, H.T.; Yang, X.M.; Drury, C.F.; Yang, J.Y.; Zhang, X.D. Predicting Soil Organic Carbon and Total Nitrogen Using Mid- and near-Infrared Spectra for Brookston Clay Loam Soil in Southwestern Ontario, Canada. Can. J. Soil. Sci. 2011, 91, 53–63. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, X.; Drury, C.; Chantigny, M.; Gregorich, E.; Miller, J.; Bittman, S.; Reynolds, D.; Yang, J. Infrared Spectroscopy Prediction of Organic Carbon and Total Nitrogen in Soil and Particulate Organic Matter from Diverse Canadian Agricultural Regions. CJSS 2017, 98, 77–90. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Gong, P.; Amundson, R. Pedodiversity in the United States of America. Geoderma 2003, 117, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Veum, K.S.; Sudduth, K.A.; Kremer, R.J.; Kitchen, N.R. Estimating a Soil Quality Index with VNIR Reflectance Spectroscopy. Soil Sci. Soc. Am. J. 2015, 79, 637. [Google Scholar] [CrossRef]
- Xia, Y.; Ugarte, C.M.; Guan, K.; Pentrak, M.; Wander, M.M. Developing Near- and Mid-Infrared Spectroscopy Analysis Methods for Rapid Assessment of Soil Quality in Illinois. Soil Sci. Soc. Am. J. 2018, 82, 1415–1427. [Google Scholar] [CrossRef] [Green Version]
- Soil Survey Staff. Kellogg Soil Survey Laboratory Methods Manual. Soil Survey Investigations Report No 42; Version 5.0; U.S. Department of Agriculture, Natural Resources Conservation Service: Washington, DC, USA, 2014.
- Savitzky, A.; Golay, M.J. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-Regression: A Basic Tool of Chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings of the AI’92; Adams, S., Ed.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
- Friedman, J.H.; Roosen, C.B. An Introduction to Multivariate Adaptive Regression Splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Soil Survey Staff. Keys to Soil Taxonomy; U.S. Department of Agriculture, Natural Resources Conservation Service: Lincoln, NE, USA, 2014.
- Orgiazzi, A.; Ballabio, C.; Panagos, P.; Jones, A.; Fernández-Ugalde, O. LUCAS Soil, the Largest Expandable Soil Dataset for Europe: A Review. Eur. J. Soil Sci. 2018, 69, 140–153. [Google Scholar] [CrossRef] [Green Version]
- Mevik, B.-H. VIP.R: Implementation of VIP (Variable Importance in Projection) for the “pls” Package. Available online: http://mevik.net/work/software/VIP.R (accessed on 22 February 2017).
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Soft. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Clark, R.N. Chapter 1: Spectroscopy of Rocks and Minerals, and Principles of Spectroscopy. In Remote Sensing for the Earth Sciences; Rencz, A.N., Ed.; Manual of Remote Sensing; John Wiley & Sons: New York, NY, USA, 1999; Volume 3, pp. 3–58. [Google Scholar]
- Bishop, J.L.; Lane, M.D.; Dyar, M.D.; King, S.J.; Brown, A.J.; Swayze, G.A. Spectral Properties of Ca-Sulfates: Gypsum, Bassanite, and Anhydrite. Am. Mineral. 2014, 99, 2105–2115. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Irons, J.R.; Epema, G.F. Soil Reflectance. In Manual of Remote Sensing; Rencz, A.N., Ryerson, R.A., Eds.; J. Wiley: New York, NY, USA, 1999; Volume 3, pp. 111–188. ISBN 978-0-471-29406-1. [Google Scholar]
- Knox, N.M.; Skidmore, A.K.; Schlerf, M.; de Boer, W.F.; van Wieren, S.E.; van der Waal, C.; Prins, H.H.T.; Slotow, R. Nitrogen Prediction in Grasses: Effect of Bandwidth and Plant Material State on Absorption Feature Selection. Int. J. Remote Sens. 2010, 31, 691–704. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Zheng, L.; Qin, Q.; Lee, W.S. Spectral Features Extraction for Estimation of Soil Total Nitrogen Content Based on Modified Ant Colony Optimization Algorithm. Geoderma 2019, 333, 23–34. [Google Scholar] [CrossRef]
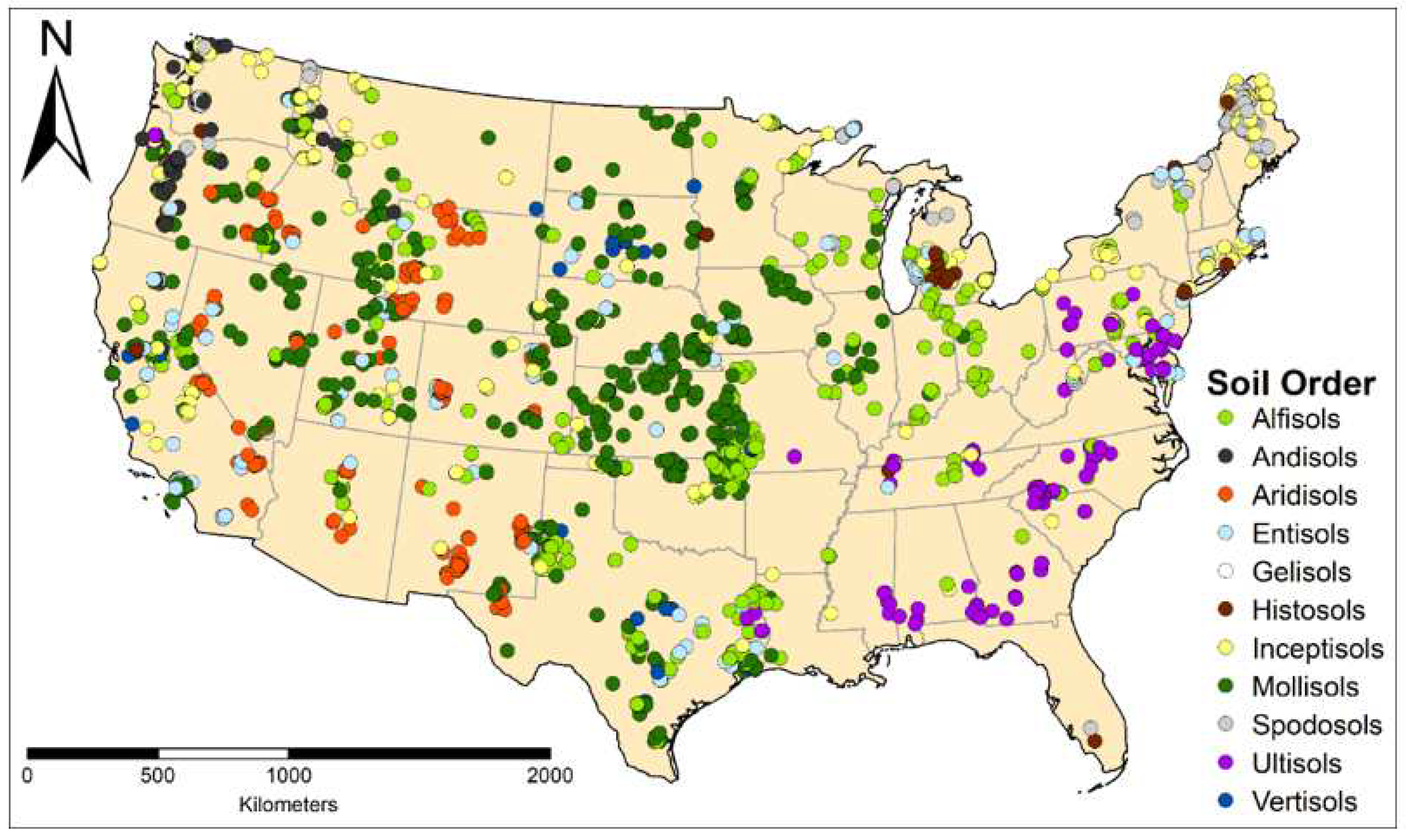

| Soil Order | n | % | Suborders Represented |
|---|---|---|---|
| Alfisols | 418 | 16.0 | 5/5 |
| Andisols | 90 | 3.4 | 6/8 |
| Aridisols | 202 | 7.7 | 7/7 |
| Entisols | 236 | 9.0 | 6/6 |
| Gelisols | 25 | 1.0 | 3/3 |
| Histosols | 76 | 2.9 | 5/5 |
| Inceptisols | 323 | 12.3 | 7/7 |
| Mollisols | 838 | 32.0 | 6/8 |
| Oxisols | 0 | 0.0 | 0/5 |
| Spodosols | 174 | 6.7 | 4/5 |
| Ultisols | 194 | 7.4 | 3/5 |
| Vertisols | 42 | 1.6 | 5/6 |
| Total | 2618 | 100 | 57/70 |
| Horizon Designation | Dominant Horizon | Subordinate Horizon |
|---|---|---|
| O | 564 | 40 |
| L | 6 | - |
| A | 3695 | 193 |
| E | 551 | 297 |
| B | 7281 | 379 |
| C | 2328 | 807 |
| R | 3 | 1 |
| Soil Properties Procedure Codes | Min. | Q1 | Mean | Median | Q3 | Max. | Range | IQR | SD | CV | Skew. | Kurt. | NAs | Zeros |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil Organic C (%) Codes: 4H2a and 4E1a1a1a1 | 0.00 | 0.18 | 2.50 | 0.52 | 1.46 | 57.2 | 57.2 | 1.28 | 7.42 | 2.97 | 5.15 | 30.4 | 1 | 288 |
| Total N (%) Code: 4H2a | 0.00 | 0.03 | 0.16 | 0.07 | 0.14 | 4.17 | 4.17 | 0.12 | 0.35 | 2.24 | 5.51 | 38.3 | 10 | 1156 |
| Total S (%) Code: 4H2a | 0.00 | 0.00 | 0.17 | 0.01 | 0.02 | 25.2 | 25.2 | 0.02 | 1.24 | 7.18 | 11.5 | 147 | 10 | 4562 |
| Total Clay (%) Code: 3A1a1a | 0.00 | 7.90 | 21.4 | 19.6 | 31.5 | 96.1 | 96.1 | 23.5 | 15.9 | 0.70 | 0.70 | 3.20 | 341 | 231 |
| Sand (%) Code: 3A1a1a | 0.20 | 16.2 | 42.6 | 38.7 | 66.2 | 100 | 99.8 | 50.0 | 29.4 | 0.70 | 0.30 | 1.90 | 341 | 0 |
| Exch. Ca (cmol+ kg−1) Code: 4B1a2a | 0.00 | 2.10 | 22.7 | 10.5 | 27.4 | 372 | 372 | 25.3 | 38.7 | 1.70 | 4.50 | 29.7 | 146 | 858 |
| CEC (cmol+ kg−1) Code: 4B1a2a | 0.00 | 6.40 | 17.3 | 13.3 | 21.8 | 585 | 585 | 15.4 | 20.6 | 1.20 | 5.90 | 75.3 | 146 | 10 |
| pH 1:2 0.01M CaCl2 Code: 4C1a2a2 | 2.30 | 4.80 | 6.00 | 5.80 | 7.4 | 10.5 | 8.20 | 2.60 | 1.40 | 0.20 | 0.20 | 1.90 | 173 | 0 |
| Property | Method | Pretreat. | N * | CV | Validation | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | Bias | RMSE | RPD | RPIQ | ||||
| SOC (%) | PLSR | LOG | 148 | 0.88 | 2.59 | 0.88 | 0.03 | 2.48 | 2.90 | 0.53 |
| RF | SG-1d | 0.94 | 1.78 | 0.95 | 0.02 | 1.68 | 4.24 | 0.79 | ||
| Cubist | CR-S | 0.94 | 1.82 | 0.95 | 0.00 | 1.62 | 4.39 | 0.81 | ||
| MARS | SG-1d | 26 | 0.92 | 2.09 | 0.91 | −0.05 | 2.10 | 3.40 | 0.63 | |
| TN (%) | PLSR | LOG | 197 | 0.83 | 0.145 | 0.84 | 0.00 | 0.14 | 2.50 | 0.76 |
| RF | SG-1d | 0.91 | 0.110 | 0.89 | 0.01 | 0.11 | 2.98 | 1.05 | ||
| Cubist | CR-D | 0.92 | 0.100 | 0.91 | 0.00 | 0.09 | 3.32 | 1.16 | ||
| MARS | CR-D | 43 | 0.86 | 0.135 | 0.84 | 0.00 | 0.13 | 2.44 | 0.85 | |
| TS (%) | PLSR | SNV | 48 | 0.93 | 0.310 | 0.87 | 0.00 | 0.37 | 2.79 | 0.06 |
| RF | SG-1d | 0.91 | 0.317 | 0.96 | 0.01 | 0.25 | 5.13 | 0.09 | ||
| Cubist | CR-D | 0.92 | 0.260 | 0.96 | 0.00 | 0.25 | 5.28 | 0.09 | ||
| MARS | CR-D | 30 | 0.89 | 0.348 | 0.95 | 0.00 | 0.31 | 4.22 | 0.07 | |
| Clay (%) | PLSR | SNV | 58 | 0.65 | 9.35 | 0.67 | 0.17 | 9.03 | 1.75 | 2.58 |
| RF | SG-1d | 0.76 | 7.80 | 0.77 | 0.01 | 7.97 | 2.01 | 3.01 | ||
| Cubist | SNV | 0.85 | 6.23 | 0.84 | 0.15 | 6.35 | 2.53 | 3.78 | ||
| MARS | SG-1d | 50 | 0.73 | 8.14 | 0.74 | 0.10 | 8.19 | 1.96 | 2.93 | |
| Sand (%) | PLSR | SG-S | 158 | 0.56 | 19.5 | 0.57 | −0.14 | 19.30 | 1.51 | 2.54 |
| RF | SG-1d | 0.69 | 16.3 | 0.72 | 0.15 | 16.61 | 1.78 | 3.04 | ||
| Cubist | SNV | 0.75 | 14.8 | 0.75 | −0.01 | 14.68 | 2.02 | 3.44 | ||
| MARS | SG-1d | 50 | 0.60 | 18.6 | 0.61 | −0.19 | 18.42 | 1.61 | 2.74 | |
| Caex (cmol+ kg−1) | PLSR | CR-D | 72 | 0.82 | 16.2 | 0.79 | 0.03 | 16.23 | 2.19 | 1.51 |
| RF | SG-1d | 0.87 | 13.2 | 0.88 | 0.35 | 13.79 | 2.86 | 1.84 | ||
| Cubist | CR-D | 0.90 | 11.4 | 0.91 | 0.28 | 12.08 | 3.27 | 2.10 | ||
| MARS | SG-1d | 45 | 0.83 | 15.0 | 0.86 | −0.24 | 15.00 | 2.63 | 1.69 | |
| CEC (cmol+ kg−1) | PLSR | LOG | 159 | 0.74 | 10.4 | 0.70 | 0.00 | 11.66 | 1.84 | 1.30 |
| RF | SG-1d | 0.84 | 8.71 | 0.84 | 0.19 | 7.38 | 2.49 | 2.12 | ||
| Cubist | SNV | 0.86 | 7.98 | 0.86 | −0.20 | 6.92 | 2.66 | 2.26 | ||
| MARS | SG-1d | 50 | 0.73 | 11.6 | 0.76 | 0.06 | 9.19 | 2.00 | 1.70 | |
| pH | PLSR | SG-2d | 71 | 0.74 | 0.715 | 0.73 | 0.00 | 0.74 | 1.91 | 3.55 |
| RF | SG-1d | 0.80 | 0.633 | 0.82 | 0.00 | 0.62 | 2.29 | 4.28 | ||
| Cubist | CR-D | 0.86 | 0.524 | 0.87 | 0.00 | 0.52 | 2.75 | 5.15 | ||
| MARS | SG-2d | 50 | 0.74 | 0.719 | 0.75 | 0.01 | 0.71 | 2.01 | 3.76 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clingensmith, C.M.; Grunwald, S. Predicting Soil Properties and Interpreting Vis-NIR Models from across Continental United States. Sensors 2022, 22, 3187. https://doi.org/10.3390/s22093187
Clingensmith CM, Grunwald S. Predicting Soil Properties and Interpreting Vis-NIR Models from across Continental United States. Sensors. 2022; 22(9):3187. https://doi.org/10.3390/s22093187
Chicago/Turabian StyleClingensmith, Christopher M., and Sabine Grunwald. 2022. "Predicting Soil Properties and Interpreting Vis-NIR Models from across Continental United States" Sensors 22, no. 9: 3187. https://doi.org/10.3390/s22093187
APA StyleClingensmith, C. M., & Grunwald, S. (2022). Predicting Soil Properties and Interpreting Vis-NIR Models from across Continental United States. Sensors, 22(9), 3187. https://doi.org/10.3390/s22093187







