Evaluation of Creep Behavior of Soft Soils by Utilizing Multisensor Data Combined with Machine Learning
Abstract
:1. Introduction
2. Methods and Methodology of Soil Creep Prediction Based on Multisensor Data
2.1. Constitutive Law Used for Numerical Modeling
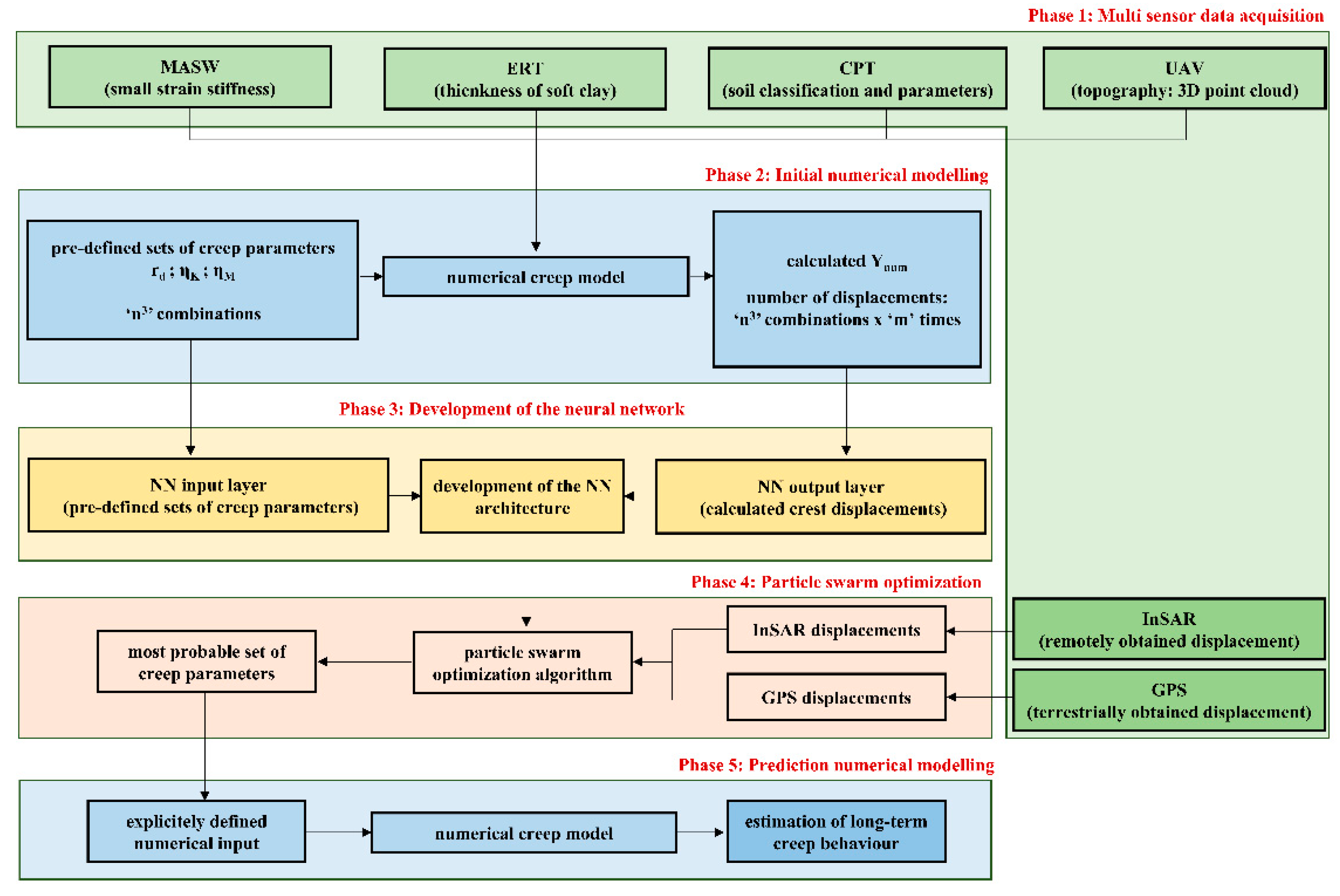
2.2. Methodology Phases
2.3. Development of NetCREEP Neural Network and PSO Optimization
3. Investigation Methods and Multisensor Data
3.1. Remote Sensing Data Acquisition
3.1.1. Unmanned Aerial Vehicle (UAV) for Terrain Topography
3.1.2. Satellite Monitoring of Ground Displacements
3.2. Geophysical Near-Surface Nondestructive Methods
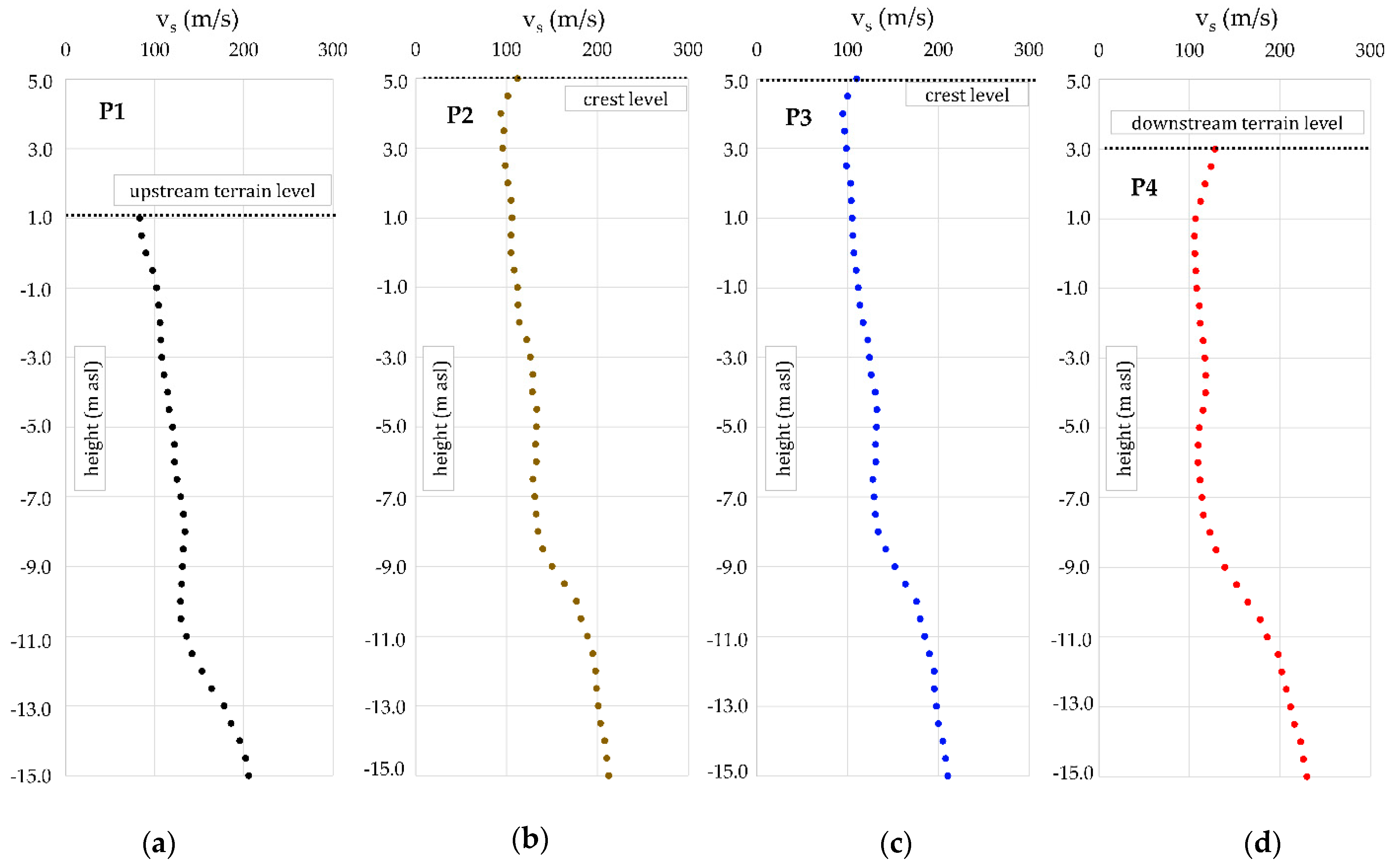
3.2.1. MASW for Determination of a Small-Strain Soil Stiffness
3.2.2. Electrical Resistivity Tomography (ERT) for Determination of Deposit Thicknesses
3.2.3. Cone Penetration Testing (CPT) for Soil Classification and Determination of Its Physical-Mechanical Parameters
4. Validation of the Methodology—Oostmolendijk Embankment
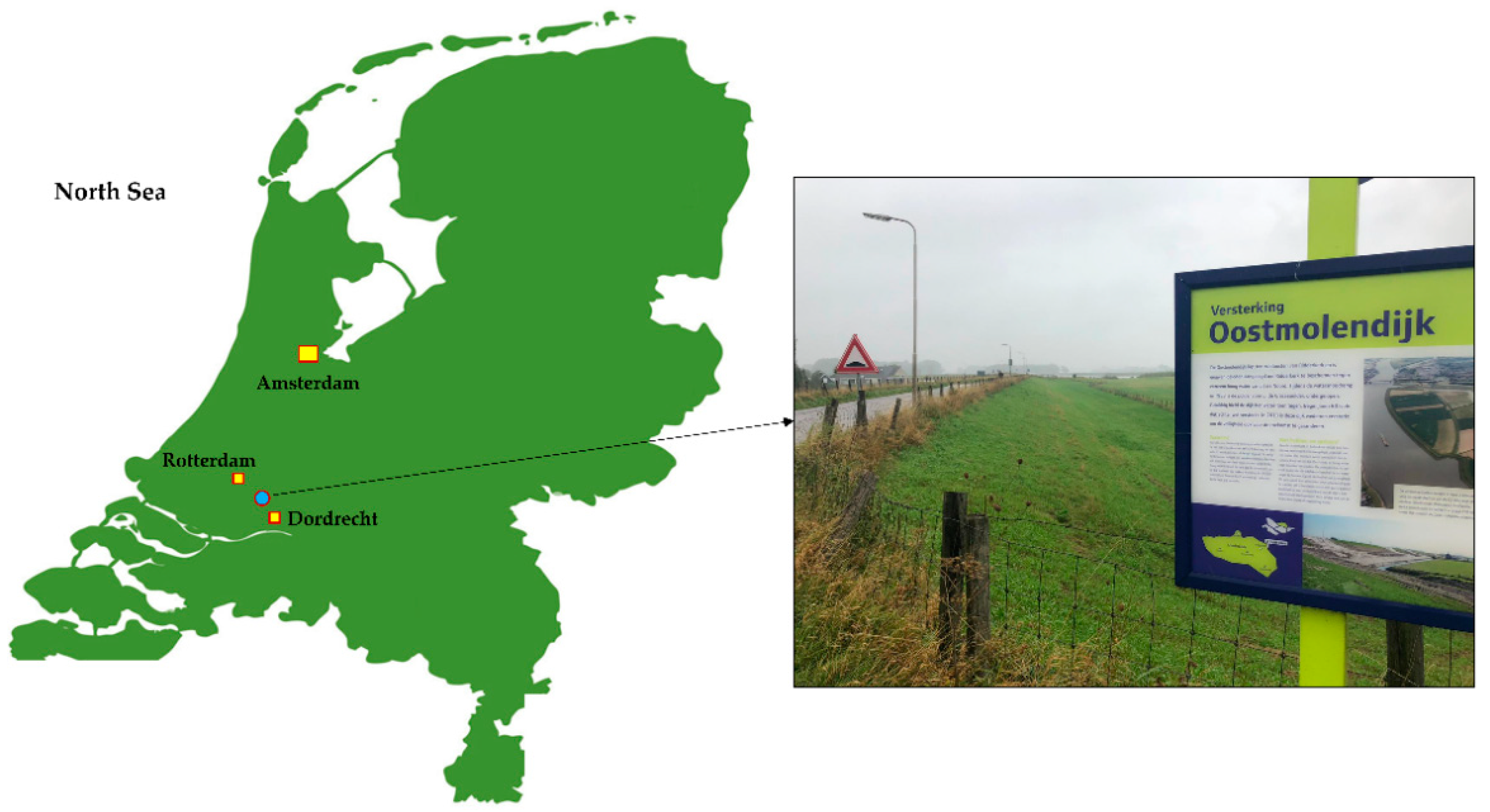
4.1. Description of the Case Study Area
4.2. Conducted Investigations and Obtained Results
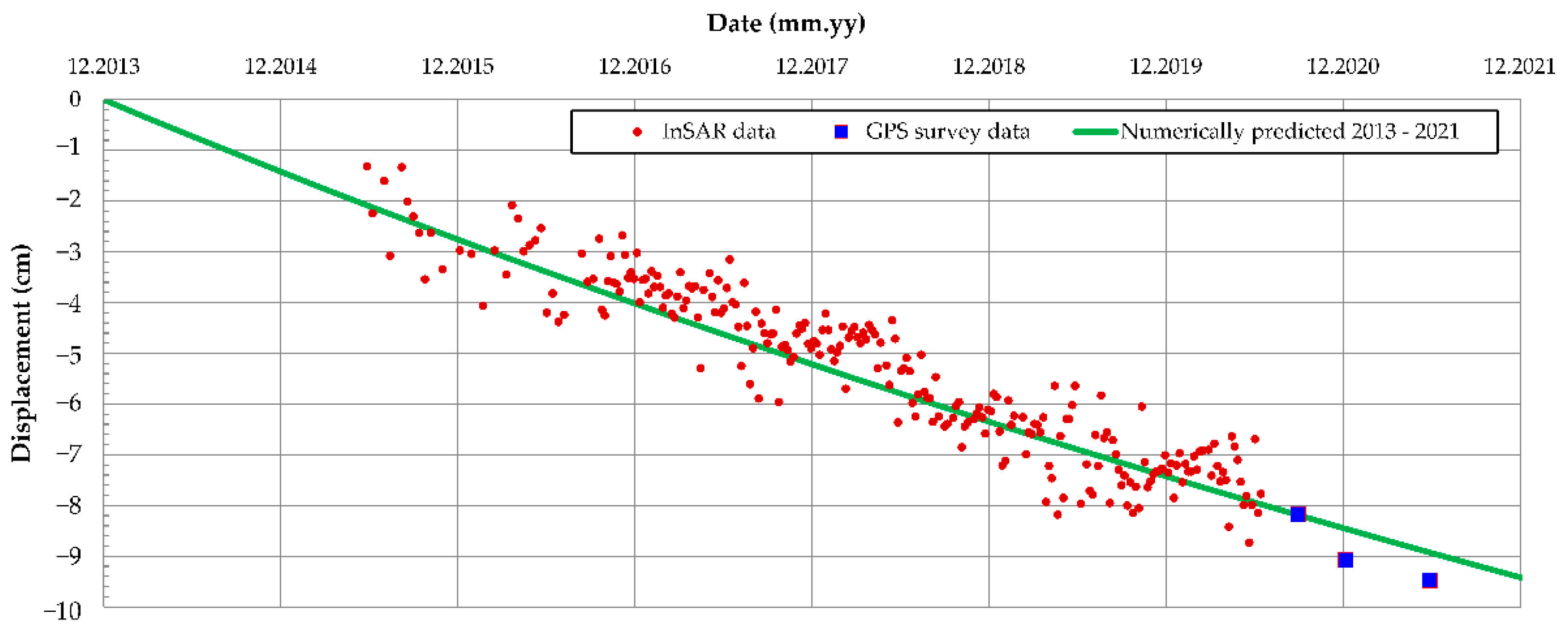
4.3. Long-Term Monitoring Data
4.4. Results and Discussion
4.4.1. Implementation of NetCREEP and PSO
4.4.2. Prediction of Oostmolendijk Long-Term Behavior
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Terzaghi, K. Erdbaumechanik auf Bodenphysikalischer Grundlage; Leipzig, U., Wien, F., Eds.; Deuticke: Vienna, Austria, 1925. (In German) [Google Scholar]
- Buisman, A.S.K. Results of Long Duration Settlement Tests. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Cambridge, MA, USA, 22–26 June 1936; Graduate School of Engineering, Harvard University: Cambridge, MA, USA, 1936; Volume 1, pp. 103–106. [Google Scholar]
- Bjerrum, L. Problems of Soil Mechanics and Construction on Soft Clays. In State-of-the-Art-Paper to Session IV, 8th ed.; ICSM & FE: Moscow, Russia, 1973; Volume 3, pp. 124–134. [Google Scholar]
- Garlanger, J.E. The consolidation of soils exhibiting creep under constant effective stress. Géotechnique 1972, 22, 71–78. [Google Scholar] [CrossRef]
- Mesri, G.; Godlewski, P.M. Time- and stress-compressibility inter-relationship. J. Geotech. Eng. Div. 1977, 103, 417–430. [Google Scholar] [CrossRef]
- Kaczmarek, Ł.; Dobak, P. Contemporary overview of soil creep phenomenon. Contemp. Trends Geosci. 2017, 6, 28–40. [Google Scholar] [CrossRef]
- Vermeer, P.A.; Neher, H.P. A soft soil model that accounts for creep. In Proceedings of the International Symposium on Beyond 2000 in Computational Geotechnics, Amsterdam, The Netherlands, 18–20 March 1999; CRC Press: Amsterdam, The Netherlands, 1999; pp. 249–261. [Google Scholar]
- Karstunen, M.; Yin, Z.-Y. Modelling time-dependent behaviour of Murro test embankment. Géotechnique 2010, 60, 735–749. [Google Scholar] [CrossRef]
- Zhu, G.; Yin, J.-H.; Graham, J. Consolidation modelling of soils under the test embankment at Chek Lap Kok International Airport in Hong Kong using a simplified finite element method. Can. Geotech. J. 2001, 38, 349–363. [Google Scholar] [CrossRef]
- Gnanendran, C.T.; Manivannan, G.; Lo, S.-C.R. Influence of using a creep, rate, or an elastoplastic model for predicting the behaviour of embankments on soft soils. Can. Geotech. J. 2006, 43, 134–154. [Google Scholar] [CrossRef]
- Karim, R. Modeling the Long Term Behavior of Soft Soils. Ph.D. Thesis, University of New South Wales, Canberra, Australia, 2011. [Google Scholar]
- Stolle, D.F.E.; Vermeer, P.A.; Bonnier, P.G. A consolidation model for a creeping clay. Can. Geotech. J. 1999, 36, 754–759. [Google Scholar] [CrossRef]
- Sivasithamparam, N.; Karstunen, M.; Bonnier, P. Modelling creep behavior of anisotropic soft soils. Comput. Geotech. 2015, 69, 46–57. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Y.; Wang, Y.; Dong, Y. Modified Mesri creep modelling of soft clays in the coastal area of Tianjin (China). Tech. Gaz. 2017, 24, 1113–1121. [Google Scholar] [CrossRef] [Green Version]
- Larsson, S.; Adevik, S.; Ignat, R.; Baker, S. A case study of the effect of using surcharge fill as a complement to ground improvement with dry deep mixing. In Proceedings of the DFI-EFFC International Conference on Piling and Deep Foundations, Stockholm, Sweden, 23–31 May 2014; Deep Foundations Institute: Hawthorne, NJ, USA, 2014. [Google Scholar]
- Long, M.; Grimstad, G.; Trafford, A. Prediction of embankment settlement on Swedish peat using the Soft Soil Creep model. Proc. Inst. Civ. Eng.-Geotech. Eng. 2020. [Google Scholar] [CrossRef]
- Lo, S.R.; Mak, J.; Gnanendran, C.T.; Zhang, R.; Manivannan, G. Long-term performance of a wide embankment on soft clay improved with prefabricated vertical drains. Can. Geotech. J. 2008, 45, 1073–1091. [Google Scholar] [CrossRef]
- Vesterberg, B.; Andersson, M. Settlement and pore pressure behaviour and predictions of test embankments on an organic clay. Int. J. Geotech. Eng. 2022. [Google Scholar] [CrossRef]
- Long, M.; Boylan, N. Predictions of settlement in peat soils. Q. J. Eng. Geol. Hydrogeol. 2013, 46, 303–322. [Google Scholar] [CrossRef] [Green Version]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Recent Advances and Future Challenges for Artificial Neural Systems in Geotechnical Engineering Applications. Adv. Artif. Neural Syst. 2009, 2009, 308239. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosallanezhad, M.; Rashid, A.S.A.; Jusoh, W.A.W.; Muazu, M.A. A systematic review and meta-analysis of artificial neural network application in geotechnical engineering: Theory and applications. Neural Comput. Appl. 2020, 32, 495–518. [Google Scholar] [CrossRef]
- Das, S.K. Artificial Neural Networks in Geotechnical Engineering. In Metaheuristics in Water, Geotechnical and Transport Engineering; Elsevier: London, UK, 2013; pp. 231–270. [Google Scholar] [CrossRef]
- Jaksa, M.; Liu, Z. Editorial for Special Issue “Applications of Artificial Intelligence and Machine Learning in Geotechnical Engineering”. Geosciences 2021, 11, 399. [Google Scholar] [CrossRef]
- Jeremiah, J.J.; Abbey, S.J.; Booth, C.A.; Kashyap, A. Results of Application of Artificial Neural Networks in Predicting Geo-Mechanical Properties of Stabilised Clays—A Review. Geotechnics 2021, 1, 147–171. [Google Scholar] [CrossRef]
- Kovačević, M.S.; Bačić, M.; Gavin, K. Application of neural networks for the reliability design of a tunnel in karst rock mass. Can. Geotech. J. 2021, 58, 455–467. [Google Scholar] [CrossRef]
- Kovačević, M.S.; Bačić, M.; Gavin, K.; Stipanović, I. Assessment of long-term deformation of a tunnel in soft rock by utilizing particle swarm optimized neural network. Tunn. Undergr. Space Technol. 2021, 110, 103838. [Google Scholar] [CrossRef]
- Reale, C.; Gavin, K.; Librić, L.; Jurić-Kaćunić, D. Automatic classification of fine-grained soils using CPT measurements and Artificial Neural Networks. Adv. Eng. Inform. 2018, 36, 207–215. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Lai, X.; Luo, T.; Yuan, K.; Cui, F. Study on the viscoelastic–viscoplastic model of layered siltstone using creep test and RBF neural network. Open Geosci. 2021, 13, 72–84. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabashi, Y. Rheological parameter estimation for the prediction of long-term deformations in conventional tunnelling. Tunn. Undergr. Space Technol. 2009, 24, 250–259. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Yin, Z.-Y.; Jin, Y.-F.; Chan, T.H.T. A novel hybrid surrogate intelligent model for creep index prediction based on particle swarm optimization and random forest. Eng. Geol. 2019, 265, 105328. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, Z.M.; Wang, Y.; Liu, Y.M.; Chen, Y.J.; Lin, H. Study on Deformation Property of Soft Soil Based on Neural Networks. Appl. Mech. Mater. 2013, 353–356, 270–273. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Xiao, Y. ANN based creep constitutive model for marine sediment clay. J. Eng. Geol. 2008, 16, 507–511. [Google Scholar]
- Lee, J.; Seo, J.I.; Lee, J.-H.; Im, S. A Performance Comparison of Machine Learning Classification Methods for Soil Creep Susceptibility Assessment. J. Korean Soc. For. Sci. 2021, 110, 610–662. [Google Scholar] [CrossRef]
- Kurnaz, T.F.; Dagdeviren, U.; Yildiz, M.; Ozkan, O. Prediction of compressibility parameters of the soils using artificial neural network. SpringerPlus 2016, 5, 1801. [Google Scholar] [CrossRef] [Green Version]
- Itasca. FLAC Manual, Section Creep Material Models; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2020. [Google Scholar]
- Kovačević, M.S.; Gavin, K.G.; Reale, C.; Librić, L. The use of neural networks to develop CPT correlations for soils in northern Croatia. In Proceedings of the 4th International Symposium on Cone Penetration Testing (CPT’18), Delft, The Netherlands, 21–22 June 2018; Taylor & Francis: Oxfordshire, UK, 2018; pp. 377–382. [Google Scholar]
- Sheela, K.G.; Deepa, S.N. Review on Methods to Fix Number of Hidden Neurons in Neural Networks. Math. Probl. Eng. 2013, 2013, 425740. [Google Scholar] [CrossRef] [Green Version]
- Hammerstrom, D. Neural networks at work. IEEE Spectr. 1993, 30, 26–32. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE Neural Networks Council: New York, NY, USA, 1995; pp. 1942–1945. [Google Scholar]
- Meier, J.; Schaedler, W.; Borgatti, L.; Corsini, A.; Schanz, T. Inverse Parameter Identification Technique Using PSO Algorithm Applied to Geotechnical Modeling. J. Artif. Evol. Appl. 2008, 2008, 574613. [Google Scholar] [CrossRef] [Green Version]
- Hajihassani, M.; Armaghani, D.J.; Kalatehjari, R. Applications of Particle Swarm Optimization in Geotechnical Engineering: A Comprehensive Review. Geotech. Geol. Eng. 2018, 36, 705–722. [Google Scholar] [CrossRef]
- MathWorks. Matlab Software; MathWorks: Natick, MA, USA, 2021. [Google Scholar]
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Car, M.; Gajski, D.; Kovačević, M.S. Remote surveying of flood protection embankments. In Proceedings of the 15th International Symposium Water Management and Hydraulics Engineering, Primosten, Croatia, 6–8 September 2017; Faculty of Civil Engineering, University of Zagreb: Zagreb, Croatia, 2017; pp. 224–232. [Google Scholar]
- Gebrehiwot, A.; Hashemi-Beni, L.; Thompson, G.; Kordjamshidi, P.; Langan, T.E. Deep Convolutional Neural Network for Flood Extent Mapping Using Unmanned Aerial Vehicles Data. Sensors 2019, 19, 1486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saraereh, O.A.; Alsaraira, A.; Khan, I.; Uthansakul, P. Performance Evaluation of UAV-Enabled LoRa Networks for Disaster Management Applications. Sensors 2020, 20, 2396. [Google Scholar] [CrossRef] [PubMed]
- Tarchi, D.; Casagli, N.; Fanti, R.; Leva David, D.; Luzi, G.; Pasuto, A.; Pieraccini, M.; Silvano, S. Landslide Monitoring by Using Ground-Based SAR Interferometry: An Example of Application to the Tesina Landslide in Italy. Eng. Geol. 2003, 68, 15–30. [Google Scholar] [CrossRef]
- Canuti, P.; Casagli, N.; Catani, F.; Falorni, G.; Farina, P. Integration of Remote Sensing Techniques in Different Stages of Landslide Report (Chapter 18). In Progress in Landslide Science; Sassa, K., Fukuoka, H., Wang, F., Wang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 251–260. [Google Scholar]
- Cascini, L.; Peduto, D.; Fornaro, G.; Lanari, R.; Zeni, G.; Guzzetti, F. Spaceborn Radar Interferometry for Landslide Monitoring. In Proceedings of the First Italian Workshop on Landslides, Rainfall–Induced Landslides, Napoli, Italy, 8–10 June 2009; Doppiavoce: Napoli, Italy, 2009; pp. 138–144. [Google Scholar]
- Karimzadeh, S.; Matsuoka, M. Ground Displacement in East Azerbaijan Province, Iran, Revealed by L-band and C-band InSAR Analyses. Sensors 2020, 20, 6913. [Google Scholar] [CrossRef]
- Podolszki, L.; Kosović, I.; Novosel, T.; Kurečić, T. Multi-Level Sensing Technologies in Landslide Research—Hrvatska Kostajnica Case Study, Croatia. Sensors 2022, 22, 177. [Google Scholar] [CrossRef]
- Mihalinec, Z.; Bačić, M.; Kovačević, M.-S. Risk identification in landslide monitoring. Građevinar 2013, 65, 523–536. [Google Scholar] [CrossRef]
- Kovačević, M.S.; Marčić, D.; Gazdek, M. Application of geophysical investigations in underground engineering. Tech. Gazzette 2013, 20, 1111–1117. [Google Scholar]
- McDowell, P.W. Geophysics in Engineering Investigation; CIRIA C562: Westminster, UK, 2002. [Google Scholar]
- Bačić, M.; Librić, L.; Kaćunić, D.J.; Kovačević, M.S. The Usefulness of Seismic Surveys for Geotechnical Engineering in Karst: Some Practical Examples. Geosciences 2020, 10, 406. [Google Scholar] [CrossRef]
- Nazarian, S.; Stokoe, K.H.; Hudson, W.R. Use of Spectral Analysis of Surface Waves Method for Determination of Moduli and Thicknesses of Pavement Systems; Transportation Research Record 930: Washington, DC, USA, 1983; pp. 38–45. [Google Scholar]
- Hallof, P.G. On the Interpretation of Resistivity and Induced Polarization Results. Ph.D. Thesis, M.I.T. Department of Geology and Geophysics, Cambridge, UK, 1957. [Google Scholar]
- Kovačević, M.S.; Bačić, M.; Librić, L.; Žužul, P.; Gavin, K.; Reale, C. A novel algorithm for vertical soil layering by utilizing the CPT data. In Proceedings of the 6th International Conference on Road and Rail Infrastructure-CETRA 2020, Zagreb, Croatia, 20–21 May 2021; Lakušić, S., Ed.; University of Zagreb, Faculty of Civil Engineering: Zagreb, Croatia, 2021; pp. 327–334. [Google Scholar] [CrossRef]
- Pieczyńska-Kozłowska, J.; Bagińska, I.; Kawa, M. The Identification of the Uncertainty in Soil Strength Parameters Based on CPTu Measurements and Random Fields. Sensors 2021, 21, 5393. [Google Scholar] [CrossRef] [PubMed]
- Robertson, P.K. Cone penetration test (CPT)-based soil behaviour type (SBT) classification system—An update. Can. Geotech. J. 2016, 53, 1910–1927. [Google Scholar] [CrossRef]
- Speijker, L.J.P.; van Noortwijk, J.M.; Kok, M.; Cooke, R.M. Optimal Maintenance Decisions for Dikes. Probab. Eng. Inf. Sci. 2000, 14, 101–121. [Google Scholar] [CrossRef] [Green Version]
- Jorissen, R.E.; van Noortwijk, J.M. Instrumenten Voor Optimaal Beheer van Waterkeringen Gepubliceerd; Het Waterschap Jaargang: Lelystad, The Netherlands, 2000; Volume 83. (In Dutcth) [Google Scholar]
- DINOloket (Data en Informatie van de Nederlandse Ondergrond Hoofdnavigatie). Available online: www.dinoloket.nl (accessed on 28 December 2021).
- Bodemdalingskaart. Available online: https://bodemdalingskaart.portal.skygeo.com (accessed on 5 January 2021).
- Robertson, P.K. Soil behaviour type from the CPT: An update. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010; Technical Papers, Session 2: Interpretation. Volumes 2–3. [Google Scholar]













| Soil Layering/Parameters | |||||||
| Type | Total no. of investigation profiles or points | No. of profiles (points) on the crest | No. of profiles (points) upstream/downstream | Length of each profile (m) | Depth of investigation (m) | Source | |
| MASW | 4 | 2 | 1/1 | 100 | 26 | In situ | |
| ERT | 4 | 2 | 1/1 | 75 | 15 | In situ | |
| CPT | 4 | 2 | 0/2 | - | 20 | [63] | |
| Terrain Topography | |||||||
| Type | Flight height (m) | Scanned area (m × m) | Photo overlapping | No. of photos | No. of 3D points (million) | GSD (cm) | Source |
| UAV | 30 | 70 × 130 | front 70% side 70% | 87 | 63.6 | 0.83 | In situ |
| Displacement Measurement | |||||||
| Type | Measurement period | Satellite | Point ID from database [56] | Coordinates (EPSG:28992) of measurement point * | No. of measurements | Source | |
| InSAR | from May 2015 to June 2020 | WEST-1 | L00019660P00016545 | N 102968.0 E 430885.0 | 251 | [64] | |
| GPS | from June 2020 to June 2021 | - | - | N 102969.6 E 430885.8 | 3 | IM ** | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovačević, M.S.; Bačić, M.; Librić, L.; Gavin, K. Evaluation of Creep Behavior of Soft Soils by Utilizing Multisensor Data Combined with Machine Learning. Sensors 2022, 22, 2888. https://doi.org/10.3390/s22082888
Kovačević MS, Bačić M, Librić L, Gavin K. Evaluation of Creep Behavior of Soft Soils by Utilizing Multisensor Data Combined with Machine Learning. Sensors. 2022; 22(8):2888. https://doi.org/10.3390/s22082888
Chicago/Turabian StyleKovačević, Meho Saša, Mario Bačić, Lovorka Librić, and Kenneth Gavin. 2022. "Evaluation of Creep Behavior of Soft Soils by Utilizing Multisensor Data Combined with Machine Learning" Sensors 22, no. 8: 2888. https://doi.org/10.3390/s22082888
APA StyleKovačević, M. S., Bačić, M., Librić, L., & Gavin, K. (2022). Evaluation of Creep Behavior of Soft Soils by Utilizing Multisensor Data Combined with Machine Learning. Sensors, 22(8), 2888. https://doi.org/10.3390/s22082888









