0.3-Volt Rail-to-Rail DDTA and Its Application in a Universal Filter and Quadrature Oscillator
Abstract
:1. Introduction
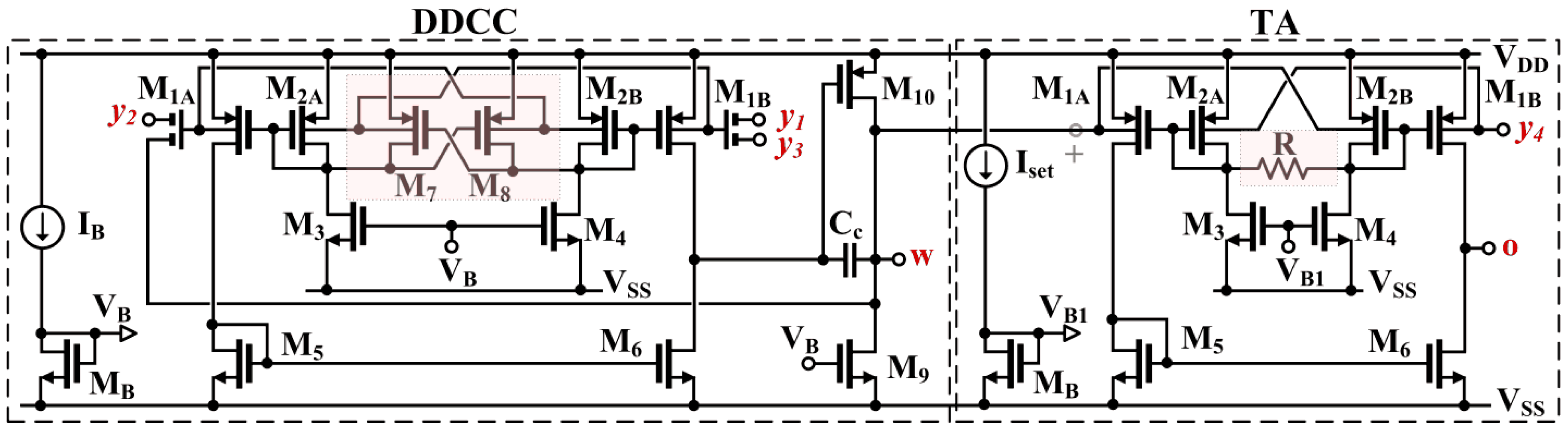
2. DDTA and Its CMOS Structure
3. Proposed Applications
3.1. Proposed Universal Filter
3.2. Proposed Quadrature Oscillator
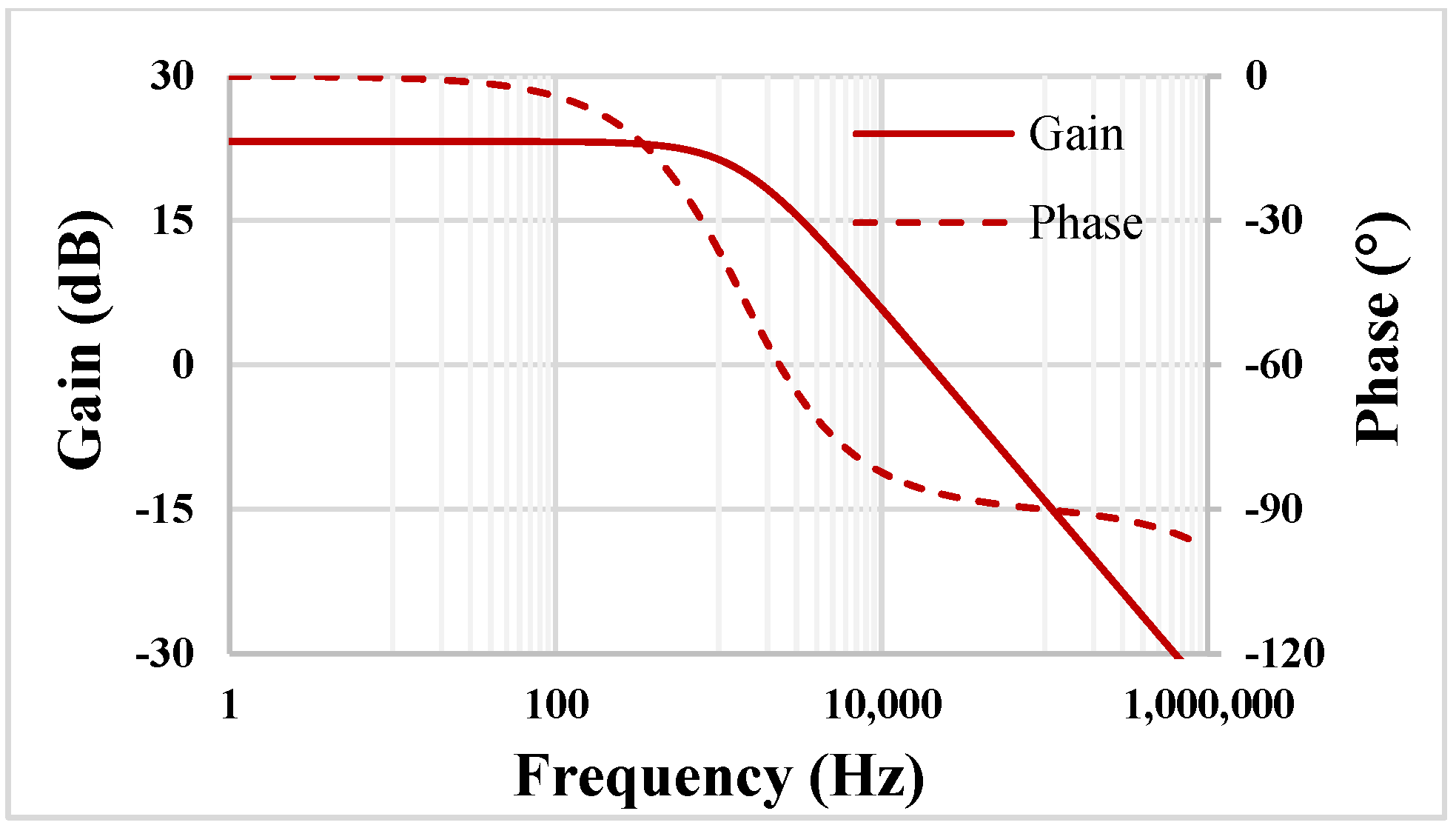
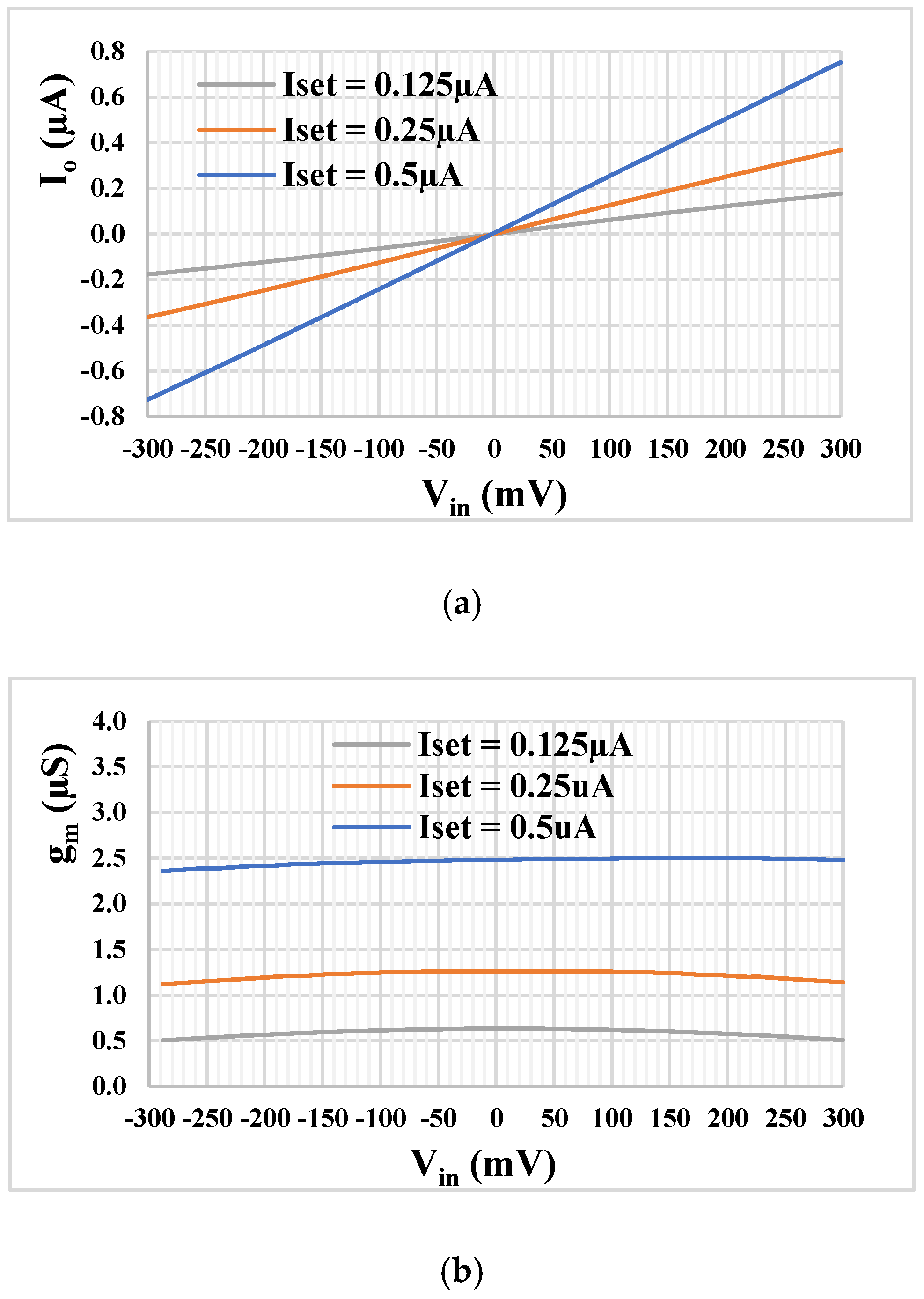
3.3. Non-Idealities Analysis
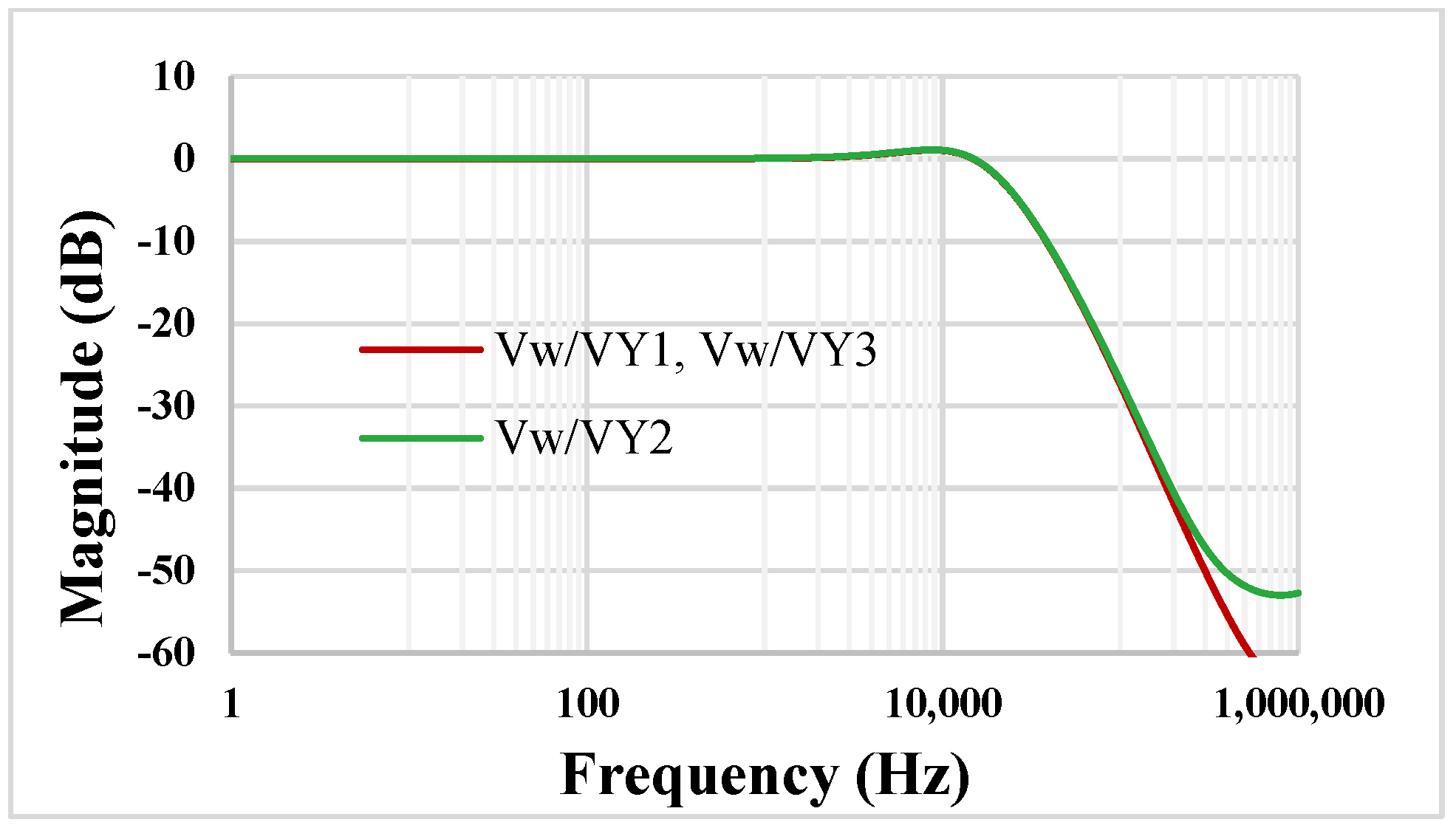
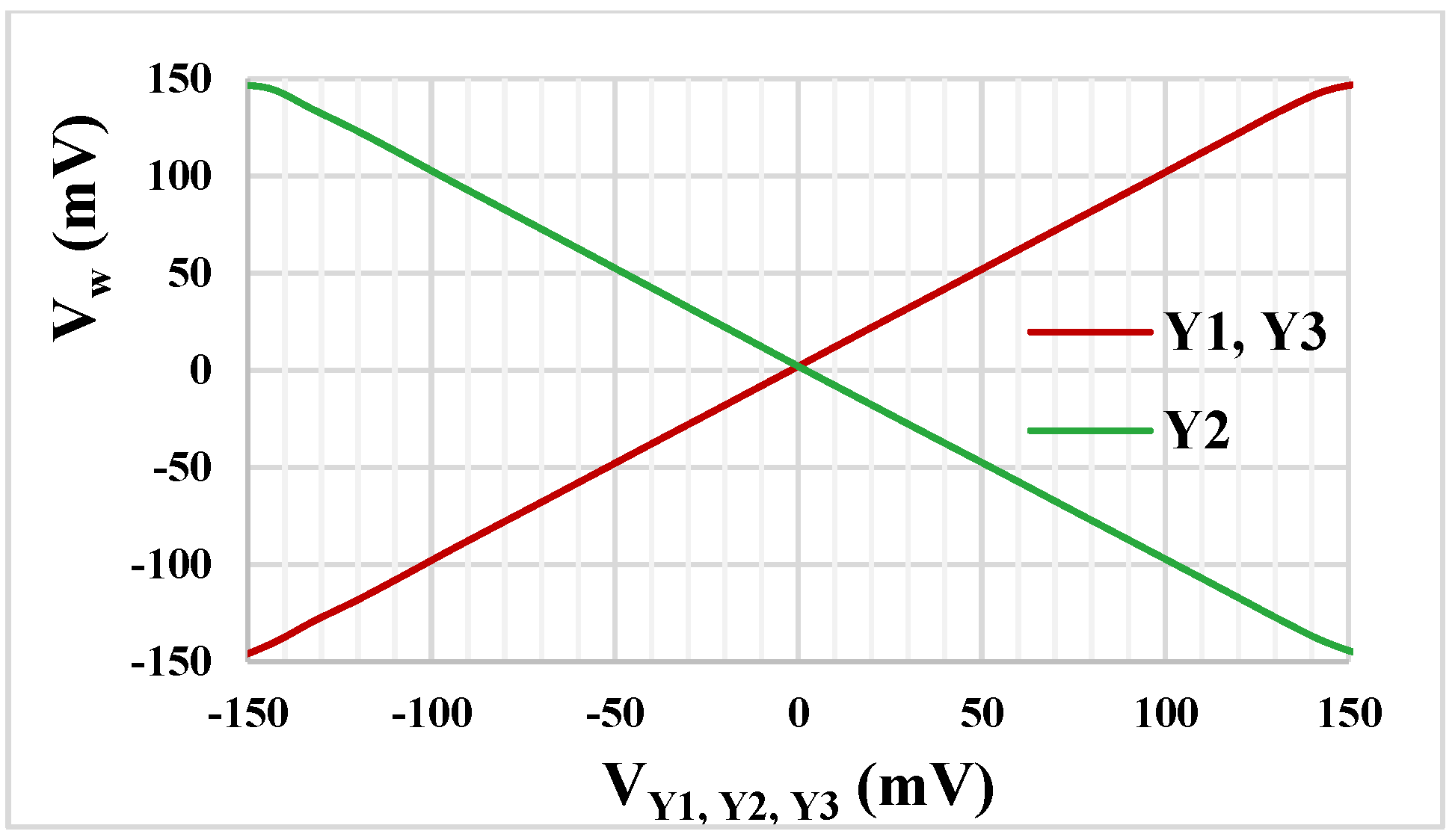
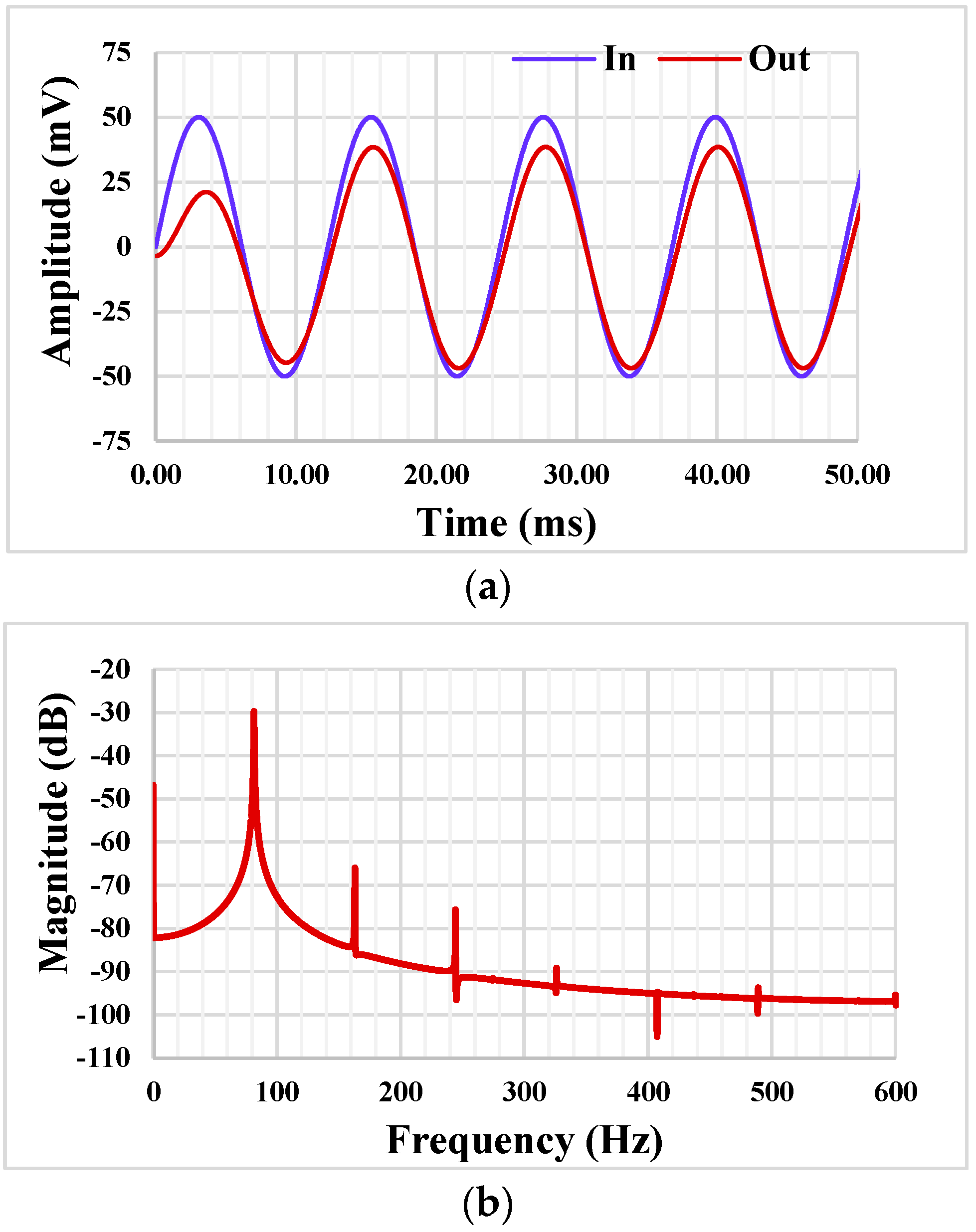
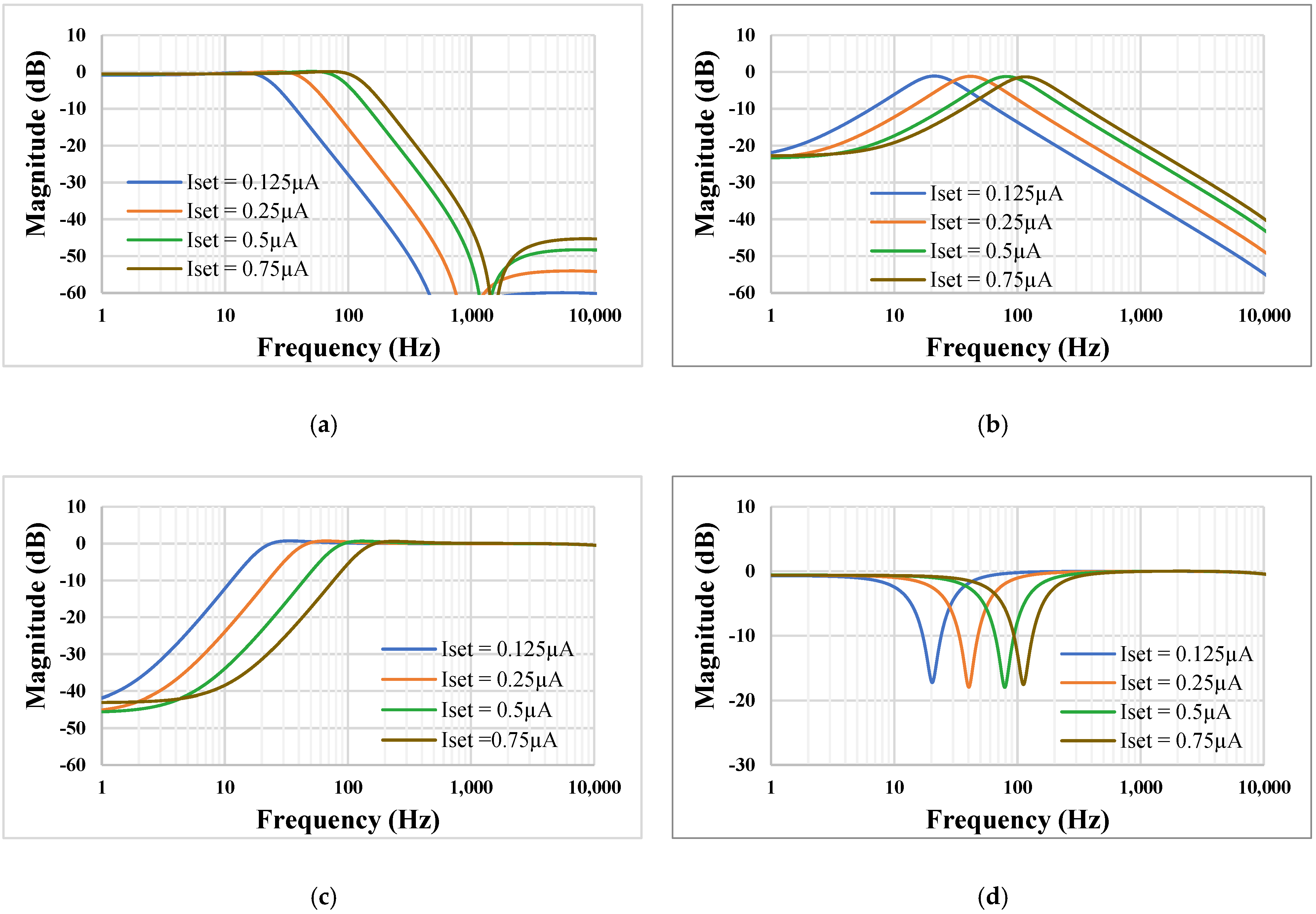
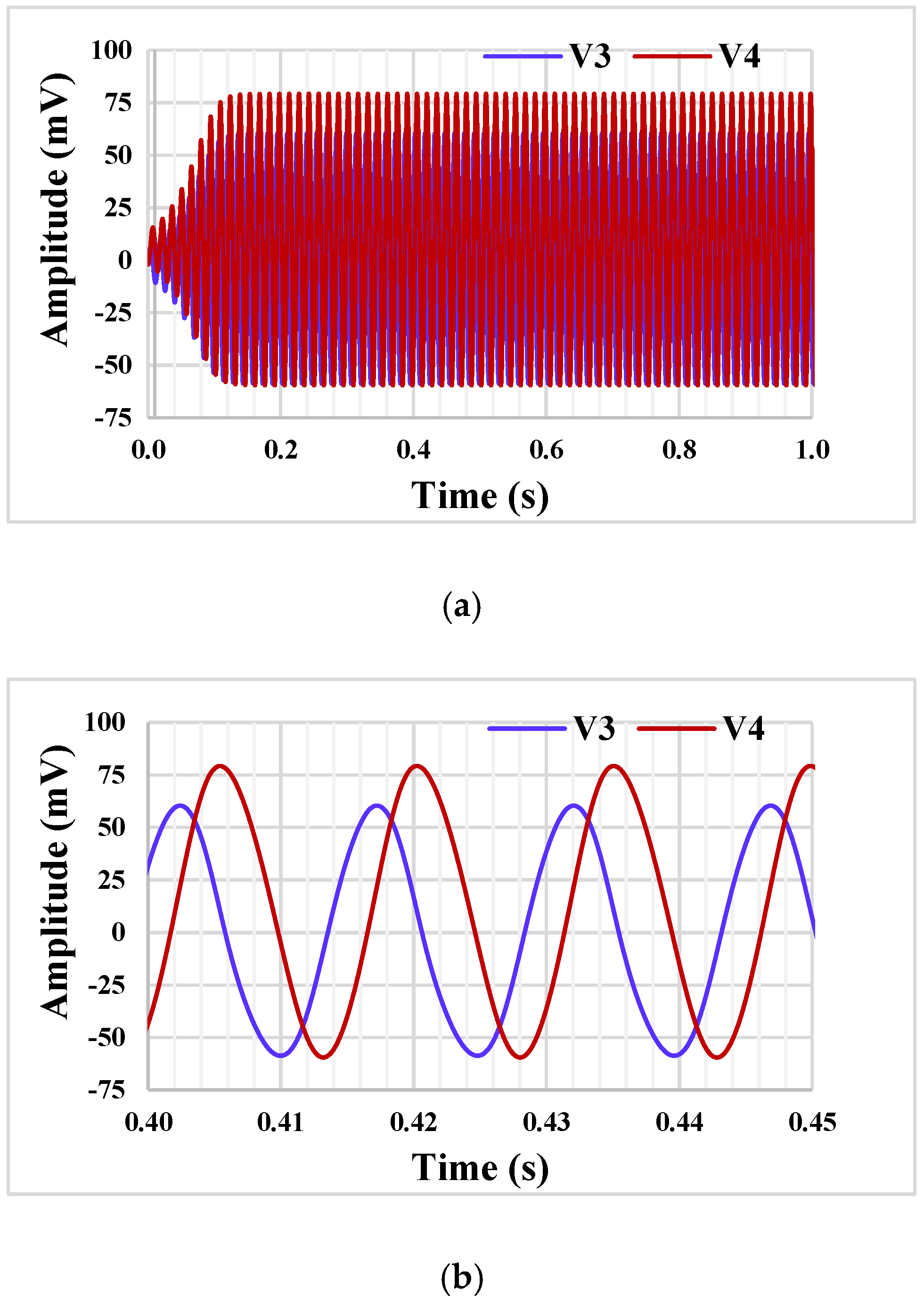
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kulej, T. 0.5 V bulk driven CMOS operational amplifier. IET Circuits Dev. Syst. 2013, 7, 352–360. [Google Scholar] [CrossRef]
- Kulej, T. 0.4-V bulk-driven operational amplifier with improved input stage. Circuits Syst. Signal Processing 2015, 34, 1167–1185. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. Design and implementation of sub 0.5-V OTAs in 0.18 µm CMOS. Int. J. Circuit Theory Appl. 2018, 46, 1129–1143. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F.; Arbet, D.; Stopjakova, V. A 0.3-V high linear rail-to-rail bulk-driven OTA in 0.13 µm CMOS. IEEE Trans. Circuits Syst.—II Express Briefs 2022, 69, 2046–2050. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Steffan, P. 0.3-V bulk-driven nanopower OTA-C integrator in 0.18 µm CMOS. Circuits Syst. Signal Process 2019, 38, 1333–1341. [Google Scholar] [CrossRef]
- Colletta, G.D.; Ferreira, L.H.C.; Pimenta, T.C. A 0.25-V 22-nS symmetrical bulk-driven OTA for low frequency Gm–C applications in 130-nm digital CMOS process. Analog Integr. Circuits Signal Process 2014, 81, 377–383. [Google Scholar] [CrossRef]
- Cotrim, E.D.; Ferreira, L.H.C. An ultra-low-power CMOS symmetrical OTA for low-frequency Gm-C applications. Analog Integr. Circuits Signal Process 2012, 71, 275–282. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Torelli, G.; Valverde, R.P.; Duque-Carrillo, J.F. 1-V Rail-to-Rail CMOS OpAmp with Improved Bulk-Driven Input Stage. IEEE J. Solid-State Circuits 2007, 42, 508–517. [Google Scholar] [CrossRef]
- Vlassis, S.; Raikos, G. Bulk-driven differential voltage follower. Electron. Lett. 2009, 45, 1276–1277. [Google Scholar] [CrossRef]
- Raikos, G.; Vlassis, S. 0.8 V bulk-driven operational amplifier. Analog Integr. Circ. Signal Process 2010, 63, 425–432. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Torelli, G.; Domínguez, M.A.; Pérez-Aloe, R.; Valverde, J.M.; Duque-Carrillo, J.F. A Family of Low-Voltage Bulk-Driven CMOS Continuous-Time CMFB Circuits. IEEE Trans. Circuits Syst. II 2010, 57, 863–867. [Google Scholar] [CrossRef]
- Raikos, G.; Vlassis, S.; Psychalinos, C. 0.5 V bulk-driven analog building blocks. Int. J. Electron. Commun. (AEÜ) 2012, 66, 920–927. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. 0.4-V bulk-driven differential-difference amplifier. Microelectron. J. 2015, 46, 362–369. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T. Design and implementation of a 0.3-V differential difference amplifier. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 513–523. [Google Scholar] [CrossRef]
- Lopez-Martin, A.J.; Ramirez-Angulo, J.; Carvajal, R.G.; Acosta, L. CMOS Transconductors with Continuous Tuning Using FGMOS Balanced Output Current Scaling. IEEE J. Solid State Circuits 2008, 43, 1313–1323. [Google Scholar] [CrossRef]
- Rico-Aniles, H.D.; Ramirez-Angulo, J.; Lopez-Martin, A.J.; Carvajal, R.G. 360 nW Gate-Driven Ultra-Low Voltage CMOS Linear Transconductor with 1 MHz Bandwidth and Wide Input Range. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2332–2336. [Google Scholar] [CrossRef]
- Khateb, F.; Prommee, P.; Kulej, T. MIOTA-based Filters for Noise and Motion Artifact Reductions in Biosignal Acquisition. IEEE Access 2022, 10, 14325–14338. [Google Scholar] [CrossRef]
- Kumngern, M.; Aupithak, N.; Khateb, F.; Kulej, T. 0.5V Fifth-Order Butterworth Low-Pass Filter Using Multiple-Input OTA for ECG Applications. Sensors 2020, 20, 7343. [Google Scholar] [CrossRef]
- Jaikla, W.; Khateb, F.; Kumngern, M.; Kulej, T.; Ranjan, R.K.; Suwanjan, P. 0.5 V Fully Differential Universal Filter Based on Multiple Input OTAs. IEEE Access 2020, 8, 187832–187839. [Google Scholar] [CrossRef]
- Prommee, P.; Karawanich, K.; Khateb, F.; Kulej, T. Voltage-Mode Elliptic Band-Pass Filter Based on Multiple-Input Transconductor. IEEE Access 2021, 9, 32582–32590. [Google Scholar] [CrossRef]
- Kumngern, M.; Kulej, T.; Stopjakova, V.; Khateb, F. 0.5 V Sixth-order Chebyshev band-pass filter based on multiple-input bulk-driven OTA. AEU-Int. J. Electron. Commun. 2019, 111, 152930. [Google Scholar] [CrossRef]
- Kumngern, M.; Kulej, T.; Khateb, F.; Stopjakova, V.; Ranjan, R.K. Nanopower multiple-input DTMOS OTA and its applications to high-order filters for biomedical systems. AEU-Int. J. Electron. Commun. 2021, 130, 153576. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T.; Psychalinos, C. Multiple-Input Universal Filter and Quadrature Oscillator Using Multiple-Input Operational Transconductance Amplifiers. IEEE Access 2021, 9, 56253–56263. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Kumngern, M. 0.5-V High Linear and Wide Tunable OTA for Biomedical Applications. IEEE Access 2021, 9, 103784–103794. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Psychalinos, C. Multiple-input bulk-driven MOS transistor for low-voltage low-frequency applications. Circuits Syst. Signal Processing 2019, 38, 2829–2845. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Veldandi, H.; Jaikla, W. Multiple-input bulk-driven quasi-floating-gate MOS transistor for low-voltage low-power integrated circuits. AEU-Int. J. Electron. Commun. 2019, 100, 32–38. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Jaikla, W.; Ranjan, R.K. Comparative performance study of multiple-input Bulk-driven and multiple-input Bulk-driven Quasi-floating-gate DDCCs. AEU-Int. J. Electron. Commun. 2019, 108, 19–28. [Google Scholar] [CrossRef]
- Jaikla, W.; Khateb, F.; Kulej, T.; Pitaksuttayaprot, K. Universal Filter Based on Compact CMOS Structure of VDDDA. Sensors 2021, 21, 1683. [Google Scholar] [CrossRef]
- Jaikla, W.; Bunrueangsak, S.; Khateb, F.; Kulej, T.; Suwanjan, P.; Supavarasuwat, P. Inductance Simulators and Their Application to the 4th Order Elliptic Lowpass Ladder Filter Using CMOS VD-DIBAs. Electronics 2021, 10, 684. [Google Scholar] [CrossRef]
- Jaikla, W.; Adhan, S.; Suwanjan, P.; Kumngern, M. Current/voltage controlled quadrature sinusoidal oscillators for phase sensitive detection using commercially available IC. Sensors 2020, 20, 1319. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, M.A.; Minaei, S.; Kuntman, H.A. A 22.5 MHz current-mode KHN-biquad using deferential voltage current conveyor and grounded passive elements. AEU-Int. J. Electron. Commun. 2005, 59, 311–318. [Google Scholar] [CrossRef]
- Alexander, C.K.; Sadiku, M.K.O. Fundamentals of Electric Circuits, 6th ed.; McGraw-Hill: New York, NY, USA, 2017; pp. 655–661. [Google Scholar]
- Povoa, R.; Arya, R.; Canelas, A.; Passos, F.; Martins, R.; Lourenco, N.; Horta, N. Sub-μW Tow-Thomas based biquad filter with improved gain for biomedical applications. Microelectron. J. 2020, 95, 104675. [Google Scholar] [CrossRef]
- Masuch, J.; Restituto, M.D. Low-power quadrature generators for body area network applications. Int. J. Circuit Theory Appl. 2011, 41, 33–43. [Google Scholar] [CrossRef]
- Hu, H.; Gupta, S.; Schiavenato, M. An 143nW relaxation oscillator for ultra-low power biomedical systems. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Tangsrirat, W.; Channumsin, O. High-Input Impedance Voltage-Mode Multifunction Filter Using a Single DDCCTA and Grounded Passive Elements. Radioengineering 2011, 20, 905–910. [Google Scholar]
- Kumngern, M. DDTA and DDCCTA: New active elements for analog signal processing. In Proceedings of the 2012 IEEE International Conference on Electronics Design, Systems and Applications (ICEDSA), Kuala Lumpur, Malaysia, 5–6 November 2012; pp. 141–145. [Google Scholar]
- Kumngern, M. CMOS differential difference voltage follower transconductance amplifier. In Proceedings of the 2015 IEEE International Circuits and Systems Symposium (ICSyS), Langkawi, Malaysia, 2–4 September 2015; pp. 133–136. [Google Scholar] [CrossRef]
- Yesil, A.; Konal, M.; Kacar, F. Electronically Tunable Quadrature Oscillator Employing Single Differential Difference Transconductance Amplifier. Acta Phys. Pol. A 2017, 132, 843. [Google Scholar] [CrossRef]
- Rana, P.; Ranjan, A. Odd- and even-order electronically controlled wave active filter employing differential difference trans-conductance amplifier (DDTA). Int. J. Electron. 2021, 108, 1623–1651. [Google Scholar] [CrossRef]
- Wang, S.-F.; Chen, H.-P.; Ku, Y.; Yang, C.-M. Independently tunable voltage-mode OTA-C biquadratic filter with five inputs and three outputs and its fully-uncoupled quadrature sinusoidal oscillator application. AEU-Int. J. Electron. Commun. 2019, 110, 152822. [Google Scholar] [CrossRef]
- Wang, S.-F.; Chen, H.-P.; Kuu, Y.; Lee, C.-L. Versatile voltage-mode biquadratic filter and quadrature oscillator using four OTAs and two grounded capacitors. Electronics 2020, 9, 1493. [Google Scholar] [CrossRef]
- Wang, S.-F.; Chen, H.-P.; Ku, Y.; Lin, Y.-C. Versatile tunable voltage-mode biquadratic filter and its application in quadrature oscillator. Sensors 2019, 19, 2349. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.-F.; Chen, H.-P.; Ku, Y.; Zhong, M.-X. Analytical Synthesis of High-Pass, Band-Pass and Low-Pass Biquadratic Filters and its Quadrature Oscillator Application Using Current-Feedback Operational Amplifiers. IEEE Access 2021, 9, 13330–13343. [Google Scholar] [CrossRef]
- Faseehuddin, M.; Herencsar, N.; Albrni, M.A.; Sampe, J. Electronically Tunable Mixed-Mode Universal Filter Employing a Single Active Block and a Minimum Number of Passive Components. Appl. Sci. 2021, 11, 55. [Google Scholar] [CrossRef]
- Faseehuddin, M.; Herencsar, N.; Shireen, S.; Tangsrirat, W.; Ali, S.H.M. Voltage Differencing Buffered Amplifier-Based Novel Truly Mixed-Mode Biquadratic Universal Filter with Versatile Input/Output Features. Appl. Sci. 2022, 12, 1229. [Google Scholar] [CrossRef]
- Namdari, A.; Dolatshahi, M. Design of a low-voltage and low-power, reconfigurable universal OTA-C filter. Analog Integr. Circuits Signal Processing 2022. [Google Scholar] [CrossRef]
- Tsukutani, T.; Higashimura, M.; Takahashi, N.; Sumi, Y.; Fukui, Y. Versatile voltage-mode active-only biquad with lossless and lossy integrator loop. Int. J. Electron. 2001, 88, 1093–1102. [Google Scholar] [CrossRef]

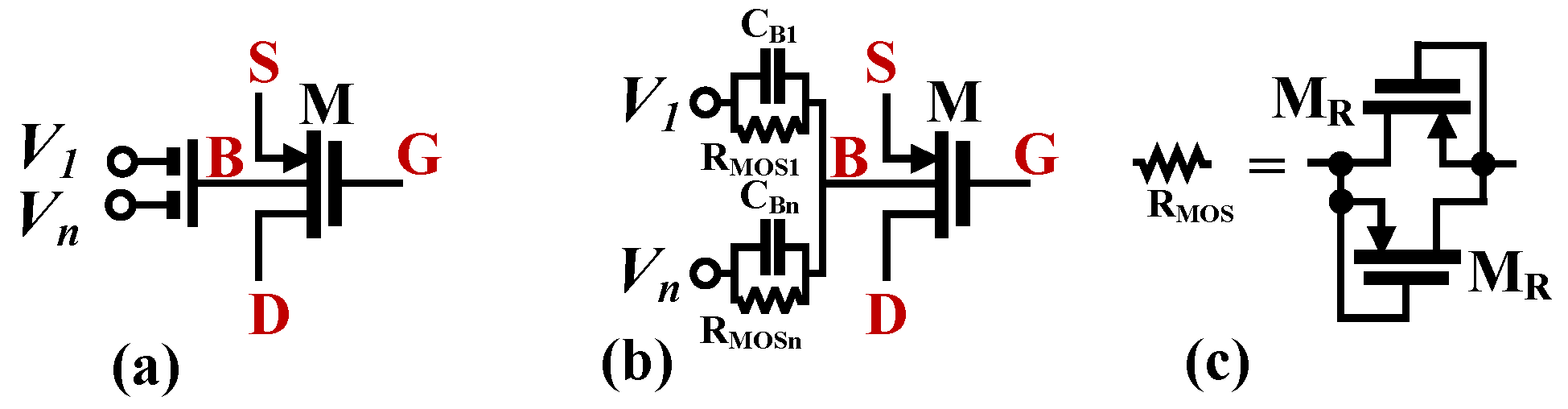




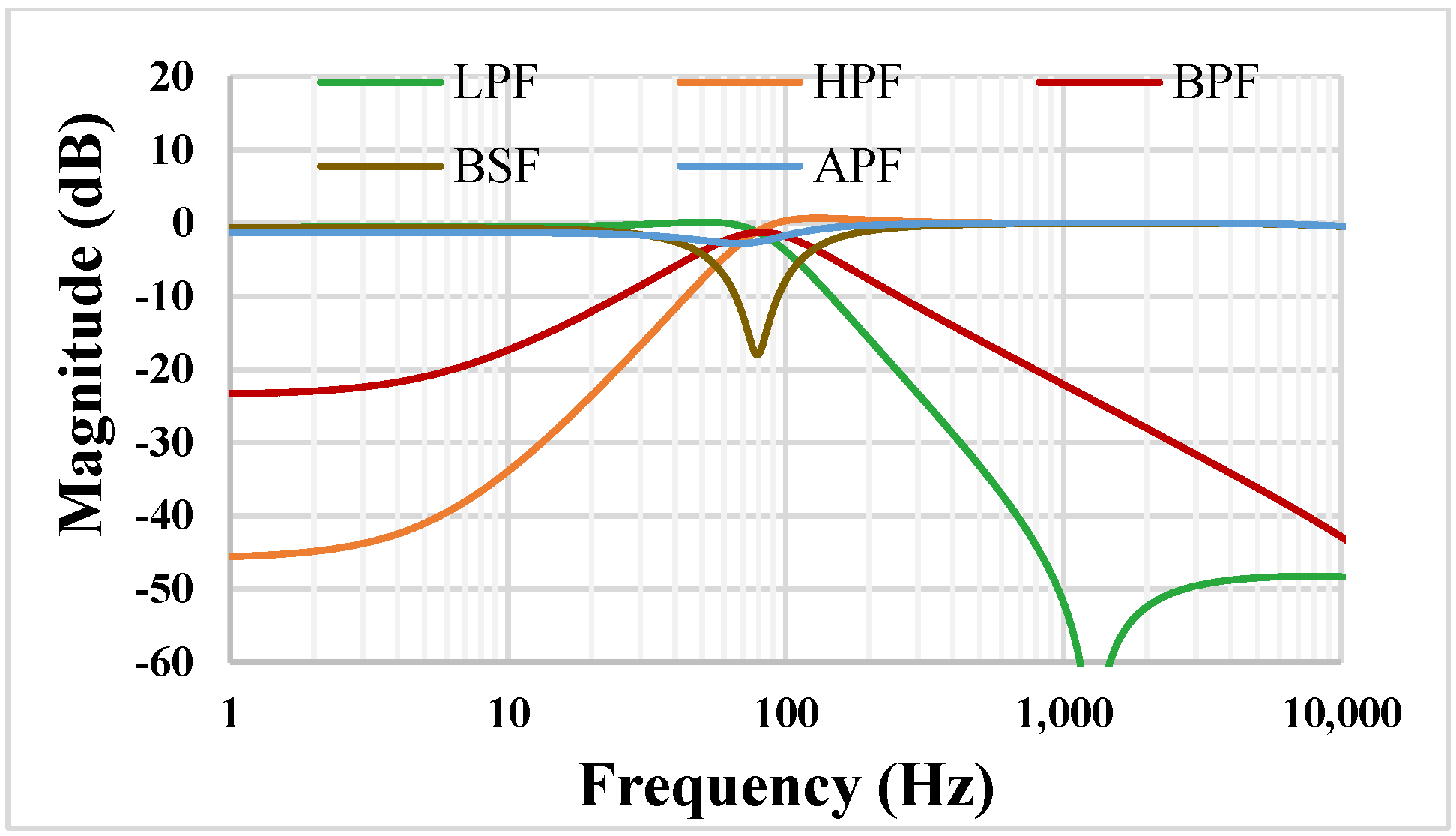
| Filtering Function | Input | Output | |
|---|---|---|---|
| LP | Non-inverting | ||
| Non-inverting | |||
| Inverting | |||
| Non-inverting | |||
| Non-inverting | |||
| Non-inverting | |||
| Inverting | |||
| BP | Non-inverting | ||
| Inverting | |||
| Non-inverting | |||
| Non-inverting | |||
| Inverting | |||
| Non-inverting | |||
| Non-inverting | |||
| Non-inverting | |||
| Inverting | |||
| Inverting | |||
| HP | Non-inverting | ||
| Inverting | |||
| Non-inverting | |||
| BS | Non-inverting | ||
| AP | Non-inverting | ||
| Device | W/L (µm/µm) |
|---|---|
| M1A, M2A, M1B, M2B | 20/3 |
| M7, M8 | 15/3 |
| M3–M6, MB | 10/3 |
| M9 | 6 × 10/3 |
| M10 | 6 × 20/3 |
| MR | 5/3 |
| MIM capacitor: CB = 0.2 pF, Cc = 4 pF | |
| Poly-resistor R = 90 kΩ | |
| DDCC | min. | nom. | max. |
|---|---|---|---|
| P/V/T | P/V/T | ||
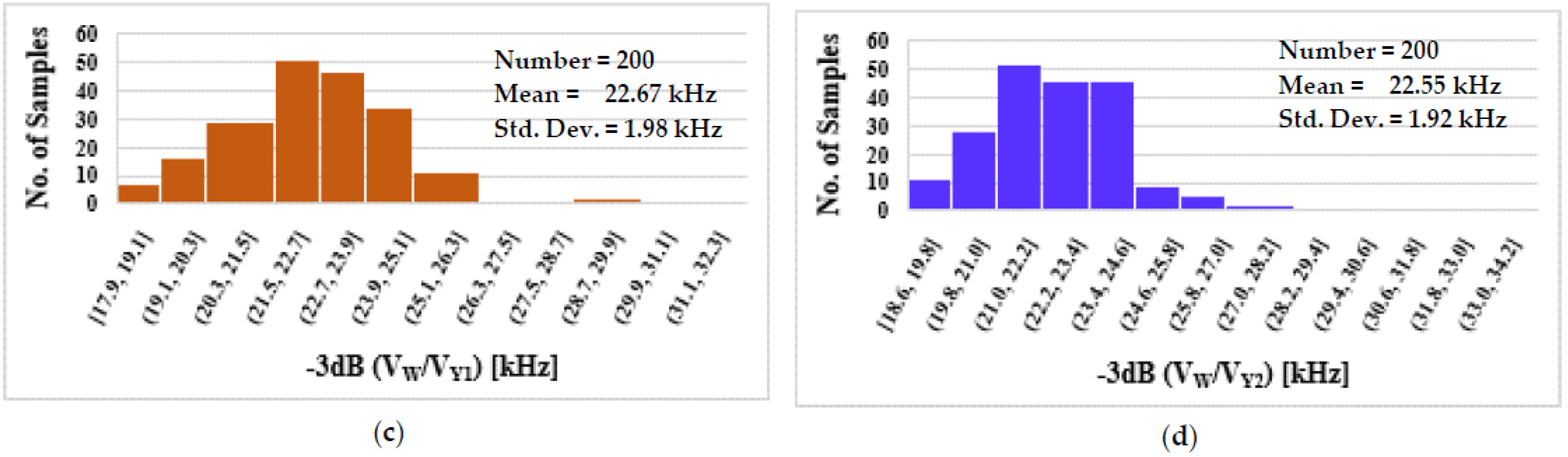
| Gain VW/VY1 [mdB] | −75.3/9.8/−224 | 14 | 29.4/14/14 |
| Gain VW/VY2 [mdB] | −14.1/45.8/−75 | 57 | 101/67.3/57 |
| −3 dB VW/VY1 [kHz] | 20.2/22/21 | 22.24 | 25.2/22.1/23.7 |
| −3 dB VW/VY2 [kHz] | 20.1/22/20.8 | 22.23 | 25/22.7/23.4 |
| TA | min. | nom. | max. |
|---|---|---|---|
| P/V/T | P/V/T | ||
| Gain [dB] | 23/20.6/21.9 | 23.19 | 23.2/25.2/24 |
| Phase error [°] | 3.7/2.9/3.4 | 3.8 | 3.8/5.1/4.3 |
| Gm [µS] | 2.2/2.2/2.2 | 2.48 | 2.5/2.5/2.4 |
| Features | Proposed | Ref. [23] | Ref. [41] | Ref. [42] | Ref. [44] | Ref. [46] | Ref. [47] |
|---|---|---|---|---|---|---|---|
| Active and passive elements | 2 DDTA, 2 C | 5 OTA, 2 C | 5 OTA, 2 C | 4 OTA, 2 C | 3 CFOA, 2 C, 4 R | 3 VDBA, 2 C, 1 R (Figure 2) | 8 OTA, 2 C (Figure 3) |
| Realization | CMOS structure (130 nm) | CMOS structure (180 nm) & commercial IC | commercial IC | commercial IC | CMOS structure (180 nm) | CMOS structure (180 nm) | CMOS structure (180 nm) |
| Filter type | MIMO | MISO | MIMO | MIMO | MOMO | MISO | MIMO |
| Number of filtering functions | 22 (VM) | 11 (VM) | 13 (VM) | 9 (VM) | 5 (VM) | 20 (Mixed-mode) | 20 (Mixed-mode) |
| Offer universal filter and oscillator | Yes | Yes | Yes | Yes | Yes | No | No |
| Electronic control of parameter | Yes | Yes | Yes | Yes | No | Yes | Yes |
| Natural frequency (kHz) | 0.08147 | 1 | 217 | 144.7 | 757.88. | 16.631 × 103 | 5.77 |
| Total harmonic distortion (%) | 0.5@100 mVpp | 1.67@600 mVpp | 1.93@200 mVpp | 3.83@170 mVpp | 3.18@1.2 Vpp | <3@500 mVpp | <2@200 mVpp |
| Power supply voltages (V) | 0.3 | 1.2 | ±15 | ±15 | ±0.9 | ±1.25 | ±0.3 |
| Simulated power consumption (µW) | 0.715 | 96 | 860 × 103 | 0.92 × 106 | 5.4 × 103 | 5.482 × 103 | 5.77 |
| Verification of result | Sim | Sim/Exp | Sim/Exp | Sim/Exp | Sim/Exp | Sim/Exp | Sim |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khateb, F.; Kumngern, M.; Kulej, T.; Biolek, D. 0.3-Volt Rail-to-Rail DDTA and Its Application in a Universal Filter and Quadrature Oscillator. Sensors 2022, 22, 2655. https://doi.org/10.3390/s22072655
Khateb F, Kumngern M, Kulej T, Biolek D. 0.3-Volt Rail-to-Rail DDTA and Its Application in a Universal Filter and Quadrature Oscillator. Sensors. 2022; 22(7):2655. https://doi.org/10.3390/s22072655
Chicago/Turabian StyleKhateb, Fabian, Montree Kumngern, Tomasz Kulej, and Dalibor Biolek. 2022. "0.3-Volt Rail-to-Rail DDTA and Its Application in a Universal Filter and Quadrature Oscillator" Sensors 22, no. 7: 2655. https://doi.org/10.3390/s22072655
APA StyleKhateb, F., Kumngern, M., Kulej, T., & Biolek, D. (2022). 0.3-Volt Rail-to-Rail DDTA and Its Application in a Universal Filter and Quadrature Oscillator. Sensors, 22(7), 2655. https://doi.org/10.3390/s22072655








