Condition Monitoring of Ball Bearings Based on Machine Learning with Synthetically Generated Data
Abstract
:1. Introduction
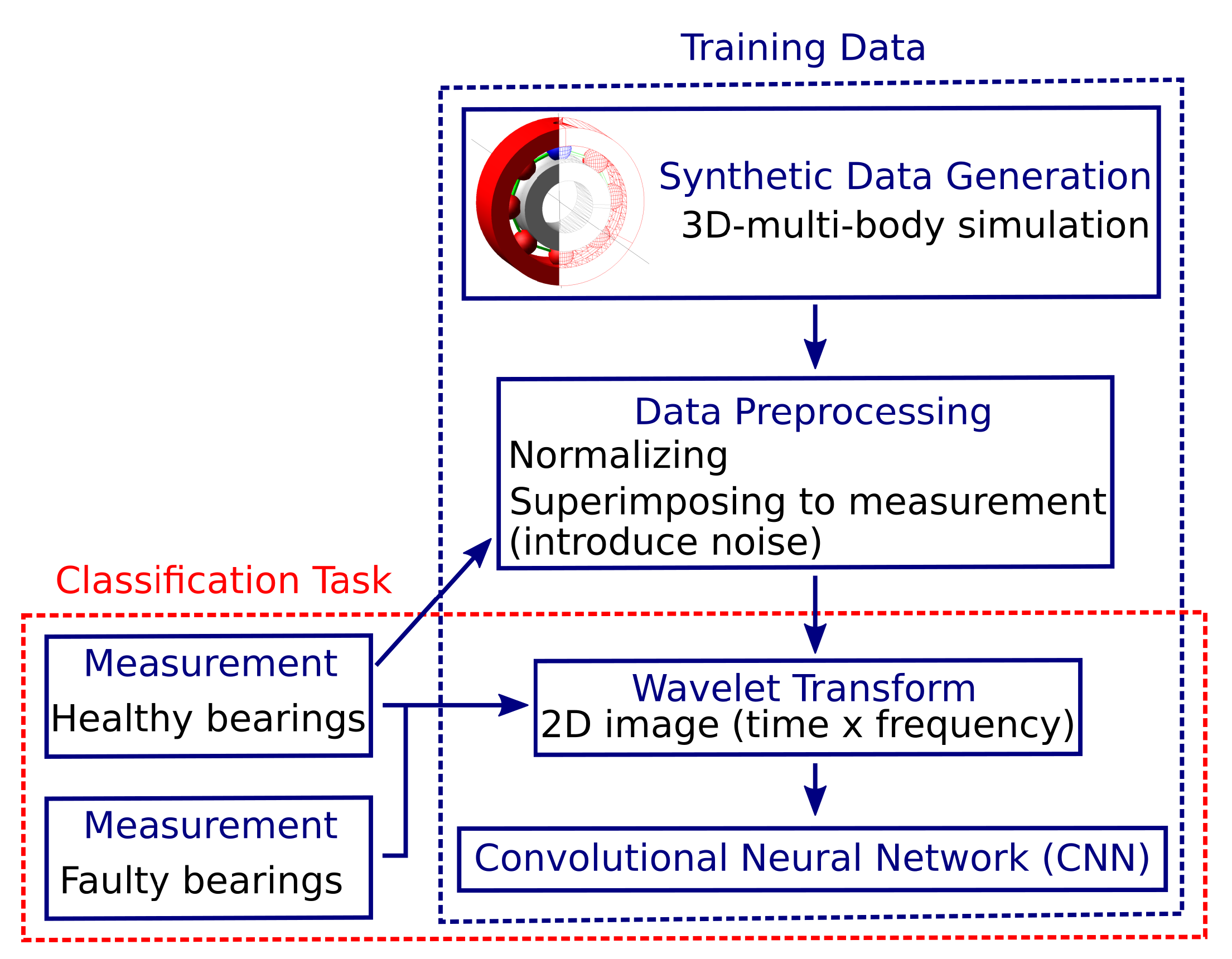
2. Synthetic Data for Training
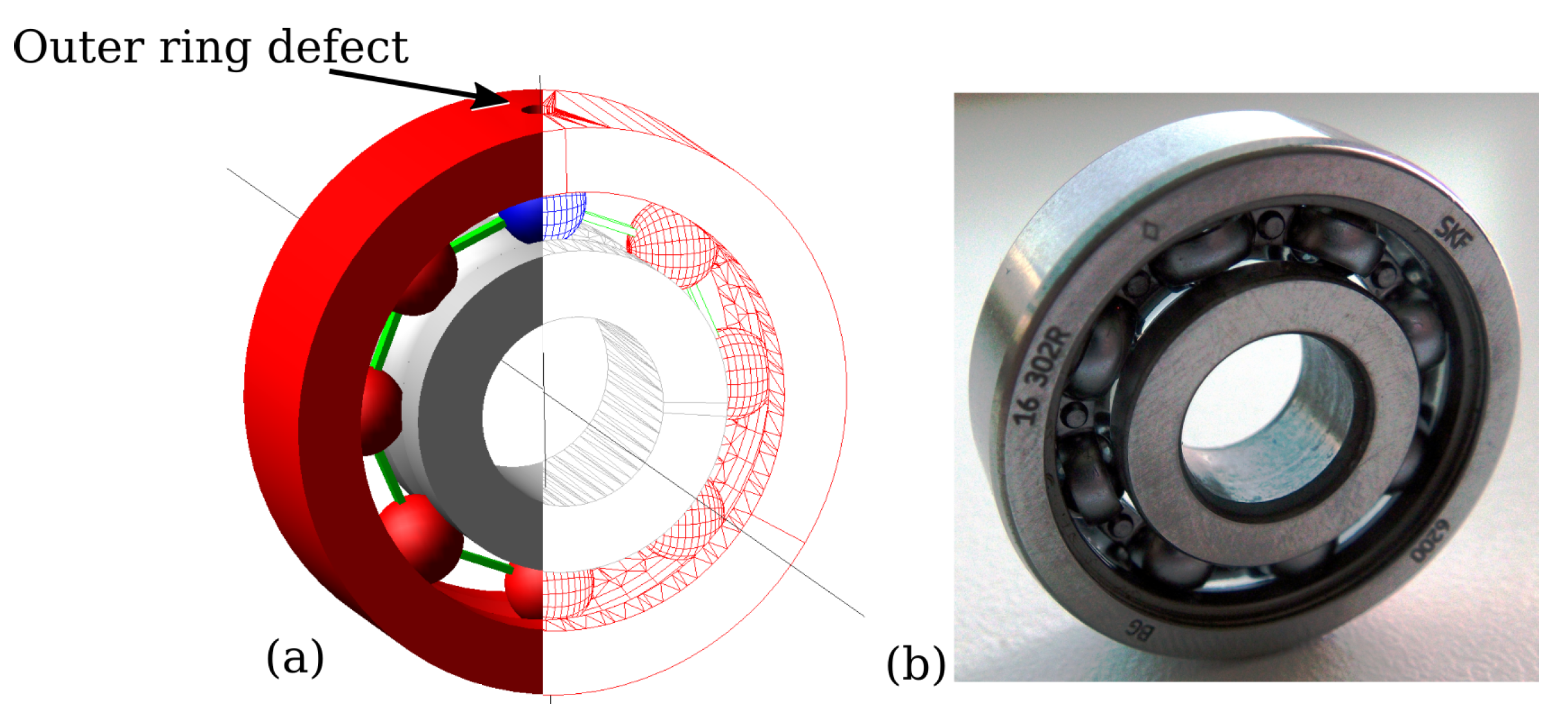
2.1. Simulation Setting
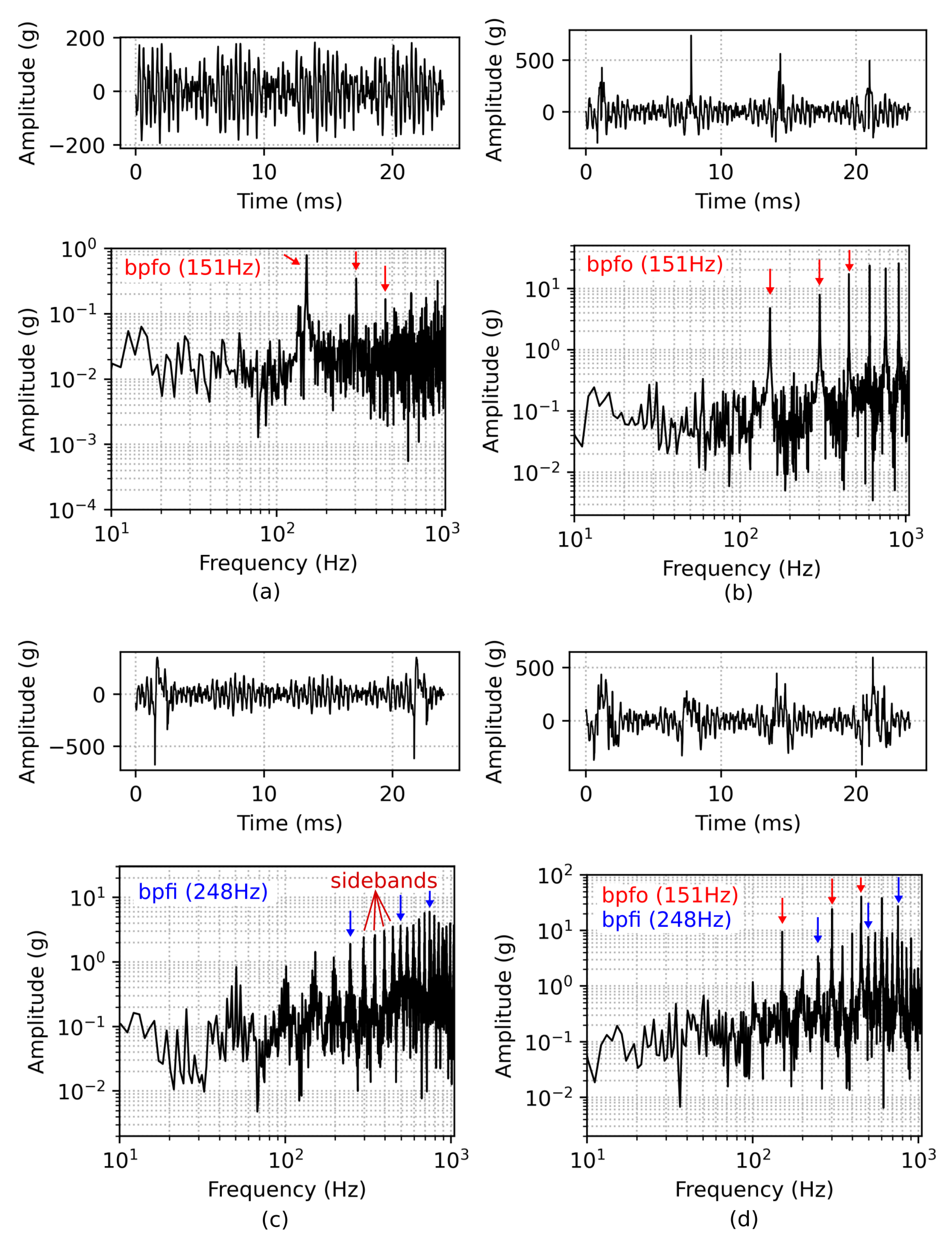
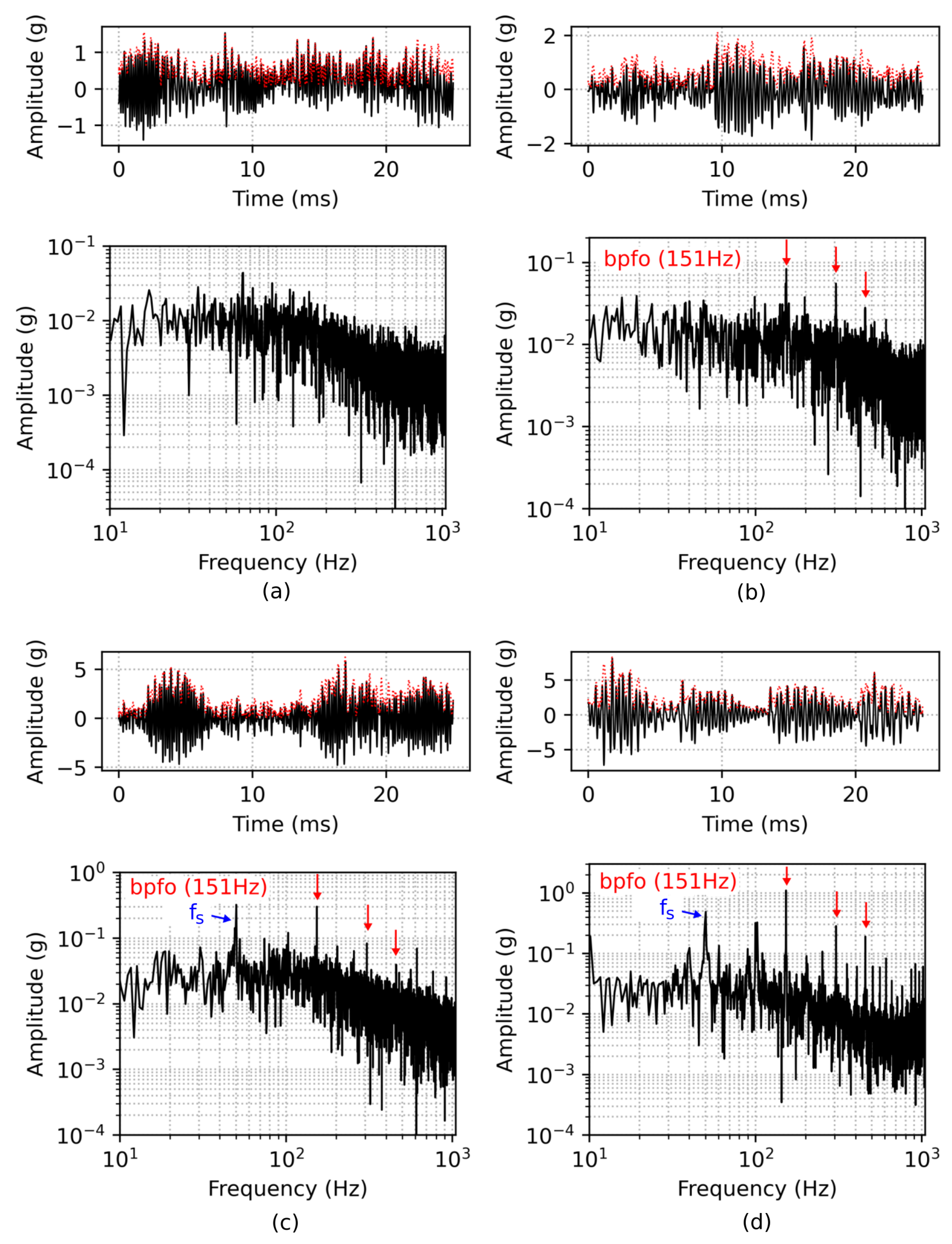
2.2. Simulation Results
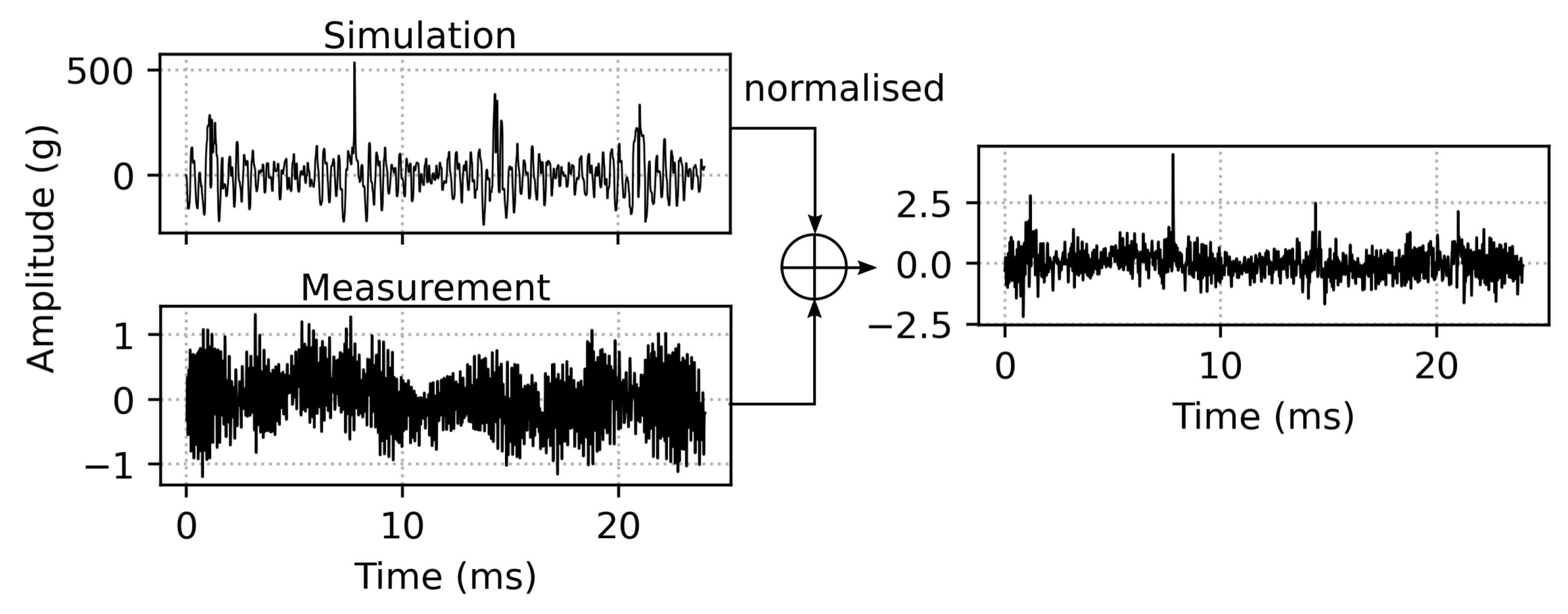
3. Measurement
Measurement Results
4. Convolutional Neural Network
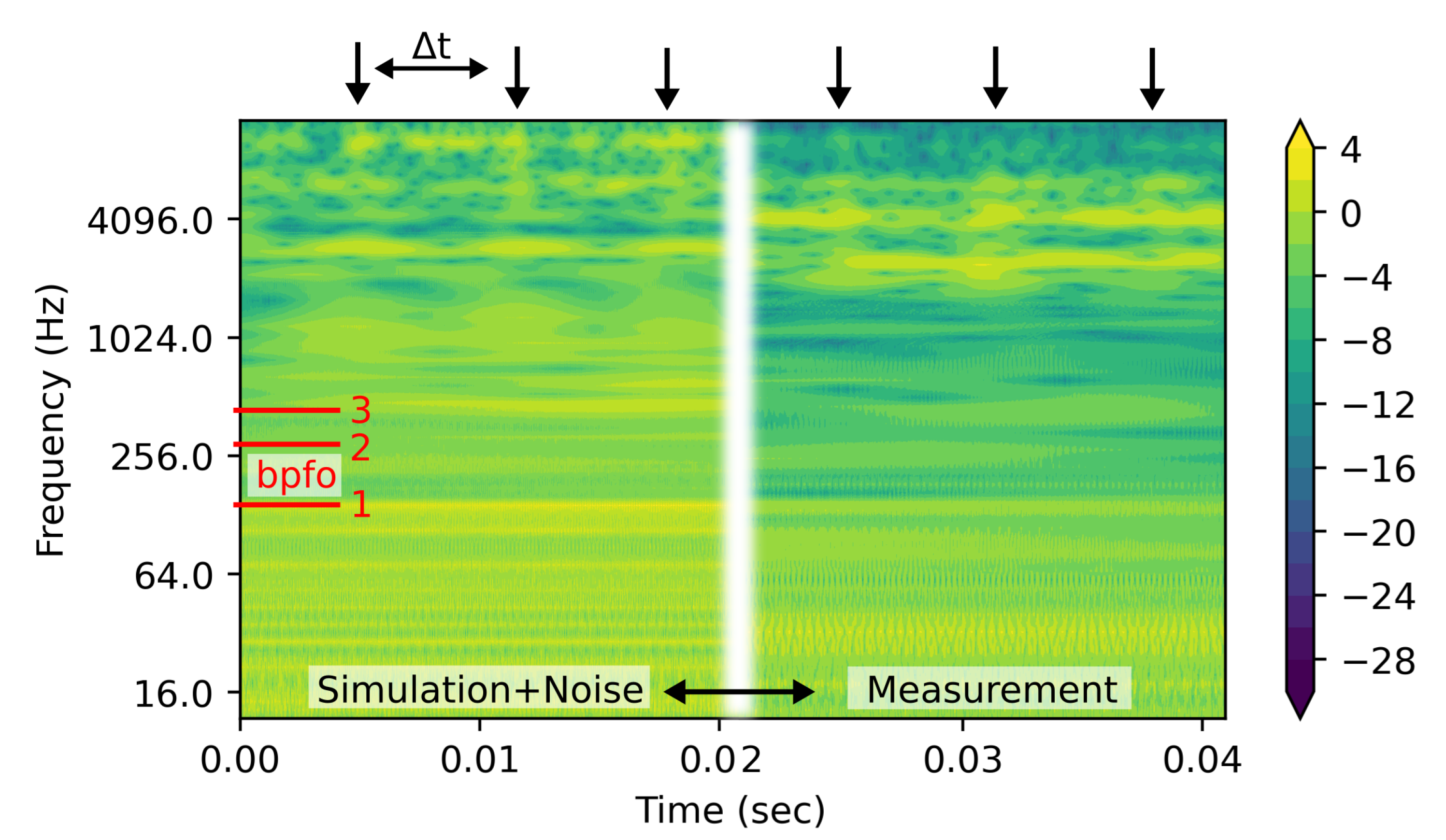
4.1. Data Preprocessing
4.2. Wavelet Transformation and Image Compilation
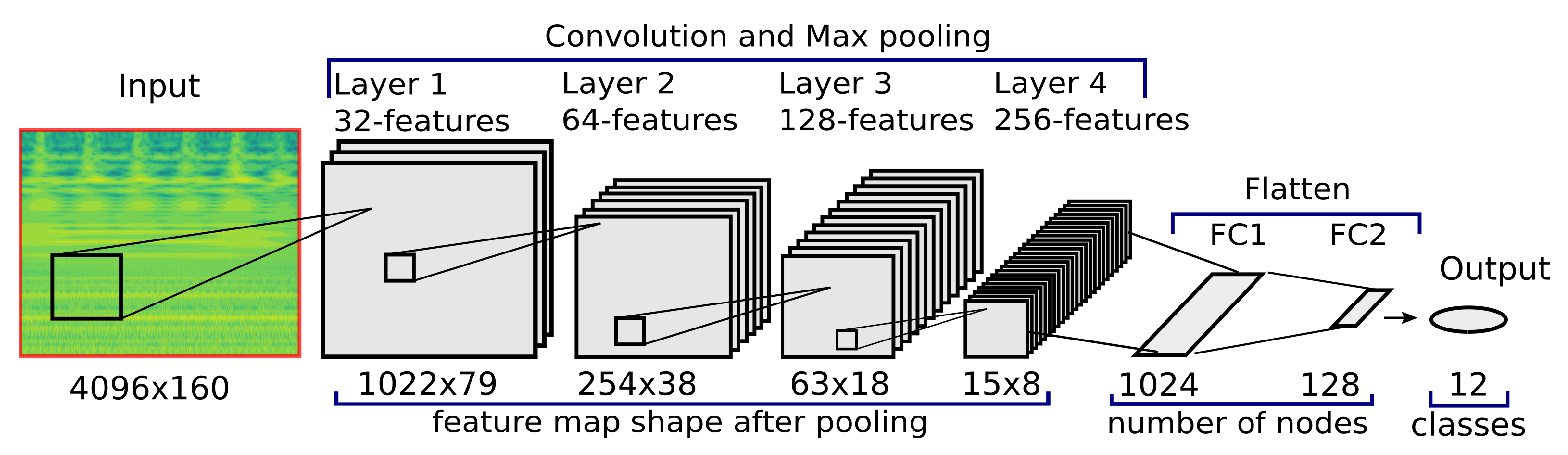
4.3. CNN-Network Architecture
5. Results
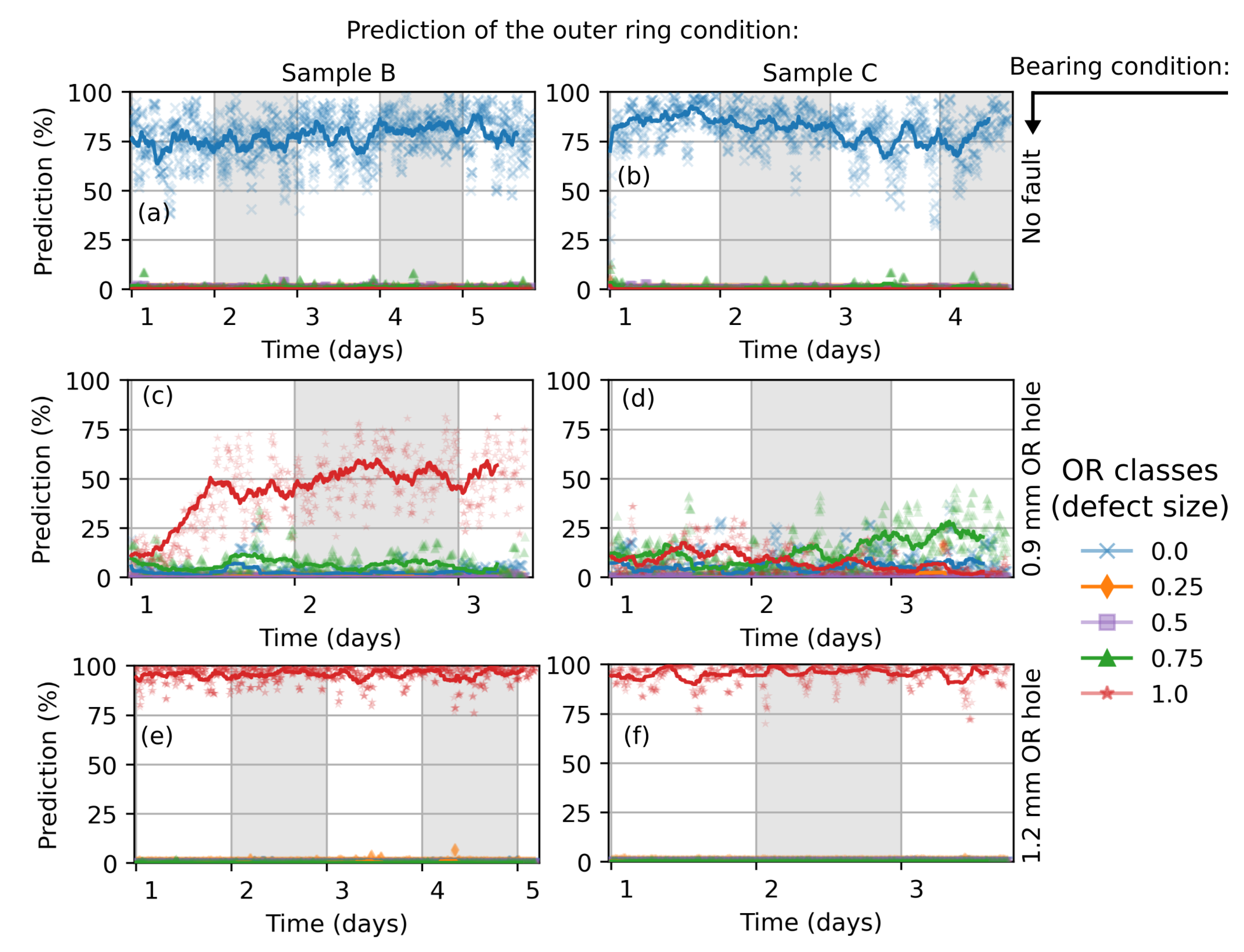
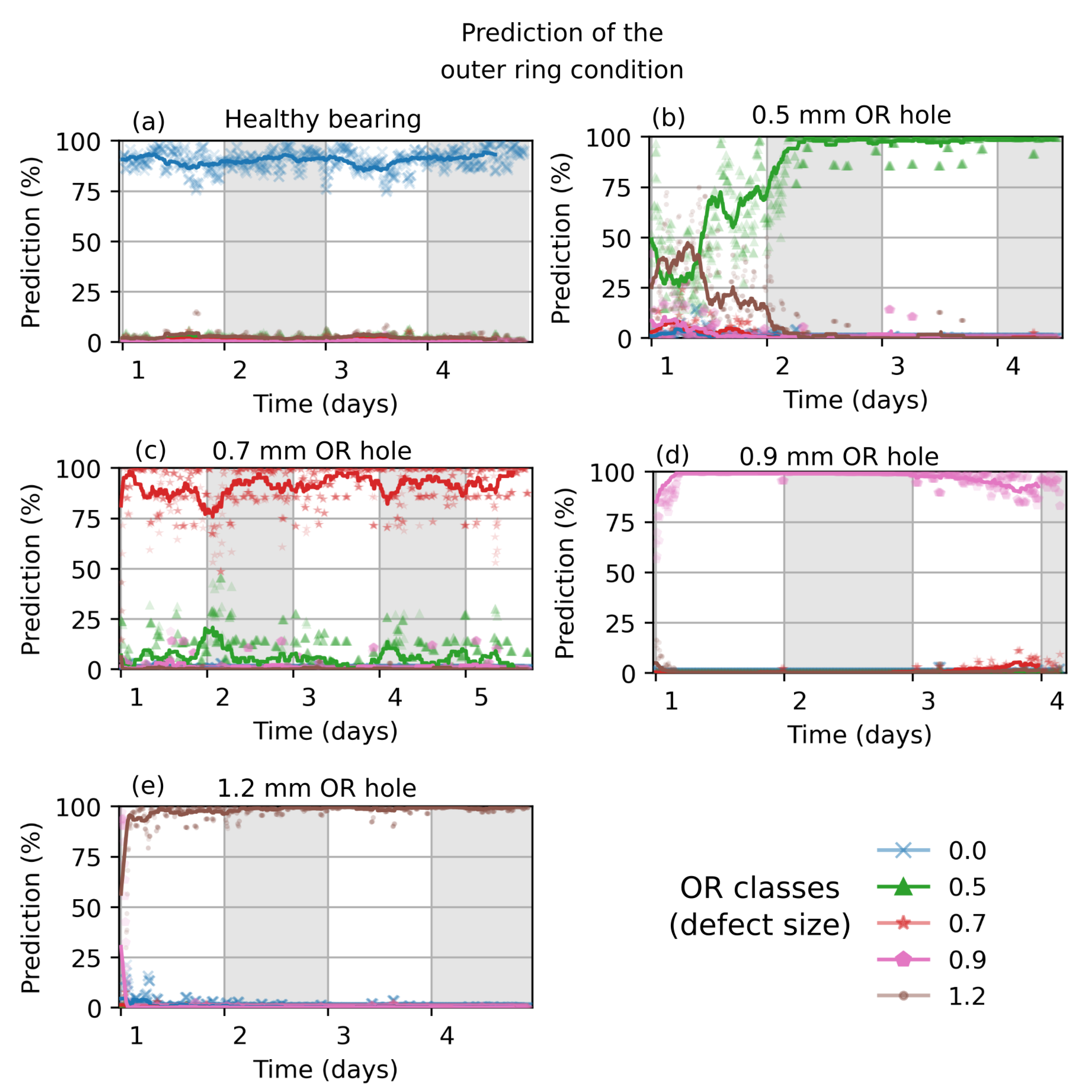
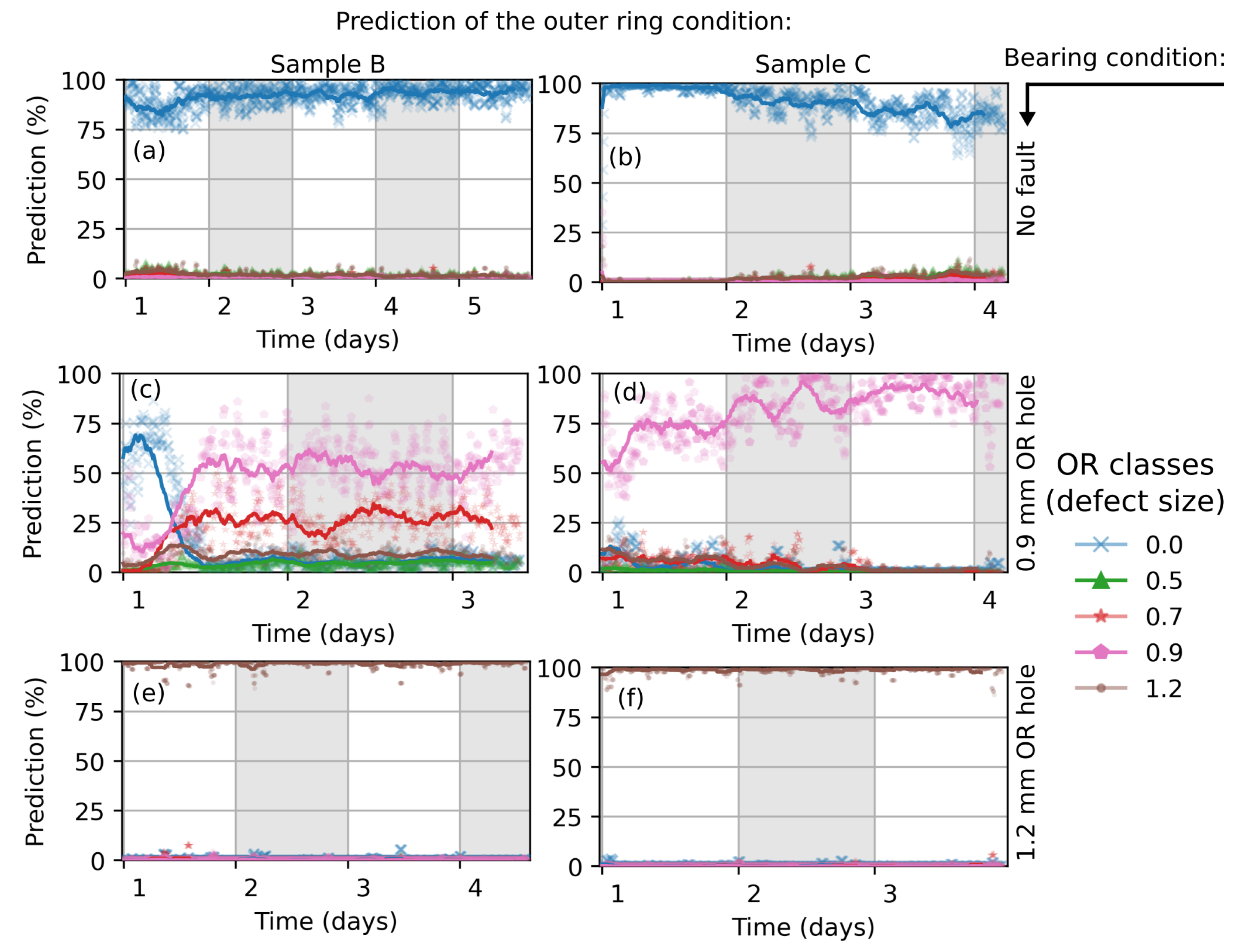
5.1. CNN-Trained with Simulation Data
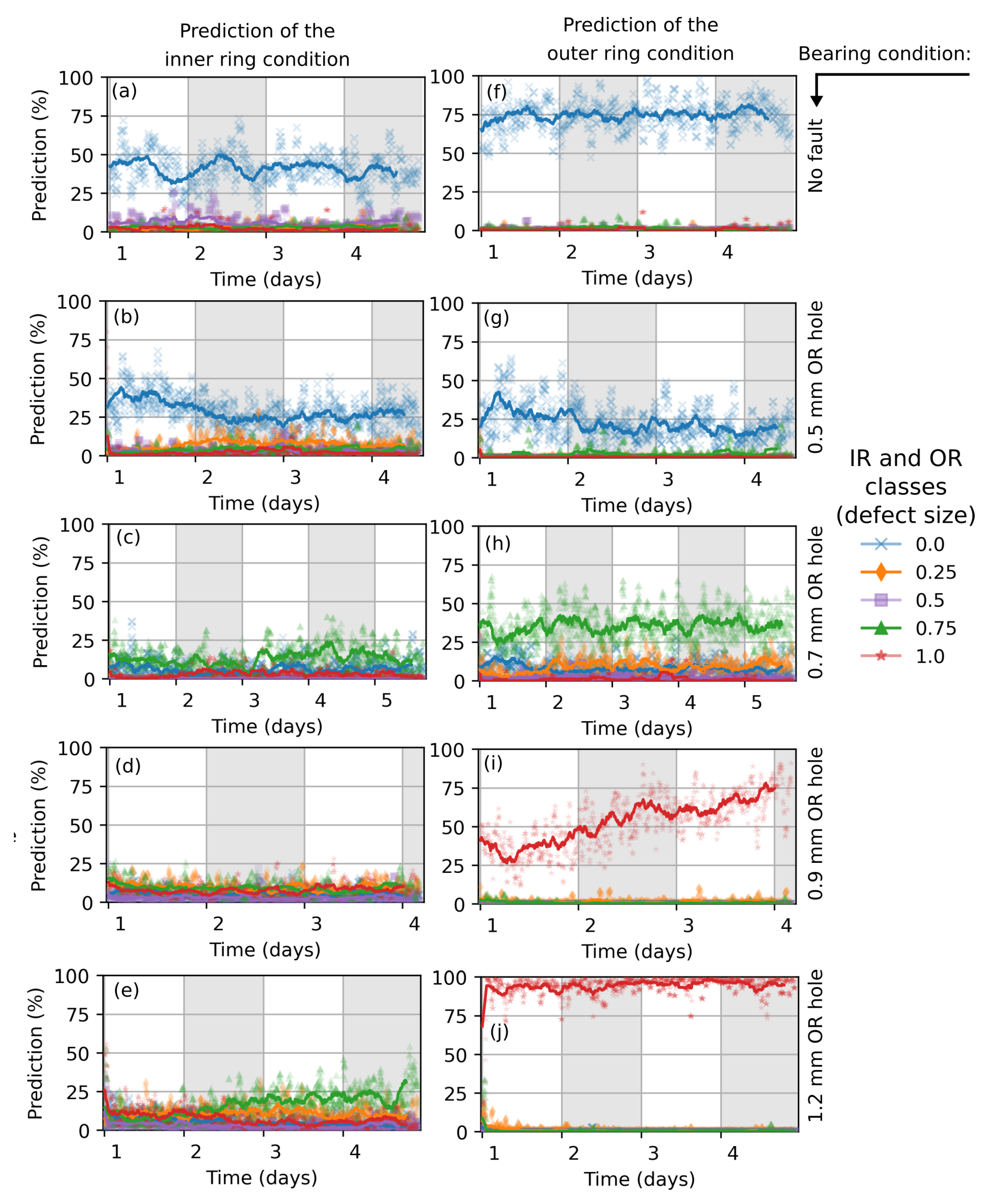
5.2. CNN-Trained with Measurement Data
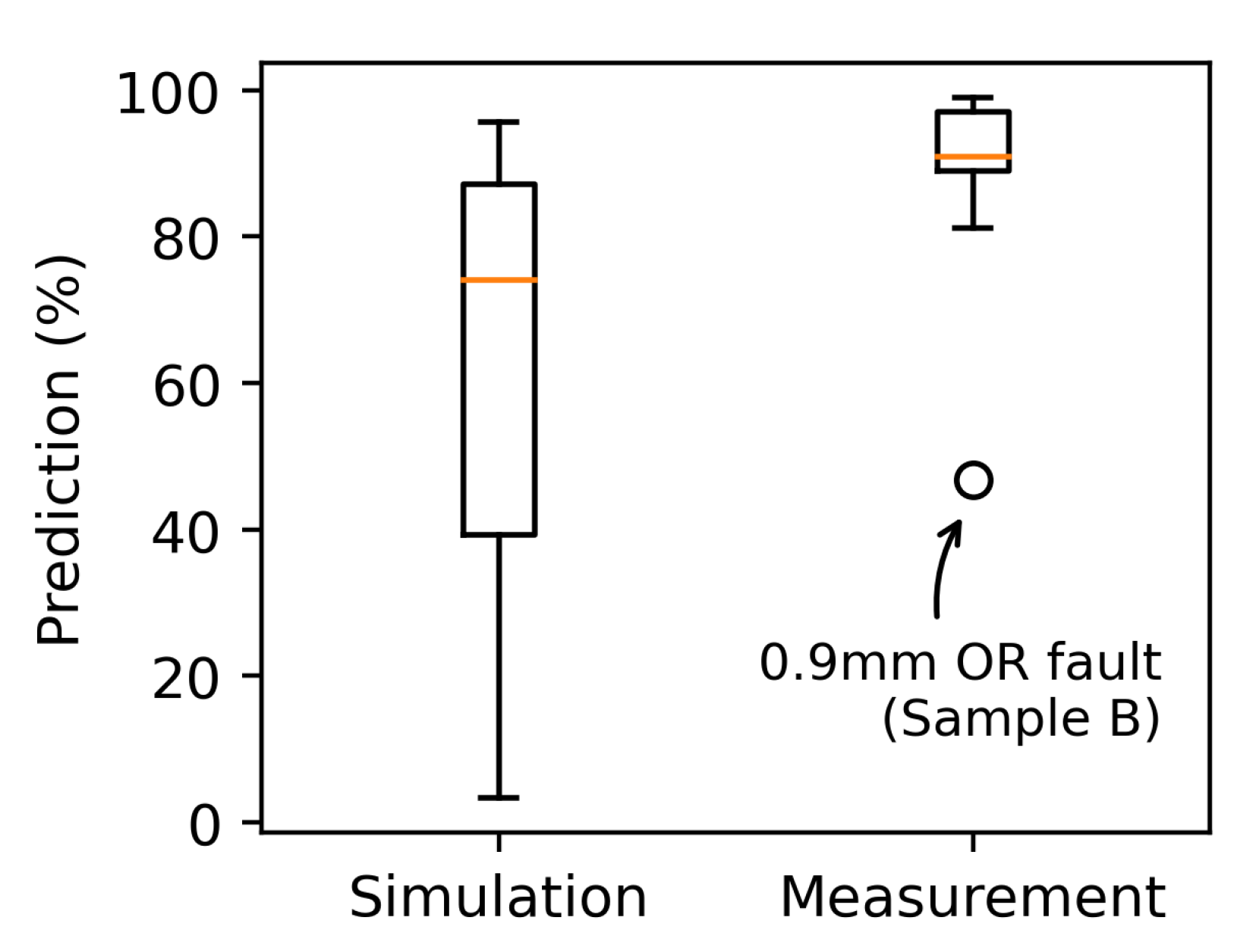
6. Discussion and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, G.K. Induction machine drive condition monitoring and diagnostic research—A survey. Electr. Power Syst. Res. 2003, 64, 145–158. [Google Scholar]
- Bonnett, A.H. Root cause AC motor failure analysis with a focus on shaft failures. IEEE Trans. Ind. Appl. 2000, 36, 1435–1448. [Google Scholar]
- Motor Reliability Working Group. Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part I. IEEE Trans. Ind. Appl. 1985, IA-21, 853–864. [Google Scholar]
- Zhang, X.; Wang, B.; Chen, X. Intelligent fault diagnosis of roller bearings with multivariable ensemble-based incremental support vector machine. Knowl.-Based Syst. 2015, 89, 56–85. [Google Scholar]
- Dolenc, B.; Boškoski, P.; Juričić, Đ. Distributed bearing fault diagnosis based on vibration analysis. Mech. Syst. Signal Process. 2016, 66–67, 521–532. [Google Scholar]
- Li, C.; De Oliveira, J.V.; Cerrada, M.; Pacheco, F.; Cabrera, D.; Sanchez, V.; Zurita, G. Observer-biased bearing condition monitoring: From fault detection to multi-fault classification. Eng. Appl. Artif. Intell. 2016, 50, 287–301. [Google Scholar]
- Shao, H.; Jiang, H.; Li, X.; Wu, S. Intelligent fault diagnosis of rolling bearing using deep wavelet auto-encoder with extreme learning machine. Knowl.-Based Syst. 2018, 140, 1–14. [Google Scholar]
- Chen, H.-Y.; Lee, C.-H. Deep Learning Approach for Vibration Signals Applications. Sensors 2021, 21, 3929. [Google Scholar] [PubMed]
- Zhang, J.; Jiang, Y.; Wu, S.; Li, X.; Luo, H.; Yin, S. Prediction of remaining useful life based on bidirectional gated recurrent unit with temporal self-attention mechanism. Reliab. Eng. Syst. Saf. 2022, 221, 108297. [Google Scholar]
- Zhu, J.; Nostr, T.; Spiegel, C.; Morton, B. Survey of Condition Indicators for Condition Monitoring Systems. In Proceedings of the Annual Conference of the PHM Society, Zhangjiajie, China, 29 September–2 October 2014. [Google Scholar]
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60–61, 252–272. [Google Scholar]
- Mishra, C.; Samantaray, A.K.; Chakraborty, G. Ball bearing defect models: A study of simulated and experimental fault signatures. J. Sound Vib. 2017, 400, 86–112. [Google Scholar]
- Sobie, C.; Freitas, C.; Nicolai, M. Simulation-driven machine learning: Bearing fault classification. Mech. Syst. Signal Process. 2018, 99, 403–419. [Google Scholar]
- Jiang, Y.; Yin, S.; Dong, J.; Kaynak, O. A Review on Soft Sensors for Monitoring, Control, and Optimization of Industrial Processes. IEEE Sens. J. 2021, 21, 12868–12881. [Google Scholar]
- Wang, J.; Mo, Z.; Zhang, H.; Miao, Q. A Deep Learning Method for Bearing Fault Diagnosis Based on Time-Frequency Image. IEEE Access 2019, 7, 42373–42383. [Google Scholar]
- Zhang, Y.; Xing, K.; Bai, R.; Sun, D.; Meng, Z. An enhanced convolutional neural network for bearing fault diagnosis based on time-frequency image. Measurement 2020, 157, 107667. [Google Scholar]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark dataset for Data-Driven Classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Hemmer, M.; Van Khang, H.; Robbersmyr, K.G.; Waag, T.I.; Meyer, T.J. Fault Classification of Axial and Radial Roller Bearings Using Transfer Learning through a Pretrained Convolutional Neural Network. Designs 2018, 2, 56. [Google Scholar]
- Mechanical Failures Prevention Group (MFPT) Society (a Division of the Vibration Institute). Available online: http://www.mfpt.org/FaultData/FaultData.htm (accessed on 16 July 2021).
- Machinery Fault Simulator. Available online: http://www02.smt.ufrj.br/~offshore/mfs/page_01.html (accessed on 16 July 2021).
- Huang, H.; Baddour, N. Bearing Vibration Data under Time-varying Rotational Speed Conditions. Mendeley Data V2. Available online: https://data.mendeley.com/datasets/v43hmbwxpm/2 (accessed on 16 July 2021).
- Lee, J.; Lee, J.; Qiu, H.; Yu, G.; Lin, J.; Rexnord Technical Services. Bearing Data Set; IMS, University of Cincinnati, NASA Ames Research Center: Moffett Field, CA, USA, 2007. Available online: http://https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/ (accessed on 16 July 2021).
- McFadden, P.D.; Smith, J.D. Model for the vibration produced by a single point defect in a rolling element bearing. J. Sound Vib. 1984, 96, 69–82. [Google Scholar]
- McFadden, P.D.; Smith, J.D. The vibration produced by multiple point defects in a rolling element bearing. J. Sound Vib. 1985, 98, 263–273. [Google Scholar]
- Su, Y.-T.; Lin, S.-J. On Initial Fault Detection of a Tapered Roller Bearing: Frequency Domain Analysis. J. Sound Vib. 1992, 155, 75–84. [Google Scholar]
- Su, Y.T.; Lin, M.H.; Lee, M.S. The Effects of Surface Irregularities on Roller Bearing Vibrations. J. Sound Vib. 1993, 165, 455–466. [Google Scholar]
- Ho, D.; Randall, R.B. Optimisation of Bearing Diagnostic Techniques Using Simulated and Actual Bearing Fault Signals. Mech. Syst. Signal Process. 2000, 14, 763–788. [Google Scholar]
- Gupta, P.K. Transient Ball Motion and Skid in Ball Bearings. ASME J. Lubr. Technol. 1975, 97, 261–269. [Google Scholar]
- Fukata, S.; Gad, E.H.; Kondou, T.; Ayabe, T.; Tamura, H. On the Radial Vibration of Ball Bearings: Computer Simulation. Bull. JSME 1985, 28, 899–904. [Google Scholar]
- Leturiondo, U.; Salgado, O.; Galar, D. Methodology for the Physics-Based Modelling of Multiple Rolling Element Bearing Configurations. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2017, 231, 194–212. [Google Scholar]
- Kong, F.; Huang, W.; Jiang, Y.; Wang, W.; Zhao, X. A Vibration Model of Ball Bearings with a Localized Defect Based on the Hertzian Contact Stress Distribution. Shock Vib. 2018, 2018, 5424875. [Google Scholar]
- MSCAdams-Multibody Dynamics Simulation, MSC Software. Available online: https://www.mscsoftware.com/product/adams (accessed on 25 August 2021).
- SKF. Deep Groove Ball Bearing 6200. Available online: https://www.skf.com/uk/products/rolling-bearings/ball-bearings/deep-groove-ball-bearings/productid-6200 (accessed on 9 December 2021).
- RAPID—Robust and Accurate Polygon Interference Detection, GAMMA Research Group, University of North Carolina. Available online: http://gamma.cs.unc.edu/OBB/ (accessed on 25 August 2021).
- Gottschalk, S.; Lin, M.C.; Manocha, D. OBBTree: A Hierarchical Structure for Rapid Interference Detection. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 171–180. [Google Scholar]
- Dempsey, P.J.; Lewicki, D.G.; Decker, H.J. Transmission Bearing Damage Detection Using Decision Fusion Analysis; Technical Memorandum (TM); NASA: Washington, DC, USA, 2004. [Google Scholar]
- Broderick, J.J.; Burchill, R.F.; Clark, H.L. Design and Fabrication of Prototype System for Early Warning of Impending Bearing Failure; MTI-71TR Contractor Report (CR); NASA: Washington, DC, USA, 1972. [Google Scholar]
- Nikolaou, N.G.; Antoniadis, I.A. Demodulation of Vibration Signals Generated by Defects in Rolling Element Bearings Using Complex Shifted Morlet Wavelets. Mech. Syst. Signal Process. 2002, 16, 677–694. [Google Scholar]
- Çınar, Z.M.; Abdussalam Nuhu, A.; Zeeshan, Q.; Korhan, O.; Asmael, M.; Safaei, B. Machine Learning in Predictive Maintenance towards Sustainable Smart Manufacturing in Industry 4.0. Sustainability 2020, 12, 8211. [Google Scholar]
- Wang, S.; Xiang, J.; Zhong, Y.; Zhou, Y. Convolutional neural network-based hidden Markov models for rolling element bearing fault identification. Knowl.-Based Syst. 2018, 144, 65–76. [Google Scholar]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; De Silva, C.W. Fault Diagnosis for Rotating Machinery Using Multiple Sensors and Convolutional Neural Networks. IEEE/ASME Trans. Mechatron. 2018, 23, 101–110. [Google Scholar]
- Lu, C.; Wang, Z.; Zhou, B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv. Eng. Inform. 2017, 32, 139–151. [Google Scholar]
- Tra, V.; Khan, S.A.; Kim, J. Diagnosis of bearing defects under variable speed conditions using energy distribution maps of acoustic emission spectra and convolutional neural networks. J. Acoust. Soc. Am. 2018, 144, EL322–EL327. [Google Scholar] [PubMed]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar]
- Chernogor, L.F.; Lazorenko, O.V. Application of the wavelet analysis for detecting ultra-wideband signals in noise. In Proceedings of the 2000 International Conference on Mathematical Methods in Electromagnetic Theory, Kharkov, Ukraine, 12–15 September 2000; Volume 1, pp. 233–235. [Google Scholar]
- Rafiee, J.; Arvani, F.; Harifi, A.; Sadeghi, M.H. Intelligent condition monitoring of a gearbox using artificial neural network. Mech. Syst. Signal Process. 2007, 21, 1746–1754. [Google Scholar]
- Tóth, L.; Tóth, T. On Finding Better Wavelet Basis for Bearing Fault Detection. Acta Polytech. Hung. 2013, 10, 17–35. [Google Scholar]
- Keras. Open-Source Software Library for Artificial Neural Networks (Python). Available online: https://keras.io/ (accessed on 13 March 2022).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahr, M.; Kovács, G.; Loinig, M.; Brückl, H. Condition Monitoring of Ball Bearings Based on Machine Learning with Synthetically Generated Data. Sensors 2022, 22, 2490. https://doi.org/10.3390/s22072490
Kahr M, Kovács G, Loinig M, Brückl H. Condition Monitoring of Ball Bearings Based on Machine Learning with Synthetically Generated Data. Sensors. 2022; 22(7):2490. https://doi.org/10.3390/s22072490
Chicago/Turabian StyleKahr, Matthias, Gabor Kovács, Markus Loinig, and Hubert Brückl. 2022. "Condition Monitoring of Ball Bearings Based on Machine Learning with Synthetically Generated Data" Sensors 22, no. 7: 2490. https://doi.org/10.3390/s22072490
APA StyleKahr, M., Kovács, G., Loinig, M., & Brückl, H. (2022). Condition Monitoring of Ball Bearings Based on Machine Learning with Synthetically Generated Data. Sensors, 22(7), 2490. https://doi.org/10.3390/s22072490






