Multiple-Actuator Fault Isolation Using a Minimal ℓ1-Norm Solution with Applications in Overactuated Electric Vehicles
Abstract
:1. Introduction
- Simultaneously occurring multiple-actuator faults are considered for FDI with fully utilizing the characteristics of overactuated system.
- With representing the residual equation of the overactuated system as an underdetermined linear system, fault isolation can be achieved by obtaining the sparsest nonzero component of the residuals from the minimal -norm solution. The computational load is consistently low regardless of the isolated number of faults.
- The experiments with a scaled-down overactuated EV are performed to support the effectiveness of the proposed method. In addition, because the sparsity condition highly depends on the system characteristics, a quantitative analysis of sparsity for the target EV is discussed.
2. Brief Summary of Structural Residual Analysis with Parity Relations
2.1. Fault Model
2.2. Multiple Fault Isolation with Structural Residual Analysis
| Algorithm 1 Fault isolation with structural residual analysis. | |
| Input: R(s) | |
| 1: | k: the assumed number of simultaneously occurring faults |
| 2: | is_ fault ← False |
| 3: | if > threshold then |
| 4: | is_ fault ← true |
| 5: | if is_ fault then |
| 6: | for do |
| 7: | for do |
| 8: | Implement s |
| 9: | |
| 10: | if is isolated successfully then |
| 11: | break |
3. Multiple Fault Isolation for an Overactuated System with a Minimal -Norm Solution
3.1. Residual Equation for Overactuated Systems
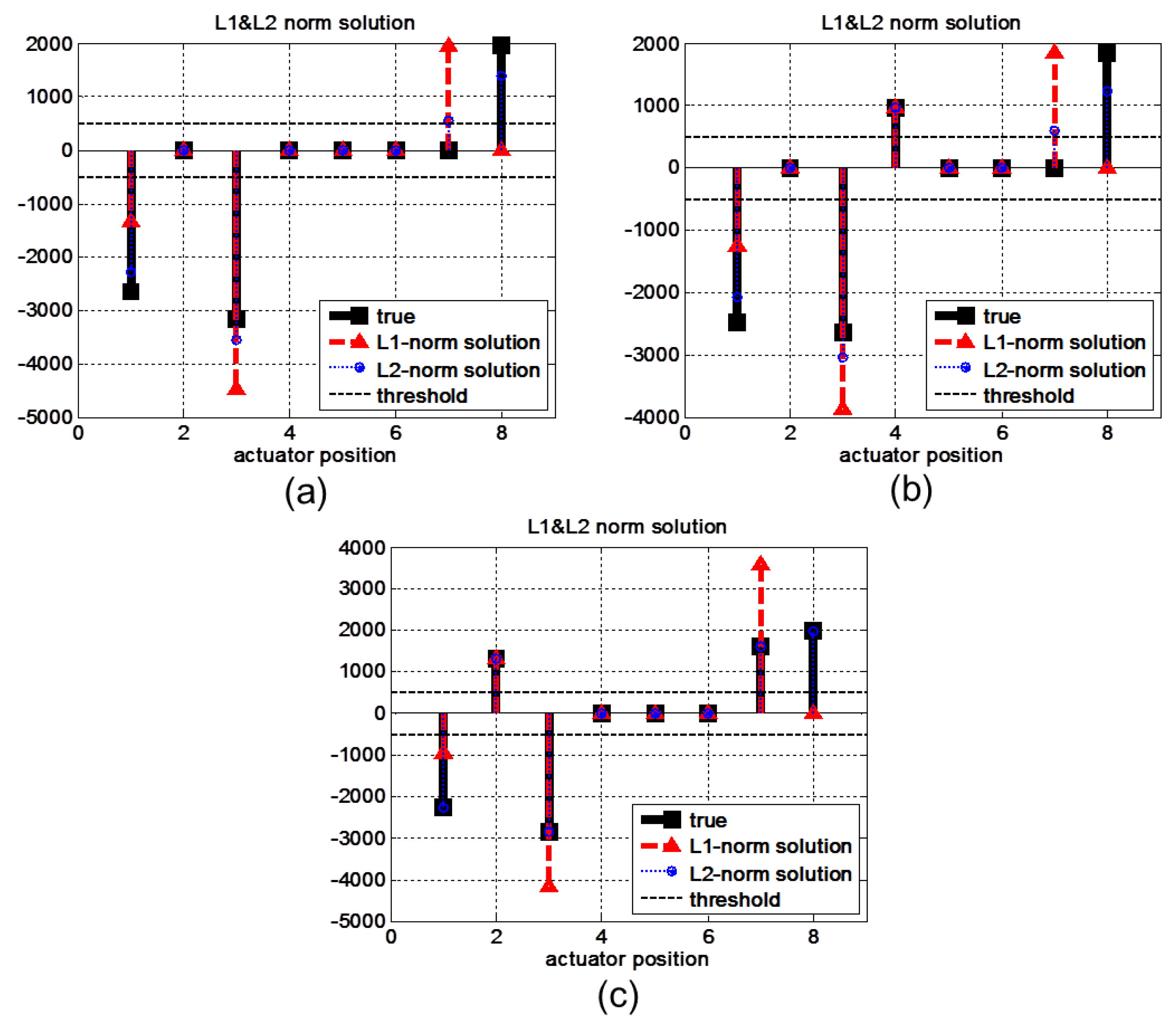
3.2. -Norm Minimization for the Sparsest Solution
| Algorithm 2 Fault isolation with the minimal -norm solution. | |
| Input: , r(t) | |
| 1: | |
| 2: | |
| 3: | is_ fault ← False |
| 4: | if > threshold then |
| 5: | is_ fault ← true |
| 6: | if is_ fault & steady state then |
| 7: | for do |
| 8: | ← |
| 9: | |
| 10: | |
| 11: | ← primal-dual algorithm() |
| 12: | return the number and locations of the nonzero components of |
4. Application to an Overactuated EV
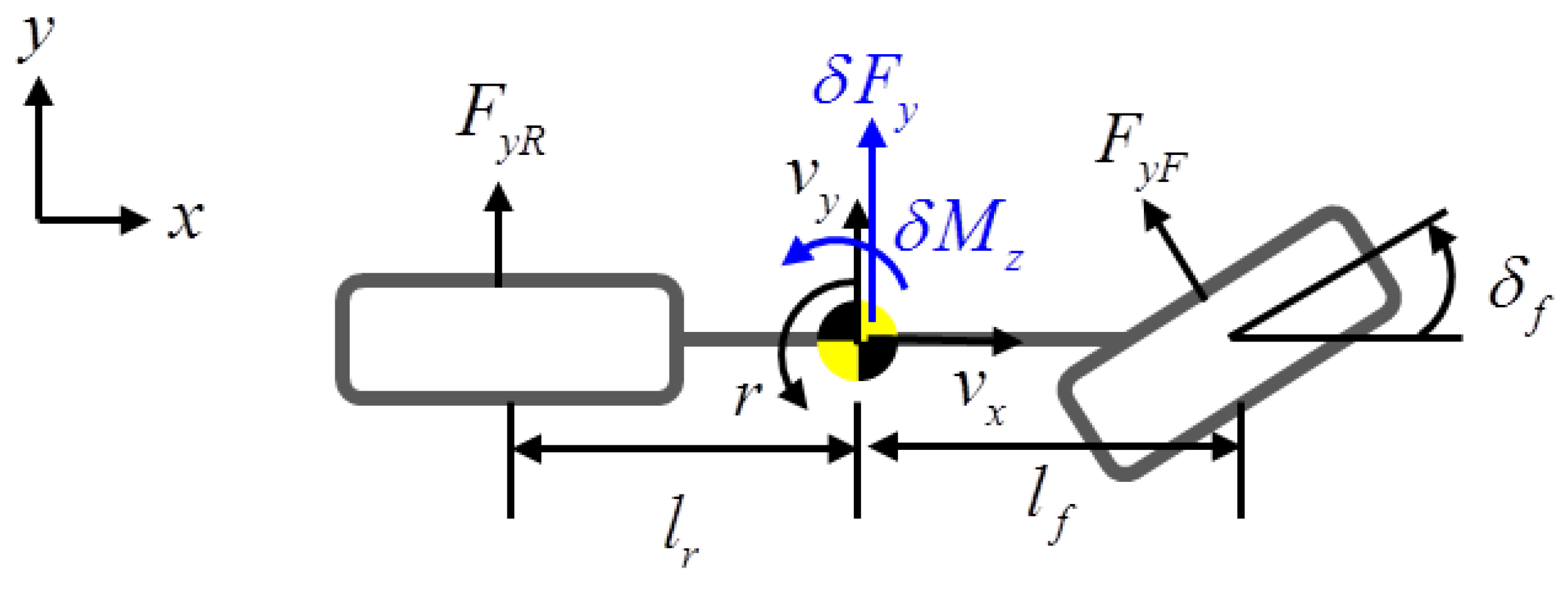
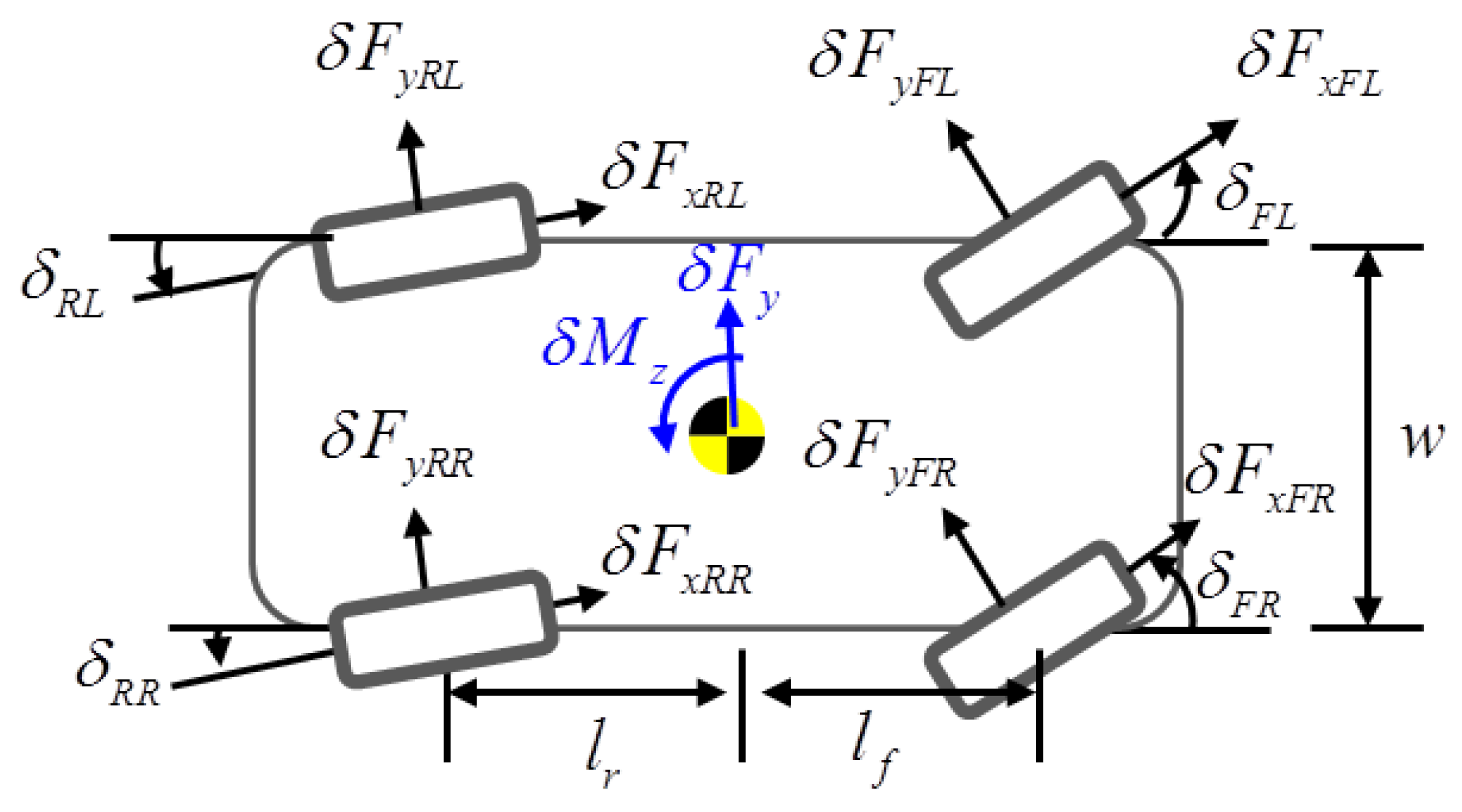
4.1. Dynamic Vehicle Model
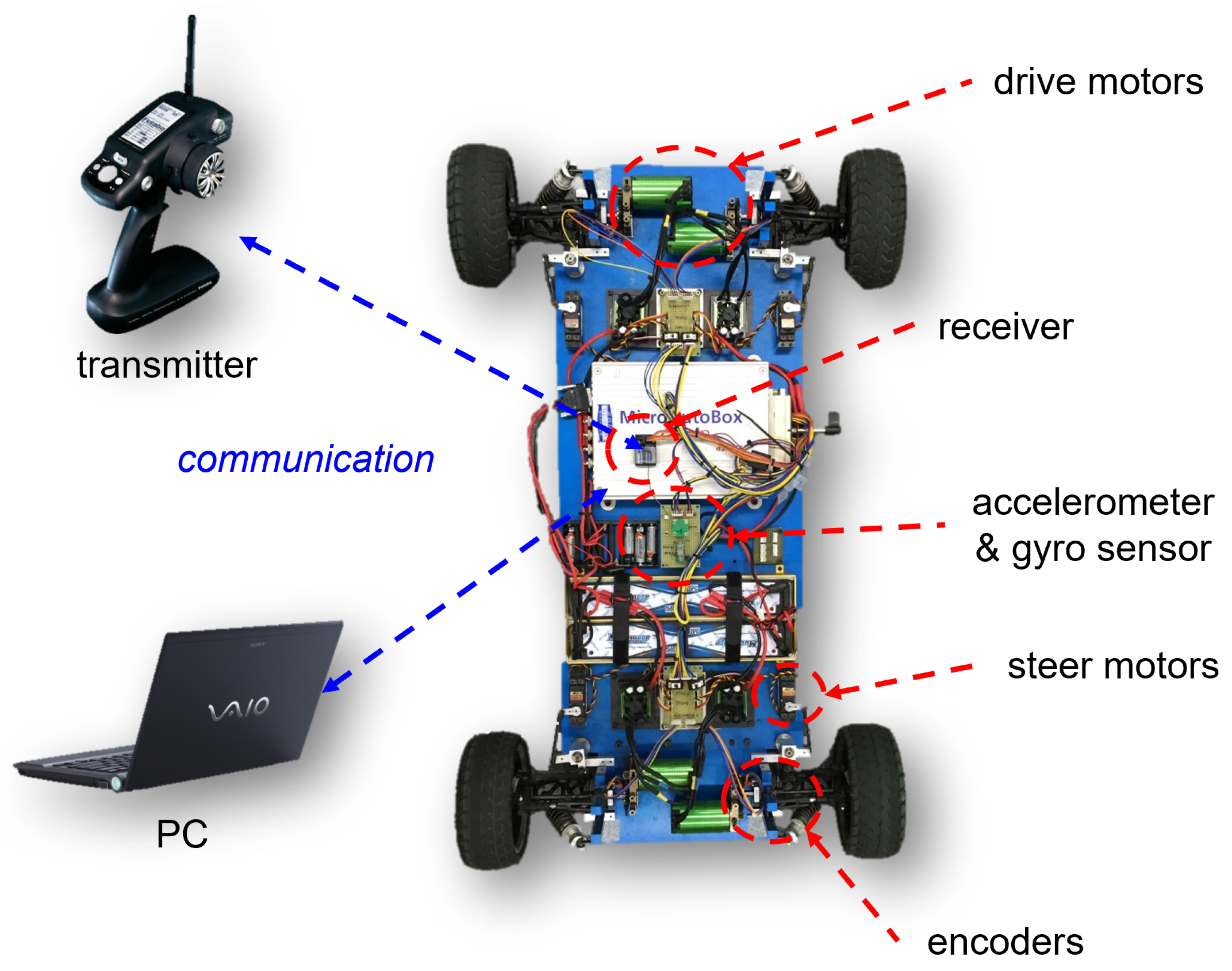
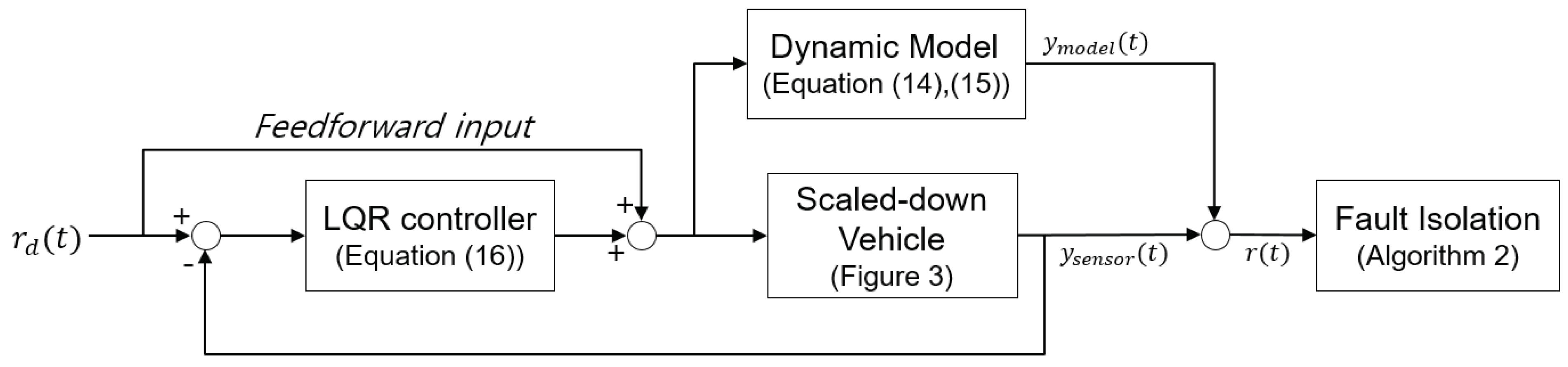
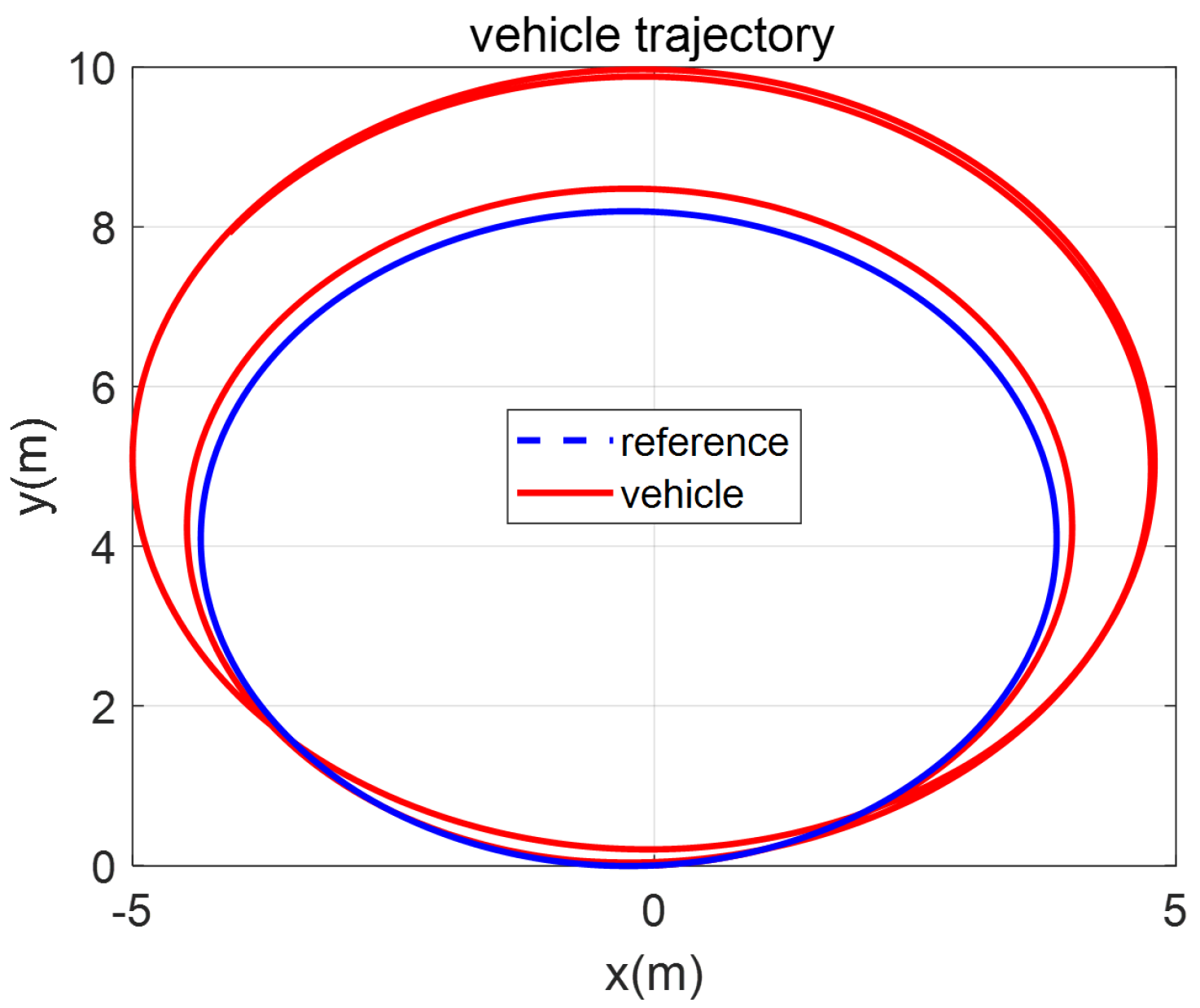
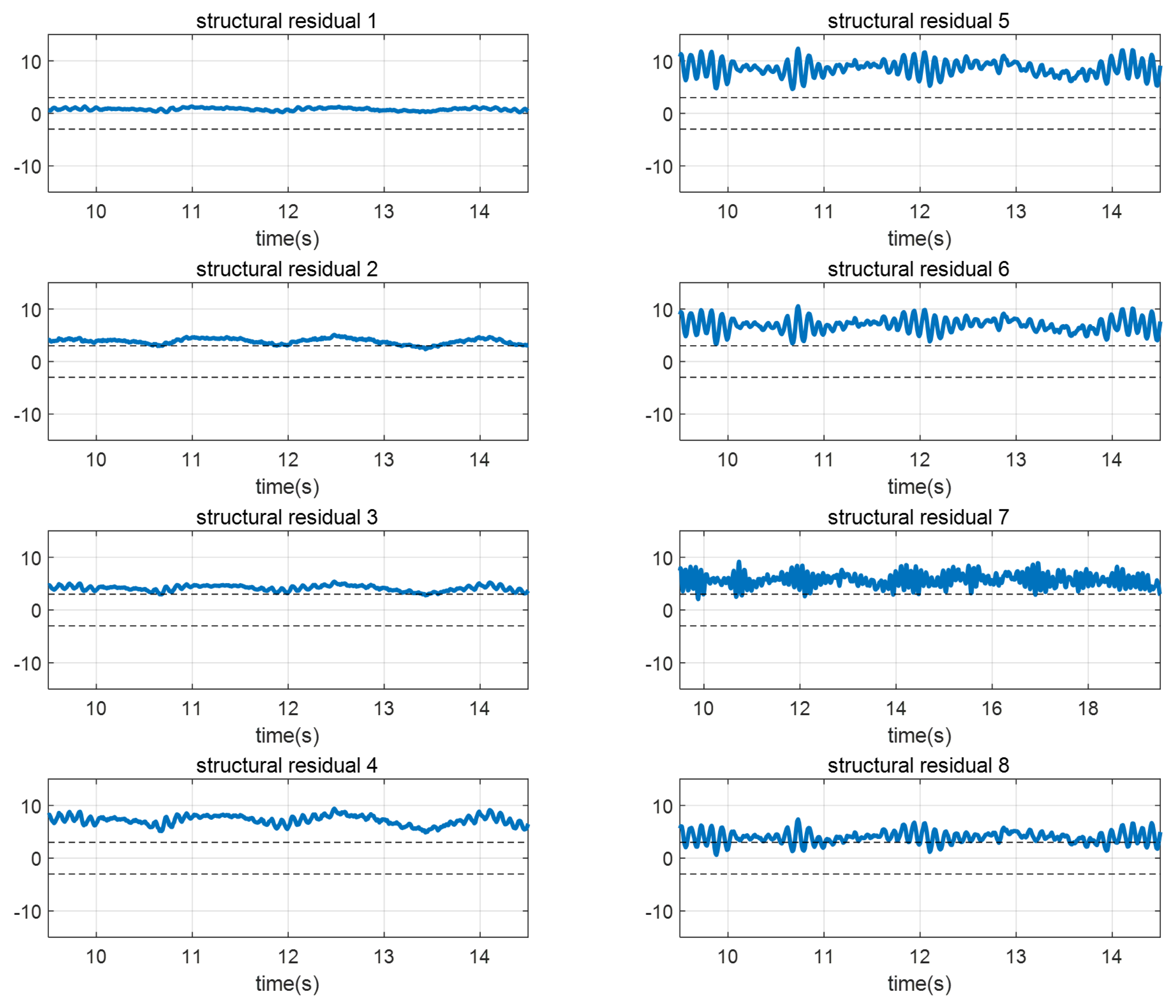
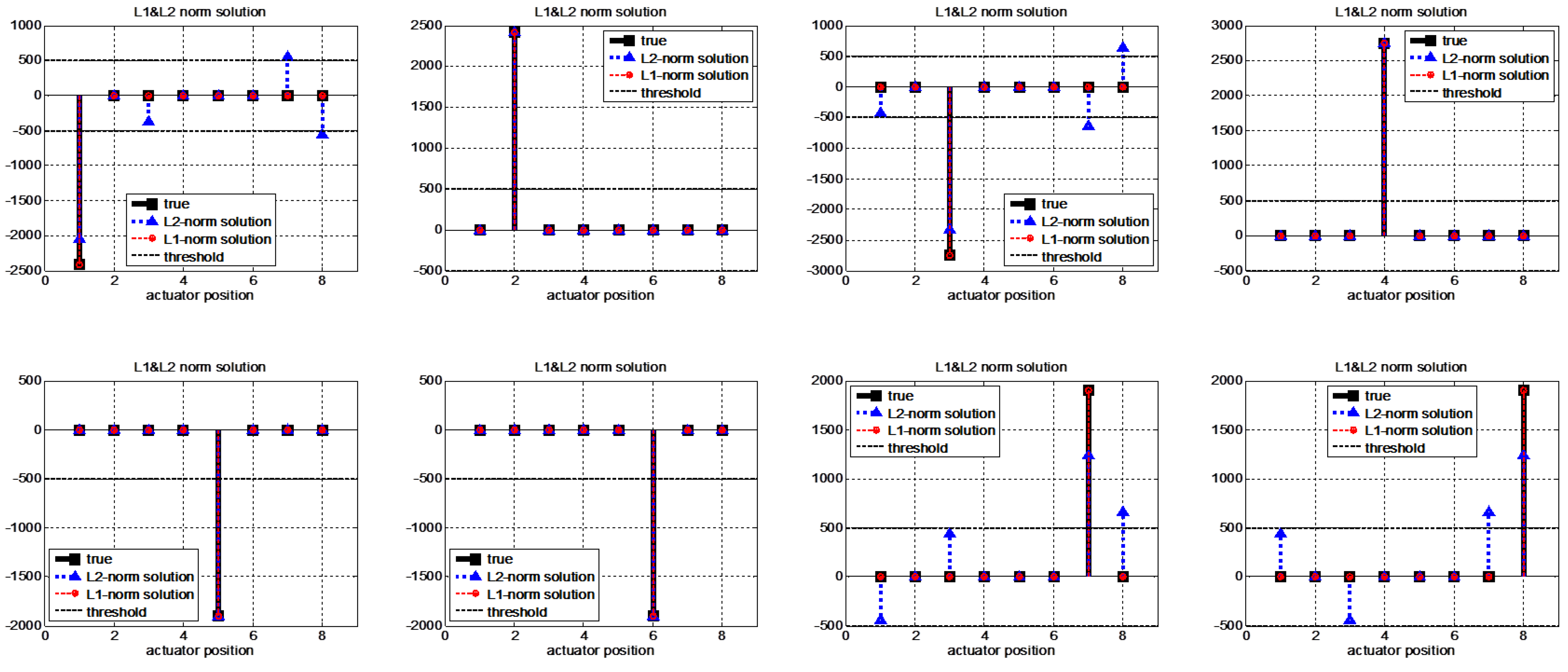
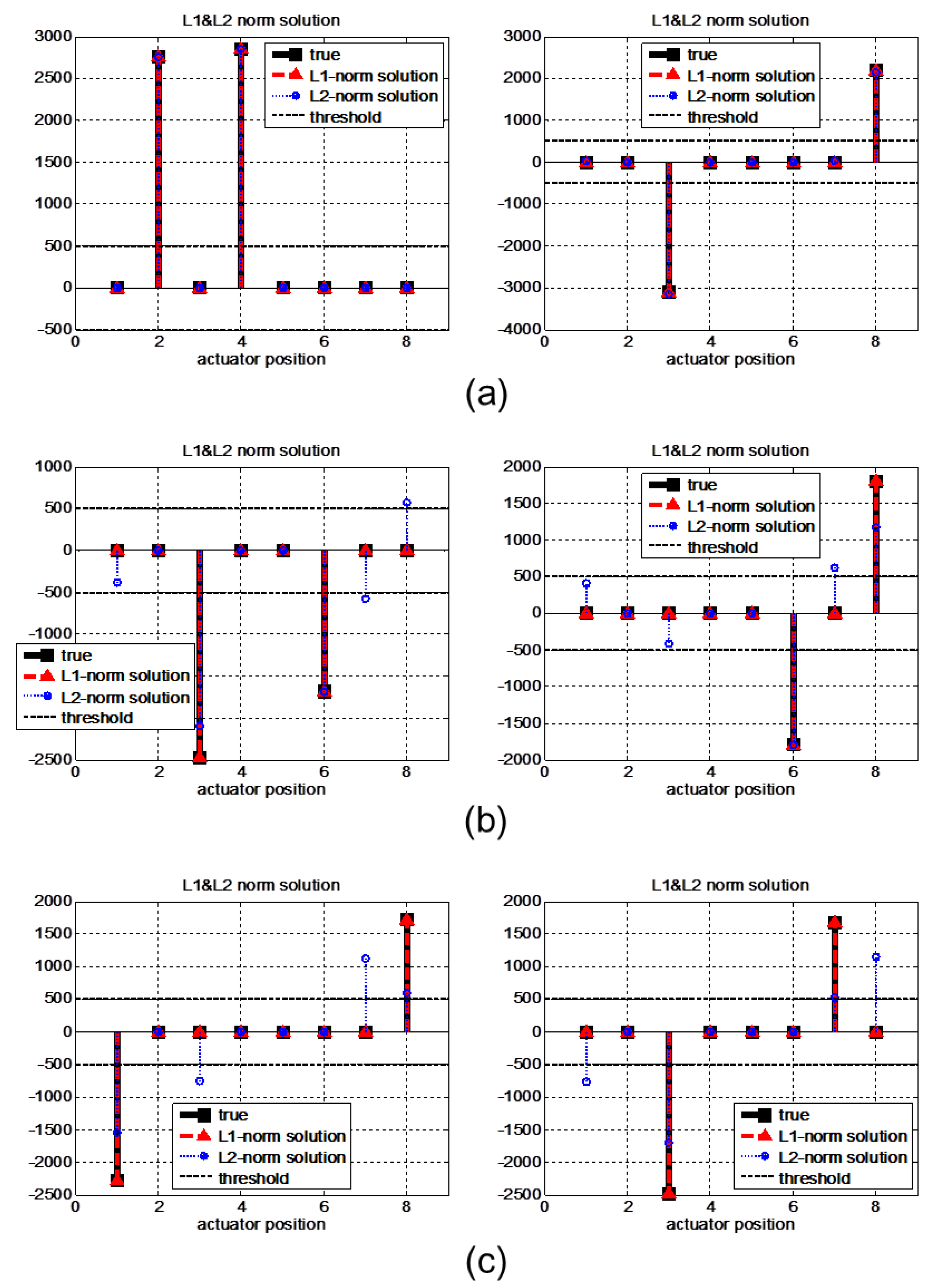
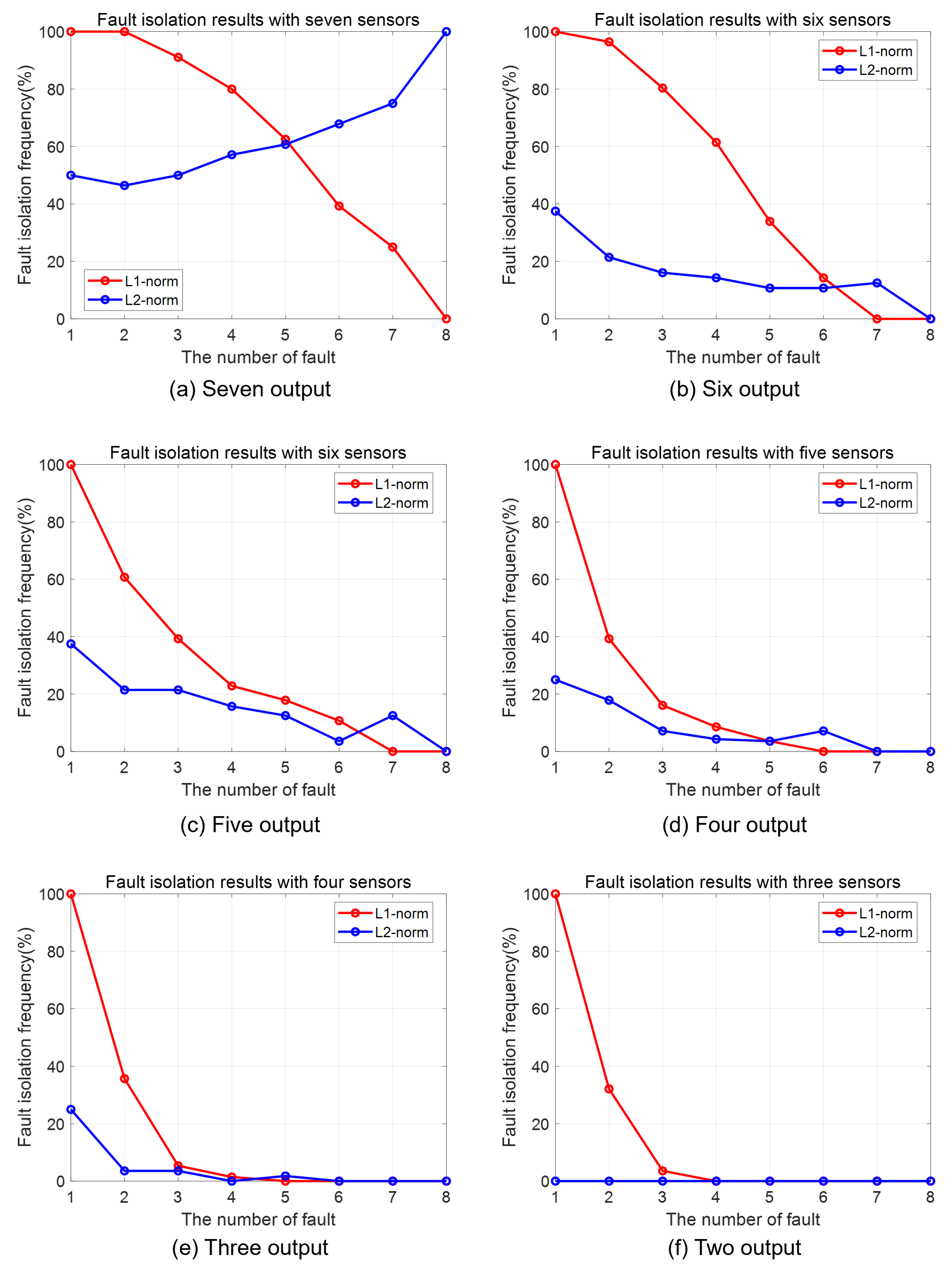
4.2. Experimental Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Minimal ℓ2 -Norm Solution
Appendix B. Sensor Fault Isolation with Minimal ℓ1 -Norm Solution
- If the residual value is nonzero due to the faults, obtain fault isolation results from the minimal -norm solution.
- If the fault isolation results are nonzero, we can decide that there are actuator faults in an isolated location.
- If the fault isolation results are zero in spite of nonzero residual occurrence, then we can decide that there are sensor faults rather than actuator faults. Furthermore, for the case of sensor faults, the position of nonzero residual components are directly the locations of sensor faults. Therefore, sensor fault isolation can be achieved easily.
References
- Murata, S. Innovation by in-wheel motor drive unit. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2012, 5, 807–830. [Google Scholar] [CrossRef]
- Shino, M.; Nagai, M. Independent wheel torque control of small-scale electric vehicle for handling and stability improvement. JSAE Rev. 2003, 24, 449–456. [Google Scholar] [CrossRef]
- Khelassi, A.; Weber, P.; Theilliol, D. Reconfigurable control design for over-actuated systems based on reliability indicators. In Proceedings of the Conference on Control and Fault-Tolerant Systems, Nice, France, 6–8 October 2010; pp. 365–370. [Google Scholar]
- Wang, J.; Longoria, R.G. Coordinated Vehicle Dynamic Control with Control Distribution. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 5348–5353. [Google Scholar]
- Alwi, H.; Edwards, C. Fault tolerant control using sliding modes with on-line control allocation. Automatica 2008, 44, 1859–1866. [Google Scholar] [CrossRef] [Green Version]
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A Survey of Fault Detection, Isolation, and Reconfiguration Methods. IEEE Trans. Control Syst. Technol. 2010, 18, 636–653. [Google Scholar] [CrossRef]
- Wang, H.; Daley, S. Actuator Fault Diagnosis: An Adaptive Observer-Based Technique. IEEE Trans. Autom. Control 1996, 41, 1073–1078. [Google Scholar] [CrossRef]
- Wang, D.; Lum, K.-Y. Adaptive unknown input observer approach for aircraft actuator fault detection and isolation. Int. J. Adapt. Control Signal Process. 2017, 21, 31–48. [Google Scholar] [CrossRef]
- Chen, W.; Saif, M. Adaptive actuator fault detection, isolation and accommodation in uncertain systems. In. J. Control 2007, 80, 45–63. [Google Scholar] [CrossRef]
- Isermann, R. Fault-Diagnosis Systems; Springer: Berlin, Germany, 2006. [Google Scholar]
- Frank, P.M. Fault Diagnosis in Dynamics Systems Using Analytical and Knowledge-based Redundancy—A Survey and Some New Results. Automatica 1990, 26, 459–474. [Google Scholar] [CrossRef]
- Patton, R.J.; Chen, J. Optimal Unknown Input Distribution Matrix Selection in Robust Fault Diagnosis. Automatica 1993, 29, 837–841. [Google Scholar] [CrossRef]
- Gertler, J. Analytical Redundancy Methods in Fault Detection and Isolation. In Proceedings of the IFAC/IMACS Symposium SAFEPROCES91, Baden-Baden, Germany, 10–13 September 1991; pp. 9–21. [Google Scholar]
- Xiao, C.; Yu, M.; Wang, H.; Zhang, B.; Wang, D. Prognosis of electric Scooter with Intermittent Faults: Dual Degradation Processes Approach. IEEE Trans. Veh. Technol. 2021, 71, 1411–1425. [Google Scholar] [CrossRef]
- Termeche, A.; Benazzouz, D.; Bouamama, B.O.; Abdallah, I. Augmented analytical redundancy relations to improve the fault isolation. Mechatronics 2018, 55, 129–140. [Google Scholar] [CrossRef]
- Levy, R.; Arogeti, S.; Wang, D.; Fivel, O. Improved diagnosis of hybrid systems using instantaneous sensitivity matrices. Mech. Mach. Theory 2015, 91, 240–257. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 241–265. [Google Scholar] [CrossRef]
- Long, J.; Sun, Z.; Li, C.; Hong, Y.; Bai, Y.; Zhang, S. A Novel Sparse Echo Autoencoder Network for Data-Driven Fault Diagnosis of Delta 3-D Printers. IEEE Trans. Instrum. Meas. 2020, 69, 683–692. [Google Scholar] [CrossRef]
- Reddy, K.K.; Sarkar, S.; Venugopalan, V.; Giering, M. Anomaly Detection and Fault Disambiguation in Large Flight Data A Multi-modal Deep Auto-encoder Approach. Annu. Conf. Progn. Health Manag. Soc. 2016, 7. [Google Scholar]
- Chen, R.H.; Speyer, J.L. Sensor and Actuator Fault Reconstruction. J. Guid. Control Dyn. 2004, 27, 186–196. [Google Scholar] [CrossRef]
- Meskin, N.; Khorasani, K. Fault Detection and Isolation of Actuator Faults in Overactuated Systems. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 28–31 October 2007. [Google Scholar]
- Hurley, N.; Rickard, S. Comparing Measures of Sparsity. IEEE Trans. Inf. Theory 2009, 55, 4723–4741. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. For Most Large Underdetermined Systems of Linear Equations the Minimal ℓ1-norm Solution Is Also the Sparsest Solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Lin, Y. ℓ1-Norm Sparse Bayesian Learning: Theory and Applications. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2008. [Google Scholar]
- Xie, L.; Lin, X.; Zeng, J. Shrinking principal component analysis for enhanced process monitoring and fault isolation. Ind. Eng. Chem. Res. 2013, 52, 17475–17486. [Google Scholar] [CrossRef]
- Collins, E.G., Jr.; Song, T. Robust ℓ1 estimation using the Popov-Tsypkin multiplier with application to robust fault detection. Int. J. Control 2001, 74, 303–313. [Google Scholar] [CrossRef]
- Curry, T.; Collins, E.G. Robust Fault Detection and Isolation Using Robust ℓ1 Estimation. J. Guid. Control Dyn. 2005, 28, 1131–1139. [Google Scholar] [CrossRef]
- Borguet, S.; Olivier, L. A sparse estimation approach to fault isolation. J. Eng. Gas Turbines Power 2010, 132, 021601. [Google Scholar] [CrossRef]
- Benosman, M.; Lum, K.-Y. Passive Actuators Fault-Tolerant Control for Affine Nonlinear Systems. IEEE Trans. Control Syst. Technol. 2010, 10, 152–163. [Google Scholar] [CrossRef]
- Theilliol, D.; Join, C.; Zhang, Y. Actuator Fault Tolerant Control Design based on A Reconfigurable Reference Input. Int. J. Appl. Math. Comput. Sci. 2008, 18, 553–560. [Google Scholar] [CrossRef]
- Jin, J.; Ko, S.; Ryoo, C.-K. Fault tolerant control for satellites with four reaction wheels. Control Eng. Pract. 2008, 16, 1250–1258. [Google Scholar] [CrossRef]
- Park, J.; Park, Y. Optimal Input Design for Fault Identification of Overactuated Electric Ground Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 1912–1923. [Google Scholar] [CrossRef]
- Huang, K.; King, I.; Lyu, M.R. Direct Zero-norm Optimization for Feature Selection. In Proceedings of the Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 845–850. [Google Scholar]
- Weston, J.; Elisseeff, A.; Schölkopf, B.; Tipping, M. Use of the Zero-Norm with Linear Models and Kernel Methods. J. Mach. Learn. Res. 2003, 3, 1439–1461. [Google Scholar]
- Milman, V.D.; Schechtman, G. Asymptotic Theory of Finite-Dimensional Normed Spaces; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1986; Volume 1200. [Google Scholar]
- Candès, E.; Romberg, J. ℓ1-Magic: Recovery of Sparse Signals via Convex Programming; California Institute of Technology: Pasadena, CA, USA, 2007. [Google Scholar]
- Park, J.; Park, Y. Experimental Verification of Fault Identification for Overactuated System With a Scaled-Down Electric Vehicle. Int. J. Automot. Technol. 2020, 21, 1037–1045. [Google Scholar] [CrossRef]
- Hac, A.; Doman, D.; Oppenheimer, M. Unified Control of Brake- and Steer-by-Wire Systems Using Optimal Control Allocation Methods; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2006. [Google Scholar]


| Parameters | Values |
|---|---|
| m | 14.75 kg |
| 0.374 m | |
| 0.366 m | |
| w | 0.48 m |
| 0.08 m | |
| 1.077 m | |
| 555 Ns/rad | |
| 450 Ns/rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Park, Y. Multiple-Actuator Fault Isolation Using a Minimal ℓ1-Norm Solution with Applications in Overactuated Electric Vehicles. Sensors 2022, 22, 2144. https://doi.org/10.3390/s22062144
Park J, Park Y. Multiple-Actuator Fault Isolation Using a Minimal ℓ1-Norm Solution with Applications in Overactuated Electric Vehicles. Sensors. 2022; 22(6):2144. https://doi.org/10.3390/s22062144
Chicago/Turabian StylePark, Jinseong, and Youngjin Park. 2022. "Multiple-Actuator Fault Isolation Using a Minimal ℓ1-Norm Solution with Applications in Overactuated Electric Vehicles" Sensors 22, no. 6: 2144. https://doi.org/10.3390/s22062144
APA StylePark, J., & Park, Y. (2022). Multiple-Actuator Fault Isolation Using a Minimal ℓ1-Norm Solution with Applications in Overactuated Electric Vehicles. Sensors, 22(6), 2144. https://doi.org/10.3390/s22062144






