Compact Finite Field Multiplication Processor Structure for Cryptographic Algorithms in IoT Devices with Limited Resources
Abstract
:1. Introduction
1.1. Related Work
1.2. Paper Contribution
1.3. Paper Organization
2. Formulation of the Multiplication Algorithm
| Algorithm 1 Finite Field Multiplication Algorithm based on AOP polynomial. |
Input: E, H, and U Output: D Initialization: , Algorithm:
|
| Algorithm 2 Finite Field Multiplication Algorithm in the bit-level formate. |
Input: , Output: Initialization: Algorithm:
|
3. Construction of Algorithm Dependence Graph
4. Two-Dimensional SISO Multiplier
4.1. Non-Linear Task Scheduling
4.2. Non-Linear Task Projection
- At the first time instance , the controller activates the MUX with select signal () to allow the l most significant bits (MSB) of variable K to reach out to the input of the processor array block as shown in Figure 4. To ensure V variable has zero initial value as described in Algorithm 1, the controller resets the shift register SR-V at the first time instance. At the same time instance, the least significant l bits of variable H are transmitted horizontally to the PEs nodes of the processor array block. Notice that the H word transferred at this time instance should be hold for the following time instances.
- At time instances , the controller still activates the MUX with select signal () to enable the remaining words of input K to reach out to the processor array input. These words, together with the previously held H words at the first time instance, are used to calculate in sequence the partial words of V and K. The V words resulted from the output of the processor array block () are looped back to its input through the shift register SR-V. The K words resulted from the output of the processor array block are looped back to its input through the shift registers SR-K, SR-Ke, SR-Kfe, and the MUX controlled by the select signal S as displayed in Figure 4. It is worth noticing that the depth of the shift register SR-V keeps the initial values of V having zero values during these time instances.
- During times , and , the controller deactivates the MUX controlled by the select signal S (), see Figure 4, to pass the signal to be concatenated with the word. At the same time instances, the controller deactivates the MUX controlled by the select signal () to transfer the whole partial word of K to the input of the processor array block as displayed in Figure 4.
- During times , , the controller activates the MUX controlled by the select signal S (), see Figure 4, to pass the signal to be concatenated with the word. At the same time instances, the controller deactivates the MUX controlled by the select signal () to transfer the whole partial word of K to the input of the processor array block as displayed in Figure 4.
- At times , , the remaining H words are transferred to the input of the processor array block to be used alongside the word inputs , in updating the partial words of variable V ().
- Starting at time , the output words of product D will be available in sequence at the output bus.
5. Experimental Results and Discussion
- ∎
- l denotes the word size of the multiplier constructions.
- ∎
- denotes the delay of the fundamental 2-input AND gate.
- ∎
- denotes the delay of the fundamental 2-input XOR gate.
- ∎
- denotes the delay of the 2-input MUX.
- ∎
- expresses the overall number of FFs employed in the multiplier construction of Pan [20].
- ∎
- expresses the overall number of FFs employed in the multiplier construction of Hua [33].
- ∎
- expresses the overall number of FFs employed in the multiplier construction of Chen [34].
- ∎
- designates the latency of the multiplier construction of Chen [34].
- ∎
- is the approximated CPD of Pan’s multiplier construction [20].
- ∎
- is the approximated CPD of Hua’s multiplier construction [33].
- ∎
- is the approximated CPD of Chen’s multiplier construction [34].
- ∎
- is the approximated CPD of the suggested multiplier construction.
- Except for the MUXes and FFs of the recommended multiplier structure, which have area complexity of order and , all other components have area complexity of order .
- In comparison to the other multipliers, the suggested multiplier has the smallest number of FFs. This is due to the suggested multiplier having an area complexity of order , as opposed to and for the other multiplier structures.
- The number of FFs in the proposed multiplier structure does not rise significantly as the word size l is increased. This is due to the fact that the proposed multiplier structure’s FFs have an area complexity of order .
- When compared to the other multiplier constructions, the multiplier of Hua [33] has the lowest latency.
- The latency findings in Table 3, for the field size and word sizes , indicate that the suggested multiplier structure’s latency expression will result in a larger latency than the multiplier constructions in [20,23], and inexpensive latency compared to the Hua [33] and Chen [34] multiplier constructions.
- When the word size l increases, the latency reduces. This is due to the fact that latency expressions are inversely related to l.
- CPD expressions of Pan [20] and the proposed multiplier structure are both directly dependent on l. As a result, the CPD values of these multipliers will rise as l rises.
- In terms of area (A), the proposed multiplier structure is superior to all existing multiplier structures. It greatly decreases area for all embedded word sizes l, with reduction rates ranging from 67.3% to 97.7%. The reduction in area is primarily due to the proposed multiplier structure’s area, which is mainly determined by the field size l, drastically reducing the number of counted logic gates when compared to most other existing multiplier structures. Furthermore, due to the systolic nature of the suggested multiplier, the majority of its connections are local, leading to a reduction in the area to a large extent.
- In terms of the area-time product (AT), Pan’s multiplier structure [20] surpasses all other multiplier structures, including the suggested one, at . This is mainly attributed to the significant reduction in its latency compared to the other multiplier constructions at this word size. At this embedded size, it outperforms the offered design by 37.9%. The proposed architecture, on the other hand, surpasses Pan’s multiplier structure for and . At , it reduces AT by 26.3%, while at , it reduces AT by 49.2%. Furthermore, the suggested multiplier structure outperforms all alternative multiplier structures by percentages ranging from 21.1% to 99.4% based on the embedded word size.The reduction in AT over the other multiplier structures is mainly due to the significant savings in area complexity of the suggested multiplier structure.
- In terms of consumed power (P), the proposed multiplier outperforms the other multiplier structures at all embedded word sizes. It reduces power consumption at all l values by percentages ranging from 64.4% to 99.5%. The power reduction is attributed to the substantial reduction in the consumed area of the proposed design when compared to the consumed area of the other multiplier designs. The reduced area minimises parasitic capacitance and, as a result, the circuit’s dynamic power significantly reduces. The systolic nature of the proposed design reduces the switching activities of the proposed design compared to the other conventional designs. The switching activities is one of the major parameters that significantly affects the dynamic power consumption.
- In terms of consumed energy (E), the offered multiplier construction surpasses the other multiplier constructions at all embedded sizes. It saves energy at rates ranging from 70.6% to 99.2%. The energy savings are due to the massive reduction in consumed power and the reasonable computation time of the offered multiplier construction compared to the other multiplier structures.
6. Summary and Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| ASIC | Application Specific Integrated Circuit |
| ECC | Elliptic Curve Cryptography |
| DG | Dependency Graph |
| AOP | All-One Polynomial |
| VLSI | Very Large Scale Integrated Circuit |
| L | Cyclic-Shift-Left |
| DSA | Digital Signature Algorithm |
| FFs | Flip-Flops |
| RSA | Rivest, Shamir, and Adleman |
| SISO | Serial-In/Serial-Out |
| SIPO | Serial-In/Parallel-Out |
| PISO | Parallel-In/Serial-Out |
| CPD | Critical Path Delay |
References
- Rondon, L.P.; Babun, L.; Aris, A.; Akkaya, K.; Uluagac, A.S. Survey on enterprise Internet-of-Things systems (E-IoT): A security perspective. Ad Hoc Netw. 2022, 125, 102728. [Google Scholar] [CrossRef]
- Sowjanya, K.; Dasgupta, M.; Ray, S. An elliptic curve cryptography based enhanced anonymous authentication protocol for wearable health monitoring systems. Int. J. Inf. Secur. 2020, 19, 129–146. [Google Scholar] [CrossRef]
- Rana, M.; Mamun, Q.; Islam, R. Lightweight cryptography in IoT networks: A survey. Future Gener. Comput. Syst. 2022, 129, 77–89. [Google Scholar] [CrossRef]
- Omolara, A.E.; Alabdulatif, A.; Abiodun, O.I.; Alawida, M.; Alabdulatif, A.; Alshours, W.H.; Arshad, H. The internet of things security: A survey encompassing unexplored areas and new insights. Comput. Secur. 2022, 112, 102494. [Google Scholar] [CrossRef]
- Liu, J.; Liu, H.; Chakraborty, C.; Yu, K.; Shao, X.; Ma, Z. Cascade Learning Embedded Vision Inspection of Rail Fastener by Using a Fault Detection IoT Vehicle. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Heninger, N. RSA, DH, and DSA in the Wild. Cryptology ePrint Archive. 2022. Available online: https://eprint.iacr.org/2022/048.pdf (accessed on 5 February 2022).
- Dong, J.; Zheng, F.; Lin, J.; Liu, Z.; Xiao, F.; Fan, G. EC-ECC: Accelerating Elliptic Curve Cryptography for Edge Computing on Embedded GPU TX2. IACM Trans. Embed. Comput. Syst. (TECS) 2022, 21, 1–25. [Google Scholar] [CrossRef]
- Chiou, C.W.; Lee, C.Y.; Deng, A.W.; Lin, J.M. Concurrent error detection in Montgomery multiplication over GF(2m). IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2006, E89-A, 566–574. [Google Scholar] [CrossRef]
- Kim, K.W.; Jeon, J.C. Polynomial Basis Multiplier Using Cellular Systolic Architecture. IETE J. Res. 2014, 60, 194–199. [Google Scholar] [CrossRef]
- Choi, S.; Lee, K. Efficient systolic modular multiplier/squarer for fast exponentiation over GF(2m). IEICE Electron. Express 2015, 12, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.W.; Kim, S.H. Efficient bit-parallel systolic architecture for multiplication and squaring over GF(2m). IEICE Electron. Express 2018, 15, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Mathe, S.E.; Boppana, L. Bit-parallel systolic multiplier over GF(2m) for irreducible trinomials with ASIC and FPGA implementations. IET Circuits Desvices Syst. 2018, 12, 315–325. [Google Scholar] [CrossRef]
- Devi, S.; Mahajan, R.; Bagai, D. Low complexity design of bit parallel polynomial basis systolic multiplier using irreducible polynomials. Egypt. Inform. J. 2022, 23, 105–112. [Google Scholar] [CrossRef]
- Pillutla, S.R.; Boppana, L. An area-efficient bit-serial sequential polynomial basis finite field GF(2m) multiplier. AEU- Int. J. Electron. Commun. 2020, 114, 153017. [Google Scholar] [CrossRef]
- Imana, J.L. LFSR-Based Bit-Serial GF(2m) Multipliers Using Irreducible Trinomials. IEEE Trans. Comput. 2020, 70, 156–162. [Google Scholar]
- Pillutla, S.R.; Boppana, L. Low-Hardware Digit-Serial Sequential Polynomial Basis Finite Field GF(2m) Multiplier for Trinomials. Adv. Commun. Signal Process. VLSI Trans. Comput. 2021, 722, 401–410. [Google Scholar]
- Kim, C.H.; Hong, C.P.; Kwon, S. A digit-serial multiplier for finite Field GF(2m). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2005, 13, 476–483. [Google Scholar]
- Talapatra, S.; Rahaman, H.; Mathew, J. Low complexity digit serial systolic montgomery multipliers for special class of GF(2m). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2010, 18, 847–852. [Google Scholar] [CrossRef]
- Guo, J.H.; Wang, C.L. Hardware-efficient Systolic Architecture for Inversion and Division in GF(2m). IEE Proc. Comput. Digit. Tech. 1998, 145, 272–278. [Google Scholar] [CrossRef]
- Pan, J.S.; Lee, C.Y.; Meher, P.K. Low-Latency Digit-Serial and Digit-Parallel Systolic Multipliers for Large Binary Extension Fields. IEEE Trans. Circuits Syst. 2013, 60, 3195–3204. [Google Scholar] [CrossRef]
- Lee, C.Y.; Fan, C.C.; Yuan, S.M. New Digit-Serial Three-Operand Multiplier over Binary Extension Fields for High-Performance Applications. In Proceedings of the 2017 2nd IEEE International Conference on Computational Intelligence and Applications, Beijing, China, 8–11 September 2017; pp. 498–502. [Google Scholar]
- Lee, C.Y. Super digit-serial systolic multiplier over GF(2m). In Proceedings of the 2012 Sixth International Conference on Genetic and Evolutionary Computing, Kitakyushu, Japan, 25–28 August 2012; pp. 509–513. [Google Scholar]
- Xie, J.; Meher, P.K.; Mao, Z. Low-latency high-throughput systolic multipliers over GF(2m) for NIST recommended pentanomials. IEEE Trans. Circuits Syst. 2015, 62, 881–890. [Google Scholar] [CrossRef]
- Namin, A.H.; Wu, H.; Ahmadi, M. A word-level finite field multiplier using normal basis. IEEE Trans. Comput. 2011, 60, 890–895. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chiou, C.W.; Lin, J.M.; Chang, C.C. Scalable and systolic Montgomery multiplier over generated by trinomials. IET Circuits Devices Syst. 2007, 1, 477–484. [Google Scholar] [CrossRef]
- Chen, L.H.; Chang, P.L.; Lee, C.Y.; Yang, Y.K. Scalable and systolic dual basis multiplier Over GF(2m). Int. J. Innov. Comput. Inf. Control 2011, 7, 1193–1208. [Google Scholar]
- Bayat-Sarmadi, S.; Kermani, M.M.; Azarderakhsh, R.; Lee, C.Y. Dual-Basis Superserial Multipliers for Secure Applications and Lightweight Cryptographic Architectures. IEEE Trans. Circ. Syst.-II 2014, 61, 125–129. [Google Scholar] [CrossRef]
- Ibrahim, A.; Gebali, F. Scalable and Unified Digit-Serial Processor Array Architecture for Multiplication and Inversion over GF(2m). IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 22, 2894–2906. [Google Scholar] [CrossRef]
- Gebali, F. Algorithms and Parallel Computers; John Wiley: New York, NY, USA, 2011. [Google Scholar]
- Ibrahim, A.; Elsimary, H.; Gebali, F. New systolic array architecture for finite field division. IEICE Electron. Express 2018, 15, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, A. Scalable digit-serial processor array architecture for finite field division. Microelectron. J. 2019, 85, 83–91. [Google Scholar] [CrossRef]
- Meher, P.K.; Lou, X. Low-Latency, Low-Area, and Scalable Systolic-Like Modular Multipliers for GF(2m) Based on Irreducible All-One Polynomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 64, 399–408. [Google Scholar] [CrossRef]
- Hua, Y.Y.; Lin, J.M.; Chiou, C.W.; Lee, C.Y.; Liu, Y.H. Low Space-Complexity Digit-Serial Dual Basis Systolic Multiplier over GF(2m) Using Hankel Matrix and Karatsuba Algorithm. IET Inf. Secur. 2013, 7, 75–86. [Google Scholar]
- Chen, C.C.; Lee, C.Y.; Lu, E.H. Scalable and Systolic Montgomery Multipliers Over GF(2m). IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2008, E91-A, 1763–1771. [Google Scholar] [CrossRef]
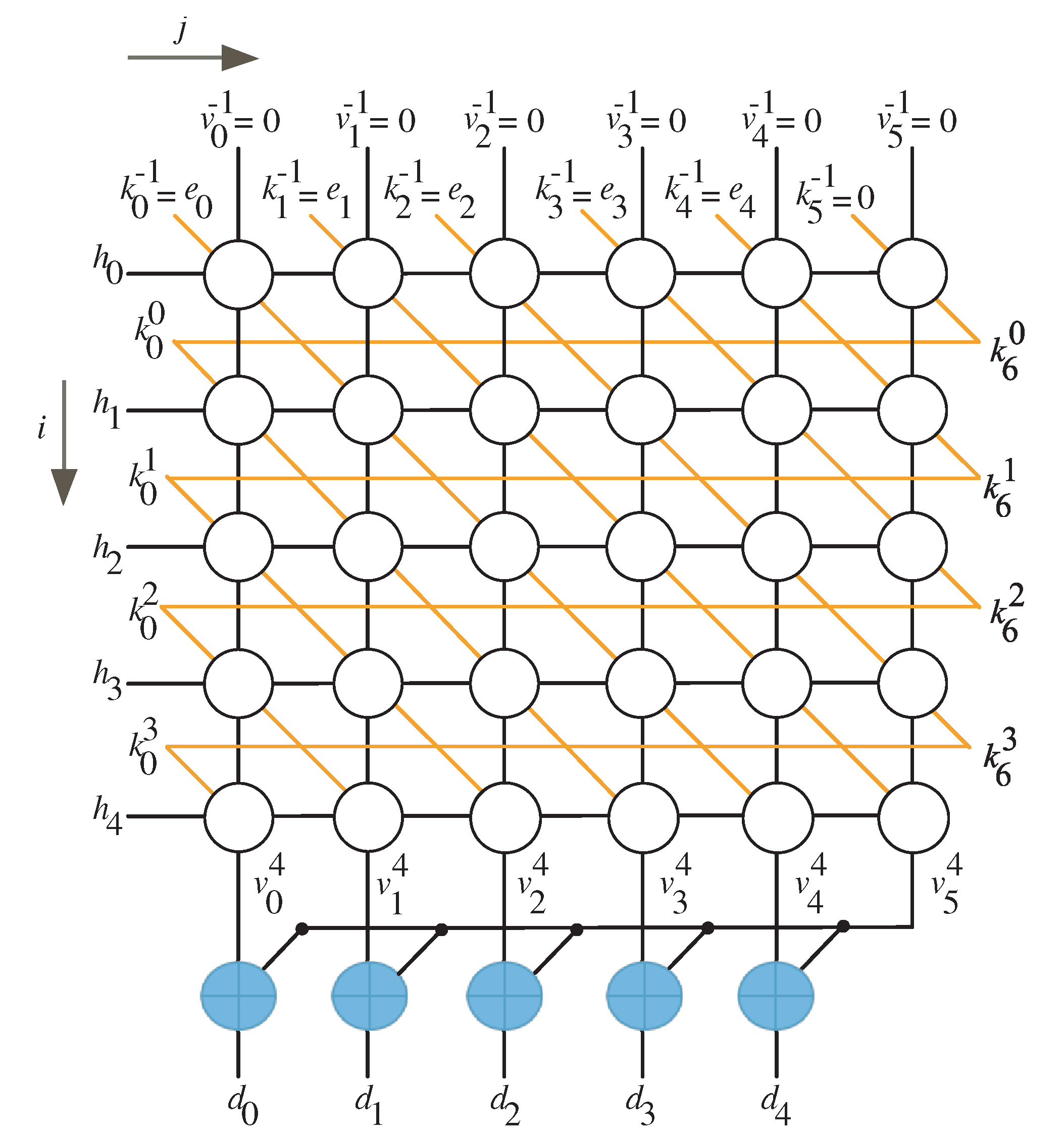
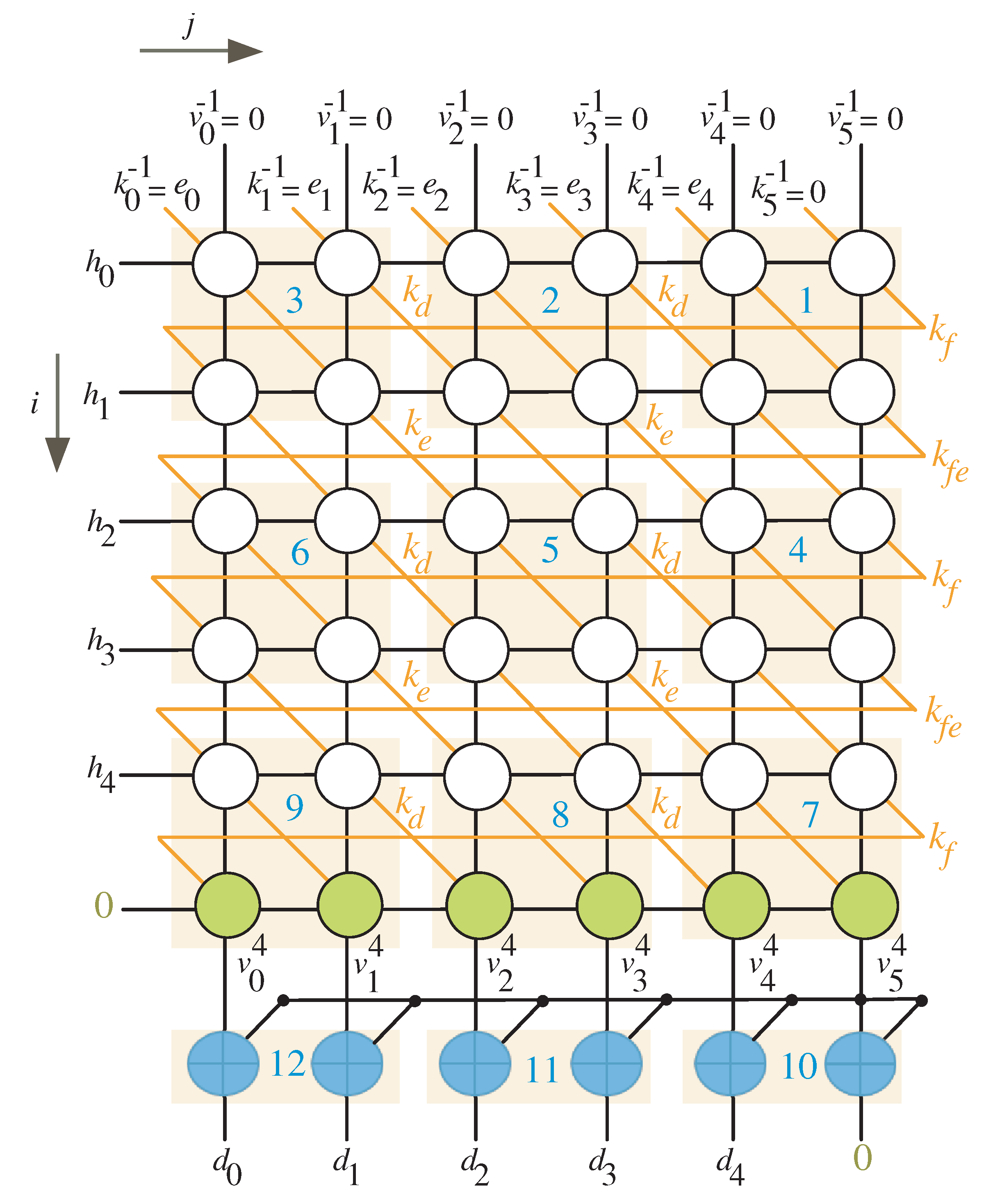


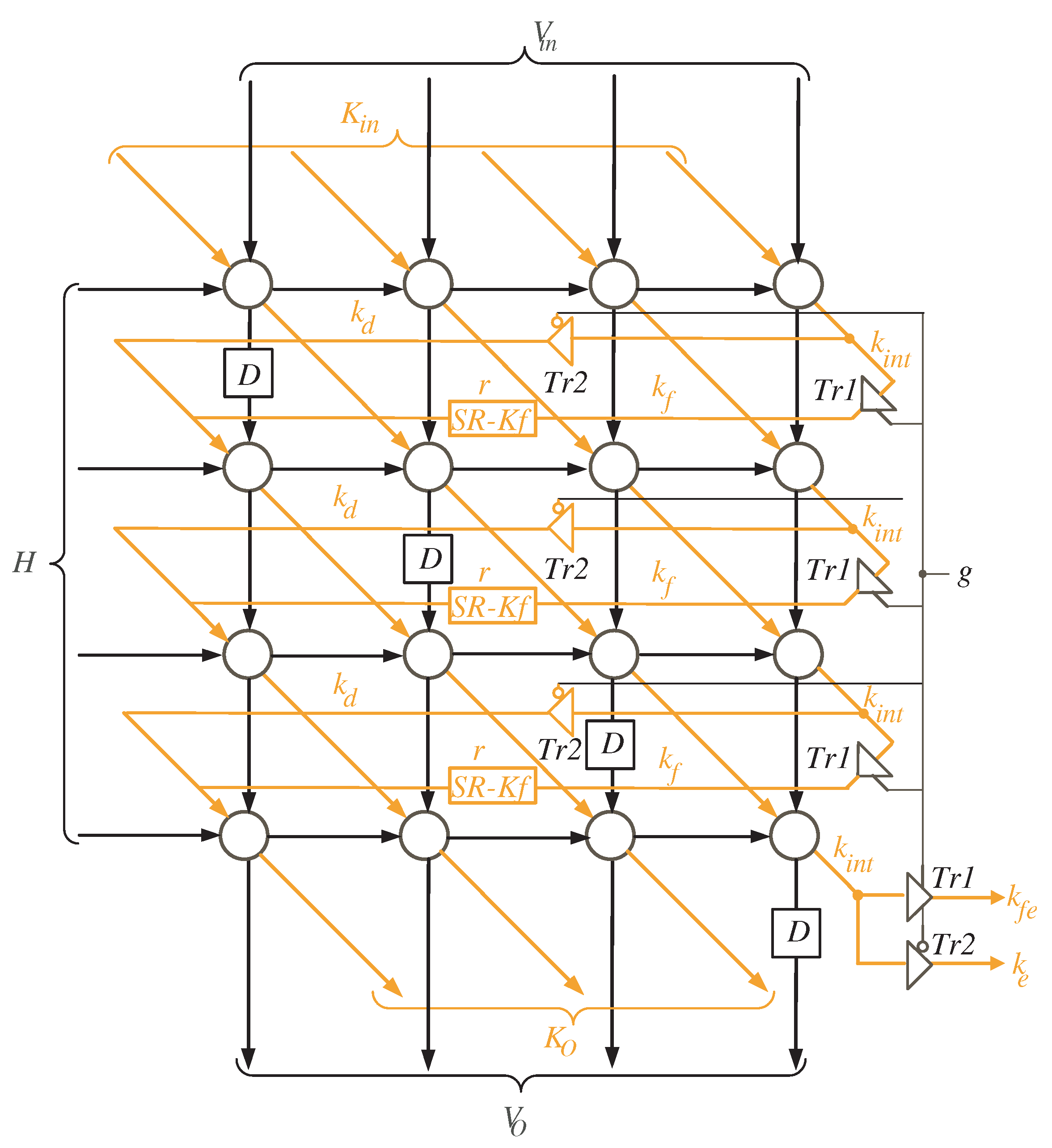
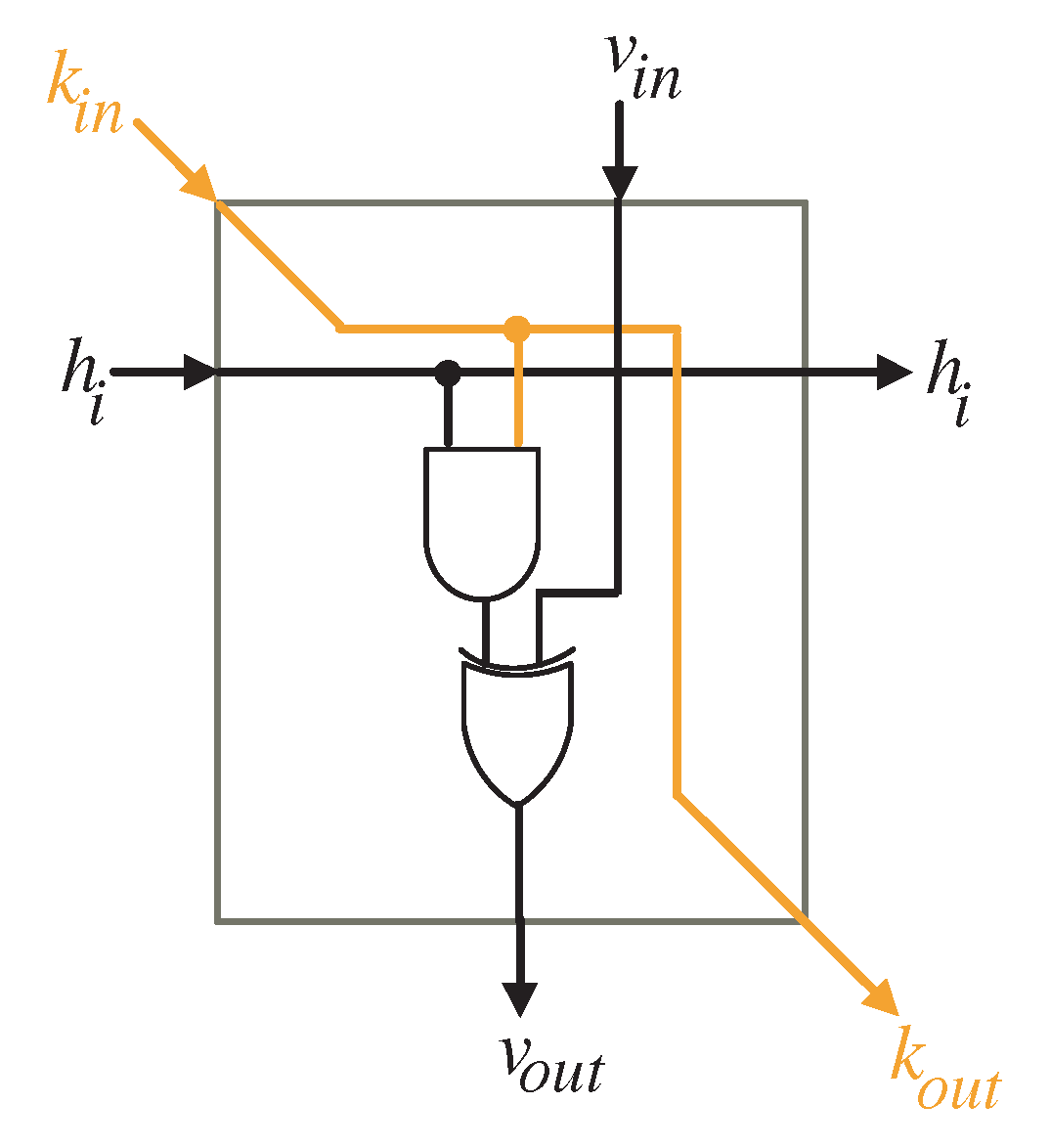
| I/O | Time Instance |
|---|---|
| North input () | k |
| East output () | k |
| West input () | |
| South output () |
| Design | Tri-State | AND | XOR | MUXs | FFs | Latency | CPD |
|---|---|---|---|---|---|---|---|
| Xie [23] | 0 | 0 | |||||
| Pan [20] | 0 | 0 | |||||
| Hua [33] | 0 | 0 | |||||
| Chen [34] | 0 | ||||||
| Proposed |
| Multiplier | l | Latency | Area (A) | CPD | Time (T) | Power (P) | Energy (E) | AT | %A | %AT | %P | %E |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Kgates) | (ps) | (ns) | (nW) | (fJ) | ||||||||
| 8 | 386 | 110.7 | 67.1 | 25.9 | 268.5 | 7 | 2866.4 | 97.3 | 21.1 | 99.4 | 82.9 | |
| Xie [23] | 16 | 205 | 174.9 | 67.1 | 13.7 | 447.4 | 6.1 | 2396.5 | 97.7 | 43.6 | 99.4 | 86.1 |
| 32 | 117 | 232.2 | 67.1 | 7.8 | 568.1 | 4.4 | 1810.9 | 97.8 | 47.3 | 99.3 | 84.6 | |
| 8 | 58 | 115.9 | 245.5 | 14 | 301.1 | 4.2 | 1622.7 | 97.4 | −37.9 | 99.5 | 72.0 | |
| Pan [20] | 16 | 43 | 147.6 | 290.8 | 12.5 | 380.9 | 4.8 | 1844.5 | 97.3 | 26.3 | 99.3 | 82.3 |
| 32 | 29 | 195.5 | 336.2 | 9.6 | 505.9 | 4.9 | 1876.9 | 97.4 | 49.2 | 99.2 | 86.1 | |
| 8 | 308,905 | 9.5 | 87.3 | 26,981.6 | 5.2 | 141.3 | 256,864.8 | 68.8 | 99.1 | 70.5 | 99.2 | |
| Hua [33] | 16 | 154,453 | 12.4 | 87.3 | 13,490.8 | 7.0 | 94.7 | 166,962.1 | 67.3 | 99.2 | 64.4 | 99.1 |
| 32 | 77,227 | 23.8 | 87.3 | 6745.4 | 13.2 | 89.1 | 160,540.5 | 79.0 | 99.4 | 71.2 | 99.2 | |
| 8 | 14,216 | 12.1 | 65.7 | 933.8 | 6.1 | 5.7 | 11,334.5 | 75.5 | 80.0 | 74.5 | 79.4 | |
| Chen [34] | 16 | 4377 | 16.1 | 65.7 | 287.5 | 9.9 | 2.9 | 4618.7 | 74.8 | 70.7 | 75.0 | 70.6 |
| 32 | 1871 | 31.7 | 65.7 | 122.9 | 19.0 | 2.3 | 3890.3 | 84.2 | 75.5 | 80.0 | 71.4 | |
| 8 | 3281 | 2.9 | 231.8 | 760.5 | 1.547 | 1.2 | 2262.5 | - | - | - | - | |
| Proposed | 16 | 837 | 4.0 | 400.2 | 334.8 | 2.5 | 0.8 | 1354.6 | - | - | - | - |
| 32 | 218 | 4.9 | 876.1 | 190.8 | 3.8 | 0.7 | 953.6 | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, A.; Gebali, F. Compact Finite Field Multiplication Processor Structure for Cryptographic Algorithms in IoT Devices with Limited Resources. Sensors 2022, 22, 2090. https://doi.org/10.3390/s22062090
Ibrahim A, Gebali F. Compact Finite Field Multiplication Processor Structure for Cryptographic Algorithms in IoT Devices with Limited Resources. Sensors. 2022; 22(6):2090. https://doi.org/10.3390/s22062090
Chicago/Turabian StyleIbrahim, Atef, and Fayez Gebali. 2022. "Compact Finite Field Multiplication Processor Structure for Cryptographic Algorithms in IoT Devices with Limited Resources" Sensors 22, no. 6: 2090. https://doi.org/10.3390/s22062090
APA StyleIbrahim, A., & Gebali, F. (2022). Compact Finite Field Multiplication Processor Structure for Cryptographic Algorithms in IoT Devices with Limited Resources. Sensors, 22(6), 2090. https://doi.org/10.3390/s22062090







