Preprocessing Methods for Ambulatory HRV Analysis Based on HRV Distribution, Variability and Characteristics (DVC)
Abstract
:1. Introduction
1.1. Related Work
1.2. Paper Contribution
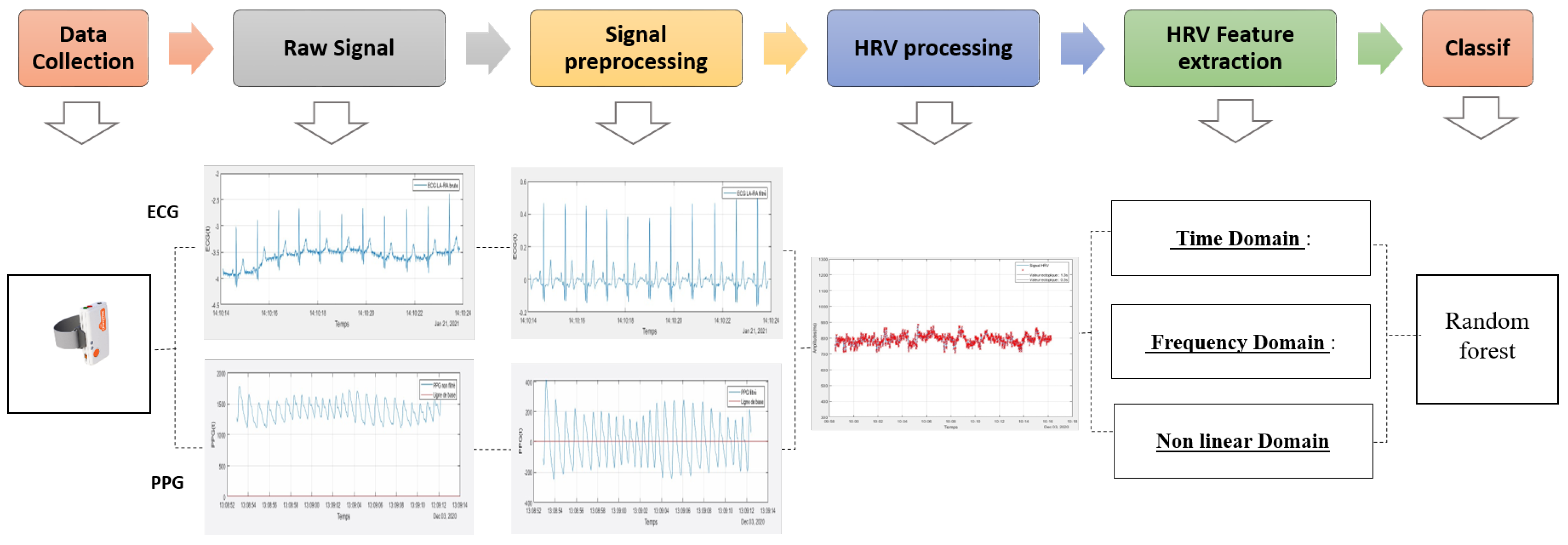
2. Materials and Methods
2.1. Data Collection
- 1.
- Relaxation: Subjects followed guided meditation for 15 min via an audio track with closed eyes, while sitting in a comfortable position, in a dark environment.
- 2.
- Stress: Participants perform stressful tasks such as the Stroop color word test, mental arithmetic, and a speed game, all proven to induce mental stress, for about 20 min [22,23]. A red timer and a visible score were used as social threats to increase the stress response. In addition, subjects were not aware that this step was to induce stress. Instead, they were told an IQ score will be computed to compare them to subjects of the same age category. This is perceived as a threat to one’s social esteem or social status, which activates the stress response as supported by the Social Self-Preservation Theory [24,25].
2.2. Signal Prepocessing
2.2.1. ECG Processing
2.2.2. PPG Processing
2.3. Proposed Method for HRV Processing Based on HRV Distribution, Variability, and Characteristics DVC
2.3.1. Ectopic Beats Filtering
| 1. 0.3 s < < 1.3 s, |
|---|
| 2. Deviation () between the new and the following RR interval must be lower than deviation computed over last 10 values |
| where: |
| where: |
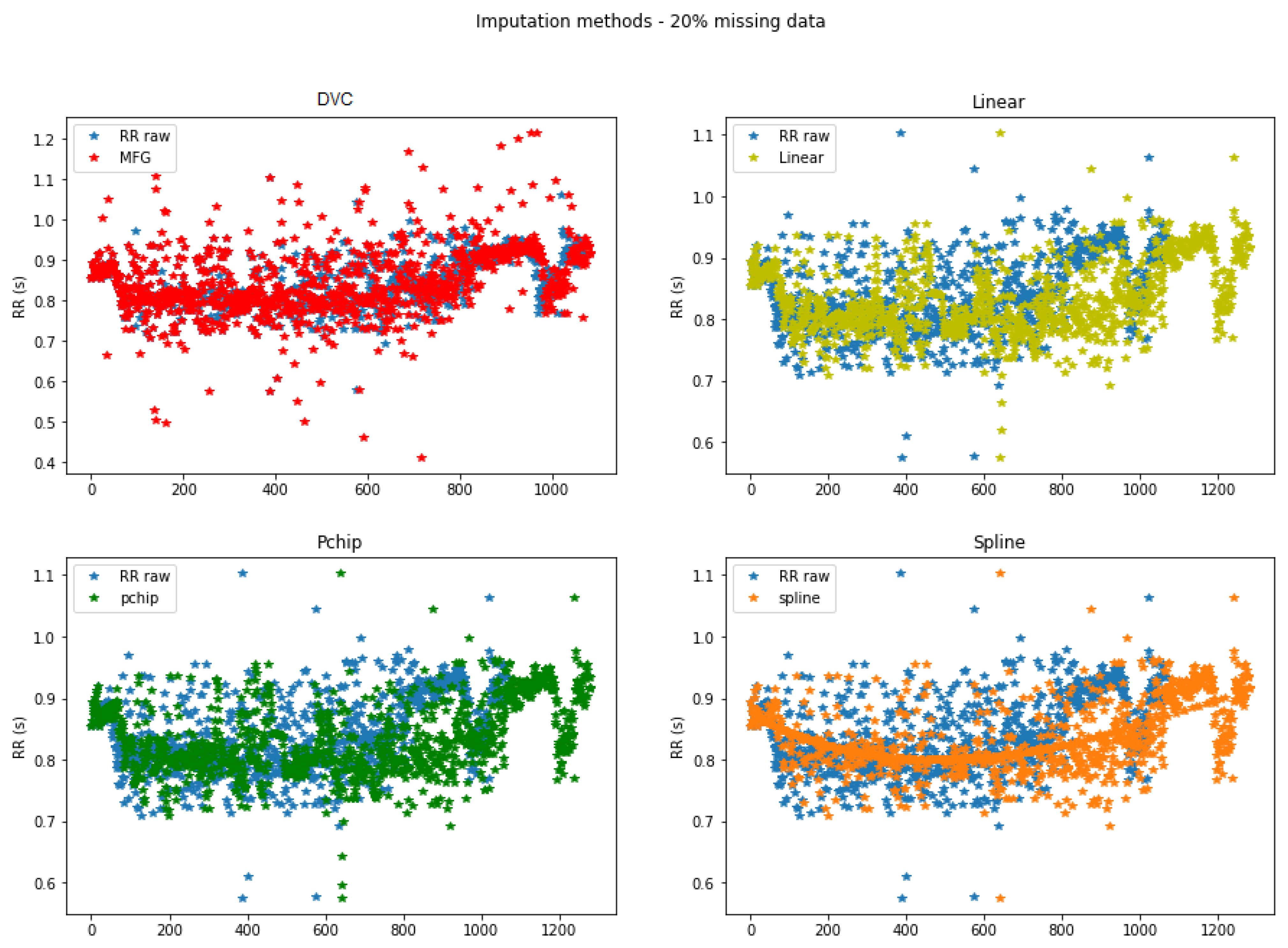
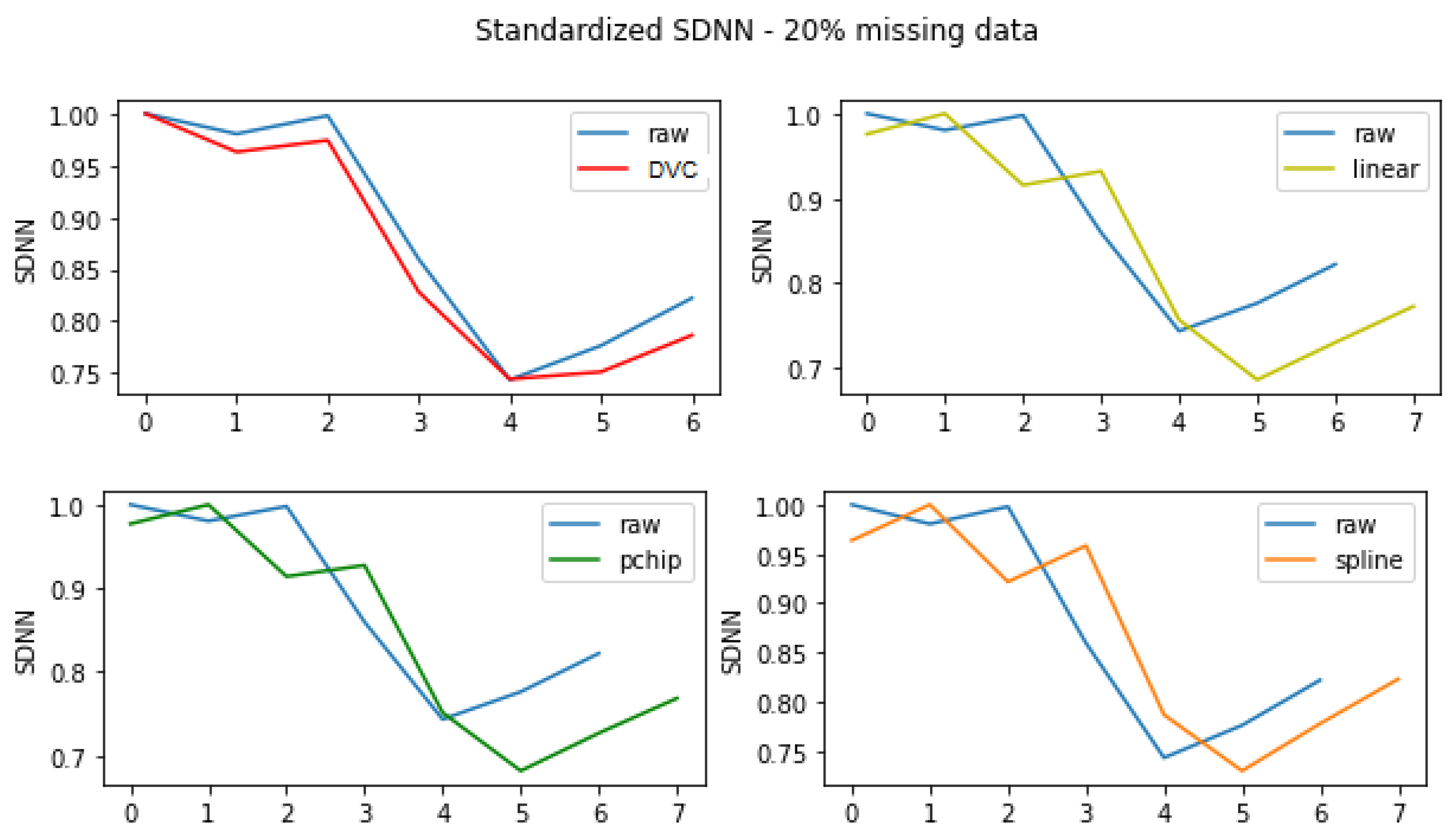
2.3.2. Data Imputation
| Algorithm 1 HRV filtering procedure |
|
2.4. HRV Feature Extraction
2.4.1. Time Domain
2.4.2. Frequency Domain
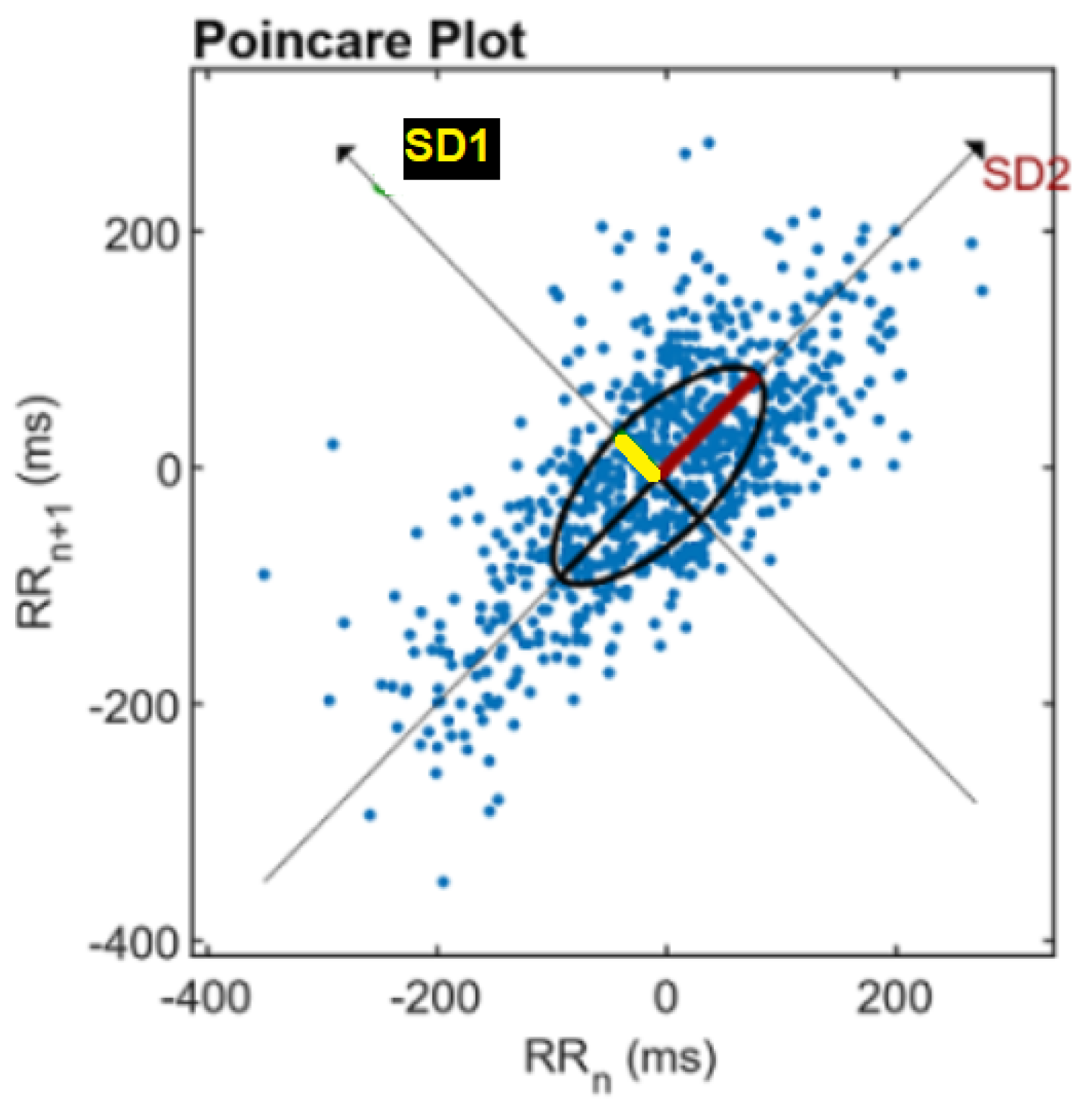
2.4.3. Non Linear Domain
2.5. Classification Model
2.6. Validation
- TP = True Positive, HRV windows from stress classified as stress,
- FP = False Positive, HRV windows from relaxation classified as stress,
- FN = False Negative, HRV windows from stress classified as relaxation.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Task Force of the European Society of Cardiology the North American Society of Pacing Electrophysiology. Heart rate variability: Standards of measurement, physiological interpretation and clinical use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.Y.; Lee, M.; Park, H.; Youn, I. Stress resilience measurement with heart-rate variability during mental and physical stress. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 5290–5293. [Google Scholar]
- Wu, M.; Cao, H.; Nguyen, H.L.; Surmacz, K.; Hargrove, C. Modeling perceived stress via HRV and accelerometer sensor streams. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 1625–1628. [Google Scholar]
- Wac, K.; Tsiourti, C. Ambulatory assessment of affect: Survey of sensor systems for monitoring of autonomic nervous systems activation in emotion. IEEE Trans. Affect. Comput. 2014, 5, 251–272. [Google Scholar] [CrossRef]
- Choi, A.; Shin, H. Quantitative analysis of the effect of an ectopic beat on the heart rate variability in the resting condition. Front. Physiol. 2018, 9, 922. [Google Scholar] [CrossRef]
- Colak, O.H. Preprocessing effects in time–frequency distributions and spectral analysis of heart rate variability. Digit. Signal Process. 2009, 19, 731–739. [Google Scholar] [CrossRef]
- Kumaravel, N.; Santhi, C. Nonlinear filters for preprocessing heart rate variability signals. Int. J. Comp. Sci. Netw. Secur. 2010, 10, 250–254. [Google Scholar]
- Kim, K.K.; Lim, Y.G.; Kim, J.S.; Park, K.S. Effect of missing RR-interval data on heart rate variability analysis in the time domain. Physiol. Meas. 2007, 28, 1485–1494. [Google Scholar] [CrossRef] [PubMed]
- Benchekroun, M.; Chevallier, B.; Zalc, V.; Istrate, D.; Lenne, D.; Vera, N. Analysis of the Impact of Inter-Beat-Interval Interpolation on real-time HRV Feature Estimation for e-Health Applications. In Proceedings of the JETSAN 2021—E-health and Biomedical Devices Study Conference 2021, Blagnac, France, 31 May 2021. [Google Scholar]
- Heiss, S.; Vaschillo, B.; Vaschillo, E.G.; Timko, C.A.; Hormes, J.M. Heart rate variability as a biobehavioral marker of diverse psychopathologies: A review and argument for an “ideal range”. Neurosci. Biobehav. Rev. 2021, 121, 144–155. [Google Scholar] [CrossRef]
- Berntson, G.G.; Stowell, J.R. ECG artifacts and heart period variability: Don’t miss a beat! Psychophysiology 1998, 35, 127–132. [Google Scholar] [CrossRef] [PubMed]
- Thuraisingham, R.A. Preprocessing RR interval time series for heart rate variability analysis and estimates of standard deviation of RR intervals. Comput. Methods Programs Biomed. 2006, 83, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Rahul, J.; Sora, M.; Sharma, L.D.; Bohat, V.K. An improved cardiac arrhythmia classification using an RR interval-based approach. Biocybern. Biomed. Eng. 2021, 41, 656–666. [Google Scholar] [CrossRef]
- Conen, D.; Adam, M.; Roche, F.; Barthelemy, J.C.; Felber Dietrich, D.; Imboden, M.; Künzli, N.; von Eckardstein, A.; Regenass, S.; Hornemann, T.; et al. Premature atrial contractions in the general population: Frequency and risk factors. Circulation 2012, 126, 2302–2308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bikkina, M.; Larson, M.G.; Levy, D. Prognostic implications of asymptomatic ventricular arrhythmias: The Framingham Heart Study. Ann. Intern. Med. 1992, 117, 990–996. [Google Scholar] [CrossRef] [PubMed]
- Peltola, M. Role of editing of RR intervals in the analysis of heart rate variability. Front. Physiol. 2012, 3, 148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eguchi, K.; Aoki, R.; Shimauchi, S.; Yoshida, K.; Yamada, T. RR interval outlier processing for heart rate variability analysis using wearable ECG devices. Adv. Biomed. Eng. 2018, 7, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Buchheit, M.; Solano, R.; Millet, G.P. Heart-rate deflection point and the second heart-rate variability threshold during running exercise in trained boys. Pediatr. Exerc. Sci. 2007, 19, 192–204. [Google Scholar] [CrossRef] [PubMed]
- Al Osman, H.; Eid, M.; El Saddik, A. A pattern-based windowed impulse rejection filter for nonpathological HRV artifacts correction. IEEE Trans. Instrum. Meas. 2014, 64, 1944–1957. [Google Scholar] [CrossRef]
- Wessel, N.; Voss, A.; Malberg, H.; Ziehmann, C.; Voss, H.U.; Schirdewan, A.; Meyerfeldt, U.; Kurths, J. Nonlinear analysis of complex phenomena in cardiological data. Herzschrittmachertherapie Elektrophysiol. 2000, 11, 159–173. [Google Scholar] [CrossRef]
- Clifford, G.D.; Tarassenko, L. Quantifying errors in spectral estimates of HRV due to beat replacement and resampling. IEEE Trans. Biomed. Eng. 2005, 52, 630–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dickerson, S.S.; Kemeny, M.E. Acute stressors and cortisol responses: A theoretical integration and synthesis of laboratory research. Psychol. Bull. 2004, 130, 355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giannakakis, G.; Grigoriadis, D.; Giannakaki, K.; Simantiraki, O.; Roniotis, A.; Tsiknakis, M. Review on psychological stress detection using biosignals. IEEE Trans. Affect. Comput. 2019, 13, 440–460. [Google Scholar] [CrossRef]
- Dickerson, S.S.; Kemeny, M.E.; Aziz, N.; Kim, K.H.; Fahey, J.L. Immunological effects of induced shame and guilt. Psychosom. Med. 2004, 66, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Dickerson, S.S.; Gruenewald, T.L.; Kemeny, M.E. Psychobiological responses to social self threat: Functional or detrimental? Self Identity 2009, 8, 270–285. [Google Scholar] [CrossRef]
- Benchekroun, M.; Istrate, D.; Zalc, V.; Lenne, D. MMSD: A Multi-modal Dataset for Real-time, Continuous Stress Detection from Physiological Signals. In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies—HEALTHINF, Online, 9–11 February 2022; pp. 240–248. [Google Scholar] [CrossRef]
- Sedghamiz, H. Complete Pan-Tompkins Implementation ECG QRS Detector. Matlab Central: Community Profile. 2014. Available online: http://www.mathworks.com/matlabcentral/profile/authors/2510422-hooman-sedghamiz (accessed on 19 December 2021).
- Elgendi, M.; Jonkman, M.; DeBoer, F. Heart rate variability and the acceleration plethysmogram signals measured at rest. In Proceedings of the International Joint Conference on Biomedical Engineering Systems and Technologies, Valencia, Spain, 20–23 January 2010; pp. 266–277. [Google Scholar]
- Kleiger, R.E.; Miller, J.P.; Bigger, J.T., Jr.; Moss, A.J. Decreased heart rate variability and its association with increased mortality after acute myocardial infarction. Am. J. Cardiol. 1987, 59, 256–262. [Google Scholar] [CrossRef]
- Bartels, R.; Peçanha, T. HRV: A Pythonic package for Heart Rate Variability Analysis. J. Open Source Softw. 2020, 5. Available online: https://github.com/rhenanbartels/hrv/tree/0.2.8 (accessed on 29 October 2021). [CrossRef]
- Shaffer, F.; Ginsberg, J. An overview of heart rate variability metrics and norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [Green Version]
- Acharya, U.R.; Joseph, K.P.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef]
- Salahuddin, L.; Jeong, M.G.; Kim, D.; Lim, S.K.; Won, K.; Woo, J.M. Dependence of heart rate variability on stress factors of stress response inventory. In Proceedings of the 2007 9th International Conference on E-Health Networking, Application and Services, Taipei, Taiwan, 19–22 June 2007; pp. 236–239. [Google Scholar]
- Nayak, S.K.; Bit, A.; Dey, A.; Mohapatra, B.; Pal, K. A review on the nonlinear dynamical system analysis of electrocardiogram signal. J. Healthc. Eng. 2018, 2018, 6920420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarvainen, M.P.; Niskanen, J.P. Kubios HRV; Biosignal Analysis and Medical Imaging Group (BSAMIG), Department of Applied Physics, University of Eastern Finland: Kuopio, Finland, 2012; p. 39. [Google Scholar]



| RF Hyper-Parameters |
|---|
| criterion = ’entropy’, max_features = 0.6, min_samples_split = 3, n_estimators = 500 |
| F1 Scores | |||||
|---|---|---|---|---|---|
| % <0.3 s | % Missing | DVC | Pchip | Linear | Spline |
| 5% | 5% | 0.63 | 0.54 | 0.53 | 0.56 |
| 5% | 10% | 0.62 | 0.52 | 0.51 | 0.54 |
| 5% | 15% | 0.61 | 0.48 | 0.47 | 0.55 |
| 5% | 20% | 0.61 | 0.45 | 0.45 | 0.55 |
| 5% | 25% | 0.61 | 0.44 | 0.43 | 0.55 |
| 5% | 30% | 0.61 | 0.44 | 0.43 | 0.55 |
| 5% | 35% | 0.61 | 0.44 | 0.43 | 0.55 |
| Method | Advantages | Disadvantages |
|---|---|---|
| Linear | - Assumes less than the other methods - Simple and efficient for good quality signals | - Less effective for signals with lots of missing data - Loss of time dependency |
| Pchip | - Preserves the linear trend and the slightly non linear contributions in the RR time-series [32] | - Less effective for signals with lots of missing data - Loss of time dependency |
| Spline | - Can capture abrupt variations when data quality is good | - Introduces outliers due to oscillation of the interpolation function [9] - Less effective for signals with lots of missing data - Loss of time dependency |
| DVC | - Adaptive to data distribution and variability - No ectopic values in the processed signal - Preserves signal’s time dependency - Effective for low quality signals | - Computationally expensive - Algorithm could be optimised |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benchekroun, M.; Chevallier, B.; Istrate, D.; Zalc, V.; Lenne, D. Preprocessing Methods for Ambulatory HRV Analysis Based on HRV Distribution, Variability and Characteristics (DVC). Sensors 2022, 22, 1984. https://doi.org/10.3390/s22051984
Benchekroun M, Chevallier B, Istrate D, Zalc V, Lenne D. Preprocessing Methods for Ambulatory HRV Analysis Based on HRV Distribution, Variability and Characteristics (DVC). Sensors. 2022; 22(5):1984. https://doi.org/10.3390/s22051984
Chicago/Turabian StyleBenchekroun, Mouna, Baptiste Chevallier, Dan Istrate, Vincent Zalc, and Dominique Lenne. 2022. "Preprocessing Methods for Ambulatory HRV Analysis Based on HRV Distribution, Variability and Characteristics (DVC)" Sensors 22, no. 5: 1984. https://doi.org/10.3390/s22051984
APA StyleBenchekroun, M., Chevallier, B., Istrate, D., Zalc, V., & Lenne, D. (2022). Preprocessing Methods for Ambulatory HRV Analysis Based on HRV Distribution, Variability and Characteristics (DVC). Sensors, 22(5), 1984. https://doi.org/10.3390/s22051984









