Indirect-Neural-Approximation-Based Fault-Tolerant Integrated Attitude and Position Control of Spacecraft Proximity Operations
Abstract
:1. Introduction
- Both the relative attitude control law and relative position control law are designed by integrating with the neural approximation. Benefiting from this design, the proposed controller is model-free and strongly robust against the lumped unknowns in 6-DOF dynamics;
- Rather than the conventional intelligent approximation [28,29,30], in which the NNs and fuzzy logic systems are introduced to directly approximate the lumped unknowns, the indirect neural approximation is exploited in this paper by adopting the NNs to approximate the upper bound of the lumped unknowns. In this way, only two adaptive parameters are required for the indirect neural approximation, and the online calculation burden of the proposed controller is therefore significantly reduced;
- Lyapunov analysis shows that the overall closed-loop system is ultimately uniformly bounded. The proposed controller can ensure that the relative attitude, angular velocity, position, and velocity stabilize into the small neighborhoods around the origin.
2. Problem Statement and Preliminaries
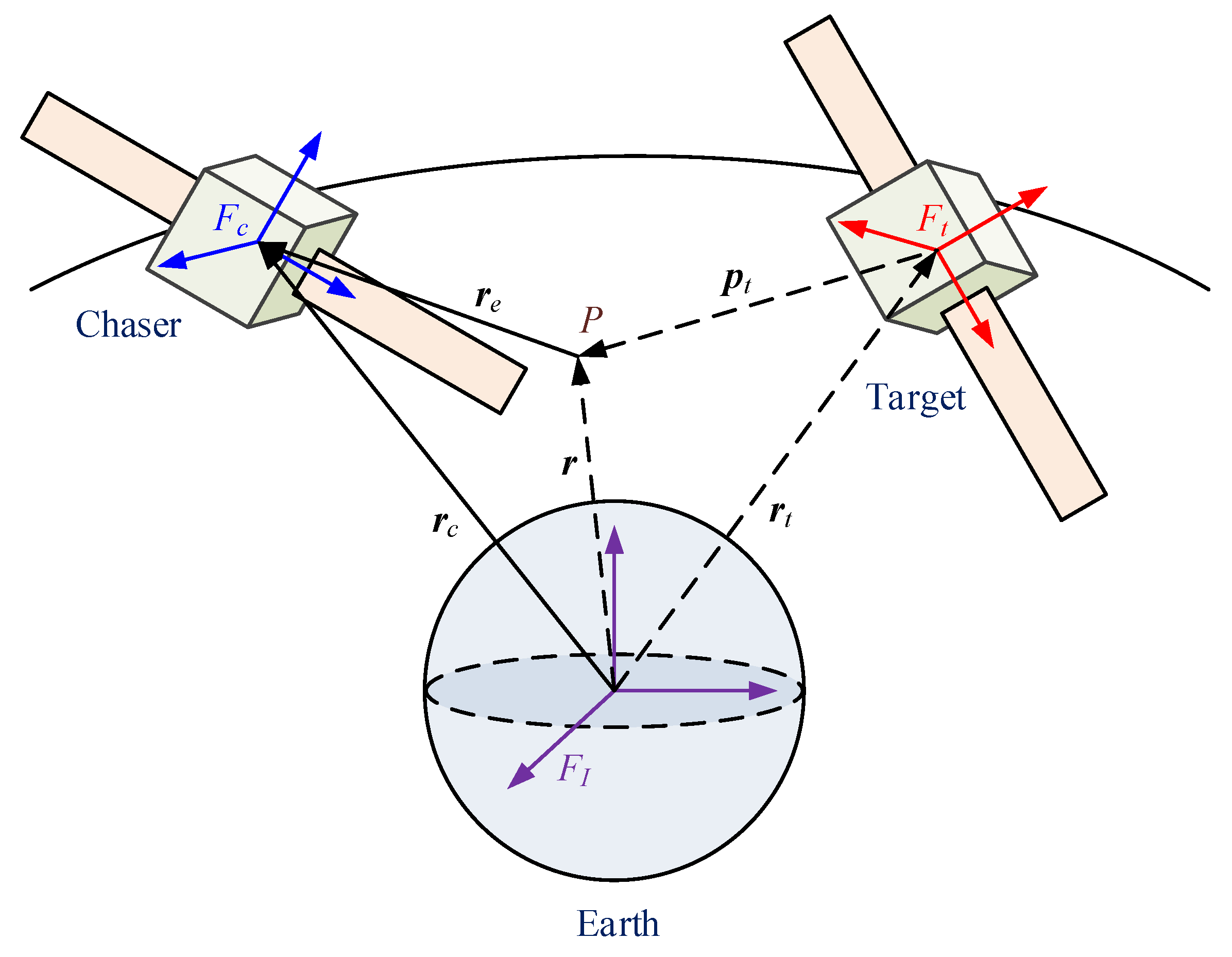
2.1. The 6-DOF Dynamics of Spacecraft Proximity Operations
2.2. Purpose
2.3. Neural Approximation
3. Control Design Methodology
3.1. Architecture of the Whole Control Design
3.2. Relative Attitude Control Design
3.3. Relative Position Control Design
4. Simulated Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singla, P.; Subbarao, K.; Junkins, J.L. Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty. J. Guid. Control Dyn. 2006, 29, 892–902. [Google Scholar] [CrossRef]
- Kristiansen, R.; Nicklasson, P.J.; Gravdahl, J.T. Spacecraft coordination control in 6DOF: Integrator backstepping vs passivity-based control. Automatica 2008, 44, 2896–2901. [Google Scholar] [CrossRef]
- Xin, M.; Pan, H. Integrated nonlinear optimal control of spacecraft in proximity operations. Int. J. Control 2010, 83, 347–363. [Google Scholar] [CrossRef]
- Xin, M.; Pan, H. Indirect robust control of spacecraft via optimal control solution. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1798–1809. [Google Scholar] [CrossRef]
- Zhang, F.; Duan, G. Robust adaptive integrated translation and rotation control of a rigid spacecraft with control saturation and actuator misalignment. Acta Astronaut. 2013, 86, 167–187. [Google Scholar] [CrossRef]
- Pukdeboon, C. Inverse optimal sliding mode control of spacecraft with coupled translation and attitude dynamics. Int. J. Syst. Sci. 2015, 46, 2421–2438. [Google Scholar] [CrossRef] [Green Version]
- Pukdeboon, C.; Kumam, P. Robust optimal sliding mode control for spacecraft position and attitude maneuvers. Aerosp. Sci. Technol. 2015, 43, 329–342. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W. 6-DOF integrated adaptive backstepping control for spacecraft proximity operations. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2433–2443. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W. Robust adaptive relative position tracking and attitude synchronization for spacecraft rendezvous. Aerosp. Sci. Technol. 2015, 41, 28–35. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Adaptive relative pose control of spacecraft with model couplings and uncertainties. Acta Astronaut. 2018, 143, 29–36. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Disturbance observer-based robust saturated control for spacecraft proximity maneuvers. IEEE Trans. Control Syst. Technol. 2018, 26, 684–692. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W.; Jiao, Z. Disturbance observer-based robust relative pose control for spacecraft rendezvous and proximity operations under input saturation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1605–1617. [Google Scholar] [CrossRef]
- Hu, Q.; Shao, X.; Chen, W.-H. Robust fault-tolerant tracking control for spacecraft proximity operations using time-varying sliding mode. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2–17. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ji, H. Integrated relative position and attitude control for spacecraft rendezvous with ISS and finite-time convergence. Aerosp. Sci. Technol. 2019, 85, 234–245. [Google Scholar] [CrossRef]
- Sun, L. Adaptive fault-tolerant constrained control of cooperative spacecraft rendezvous and docking. IEEE Trans. Ind. Electron. 2020, 67, 3107–3115. [Google Scholar] [CrossRef]
- Zhou, B.-Z.; Liu, X.-F.; Cai, G.-P. Robust adaptive position and attitude-tracking controller for satellite proximity operations. Acta Astronaut. 2020, 167, 135–145. [Google Scholar] [CrossRef]
- Huang, Y.; Jia, Y. Adaptive fixed-time relative position tracking and attitude synchronization control for non-cooperative target spacecraft fly-around mission. J. Frankl. Inst. 2017, 354, 8461–8489. [Google Scholar] [CrossRef]
- Huang, Y.; Jia, Y. Robust adaptive fixed-time tracking control of 6-DOF spacecraft fly-around mission for noncooperative target. Int. J. Robust Nonlinear Control 2018, 28, 2598–2618. [Google Scholar] [CrossRef]
- Huang, Y.; Jia, Y. Adaptive fixed-time six-DOF tracking control for noncooperative spacecraft fly-around mission. IEEE Trans. Control Syst. Technol. 2019, 27, 1796–1804. [Google Scholar] [CrossRef]
- Wang, J.; Liang, H.; Sun, Z.; Zhang, S.; Liu, M. Finite-time control for spacecraft formation with dual-number-based description. J. Guid. Control Dyn. 2012, 35, 950–962. [Google Scholar] [CrossRef]
- Filipe, N.; Tsiotras, P. Adaptive position and attitude-tracking controller for satellite proximity operations using dual quaternions. J. Guid. Control Dyn. 2015, 38, 566–577. [Google Scholar] [CrossRef] [Green Version]
- Filipe, N.; Valverde, A.; Tsiotras, P. Pose tracking without linear- and angular-velocity feedback using dual quaternions. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 411–422. [Google Scholar] [CrossRef]
- Gui, H.; Vukovich, G. Dual-quaternion-based adaptive motion tracking of spacecraft with reduced control effort. Nonlinear Dyn. 2016, 83, 597–614. [Google Scholar] [CrossRef]
- Gui, H.; Vukovich, G. Finite-time output-feedback position and attitude tracking of a rigid body. Automatica 2016, 74, 270–278. [Google Scholar] [CrossRef]
- Vukovich, G.; Gui, H. Robust adaptive tracking of rigid-body motion with applications to asteroid proximity operations. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 419–430. [Google Scholar] [CrossRef]
- Tsiotras, P.; Valverde, A. Dual quaternions as a tool for modeling, control, and estimation for spacecraft robotic servicing missions. J. Astronaut. Sci. 2020, 67, 595–629. [Google Scholar] [CrossRef]
- Stanfield, K.; Younes, A.B. Dual-quaternion analytic LQR control design for spacecraft proximity operations. Sensors 2020, 21, 3597. [Google Scholar] [CrossRef]
- Xia, K.; Huo, W. Robust adaptive backstepping neural networks control for spacecraft rendezvous and docking with uncertainties. Nonlinear Dyn. 2016, 84, 1683–1695. [Google Scholar] [CrossRef]
- Xia, K.; Huo, W. Robust adaptive backstepping neural networks control for spacecraft rendezvous and docking with input saturation. ISA Trans. 2016, 62, 249–257. [Google Scholar] [CrossRef]
- Sun, L.; He, W.; Sun, C. Adaptive fuzzy relative pose control of spacecraft during rendezvous and proximity maneuvers. IEEE Trans. Fuzzy Syst. 2018, 26, 3440–3451. [Google Scholar] [CrossRef]
- Sanner, R.M.; Slotine, J.-J.E. Gaussian networks for direct adaptive control. IEEE Trans. Neural Netw. 1992, 3, 837–863. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Na, J.; Gao, G. Adaptive dynamic programming based robust control of nonlinear systems with unmatched uncertainties. Neurocomputing 2020, 395, 56–65. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, B.; Liu, D. Fault tolerant tracking control for nonlinear systems with actuator failures through particle swarm optimization-based adaptive dynamic programming. Appl. Soft Comput. 2020, 97, 106766. [Google Scholar] [CrossRef]
- Liu, D.; Xue, S.; Zhao, B.; Luo, B.; Wei, Q. Adaptive dynamic programming for control: A survey and recent advances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 142–160. [Google Scholar] [CrossRef]
- Na, J.; Lv, F.; Zhang, K.; Zhao, J. Adaptive identifier-critic-based optimal tracking control for nonlinear systems with experimental validation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 459–472. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaade, F.W.; Yao, Q.; Al-zahrani, M.S.; Alzahrani, A.S.; Jahanshahi, H. Indirect-Neural-Approximation-Based Fault-Tolerant Integrated Attitude and Position Control of Spacecraft Proximity Operations. Sensors 2022, 22, 1726. https://doi.org/10.3390/s22051726
Alsaade FW, Yao Q, Al-zahrani MS, Alzahrani AS, Jahanshahi H. Indirect-Neural-Approximation-Based Fault-Tolerant Integrated Attitude and Position Control of Spacecraft Proximity Operations. Sensors. 2022; 22(5):1726. https://doi.org/10.3390/s22051726
Chicago/Turabian StyleAlsaade, Fawaz W., Qijia Yao, Mohammed S. Al-zahrani, Ali S. Alzahrani, and Hadi Jahanshahi. 2022. "Indirect-Neural-Approximation-Based Fault-Tolerant Integrated Attitude and Position Control of Spacecraft Proximity Operations" Sensors 22, no. 5: 1726. https://doi.org/10.3390/s22051726
APA StyleAlsaade, F. W., Yao, Q., Al-zahrani, M. S., Alzahrani, A. S., & Jahanshahi, H. (2022). Indirect-Neural-Approximation-Based Fault-Tolerant Integrated Attitude and Position Control of Spacecraft Proximity Operations. Sensors, 22(5), 1726. https://doi.org/10.3390/s22051726





