A Novel Method for Intelligibility Assessment of Nonlinearly Processed Speech in Spaces Characterized by Long Reverberation Times
Abstract
:1. Introduction
- A main utility space of a shopping mall (3 impulse responses with STIs of 0.35, 0.41, and 0.62),
- An above-ground parking hall (2 impulse responses with STIs of 0.37 and 0.58),
- A staircase of an office building (5 impulse responses with STIs of 0.33, 0.35, 0.39, 0.45, and 0.51).
1.1. State-of-the-Art of the Speech Intelligibility Assessment Methods
1.2. STI as an Objective Speech Intelligibility Measure
1.3. Limitations of STI as a Way of Assessing Speech Intelligibility
- The impact of linear transformations on the intelligibility of a speech signal (e.g., filtration, adaptive filtering, signal amplification),
- The effect of the appearance of additive disturbances (the disturbances being signals containing modulation signals, e.g., a real speech signal, are excluded).
2. Methods
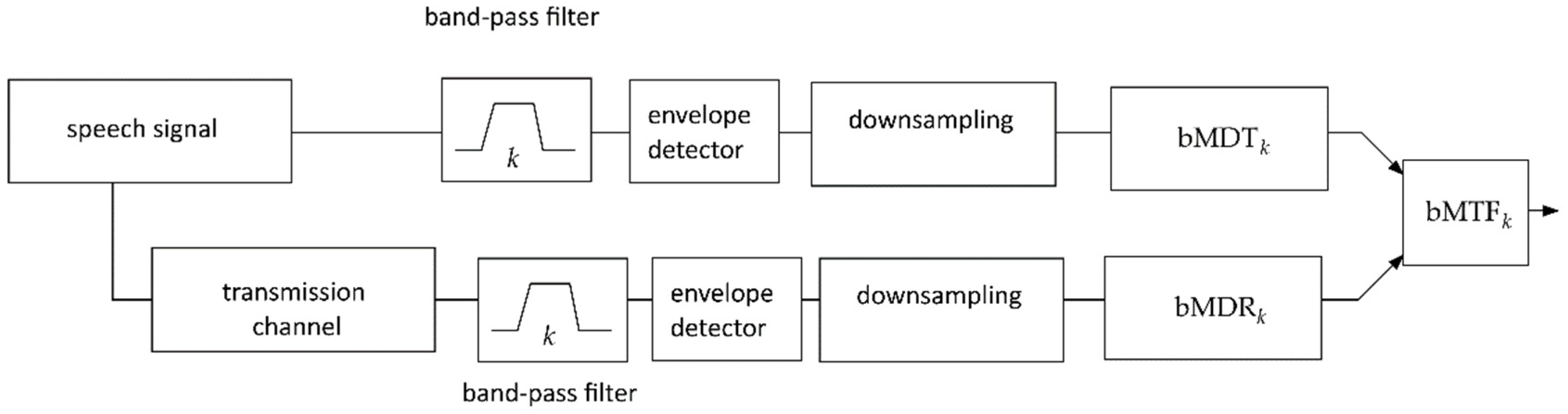
2.1. Calculation of the Broadband STI Measure (bSTI)
2.2. Practical Measurement of bSTI and Its Relation to STI
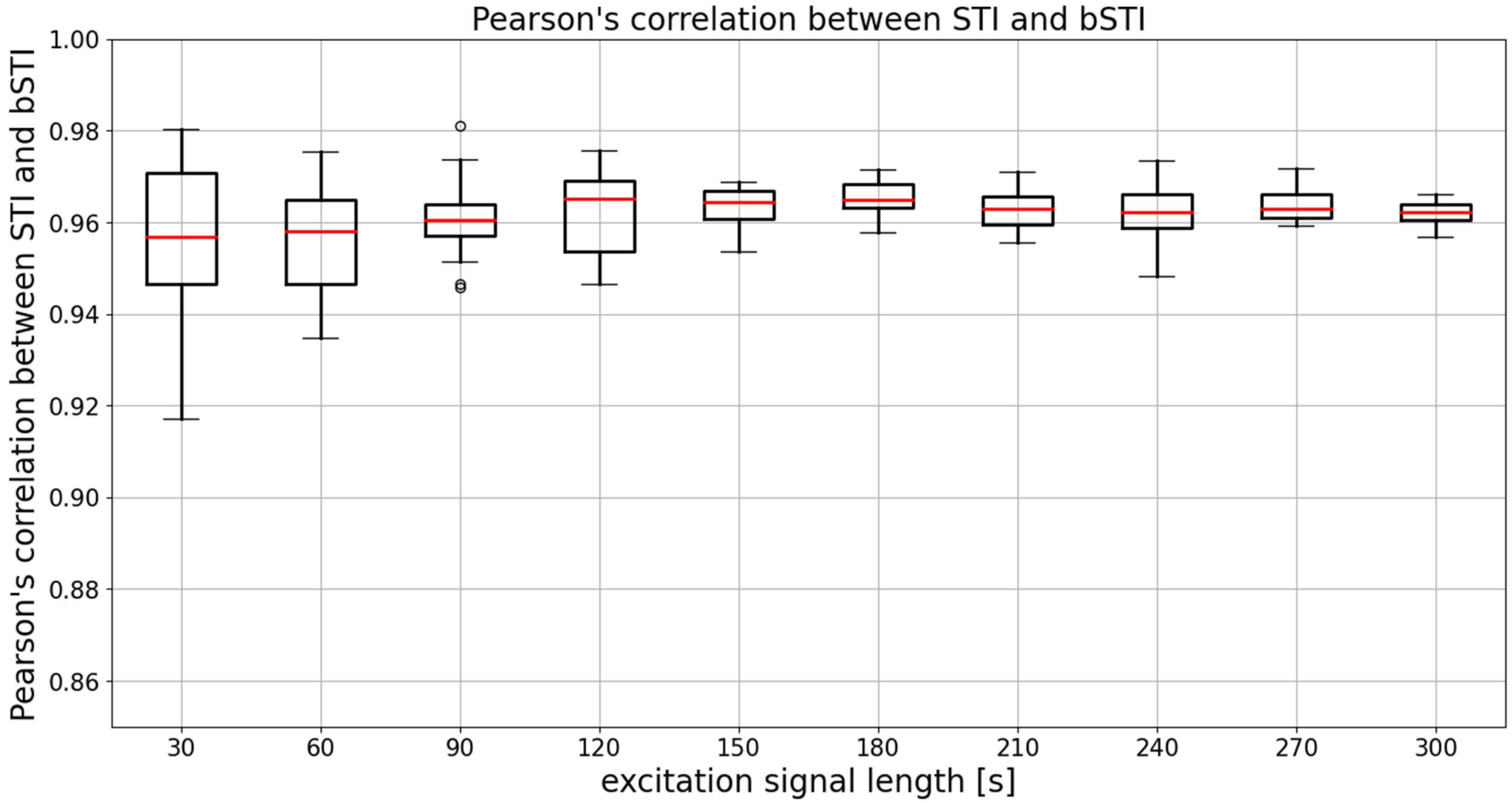
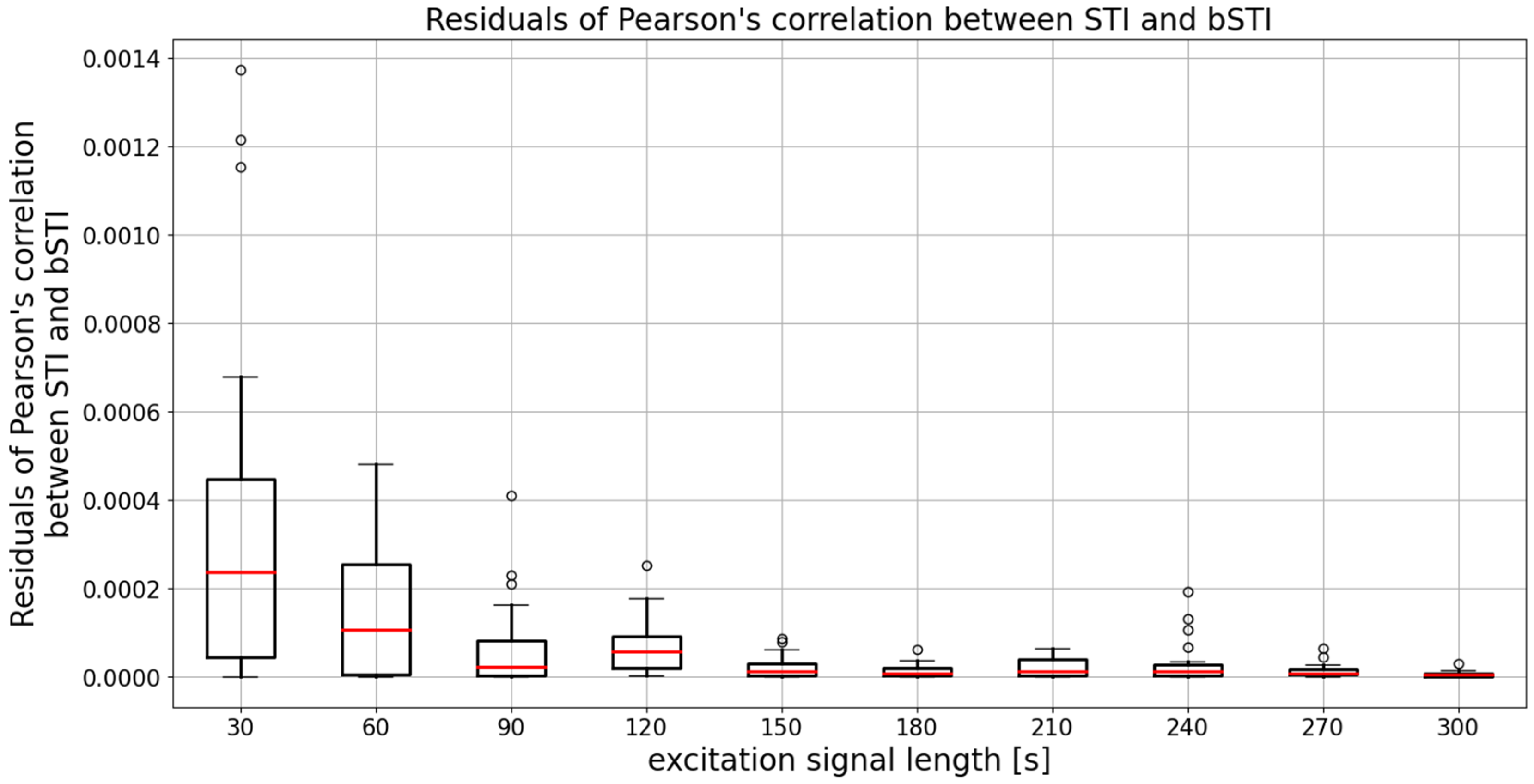
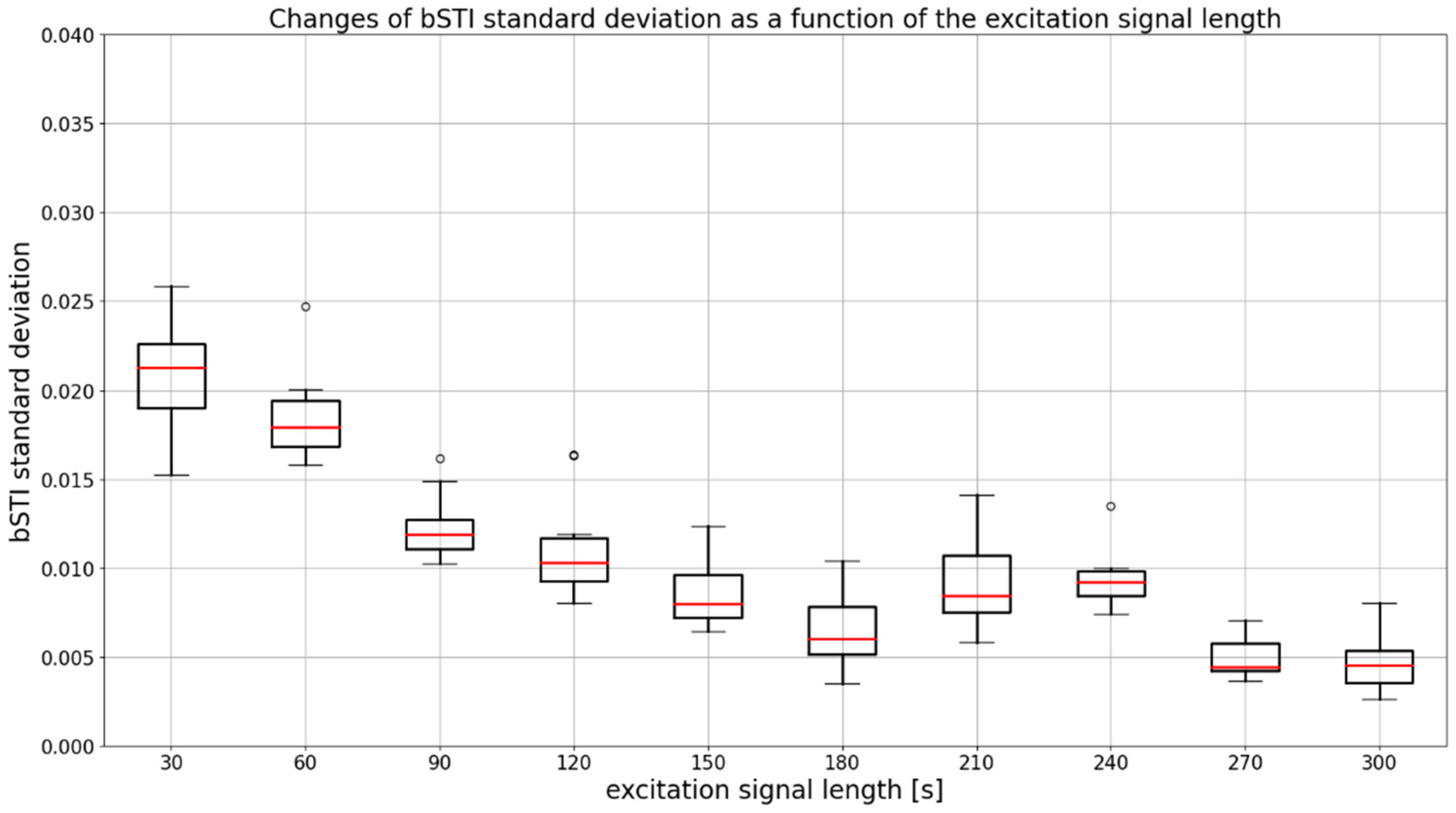
3. Results
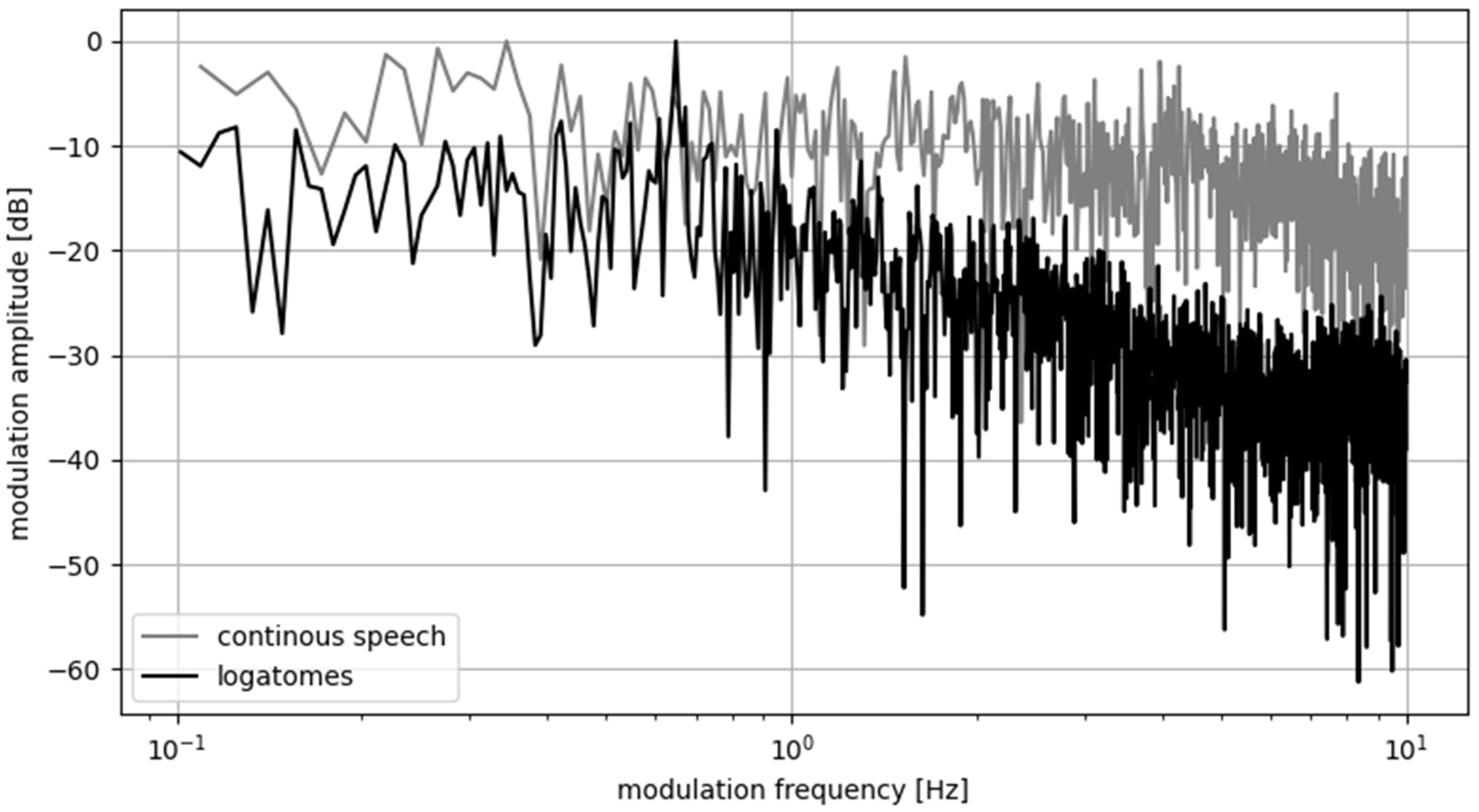
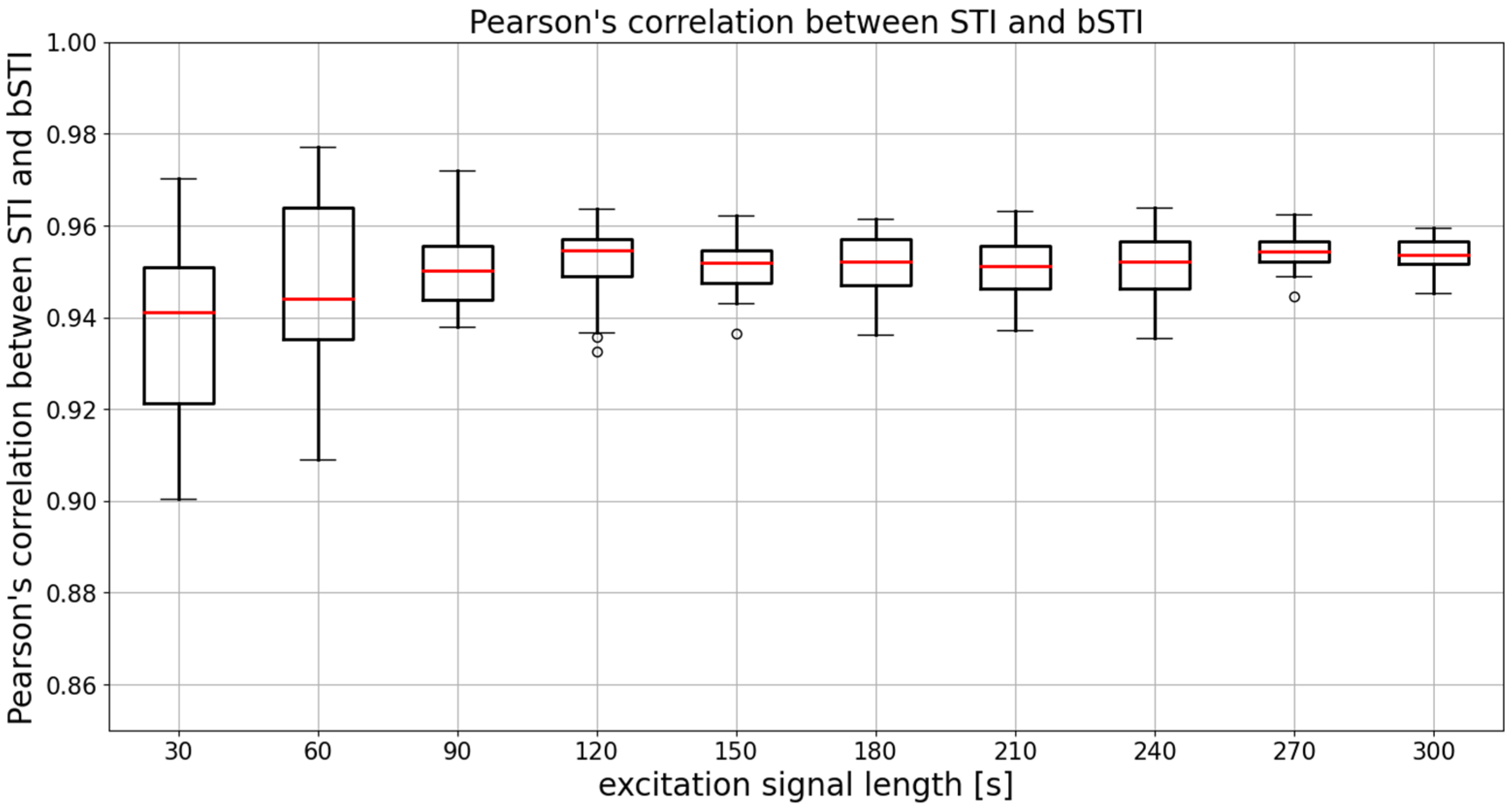
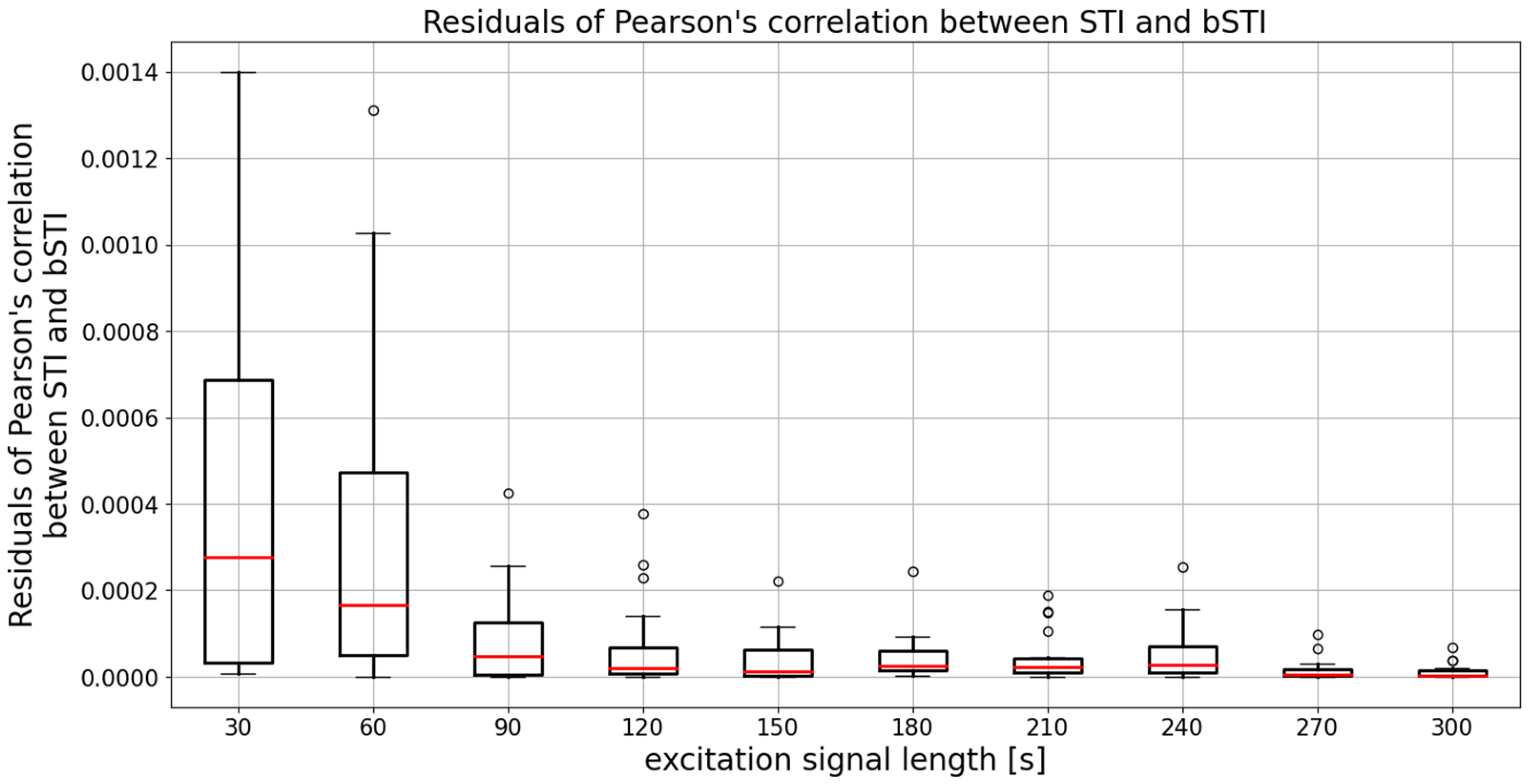
3.1. Results for Excitation Signal Synthesized from Polish Utterances
3.2. Results for Excitation Signal Synthesized from English Utterances
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phillips, F. The Circle of Innovation. J. Innov. Manag. 2016, 4, 12–31. [Google Scholar] [CrossRef]
- Johannesson, N.O. The ETSI computation model: A tool for transmission planning of telephone networks. IEEE Commun. Mag. 1997, 35, 70–79. [Google Scholar] [CrossRef]
- Ma, J.; Hu, Y.; Loizou, P.C. Objective measures for predicting speech intelligibility in noisy conditions based on new band-importance functions. J. Acoust. Soc. Am. 2009, 125, 3387–3405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Payton, K.L.; Shrestha, M. Comparison of a short-time speech-based intelligibility metric to the speech transmission index and intelligibility data. J. Acoust. Soc. Am. 2013, 134, 3818–3827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- International Telecommunication Union (ITU). BS.1534-1 Method for the Subjective Assessment of Intermediate Quality Level of Coding Systems; International Telecommunication Union: Geneva, Switzerland, 2003; pp. 1–18. [Google Scholar]
- International Telecommunication Union (ITU). P.800 Methods for Subjective Determination of Transmission Quality; International Telecommunication Union: Geneva, Switzerland, 1996. [Google Scholar]
- Korvel, G.; Kakol, K.; Kurasova, O.; Kostek, B. Evaluation of Lombard Speech Models in the Context of Speech in Noise Enhancement. IEEE Access 2020, 8, 155156–155170. [Google Scholar] [CrossRef]
- Kostek, B.; Kakol, K. Improving the quality of speech in the conditions of noise and interference. J. Acoust. Soc. Am. 2018, 144, 1905. [Google Scholar] [CrossRef]
- Fivela, B.G.; Sallustio, V.; Pede, S.; Patrocinio, D. Phonetic Complexity, Speech Accuracy and Intelligibility Assessment of Italian Dysarthric Speech. In Proceedings of the Interspeech 2021, Brno, Czechia, 30 August–3 September 2021. [Google Scholar] [CrossRef]
- Institute of Sound and Vibration Research. BS EN IEC 60268-16:2020, Sound System Equipment. Objective Rating of Speech Intelligibility by Speech Transmission Index, a Norm Document Defining the STI, STITEL and STIPA Measurement Methods; Institute of Sound and Vibration Research: Southampton, UK, 2011. [Google Scholar]
- Odya, P.; Kotus, J.; Kurowski, A.; Kostek, B. Acoustic Sensing Analytics Applied to Speech in Reverberation Conditions. Sensors 2021, 21, 6320. [Google Scholar] [CrossRef]
- Gomez-Agustina, L.; Dance, S.; Shield, B. The effects of air temperature and humidity on the acoustic design of voice alarm systems on underground stations. Appl. Acoust. 2014, 76, 262–273. [Google Scholar] [CrossRef]
- Tronchin, L. Variability of room acoustic parameters with thermo-hygrometric conditions. Appl. Acoust. 2021, 177, 107933. [Google Scholar] [CrossRef]
- Yang, W.; Moon, H.J. Cross-modal effects of noise and thermal conditions on indoor environmental perception and speech recognition. Appl. Acoust. 2018, 141, 1–8. [Google Scholar] [CrossRef]
- Assmann, P.; Summerfield, Q. The Perception of Speech Under Adverse Conditions. In Speech Processing in the Auditory System, 1st ed.; Greenberg, S., Ainsworth, W.A., Popper, A.N., Fay, R.R., Eds.; Springer: New York, NY, USA, 2004; pp. 231–308. [Google Scholar] [CrossRef]
- Steeneken, H.J.M.; Houtgast, T. A physical method for measuring speech-transmission quality. J. Acoust. Soc. Am. 1980, 67, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Houtgast, T.; Steeneken, H.J.M. A review of the MTF concept in room acoustics and its use for estimating speech intelligibility in auditoria. J. Acoust. Soc. Am. 1985, 77, 1069–1077. [Google Scholar] [CrossRef]
- French, N.R.; Steinberg, J.C. Factors Governing the Intelligibility of Speech Sounds. J. Acoust. Soc. Am. 1947, 19, 90–119. [Google Scholar] [CrossRef]
- Fletcher, H.; Galt, R.H. The Perception of Speech and Its Relation to Telephony. J. Acoust. Soc. Am. 1950, 22, 89–151. [Google Scholar] [CrossRef]
- Kryter, K.D. Methods for the Calculation and Use of the Articulation Index. J. Acoust. Soc. Am. 1962, 34, 1689–1697. [Google Scholar] [CrossRef]
- Kryter, K.D. Validation of the Articulation Index. J. Acoust. Soc. Am. 1962, 34, 1698–1702. [Google Scholar] [CrossRef]
- Parija, S.; Sahu, P.K.; Singh, S.S. Speech Enhancement by Speech Intelligibility Index in Sensor Network. In Proceedings of the 2012 Third International Conference on Computing, Communication and Networking Technologies (ICCCNT’12), Coimbatore, India, 26–28 July 2012; pp. 1–6. [Google Scholar]
- Rhebergen, K.S.; Versfeld, N.J.; Dreschler, W.A. Extended speech intelligibility index for the prediction of the speech reception threshold in fluctuating noise. J. Acoust. Soc. Am. 2006, 120, 3988–3997. [Google Scholar] [CrossRef]
- Kates, J.M. The short-time articulation index. J. Rehabil. Res. Dev. 1987, 24, 271–276. [Google Scholar]
- Kąkol, K.; Korvel, G.; Kostek, B. Improving Objective Speech Quality Indicators in Noise Conditions. In Data Science: New Issues, Challenges and Applications. Studies in Computational Intelligence; Dzemyda, G., Bernatavičienė, J., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2020; Volume 869, pp. 199–218. [Google Scholar] [CrossRef]
- Kates, J.M.; Arehart, K.H. Coherence and the speech intelligibility index. J. Acoust. Soc. Am. 2005, 117, 2224–2237. [Google Scholar] [CrossRef]
- Arifianto, D.; Asyraf, M.A.; Amelia, R.R.; Fajriyah, L. Speech Intelligibility evaluation in the presence of speech masker of cochlear implant in a reverberant room. J. Acoust. Soc. Am. 2021, 150, A340. [Google Scholar] [CrossRef]
- Goldsworthy, R.L.; Greenberg, J.E. Analysis of speech-based speech transmission index methods with implications for nonlinear operations. J. Acoust. Soc. Am. 2004, 116, 3679–3689. [Google Scholar] [CrossRef] [PubMed]
- Thiede, T.; Treurniet, W.C.; Bitto, R.; Schmidmer, C.; Sporer, T.; Beerends, J.G.; Colomes, C. PEAQ-The ITU standard for objective measurement of perceived audio quality. J. Audio Eng. Soc. 2000, 48, 3–29. [Google Scholar]
- Rix, A.W.; Beerends, J.G.; Hollier, M.P.; Hekstra, A.P. Perceptual evaluation of speech quality (PESQ)-A new method for speech quality assessment of telephone networks and codecs. In Proceedings of the Acoustics, Speech, and Signal Processing. IEEE Computer Society, Salt Lake City, UT, USA, 7–11 May 2001; pp. 749–752. [Google Scholar] [CrossRef]
- Rix, A.W.; Beerends, J.G.; Hollier, M.P.; Hekstra, A.P. PESQ–the new ITU standard for end-to-end speech quality assessment”. In Proceedings of the 109th Audio Engineering Society Convention, Los Angeles, CA, USA, 22–25 September 2020; pre-print no. 5260. pp. 1–4. [Google Scholar]
- ITU-T. Perceptual Evaluation of Speech Quality (PESQ), an Objective Method for End-to-End Speech Quality Assessment of Narrow Band Telephone Networks and Speech Codecs. Recommendation P.862; ITU: Geneva, Switzerland, 2001. [Google Scholar]
- Beerends, J.G.; Schmidmer, C.; Berger, J.; Obermann, M.; Ullmann, R.; Pomy, J.; Keyhl, M. Perceptual Objective Listening Quality Assessment (POLQA), The Third Generation ITUT Standard for End-to-End Speech Quality Measurement Part II Perceptual Model. J. Audio Eng. Soc. 2013, 61, 385–402. [Google Scholar]
- Malfait, L.; Gray, P.; Reed, M.J. Objective Listening Quality Assessment of Speech Communication Systems Introducing Con-tinuously Varying Delay (Time-Warping): A Time Alignment Issue. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 4213–4216. [Google Scholar]
- Avila, A.R.; Gamper, H.; Reddy, C.; Cutler, R.; Tashev, I.; Gehrke, J. Non-Intrusive Speech Quality Assessment Using Neural Networks. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 631–635. [Google Scholar]
- Serrà, J.; Pons, J.; Pascual, S. SESQA: Semi-Supervised Learning for Speech Quality Assessment. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 381–385. [Google Scholar]
- Mittag, G.; Naderi, B.; Chehadi, A.; Möller, S. NISQA: A Deep CNN-Self-Attention Model for Multidimensional Speech Quality Prediction with Crowdsourced Datasets. In Proceedings of the Interspeech 2021, Brno, Czechia, 30 August–3 September 2021. [Google Scholar] [CrossRef]
- Chen, Y.-W.; Tsao, Y. InQSS: A Speech Intelligibility Assessment Model Using a Multi-Task Learning Network. arXiv 2021, arXiv:2111.02585 2021. [Google Scholar]
- IEEE. IEEE Recommended Practice for Speech Quality Measurements; IEEE: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Reinhart, P.N.; Souza, P.E. Intelligibility and Clarity of Reverberant Speech: Effects of Wide Dynamic Range Compression Release Time and Working Memory. J. Speech Lang. Hear. Res. 2016, 59, 1543–1554. [Google Scholar] [CrossRef] [Green Version]
- Kruger, K.; Gough, K.; Hill, P. A comparison of subjective speech intelligibility tests in reverberant environments. Can. Acoust. 1991, 19, 23–24. [Google Scholar]
- Hodoshima, N.; Arai, T. Effect of talker variability on speech perception by elderly people in reverberation. In Proceedings of the International Symposium on Auditory and Audiological Research, Helsingor, Denmark, 29–31 August 2007; pp. 383–388. [Google Scholar]
- Brachmański, S. Automation of the logatom intelligibility measurements in rooms. Archiv. Acoust. 2007, 32, 159–164. [Google Scholar]
- Bellanova, M. Development of a Logatome Test for the Evaluation of Signal Processing Algorithms in Hearing Aids on a Microscopic Level. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2016. [Google Scholar]
- Lavandier, M.; Culling, J.F. Speech segregation in rooms: Monaural, binaural, and interacting effects of reverberation on target and interferer. J. Acoust. Soc. Am. 2008, 123, 2237–2248. [Google Scholar] [CrossRef]
- Ozimek, E.; Kutzner, D.; Libiszewski, P.; Warzybok, A.; Kociński, J. The new Polish tests for speech intelligibility meas-urements. In Proceedings of the IEEE Signal Processing Algorithms, Architectures, Arrangements, and Applications SPA, Poznan, Poland, 24–26 September 2009; pp. 163–168. [Google Scholar]
- Kitapci, K.; Galbrun, L. Comparison of speech intelligibility between English, Polish, Arabic and Mandarin. In Proceedings of the Forum Acusticum 2014, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Kitapci, K.; Galbrun, L. Subjective speech intelligibility and soundscape perception of English, Polish, Arabic and Mandarin. In Proceedings of the 44th International Congress and Exposition on Noise Control Engineering, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- George, E.L.J.; Festen, J.M.; Houtgast, T. The combined effects of reverberation and nonstationary noise on sentence intelligibility. J. Acoust. Soc. Am. 2008, 124, 1269–1277. [Google Scholar] [CrossRef]
- Rhebergen, K.S.; Versfeld, N.J. A Speech Intelligibility Index-based approach to predict the speech reception threshold for sentences in fluctuating noise for normal-hearing listeners. J. Acoust. Soc. Am. 2005, 117, 2181–2192. [Google Scholar] [CrossRef] [Green Version]
- Van Wijngaarden, S.J.; Drullman, R. Binaural intelligibility prediction based on the speech transmission index. J. Acoust. Soc. Am. 2008, 123, 4514–4523. [Google Scholar] [CrossRef] [PubMed]
- Möller, H. A Review of STI Measurements. In Proceedings of the Forum Acusticum, Lyon, France, 7–11 December 2020; pp. 173–176. [Google Scholar]
- McCarthy, B. Sound Systems: Design and Optimization, 2nd ed.; Focal Press: Boston, MA, USA, 2010; ISBN 978-0-240-52156-5. [Google Scholar]
- Licklider, J.C.R.; Bindra, D.; Pollack, I. The Intelligibility of Rectangular Speech-Waves. Am. J. Psychol. 1948, 61, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Czyzewski, A.; Kostek, B.; Bratoszewski, P.; Kotus, J.; Szykulski, M. An audio-visual corpus for multimodal automatic speech recognition. J. Intell. Inf. Syst. 2017, 49, 167–192. [Google Scholar] [CrossRef] [Green Version]
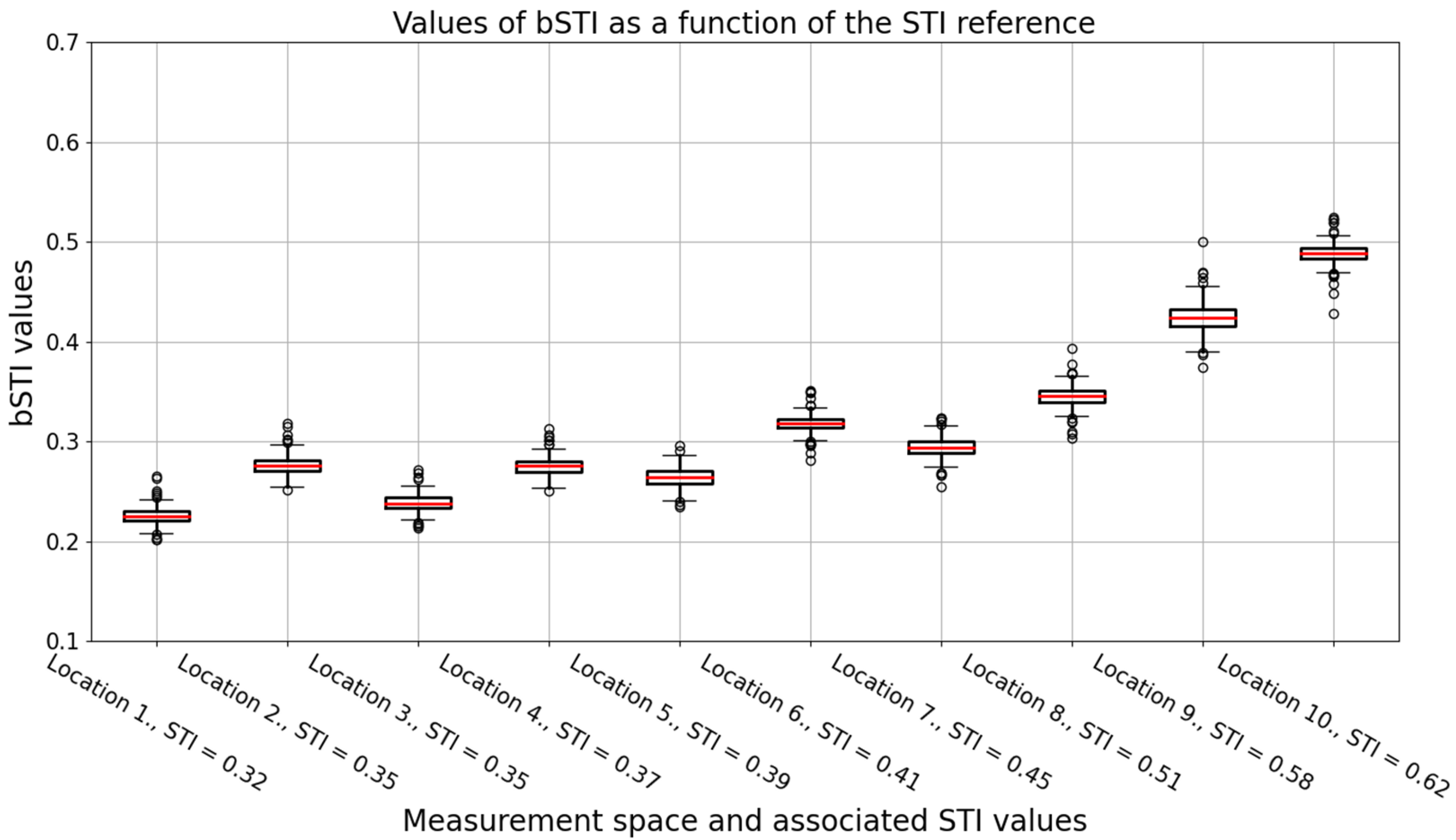
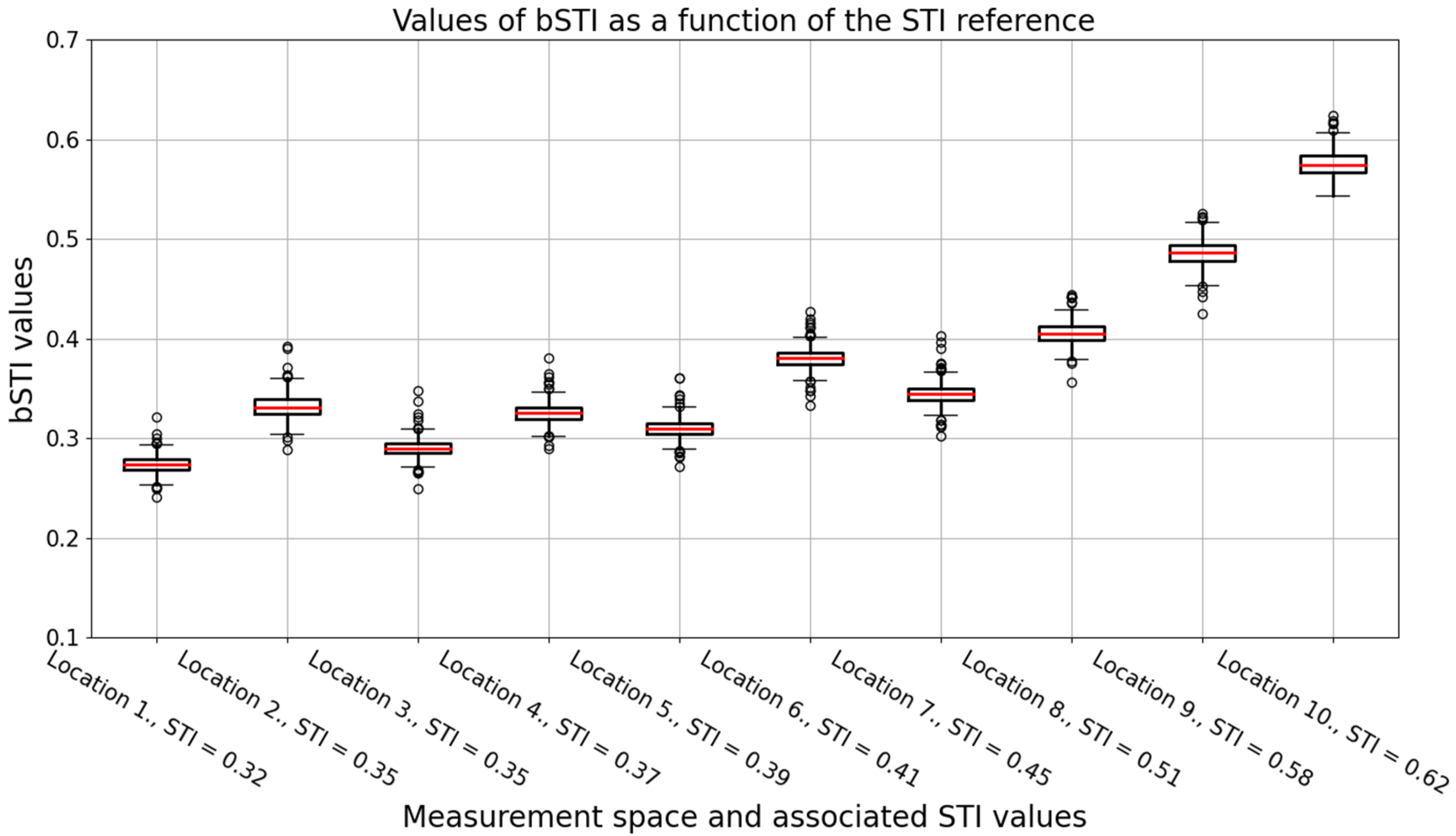
| Location | Interior | RT 250 | RT 500 | RT 1000 | RT 2000 | RT 4000 | RT 8000 | RT AVG | STIPA |
|---|---|---|---|---|---|---|---|---|---|
| 1 | C | 4.331 | 3.749 | 3.140 | 2.744 | 2.036 | 1.027 | 2.838 | 0.32 |
| 2 | A | 2.223 | 2.624 | 2.520 | 2.623 | 2.026 | 1.507 | 2.254 | 0.35 |
| 3 | C | 3.388 | 3.129 | 3.384 | 2.684 | 1.909 | 1.002 | 2.583 | 0.35 |
| 4 | B | 3.103 | 2.934 | 2.674 | 2.412 | 2.067 | 1.452 | 2.440 | 0.37 |
| 5 | C | 3.205 | 3.196 | 3.347 | 2.599 | 1.892 | 1.060 | 2.550 | 0.39 |
| 6 | A | 2.343 | 2.594 | 2.648 | 2.579 | 2.033 | 1.412 | 2.268 | 0.41 |
| 7 | C | 1.363 | 2.063 | 2.050 | 1.805 | 1.437 | 0.830 | 1.591 | 0.45 |
| 8 | C | 1.516 | 1.211 | 1.399 | 1.269 | 0.997 | 0.653 | 1.174 | 0.51 |
| 9 | B | 2.133 | 1.964 | 1.765 | 1.438 | 1.079 | 0.858 | 1.540 | 0.58 |
| 10 | A | 2.013 | 2.358 | 2.372 | 2.439 | 1.676 | 1.277 | 2.023 | 0.62 |
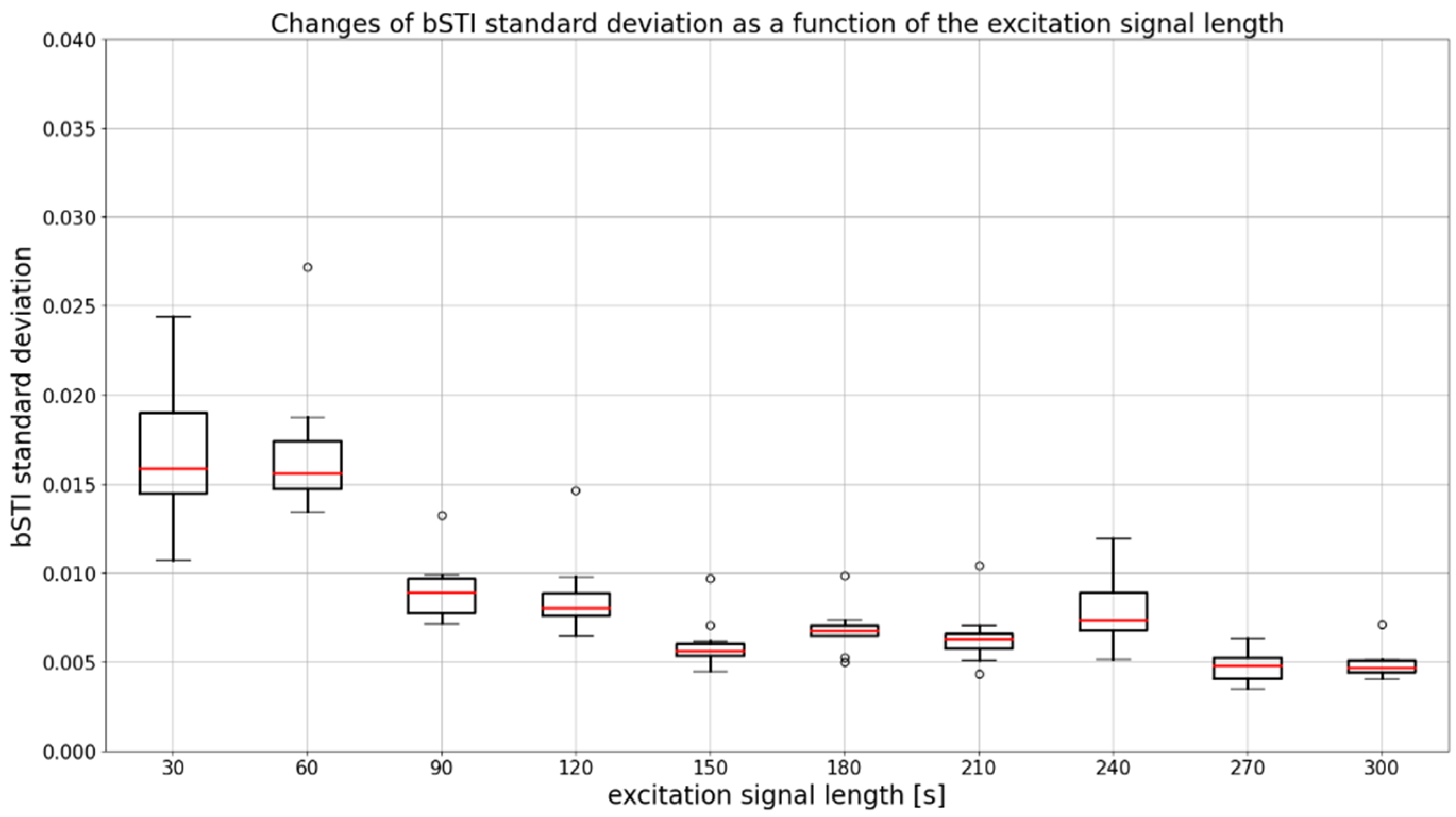
| Duration [s] | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|
| 30 | – | 0.975 | 0.065 | 0.034 | < | < | < | 0.004 | < | < |
| 60 | 0.975 | – | 0.070 | 0.037 | < | < | < | 0.005 | < | < |
| 90 | 0.065 | 0.070 | – | 0.781 | 0.007 | 0.074 | 0.021 | 0.316 | < | < |
| 120 | 0.034 | 0.037 | 0.781 | – | 0.015 | 0.131 | 0.042 | 0.469 | < | < |
| 150 | < | < | 0.007 | 0.015 | – | 0.359 | 0.694 | 0.089 | 0.215 | 0.241 |
| 180 | < | < | 0.074 | 0.131 | 0.359 | – | 0.600 | 0.432 | 0.031 | 0.037 |
| 210 | < | < | 0.021 | 0.042 | 0.694 | 0.600 | – | 0.190 | 0.102 | 0.118 |
| 240 | 0.004 | 0.005 | 0.316 | 0.469 | 0.089 | 0.432 | 0.190 | – | 0.003 | 0.004 |
| 270 | < | < | < | < | 0.215 | 0.031 | 0.102 | 0.003 | – | 0.945 |
| 300 | < | < | < | < | 0.241 | 0.037 | 0.118 | 0.004 | 0.945 | – |
| Duration [s] | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|
| 30 | – | 0.233 | 0.004 | 0.237 | < | < | < | 0.001 | < | < |
| 60 | 0.233 | – | 0.090 | 0.991 | 0.022 | 0.002 | 0.018 | 0.043 | 0.004 | < |
| 90 | 0.004 | 0.090 | – | 0.088 | 0.546 | 0.148 | 0.507 | 0.741 | 0.221 | 0.014 |
| 120 | 0.237 | 0.991 | 0.088 | – | 0.021 | 0.002 | 0.018 | 0.042 | 0.003 | < |
| 150 | < | 0.022 | 0.546 | 0.021 | – | 0.400 | 0.952 | 0.785 | 0.535 | 0.064 |
| 180 | < | 0.002 | 0.148 | 0.002 | 0.400 | – | 0.435 | 0.265 | 0.825 | 0.312 |
| 210 | < | 0.018 | 0.507 | 0.018 | 0.952 | 0.435 | – | 0.739 | 0.575 | 0.073 |
| 240 | 0.001 | 0.043 | 0.741 | 0.042 | 0.785 | 0.265 | 0.739 | – | 0.372 | 0.034 |
| 270 | < | 0.004 | 0.221 | 0.003 | 0.535 | 0.825 | 0.575 | 0.372 | – | 0.218 |
| 300 | < | < | 0.014 | < | 0.064 | 0.312 | 0.073 | 0.034 | 0.218 | – |
| Duration [s] | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|
| 30 | – | 0.683 | 0.074 | 0.014 | < | < | < | 0.001 | < | < |
| 60 | 0.683 | – | 0.168 | 0.040 | 0.001 | < | 0.002 | 0.003 | < | < |
| 90 | 0.074 | 0.168 | – | 0.503 | 0.043 | 0.001 | 0.080 | 0.118 | < | < |
| 120 | 0.014 | 0.040 | 0.503 | – | 0.177 | 0.009 | 0.281 | 0.371 | < | < |
| 150 | < | 0.001 | 0.043 | 0.177 | – | 0.201 | 0.787 | 0.649 | 0.028 | 0.023 |
| 180 | < | < | 0.001 | 0.009 | 0.201 | – | 0.121 | 0.083 | 0.359 | 0.320 |
| 210 | < | 0.002 | 0.080 | 0.281 | 0.787 | 0.121 | – | 0.853 | 0.014 | 0.011 |
| 240 | 0.001 | 0.003 | 0.118 | 0.371 | 0.649 | 0.083 | 0.853 | – | 0.008 | 0.006 |
| 270 | < | < | < | < | 0.028 | 0.359 | 0.014 | 0.008 | – | 0.939 |
| 300 | < | < | < | < | 0.023 | 0.320 | 0.011 | 0.006 | 0.939 | – |
| Duration [s] | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|
| 30 | – | 0.650 | 0.025 | 0.006 | < | 0.012 | 0.002 | 0.010 | < | < |
| 60 | 0.650 | – | 0.074 | 0.021 | 0.001 | 0.039 | 0.007 | 0.032 | < | < |
| 90 | 0.025 | 0.074 | – | 0.602 | 0.112 | 0.781 | 0.352 | 0.722 | 0.005 | 0.005 |
| 120 | 0.006 | 0.021 | 0.602 | – | 0.285 | 0.808 | 0.682 | 0.868 | 0.024 | 0.022 |
| 150 | < | 0.001 | 0.112 | 0.285 | – | 0.190 | 0.510 | 0.217 | 0.233 | 0.224 |
| 180 | 0.012 | 0.039 | 0.781 | 0.808 | 0.190 | – | 0.514 | 0.939 | 0.012 | 0.012 |
| 210 | 0.002 | 0.007 | 0.352 | 0.682 | 0.510 | 0.514 | – | 0.564 | 0.064 | 0.061 |
| 240 | 0.010 | 0.032 | 0.722 | 0.868 | 0.217 | 0.939 | 0.564 | – | 0.015 | 0.014 |
| 270 | < | < | 0.005 | 0.024 | 0.233 | 0.012 | 0.064 | 0.015 | – | 0.983 |
| 300 | < | < | 0.005 | 0.022 | 0.224 | 0.012 | 0.061 | 0.014 | 0.983 | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurowski, A.; Kotus, J.; Odya, P.; Kostek, B. A Novel Method for Intelligibility Assessment of Nonlinearly Processed Speech in Spaces Characterized by Long Reverberation Times. Sensors 2022, 22, 1641. https://doi.org/10.3390/s22041641
Kurowski A, Kotus J, Odya P, Kostek B. A Novel Method for Intelligibility Assessment of Nonlinearly Processed Speech in Spaces Characterized by Long Reverberation Times. Sensors. 2022; 22(4):1641. https://doi.org/10.3390/s22041641
Chicago/Turabian StyleKurowski, Adam, Jozef Kotus, Piotr Odya, and Bozena Kostek. 2022. "A Novel Method for Intelligibility Assessment of Nonlinearly Processed Speech in Spaces Characterized by Long Reverberation Times" Sensors 22, no. 4: 1641. https://doi.org/10.3390/s22041641
APA StyleKurowski, A., Kotus, J., Odya, P., & Kostek, B. (2022). A Novel Method for Intelligibility Assessment of Nonlinearly Processed Speech in Spaces Characterized by Long Reverberation Times. Sensors, 22(4), 1641. https://doi.org/10.3390/s22041641






