All-Directional DOA Estimation for Ultra-Wideband Regular Tetrahedral Array Using Wrapped PDoA
Abstract
:1. Introduction
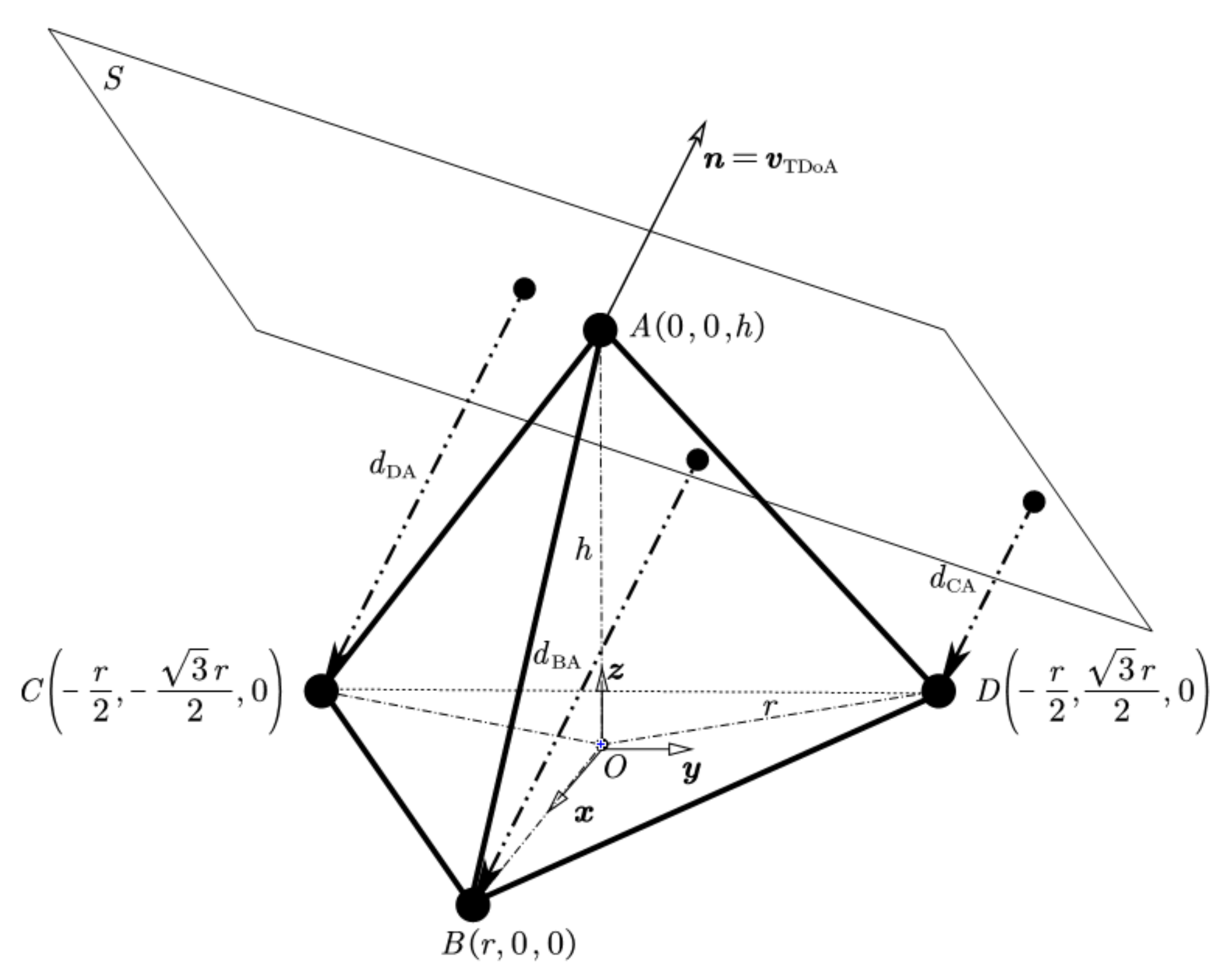
2. Coarse Estimate for RTA Using TDOA
3. Combined TDoA and Wrapped PDoA for RTA
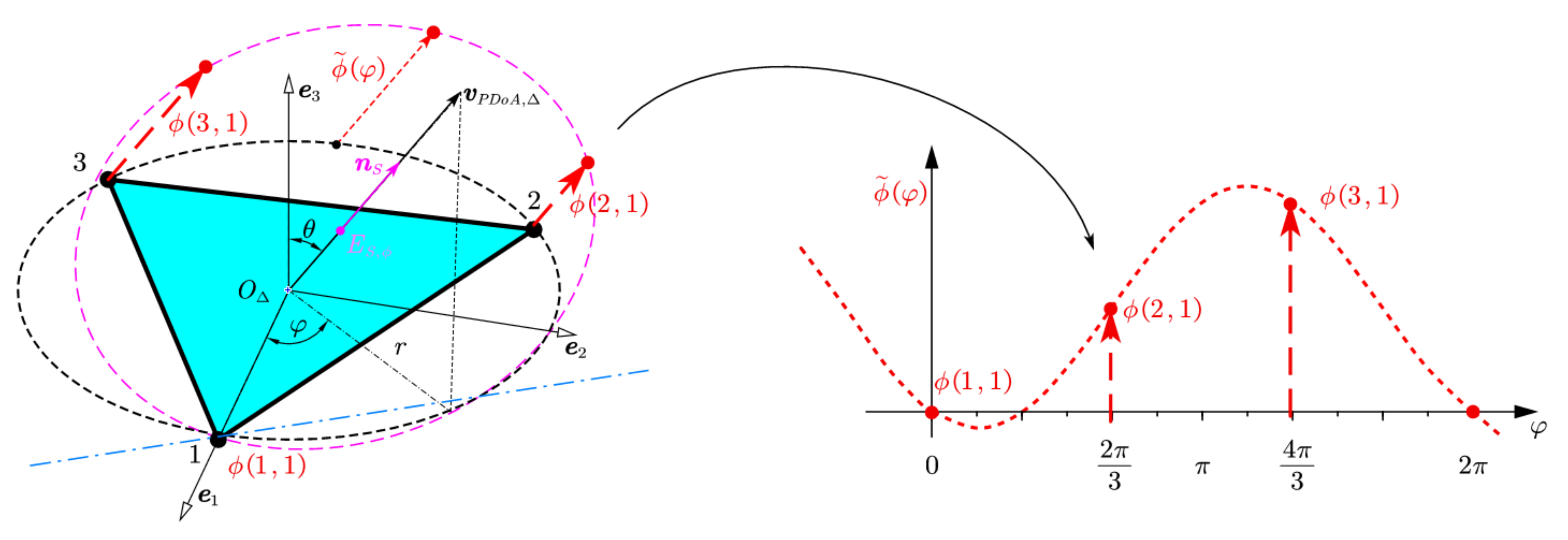
3.1. Wrapped PDoA for RTA
3.1.1. Spatial Subarray Decompose of RTA
3.1.2. Solve Phased UCA Utilizing Fourier Analysis
3.2. Ambiguity Resolution Algorithm
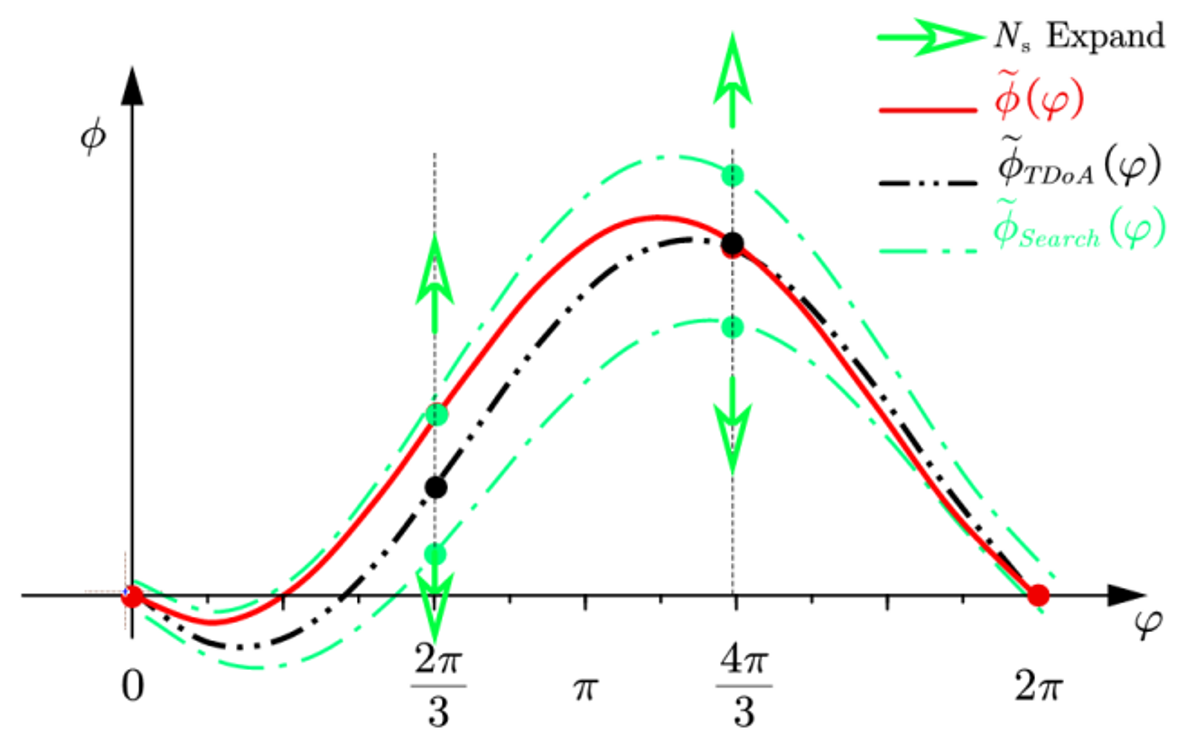
3.2.1. Geometric Identical Cost Function
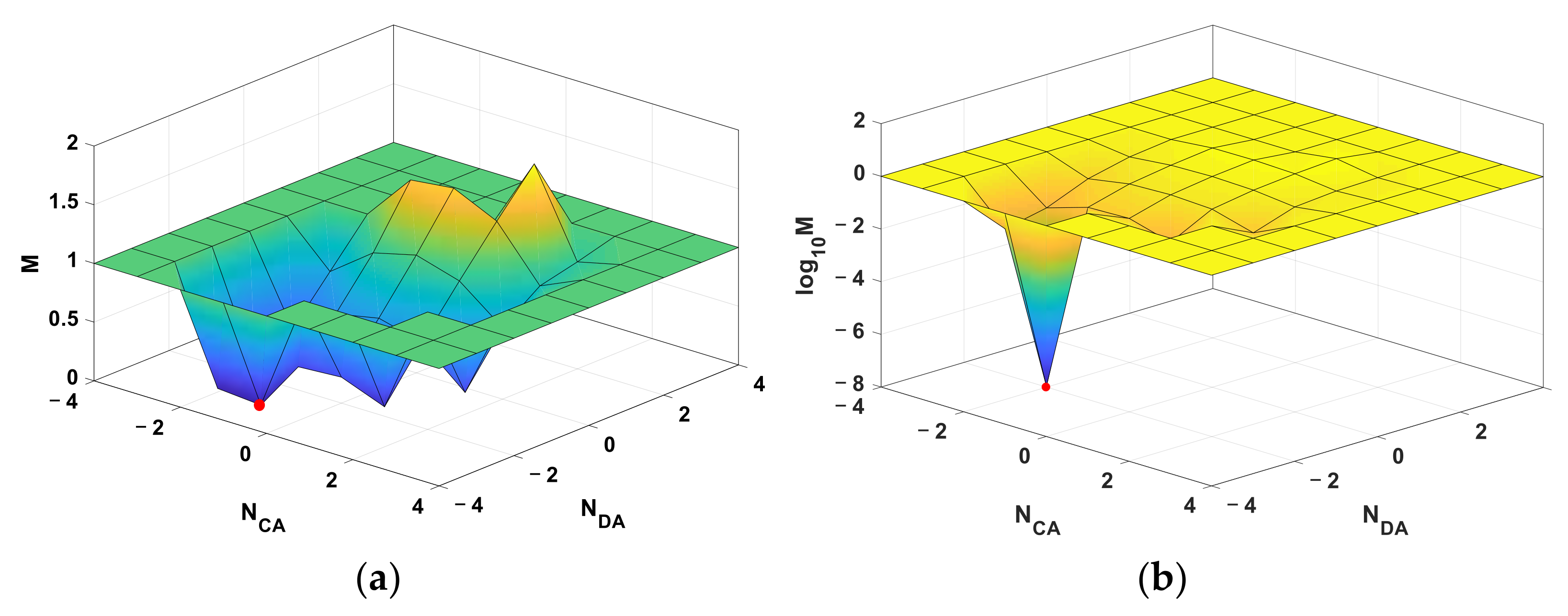
3.2.2. Ambiguity Integer Search Strategy
Initial Value
Variable Neighborhood Search
3.2.3. Spatial Subarray Vote Mechanism
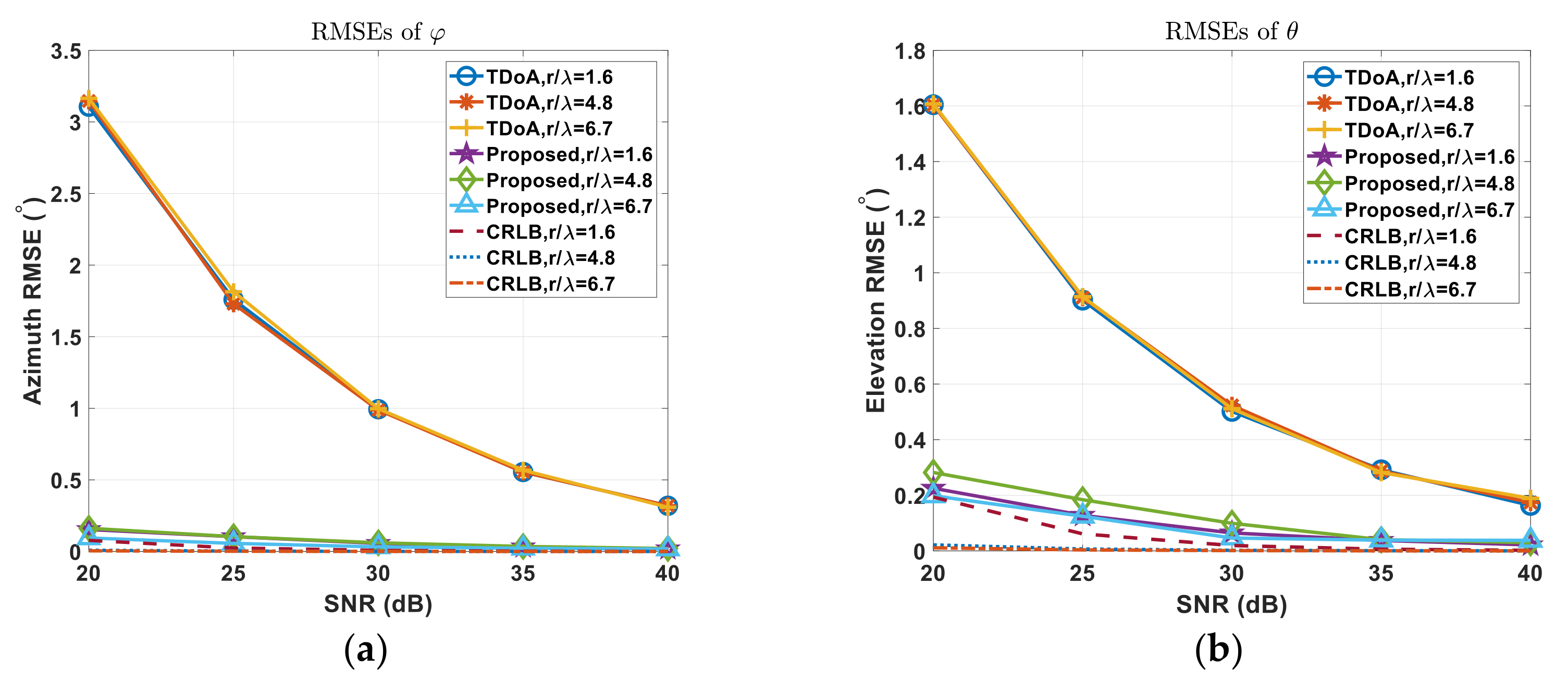
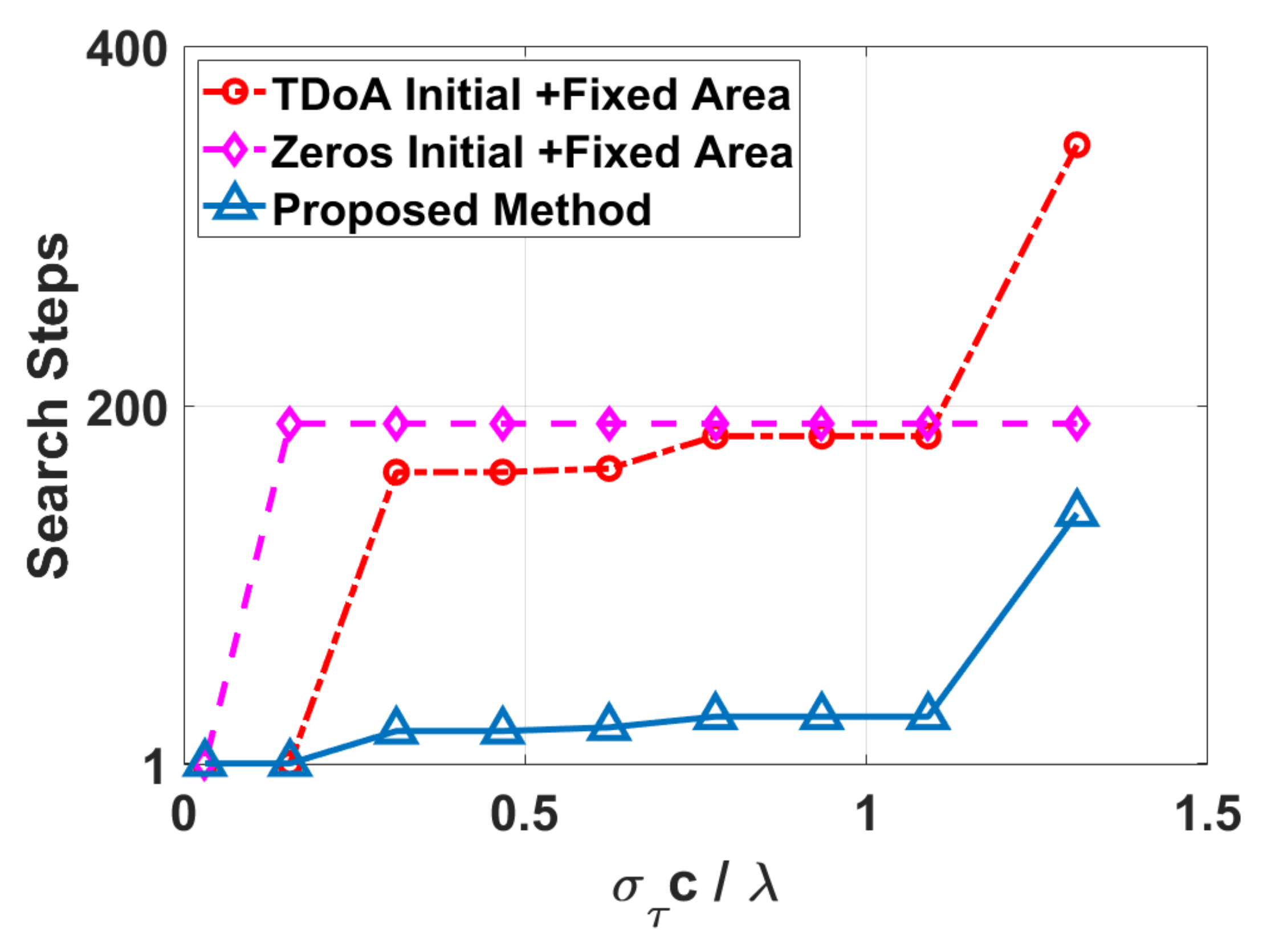
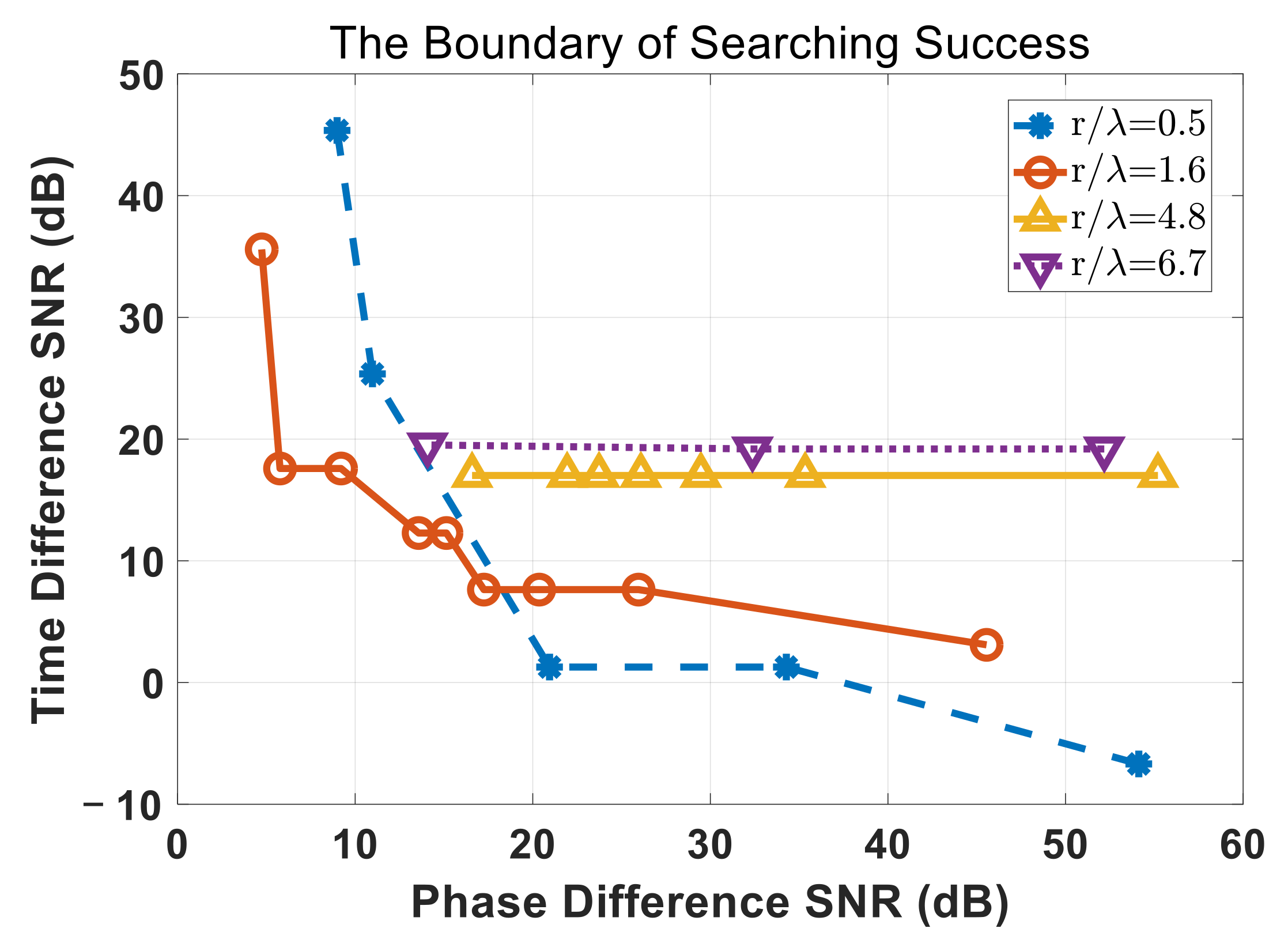
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ge, F.; Shen, Y. Single-Anchor Ultra-Wideband Localization System Using Wrapped PDoA. IEEE Trans. Mob. Comput. 2021, 1. [Google Scholar] [CrossRef]
- D’Alu, S.; Iova, O.; Simonin, O.; Rivano, H. Demo: In-Flight Localisation of Micro-UAVs Using Ultra-Wide Band. In Proceedings of the International Conference on Embedded Wireless Systems and Networks, Lyon, France, 17–19 February 2020. [Google Scholar]
- Sorbelli, F.B. Localization of Terrestrial Objects Using a Drone with UWB Antennas. Ph.D. Thesis, Università degli Studi di Perugia, Umbria, Italy, 2018. [Google Scholar]
- Acres, K.T.; Barca, J.C. Tetrahedra and Relative Directions in Space Using 2 and 3-Space Simplexes for 3-Space Localization. Arxiv Preprint 2018, arXiv:1810.07316.28. [Google Scholar]
- Cao, Y.; Dhekne, A. Homecoming: A Wireless Homing Device for UAVs. In Proceedings of the 26th Annual International Conference on Mobile Computing and Networking, London, UK, 21–25 September 2020; pp. 1–3. [Google Scholar]
- Hoeller, D.; Ledergerber, A.; Hamer, M.; D’Andrea, R. Augmenting Ultra-Wideband Localization with Computer Vision for Accurate Flight. IFAC-Pap. 2017, 50, 12734–12740. [Google Scholar] [CrossRef]
- Wang, D. Cooperative V2X Relative Navigation Using Tight-Integration of DGPS and V2X UWB Range and Simulated Bearing. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2015. [Google Scholar] [CrossRef]
- Tiemann, J.; Fuhr, O.; Wietfeld, C. CELIDON: Supporting First Responders through 3D AOA-Based UWB Ad-Hoc Localization. In Proceedings of the 2020 16th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob) (50308), Thessaloniki, Greece, 12 October 2020; pp. 20–25. [Google Scholar]
- Zhao, M.; Chang, T.; Arun, A.; Ayyalasomayajula, R.; Zhang, C.; Bharadia, D. ULoc: Low-Power, Scalable and Cm-Accurate UWB-Tag Localization and Tracking for Indoor Applications. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2021, 5, 1–31. [Google Scholar] [CrossRef]
- Dotlic, I.; Connell, A.; Ma, H.; Clancy, J.; McLaughlin, M. Angle of Arrival Estimation Using Decawave DW1000 Integrated Circuits. In Proceedings of the 2017 14th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2017; pp. 1–6. [Google Scholar]
- Friedlander, B.; Weiss, A.J. Direction Finding in the Presence of Mutual Coupling. IEEE Trans. Antennas Propag. 1991, 39, 273–284. [Google Scholar] [CrossRef]
- Dorsey, W.M.; Mital, R.; Scholnik, D.P. Phase-Only Synthesis of Omnidirectional Patterns with Multiple Nulls from a Uniform Circular Array. In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation (APSURSI), Fajardo, PR, USA, 26 June–1 July 2016; pp. 765–766. [Google Scholar]
- Zuo, L.; Pan, J.; Shen, Z. Analytical Algorithm for 3-D Localization of a Single Source With Uniform Circular Array. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 323–326. [Google Scholar] [CrossRef]
- Zuo, L.; Pan, J. Accurate 2-D AOA Estimation and Ambiguity Resolution for a Single Source under Fixed Uniform Circular Arrays. Int. J. Antennas Propag. 2017, 2017, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kitavi, D.M.; Lin, T.-C.; Wong, K.T. A Tetrahedral Array of Isotropic Sensors, Each Suffering a Random Complex Gain—The Resulting Hybrid Cramér-Rao Bound for Direction Finding. In Proceedings of the 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), Dayton, OH, USA, 26–29 July 2016; pp. 412–415. [Google Scholar]
- Phalak, Y.; Chiddarwar, S. Tetrahedron and Euclidean Distance Based Decentralized Relative Localization for Multi-Robot Systems. In Proceedings of the 2020 IEEE International Conference for Innovation in Technology (INOCON), Bangluru, India, 6 November 2020; pp. 1–6. [Google Scholar]
- Shen, Y.; Win, M. On the Accuracy of Localization Systems Using Wideband Antenna Arrays. IEEE Trans. Commun. 2010, 58, 270–280. [Google Scholar] [CrossRef]
- Xin, J.; Liao, G.; Yang, Z.; Shen, H. Ambiguity Resolution for Passive 2-D Source Localization with a Uniform Circular Array. Sensors 2018, 18, 2650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Liu, Z.; Wei, X. Ambiguity Resolution for Phase-Based 3-D Source Localization under Fixed Uniform Circular Array. Sensors 2017, 17, 1086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wax, M.; Tweg, R. Direction of Arrival Tracking below the Ambiguity Threshold. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 354–363. [Google Scholar] [CrossRef]
- Chen, H.; Ballal, T.; Saeed, N.; Alouini, M.-S.; Al-Naffouri, T.Y. A Joint TDOA-PDOA Localization Approach Using Particle Swarm Optimization. IEEE Wirel. Commun. Lett. 2020, 9, 1240–1244. [Google Scholar] [CrossRef] [Green Version]
- Kitavi, D.M.; Tan, H.; Wong, K.T. A Regular Tetrahedral Array Whose Constituent Sensors Fail Randomly—A Lower Bound for Direction-of-Arrival Estimation. In Proceedings of the 2016 Loughborough Antennas & Propagation Conference (LAPC), Loughborough, Leicestershire, UK, 14–15 November 2016; pp. 1–5. [Google Scholar]
- Zuo, L.; Pan, J. An Optimum 2-D DOA Estimation Algorithm with Uniform Circular Array and Its Performance Analysis. Int. J. Electron. Lett. 2019, 7, 262–275. [Google Scholar] [CrossRef]
- Jain, P.; Kar, P. Non-Convex Optimization for Machine Learning. Found. Trends Mach. Learn. 2017, 10, 142–336. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Zhang, J.; Yang, H.; Guan, Y. All-Directional DOA Estimation for Ultra-Wideband Regular Tetrahedral Array Using Wrapped PDoA. Sensors 2022, 22, 1532. https://doi.org/10.3390/s22041532
Luo J, Zhang J, Yang H, Guan Y. All-Directional DOA Estimation for Ultra-Wideband Regular Tetrahedral Array Using Wrapped PDoA. Sensors. 2022; 22(4):1532. https://doi.org/10.3390/s22041532
Chicago/Turabian StyleLuo, Jinglin, Jingjing Zhang, Haidong Yang, and Yisheng Guan. 2022. "All-Directional DOA Estimation for Ultra-Wideband Regular Tetrahedral Array Using Wrapped PDoA" Sensors 22, no. 4: 1532. https://doi.org/10.3390/s22041532
APA StyleLuo, J., Zhang, J., Yang, H., & Guan, Y. (2022). All-Directional DOA Estimation for Ultra-Wideband Regular Tetrahedral Array Using Wrapped PDoA. Sensors, 22(4), 1532. https://doi.org/10.3390/s22041532






