Damage Detection in Largely Unobserved Structures under Varying Environmental Conditions: An AutoRegressive Spectrum and Multi-Level Machine Learning Methodology
Abstract
:1. Introduction
2. Parametric Spectral-Based Feature Extraction by AR Modeling
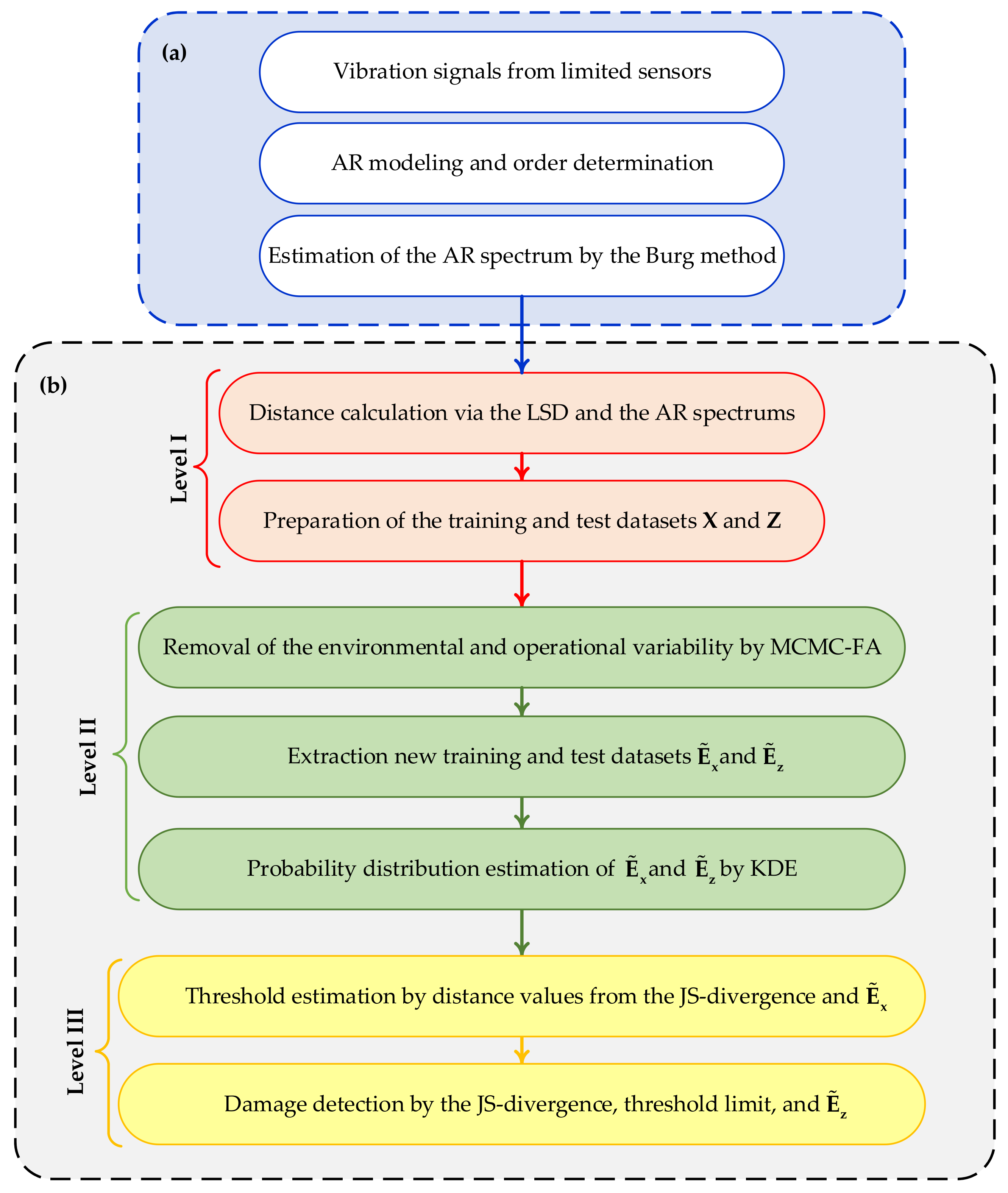
3. Proposed Multi-Level Machine Learning Method
3.1. Level I: Training and Test Data Generation by Log-Dpectral Distance
3.2. Level II: Feature Normalization by MCMC-FA
3.2.1. Classical Factor Analysis
3.2.2. Markov Chain Monte Carlo Factor Analysis
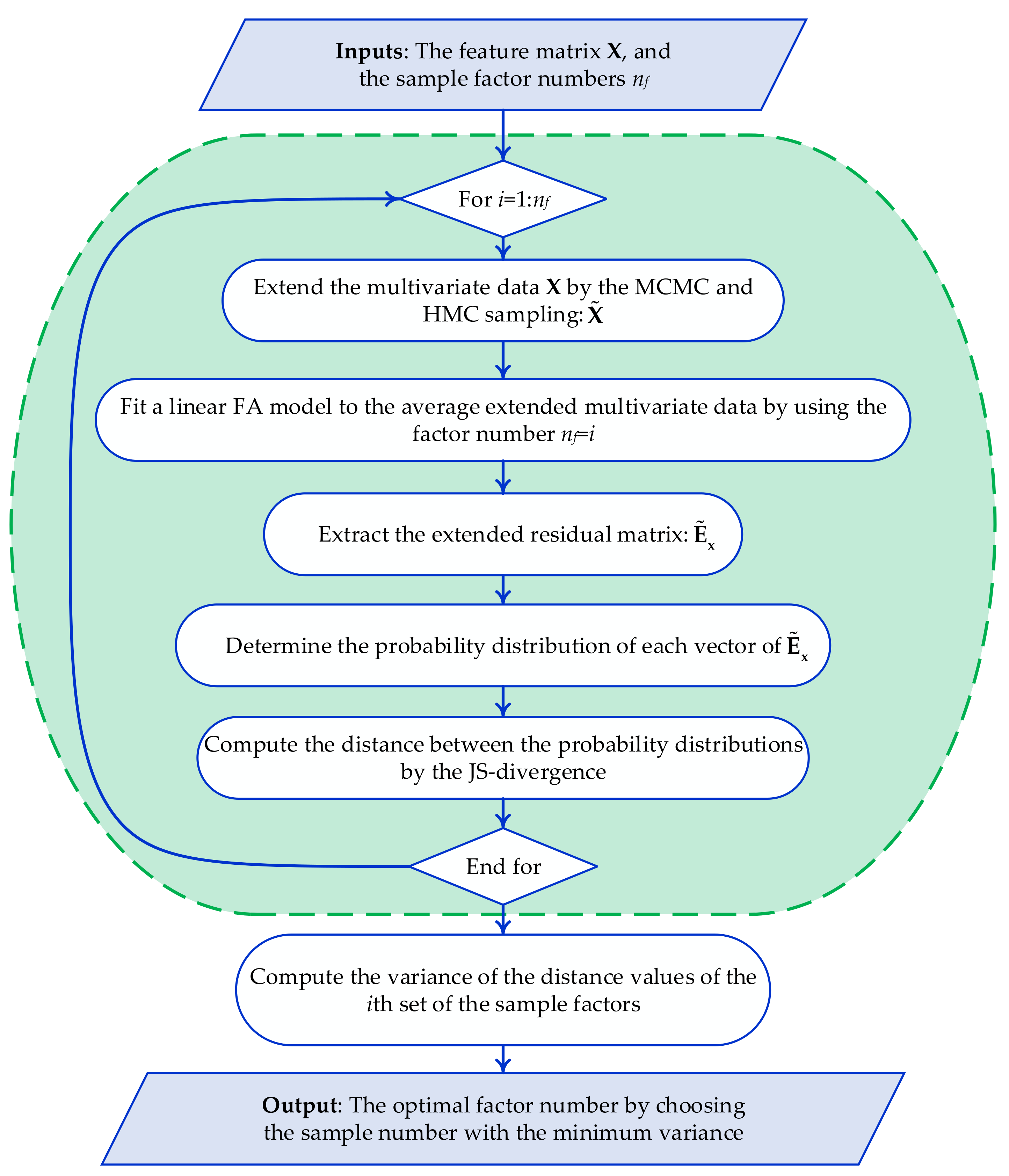
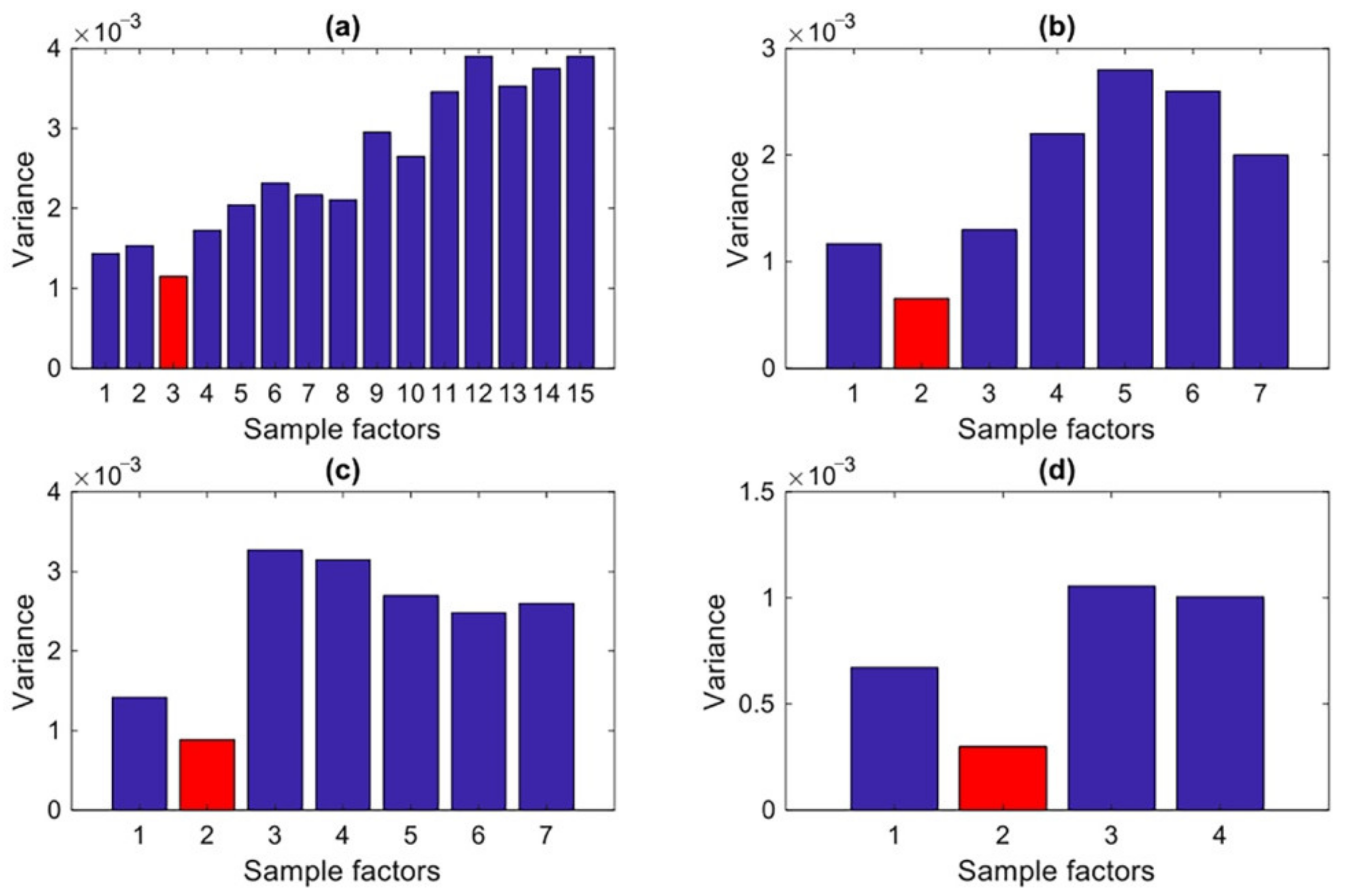
3.2.3. Determination of the Number of Factors
3.3. Level III: Decision-Making by Jensen-Shannon Divergence
3.3.1. Relative Entropy Measures in Information Theory
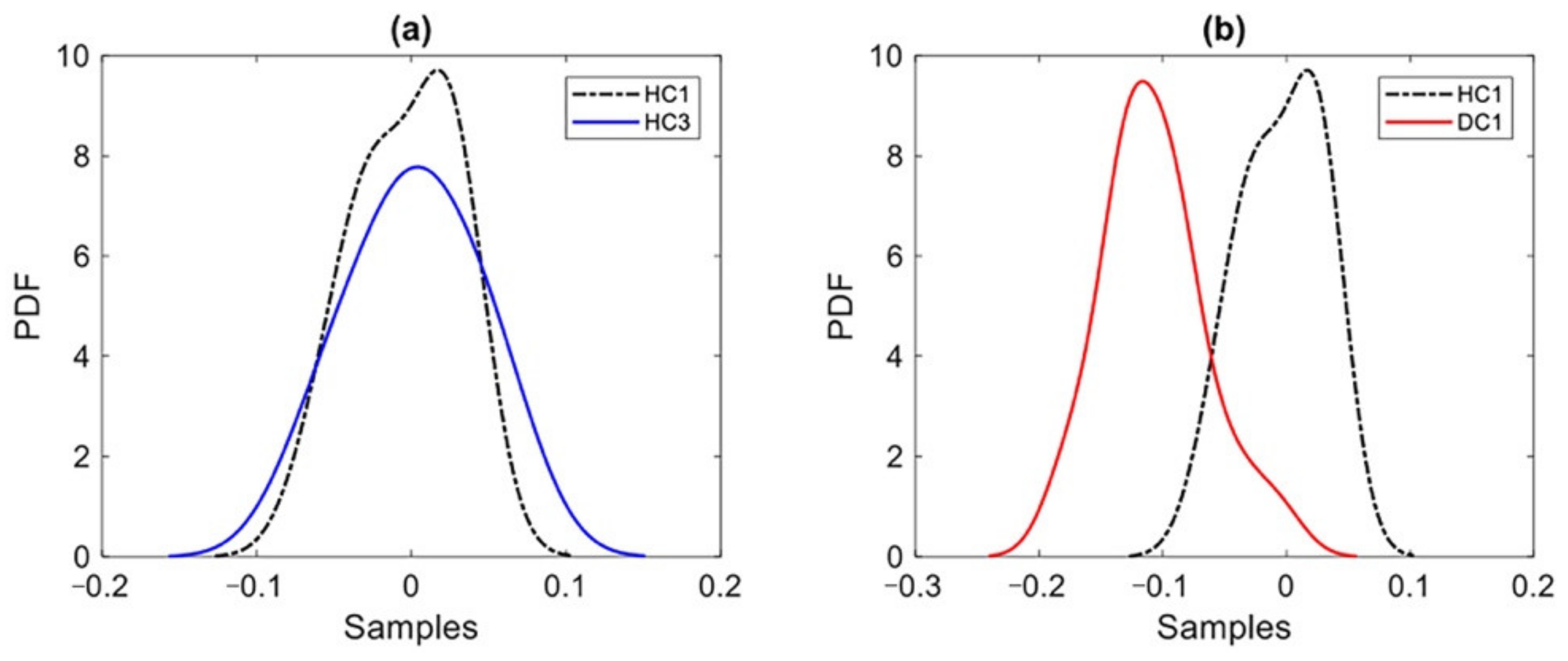
3.3.2. Damage Detection Scheme
4. Case Study: The Wooden Bridge
4.1. Response Modeling and Feature Extraction
4.2. Damage Detection with Limited Sensor Deployment and Under Environmental Effects
4.3. Comparative Studies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Entezami, A.; Sarmadi, H.; Behkamal, B.; Mariani, S. Big data analytics and structural health monitoring: A statistical pattern recognition-based approach. Sensors 2020, 20, 2328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarmadi, H. Investigation of Machine Learning Methods for Structural Safety Assessment under Variability in Data: Comparative Studies and New Approaches. J. Perform. Constr. Facil. 2021, 35, 04021090. [Google Scholar] [CrossRef]
- Kullaa, J. Damage Detection and Localization under Variable Environmental Conditions Using Compressed and Reconstructed Bayesian Virtual Sensor Data. Sensors 2022, 22, 306. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.; Zhou, Z. Two-Step Approach to Processing Raw Strain Monitoring Data for Damage Detection of Structures under Operational Conditions. Sensors 2021, 21, 6887. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; De Michele, C. Non-parametric empirical machine learning for short-term and long-term structural health monitoring. Struct. Health Monit. 2022, in press. [Google Scholar]
- Spencer, B.F.; Hoskere, V.; Narazaki, Y. Advances in Computer Vision-Based Civil Infrastructure Inspection and Monitoring. Engineering 2019, 5, 199–222. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W. Review of machine-vision based methodologies for displacement measurement in civil structures. J. Civ. Struct. Health Monit. 2018, 8, 91–110. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, T.; Shariati, A. Monitoring of Structures and Mechanical Systems Using Virtual Visual Sensors for Video Analysis: Fundamental Concept and Proof of Feasibility. Sensors 2013, 13, 16551–16564. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Ferreira, J.; Martins, T. Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 2014, 75, 164–180. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Ghalehnovi, M. On model-based damage detection by an enhanced sensitivity function of modal flexibility and LSMR-Tikhonov method under incomplete noisy modal data. Eng. Comput. 2020, in press. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Sarmadi, H.; Entezami, A. A hybrid sensitivity function and Lanczos bidiagonalization-Tikhonov method for structural model updating: Application to a full-scale bridge structure. Appl. Math. Model. 2021, 89, 860–884. [Google Scholar] [CrossRef]
- Daneshvar, M.H.; Saffarian, M.; Jahangir, H.; Sarmadi, H. Damage identification of structural systems by modal strain energy and an optimization-based iterative regularization method. Eng. Comput. 2022, in press. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Ghalehnovi, M. Damage detection by updating structural models based on linear objective functions. J. Civ. Struct. Health Monit. 2014, 4, 165–176. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-driven structural health monitoring and damage detection through deep learning: State-of-the-art review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Karamodin, A. Data-driven damage diagnosis under environmental and operational variability by novel statistical pattern recognition methods. Struct. Health Monit. 2019, 18, 1416–1443. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Karamodin, A. Improving feature extraction via time series modeling for structural health monitoring based on unsupervised learning methods. Sci. Iran. 2020, 27, 1001–1018. [Google Scholar]
- Rezaiee-Pajand, M.; Entezami, A.; Shariatmadar, H. An iterative order determination method for time-series modeling in structural health monitoring. Adv. Struct. Eng. 2017, 21, 300–314. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons Ltd.: Chichester, UK, 2013. [Google Scholar]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal Processing Techniques for Vibration-Based Health Monitoring of Smart Structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Sarmadi, H.; Karamodin, A. A novel anomaly detection method based on adaptive Mahalanobis-squared distance and one-class kNN rule for structural health monitoring under environmental effects. Mech. Syst. Sig. Process. 2020, 140, 106495. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Saeedi Razavi, B.; Yuen, K.-V. Ensemble learning-based structural health monitoring by Mahalanobis distance metrics. Struct. Contr. Health Monit. 2021, 28, e2663. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Daneshvar Khorram, M. Energy-based damage localization under ambient vibration and non-stationary signals by ensemble empirical mode decomposition and Mahalanobis-squared distance. J. Vibrat. Control. 2020, 26, 1012–1027. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Mariani, S. Fast unsupervised learning methods for structural health monitoring with large vibration data from dense sensor networks. Struct. Health Monit. 2020, 19, 1685–1710. [Google Scholar] [CrossRef]
- Yan, W.-J.; Chronopoulos, D.; Yuen, K.-V.; Zhu, Y.-C. Structural anomaly detection based on probabilistic distance measures of transmissibility function and statistical threshold selection scheme. Mech. Syst. Sig. Process. 2022, 162, 108009. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H. Structural health monitoring by a new hybrid feature extraction and dynamic time warping methods under ambient vibration and non-stationary signals. Measurement 2019, 134, 548–568. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H. An unsupervised learning approach by novel damage indices in structural health monitoring for damage localization and quantification. Struct. Health Monit. 2018, 17, 325–345. [Google Scholar] [CrossRef]
- Daneshvar, M.H.; Gharighoran, A.; Zareei, S.A.; Karamodin, A. Structural health monitoring using high-dimensional features from time series modeling by innovative hybrid distance-based methods. J. Civ. Struct. Health Monit. 2021, 11, 537–557. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; Mariani, S. Health Monitoring of Large-Scale Civil Structures: An Approach Based on Data Partitioning and Classical Multidimensional Scaling. Sensors 2021, 21, 1646. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Salar, M.; De Michele, C.; Nadir Arslan, A. A novel data-driven method for structural health monitoring under ambient vibration and high dimensional features by robust multidimensional scaling. Struct. Health Monit. 2021, in press. [CrossRef]
- Liu, Z.; Yu, Y.; Liu, G.; Wang, J.; Mao, X. Design of a wireless measurement system based on WSNs for large bridges. Measurement 2014, 50, 324–330. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S.; Azam, S.E. Optimal design of sensor networks for damage detection. Procedia Eng. 2017, 199, 1864–1869. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S. Cost-benefit optimization of sensor networks for SHM applications. Proceedings 2018, 2, 132. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Saha, P. A review of some advanced sensors used for health diagnosis of civil engineering structures. Measurement 2018, 129, 68–90. [Google Scholar] [CrossRef]
- Yang, Y.; Nagarajaiah, S. Output-only modal identification with limited sensors using sparse component analysis. J. Sound Vib. 2013, 332, 4741–4765. [Google Scholar] [CrossRef]
- Lu, W.; Wen, R.; Teng, J.; Li, X.; Li, C. Data correlation analysis for optimal sensor placement using a bond energy algorithm. Measurement 2016, 91, 509–518. [Google Scholar] [CrossRef] [Green Version]
- Bagheri, A.; Zare Hosseinzadeh, A.; Rizzo, P.; Ghodrati Amiri, G. Time domain damage localization and quantification in seismically excited structures using a limited number of sensors. J. Vibrat. Control. 2017, 23, 2942–2961. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, J.; Li, J.; Hao, H.; Ma, H. Bridge condition monitoring under moving loads using two sensor measurements. Struct. Health Monit. 2020, 19, 917–937. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A. Application of supervised learning to validation of damage detection. Arch. Appl. Mech. 2021, 91, 393–410. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Salar, M.; De Michele, C. Bridge health monitoring in environmental variability by new clustering and threshold estimation methods. J. Civ. Struct. Health Monit. 2021, 11, 629–644. [Google Scholar] [CrossRef]
- Balsamo, L.; Betti, R. Data-based structural health monitoring using small training data sets. Struct. Contr. Health Monit. 2015, 22, 1240–1264. [Google Scholar] [CrossRef]
- Castanié, F. Spectral Analysis: Parametric and Non-Parametric Digital Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yao, R.; Pakzad, S.N. Autoregressive statistical pattern recognition algorithms for damage detection in civil structures. Mech. Syst. Sig. Process. 2012, 31, 355–368. [Google Scholar] [CrossRef]
- Bos, R.; De Waele, S.; Broersen, P.M. Autoregressive spectral estimation by application of the Burg algorithm to irregularly sampled data. IEEE Trans. Instrum. Meas. 2002, 51, 1289–1294. [Google Scholar] [CrossRef] [Green Version]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1997; Volume 1. [Google Scholar]
- Entezami, A.; Shariatmadar, H.; Sarmadi, H. Condition assessment of civil structures for structural health monitoring using supervised learning classification methods. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 51–66. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Mariani, S. Structural health monitoring for condition assessment using efficient supervised learning techniques. Proceedings 2020, 42, 17. [Google Scholar] [CrossRef] [Green Version]
- Sarmadi, H.; Yuen, K.-V. Early damage detection by an innovative unsupervised learning method based on kernel null space and peak-over-threshold. Comput. Aided Civ. Inf. 2021, 36, 1150–1167. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Juang, B.H. Fundamentals of Speech Recognition; PTR Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances, 3rd ed.; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Mulaik, S.A. Foundations of Factor Analysis; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Hashemi, F.; Naderi, M.; Jamalizadeh, A.; Bekker, A. A flexible factor analysis based on the class of mean-mixture of normal distributions. Comput. Stat. Data Anal. 2021, 157, 107162. [Google Scholar] [CrossRef]
- Van Ravenzwaaij, D.; Cassey, P.; Brown, S.D. A simple introduction to Markov Chain Monte–Carlo sampling. Psychon. Bull. Rev. 2018, 25, 143–154. [Google Scholar] [CrossRef] [Green Version]
- Neal, R.M. MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Song, J.; Belin, T.R. Choosing an appropriate number of factors in factor analysis with incomplete data. Comput. Stat. Data Anal. 2008, 52, 3560–3569. [Google Scholar] [CrossRef]
- Reisen, V.A.; Sgrancio, A.M.; Lévy-Leduc, C.; Bondon, P.; Monte, E.Z.; Cotta, H.H.A.; Ziegelmann, F.A. Robust factor modelling for high-dimensional time series: An application to air pollution data. Appl. Math. Comput. 2019, 346, 842–852. [Google Scholar] [CrossRef]
- Nanda, A.K.; Chowdhury, S. Shannon’s Entropy and Its Generalisations Towards Statistical Inference in Last Seven Decades. Int. Stat. Rev. 2021, 89, 167–185. [Google Scholar] [CrossRef]
- Nielsen, F. On a generalization of the Jensen–Shannon divergence and the Jensen–Shannon centroid. Entropy 2020, 22, 221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: Hobokken, NJ, USA, 2015. [Google Scholar]
- Kullaa, J. Distinguishing between sensor fault, structural damage, and environmental or operational effects in structural health monitoring. Mech. Syst. Sig. Process. 2011, 25, 2976–2989. [Google Scholar] [CrossRef]
- Giglioni, V.; García-Macías, E.; Venanzi, I.; Ierimonti, L.; Ubertini, F. The use of receiver operating characteristic curves and precision-versus-recall curves as performance metrics in unsupervised structural damage classification under changing environment. Eng. Struct. 2021, 246, 113029. [Google Scholar] [CrossRef]







| Day | Condition | Label | Added Mass (g) | Phase |
|---|---|---|---|---|
| 18 May | Undamaged | HC1 | - | Baseline |
| 25 May | Undamaged | HC2 | - | |
| 29 May | Undamaged | HC3 | - | Monitoring |
| 29 May | Damaged | DC1 | 23.5 | |
| DC2 | 47.0 | |||
| DC3 | 70.5 | |||
| DC4 | 123.2 | |||
| DC5 | 193.7 |
| Deployment Case | Labels of Active Sensors | Description |
|---|---|---|
| 1 | 1–15 | 100% of deployed sensors |
| 2 | 2,4,6,7,9,10,14 | ~50% of deployed sensors |
| 3 | 1,3,5,8,11,12,15 | ~50% of deployed sensors with no sensors installed on the damaged area |
| 4 | 2,5,11,15 | ~25% of deployed sensors with no sensors installed on the damaged area |
| Number of Chains (C) | Number of Samples (N) | Burn-in Value | Probability Type |
|---|---|---|---|
| 10 | 1000 | 1000 | Multivariate Gaussian |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Entezami, A.; Mariani, S.; Shariatmadar, H. Damage Detection in Largely Unobserved Structures under Varying Environmental Conditions: An AutoRegressive Spectrum and Multi-Level Machine Learning Methodology. Sensors 2022, 22, 1400. https://doi.org/10.3390/s22041400
Entezami A, Mariani S, Shariatmadar H. Damage Detection in Largely Unobserved Structures under Varying Environmental Conditions: An AutoRegressive Spectrum and Multi-Level Machine Learning Methodology. Sensors. 2022; 22(4):1400. https://doi.org/10.3390/s22041400
Chicago/Turabian StyleEntezami, Alireza, Stefano Mariani, and Hashem Shariatmadar. 2022. "Damage Detection in Largely Unobserved Structures under Varying Environmental Conditions: An AutoRegressive Spectrum and Multi-Level Machine Learning Methodology" Sensors 22, no. 4: 1400. https://doi.org/10.3390/s22041400
APA StyleEntezami, A., Mariani, S., & Shariatmadar, H. (2022). Damage Detection in Largely Unobserved Structures under Varying Environmental Conditions: An AutoRegressive Spectrum and Multi-Level Machine Learning Methodology. Sensors, 22(4), 1400. https://doi.org/10.3390/s22041400








