High-Resolution Permanent Magnet Drive Using Separated Observers for Acceleration Estimation and Control †
Abstract
:1. Introduction
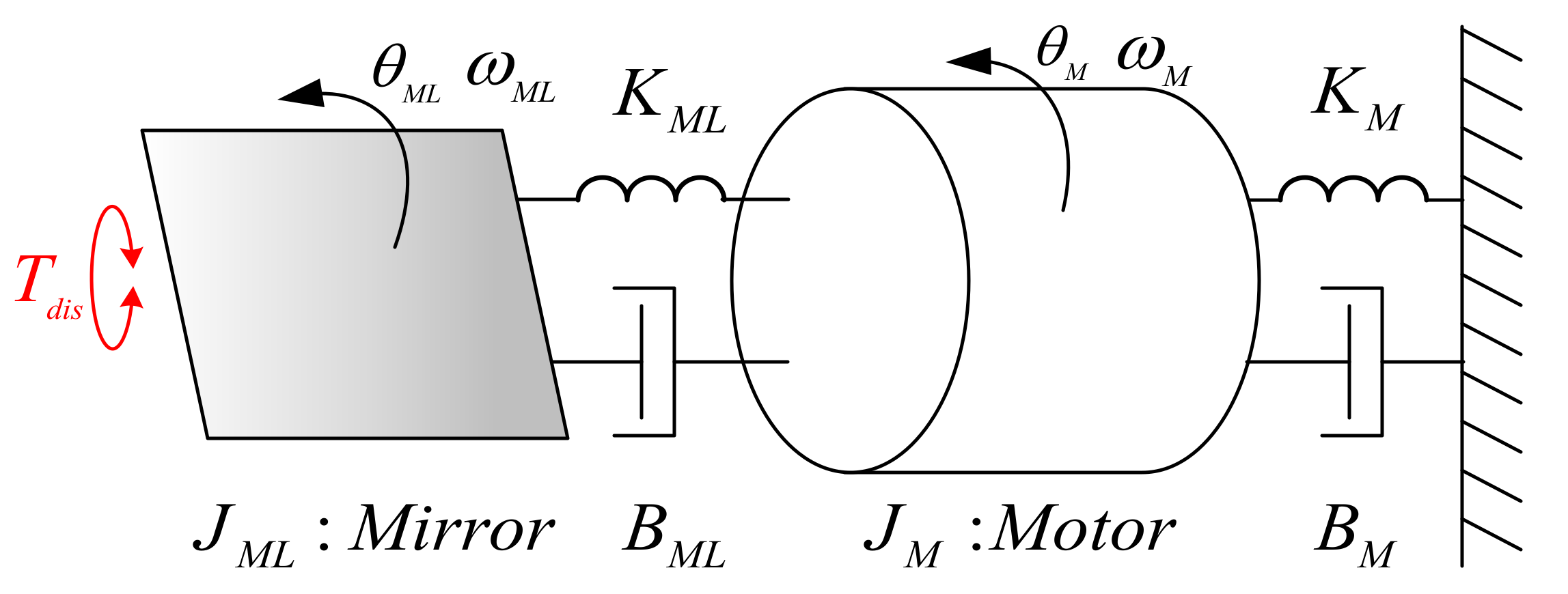
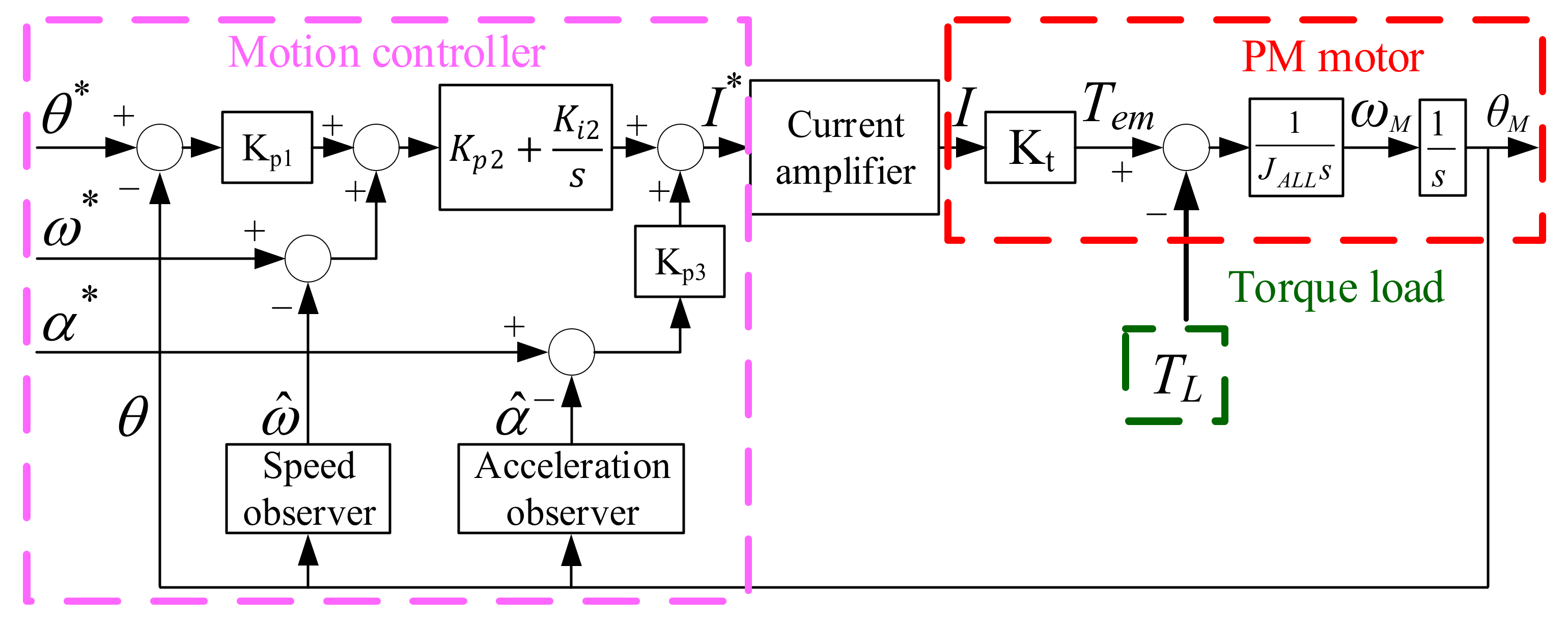
2. PM Motor System
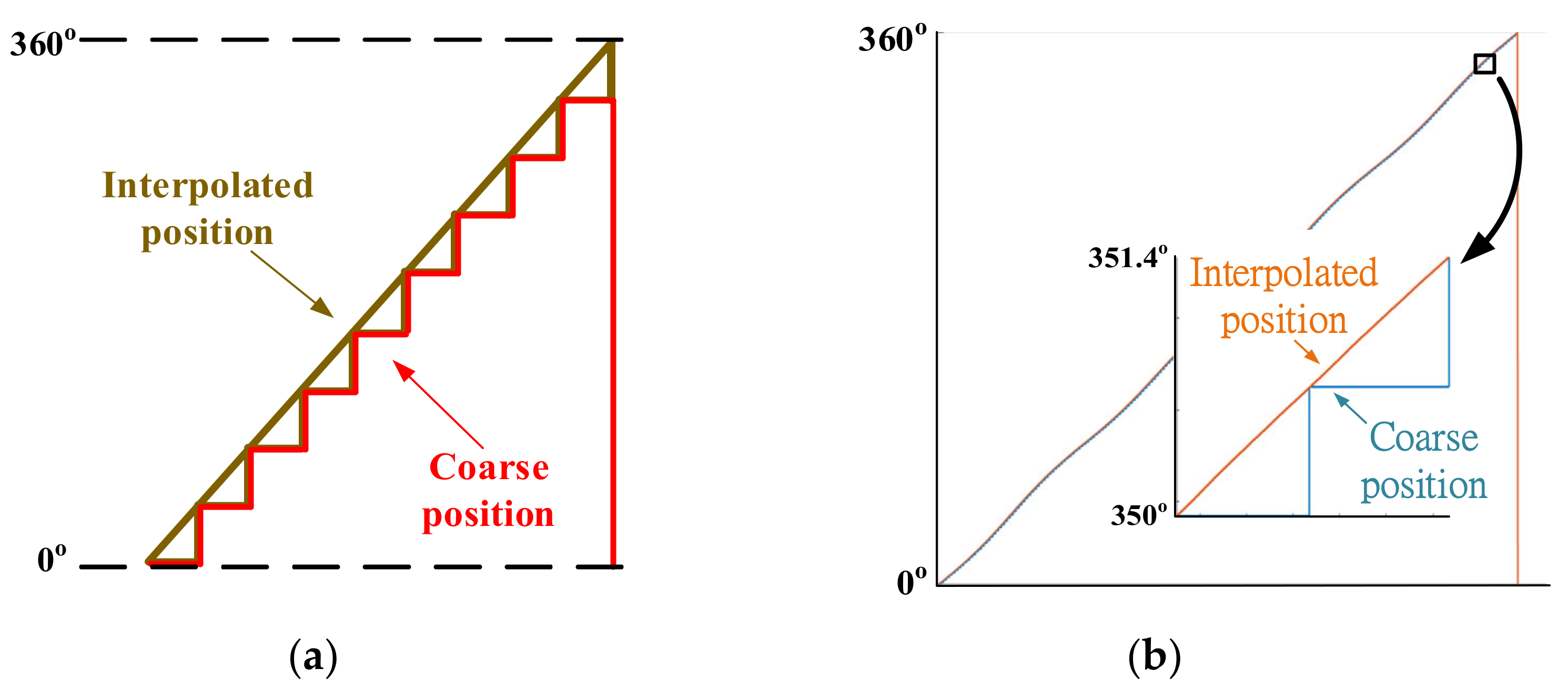
3. High-Resolution Position Sensing
4. Dynamic Model of PM Motor
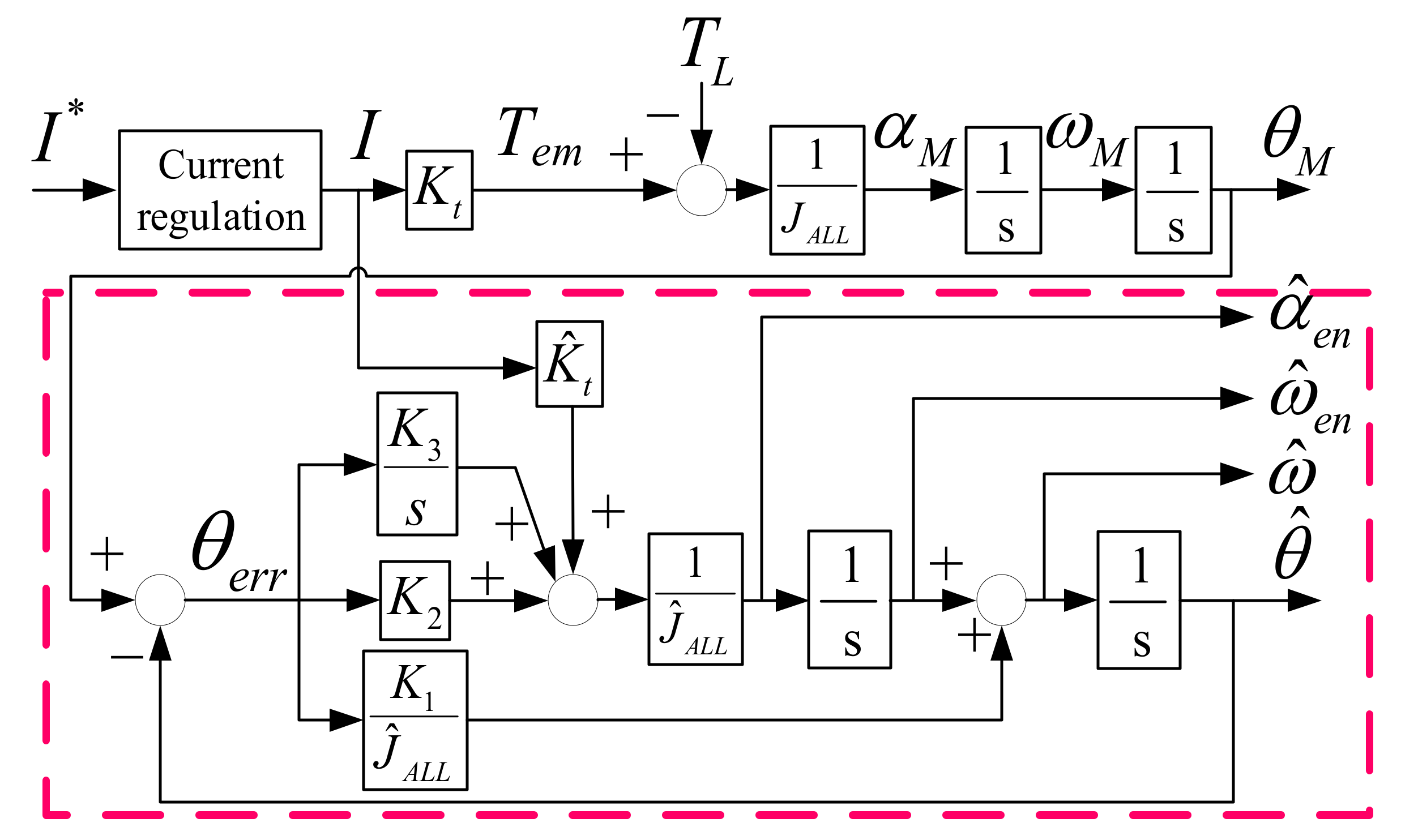
5. Observer-Based Speed Estimation
5.1. Proposed Speed Observer
5.2. Differentiation Noises Elimination
5.3. Simulation Result
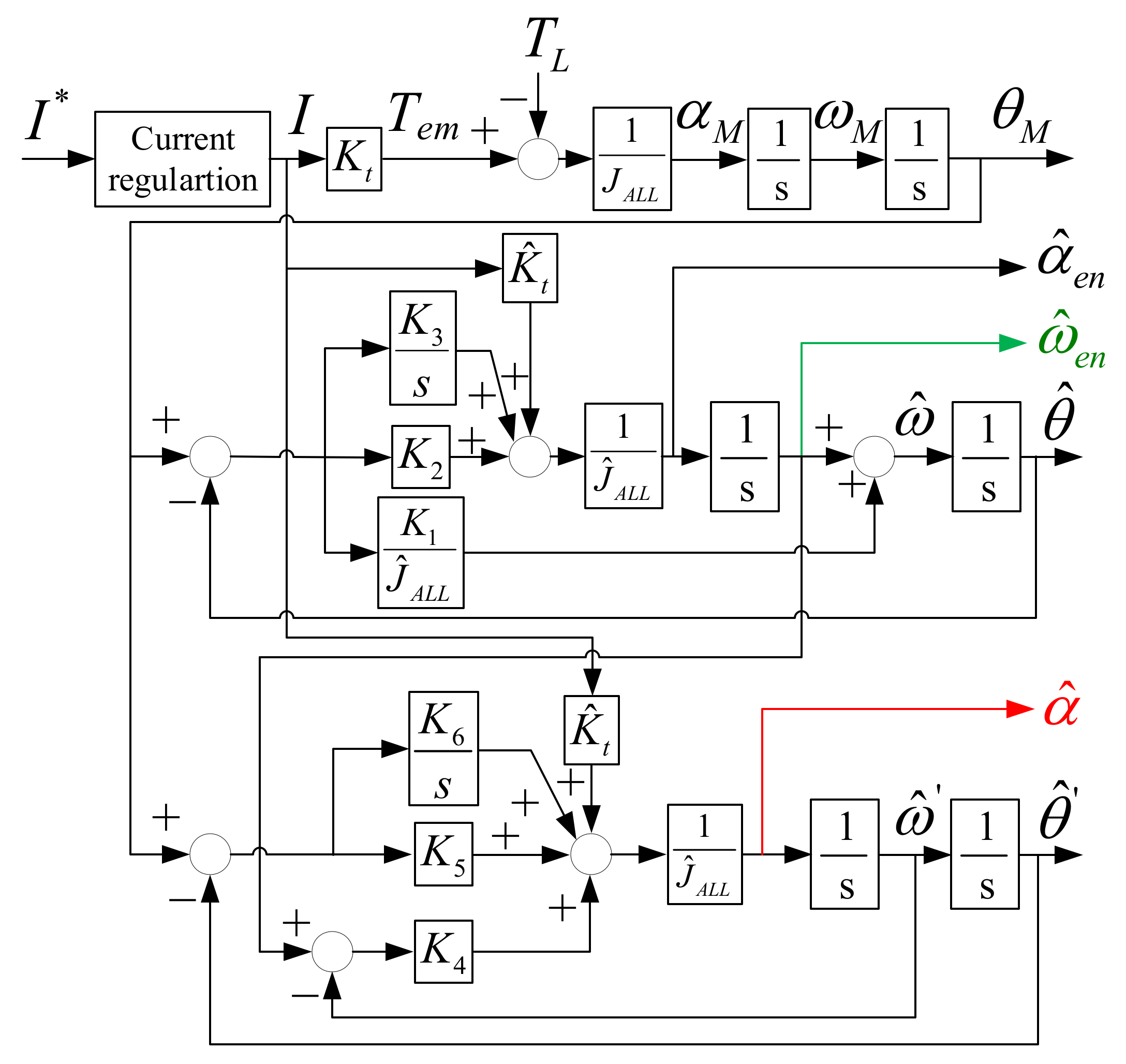
6. Acceleration Estimation and Control
6.1. Acceleration Feedback Control
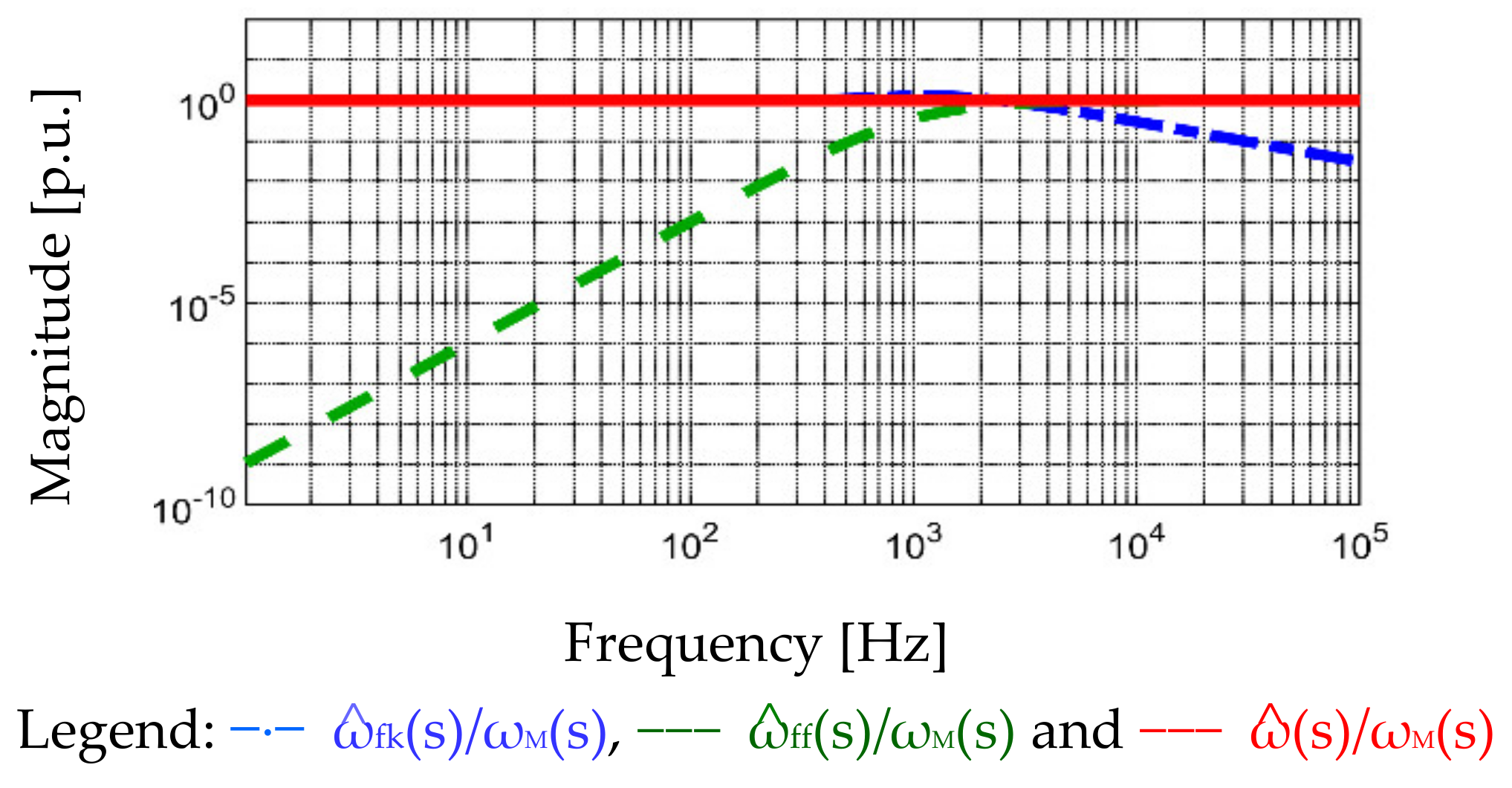
6.2. Acceleration Estimation
6.3. Simulation Results
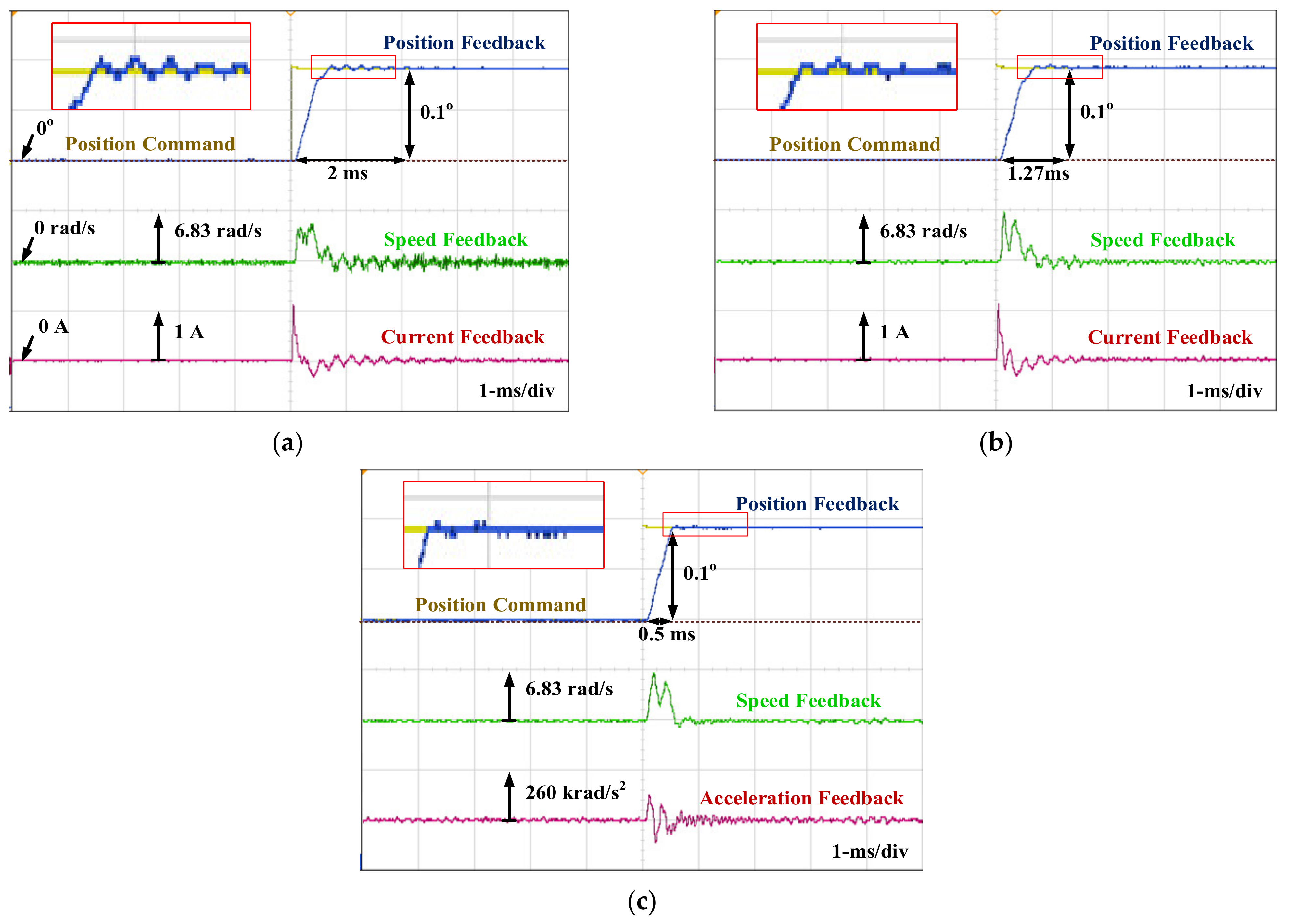
7. Experimental Results
7.1. High-Resolution Position Interpolation
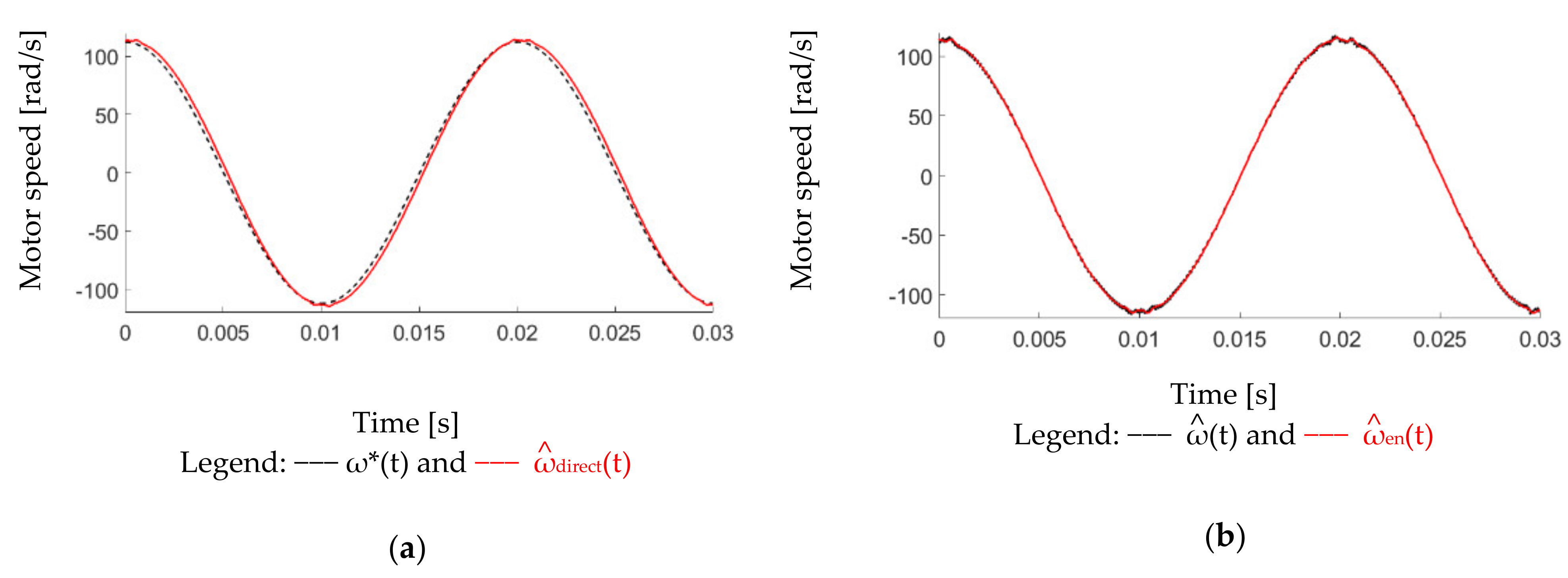
7.2. Observer-Based Speed Estimation
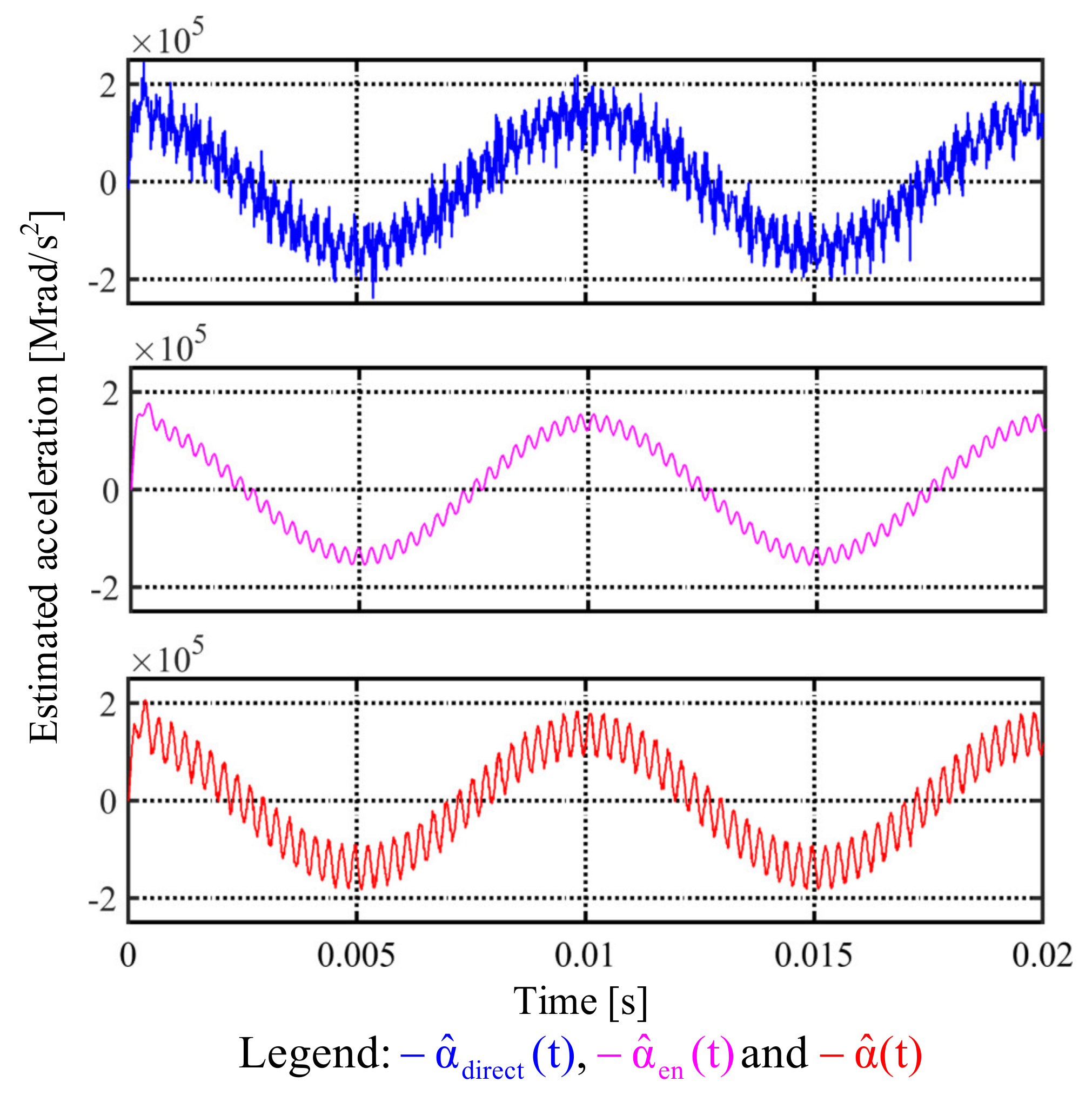
7.3. Observer-Based Acceleration Estimation
7.4. Motion Control Response
8. Comparison between Simulation and Experimental Results
9. Conclusions
- A position interpolation is used to increase the position resolution. The high-performance speed and acceleration estimations are implemented with this interpolation process.
- The proposed speed observer reduces the differentiation noise on speed estimation. A better dynamic response of the PM motor is achieved.
- A separated acceleration observer is proposed for acceleration estimation. The lowest steady-state error is achieved through acceleration control to suppress the high-frequency mirror vibrational harmonics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ueda, S.; Hirata, M. Final-state control for a galvano scanner: Minimizing mirror vibration in an inclined direction relative to the rotation axis. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 3289–3294. [Google Scholar]
- Michigami, N.; Yamaga, M.; Kawamura, M.; Kuze, O.; Nakamura, S. High-performance Printed Circuit Board Production Equipment for Ultra-high Density Multi-layer Wiring. Hitachi Rev. 2011, 60, 216–221. [Google Scholar]
- Matsuka, D.; Tanaka, T.; Iwasaki, M. Thermal Demagnetization Compensation for Fast and Precise Positioning in Galvanometer Scanners. IEEE Trans. Ind. Electron. 2016, 63, 5514–5522. [Google Scholar] [CrossRef]
- Secrest, C.W.; Pointer, J.S.; Buehner, M.R.; Lorenz, R.D. Improving position sensor accuracy through spatial harmonic decoupling, and sensor scaling, offset, and orthogonality correction using self-commissioning MRAS-methods. IEEE Trans. Ind Appl. 2015, 51, 4492–4504. [Google Scholar] [CrossRef]
- Hoang, H.V.; Jeon, J.W. An Efficient Approach to Correct the Signals and Generate High-Resolution Quadrature Pulses for Magnetic Encoders. IEEE Trans. Ind. Electron. 2011, 58, 3634–3646. [Google Scholar] [CrossRef]
- Dogša, T.; Solar, M.; Jarc, B. Precision Delay Circuit for Analog Quadrature Signals in Sin/Cos Encoders. IEEE Trans. Instrum. Meas. 2014, 63, 2795–2803. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, G.; Liu, H.; Lei, B.; Li, X.; Han, W.; Liu, H. Electronic Interpolation Interface Based on Linear Subdivision Method for Sinusoidal Optical Encoders. Sensors 2020, 20, 3646–3654. [Google Scholar] [CrossRef]
- Qamar, N.A.; Hatziadoniu, C.J.; Wang, H. Speed error mitigation for a DSP-based resolver-to-digital converter using autotuning filters. IEEE Trans. Ind. Electron. 2015, 62, 1134–1139. [Google Scholar] [CrossRef] [Green Version]
- Texas Instruments Corporation. TI Designs-Interface to Sin/Cos Encoders with High-Resolution Position Interpolation. Available online: http://www.ti.com/lit/ug/tidua05a/tidua05a.pdf (accessed on 21 June 2021).
- Feng, J.; Zhi, J. Digital implementation of a galvanometric optical scanner based on DSP and FPGA. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 1899–1902. [Google Scholar]
- Kim, H.-J.; Park, H.-S.; Kim, J.-M. Expansion of Operating Speed Range of High-Speed BLDC Motor Using Hybrid PWM Switching Method Considering Dead Time. Energies 2020, 13, 5212. [Google Scholar] [CrossRef]
- Iwasaki, M.; Seki, K.; Maeda, Y. High-Precision Motion Control Techniques: A Promising Approach to Improving Motion Performance. IEEE Ind. Electron. Mag. 2012, 6, 32–40. [Google Scholar] [CrossRef]
- Yen, S.-H.; Tang, P.-C.; Lin, Y.-C.; Lin, C.-Y. A Sensorless and Low-Gain Brushless DC Motor Controller Using a Simplified Dynamic Force Compensator for Robot Arm Application. Sensors 2019, 19, 3171. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Jiao, Z.; Ma, D. Adaptive Robust Control of DC Motors With Extended State Observer. IEEE Trans. Ind. Electron. 2014, 61, 3630–3637. [Google Scholar] [CrossRef]
- Gamazo-Real, J.C.; Vázquez-Sánchez, E.; Gómez-Gil, J. Position and Speed Control of Brushless DC Motors Using Sensorless Techniques and Application Trends. Sensors 2010, 10, 6901–6947. [Google Scholar] [CrossRef] [Green Version]
- Sikora, A.; Woźniak, M. Impact of Current Pulsation on BLDC Motor Parameters. Sensors 2021, 21, 587. [Google Scholar] [CrossRef]
- Allotta, B.; Giorgetti, F.; Nincheri, M.; Pugi, L. Modelling and control of a galvanometer for the application to a laser engraving system. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 595–600. [Google Scholar]
- Liu, W.; Liu, D.; Wu, J.; Chang, K.; Chou, M.; Fu, L. Precision sinusoidal tracking for galvanometer scanner with smith predictor-based adaptive sliding mode control. In Proceedings of the 2016 International Automatic Control Conference (CACS), Taichung, Taiwan, 9–11 November 2016; pp. 100–105. [Google Scholar]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Nakade, K.; Wakui, S. Modeling of the galvano mirror by lumped mass system and verification for the model through the experiments. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, JAMDSM0032. [Google Scholar] [CrossRef] [Green Version]
- Buja, G.S.; Menis, R.; Valla, M.I. Disturbance torque estimation in a sensorless DC drive. IEEE Trans. Ind. Electron. 1995, 42, 351–357. [Google Scholar] [CrossRef]
- Godler, I.; Inoue, M.; Ninomiya, T.; Yamashita, T. Robustness comparison of control schemes with disturbance observer and with acceleration control loop. In Proceedings of the ISIE ’99, IEEE International Symposium on Industrial Electronics (Cat. No.99TH8465), Bled, Slovenia, 12–16 July 1999; Volume 1033, pp. 1035–1040. [Google Scholar]
- Fang, J.; Zhou, X.; Liu, G. Precise Accelerated Torque Control for Small Inductance Brushless DC Motor. IEEE Trans. Power Electron. 2013, 28, 1400–1412. [Google Scholar] [CrossRef]
- Deng, C.; Tang, T.; Mao, Y.; Ren, G. Enhanced Disturbance Observer Based on Acceleration Measurement for Fast Steering Mirror Systems. IEEE Photonics J. 2017, 9, 1–11. [Google Scholar]
- Cristalli, C.; Paone, N.; Rodríguez, R.M. Mechanical fault detection of electric motors by laser vibrometer and accelerometer measurements. Mech. Syst. Signal Process. 2006, 20, 1350–1361. [Google Scholar] [CrossRef]
- Schmidt, P.B.; Lorenz, R.D. Design principles and implementation of acceleration feedback to improve performance of DC drives. IEEE Trans. Ind Appl. 1992, 28, 594–599. [Google Scholar] [CrossRef]
- Lin, Y.J.; Chou, P.H.; Wu, C.J.; Yang, S.C. Sensorless Acceleration Estimation and Acceleration Feedback Control to Improve the Disturbance Torque Rejection on Galvano Motor System. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 5048–5052. [Google Scholar]
- Digital Encoder Galvano Scanner GM-1000 Series. Available online: https://www.usa.canon.com/internet/portal/us/home/products/details/optoelectronic-products/digital-laser-scanner-system/gm-series (accessed on 22 June 2021).
- Lin, D.; Zhou, P.; Cendes, Z.J. In-Depth Study of the Torque Constant for Permanent-Magnet Machines. IEEE Trans. Magn. 2009, 45, 5383–5387. [Google Scholar] [CrossRef]
- Hendershot, J.R.; Miller, T.J.E. Design of Brushless Permanent-Magnet Machines; Motor Design Books: Venice, FL, USA, 2010. [Google Scholar]
- Luenberger, D. An introduction to observers. IEEE Trans. Automat. Contr. 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Banerjee, K.; Dam, B.; Majumdar, K. An FPGA-based integrated signal conditioner for measurement of position, velocity and acceleration of a rotating shaft using an incremental encoder. In Proceedings of the 2016 IEEE First International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2016; pp. 440–444. [Google Scholar]
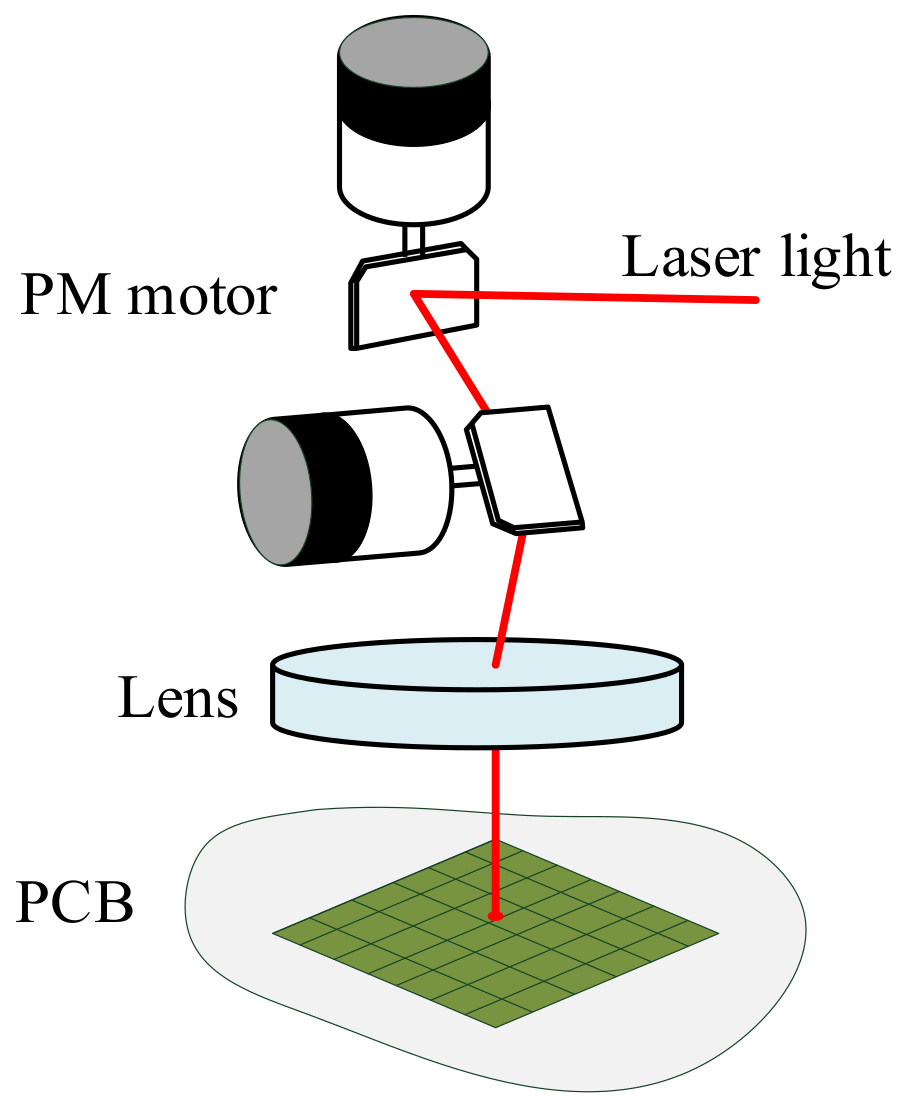
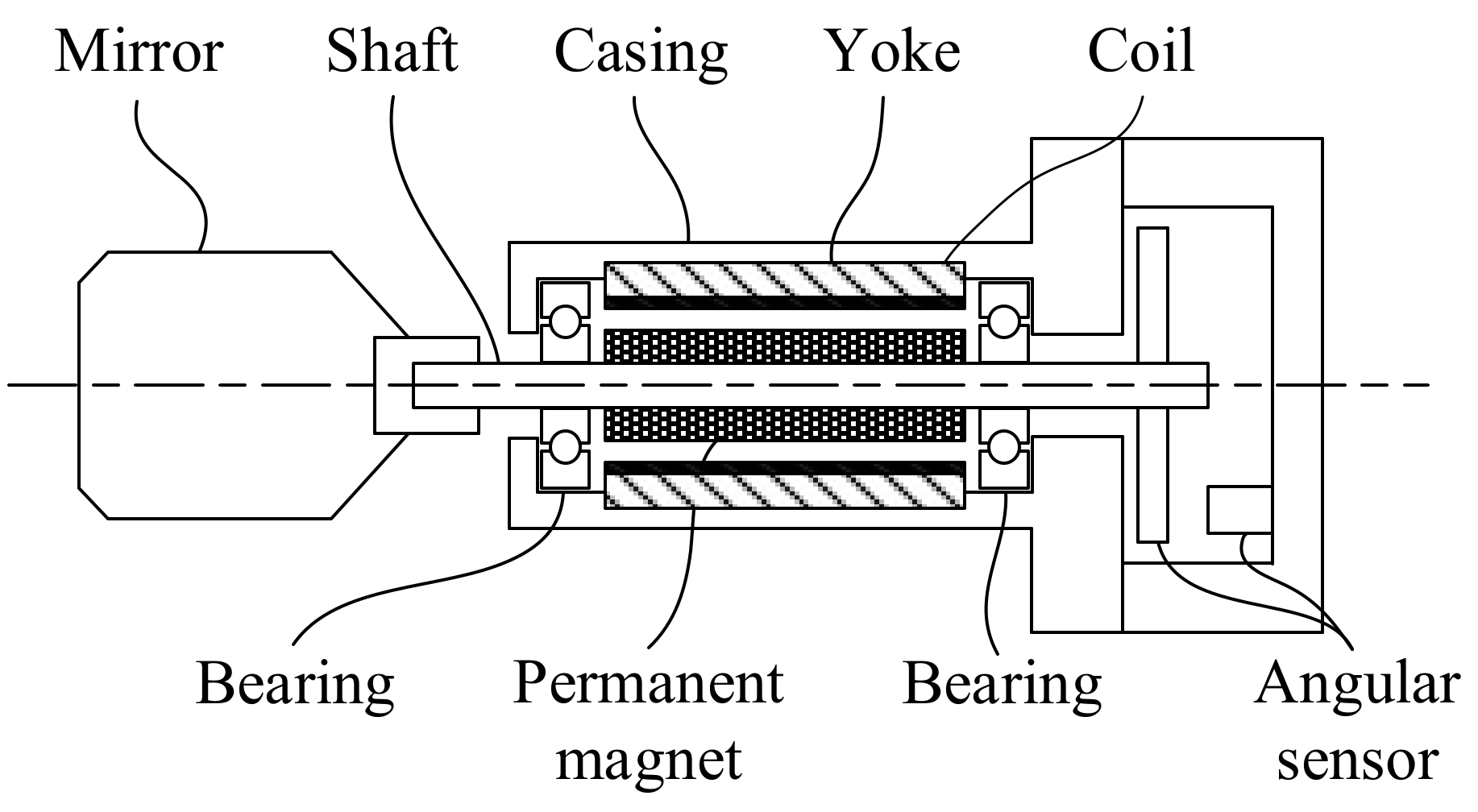
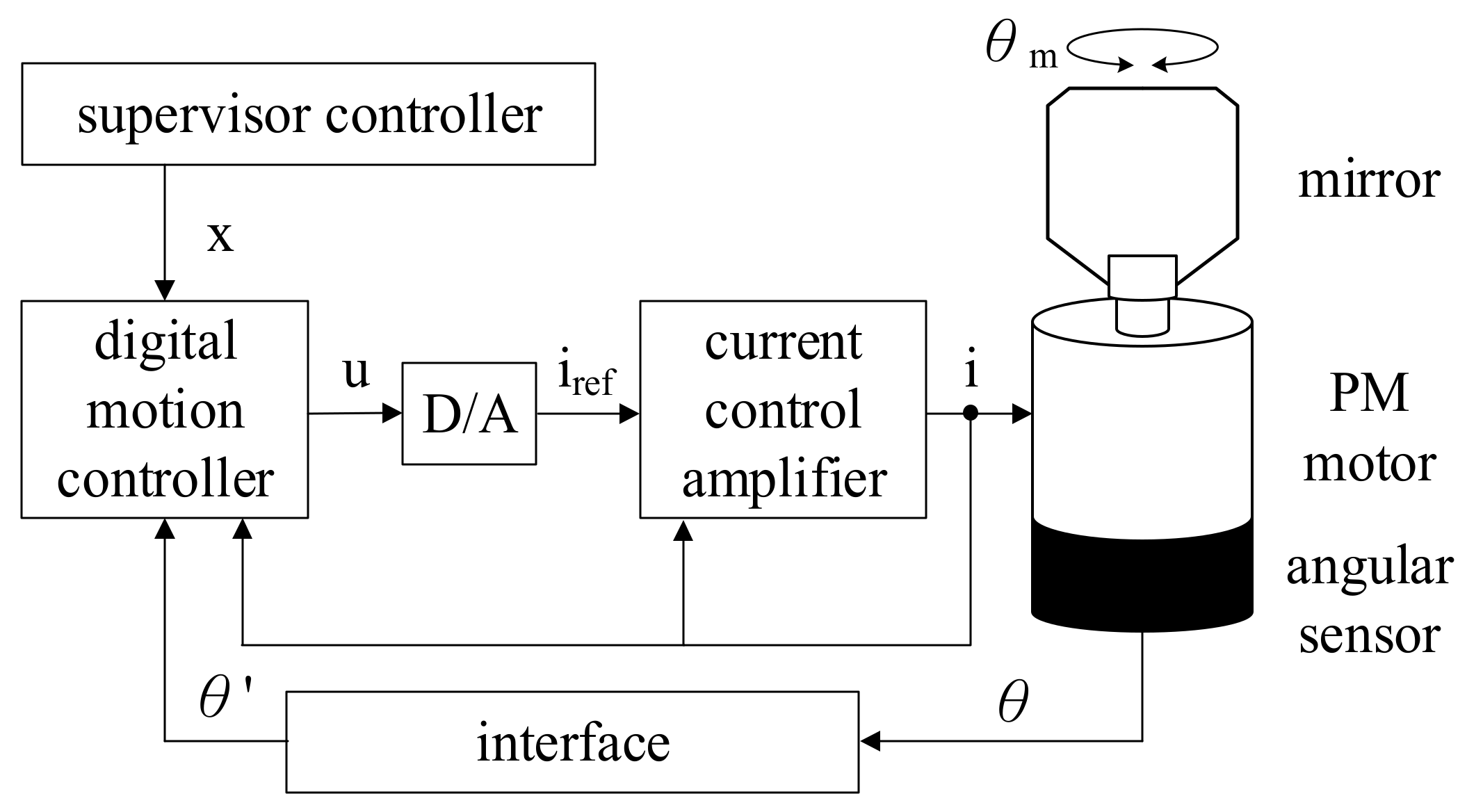
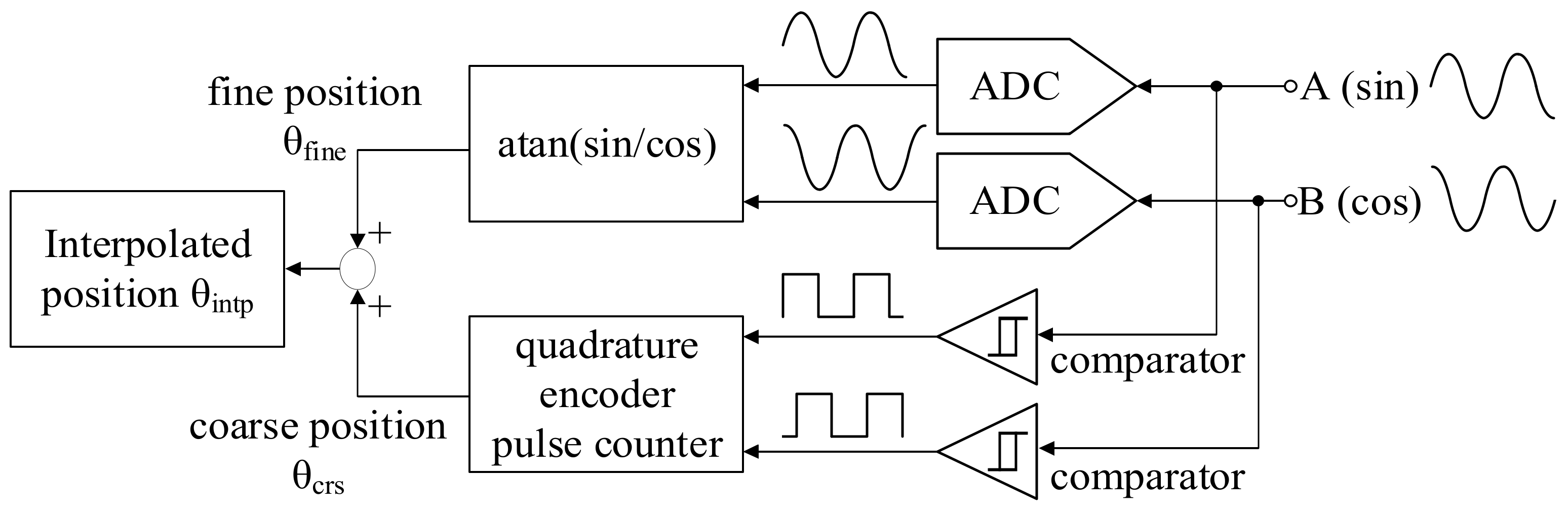







| Characteristics | Values |
|---|---|
| Rotor poles | 4-pole |
| Rated torque | 0.0127 Nm |
| Rated current | 1 A |
| Position rotation | 40 deg (maximum) |
| Resistance | 1.7 Ω |
| Inductance | 0.22 mH |
| Rated voltage | ±15 V |
| Inertia | 0.82 g·cm2 |
| Sample frequency | 100 kHz |
| Resolution per degree | 40 mm/360 deg = 111 μm/deg |
| Control accuracy (existing drive) | 4.41 × 10−5 deg |
| Control accuracy (proposed drive) | 1.08 × 10−5 deg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-J.; Chou, P.-H.; Yang, S.-C. High-Resolution Permanent Magnet Drive Using Separated Observers for Acceleration Estimation and Control. Sensors 2022, 22, 725. https://doi.org/10.3390/s22030725
Lin Y-J, Chou P-H, Yang S-C. High-Resolution Permanent Magnet Drive Using Separated Observers for Acceleration Estimation and Control. Sensors. 2022; 22(3):725. https://doi.org/10.3390/s22030725
Chicago/Turabian StyleLin, Yi-Jen, Po-Huan Chou, and Shih-Chin Yang. 2022. "High-Resolution Permanent Magnet Drive Using Separated Observers for Acceleration Estimation and Control" Sensors 22, no. 3: 725. https://doi.org/10.3390/s22030725
APA StyleLin, Y.-J., Chou, P.-H., & Yang, S.-C. (2022). High-Resolution Permanent Magnet Drive Using Separated Observers for Acceleration Estimation and Control. Sensors, 22(3), 725. https://doi.org/10.3390/s22030725






