Semi-Empirical Model of Remote-Sensing Reflectance for Chosen Areas of the Southern Baltic
Abstract
:1. Introduction
1.1. Context of the Study
1.2. State of Knowledge
1.3. Research Objectives
- determination of a mathematical description of the relationship between the selected optical properties (absorption coefficient of phytoplankton (aph(λi)), absorption coefficient by non-algal particles (ad(λi)), the coloured dissolved organic matter absorption coefficient (aCDOM(λi)), backscattering coefficient of particles (bbp(λi))) and the concentrations and physicochemical properties of natural water components (Chl a, SPM, surface concentrations of absorption coefficients of coloured dissolved organic matter for wavelength 400 nm (aCDOM(400)), sum of surface concentrations of accessory pigments (∑C), SPMinorg) in selected areas of the southern Baltic;
- development of a semi-empirical model of Rrs(λi) enabling the determination of Rrs(λi) spectra in the visible light range based on the known spectra of a(λi) and bb(λi) in coastal waters of the southern Baltic or based on knowledge of the concentration of admixture components.
2. Materials and Methods
2.1. The Conception of the Five-Parameter Model of Rrs
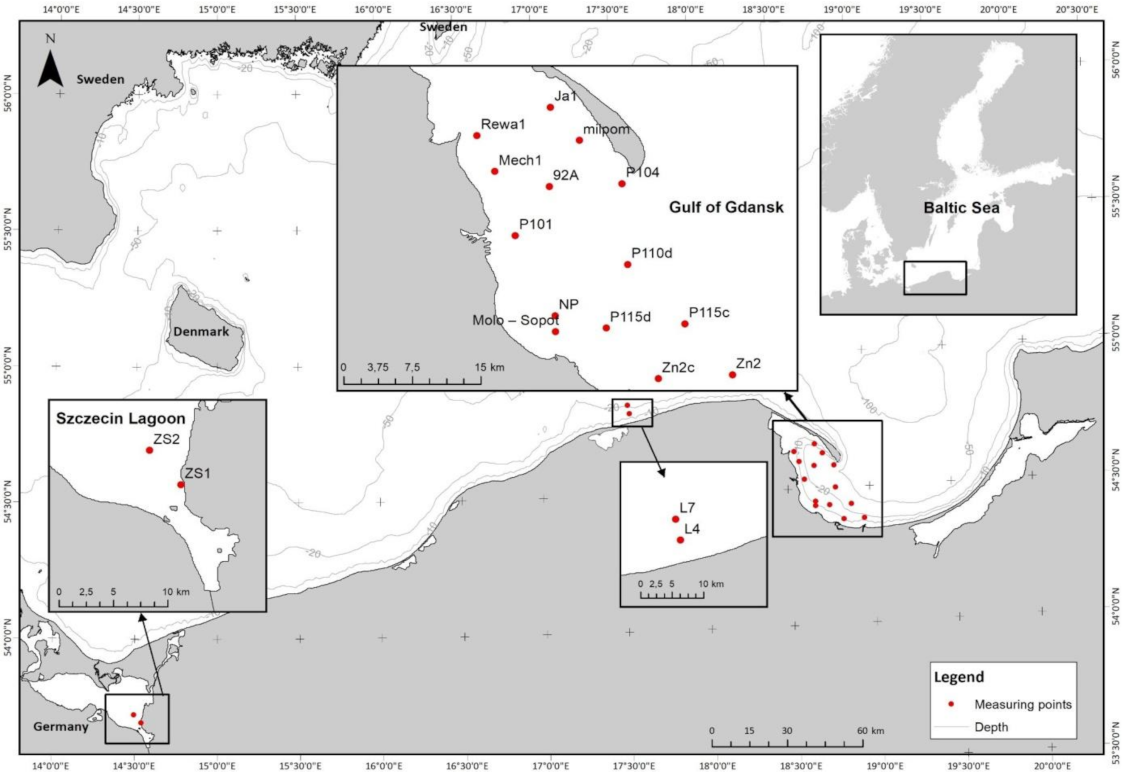
2.2. The Study Area
2.3. Data Acquisition and Processing
3. Results
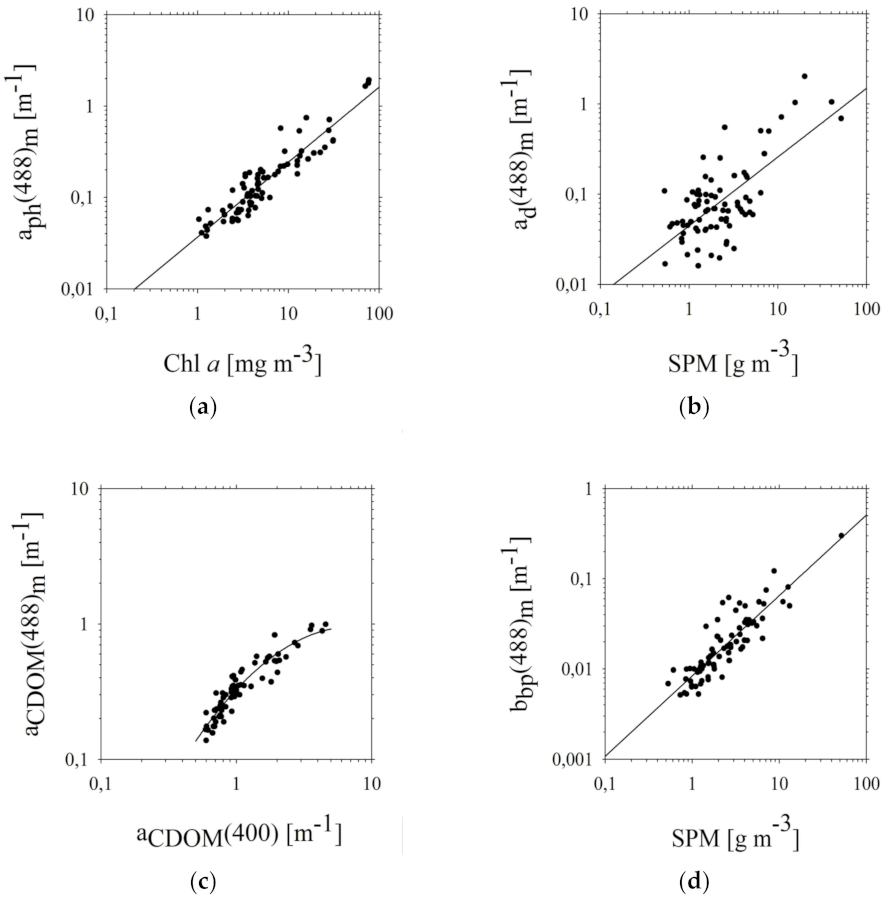
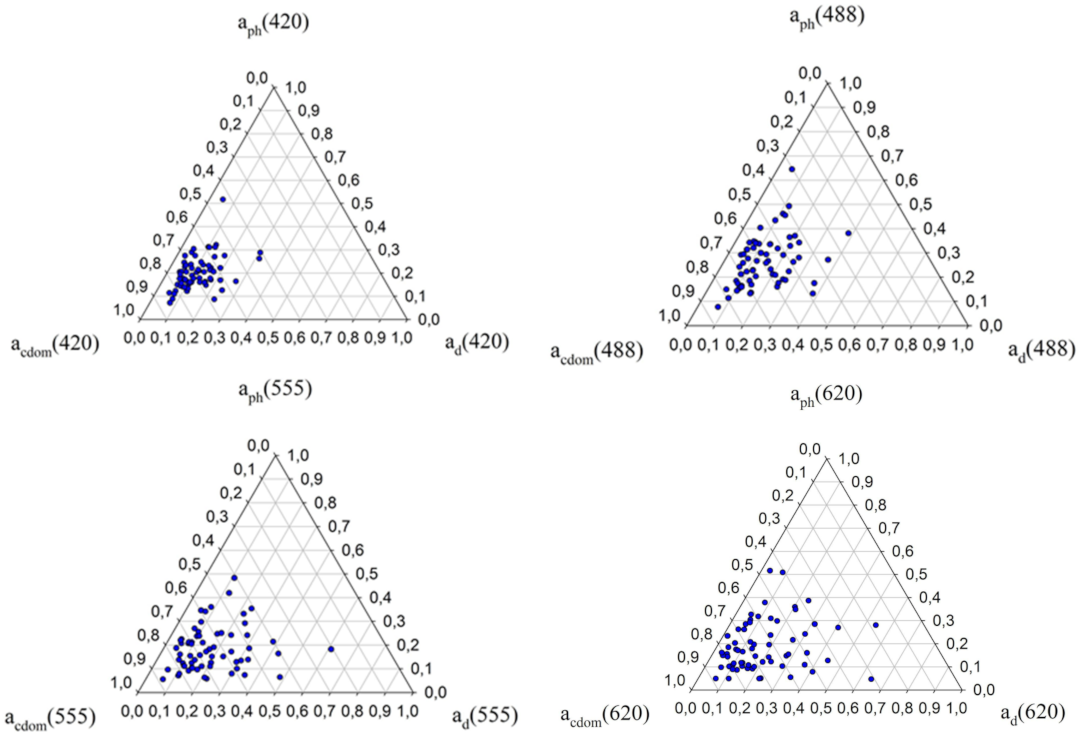
3.1. Analysis of the Impact of Biogeochemical Components on the Optical Properties of the Southern Baltic Coastal Waters
- relative mean error (systematic error):
- 2.
- standard deviation (statistical error) of ε (RMSE-root mean square error):
- 3.
- mean logarithmic error:
- 4.
- standard error factor:
- 5.
- statistical logarithmic errors:
- 6.
- 7.
3.2. The Five-Parameter Semi-Empirical Model of Rrs(λi) of the Southern Baltic Coastal Waters
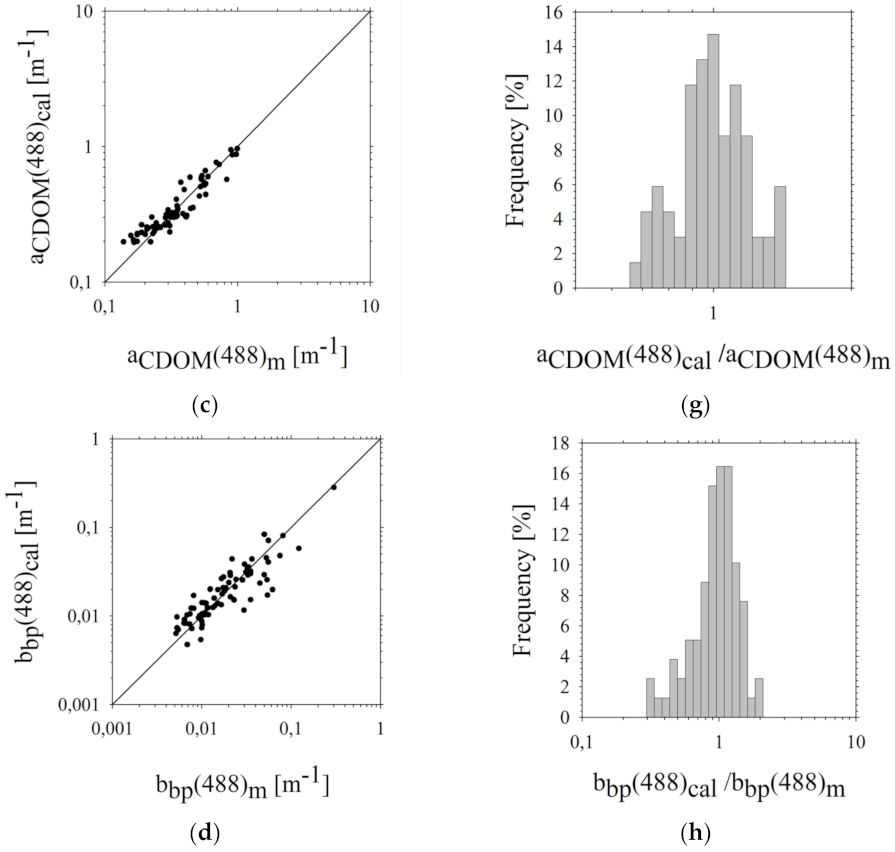
3.3. Assessment of Estimation Errors of the Five-Parameter Rrs(λi) Model
4. Discussion
4.1. Reference to the Main Research Objectives
4.2. Summary of the Main Findings of the Article
4.3. Limitations of Our Research
4.4. Recommendations for Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, R.L.; Mckee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Meler, J. Modelling Water Colour Characteristics in an Optically Complex Nearshore Environment in the Baltic Sea; Quantitative Interpretation of the Forel-Ule Scale and Algorithms for the Remote Estimation of Seawater Composition. Remote Sens. 2020, 12, 2852. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Woźniak, B.; Dera, J. Light Absorption in Sea Water; Springer: New York, NY, USA, 2007; p. 452. [Google Scholar]
- Bricaud, A.; Roesler, C.; Zaneveld, J.R.V. In Situ methods for measuring the inherent optical properties of ocean waters. Limnol. Oceanogr. 1995, 40, 393–410. [Google Scholar]
- Arst, H. Properties and Remote Sensing of Multicomponental Water Bodies; Springer: Berlin/Heidelberg, Germany, 2003; p. 231. [Google Scholar]
- Babin, M.; Morel, A.; Fournier-Sicre, V.; Fell, F.; Stramski, D. Light scattering properties of marine particles in coastal and oceanic waters as related to the particle mass concentration. Limnol. Oceanogr. 2003, 48, 843–859. [Google Scholar] [CrossRef]
- Sathyendranath, S. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex Waters; International Ocean Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2000; p. 140. [Google Scholar]
- Woźniak, B.; Krężel, A.; Dera, J. Development of a satellite method for Baltic ecosystem monitoring (DESAMBEM)—An ongoing project in Poland. Oceanologia 2004, 46, 445–455. [Google Scholar]
- Zapadka, T.; Krężel, A.; Woźniak, B. Longwave radiation budget at the Baltic Sea surface from satellite and atmospheric model data. Oceanologia 2008, 50, 147–166. [Google Scholar]
- D’Alimonte, D.; Zibordi, G.; Berthon, J.-F.; Canuti, E.; Kajiyama, T. Performance and applicability of bio-optical algorithms in different European seas. Remote Sens. Environ. 2012, 124, 402–412. [Google Scholar] [CrossRef]
- Saba, V.S.; Friedrichs, M.A.M.; Carr, M.-E.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Aumont, O.; Bates, N.R.; Behrenfeld, M.J.; Bennington, V.; et al. Challenges of Modeling Depthintegratedmarine Primary Productivity over Multiple Decades: A Case Study at BATS and HOT. Glob. Biogeochem. Cycles 2010, 24, GB3020. [Google Scholar] [CrossRef]
- Miller, R.L.; Del Castillo, C.E.; Mckee, B.A. Remote Sensing of Coastal Aquatic Environments; Springer: Dordrecht, The Netherlands, 2010; p. 346. [Google Scholar]
- Kostianoy, A.G.; Lavrova, O.Y.; Mityagina, M.I.; Solovyov, D.M.; Lebedev, S.A. Satellite Monitoring of Oil Pollution in the Southeastern Baltic Sea. In Oil Pollution in the Baltic Sea; The Handbook of Environmental Chemistry Book Series; Springer: Berlin/Heidelberg, Germany, 2013; pp. 125–153. [Google Scholar]
- Baszanowska, E.; Otremba, Z.; Piskozub, J. Modeling Remote Sensing Reflectance to Detect Dispersed Oil at Sea. Sensors 2020, 20, 863. [Google Scholar] [CrossRef] [Green Version]
- Haule, K.; Freda, W. The effect of dispersed Petrobaltic oil droplet size on photosynthetically active radiation in marine environment. Environ. Sci. Pollut. Res. 2016, 23, 6506–6516. [Google Scholar] [CrossRef] [PubMed]
- Haule, K.; Toczek, H.; Borzycka, K.; Darecki, M. Influence of Dispersed Oil on the Remote Sensing Reflectance-Field Experiment in the Baltic Sea. Sensors 2021, 21, 5733. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (Case I waters). J. Geophys. Res. 1988, 93, 10749–10768. [Google Scholar] [CrossRef] [Green Version]
- Carder, K.L.; Chen, F.R.; Lee, Z.P.; Hawes, S.K.; Kamykowski, D. Semi-analytic Moderate-Resolution Imaging Spectrometer algorithms for chlorophyll a and absorption with bio-optical domains based on nitrate-depletion temperatures. J. Geophys. Res. 1999, 104, 5403–5422. [Google Scholar] [CrossRef]
- Maritorena, S.; Siegel, D.A.; Peterson, A. Optimization of a semi-analytical ocean color model for global scale applications. Appl. Optics 2002, 41, 2705–2714. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Hansell, D.A.; Lorenzi-Kayser, M. Global ocean distribution and dynamics of colored dissolved and detrital organic materials. J. Geophys. Res. 2002, 107, 3228. [Google Scholar] [CrossRef]
- Haltrin, V.I.; Arnone, R.A. An algorithm to estimate concentrations of suspended particles in seawater from satellite optical images. In Proceedings of the II International Conference “Current Problems in Optics of Natural Waters, St. Petersbur, Russia, 8–12 September 2009; Livin, I., Gilbert, G., Eds.; Citeseer: St. Petersbur, Russia, 2009. [Google Scholar]
- Darecki, M.; Ficek, D.; Krężel, A.; Ostrowska, M.; Majchrowski, R.; Woźniak, S.B.; Bradtke, K.; Dera, J.; Woźniak, B. Algorithms for the remote sensing of the Baltic ecosystem (DESAMBEM). Part 2: Empirical validation. Oceanologia 2008, 50, 509–538. [Google Scholar]
- Woźniak, S.B.; Meler, J.; Lednicka, B.; Zdun, A.; Stoń-Egiert, J. Inherent optical properties of suspended particulate matter in the southern Baltic Sea. Oceanologia 2011, 53, 691–729. [Google Scholar]
- Lee, Z.P.; Carder, K.L.; Arnone, R. Deriving inherent optical properties from water color: A multi-band quasi-analytical algorithm for optically deep waters. Appl. Optics 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Woźniak, S.B. Simple statistical formulas for estimating biogeochemical properties of suspended particulate matter in the southern Baltic Sea potentially useful for optical remote sensing applications. Oceanologia 2014, 56, 7–39. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Sathyendranath, S.; Prieur, L.; Morel, A. A three-component model of ocean colour and its application to remote sensing of phytoplankton pigments in coastal waters. Int. J. Remote Sensing. 1989, 10, 1373–1394. [Google Scholar] [CrossRef]
- McKee, D.; Cunningham, A. Identification and characterisation of two optical water types in the Irish Sea from in situ inherent optical properties and seawater constituents. Estuar. Coast. Shelf Sci. 2006, 68, 305–316. [Google Scholar] [CrossRef]
- Meler, J.; Kowalczuk, P.; Ostrowska, M.; Ficek, D.; Zabłocka, M.; Zdun, A. Parameterization of the light absorption properties of chromophoric dissolved organic matter in the Baltic Sea and Pomeranian lakes. Ocean. Sci. 2016, 12, 1013–1032. [Google Scholar] [CrossRef] [Green Version]
- Meler, J.; Ostrowska, M.; Ficek, D.; Zdun, A. Light absorption by phytoplankton in the southern Baltic and Pomeranian lakes: Mathematical expressions for remote sensing applications. Oceanologia 2017, 59, 195–212. [Google Scholar] [CrossRef]
- Kahru, M.; Mitchell, B.G. Seasonal and nonseasonal variability of satellite-derived chlorophyll and colored dissolved organic matter concentration in the California Current. J. Geophys. Res. 2001, 106, 2517–2529. [Google Scholar] [CrossRef]
- Reynolds, R.A.; Stramski, D.; Mitchell, B.G. A chlorophyll dependent semianalytical reflectance model derived from field measurements of absorption and backscattering coefficients within the SouthernOcean. J. Geophys. Res. 2001, 106, 7125–7138. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L. Bio-optical properties in waters influenced by the Mississippi River during low flow conditions. Remote Sens. Environ. 2003, 84, 538–549. [Google Scholar] [CrossRef]
- Meler, J.; Woźniak, S.B.; Stoń-Egiert, J.; Woźniak, B. Parameterization of phytoplankton spectral absorption coefficients in the Baltic Sea: General, monthly and two-component variants of approximation formulas. Ocean. Sci. 2018, 14, 1523–1545. [Google Scholar] [CrossRef] [Green Version]
- Kirk, J.T.O. Light & Photosynthesis in Aquatic Ecosystems; University Press Cambridge: Cambridge, UK, 1994. [Google Scholar]
- Kalle, K. The problem of the Gelbstraff in the sea. Oceanogr. Mar. Biol. Annu. 1966, 4, 91–104. [Google Scholar]
- Bukata, R.P.; Jerome, J.H.; Kondratyev, K.Y.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Dera, J. Fizyka Morza; PWN: Warszawa, Poland, 1983. [Google Scholar]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Optics 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Morel, A. Optical properties of pure water and pure seawater. In Optical Aspects of Oceanography; Jerlov, N.G., Steeman, E., Eds.; Academic Press: London, UK, 1974; pp. 1–24. [Google Scholar]
- Statistical Yearbook of Maritime Economy 2019; Gdynia Maritime University: Gdynia, Poland, 2020; ISBN 978-83-7421-307-3.
- Urbański, J. Upwellingi polskiego wybrzeża Bałtyku. Przegląd Geofiz. 1995, XL, 141–153. [Google Scholar]
- Filipkowska, A.; Pavoni, B.; Kowalewska, G. Organotin compounds in surface sediments of the Southern Baltic coastal zone: A study on the main factors for their accumulation and degradation. Environ. Sci. Pollut. Res. 2014, 21, 2077–2087. [Google Scholar] [CrossRef] [Green Version]
- Majewski, A. Ogólna Charakterystyka Morfometryczna Zatoki Gdańskiej; Wydawnictwa Geologiczne: Warszawa, Poland, 1990. [Google Scholar]
- Mohrholz, V.; Lass, H.U.; Matthäus, W.; Pastuszak, M. Oder water and nutrient discharge and salinity distribution in the Pomeranian Bight during the Oder Flood. (Abstract). In Proceedings of the HELCOM Scientific Workshop: The Effects of The 1997 Flood of the Odra and Vistula Rivers, Hamburg, Germany, 12–14 January 1998; p. 33, Hamburg, Rostock: Bundesamt für Seeeschiffahrt und Hydrographie (Berichte des Bundesamtes für Seeeschiffahrt und Hydrographie; 13). [Google Scholar]
- Jaroszewski, W.; Marks, L.; Radomski, A. Słownik Geologii Dynamicznej; Wydawnictwa Geologiczne: Warszawa, Poland, 1985. [Google Scholar]
- Radziejewska, T.; Schernewski, G. The Szczecin (Oder-) La-goon. In Ecology of Baltic Coastal Waters Series; Schiewer, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 197, pp. 115–129. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Moon, J.E.; Gallegos, S. Development of suspended particulate matter algorithms for ocean color remote sensing. Korean J. Remote Sens. 2001, 17, 285–295. [Google Scholar]
- Woźniak, S.B.; Darecki, M.; Zabłocka, M.; Burska, D.; Dera, J. New simple statistical formulas for estimating surface concentrations of suspended particulate matter (SPM) and particulate organic carbon (POC) from remote-sensing reflectance in the southern Baltic Sea. Oceanologia 2016, 58, 161–175. [Google Scholar] [CrossRef] [Green Version]
- Sartory, D.P.; Grobbelaar, J.U. Extraction of chlorophyll a from freshwater phytoplankton for spectrophotometric analysis. Hydrobiologia 1984, 114, 177–187. [Google Scholar] [CrossRef]
- Guidelines for the Baltic Monitoring Program 1988. Available online: https://earth.esa.int/eogateway/documents/20142/37627/Proceedings%20from%20the%20Ocean%20Colour%20Workshop (accessed on 15 November 2021).
- Strickland, J.D.H.; Parsons, T.R. A Practical Handbook of Seawater Analysis, 2nd ed.; Bulletin Fisheries Research Board of Canada: Toronto, ON, Canada, 1972; pp. 1–310. [Google Scholar]
- Parsons, T.R.; Maita, Y.; Lalli, C.M. A Manual of Chemical and Biological Methods for Seawater Analysis, 1st ed.; Pergamon Press Ltd.: Oxford, UK, 1984. [Google Scholar]
- Mantoura, R.F.C.; Repeta, D.J. Calibration Methods for HPLC, Phytoplankton Pigments in Oceanography: Guidelines to Modern Methods; UNESCO Publishing: Paris, France, 1997; pp. 407–428. [Google Scholar]
- Reuter, R.; Albers, W.; Brandt, K.; Diebel-Langohr, D.; Doerffer, R.; Dorre, F.; Hengstermann, T. Ground Truth Techniques and Procedures for Gelbstoff Measurements, The Influence of Yellow Substances on Remote Sensing of Seawater Constituents from Space; Rep. ESA Contract No. RFQ 3–5060/84/NL/MD; GKSS Research Centre: Geesthacht, Germany, 1986. [Google Scholar]
- Kowalczuk, P. The absorption of yellow substance in the Baltic Sea. Oceanologia 2002, 44, 287–288. [Google Scholar]
- Mitchell, B.G.; Kahru, M.; Wieland, J.; Stramska, M. Determination of spectral absorption coefficients of particles, dissolved material and phytoplankton for discrete water samples. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2002. [Google Scholar]
- Tassan, S.; Ferrari, G.M. An alternative approach to absorption measurements of aquatic particles retained on filters. Limnol. Oceanogr. 1995, 40, 1358–1368. [Google Scholar] [CrossRef] [Green Version]
- Maffione, R.A.; Dana, D.R. Instruments and methods for measuring the backward scattering coefficient of ocean waters. Appl. Optics 1997, 36, 6057–6067. [Google Scholar] [CrossRef]
- Dana, D.R.; Maffione, R.A. Determining the backward scattering coefficient with fixed-angle backscattering sensors—Revisited. In Proceedings of the Ocean Optics XVI Conference, Santa Fe, NM, USA, 18–22 November 2002. [Google Scholar]
- HOBI Labs (Hydro-Optics, Biology, and Instrument. Lab. Inc.). HydroScat-4 Spectral Backscattering Sensor. User’s Manual; Bellevue: Washington, WA, USA, 2008; 65p, Rev. 4. [Google Scholar]
- Gordon, H.R.; Ding, K. Self-shading of in-water optical instruments. Limnol. Oceanogr. 1992, 37, 491–500. [Google Scholar] [CrossRef]
- Zibordi, G.; Ferrari, M. Instrument self-shading in underwater optical measurements: Experimental data. Appl. Optics 1995, 34, 2750–2754. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. II Bidirectional aspects. Appl. Optics 1993, 32, 6864–6879. [Google Scholar] [CrossRef] [PubMed]
- Loisel, H.; Morel, A. Non-isotropy of the upward-radiance field in typical coastal case 2 waters. Int. J. Remote Sens. 2001, 22, 275–295. [Google Scholar] [CrossRef]
- Tzortziou, M.; Herman, J.; Gallegos, C.; Neale, P.; Subramaniam, A.; Harding, L.; Ahmad, Z. Bio-optics of the Chesapeake Bay from measurements and radiative transfer closure. Estuarine Coastal Shelf Sci. 2006, 68, 348–362. [Google Scholar] [CrossRef]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional Reflectance of Oceanic Waters: Accounting for Raman Emission and Varying Particle Scattering Phase Function. Appl. Optics 2002, 41, 6289–6306. [Google Scholar] [CrossRef] [PubMed]
- Voss, K.; Morel, A. Bidirectional reflectance function for oceanic waters with varying chlorophyll concentrations: Measurements versus predictions. Limnol. Oceanogr. 2005, 50, 698–705. [Google Scholar] [CrossRef]
- Shifrin, K.S. Introduction to Ocean Optics; Gidrometeoizdat: Leningrad, Russia, 1983; p. 278. [Google Scholar]
- Woźniak, B.; Dera, J.; Ficek, D.; Majchrowski, R.; Kaczmarek, S.; Ostrowska, M.; Koblentz-Mishke, O.I. Model of the ‘in vivo’ spectral absorption of algal pigments. Part 1. Mathematical apparatus. Oceanologia 2000, 42, 177–190. [Google Scholar]


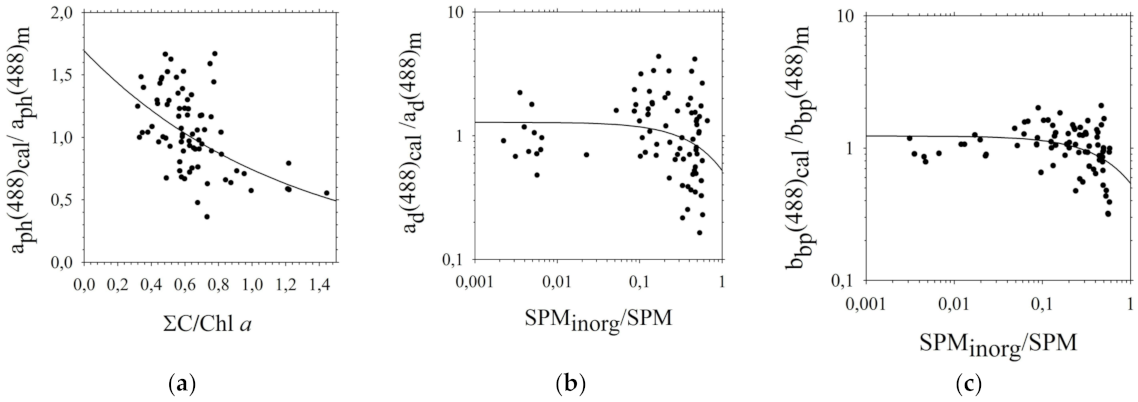
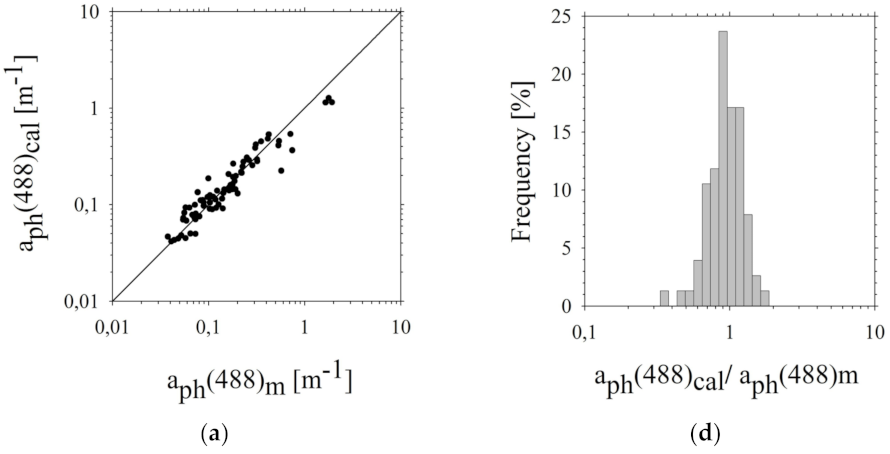
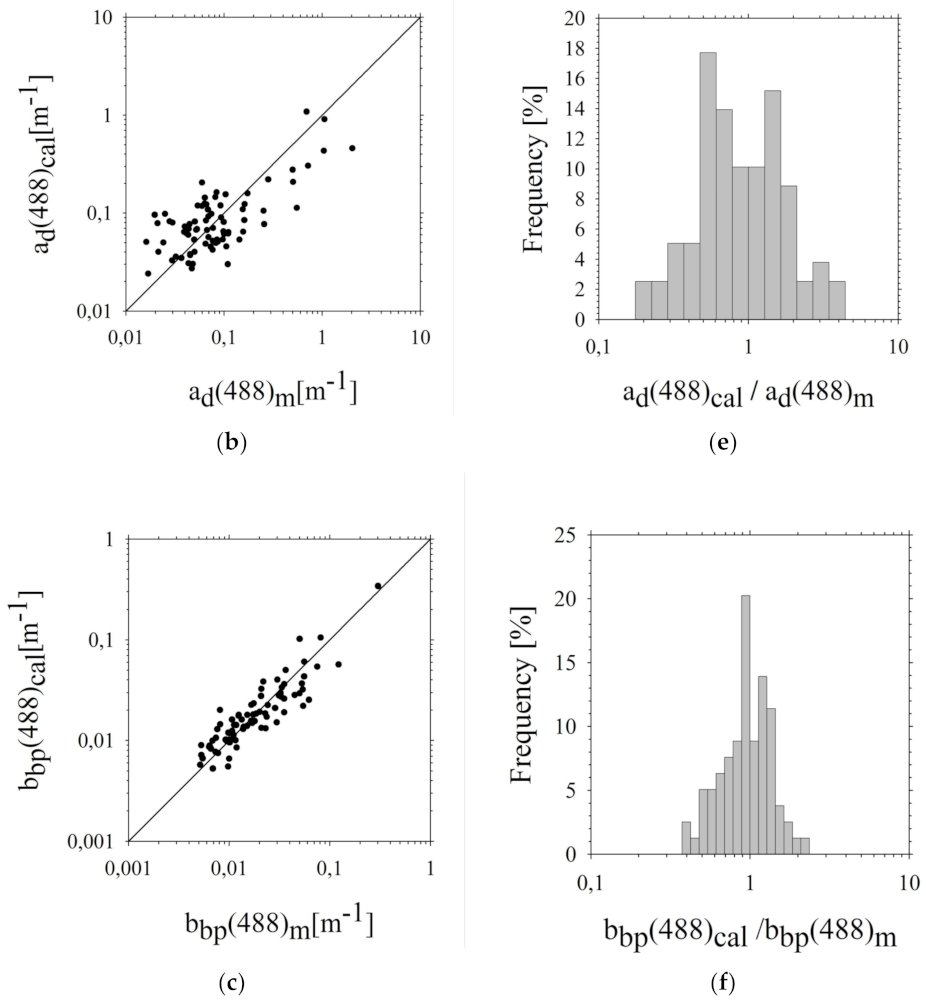

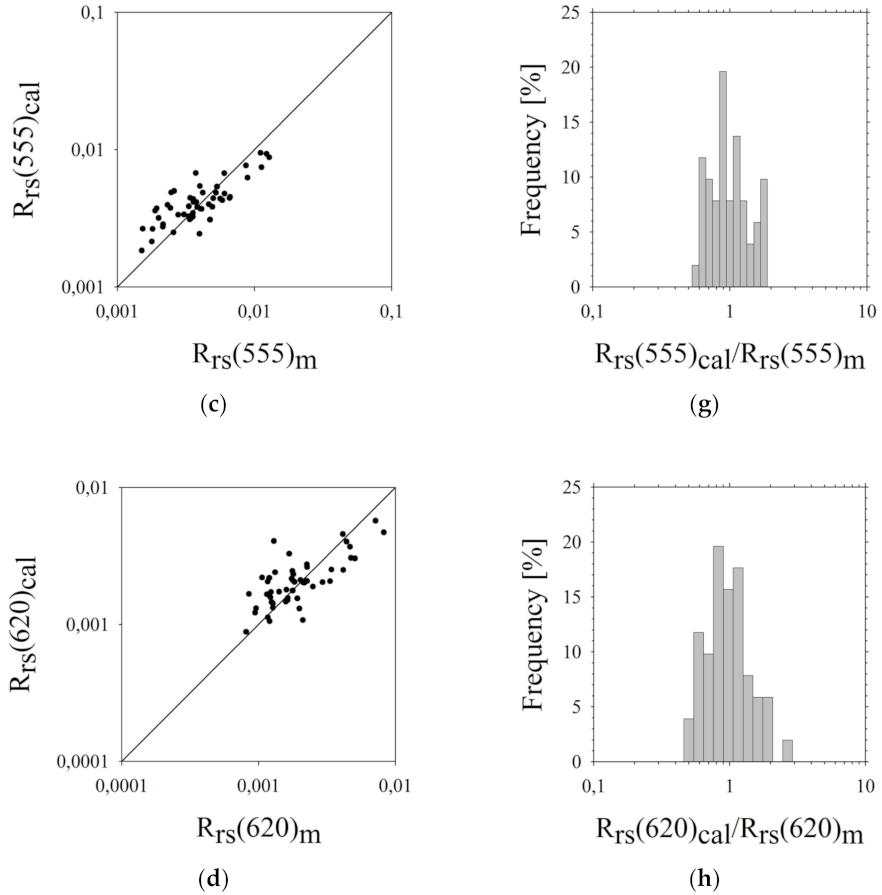
| Step 1. 1-Parameter Model of IOPs | Arithmetic Statistic | Logarithmic Statistic | ||||
|---|---|---|---|---|---|---|
| Systematic Error | Statistical Error | Systematic Error | Standard Error Factor | Statistical Error | ||
| <ε> [%] | σε [%] | <ε>g [%] | x | σε+ [%] | σε− [%] | |
| aph(420) Equation (7) | 4.39 | 30.97 | −1.54 × 10 −2 | 1.35 | 34.66 | −25.74 |
| aph(488) Equation (8) | 4.91 | 31.10 | 7.1 × 10 −3 | 1.38 | 37.97 | −27.52 |
| aph(555) Equation (9) | 4.46 | 30.80 | 3.3 × 10 −3 | 1.35 | 35.01 | −25.93 |
| aph(620) Equation (10) | 5.46 | 34.01 | 1.1 × 10 −3 | 1.40 | 39.90 | −28.52 |
| ad(420) Equation (11) | 23.7 | 86.1 | −1.4 × 10 −3 | 1.94 | 94.3 | −48.5 |
| ad(488) Equation (12) | 26.4 | 89.7 | −5.9 × 10 −3 | 2.03 | 103.2 | −50.8 |
| ad(555) Equation (13) | 38.1 | 115.9 | 2.7 × 10 −3 | 2.30 | 130.4 | −56.6 |
| ad(620) Equation (14) | 65.5 | 188.9 | 9.1 × 10 −3 | 2.79 | 179.1 | −64.2 |
| aCDOM(420) Equation (19) | 0.23 | 7.08 | −0.01 | 1.07 | 7.25 | −6.76 |
| aCDOM(488) Equation (20) | 1.69 | 18.60 | 0.01 | 1.20 | 20.31 | −16.88 |
| aCDOM(555) Equation (21) | 4.71 | 32.91 | 0.01 | 1.35 | 35.37 | −26.13 |
| aCDOM(620) Equation (22) | 6.94 | 40.23 | 0.01 | 1.45 | 44.52 | −30.81 |
| bbp(420) Equation (15) | 8.87 | 44.52 | 8.25 × 10 −3 | 1.53 | 52.93 | −34.61 |
| bbp(488) Equation (16) | 7.16 | 37.44 | 2.8 × 10 −4 | 1.48 | 48.39 | −32.61 |
| bbp(555) Equation (17) | 6.97 | 36.14 | −2.22 × 10 −3 | 1.48 | 48.20 | −32.52 |
| bbp(620) Equation (18) | 9.95 | 45.88 | 2 × 10 −5 | 1.59 | 58.90 | −37.07 |
| Step 2. 2-Parameter Model of IOPs | Arithmetic Statistic | Logarithmic Statistic | ||||
|---|---|---|---|---|---|---|
| Systematic Error | Statistical Error | Systematic Error | Standard Error Factor | Statistical Error | ||
| <ε> [%] | σε [%] | <ε>g [%] | x | σε+ [%] | σε− [%] | |
| aph(420) Equation (31) | 3.86 | 28.90 | 6 × 10 −4 | 1.32 | 32.16 | −24.33 |
| aph(488) Equation (32) | 3.62 | 27.28 | −2 × 10 −4 | 1.32 | 31.56 | −23.99 |
| aph(555) Equation (33) | 4.21 | 29.84 | 1.3 × 10 −3 | 1.34 | 33.96 | −25.35 |
| aph(620) Equation (34) | 5.37 | 33.86 | −8 × 10 −4 | 1.39 | 39.35 | −28.23 |
| ad(420) Equation (35) | 23.5 | 88.9 | −2.2 × 10 −3 | 1.91 | 91.1 | −47.7 |
| ad(488) Equation (36) | 25.9 | 91.7 | 7 × 10 −4 | 1.99 | 98.6 | −49.7 |
| ad(555) Equation (37) | 36.3 | 114.1 | −1.6 × 10 −3 | 2.23 | 123.2 | −55.2 |
| ad(620) Equation (38) | 58.0 | 165.8 | 2 × 10 −4 | 2.67 | 166.7 | −62.5 |
| bbp(420) Equation (39) | 8.86 | 45.31 | 7 × 10 −4 | 1.52 | 52.26 | −34.32 |
| bbp(488) Equation (40) | 6.55 | 38.07 | 3 × 10 −4 | 1.44 | 44.04 | −30.58 |
| bbp(555) Equation (41) | 6.02 | 36.19 | −4.4 × 10 −3 | 1.42 | 42.04 | −29.60 |
| bbp(620) Equation (42) | 8.21 | 43.85 | −1.2 × 10 −3 | 1.50 | 50.01 | −33.34 |
| λ | C | B | D | K | J | L | aw | bbw |
|---|---|---|---|---|---|---|---|---|
| 420 | 0.009 | 0.911 | 0.337 | 0.057 | 0.807 | 0.750 | 0.0045 | 0.0023 |
| 488 | 0.006 | 0.891 | 0.827 | 0.035 | 0.762 | 0.903 | 0.0147 | 0.0012 |
| 555 | 0.005 | 0.935 | 0.977 | 0.022 | 0.646 | 1.157 | 0.0596 | 0.0007 |
| 620 | 0.004 | 0.881 | 1.230 | 0.015 | 0.592 | 1.542 | 0.2755 | 0.0004 |
| λ | F | G | H | M | N | P | f/Q | |
| 420 | 0.827 | 0.041 | 0.493 | 0.077 | 1.006 | 0.132 | 0.07 | |
| 488 | 0.820 | 0.022 | 0.824 | 0.624 | 1.077 | 0.485 | 0.10 | |
| 555 | 0.815 | 0.011 | 0.257 | 1.037 | 1.072 | 0.689 | 0.12 | |
| 620 | 0.926 | 0.007 | 0.261 | 1.488 | 1.136 | 0.794 | 0.13 |
| Step 3. 5-Parameter Model of Rrs(λi) | Arithmetic Statistic | Logarithmic Statistic | ||||
|---|---|---|---|---|---|---|
| Systematic Error | Statistical Error | Systematic Error | Standard Error Factor | Statistical Error | ||
| <ε> [%] | σε [%] | <ε>g [%] | x | σε+ [%] | σε− [%] | |
| Rrs(420) | 11.10 | 34.71 | 6.13 | 1.35 | 35.49 | −26.19 |
| Rrs(488) | 10.16 | 34.53 | 5.46 | 1.34 | 34.13 | −25.44 |
| Rrs(555) | 11.68 | 37.98 | 5.,94 | 1.38 | 38.25 | −27.67 |
| Rrs(620) | 13.62 | 47.52 | 5.78 | 1.45 | 45.12 | −31.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lednicka, B.; Kubacka, M. Semi-Empirical Model of Remote-Sensing Reflectance for Chosen Areas of the Southern Baltic. Sensors 2022, 22, 1105. https://doi.org/10.3390/s22031105
Lednicka B, Kubacka M. Semi-Empirical Model of Remote-Sensing Reflectance for Chosen Areas of the Southern Baltic. Sensors. 2022; 22(3):1105. https://doi.org/10.3390/s22031105
Chicago/Turabian StyleLednicka, Barbara, and Maria Kubacka. 2022. "Semi-Empirical Model of Remote-Sensing Reflectance for Chosen Areas of the Southern Baltic" Sensors 22, no. 3: 1105. https://doi.org/10.3390/s22031105
APA StyleLednicka, B., & Kubacka, M. (2022). Semi-Empirical Model of Remote-Sensing Reflectance for Chosen Areas of the Southern Baltic. Sensors, 22(3), 1105. https://doi.org/10.3390/s22031105






