Paper-Based Microfluidics Perform Mixing Effects by Utilizing Planar Constricted–Expanded Structures to Enhance Chaotic Advection
Abstract
:1. Introduction
2. Theory and Numerical Model
3. Materials and Methods
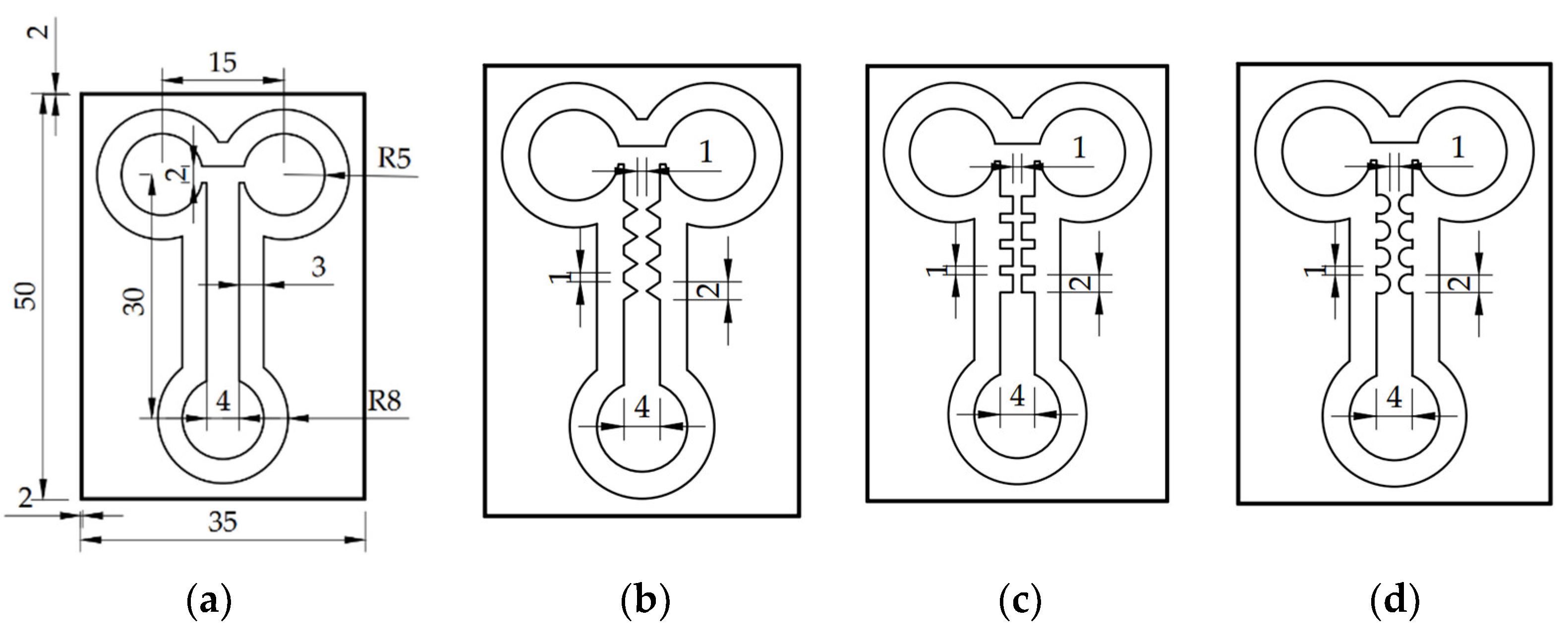
3.1. Design and Fabrication
3.2. Experimental Testing
4. Results and Discussion
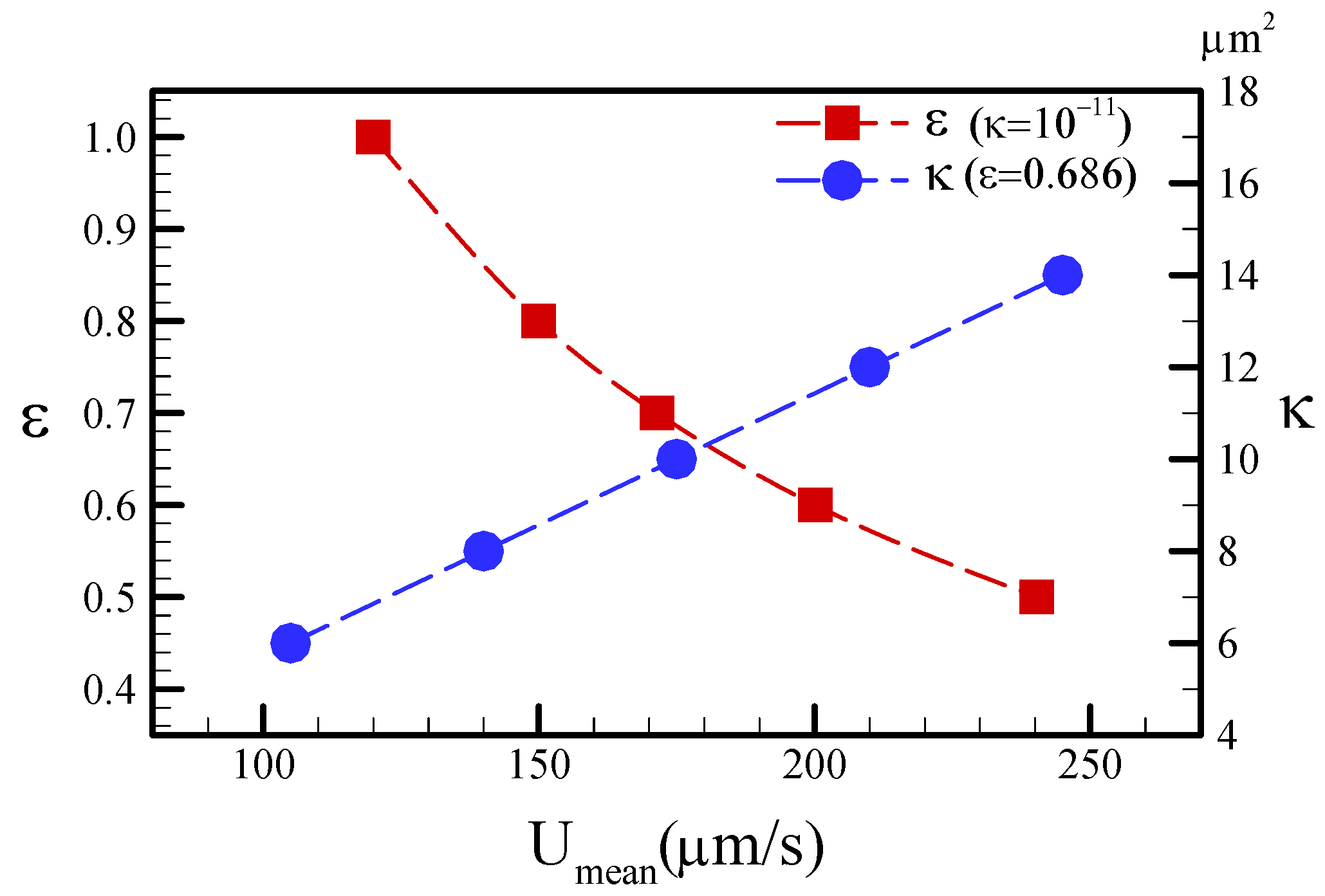
4.1. Characterization of the Numerical Simulation
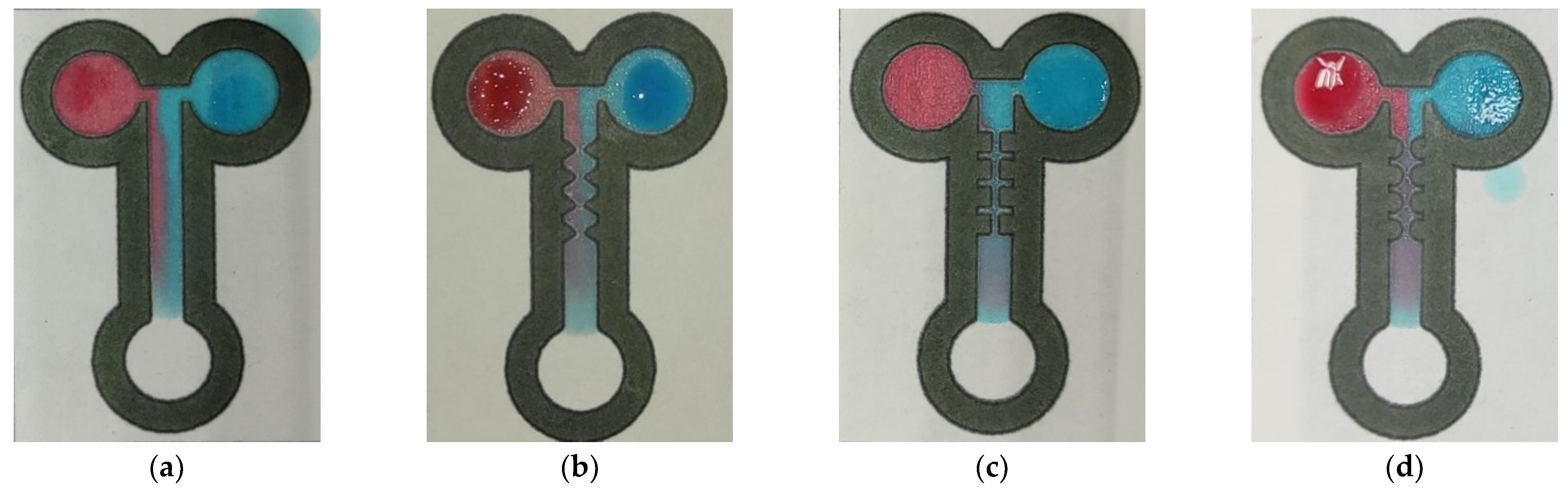
4.2. Characterization of the Mixing Performance
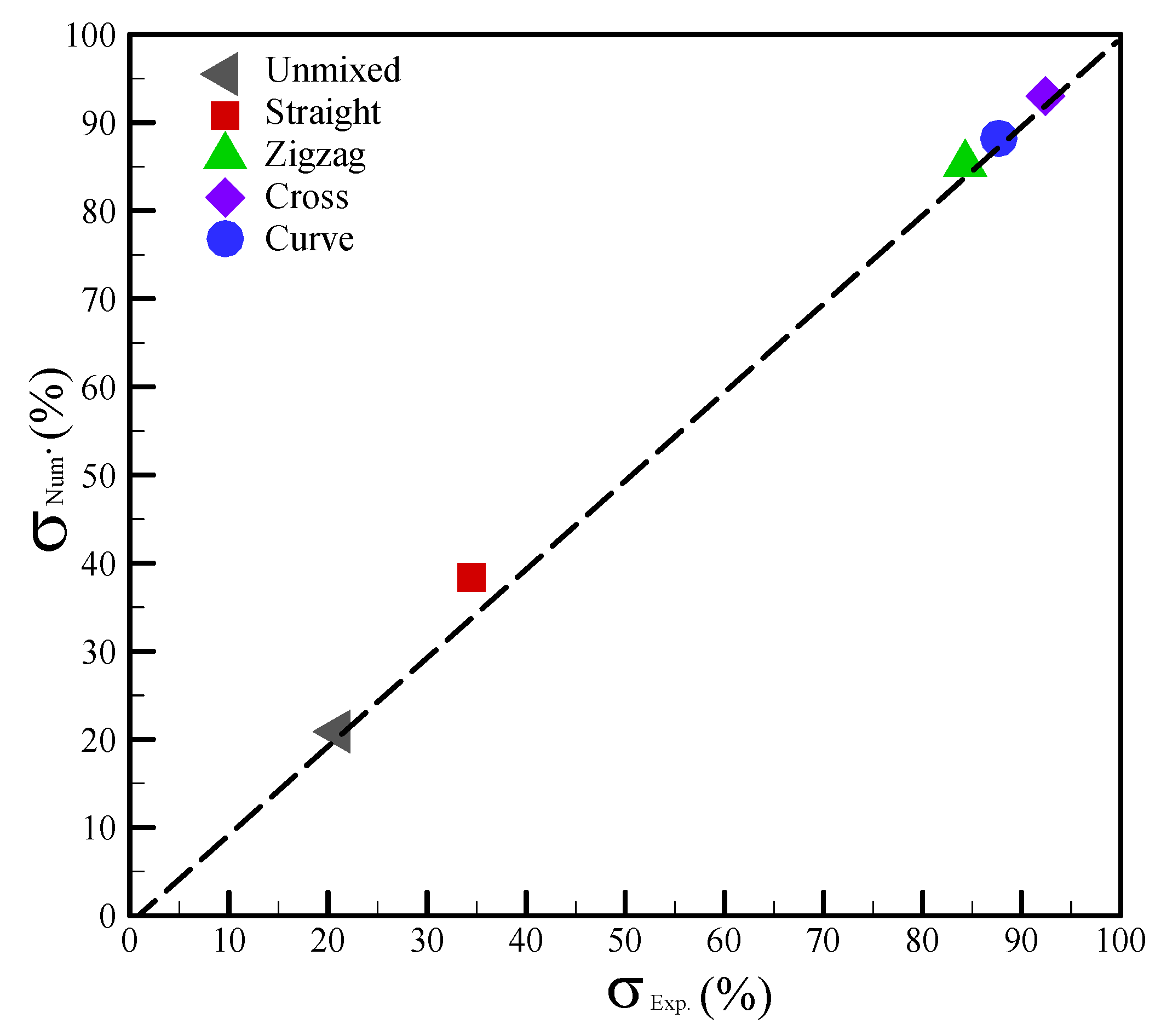
4.3. Numerical Verification of the Mixing Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, C.-Y.; Fu, L.-M. Recent advances and applications of micromixers. Sens. Actuators B Chem. 2018, 259, 677–702. [Google Scholar] [CrossRef]
- Ottino, J.M. The mixing of fluids. Sci. Am. 1989, 260, 56–67. [Google Scholar] [CrossRef]
- Nguyen, N.-T.; Wu, Z. Micromixers—A review. J. Micromech. Microeng. 2005, 15, R1–R16. [Google Scholar] [CrossRef]
- Gaozhe Cai, G.; Li Xue, L.; Zhang, H.; Lin, J. A review on micromixers. Micromachines 2017, 8, 274. [Google Scholar]
- Annabestani, M.; Azizmohseni, S.; Esmaeili-Dokht, P.; Bagheri, N.; Aghassizadeh, A.; Fardmanesh, M. Multiphysics Analysis and Practical Implementation of a Soft μ-Actuator-Based Microfluidic Micromixer. J. Microelectromech. Syst. 2020, 29, 268–276. [Google Scholar] [CrossRef]
- Annabestani, M.; Mohammadzadeh, H.; Aghassizadeh, A.; Azizmohseni, S.; Fardmanesh, M. Active Microfluidic Micromixer Design using Ionic Polymer-Metal Composites. In Proceedings of the 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 371–375. [Google Scholar]
- Meis, C.; Montazami, R.; Hashemi, N. Ionic electroactive polymer actuators as active microfluidic mixers. Anal. Methods 2015, 7, 10217–10223. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.H.; Stremler, M.A.; Sharp, K.V.; Olsen, M.G.; Santiago, J.G.; Adrian, R.J.; Aref, H.; Beebe, D.J. Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 2000, 9, 190–197. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Whitesides, G.M. Patterning flows using grooved surfaces. Anal. Chem. 2002, 74, 5306–5312. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [Green Version]
- Hong, C.-C.; Choi, J.-W.; Ahn, C.H. A novel in-plane passive microfluidic mixer with modified Tesla structures. Lab Chip 2004, 4, 109–113. [Google Scholar] [CrossRef]
- Hessel, V.; Lowe, H.; Schonfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Xia, Y.; Si, J.; Li, Z. Fabrication techniques for microfluidic paper-based analytical devices and their applications for biological testing: A review. Biosens. Bioelectron. 2016, 77, 774–789. [Google Scholar] [CrossRef] [PubMed]
- Nishat, S.; Jafry, A.T.; Martinez, A.W.; Awan, F.R. Paper-based microfluidics: Simplified fabrication and assay methods. Sens. Actuators B Chem. 2021, 336, 129681. [Google Scholar] [CrossRef]
- Boobphahom, S.; Ly, M.N.; Pyun, N.; Kwon, O.-S.; Rodthongkum, N.; Shin, K. Recent Advances in Microfluidic Paper-Based Analytical Devices toward High-Throughput Screening. Molecules 2020, 25, 2970. [Google Scholar] [CrossRef]
- He, Y.; Wu, Y.; Fu, J.-Z.; Wu, W.-B. Fabrication of paper-based microfluidic analysis devices: A review. RSC Adv. 2015, 5, 78109–78127. [Google Scholar] [CrossRef]
- Lim, H.; Jafry, A.T.; Lee, J. Fabrication, Flow Control, and Applications of Microfluidic Paper-Based Analytical Devices. Molecules 2019, 24, 2869. [Google Scholar] [CrossRef] [Green Version]
- Jafry, A.T.; Lim, H.; Kang, S.; Suk, J.W.; Lee, J. A comparative study of paper-based microfluidic devices with respect to channel geometry. Colloids Surf. A Physicochem. Eng. Aspects 2016, 492, 190–198. [Google Scholar] [CrossRef]
- Martinez, A.W.; Phillips, S.T.; Butte, M.J.; Whitesides, G.M. Patterned paper as a platform for inexpensive, low-volume, portable bioassays. Angew. Chem. Int. Ed. 2007, 46, 1318–1320. [Google Scholar] [CrossRef] [Green Version]
- Shangguan, J.-W.; Liu, Y.; Pan, J.-B.; Xu, B.-Y.; Xu, J.-J.; Chen, H.-Y. Microfluidic PDMS on paper (POP) devices. Lab Chip 2017, 17, 120–127. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, W.; Jiang, L.; Qin, J.; Lin, B. Rapid prototyping of paper-based microfluidics with wax for low-cost, portable bioassay. Electrophoresis 2009, 30, 1497–1500. [Google Scholar] [CrossRef]
- Zhong, Z.W.; Wang, Z.P.; Huang, G.X.D. Investigation of wax and paper materials for the fabrication of paper-based microfluidic devices. Microsyst. Technol. 2012, 18, 649–659. [Google Scholar] [CrossRef]
- Maejima, K.; Tomikawa, S.; Suzuki, K.; Citterio, D. Inkjet printing: An integrated and green chemical approach to microfluidic paper-based analytical devices. RSC Adv. 2013, 3, 9258–9263. [Google Scholar] [CrossRef]
- Khan, M.S.; Fon, D.; Li, X.; Tian, J.; Forsythe, J.; Garnier, G.; Shen, W. Biosurface engineering through ink jet printing. Colloids Surf. B Biointerfaces 2010, 75, 441–447. [Google Scholar] [CrossRef] [PubMed]
- Carrilho, E.; Martinez, A.W.; Whitesides, G.M. Understanding wax printing: A simple micropatterning process for paper-based microfluidics. Anal. Chem. 2009, 81, 7091–7095. [Google Scholar] [CrossRef] [PubMed]
- Sameenoi, Y.; Nongkai, P.N.; Nouanthavong, S.; Henry, C.S.; Nacapricha, D. One-step polymer screen-printing for microfluidic paper-based analytical device (μPAD) fabrication. Analyst 2014, 139, 6580–6588. [Google Scholar] [CrossRef]
- Green, H.C. Improving Paper-Based Microflfluidic Mixing with the Incorporation of Flow Disrupting Structures. Master’s Theses, Louisiana Tech University, Ruston, LA, USA, 2019. [Google Scholar]
- Rezk, A.R.; Qi, A.; Friend, J.R.; Li, W.H.; Yeo, L.Y. Uniform mixing in paper-based microfluidic systems using surface acoustic. Lab Chip 2012, 12, 773–779. [Google Scholar] [CrossRef]
- Ku, C.-H.; Yang, R.-J. A new method for paper porosity estimation. TechConnect Briefs 2018, 3, 194–197. [Google Scholar]
- Cimolin, F.; Discacciati, M. Navier–Stokes/Forchheimer models for filtration through porous media. Appl. Numer. Math. 2013, 72, 205–224. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-L.; Lee, K.-H.; Lee, G.-B. Active micro-mixers utilizing a gradient zeta potential induced by inclined buried shielding electrodes. J. Micromech. Microeng. 2006, 16, 757–768. [Google Scholar] [CrossRef]








| Fluid | Property | Symbol | Unit | Value |
|---|---|---|---|---|
| water | density | ρ | kgm−3 | 1000 |
| viscosity | μ | Pas−1 | 10−3 | |
| diffusivity | D | m2s−1 | 10−9 | |
| Schmidt number | Sc | 103 | ||
| filter paper | porosity | ε | 0.686 | |
| permeability | κ | m−2 | 10−11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, C.-H.; Hsu, P.-P.; Huang, A.-Y.; Lin, J.-L. Paper-Based Microfluidics Perform Mixing Effects by Utilizing Planar Constricted–Expanded Structures to Enhance Chaotic Advection. Sensors 2022, 22, 1028. https://doi.org/10.3390/s22031028
Weng C-H, Hsu P-P, Huang A-Y, Lin J-L. Paper-Based Microfluidics Perform Mixing Effects by Utilizing Planar Constricted–Expanded Structures to Enhance Chaotic Advection. Sensors. 2022; 22(3):1028. https://doi.org/10.3390/s22031028
Chicago/Turabian StyleWeng, Chen-Hsun, Pei-Pei Hsu, An-Yu Huang, and Jr-Lung Lin. 2022. "Paper-Based Microfluidics Perform Mixing Effects by Utilizing Planar Constricted–Expanded Structures to Enhance Chaotic Advection" Sensors 22, no. 3: 1028. https://doi.org/10.3390/s22031028
APA StyleWeng, C.-H., Hsu, P.-P., Huang, A.-Y., & Lin, J.-L. (2022). Paper-Based Microfluidics Perform Mixing Effects by Utilizing Planar Constricted–Expanded Structures to Enhance Chaotic Advection. Sensors, 22(3), 1028. https://doi.org/10.3390/s22031028







