A Survey of Blind Modulation Classification Techniques for OFDM Signals
Abstract
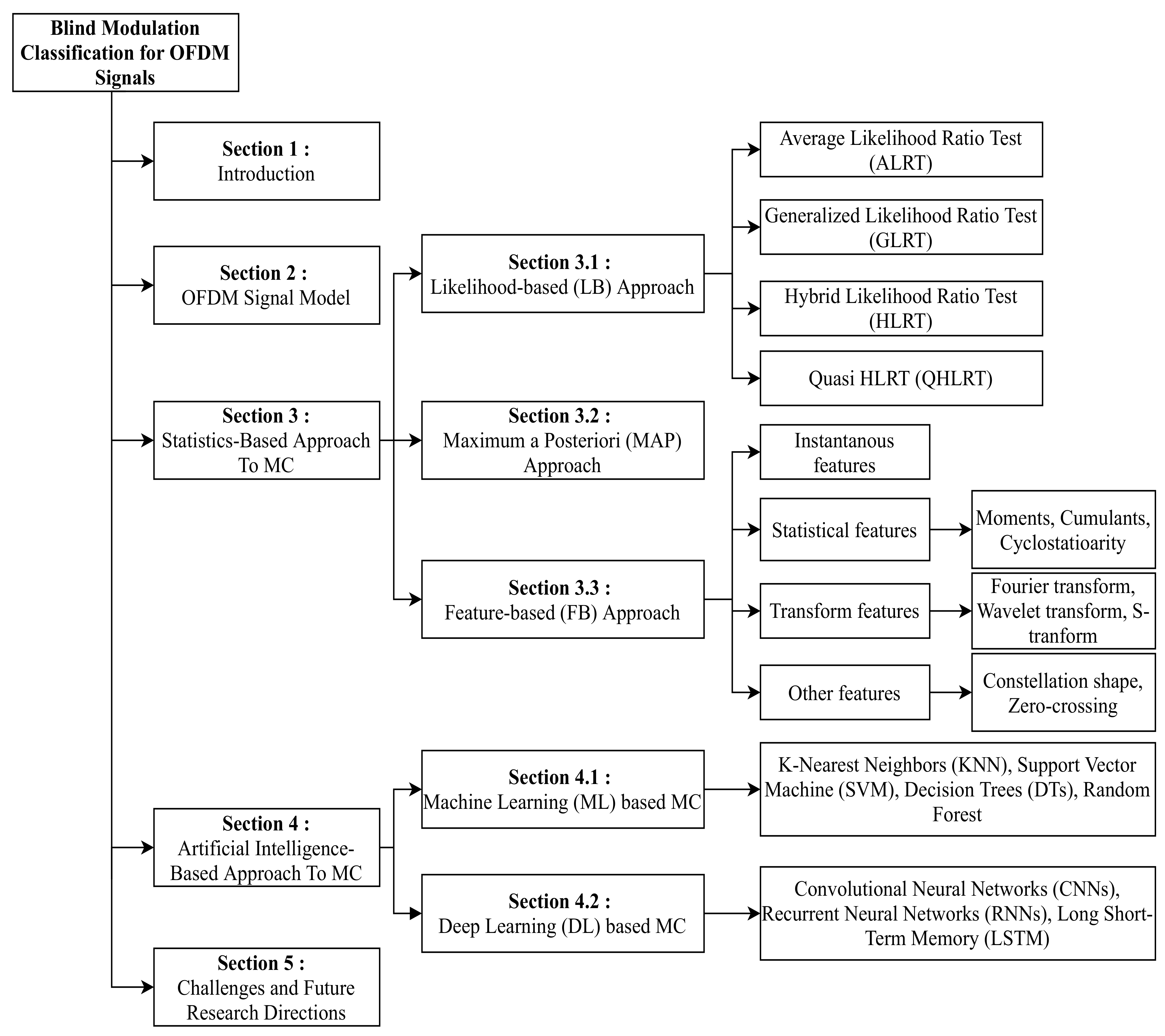
:1. Introduction
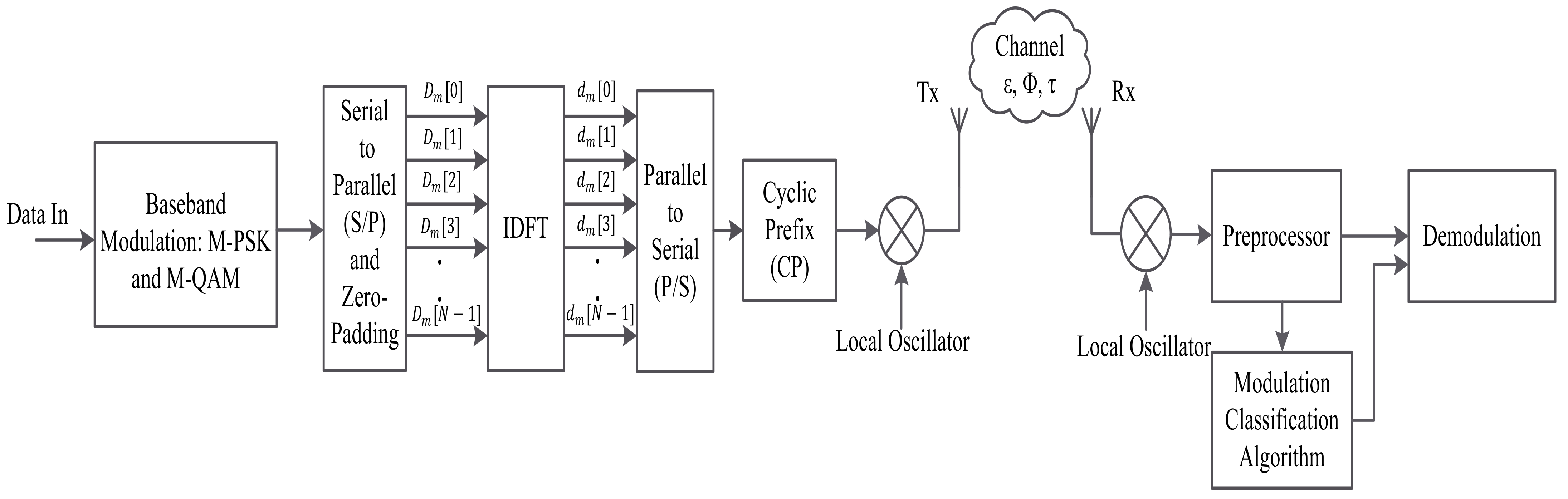
2. OFDM Signal Model
3. Statistics-Based Approach to MC
3.1. LB Approach
3.2. Maximum a Posteriori (MAP) Approach
3.3. FB Approach
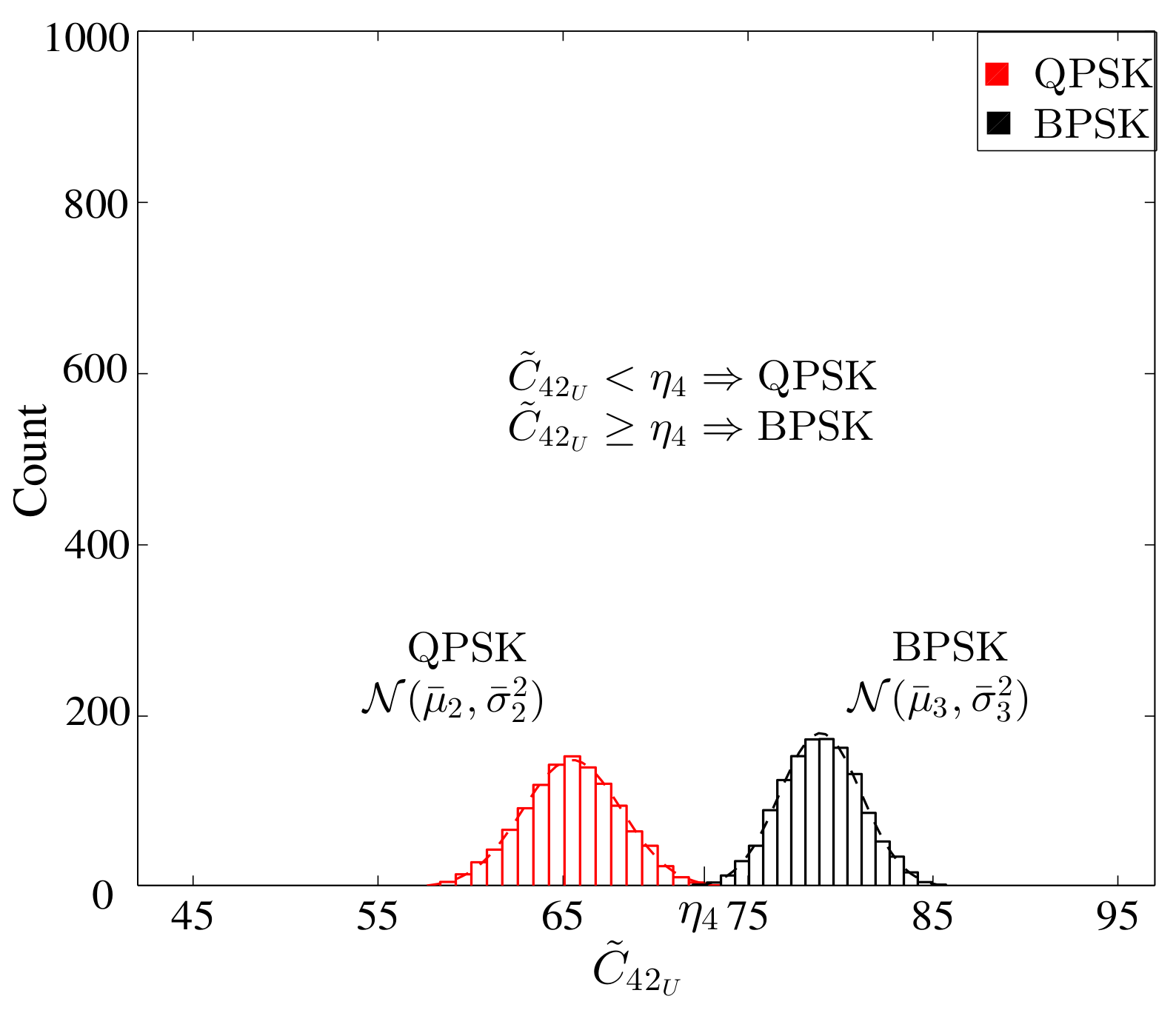
MC with Higher Order Statistics (HOS)
4. Artificial Intelligence-Based Approach to MC
4.1. ML-Based MC
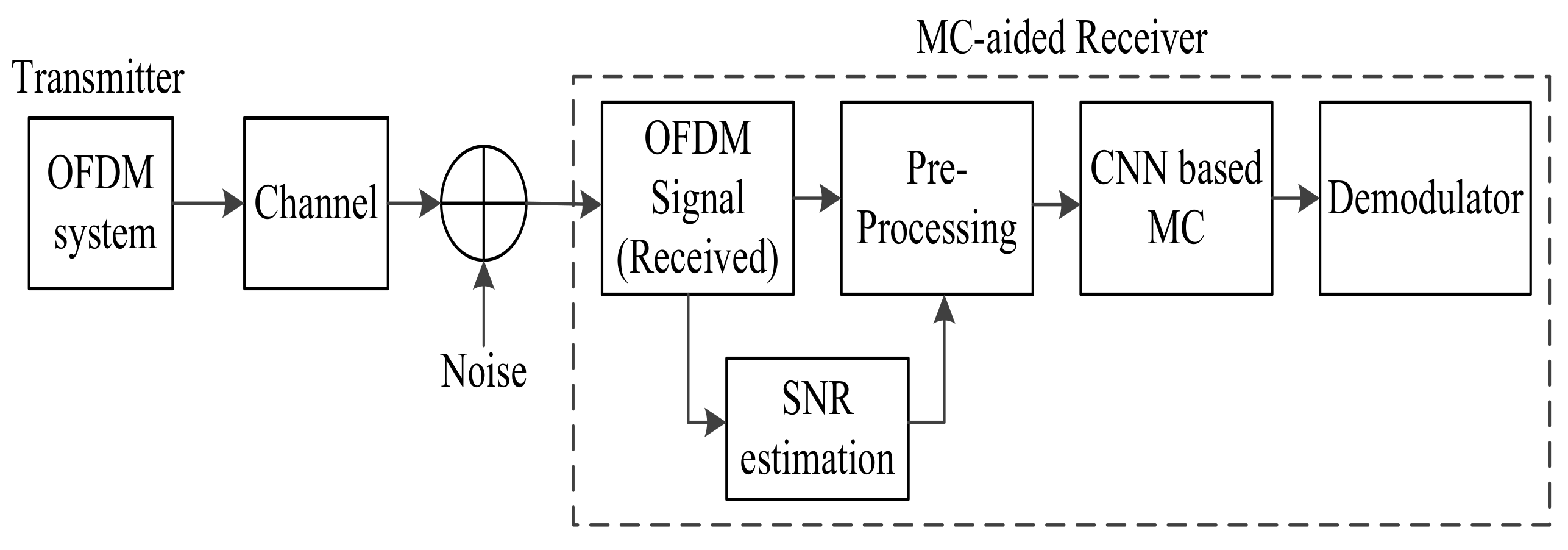
4.2. DL-Based MC
5. Challenges and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dobre, O.A.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 2007, 1, 137–156. [Google Scholar] [CrossRef] [Green Version]
- Dobre, O.A. Signal identification for emerging intelligent radios: Classical problems and new challenges. IEEE Instrum. Meas. Mag. 2015, 18, 11–18. [Google Scholar] [CrossRef]
- Eldemerdash, Y.A.; Dobre, O.A.; Öner, M. Signal identification for multiple-antenna wireless systems: Achievements and challenges. IEEE Commun. Surv. Tutor. 2016, 18, 1524–1551. [Google Scholar] [CrossRef]
- Jiang, W.; Wu, X.; Wang, Y.; Chen, B.; Feng, W.; Jin, Y. Time–Frequency-Analysis-Based Blind Modulation Classification for Multiple-Antenna Systems. Sensors 2021, 21, 231. [Google Scholar] [CrossRef]
- Gupta, R.; Majhi, S.; Dobre, O.A. Design and Implementation of a Tree-Based Blind Modulation Classification Algorithm for Multiple-Antenna Systems. IEEE Trans. Instrum. Meas. 2019, 68, 3020–3031. [Google Scholar] [CrossRef]
- Majhi, S.; Gupta, R.; Xiang, W.; Glisic, S. Hierarchical Hypothesis and Feature-Based Blind Modulation Classification for Linearly Modulated Signals. IEEE Trans. Veh. Technol. 2017, 66, 11057–11069. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.L.; Su, W.; Zhou, M. Software-Defined Radio Equipped With Rapid Modulation Recognition. IEEE Trans. Veh. Technol. 2010, 59, 1659–1667. [Google Scholar] [CrossRef]
- Majhi, S.; Kumar, M.; Xiang, W. Implementation and Measurement of Blind Wireless Receiver for Single Carrier Systems. IEEE Trans. Instrum. Meas. 2017, 66, 1965–1975. [Google Scholar] [CrossRef]
- Majhi, S.; Ho, T.S. Blind Symbol-Rate Estimation and TestBed Implementation of Linearly Modulated Signals. IEEE Trans. Veh. Technol. 2015, 64, 954–963. [Google Scholar] [CrossRef]
- Zhang, J.K.; Yuen, C.; Huang, F. Full diversity blind signal designs for unique identification of frequency selective channels. IEEE Trans. Veh. Technol. 2012, 61, 2172–2184. [Google Scholar] [CrossRef]
- Wei, W.; Mendel, J.M. Maximum-likelihood classification for digital amplitude-phase modulations. IEEE Trans. Commun. 2000, 48, 189–193. [Google Scholar] [CrossRef]
- Swami, A.; Sadler, B.M. Hierarchical digital modulation classification using cumulants. IEEE Trans. Commun. 2000, 48, 416–429. [Google Scholar] [CrossRef]
- Wu, H.C.; Saquib, M.; Yun, Z. Novel Automatic Modulation Classification Using Cumulant Features for Communications via Multipath Channels. IEEE Wirel. Commun. 2008, 7, 3098–3105. [Google Scholar]
- Oner, M.; Dobre, O.A. On the Second-Order Cyclic Statistics of Signals in the Presence of Receiver Impairments. IEEE Trans. Commun. 2011, 59, 3278–3284. [Google Scholar] [CrossRef]
- Majhi, S.; Gupta, R.; Xiang, W. Novel blind modulation classification of circular and linearly modulated signals using cyclic cumulants. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–5. [Google Scholar]
- Gupta, R.; Majhi, S.; Dobre, O.A. Blind Modulation Classification of Different Variants of QPSK and 8-PSK for Multiple-Antenna Systems with Transmission Impairments. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Daponte, P.; Mercurio, G.; Rapuano, S. A wavelet networks-based method for the digital telecommunication system monitoring. IEEE Trans. Instrum. Meas. 2001, 50, 1773–1780. [Google Scholar] [CrossRef]
- Jerjawi, W.A.; Eldemerdash, Y.A.; Dobre, O.A. Second-order cyclostationarity-based detection of LTE SC-FDMA signals for cognitive radio systems. IEEE Trans. Instrum. Meas. 2014, 64, 823–833. [Google Scholar] [CrossRef] [Green Version]
- Dobre, O.A.; Venkatesan, R.; Popescu, D.C. Second-order cyclostationarity of mobile WiMAX and LTE OFDM signals and application to spectrum awareness in cognitive radio systems. IEEE J. Sel. Top. Signal Process. 2011, 6, 26–42. [Google Scholar]
- Karami, E.; Dobre, O.A. Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclostationarity. IEEE Trans. Veh. Technol. 2014, 64, 942–953. [Google Scholar] [CrossRef]
- Punchihewa, A.; Zhang, Q.; Dobre, O.A.; Spooner, C.; Rajan, S.; Inkol, R. On the cyclostationarity of OFDM and single carrier linearly digitally modulated signals in time dispersive channels: Theoretical developments and application. IEEE Trans. Wirel. Commun. 2010, 9, 2588–2599. [Google Scholar] [CrossRef]
- Santhanavijayan, A.; Kumar, D.N.; Deepak, G. A semantic-aware strategy for automatic speech recognition incorporating deep learning models. In Intelligent System Design; Springer: Singapore, 2021; pp. 247–254. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Aslam, M.W.; Zhu, Z.; Nandi, A.K. Automatic Modulation Classification Using Combination of Genetic Programming and KNN. IEEE Trans. Wirel. Commun. 2012, 11, 2742–2750. [Google Scholar]
- Liu, X.; Zhao, C.; Wang, P.; Zhang, Y.; Yang, T. Blind modulation classification algorithm based on machine learning for spatially correlated MIMO system. IET Commun. 2017, 11, 1000–1007. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Yang, J.; Gui, G. Data-Driven Deep Learning for Automatic Modulation Recognition in Cognitive Radios. IEEE Trans. Veh. Technol. 2019, 68, 4074–4077. [Google Scholar] [CrossRef]
- Xie, W.; Hu, S.; Yu, C.; Zhu, P.; Peng, X.; Ouyang, J. Deep Learning in Digital Modulation Recognition Using High Order Cumulants. IEEE Access 2019, 7, 63760–63766. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, L.; Zhao, Y.; Yang, J.; Adebisi, B.; Gacanin, H.; Gui, G. Distributed learning for automatic modulation classification in edge devices. IEEE Wirel. Commun. Lett. 2020, 9, 2177–2181. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Ohtsuki, T.; Adachi, F. Multi-task learning for generalized automatic modulation classification under non-Gaussian noise with varying SNR conditions. IEEE Trans. Wirel. Commun. 2021, 20, 3587–3596. [Google Scholar] [CrossRef]
- Chang, S.; Huang, S.; Zhang, R.; Feng, Z.; Liu, L. Multi-Task Learning Based Deep Neural Network for Automatic Modulation Classification. IEEE Internet Things J. 2022, 9, 2192–2206. [Google Scholar] [CrossRef]
- Huang, S.; Jiang, Y.; Gao, Y.; Feng, Z.; Zhang, P. Automatic modulation classification using contrastive fully convolutional network. IEEE Wirel. Commun. Lett. 2019, 8, 1044–1047. [Google Scholar] [CrossRef]
- Huang, J.; Huang, S.; Zeng, Y.; Chen, H.; Chang, S.; Zhang, Y. Hierarchical Digital Modulation Classification Using Cascaded Convolutional Neural Network. J. Commun. Inf. Netw. 2021, 6, 72–81. [Google Scholar]
- Qi, P.; Zhou, X.; Zheng, S.; Li, Z. Automatic modulation classification based on deep residual networks with multimodal information. IEEE Trans. Cogn. Commun. Netw. 2020, 7, 21–33. [Google Scholar] [CrossRef]
- Han, H.; Ren, Z.; Li, L.; Zhu, Z. Automatic Modulation Classification Based on Deep Feature Fusion for High Noise Level and Large Dynamic Input. Sensors 2021, 21, 2117. [Google Scholar] [CrossRef] [PubMed]
- Bu, K.; He, Y.; Jing, X.; Han, J. Adversarial transfer learning for deep learning based automatic modulation classification. IEEE Signal Process. Lett. 2020, 27, 880–884. [Google Scholar] [CrossRef]
- Tu, Y.; Lin, Y.; Hou, C.; Mao, S. Complex-valued networks for automatic modulation classification. IEEE Trans. Veh. Technol. 2020, 69, 10085–10089. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, X.; Xiong, Z.; Lu, Y. Phoneme-Based Distribution Regularization for Speech Enhancement. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 726–730. [Google Scholar]
- Hwang, T.; Yang, C.; Wu, G.; Li, S.; Li, G.Y. OFDM and Its Wireless Applications: A Survey. IEEE Trans. Veh. Technol. 2009, 58, 1673–1694. [Google Scholar] [CrossRef]
- Lorincz, J.; Ramljak, I.; Begušić, D. A Survey on the Energy Detection of OFDM Signals with Dynamic Threshold Adaptation: Open Issues and Future Challenges. Sensors 2021, 21, 3080. [Google Scholar] [CrossRef]
- Qin, Z.; Ye, H.; Li, G.Y.; Juang, B.F. Deep Learning in Physical Layer Communications. IEEE Wirel. Commun. 2019, 26, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Gui, G.; Huang, H.; Song, Y.; Sari, H. Deep Learning for an Effective Nonorthogonal Multiple Access Scheme. IEEE Trans. Veh. Technol. 2018, 67, 8440–8450. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Y.; He, Z.; Nie, J.; Zhang, W. A Novel Attention Cooperative Framework for Automatic Modulation Recognition. IEEE Access 2020, 8, 15673–15686. [Google Scholar] [CrossRef]
- Nie, J.; Zhang, Y.; He, Z.; Chen, S.; Gong, S.; Zhang, W. Deep Hierarchical Network for Automatic Modulation Classification. IEEE Access 2019, 7, 94604–94613. [Google Scholar] [CrossRef]
- Ha, C.; You, Y.; Song, H. Machine Learning Model for Adaptive Modulation of Multi-Stream in MIMO-OFDM System. IEEE Access 2019, 7, 5141–5152. [Google Scholar] [CrossRef]
- Yucek, T.; Arslan, H. A novel sub-optimum maximum-likelihood modulation classification algorithm for adaptive OFDM systems. In Proceedings of the IEEE Wireless Communications and Networking Conference, Atlanta, GA, USA, 21–25 March 2004; Volume 2, pp. 739–744. [Google Scholar]
- Leinonen, J.; Juntti, M. Modulation classification in adaptive OFDM systems. In Proceedings of the IEEE 59th Vehicular Technology Conference. VTC 2004-Spring, Milan, Italy, 17–19 May 2004; Volume 3, pp. 1554–1558. [Google Scholar]
- Zheng, J.; Lv, Y. Likelihood-based automatic modulation classification in OFDM with index modulation. IEEE Trans. Veh. Technol. 2018, 67, 8192–8204. [Google Scholar] [CrossRef]
- Fang, T.; Liu, S.; Ma, L.; Zhang, L.; Khan, I.U. Subcarrier modulation identification of underwater acoustic OFDM based on block expectation maximization and likelihood. Appl. Acoust. 2021, 173, 107654. [Google Scholar] [CrossRef]
- Marey, M.; Mostafa, H. Turbo modulation identification algorithm for OFDM software-defined radios. IEEE Commun. Lett. 2021, 25, 1707–1711. [Google Scholar] [CrossRef]
- Häring, L.; Chen, Y.; Czylwik, A. Automatic modulation classification methods for wireless OFDM systems in TDD mode. IEEE Trans. Commun. 2010, 58, 2480–2485. [Google Scholar] [CrossRef]
- Häring, L.; Chen, Y.; Czylwik, A. Efficient modulation classification for adaptive wireless OFDM systems in TDD mode. In Proceedings of the IEEE Wireless Communication and Networking Conference, Sydney, Australia, 18–21 April 2010; pp. 1–6. [Google Scholar]
- Haring, L.; Chen, Y.; Czylwik, A. Utilizing side information in modulation classification for wireless OFDM systems with adaptive modulation. In Proceedings of the 2011 IEEE Vehicular Technology Conference (VTC Fall), San Francisco, CA, USA, 5–8 September 2011; pp. 1–5. [Google Scholar]
- Häring, L.; Kisters, C. MAP-based automatic modulation classification for wireless adaptive OFDM systems. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 5204–5208. [Google Scholar]
- Haering, L.; Kisters, C. Signalling-assisted modulation classification in wireless OFDM systems with adaptive modulation and coding. In Proceedings of the International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 5037–5041. [Google Scholar]
- Häring, L.; Kisters, C. Joint optimization of bit loading and modulation classification in wireless OFDM systems. In Proceedings of the IEEE 9th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Lyon, France, 7–9 October 2013; pp. 402–407. [Google Scholar]
- Haering, L.; Kisters, C. Influence of imperfect reciprocity on MAP-based automatic modulation classification for adaptive OFDM systems in TDD mode. In Proceedings of the 18th International OFDM Workshop 2014 (InOWo’14), Essen, Germany, 27–28 August 2014; pp. 1–6. [Google Scholar]
- Husmann, C.; Chen, Y. Modulation classification for adaptive mobile OFDM systems. In Proceedings of the 18th International OFDM Workshop (InOWo’14), Essen, Germany, 27–28 August 2014; pp. 1–8. [Google Scholar]
- Bahrani, S.; Derakhtian, M.; Zolghadrasli, A. Effect of channel prediction on automatic modulation classification for adaptive OFDM Systems. In Proceedings of the 20th Iranian Conference on Electrical Engineering (ICEE2012), Tehran, Iran, 15–17 May 2012; pp. 1280–1285. [Google Scholar]
- Karabacak, M.; Cırpan, H.A.; Arslan, H. Adaptive pilot based modulation identification and channel estimation for OFDM systems. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 26–30 September 2010; pp. 730–735. [Google Scholar]
- Bahrani, S.; Derakhtian, M.; Zolghadrasli, A. Performance analysis of a low-complexity MAP algorithm for automatic modulation classification in adaptive OFDM systems. IET Commun. 2016, 10, 2363–2371. [Google Scholar] [CrossRef]
- Pambudi, A.D.; Tjondronegoro, S.; Wijanto, H. Statistical properties proposed for blind classification OFDM modulation scheme. In Proceedings of the IEEE International Conference on Aerospace Electronics and Remote Sensing Technology, Yogyakarta, Indonesia, 13–14 November 2014; pp. 89–93. [Google Scholar]
- Shimbo, D.; Oka, I. A modulation classification using amplitude moments in OFDM systems. In Proceedings of the International Symposium On Information Theory & Its Applications, Taichung, Taiwan, 17–20 October 2010; pp. 288–293. [Google Scholar]
- Gupta, R.; Kumar, S.; Majhi, S. Blind Modulation Classification for Asynchronous OFDM Systems Over Unknown Signal Parameters and Channel Statistics. IEEE Trans. Veh. Technol. 2020, 69, 5281–5292. [Google Scholar] [CrossRef]
- Zhang, J.; Li, B. A new modulation identification scheme for OFDM in multipath rayleigh fading channel. In Proceedings of the International Symposium on Computer Science and Computational Technology, Shanghai, China, 20–22 December 2008; Volume 1, pp. 793–796. [Google Scholar]
- Zhu, Y.; Tian, B.; Ma, R.; Sun, Y.; An, J.; Yi, K.; Ren, Y. An OFDM modulation recognition algorithm based on spectrum analysis. In Proceedings of the 10th International Conference on Signal Processing Proceedings, Beijing, China, 24–28 October 2010; pp. 1557–1560. [Google Scholar]
- Ma, Y.; Gao, M.; Ye, Y.; Chen, W.; Wang, L.; Sha, Y.; Yan, Y. Modulation Format Identification for Adaptive Optical OFDM System. In Proceedings of the 24th OptoElectronics and Communications Conference (OECC) and International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar]
- Katayama, T.; Oka, I.; Ata, S. Modulation identification by general orthogonal modulations. In Proceedings of the International Conference on Advanced Technologies for Communications, Hanoi, Vietnam, 6–9 October 2008; pp. 12–15. [Google Scholar]
- Chen, J.; Kuo, Y.; Liu, X. Modulation identification for MIMO-OFDM signals. In Proceedings of the 2007 IET Conference on Wireless, Mobile and Sensor Networks (CCWMSN07), Shanghai, China, 12–14 December 2007. [Google Scholar]
- Li, H.; Bar-Ness, Y.; Abdi, A.; Somekh, O.S.; Su, W. OFDM modulation classification and parameters extraction. In Proceedings of the 1st International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Mykonos, Greece, 8–10 June 2006; pp. 1–6. [Google Scholar]
- Liu, Y.; Simeone, O.; Haimovich, A.M.; Su, W. Modulation classification for MIMO-OFDM signals via Gibbs sampling. In Proceedings of the IEEE 49th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 18–20 March 2015; pp. 1–6. [Google Scholar]
- Liu, Y.; Simeone, O.; Haimovich, A.M.; Su, W. Modulation classification for MIMO-OFDM signals via approximate Bayesian inference. IEEE Trans. Veh. Technol. 2016, 66, 268–281. [Google Scholar] [CrossRef] [Green Version]
- Pathy, A.K.; Kumar, A.; Gupta, R.; Kumar, S.; Majhi, S. Design and Implementation of Blind Modulation Classification for Asynchronous MIMO-OFDM System. IEEE Trans. Instrum. Meas. 2021, 70, 5504011. [Google Scholar] [CrossRef]
- Wong, M.D.; Ting, S.K.; Nandi, A.K. Naive Bayes classification of adaptive broadband wireless modulation schemes with higher order cumulants. In Proceedings of the 2nd International Conference on Signal Processing and Communication Systems, Gold Coast, Australia, 15–17 December 2008; pp. 1–5. [Google Scholar]
- El-Khamy, S.E.; Elsayed, H.A.; Rizk, M.M. C45. Classification of OFDM signals using higher order statistics and clustering techniques. In Proceedings of the 29th National Radio Science Conference (NRSC), Cairo, Egypt, 10–12 April 2012; pp. 541–549. [Google Scholar]
- Yuan, X.; Li, Y.; Gao, M.; Li, T.; Zhang, H. Automatic modulation classification for MIMO-OFDM systems with imperfect timing synchronization. In Proceedings of the IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Machida, W.; Ichijo, K.; Sugiura, Y.; Shimamura, T. Phase Correction for Automatic Modulation Classification Using Iterative Closest Point. In Proceedings of the International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Taipei, Taiwan, 3–6 December 2019; pp. 1–2. [Google Scholar]
- Zhang, Y.; Wu, G.; Wang, J.; Tang, Q. Wireless Signal Classification Based on High-Order Cumulants and Machine Learning. In Proceedings of the International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017; pp. 559–564. [Google Scholar]
- Dehri, B.; Besseghier, M.; Djebbar, A.B.; Dayoub, I. Blind digital modulation classification for STBC-OFDM system in presence of CFO and channels estimation errors. IET Commun. 2019, 13, 2827–2833. [Google Scholar] [CrossRef]
- Gu, Y.; Xu, S.; Zhou, J. Automatic Modulation Format Classification of USRP Transmitted Signals Based on SVM. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3712–3717. [Google Scholar]
- He, J.; Zhou, Y.; Shi, J.; Tang, Q. Modulation classification method based on clustering and gaussian model analysis for vlc system. IEEE Photonics Technol. Lett. 2020, 32, 651–654. [Google Scholar] [CrossRef]
- Gaohui, L.; Jiakun, C. Research on Modulation Recognition of OFDM Signal Based on Hierarchical Iterative Support Vector Machine. In Proceedings of the 2020 International Conference on Communications, Information System and Computer Engineering (CISCE), Kuala Lumpur, Malaysia, 3–5 July 2020; pp. 38–44. [Google Scholar]
- Al-Makhlasawy, R.M.; Elnaby, M.M.A.; El-Khobby, H.A.; El-Samie, F.E.A. Automatic modulation recognition in OFDM systems using cepstral analysis and a fuzzy logic interface. In Proceedings of the 8th International Conference on Informatics and Systems (INFOS), Giza, Egypt, 14–16 May 2012; pp. CC-56–CC-62. [Google Scholar]
- Li, Y.; Shao, G.; Wang, B. Automatic Modulation Classification Based on Bispectrum and CNN. In Proceedings of the IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 311–316. [Google Scholar]
- Hong, S.; Zhang, Y.; Wang, Y.; Gu, H.; Gui, G.; Sari, H. Deep Learning-Based Signal Modulation Identification in OFDM Systems. IEEE Access 2019, 7, 114631–114638. [Google Scholar] [CrossRef]
- Shi, J.; Hong, S.; Cai, C.; Wang, Y.; Huang, H.; Gui, G. Deep Learning-Based Automatic Modulation Recognition Method in the Presence of Phase Offset. IEEE Access 2020, 8, 42841–42847. [Google Scholar] [CrossRef]
- Hong, S.; Wang, Y.; Pan, Y.; Gu, H.; Liu, M.; Yang, J.; Gui, G. Convolutional neural network aided signal modulation recognition in OFDM systems. In Proceedings of the IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Meng, F.; Chen, P.; Wu, L.; Wang, X. Automatic modulation classification: A deep learning enabled approach. IEEE Trans. Veh. Technol. 2018, 67, 10760–10772. [Google Scholar] [CrossRef]
- AlNuaimi, D.H. AMC2-Pyramid: Intelligent Pyramidal Feature Engineering and Multi-Distance Decision Making for Automatic Multi-Carrier Modulation Classification. IEEE Access 2021, 9, 137560–137583. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans. Veh. Technol. 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- Park, M.C.; Han, D.S. Deep Learning-Based Automatic Modulation Classification With Blind OFDM Parameter Estimation. IEEE Access 2021, 9, 108305–108317. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, D.; Liu, J.; Xian, Y.; Wang, X. Improved deep neural network for OFDM signal recognition using hybrid grey wolf optimization. IEEE Access 2020, 8, 133622–133632. [Google Scholar] [CrossRef]
- Zhao, Z.; Wei, Z.; Wang, Z.; Zhang, Y.; Li, M.; Khan, F.N.; Fu, H. Modulation Format Recognition based on Transfer Learning for Visible Light Communication Systems. In Proceedings of the Optoelectronics and Communications Conference, Hong Kong, China, 3–7 July 2021; p. JS2B.12. [Google Scholar]
- Yin, J.; Guo, L.; Jiang, W.; Hong, S.; Yang, J. ShuffleNet-inspired lightweight neural network design for automatic modulation classification methods in ubiquitous IoT cyber-physical systems. Comput. Commun. 2021, 176, 249–257. [Google Scholar] [CrossRef]
- Kong, G.; Jung, M.; Koivunen, V. Waveform Classification in Radar-Communications Coexistence Scenarios. In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Zheng, Q.; Zhao, P.; Li, Y.; Wang, H.; Yang, Y. Spectrum interference-based two-level data augmentation method in deep learning for automatic modulation classification. Neural Comput. Appl. 2021, 33, 7723–7745. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, C.; Yan, W.; Ling, Q.; Wang, Y. Real-Time OFDM Signal Modulation Classification Based on Deep Learning and Software-Defined Radio. IEEE Commun. Lett. 2021, 25, 2988–2992. [Google Scholar] [CrossRef]
- Huynh-The, T.; Pham, Q.V.; Nguyen, T.V.; Pham, X.Q.; Kim, D.S. Deep Learning-based Automatic Modulation Classification for Wireless OFDM Communications. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 20–22 October 2021; pp. 47–49. [Google Scholar]
- Wang, F.; Wang, X. Fast and Robust Modulation Classification via Kolmogorov-Smirnov Test. IEEE Trans. Commun. 2010, 58, 2324–2332. [Google Scholar] [CrossRef]
- Mohammadkarimi, M.; Dobre, O.A. Blind identification of spatial multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov (KS) test. IEEE Commun. Lett. 2014, 18, 1711–1714. [Google Scholar] [CrossRef]
- Trees, V.; Harry, L. Detection, Estimation, and Modulation Theory-Part L-Detection, Estimation, and Linear Modulation Theory; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Azzouz, E.; Nandi, A.K. Automatic Modulation Recognition of Communication Signals; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hsue, S.Z.; Soliman, S.S. Automatic modulation classification using zero crossing. IEE Proc. Radar Signal Process. 1990, 137, 459–464, IET Digital Library. [Google Scholar] [CrossRef]
- Ramkumar, B. Automatic modulation classification for cognitive radios using cyclic feature detection. IEEE Circuits Syst. Mag. 2009, 9, 27–45. [Google Scholar] [CrossRef]
- Mobasseri, B.G. Digital modulation classification using constellation shape. Signal Process. 2000, 80, 251–277. [Google Scholar] [CrossRef]
- Lopatka, J.; Pedzisz, M. Automatic modulation classification using statistical moments and a fuzzy classifier. In Proceedings of the WCC 2000-ICSP 2000, 2000 5th International Conference on Signal Processing Proceedings, 16th World Computer Congress 2000, Beijing, China, 21–25 August 2000; Volume 3, pp. 1500–1506. [Google Scholar]
- Paris, B.P.; Orsak, G.C.; Chen, H.; Warke, N. Modulation classification in unknown dispersive environments. In Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 21–24 April 1997; Volume 5, pp. 3853–3856. [Google Scholar]
- Huo, X.; Donoho, D. A simple and robust modulation classification method via counting. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No. 98CH36181), Seattle, WA, USA, 15 May 1998; Volume 6, pp. 3289–3292. [Google Scholar]
- Dobre, O.A.; Bar-Ness, Y.; Su, W. Robust QAM modulation classification algorithm using cyclic cumulants. In Proceedings of the 2004 IEEE Wireless Communications and Networking Conference (IEEE Cat. No. 04TH8733), Atlanta, GA, USA, 21–25 March 2004; Volume 2, pp. 745–748. [Google Scholar]
- Ali, A.; Yangyu, F. Unsupervised feature learning and automatic modulation classification using deep learning model. Phys. Commun. 2017, 25, 75–84. [Google Scholar] [CrossRef]
- Muhlhaus, M.S.; Oner, M.; Dobre, O.A.; Jkel, H.U.; Jondral, F.K. Automatic modulation classification for MIMO systems using fourth-order cumulants. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012; pp. 1–5. [Google Scholar]
- Li, T.; Li, Y.; Dobre, O.A. Modulation Classification Based on Fourth-Order Cumulants of Superposed Signal in NOMA Systems. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2885–2897. [Google Scholar] [CrossRef]
- Chaudhari, M.S.; Kumar, S.; Gupta, R.; Kumar, M.; Majhi, S. Design and Testbed Implementation of Blind Parameter Estimated OFDM Receiver. IEEE Trans. Instrum. Meas. 2021. [Google Scholar] [CrossRef]
- Wang, C.X.; Di Renzo, M.; Stanczak, S.; Wang, S.; Larsson, E.G. Artificial intelligence enabled wireless networking for 5G and beyond: Recent advances and future challenges. IEEE Wirel. Commun. 2020, 27, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Zha, X.; Peng, H.; Qin, X.; Li, G.; Yang, S. A deep learning framework for signal detection and modulation classification. Sensors 2019, 19, 4042. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Am. Assoc. Adv. Sci. 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Shi, W.; Yang, Z.; Yang, J.; Gui, G. Behavioral modeling and linearization of wideband RF power amplifiers using BiLSTM networks for 5G wireless systems. IEEE Trans. Veh. Technol. 2019, 68, 10348–10356. [Google Scholar] [CrossRef]
- Gui, G.; Liu, F.; Sun, J.; Yang, J.; Zhou, Z.; Zhao, D. Flight delay prediction based on aviation big data and machine learning. IEEE Trans. Veh. Technol. 2019, 69, 140–150. [Google Scholar] [CrossRef]



| Acronym | Explanation |
|---|---|
| AI | Artificial Intelligence |
| ALRT | Average Probability Ratio Test |
| AMAP | Approximated Maximum a Posteriori |
| ASB | Amplitude Spectrum of Bispectrum |
| AWGN | Additive White Gaussian Noise |
| BAT | Bit Allocation Table |
| BFSF | Bi-Fold Signal Fortification |
| BICM-ID | Bit-Interleaved Coded Modulation Iterative Decoding |
| CNN | Convolutional Neural Network |
| CSI | Channel State Information |
| DBN | Deep Belief network |
| DVB | Digital Video Broadcasting |
| FB | Feature Based |
| FCP | False Classification Probability |
| FFT | Fast Fourier Transform |
| FNSF | Frequency Non-Selective Fading Channel |
| FPGA | Field Programmable Gate Array |
| FSF | Frequency Selective Fading Channel |
| FSST | Fourier Synchrosqueezing Transformation |
| GLRT | Generalized Likelihood Ratio Test |
| HGWO | Hybrid Grey Wolf Optimization |
| HLRT | Hybrid Likelihood Ratio Test |
| HOC | Higher Order Cumulant |
| HOS | Higher Order Statistics |
| ICI | Inter-carrier Interference |
| IQ | In-phase and Quadrature |
| IQL | Improved Q-learning |
| KNN | K-Nearest Neighbors |
| KS | Kolmogorov–Smirnov |
| LLR | Log-likelihood ratio |
| MAP | Maximum a Posteriori |
| MC | Modulation Classification |
| MFCC | Mel Frequency Cepstral Coefficient |
| MDNCC | Multi-Distance-Based Nearest Centroid Classifier |
| NOMA | Non-Orthogonal Multiple Access |
| OFDM-IM | Orthogonal Frequency Division Multiplexing with Index Modulation |
| PCC | Percentage of Correct Classification |
| Probability Density Function | |
| PER | Packet Error Ratio |
| PSO | Particle Swarm Optimization |
| SC | Single Carrier |
| SDR | Software-defined Radio |
| STFT | Short-Time Fourier Transform |
| TDD | Time Division Duplex |
| TF-HMS | Twin-Functioned Human Mental Search |
| UMP | Uniformly Most Powerful |
| VLC | Visible Light Communication |
| WOA | Whale Optimization Algorithm |
| WPS | Wavelet Packet Signals |
| WT | Wavelet Transform |
| Author(s) | Classifier(s) | Modulation(s) | Parameter(s) | Channel | Average PCC at 20 dB SNR |
|---|---|---|---|---|---|
| T. Yucek [45] | Sub-optimum algorithm | BPSK, QPSK, 16-QAM and 64-QAM | Imperfect noise variance | AWGN | 99.9% |
| J. Leinonen [46] | Quasi-log-likelihood Ratio Test based classifer | BPSK, QPSK, 16-QAM and 64-QAM | Known channel correlation between adjacent subchannels | AWGN | 98.50% |
| J. Zheng [47] | ALRT, HLRT and Energy-based detector | BPSK, QPSK, 8-PSK and 16-QAM | Known CSI, Known noise variance and unknown CSI | Rayleigh | 97.40% |
| T. Fang [48] | Expectation maximization block-quasi HLRT (EM-Block-QHLRT) | BPSK, QPSK, 8-PSK and 16-QAM | Unknown CSI and unknown noise power | Acoustic Rayleigh | 100% |
| M. Marey [49] | Iterative EM-based MC algorithm, bit-interleaved coded modulation iterative decoding (BICM-ID) scheme | QPSK, 64-QAM, 1024-QAM and 8194-QAM | Presence of synchronization error and known and unknown CSI | Rayleigh | 99% |
| Author(s) | Classifier(s) | Modulation(s) | Parameter(s) | Channel | Average PCC at 20 dB SNR |
|---|---|---|---|---|---|
| L. Häring [50] | MAP Algorithm, channel reciprocity in TDD systems | BPSK, 4-QAM, 16-QAM and 64-QAM | Perfect knowledge about data rate | Rayleigh | 99% |
| L. Häring [51] | ML and MAP Algorithm | no modulation, BPSK, QPSK, 16-QAM and 64-QAM | Perfect synchronization and unknown CSI | Rayleigh | 99% |
| L. Häring [52] | Simplified MAP algorithm that utilized frame structure, channel reciprocity, total number of transmitted data | no modulation, BPSK, QPSK,16-QAM and 64-QAM | Perfect knowledge about data rate | AWGN | 100% |
| L. Häring [53] | Improved Approximated MAP Algorithm | QPSK, 16-QAM and 64-QAM | Perfect synchronization | - | 79.5% |
| L. Häring [54] | Signalling-assisted modulation classifier | M-QAM | Known CSI, knowledge about total number of loaded bits and coding rate | AWGN | 98.5% |
| L. Häring [55] | Jointly optimizes the bit loading algorithm | M-QAM | Perfect synchronization and knowledge about signalling | AWGN | 99% |
| L. Häring [56] | Influence of imperfect reciprocity | IEEE 802.11a/n | Unknown CSI and knowledge about total number of loaded bits | Rayleigh | 100% |
| C. Husmann [57] | MAP Algorithm | BPSK, QPSK, 16-QAM and 64-QAM | Perfect time and frequency synchronization | AWGN | 97.5% |
| S. Bahrani [58] | Improved Approximated MAP Algorithm, channel prediction method | BPSK, QPSK, 16-QAM 64-QAM and no modulation | Perfect synchronization and unknown CSI | AWGN | 98% |
| M. Karabacak [59] | Adaptive Pilot Based | BPSK, QPSK, 16-QAM and 64-QAM | Perfect synchronization and known CSI | AWGN | 99.8% |
| S. bahrani [60] | Rate adaptive (RA) bit loading algorithm | BPSK, QPSK, 16-QAM and no modulation | Perfect synchronization and unknown CSI | Rayleigh | 100% |
| Author(s) | Feature(s) | Modulation(s) | Parameter(s) | Channel | Decision-Making Approaches | Average PCC at 20 dB SNR |
|---|---|---|---|---|---|---|
| A. D. Pambudi [61] | Mean, Variance, Skewness, Kurtosis and Moment Order | QPSK,16-QAM and 64-QAM | - | Rayleigh | Threshold based technique | 91% |
| D. Shimbo [62] | Amplitude, Moments and Correlation | 16-QAM and 64-QAM | Prior knowledge about CFO | AWGN | Threshold based technique | 89% |
| R. Gupta [63] | Using discrete Fourier transform (DFT) and normalized fourth-order cumulants | BPSK, QPSK, MSK, OQPSK, and 16-QAM | Unknown Signal Parameters, unknown CSI and imperfect synchronization | Rayleigh | Likelihood ratio test | 97.5% |
| J. Zhang [64] | Wavelet transform (WT), Transient characteristics | 4-FSK, QPSK, 16-QAM and OFDM | Unknown Signal Parameters | Rayleigh | - | 100% |
| Y. Zhu [65] | Kurtosis coefficient, Power spectral parameter, Energy distribution parameter | 2-ASK, 4-ASK, 2-FSK, 4-FSK and OFDM | Unknown symbol rate and carrier frequency | AWGN, FNSF, FSF and Rayleigh | Threshold based technique | 97% |
| Y. Ma [66] | Constellation cluster, number of cluster center | QPSK, 8-QAM, 16-QAM, 32-QAM and 64-QAM | Rotation plane and angle | AWGN | Peak-density clustering algorithm | 87.5% |
| Tomoya [67] | Identification estimation method, Modulation parameters of rotation planes and angles | OFDM, CDMA, a block of QAM and so on | - | AWGN | - | 92.5% |
| J. Chen [68] | Inter-class identification, Higher order cumulants | OFDM, 2-FSK, 4-FSK, 8-FSK, BPSK, QPSK, 8-PSK, 16-QAM, 32-QAM and 64-QAM | Perfect CSI | Rayleigh | Threshold based technique | 100% |
| H. Li [69] | Empirical Distribution Function-Based Gaussian Test | M-QAM | Unknown symbol duration, cyclic prefix duration and number of subcarriers | AWGN | - | 95% |
| Y. Liu [70] | Latent Dirichlet Bayesian network, Gibbs sampling method | QPSK, 8-PSK and 16-QAM | Imperfect CSI and unknown SNR | Flat fading | - | 97.5% |
| Y. Liu [71] | Optimal Bayesian Method, latent Dirichlet model, mean field variation inference | QPSK, 8-PSK, 16-QAM, and 16-PSK | Imperfect CSI and unknown SNR | Flat fading | - | 97% |
| A.K. Pathy [72] | Using DFT and normalized fourth-order and sixth-order cumulants | BPSK, QPSK, MSK, OQPSK, and 16-QAM | Unknown Signal Parameters, unknown CSI and imperfect synchronization | Rayleigh | Likelihood ratio test | 97% |
| Author(s) | Classifier(s) | Modulation(s) | Parameter(s) | Channel(s) | Average PCC at 20 dB SNR |
|---|---|---|---|---|---|
| M.L.D. Wong [73] | Optimize Shannon’s channel capacity, Naive Bayes classifier | BPSK, QPSK, 16-QAM and 64-QAM | Perfect synchronization | AWGN | 96.8% |
| S. E. El-Khamy [74] | Higher order moments and cumulants, Fuzzy K-Means and Fuzzy C-means | BPSK, QPSK, 16 QAM, and 64 QAM | - | Rayleigh | 100% |
| X. Yuan [75] | Higher-order cumulants, random forest based MC algorithm | QPSK, 16-QAM and 64-QAM | Imperfect time synchronization | Frequency- selective | 100% |
| W. Machid [76] | Least squares (LS) method and iterative closest point (ICP) | BPSK, QPSK, 16-QAM, and 64-QAM | Unknown noise variance and CSI | Flat fading | 97.5% |
| Y. Zhang [77] | High order cumulants, Decision Tree classifier | BPSK, QPSK, GFSK, 16-QAM, 64-QAM and OFDM | Presence of timing offset | Flat fading | 99.5% |
| B. Dehri [78] | Higher order statistics, pattern recognition methods, ANN or SVM, or RFC or KNN | QPSK and 16-QAM | Presence of CFO and Imperfect CSI | Rayleigh | 100% |
| Y. Gu [79] | Peaks in the distribution of amplitude, the variance of the amplitude, the variance of the phase, and the variance of the spectrum, SVM classifier | BPSK, QPSK, 16-QAM, 64-QAM, 256-QAM and GMSK | Unknown CFO | AWGN | 100% |
| J. He [80] | Clustering and Gaussian model | QPSK, 16-QAM, 64-QAM | - | AWGN | 100% |
| L. Gaohui [81] | High order cumulants and bi-spectral envelope peaks, hierarchical iterative SVM classifier model | M-QAM, MFSK and MPSK | Perfect synchronization | Rayleigh | 100% |
| Author(s) | Classifier(s) | Modulation(s) | Parameter(s) | Channel(s) | Average PCC at 20 dB SNR |
|---|---|---|---|---|---|
| R. M. Al-Makhlasawy [82] | Mel Frequency Cepstral Coefficients (MFCCs) and multi-layer feed -forward neural network | QPSK, 8-QAM, 16-QAM, 32-QAM, 64-QAM and 128-QAM | Perfect synchronization | AWGN | 100% |
| Y. Li [83] | Bispectrum and CNN Alexnet model | BPSK, 2-ASK, 2-FSK, 4-FSK, 8-FSK, LFM, and OFDM | - | AWGN | 97.5% |
| S. Hong [84] | CNN with dropout layer | BPSK, QPSK, 8-PSK, 16-QAM and 64-QAM | Perfect synchronization | Rician fading | 99% |
| J. Shi [85] | CNN, ReLU and PReLu activation | BPSK, QPSK, 8-PSK, and 16-QAM | Presence of phase offset and imperfect CSI | AWGN | 100% |
| S. Hong [86] | CNN | BPSK, QPSK, 4-PAM, 8-PSK, and 16-QAM | Perfect synchronization | Rician fading | 97.5% |
| F. Meng [87] | CNN with two step training, Transfer learning | BPSK, QPSK, 8-PSK, 16-PSK, 16-QAM, 32-PSK and 64-QAM | Unknown CFO and unknown SNR | Time invariant and frequency non-selective | 100% |
| D. H. AlNuaimi [88] | GaFP-Net, TF-HMS, MDNC, and IQL | QPSK, BPSK, DPSK, ASK, FSK, 16-QAM, 32-QAM, 64-QAM, and 128-QAM | Unknown CFO | AWGN | 86% |
| Z. Zhang [89] | CNN-LSTM | BPSK, QPSK, 8-PSK, AM-DSB, AM-SSB, CPFSK, GFSK, WBFM, 4-PAM, 16-QAM, and 64-QAM | Presence of CFO and STO | Rayleigh | 91% |
| M.C. Park [90] | IQ and FFT window bank (FWB), CNN-LSTM-based classifier | QPSK, 16-QAM, 32-QAM, and 64-QAM | - | Rayleigh | 98.5% |
| Y. Zhang [91] | Mixed order moment, hybrid grey wolf optimization (HGWO) algorithm, DNN-based classifier | QPSK, 16-QAM, 32-QAM, and 64-QAM | Presence of CFO and STO | Rayleigh | 100% |
| Z. Zhao [92] | AlexNet/GoogLeNet- TL-based classifier | BPSK, QPSK, 8-QAM, 16-QAM, 32-QAM and 64-QAM | - | AWGN | 100% |
| J. Yin [93] | Lightweight CNN (LCNN)-based Shuffle MC, FFT, regularization | BPSK, QPSK, 8-PSK, 16-QAM | - | Rician fading | 100% |
| G. Kong [94] | Fourier synchrosqueezing transformation (FSST), Independent component analysis (ICA), hierarchical CNN-based MC | 16-QAM, 64-QAM, and 256-QAM | Perfect Synchronization | Rayleigh | 90% |
| Q. Zheng [95] | Spectrum interference-based two-level data augmentation method, deep CNN | BPSK, QPSK, 8-PSK, 16-QAM, 64-QAM, GFSK, CPFSK, 4-PAM, WBFM, AM-SSB, and AM-DSB | - | Rayleigh | 89.3% |
| T. Huynh-The [97] | CNN with integrated attention and residual connections | BPSK, QPSK, 8-PSK, and 16-QAM | Presence of CFO | Rayleigh | 88% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Majhi, S.; Gui, G.; Wu, H.-C.; Yuen, C. A Survey of Blind Modulation Classification Techniques for OFDM Signals. Sensors 2022, 22, 1020. https://doi.org/10.3390/s22031020
Kumar A, Majhi S, Gui G, Wu H-C, Yuen C. A Survey of Blind Modulation Classification Techniques for OFDM Signals. Sensors. 2022; 22(3):1020. https://doi.org/10.3390/s22031020
Chicago/Turabian StyleKumar, Anand, Sudhan Majhi, Guan Gui, Hsiao-Chun Wu, and Chau Yuen. 2022. "A Survey of Blind Modulation Classification Techniques for OFDM Signals" Sensors 22, no. 3: 1020. https://doi.org/10.3390/s22031020
APA StyleKumar, A., Majhi, S., Gui, G., Wu, H.-C., & Yuen, C. (2022). A Survey of Blind Modulation Classification Techniques for OFDM Signals. Sensors, 22(3), 1020. https://doi.org/10.3390/s22031020










