Fast Iterative Shrinkage-Thresholding Algorithm with Continuation for Brain Injury Monitoring Imaging Based on Electrical Impedance Tomography
Abstract
1. Introduction
2. Methods
2.1. DLS Algorithm for Brain EIT
2.2. SB Algorithm for Brain EIT
2.3. FISTA Algorithm for Brain EIT
| Algorithm 1: FISTA for EIT |
| Inputs: A Lipschitz constant , , , and |
| Set: , , |
| while convergence criteria not satisfied, do |
| update using Equation (11); |
| update using Equation (12); |
| end |
| Outputs: |
2.4. FISTA-C Algorithm for Brain EIT
| Algorithm 2: FISTA-C for EIT |
| Inputs: A Lipschitz constant , , , , and |
| Set: , , , |
| and |
| while convergence criteria not satisfied, do |
| update using Equation (11); |
| update using Equation (12); |
| update using Equation (14); |
| end |
| Outputs: |
2.5. Experimental Framework
2.5.1. Evaluation Metrics for Image Quality
2.5.2. Numerical Simulations
2.5.3. Head Phantom Experiments
3. Results
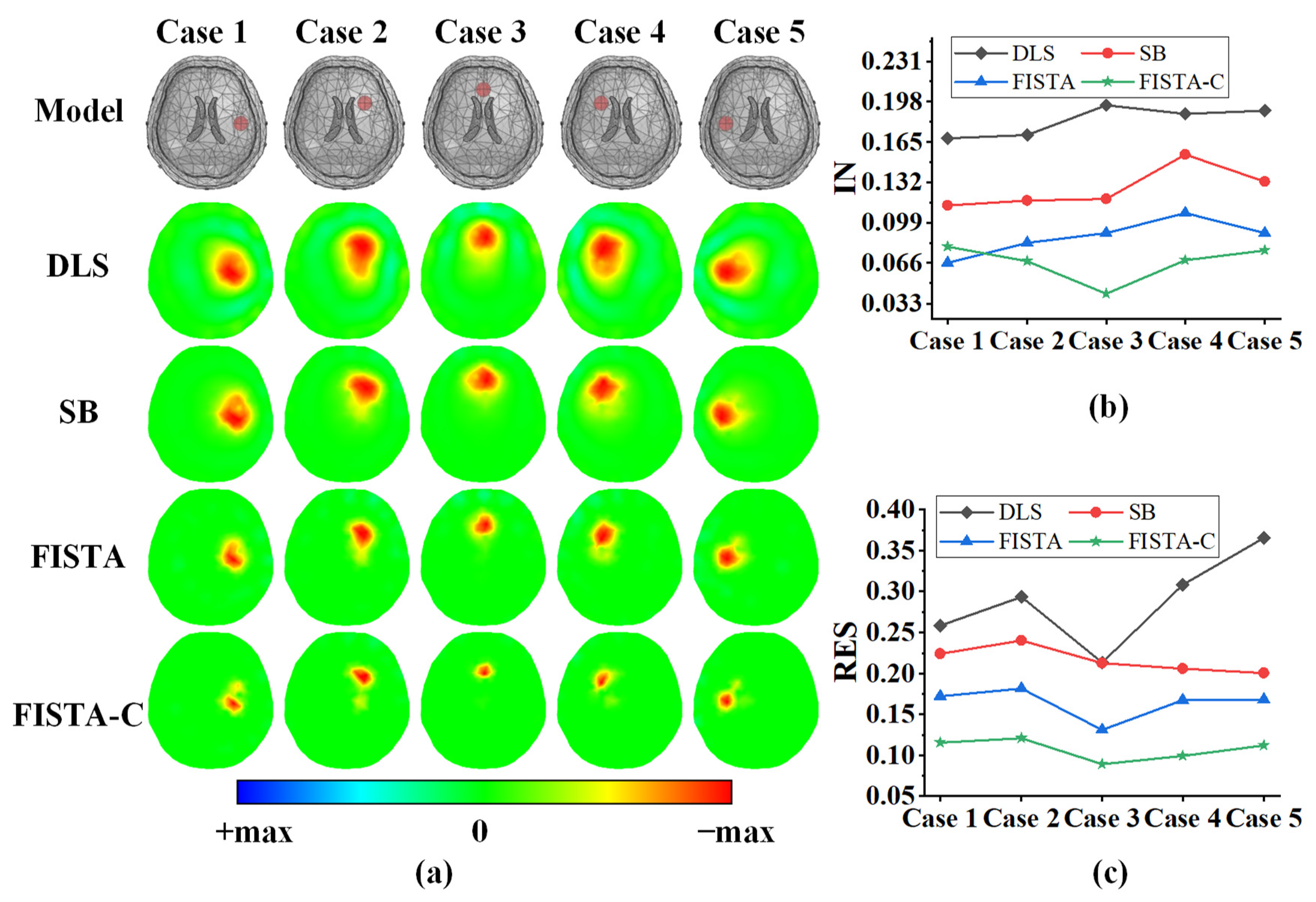
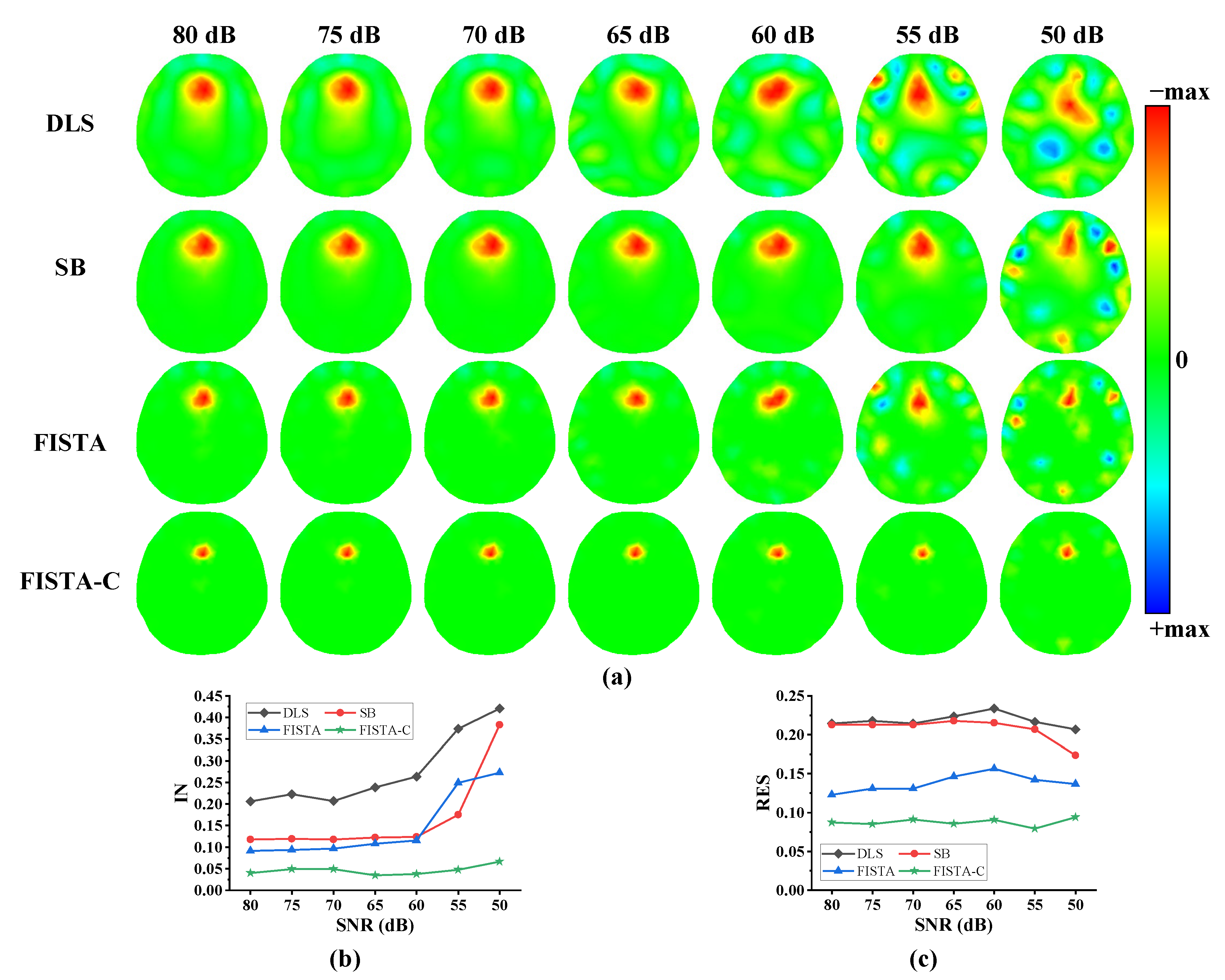
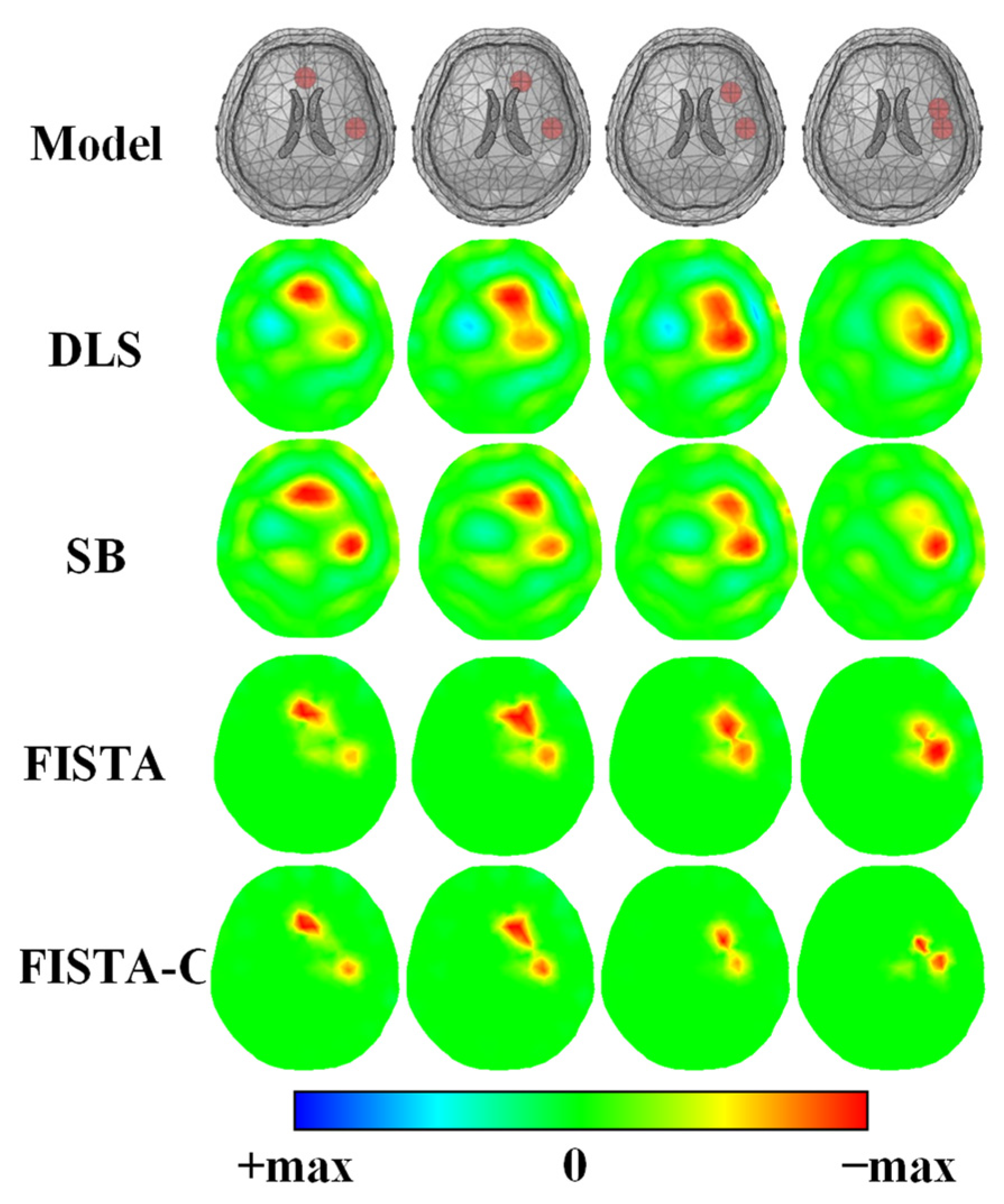
3.1. Numerical Simulations
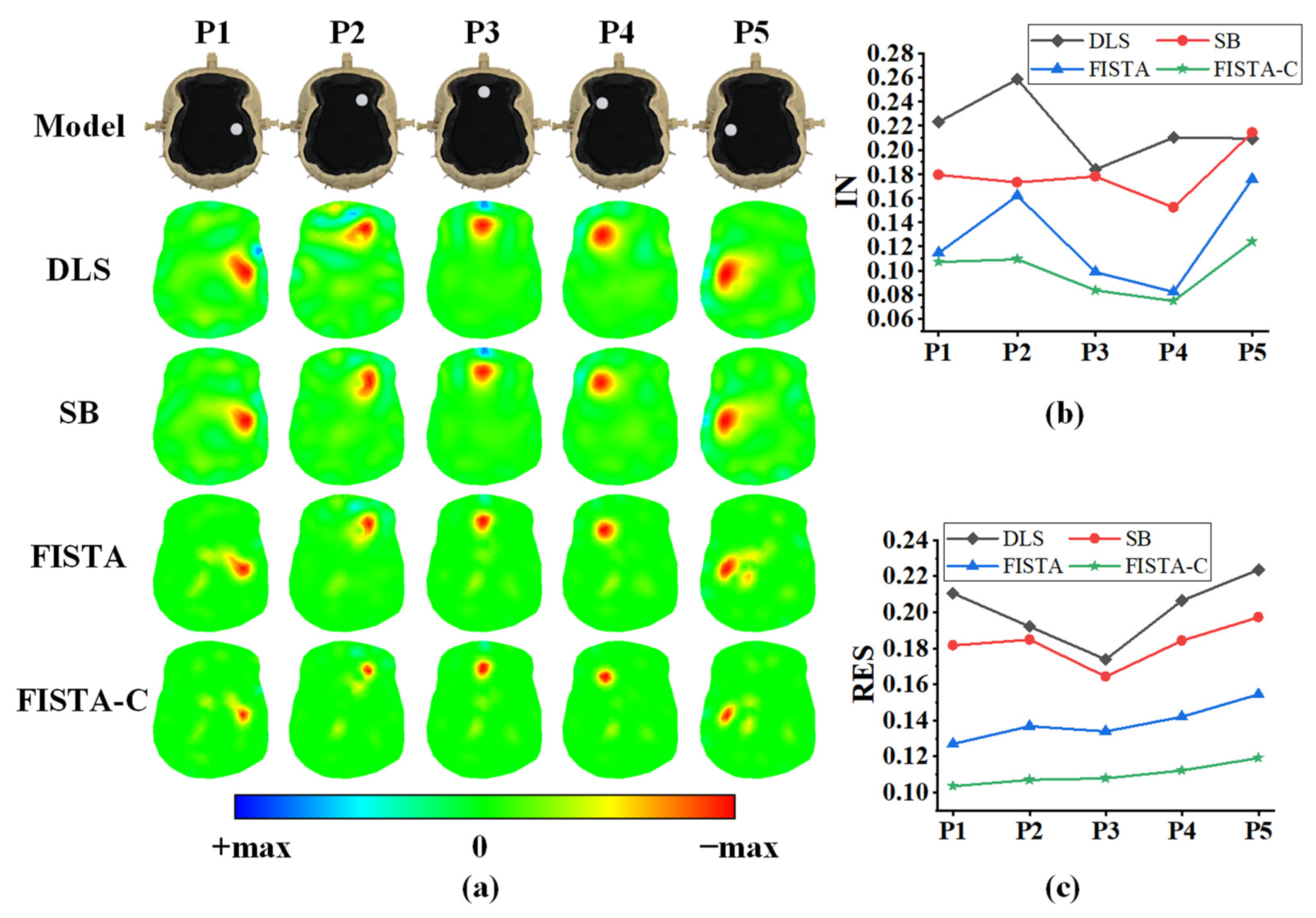
3.2. Head Phantom Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Zeng, L.; Hu, Z. Progressing haemorrhagic stroke: Categories, causes, mechanisms and managements. J. Neurol. 2014, 261, 2061–2078. [Google Scholar] [CrossRef]
- McDermott, B.; Elahi, A.; Santorelli, A.; O’halloran, M.; Avery, J.; Porter, E. Multi-frequency symmetry difference electrical impedance tomography with machine learning for human stroke diagnosis. Physiol. Meas. 2020, 41, 075010. [Google Scholar] [CrossRef]
- Menden, T.; Alcaín, G.B.; Stevenson, A.T.; Pollock, R.D.; Tank, H.; Hodkinson, P.; Jolley, C.; Smith, T.G.; Leonhardt, S.; Walter, M. Dynamic lung behavior under high G acceleration monitored with electrical impedance tomography. Physiol. Meas. 2021, 42, 094001. [Google Scholar] [CrossRef]
- Hsu, H.J.; Chang, H.T.; Zhao, Z.; Wang, P.H.; Zhang, J.H.; Chen, Y.S.; Frerichs, I.; Möller, K.; Fu, F.; Hsu, H.S.; et al. Positive end-expiratory pressure titration with electrical impedance tomography and pressure-volume curve: A randomized trial in moderate to severe ARDS. Physiol. Meas. 2021, 42, 014002. [Google Scholar] [CrossRef] [PubMed]
- Hentze, B.; Muders, T.; Hoog Antink, C.; Putensen, C.; Larsson, A.; Hedenstierna, G.; Walter, M.; Leonhardt, S. A model-based source separation algorithm for lung perfusion imaging using electrical impedance tomography. Physiol. Meas. 2021, 42, 084001. [Google Scholar] [CrossRef] [PubMed]
- Haris, K.; Vogt, B.; Strodthoff, C.; Pessoa, D.; Cheimariotis, G.A.; Rocha, B.; Petmezas, G.; Weiler, N.; Paiva, R.P.; de Carvalho, P.; et al. Identification and analysis of stable breathing periods in electrical impedance tomography recordings. Physiol. Meas. 2021, 42, 064003. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.Y.; Li, Q.; Yu, X.; Zhang, C.X.; Li, Y.; Niu, G.Y.; Tong, Z.H.; Xi, J.N.; Zhao, Z. Ventilation improvement after pneumonia treatment evaluated with electrical impedance tomography: An observational study. Physiol. Meas. 2021, 42, 104001. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Zhang, J.S.; Chen, Y.T.; Chang, H.T.; Hsu, Y.L.; Frerichs, I.; Adler, A. The use of electrical impedance tomography for individualized ventilation strategy in COVID-19: A case report. BMC Pulm. Med. 2021, 21, 38. [Google Scholar] [CrossRef]
- Hu, J.; Soleimani, M. Combining multiple boundary shapes in deformable EIT a potential use in breast imaging. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Murphy, E.K.; Mahara, A.; Wu, X.; Halter, R.J. Phantom experiments using soft-prior regularization EIT for breast cancer imaging. Physiol. Meas. 2017, 38, 1262–1277. [Google Scholar] [CrossRef]
- Dai, M.; Liu, X.C.; Li, H.T.; Xu, C.H.; Yang, B.; Wang, H.; Shi, X.T.; Dong, X.Z.; Fu, F. EIT imaging of intracranial hemorrhage in rabbit models is influenced by the intactness of cranium. BioMed Res. Int. 2018, 2018, 1321862. [Google Scholar] [CrossRef]
- Cao, L.; Li, H.; Fu, D.; Liu, X.; Ma, H.; Xu, C.; Dong, X.; Yang, B.; Fu, F. Real-time imaging of infarction deterioration after ischemic stroke in rats using electrical impedance tomography. Physiol. Meas. 2020, 41, 015004. [Google Scholar] [CrossRef]
- Dowrick, T.; Blochet, C.; Holder, D. In Vivo bioimpedance changes during haemorrhagic and ischaemic stroke in rats: Towards 3D stroke imaging using electrical impedance tomography. Physiol. Meas. 2016, 37, 765–784. [Google Scholar] [CrossRef]
- Ke, X.Y.; Hou, W.; Huang, Q.; Hou, X.; Bao, X.Y.; Kong, W.X.; Li, C.X.; Qiu, Y.Q.; Hu, S.Y.; Dong, L.H. Advances in electrical impedance tomography-based brain imaging. Mil. Med. Res. 2022, 9, 10. [Google Scholar] [CrossRef]
- Fu, F.; Li, B.; Dai, M.; Hu, S.J.; Li, X.; Xu, C.H.; Wang, B.; Yang, B.; Tang, M.X.; Dong, X.Z.; et al. Use of electrical impedance tomography to monitor regional cerebral edema during clinical dehydration treatment. PLoS ONE 2014, 9, e113202. [Google Scholar] [CrossRef]
- Yang, B.; Li, B.; Xu, C.; Hu, S.; Dai, M.; Xia, J.; Luo, P.; Shi, X.; Zhao, Z.; Dong, X.; et al. Comparison of electrical impedance tomography and intracranial pressure during dehydration treatment of cerebral edema. NeuroImage Clin. 2019, 23, 101909. [Google Scholar] [CrossRef]
- Li, H.; Ma, H.; Yang, B.; Xu, C.; Cao, L.; Dong, X.; Fu, F. Automatic evaluation of mannitol dehydration treatments on controlling intracranial pressure using electrical impedance tomography. IEEE Sens. J. 2020, 20, 4832–4839. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, D.; Liu, B.; Jin, Z.; Duan, W.; Dong, X.; Fu, F.; Yu, S.; Shi, X. Noninvasive cerebral imaging and monitoring using electrical impedance tomography during total aortic arch replacement. J. Cardiothorac. Vasc. Anesth. 2018, 32, 2469–2476. [Google Scholar] [CrossRef]
- Liu, B.; Dong, X.; Fu, F.; Shi, X.; Jin, Z.; Duan, W.; Ren, K.; Yu, S. Non-invasive imaging the relative changes in cerebral blood volume during total aortic-arch replacement using electrical impedance tomography. In Proceedings of the Third International Symposium on Image Computing and Digital Medicine—ISICDM, Xi’an, China, 24–26 August 2019; pp. 308–313. [Google Scholar] [CrossRef]
- Xu, C.; Dai, M.; You, F.; Shi, X.; Fu, F.; Liu, R.; Dong, X. An optimized strategy for real-time hemorrhage monitoring with electrical impedance tomography. Physiol. Meas. 2011, 32, 585–598. [Google Scholar] [CrossRef]
- Yang, L.; Dai, M.; Xu, C.; Zhang, G.; Li, W.; Fu, F.; Shi, X.; Dong, X. The frequency spectral properties of electrode-skin contact impedance on human head and its frequency-dependent effects on frequency-difference EIT in stroke detection from 10Hz to 1MHz. PLoS ONE 2017, 12, e0170563. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Ma, H.; Xu, C.; Yang, B.; Dai, M.; Dong, X.; Fu, F. An iterative damped least-squares algorithm for simultaneously monitoring the development of hemorrhagic and secondary ischemic lesions in brain injuries. Med. Biol. Eng. Comput. 2019, 57, 1917–1931. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Cao, L.; Xu, C.-H.; Liu, B.; Yang, B.; Dong, X.; Fu, F. Optimized method for electrical impedance tomography to image large area conductive perturbation. IEEE Access 2019, 7, 140734–140742. [Google Scholar] [CrossRef]
- Cao, L.; Li, H.; Xu, C.; Dai, M.; Ji, Z.; Shi, X.; Dong, X.; Fu, F.; Yang, B. A novel time-difference electrical impedance tomography algorithm using multi-frequency information. Biomed. Eng. OnLine 2019, 18, 84. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Li, F.; Wang, J.; Duan, X.; Li, X. Towards a combination of low rank and sparsity in EIT imaging. IEEE Access 2019, 7, 156054–156064. [Google Scholar] [CrossRef]
- Liu, S.; Jia, J.; Zhang, Y.D.; Yang, Y. Image reconstruction in electrical impedance tomography based on structure-aware sparse bayesian learning. IEEE Trans. Med. Imaging 2018, 37, 2090–2102. [Google Scholar] [CrossRef]
- Ye, J.; Wang, H.; Yang, W. Image reconstruction for electrical capacitance tomography based on sparse representation. IEEE Trans. Instrum. Meas. 2015, 64, 89–102. [Google Scholar] [CrossRef]
- Liu, D.; Khambampati, A.K.; Du, J. A parametric level set method for electrical impedance tomography. IEEE Trans. Med. Imaging 2018, 37, 451–460. [Google Scholar] [CrossRef]
- Liu, D.; Gu, D.; Smyl, D.; Deng, J.; Du, J. B-spline level set method for shape reconstruction in electrical impedance tomography. IEEE Trans. Med. Imaging 2020, 39, 1917–1929. [Google Scholar] [CrossRef]
- Liu, D.; Gu, D.; Smyl, D.; Deng, J.; Du, J. Shape reconstruction using Boolean operations in electrical impedance tomography. IEEE Trans. Med. Imaging 2020, 39, 2954–2964. [Google Scholar] [CrossRef]
- Liu, D.; Gu, D.; Smyl, D.; Khambampati, A.K.; Deng, J.; Du, J. Shape-driven EIT reconstruction using Fourier representations. IEEE Trans. Med. Imaging 2021, 40, 481–490. [Google Scholar] [CrossRef]
- Lin, Z.; Guo, R.; Zhang, K.; Li, M.; Yang, F.; Xu, S.; Abubakar, A. Neural network-based supervised descent method for 2D electrical impedance tomography. Physiol. Meas. 2020, 41, 074003. [Google Scholar] [CrossRef]
- Chen, Z.; Xiang, J.; Bagnaninchi, P.O.; Yang, Y. MMV-net: A multiple measurement vector network for multifrequency electrical impedance tomography. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Capps, M.; Mueller, J.L. Reconstruction of organ boundaries with deep learning in the D-bar method for electrical impedance tomography. IEEE Trans. Biomed. Eng. 2021, 68, 826–833. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, X.; Zhang, W.; Dai, M.; Chen, C.; Dong, X.; Liu, R.; Xu, C. Adaptive threshold split Bregman algorithm based on magnetic induction tomography for brain injury monitoring imaging. Physiol. Meas. 2021, 42, 065004. [Google Scholar] [CrossRef]
- Lu, L.; Tong, G.; Guo, G.; Liu, S. Split Bregman iteration based reconstruction algorithm for electrical capacitance tomography. Trans. Inst. Meas. Control 2019, 41, 2389–2399. [Google Scholar] [CrossRef]
- Zou, J.; Li, H.; Liu, G. Split Bregman algorithm for structured sparse reconstruction. IEEE Access 2018, 6, 21560–21569. [Google Scholar] [CrossRef]
- Wang, J.; Ma, J.; Han, B.; Li, Q. Split Bregman iterative algorithm for sparse reconstruction of electrical impedance tomography. Signal Process. 2012, 92, 2952–2961. [Google Scholar] [CrossRef]
- Adler, A.; Boyle, A. Electrical impedance tomography: Tissue properties to image measures. IEEE Trans. Biomed. Eng. 2017, 64, 2494–2504. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Babapour, S.; Lakestani, M.; Fatholahzadeh, A. AFISTA: Accelerated FISTA for sparse signal recovery and compressive sensing. Multimed. Tools Appl. 2021, 80, 20707–20731. [Google Scholar] [CrossRef]
- Adler, A.; Arnold, J.H.; Bayford, R.; Borsic, A.; Brown, B.; Dixon, P.; Faes, T.J.; Frerichs, I.; Gagnon, H.; Gärber, Y.; et al. GREIT: A unified approach to 2D linear EIT reconstruction of lung images. Physiol. Meas. 2009, 30, S35–S55. [Google Scholar] [CrossRef] [PubMed]
- Malone, E.; Sato Dos Santos, G.S.; Holder, D.; Arridge, S. Multifrequency electrical impedance tomography using spectral constraints. IEEE Trans. Med. Imaging 2014, 33, 340–350. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Wu, Y.; Wang, M.; Tian, Z.; Kong, X.; He, X. Sparse image reconstruction of intracerebral hemorrhage with electrical impedance tomography. J. Med. Imaging 2021, 8, 014501. [Google Scholar] [CrossRef]
- Tang, C.; You, F.; Cheng, G.; Gao, D.; Fu, F.; Yang, G.; Dong, X. Correlation between structure and resistivity variations of the live human skull. IEEE Trans. Biomed. Eng. 2008, 55, 2286–2292. [Google Scholar] [CrossRef]
- Gilad, O.; Horesh, L.; Holder, D.S. A modelling study to inform specification and optimal electrode placement for imaging of neuronal depolarization during visual evoked responses by electrical and magnetic detection impedance tomography. Physiol. Meas. 2009, 30, S201–S224. [Google Scholar] [CrossRef]
- Shi, X.; Dong, X.; Shuai, W.; You, F.; Fu, F.; Liu, R. Pseudo-polar drive patterns for brain electrical impedance tomography. Physiol. Meas. 2006, 27, 1071–1080. [Google Scholar] [CrossRef]
- Xu, C.; Dong, X.; Shi, X.; Fu, F.; Shuai, W.; Liu, R.; You, F. Comparison of drive patterns for single current source EIT in computational phantom. In Proceedings of the 2nd International Conference on Bioinformatics and Biomedical Engineering, Shanghai, China, 16–18 May 2008; Volume 2008, pp. 1500–1503. [Google Scholar] [CrossRef]
- Shi, X.; Li, W.; You, F.; Huo, X.; Xu, C.; Ji, Z.; Liu, R.; Liu, B.; Li, Y.; Fu, F.; et al. High-precision electrical impedance tomography data acquisition system for brain imaging. IEEE Sens. J. 2018, 18, 5974–5984. [Google Scholar] [CrossRef]
- Li, J.B.; Tang, C.; Dai, M.; Liu, G.; Shi, X.T.; Yang, B.; Xu, C.H.; Fu, F.; You, F.S.; Tang, M.X.; et al. A new head phantom with realistic shape and spatially varying skull resistivity distribution. IEEE Trans. Biomed. Eng. 2014, 61, 254–263. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, T.; Liu, X.; Yang, B.; Dai, M.; Shi, X.; Dong, X.; Fu, F.; Xu, C. Target adaptive differential iterative reconstruction (TADI): A robust algorithm for real-time electrical impedance tomography. IEEE Access 2021, 9, 141999–142011. [Google Scholar] [CrossRef]
- Lee, K.; Woo, E.J.; Seo, J.K. A fidelity-embedded regularization method for robust electrical impedance tomography. IEEE Trans. Med. Imaging 2018, 37, 1970–1977. [Google Scholar] [CrossRef]
- Paldanius, A.; Dekdouk, B.; Toivanen, J.; Kolehmainen, V.; Hyttinen, J. Sensitivity analysis highlights the importance of accurate head models for electrical impedance tomography monitoring of intracerebral hemorrhagic stroke. IEEE Trans. Biomed. Eng. 2022, 69, 1491–1501. [Google Scholar] [CrossRef]
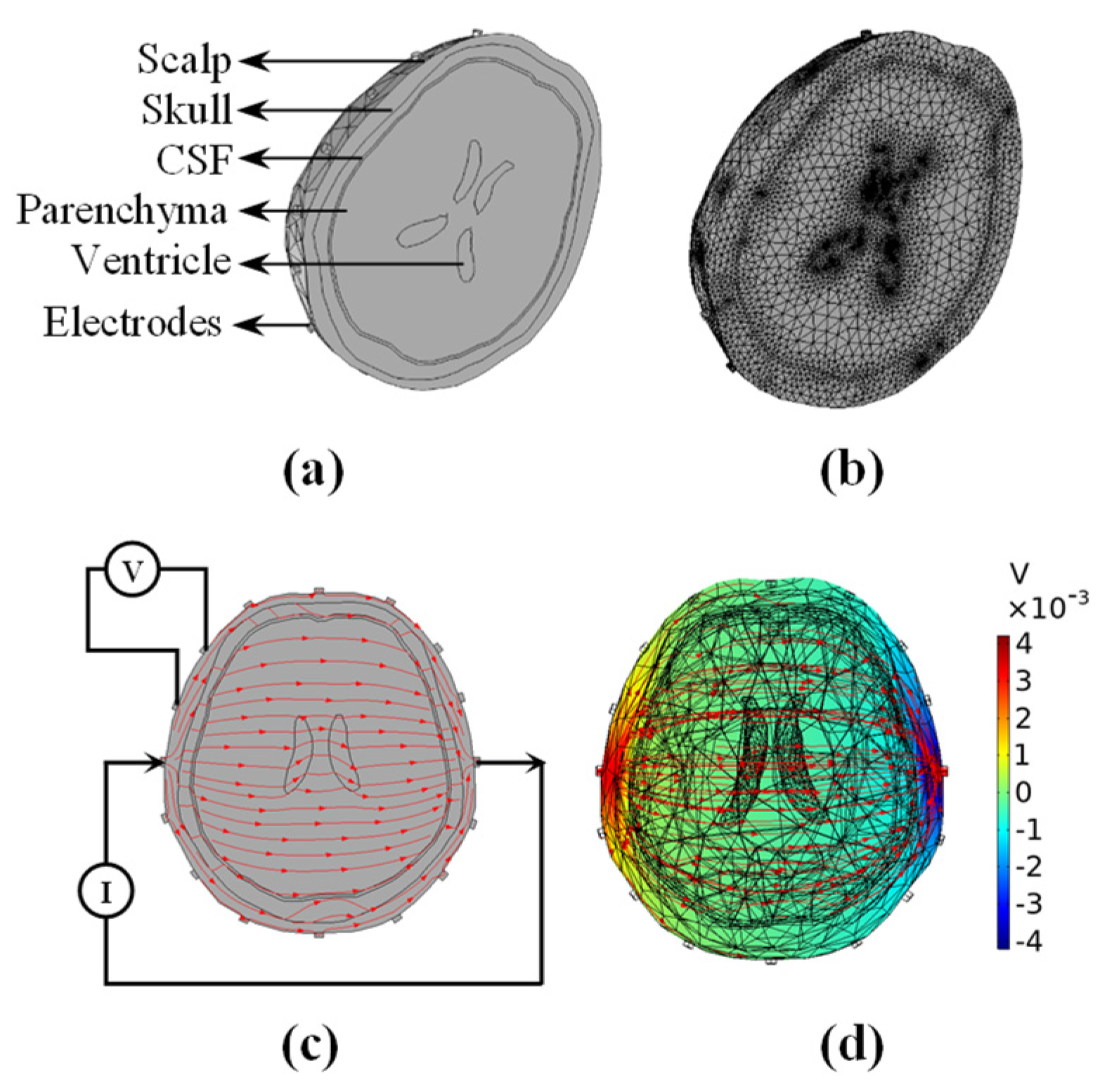
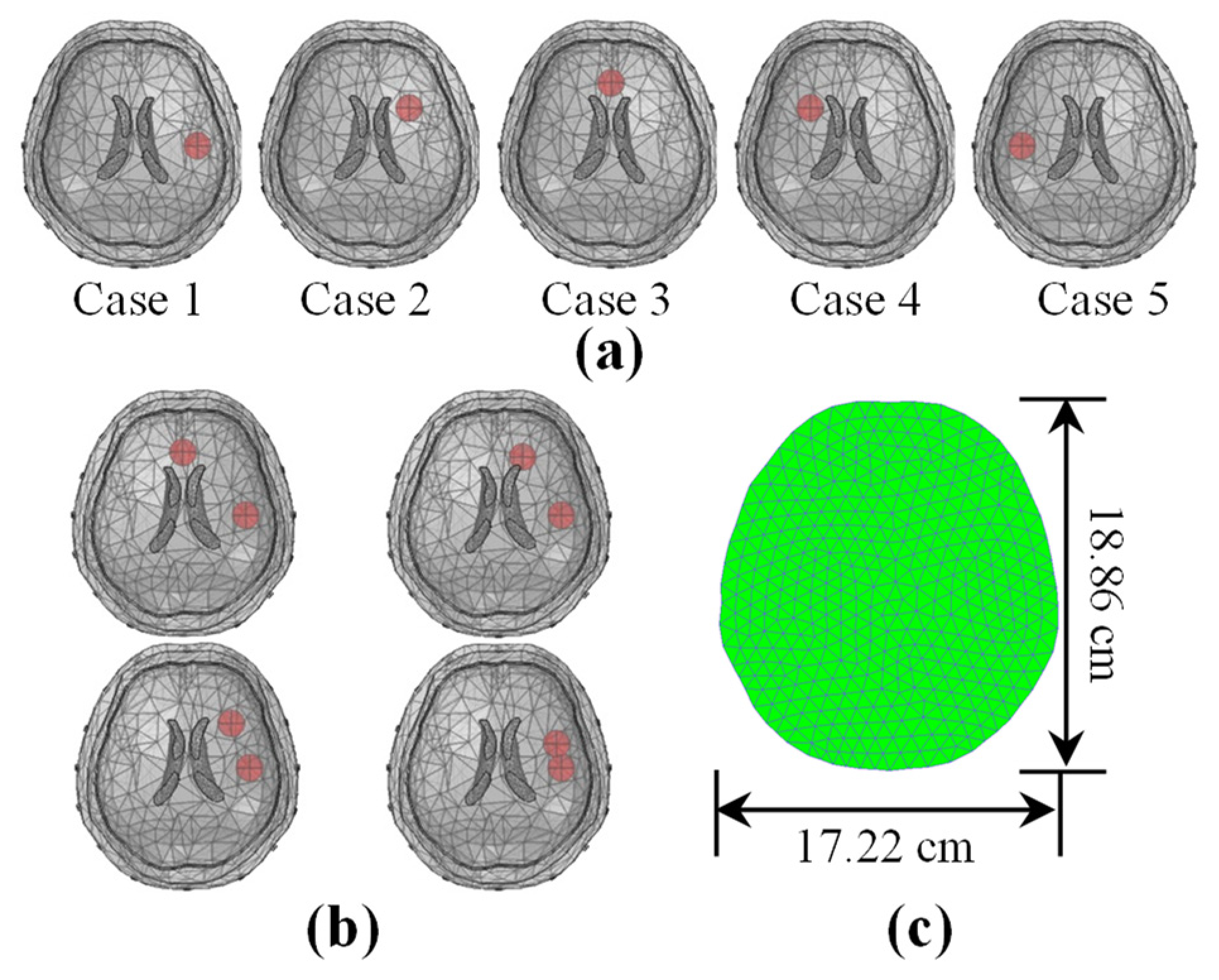


| Tissue | Conductivity (S/m) |
|---|---|
| Scalp | 0.44 |
| Skull | 0.012 |
| Parenchyma | 0.149 |
| Cerebrospinal fluid | 1.79 |
| Ventricle | 1.79 |
| Lesion | 0.67 |
| Method | IN (Mean) | RES (Mean ± Std) |
|---|---|---|
| DLS | 0.182 | 0.288 ± 0.051 |
| SB | 0.127 | 0.217 ± 0.014 |
| FISTA | 0.087 | 0.164 ± 0.017 |
| FISTA-C | 0.067 | 0.107 ± 0.011 |
| Method | IN (Mean) | RES (Mean ± Std) |
|---|---|---|
| DLS | 0.276 | 0.218 ± 0.008 |
| SB | 0.166 | 0.207 ± 0.014 |
| FISTA | 0.147 | 0.139 ± 0.010 |
| FISTA-C | 0.046 | 0.088 ± 0.004 |
| Method | IN (Mean) | RES (Mean ± Std) |
|---|---|---|
| DLS | 0.217 | 0.201 ± 0.017 |
| SB | 0.179 | 0.182 ± 0.011 |
| FISTA | 0.128 | 0.139 ± 0.009 |
| FISTA-C | 0.099 | 0.109 ± 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, T.; Ye, J.; Tian, X.; Zhang, W.; Yang, B.; Dai, M.; Xu, C.; Fu, F. Fast Iterative Shrinkage-Thresholding Algorithm with Continuation for Brain Injury Monitoring Imaging Based on Electrical Impedance Tomography. Sensors 2022, 22, 9934. https://doi.org/10.3390/s22249934
Liu X, Zhang T, Ye J, Tian X, Zhang W, Yang B, Dai M, Xu C, Fu F. Fast Iterative Shrinkage-Thresholding Algorithm with Continuation for Brain Injury Monitoring Imaging Based on Electrical Impedance Tomography. Sensors. 2022; 22(24):9934. https://doi.org/10.3390/s22249934
Chicago/Turabian StyleLiu, Xuechao, Tao Zhang, Jian’an Ye, Xiang Tian, Weirui Zhang, Bin Yang, Meng Dai, Canhua Xu, and Feng Fu. 2022. "Fast Iterative Shrinkage-Thresholding Algorithm with Continuation for Brain Injury Monitoring Imaging Based on Electrical Impedance Tomography" Sensors 22, no. 24: 9934. https://doi.org/10.3390/s22249934
APA StyleLiu, X., Zhang, T., Ye, J., Tian, X., Zhang, W., Yang, B., Dai, M., Xu, C., & Fu, F. (2022). Fast Iterative Shrinkage-Thresholding Algorithm with Continuation for Brain Injury Monitoring Imaging Based on Electrical Impedance Tomography. Sensors, 22(24), 9934. https://doi.org/10.3390/s22249934







