GradFreeBits: Gradient-Free Bit Allocation for Mixed-Precision Neural Networks
Abstract
1. Introduction
1.1. Paper Organization
1.2. Problem Definition
1.3. System Model
1.4. Our Contributions
- Our training scheme for mixed-precision QNNs optimizes the network as a whole. That is, it considers the dependencies between the layers of the neural network and the dependencies between the weights and their bit allocation.
- Our approach for optimizing the bit allocation is gradient free, and thus can handle multiple, possibly non-differentiable, hardware constraints. This enables tailoring QNNs to the resources of specific edge devices.
- We propose a bit-dependent parameterization for the quantization clipping parameters that allows for a better performance evaluation when sampling the network with a varying bit allocation.
- The systematic combination of gradient-based and gradient-free optimization algorithms can be utilized in other applications and scenarios, e.g., a search of the network’s other hyperparameters.
1.5. Related Works
1.5.1. Fixed-Precision Methods
1.5.2. Mixed-Precision Methods
1.5.3. Joint Search Methods
2. Preliminaries
2.1. Quantization-Aware Training
2.2. CMA-ES
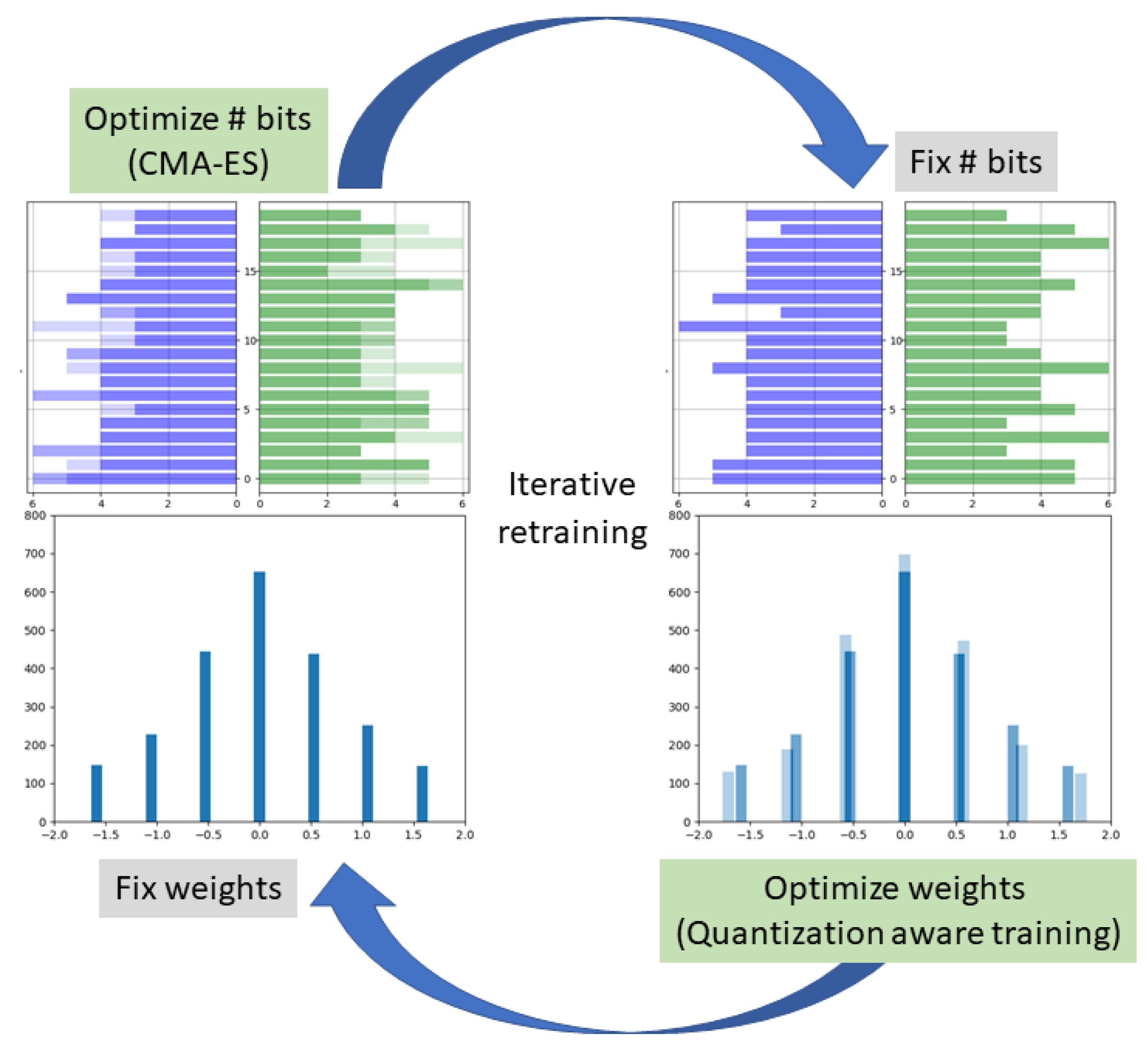
3. The GradFreeBits Method
3.1. Motivation: CMA-ES for Mixed Precision
3.2. Setting the Stage for CMA-ES
3.2.1. Search Space
3.2.2. Objective Function
3.3. Gradient-Free Rounds
| Algorithm 1 Gradient-Free Rounds. |
 |
3.4. Iterative Alternating Retraining
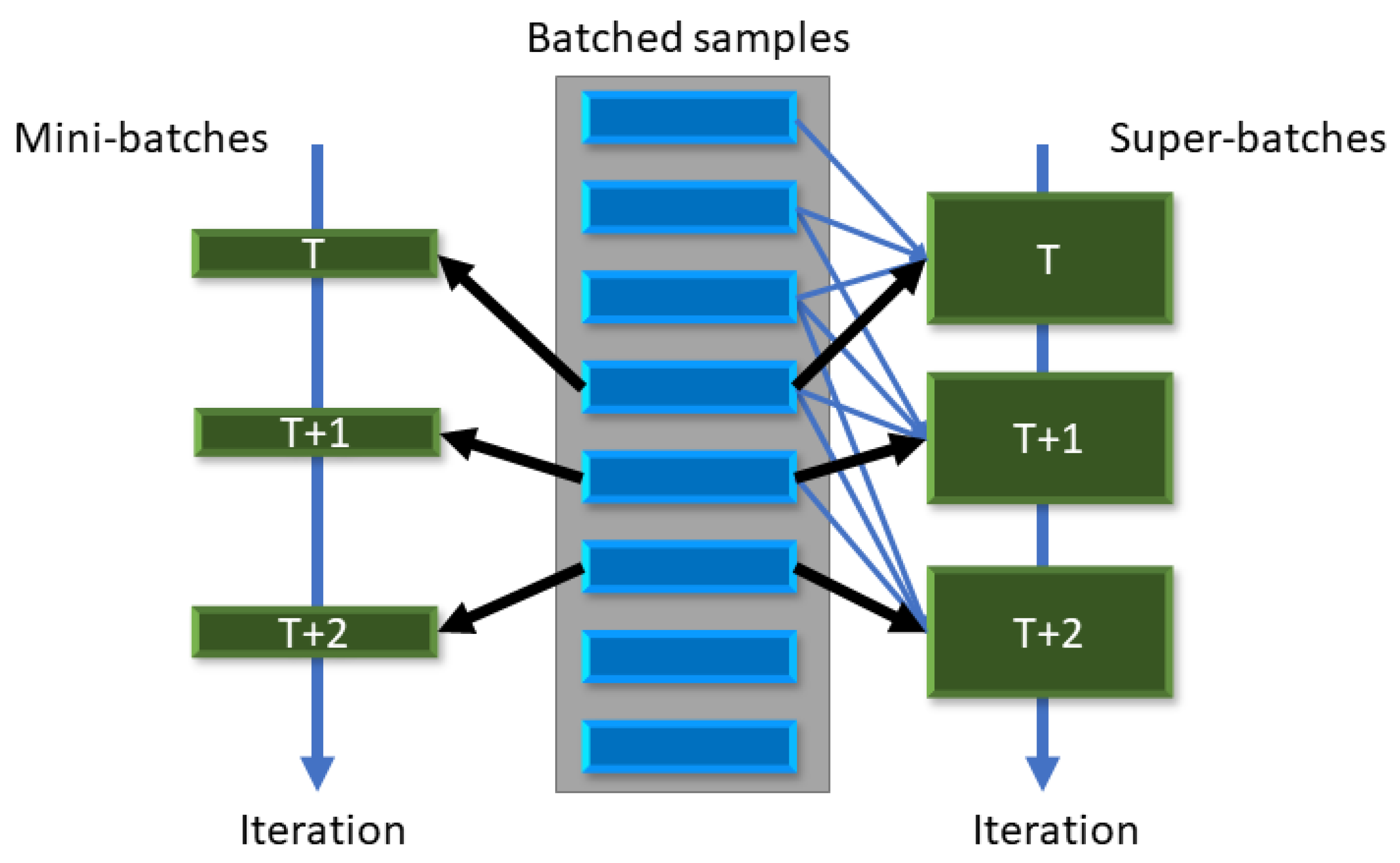
3.5. Variance Reduction in CMA-ES Sampling
Moving Super-Batches
3.6. Adapting the Clipping Parameters to Varying Bit Allocations
4. Experiments and Results
4.1. CIFAR 10/100
4.2. ImageNet
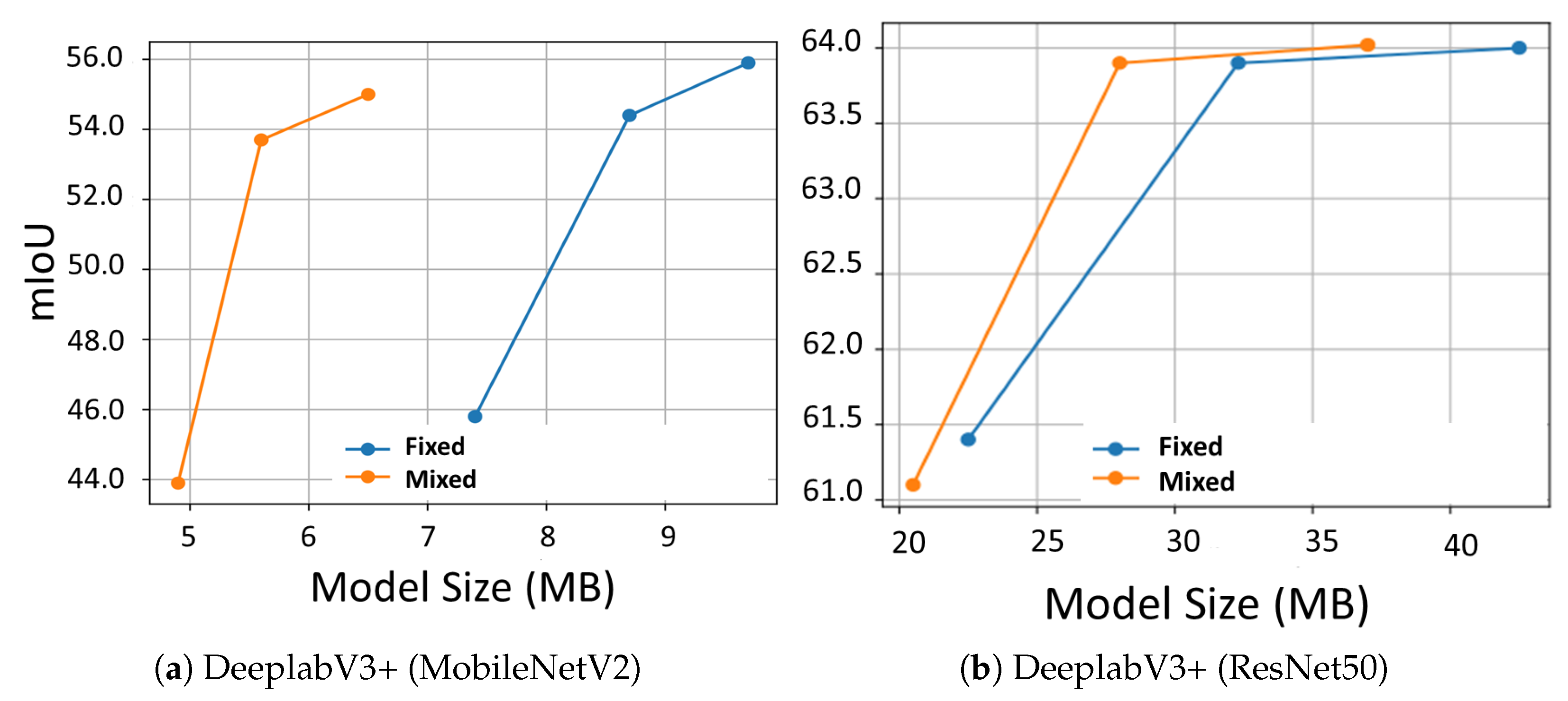
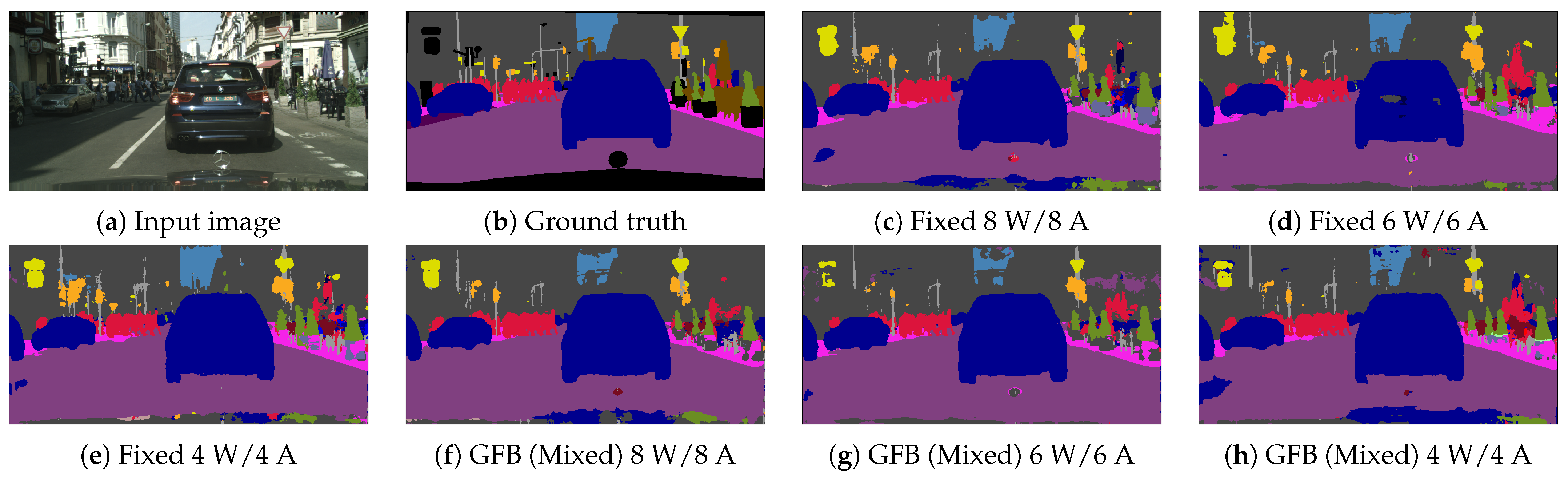
4.3. Image Semantic Segmentation
5. Ablation Study
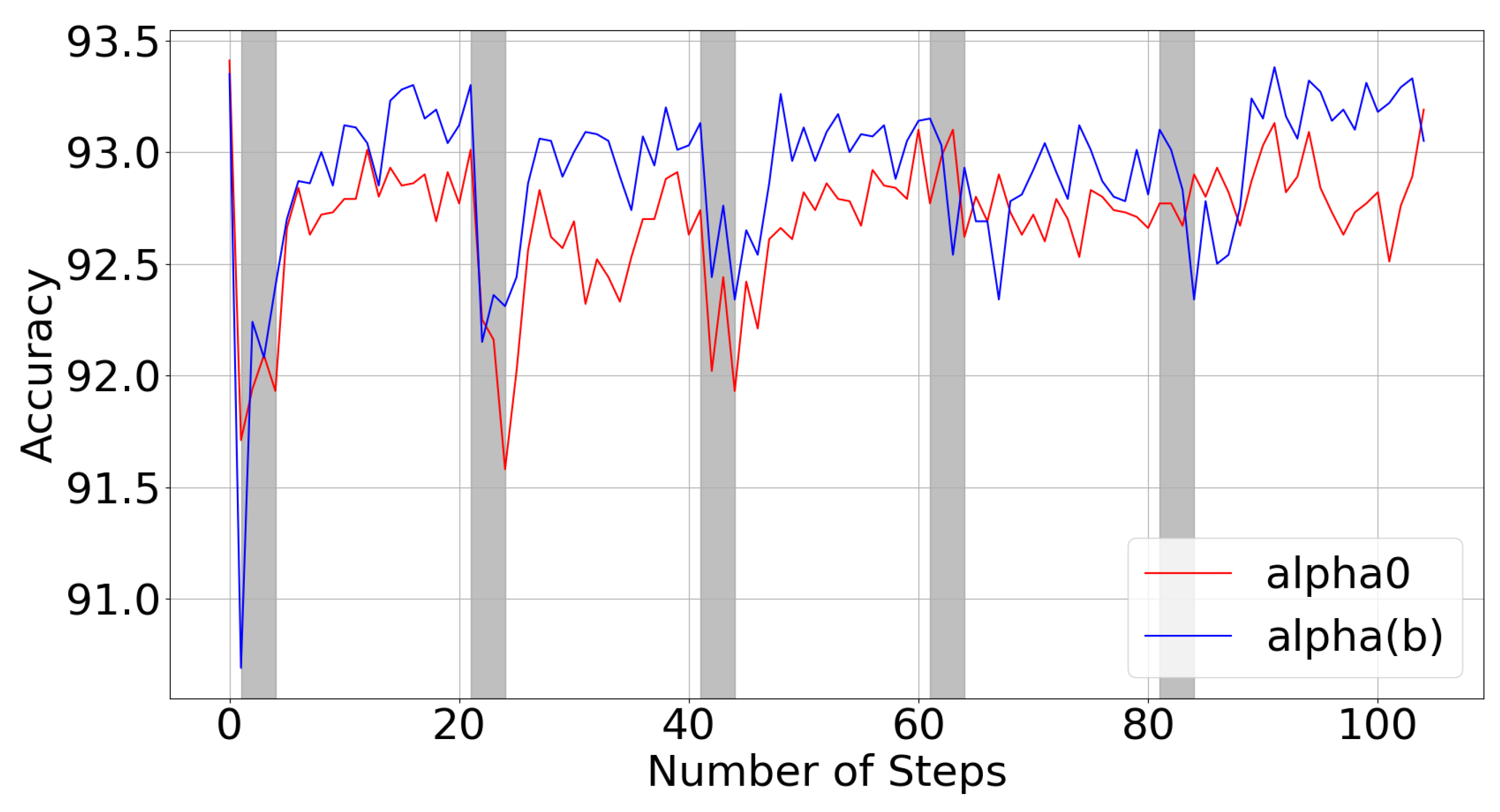
5.1. Bit-Dependent Clipping Parameters
5.2. Iterative Alternating Retraining
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. CMA-ES
Appendix A.1. Hyperparameters
Appendix A.2. Mean Update Rule
Appendix A.3. Covariance Matrix Update Rule
Appendix A.4. Step-Size Update Rule
Appendix A.5. Next Generation
Appendix B. Computational Cost
References
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS, Virtual, 6–12 December 2020; Volume 33, pp. 1877–1901. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the International Conference on Machine Learning, ICML, Long Beach, CA, USA, 9–15 June 2019; Springer: Berlin/Heidelberg, Germany, 2019; Volume 97, pp. 6105–6114. [Google Scholar]
- Kolesnikov, A.; Beyer, L.; Zhai, X.; Puigcerver, J.; Yung, J.; Gelly, S.; Houlsby, N. Big Transfer (BiT): General Visual Representation Learning. In Proceedings of the European Conference on Computer Vision, ECCV, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12350, pp. 491–507. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Y.; Song, L.; Chen, F.; Tang, T. A survey of accelerator architectures for deep neural networks. Engineering 2020, 6, 264–274. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. Model Compression and Acceleration for Deep Neural Networks: The Principles, Progress, and Challenges. IEEE Signal Process. Mag. 2018, 35, 126–136. [Google Scholar] [CrossRef]
- Blalock, D.; Gonzalez Ortiz, J.J.; Frankle, J.; Guttag, J. What is the state of neural network pruning? Proc. Mach. Learn. Syst. 2020, 2, 129–146. [Google Scholar]
- Cho, J.H.; Hariharan, B. On the Efficacy of Knowledge Distillation. In Proceedings of the International Conference on Computer Vision, ICCV, Seoul, Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4793–4801. [Google Scholar] [CrossRef]
- Tung, F.; Mori, G. Similarity-Preserving Knowledge Distillation. In Proceedings of the International Conference on Computer Vision, ICCV, Seoul, Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1365–1374. [Google Scholar] [CrossRef]
- Ren, P.; Xiao, Y.; Chang, X.; Huang, P.; Li, Z.; Chen, X.; Wang, X. A Comprehensive Survey of Neural Architecture Search: Challenges and Solutions. ACM Comput. Surv. 2022, 54, 76:1–76:34. [Google Scholar] [CrossRef]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations. J. Mach. Learn. Res. 2017, 18, 187:1–187:30. [Google Scholar]
- Tung, F.; Mori, G. Deep Neural Network Compression by In-Parallel Pruning-Quantization. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 568–579. [Google Scholar] [CrossRef] [PubMed]
- Banner, R.; Nahshan, Y.; Soudry, D. Post training 4-bit quantization of convolutional networks for rapid-deployment. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; pp. 7948–7956. [Google Scholar]
- Choi, J.; Venkataramani, S.; Srinivasan, V.; Gopalakrishnan, K.; Wang, Z.; Chuang, P. Accurate and Efficient 2-bit Quantized Neural Networks. In Proceedings of the Machine Learning and Systems, Stanford, CA, USA, 31 March–2 April 2019. [Google Scholar]
- Zhao, R.; Hu, Y.; Dotzel, J.; Sa, C.D.; Zhang, Z. Improving Neural Network Quantization without Retraining using Outlier Channel Splitting. In Proceedings of the International Conference on Machine Learning, ICML, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 7543–7552. [Google Scholar]
- Bai, H.; Cao, M.; Huang, P.; Shan, J. BatchQuant: Quantized-for-all Architecture Search with Robust Quantizer. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS, Virtual, 19 April 2021; pp. 1074–1085. [Google Scholar]
- Liu, Y.; Zhang, W.; Wang, J. Zero-Shot Adversarial Quantization. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Virtual, 19–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1512–1521. [Google Scholar] [CrossRef]
- Zhou, S.; Ni, Z.; Zhou, X.; Wen, H.; Wu, Y.; Zou, Y. DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Choi, J.; Wang, Z.; Venkataramani, S.; Chuang, P.I.; Srinivasan, V.; Gopalakrishnan, K. PACT: Parameterized Clipping Activation for Quantized Neural Networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Jin, Q.; Yang, L.; Liao, Z.; Qian, X. Neural Network Quantization with Scale-Adjusted Training. In Proceedings of the British Machine Vision Conference, BMVC, Virtual Event, UK, 7–10 September 2020. [Google Scholar]
- Cai, W.; Li, W. Weight Normalization based Quantization for Deep Neural Network Compression. arXiv 2019, arXiv:1907.00593. [Google Scholar]
- Zhang, D.; Yang, J.; Ye, D.; Hua, G. LQ-Nets: Learned Quantization for Highly Accurate and Compact Deep Neural Networks. In Proceedings of the European Conference on Computer Vision, ECCV, Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11212, pp. 373–390. [Google Scholar] [CrossRef]
- Rios, L.M.; Sahinidis, N.V. Derivative-free optimization: A review of algorithms and comparison of software implementations. J. Glob. Optim. 2013, 56, 1247–1293. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Dong, X.; Wang, W. Additive Powers-of-Two Quantization: An Efficient Non-uniform Discretization for Neural Networks. In Proceedings of the International Conference on Learning Representations, ICLR, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable Soft Quantization: Bridging Full-Precision and Low-Bit Neural Networks. In Proceedings of the International Conference on Computer Vision, ICCV, Seoul, Korea, 29 October–1 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4851–4860. [Google Scholar] [CrossRef]
- Yin, P.; Zhang, S.; Lyu, J.; Osher, S.; Qi, Y.; Xin, J. Blended coarse gradient descent for full quantization of deep neural networks. Res. Math. Sci. 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Yamamoto, K. Learnable Companding Quantization for Accurate Low-Bit Neural Networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Virtual, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5029–5038. [Google Scholar] [CrossRef]
- Wang, L.; Dong, X.; Wang, Y.; Liu, L.; An, W.; Guo, Y. Learnable Lookup Table for Neural Network Quantization. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, New Orleans, LA, USA, 18–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 12413–12423. [Google Scholar] [CrossRef]
- Elthakeb, A.T.; Pilligundla, P.; Mireshghallah, F.; Yazdanbakhsh, A.; Esmaeilzadeh, H. ReLeQ: A Reinforcement Learning Approach for Automatic Deep Quantization of Neural Networks. IEEE Micro 2020, 40, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Liu, Z.; Lin, Y.; Lin, J.; Han, S. HAQ: Hardware-Aware Automated Quantization With Mixed Precision. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Long Beach, CA, USA, 15–20 June 201; IEEE: Piscataway, NJ, USA, 2019; pp. 8612–8620. [Google Scholar] [CrossRef]
- Dong, Z.; Yao, Z.; Gholami, A.; Mahoney, M.W.; Keutzer, K. HAWQ: Hessian AWare Quantization of Neural Networks With Mixed-Precision. In Proceedings of the International Conference on Computer Vision, ICCV, Seoul, Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 293–302. [Google Scholar] [CrossRef]
- Dong, Z.; Yao, Z.; Arfeen, D.; Gholami, A.; Mahoney, M.W.; Keutzer, K. HAWQ-V2: Hessian Aware trace-Weighted Quantization of Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS, Virtual, 6–12 December 2020. [Google Scholar]
- Uhlich, S.; Mauch, L.; Cardinaux, F.; Yoshiyama, K.; García, J.A.; Tiedemann, S.; Kemp, T.; Nakamura, A. Mixed Precision DNNs: All you need is a good parametrization. In Proceedings of the International Conference on Learning Representations, ICLR, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Li, Y.; Wang, W.; Bai, H.; Gong, R.; Dong, X.; Yu, F. Efficient Bitwidth Search for Practical Mixed Precision Neural Network. arXiv 2020, arXiv:2003.07577. [Google Scholar]
- Guo, Z.; Zhang, X.; Mu, H.; Heng, W.; Liu, Z.; Wei, Y.; Sun, J. Single Path One-Shot Neural Architecture Search with Uniform Sampling. In Proceedings of the European Conference on Computer Vision, ECCV, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12361, pp. 544–560. [Google Scholar] [CrossRef]
- Yu, H.; Han, Q.; Li, J.; Shi, J.; Cheng, G.; Fan, B. Search What You Want: Barrier Panelty NAS for Mixed Precision Quantization. In Proceedings of the European Conference on Computer Vision, ECCV, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12354, pp. 1–16. [Google Scholar] [CrossRef]
- Shen, M.; Liang, F.; Gong, R.; Li, Y.; Li, C.; Lin, C.; Yu, F.; Yan, J.; Ouyang, W. Once Quantization-Aware Training: High Performance Extremely Low-bit Architecture Search. In Proceedings of the International Conference on Computer Vision, ICCV, Montreal, QC, Canada, 10–17 October 2021; IEEE: Piscatway, NJ, USA, 2021; pp. 5320–5329. [Google Scholar] [CrossRef]
- Wang, T.; Wang, K.; Cai, H.; Lin, J.; Liu, Z.; Wang, H.; Lin, Y.; Han, S. APQ: Joint Search for Network Architecture, Pruning and Quantization Policy. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscatway, NJ, USA, 2020; pp. 2075–2084. [Google Scholar] [CrossRef]
- Schorn, C.; Elsken, T.; Vogel, S.; Runge, A.; Guntoro, A.; Ascheid, G. Automated design of error-resilient and hardware-efficient deep neural networks. Neural Comput. Appl. 2020, 32, 18327–18345. [Google Scholar] [CrossRef]
- Hu, P.; Peng, X.; Zhu, H.; Aly, M.M.S.; Lin, J. OPQ: Compressing Deep Neural Networks with One-shot Pruning-Quantization. In Proceedings of the Thirty-Fifth Conference on Artificial Intelligence, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, The Eleventh Symposium on Educational Advances in Artificial Intelligence, Virtual Event, 2–9 February 2021; pp. 7780–7788. [Google Scholar]
- Yang, H.; Gui, S.; Zhu, Y.; Liu, J. Automatic Neural Network Compression by Sparsity-Quantization Joint Learning: A Constrained Optimization-Based Approach. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscatway, NJ, USA, 2020; pp. 2175–2185. [Google Scholar] [CrossRef]
- Bengio, Y.; Léonard, N.; Courville, A.C. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. arXiv 2013, arXiv:1308.3432. [Google Scholar]
- Heidrich-Meisner, V.; Igel, C. Evolution Strategies for Direct Policy Search. In Proceedings of the Parallel Problem Solving from Nature, Dortmund, Germany, 13–17 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5199, pp. 428–437. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Wagner, M. A hybrid cooperative co-evolution algorithm framework for optimising power take off and placements of wave energy converters. Inf. Sci. 2020, 534, 218–244. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. CMA-ES for Hyperparameter Optimization of Deep Neural Networks. arXiv 2016, arXiv:1604.07269. [Google Scholar]
- Hansen, N. Benchmarking a BI-population CMA-ES on the BBOB-2009 function testbed. In Proceedings of the Genetic and Evolutionary Computation Conference, Montreal, QC, Canada, 8–12 July 2009; pp. 2389–2396. [Google Scholar] [CrossRef]
- Johnson, R.; Zhang, T. Accelerating Stochastic Gradient Descent using Predictive Variance Reduction. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 315–323. [Google Scholar]
- Marcel, S.; Rodriguez, Y. Torchvision the machine-vision package of torch. Int. Conf. Multimed. 2010, 1485–1488. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems, NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; pp. 8024–8035. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning multiple layers of features from tiny images. Neural Inf. Process. Syst. 2009. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3213–3223. [Google Scholar] [CrossRef]
- Zhang, H.; Cissé, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. In Proceedings of the International Conference on Learning Representations, ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Tang, Z.; Peng, X.; Li, K.; Metaxas, D.N. Towards Efficient U-Nets: A Coupled and Quantized Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2038–2050. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chen, L.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision, ECCV, Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11211, pp. 833–851. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.G.; Zhu, M.; Zhmoginov, A.; Chen, L. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
- Eliasof, M.; Bodner, B.J.; Treister, E. Haar Wavelet Feature Compression for Quantized Graph Convolutional Networks. arXiv 2021, arXiv:2110.04824. [Google Scholar]
- Chen, M.; Wei, Z.; Huang, Z.; Ding, B.; Li, Y. Simple and Deep Graph Convolutional Networks. In Proceedings of the International Conference on Machine Learning, ICML, Virtual Event, 29 June–2 July 2020; Volume 119, pp. 1725–1735. [Google Scholar]
- Yang, Z.; Cohen, W.W.; Salakhutdinov, R. Revisiting Semi-Supervised Learning with Graph Embeddings. In Proceedings of the 33nd International Conference on Machine Learning, ICML, New York City, NY, USA, 19–24 June 2016; Volume 48, pp. 40–48. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2016, arXiv:1604.00772. [Google Scholar]

| Property | C10/100 | ImageNet | Cityscapes |
|---|---|---|---|
| [50] | [51] | [52] | |
| # Train | 50 K | 1.2 M | 2975 |
| # Test | 10 K | 150 K | 1525 |
| # classes | 10/100 | 1000 | 19 |
| Img size | 32 | 224 * | 256 * |
| Batch size | 128 | 100 | 4 |
| # Batch/S-Batch | 32 | 16 | 16 |
| Optimizer | SGD | SGD | SGD |
| lr-enc | 0.1 | 0.001 | |
| lr-dec | - | - | 0.1 |
| Momentum | 0.9 | 0.9 | 0.9 |
| 0.9 | 0.9 | 0.98 | |
| 0.98 | 0.9 | 0.98 | |
| 20.0 | 10.0 | 0.1 | |
| 0.5 | 10.0 | 0.5 | |
| Pret. epochs | 300 | 30 | 80 |
| M | 1024 | 1024 | 512 |
| 4 | 4 | 4 | |
| 16 | 5 | 16 | |
| 5 | 3 | 3 | |
| s. space | [0.0–3.0] | [0.0–3.0] | [0.0–3.6] |
| Bit s. space | 1-8b | 1-8b | 1-12b |
| CIFAR-10 with ResNet20, FP Accuracy 93.3% | |||
|---|---|---|---|
| Method | 2W/4A | 3W/3A | 4W/4A |
| PACT(F) [18] | - | 91.1 | 91.7 |
| LQN(F) [21] | - | 91.6 - | - |
| BCGD(F) [26] | 91.2 | - | 92.0 |
| DQ(M) [33] | 91.4 | - | - |
| HAWQ(M) [31] | 92.2 | - | - |
| EBS(M) [34] | - | 92.7 | 92.9 |
| BPNAS(M) [36] | - | 92.0 | 92.3 |
| GFB(M) (ours) | 93.0 | 93.2 | 93.4 |
| CIFAR10 with ResNet56, FP Accuracy 95.1% | |||
| EBS(M) [34] | - | 94.1 | 94.3 |
| GFB(M) (ours) | - | 94.7 | 94.8 |
| CIFAR100 with ResNet20, FP Accuracy 70.35% | |||
| DRFN(F) [17] | - | 68.4 | 68.9 |
| LQN(F) [21] | - | 68.4 | 69.0 |
| WNQ(F) [20] | - | 68.8 | 69.0 |
| GFB(M) (ours) | - | 69.6 | 70.6 |
| Method | 2 W/2 A | 2 W/4 A | 3 W/3 A | 4 W/4 A | 32 W/32 A | Cost (# Epochs) |
|---|---|---|---|---|---|---|
| ResNet18 | ||||||
| PACT [18] | (3.2) | - | (4.7) | (6.1) | 70.4 (46.8) | 110 |
| DSQ [25] | (3.2) | - | (4.7) | (6.1) | 69.9 (46.8) | - |
| APoT [24] | - | - | (4.7) | - | 70.7 (46.8) | 120 |
| SAT [19] | (3.2) | - | (4.7) | (6.1) | 70.2 (46.8) | 150 |
| DQ(M) [33] | - | - | - | (5.4) | 70.3 (46.8) | 160 |
| SPOS * (M) [35] | (-) | - | (-) | (-) | 70.4 (46.8) | 240 |
| GFB(M) (ours) | (3.2) | - | (4.5) | (5.4) | 70.4 (46.8) | 57 |
| ResNet50 | ||||||
| PACT [18] | (8.1) | - | (11.0) | (13.9) | 76.9 (102.2) | 110 |
| SAT [19] | (8.1) | - | (11.0) | (13.9) | 76.7 (102.2) | 150 |
| BPNAS(M) * [36] | - | - | (11.3) | (13.4) | 77.4 (102.2) | 150 |
| HAQ(M) * [30] | - | (12.2) | - | - | 76.2 (102.2) | - |
| HAWQ(M) * [31] | - | (13.2) | - | - | 77.4 (102.2) | ∼400 |
| HAWQV2(M) * [32] | - | (13.1) | - | - | 77.4 (102.2) | ∼400 |
| GFB(M) (ours) | (8.1) | (8.2) | (10.7) | (12.8) | 76.4 (102.2) | 57 |
| Bits | ZAQ-FT (F) | GFB (M) | GFB-HR (M) |
|---|---|---|---|
| W/A | [16] | (Ours) | (Ours) |
| 4/4 | (22.1) | (21.2) | (22.0) |
| 6/6 | (31.8) | (30.2) | (27.6) |
| 8/8 | (41.6) | (34.3) | (38.5) |
| Data | Classes | Label Rate | Nodes | Edges | Features |
|---|---|---|---|---|---|
| Cora | 7 | 0.052 | 2708 | 5429 | 1433 |
| Citeseer | 6 | 0.036 | 3327 | 4732 | 3703 |
| Pubmed | 3 | 0.003 | 19,717 | 44,338 | 500 |
| Benchmark | Bits | GFB (M) | Quantized GCNII [59] (F) |
|---|---|---|---|
| Cora | 8W/8A | 83.7 | 80.9 |
| FP Acc 85.4 | 8W/4A | 83.1 | 31.9 |
| 8W/2A | 81.2 | 21.1 | |
| Citeseer | 8W/8A | 72.0 | 69.8 |
| Acc 73.2 | 8W/4A | 71.8 | 24.7 |
| 8W/2A | 70.3 | 18.3 | |
| Pubmed | 8W/8A | 79.6 | 80.0 |
| Acc 80.3 | 8W/4A | 79.6 | 41.3 |
| 8W/2A | 77.8 | 40.7 |
| Variable | IAR. | PRET. | Top1 Acc. | |
|---|---|---|---|---|
| Baseline | 32 | √ | √ | 70.61 |
| Components | 32 | √ | × | 66.99 |
| 32 | × | √ | 70.33 | |
| Super-batch | 4 | √ | √ | 69.68 |
| Size | 8 | √ | √ | 70.25 |
| 16 | √ | √ | 70.18 | |
| 64 | √ | √ | 70.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodner, B.J.; Ben-Shalom, G.; Treister, E. GradFreeBits: Gradient-Free Bit Allocation for Mixed-Precision Neural Networks. Sensors 2022, 22, 9772. https://doi.org/10.3390/s22249772
Bodner BJ, Ben-Shalom G, Treister E. GradFreeBits: Gradient-Free Bit Allocation for Mixed-Precision Neural Networks. Sensors. 2022; 22(24):9772. https://doi.org/10.3390/s22249772
Chicago/Turabian StyleBodner, Benjamin Jacob, Gil Ben-Shalom, and Eran Treister. 2022. "GradFreeBits: Gradient-Free Bit Allocation for Mixed-Precision Neural Networks" Sensors 22, no. 24: 9772. https://doi.org/10.3390/s22249772
APA StyleBodner, B. J., Ben-Shalom, G., & Treister, E. (2022). GradFreeBits: Gradient-Free Bit Allocation for Mixed-Precision Neural Networks. Sensors, 22(24), 9772. https://doi.org/10.3390/s22249772





