Sensor Placement Optimization for Shape Sensing of Plates and Shells Using Genetic Algorithm and Inverse Finite Element Method
Abstract
1. Introduction
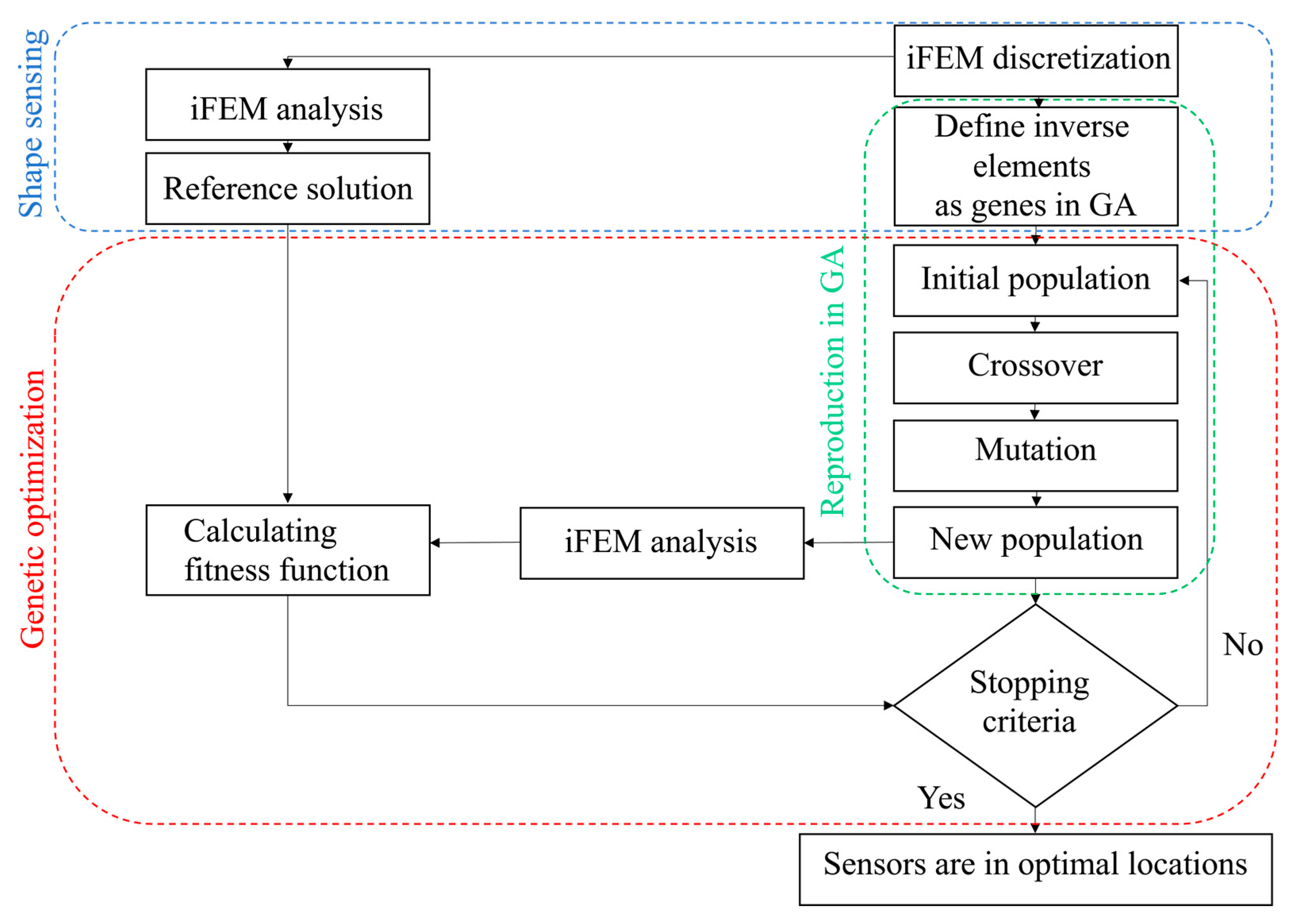
2. Mathematical Formulation of iFEM-GA Method
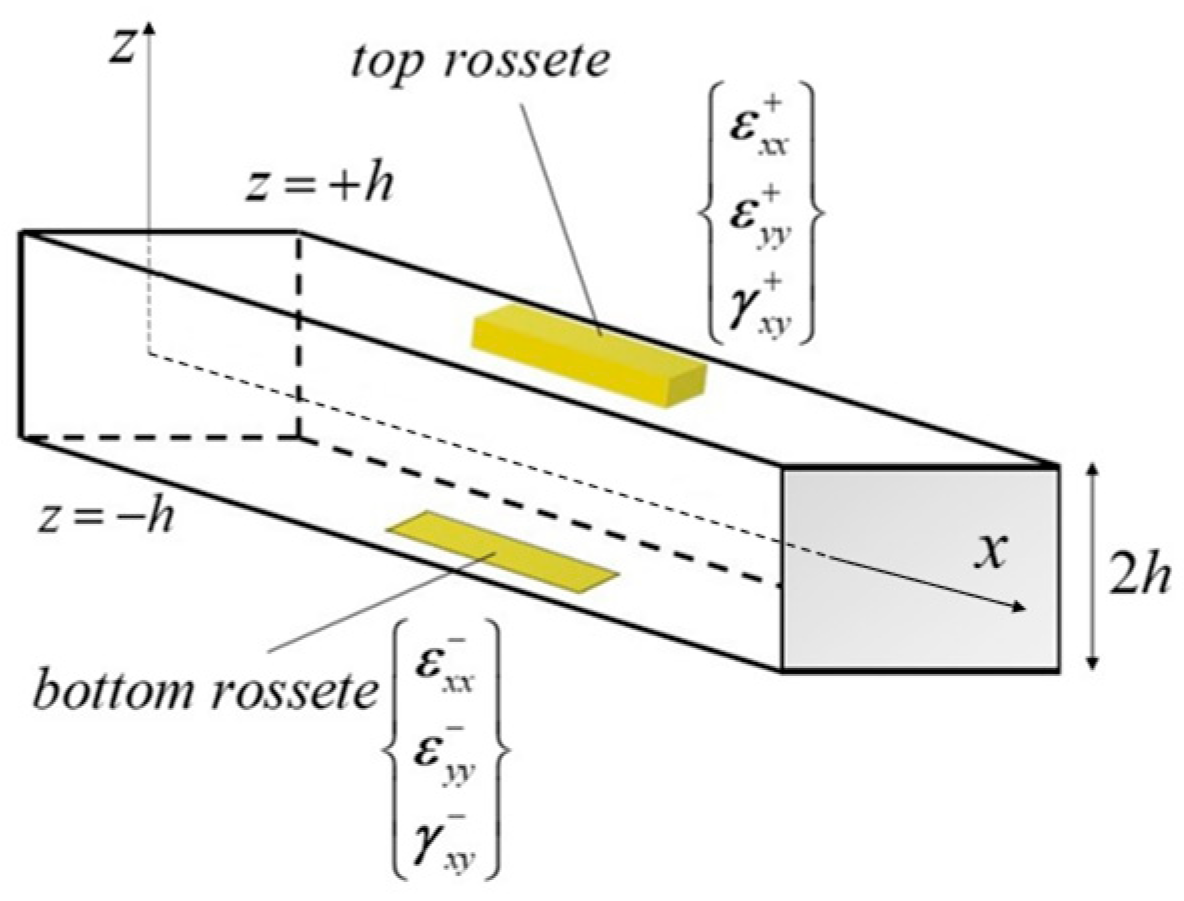
2.1. The iQS4 Inverse-Shell Element
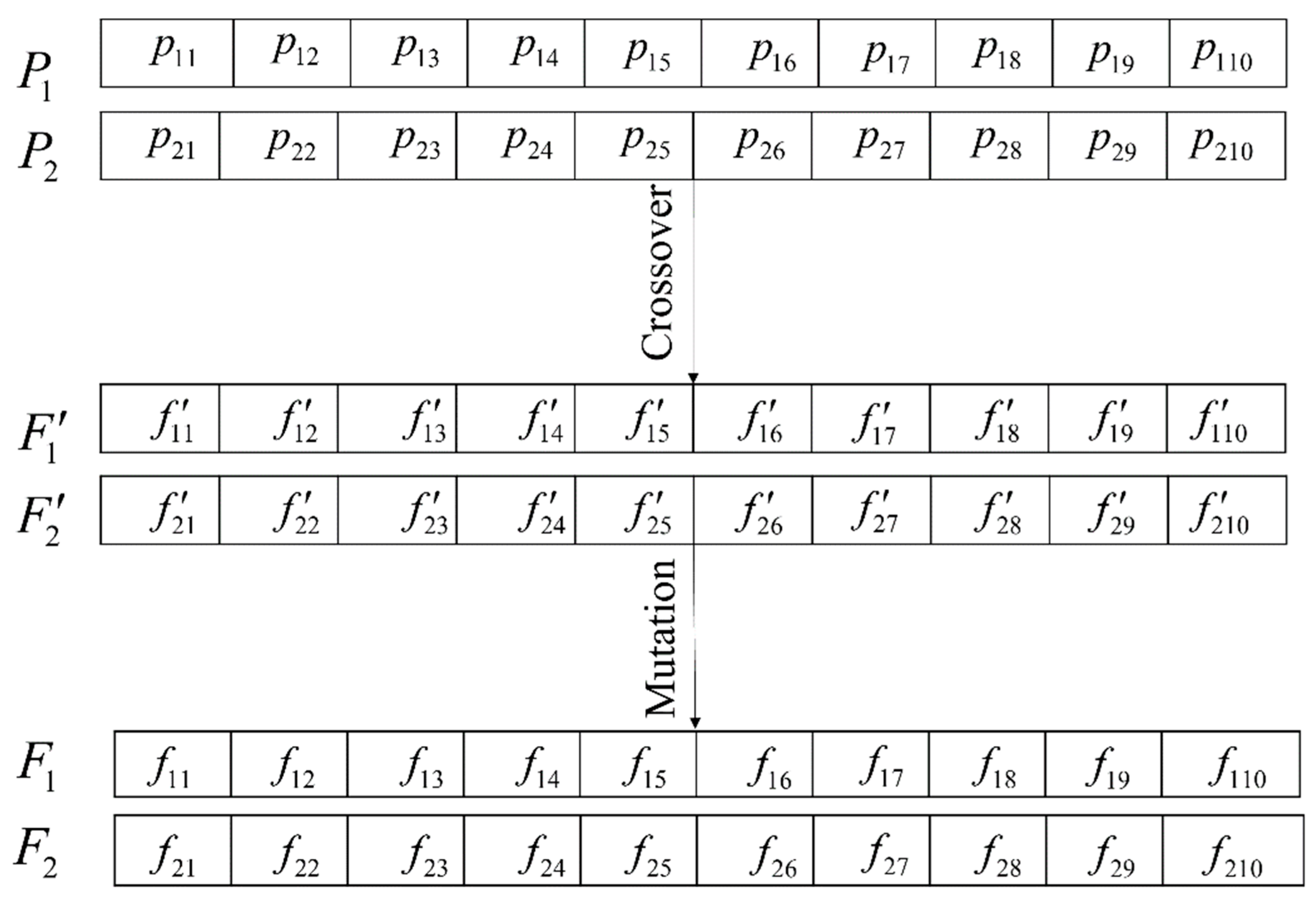
2.2. Coupling iFEM and Genetic Algorithm
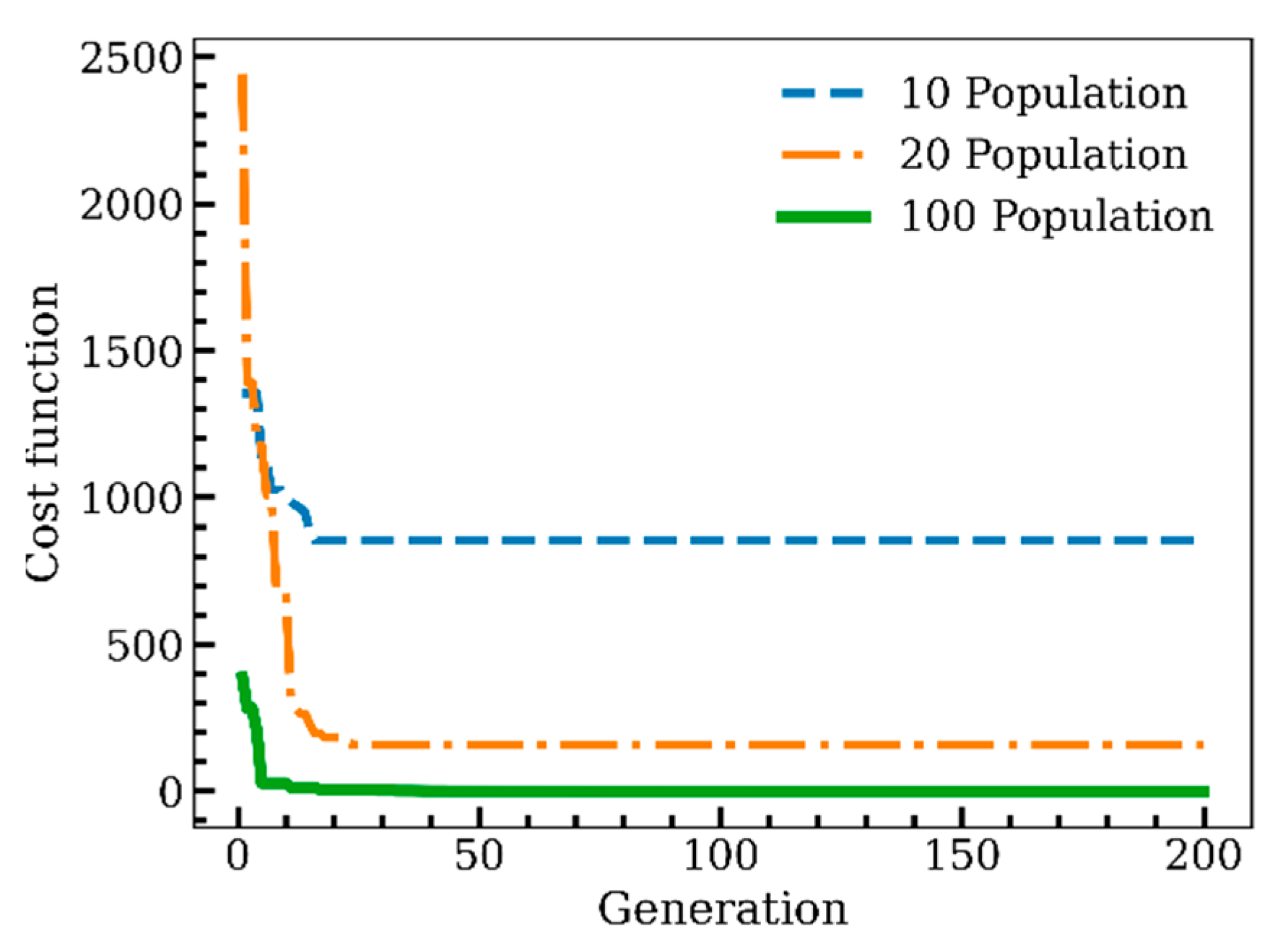
3. Numerical Examples
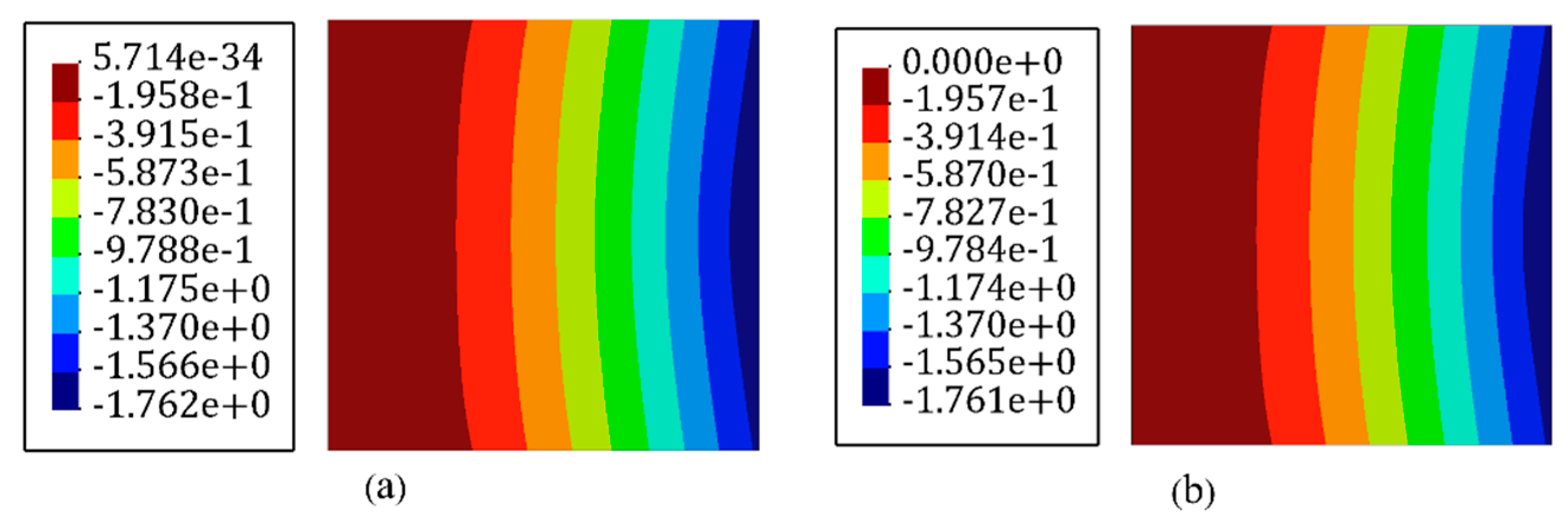
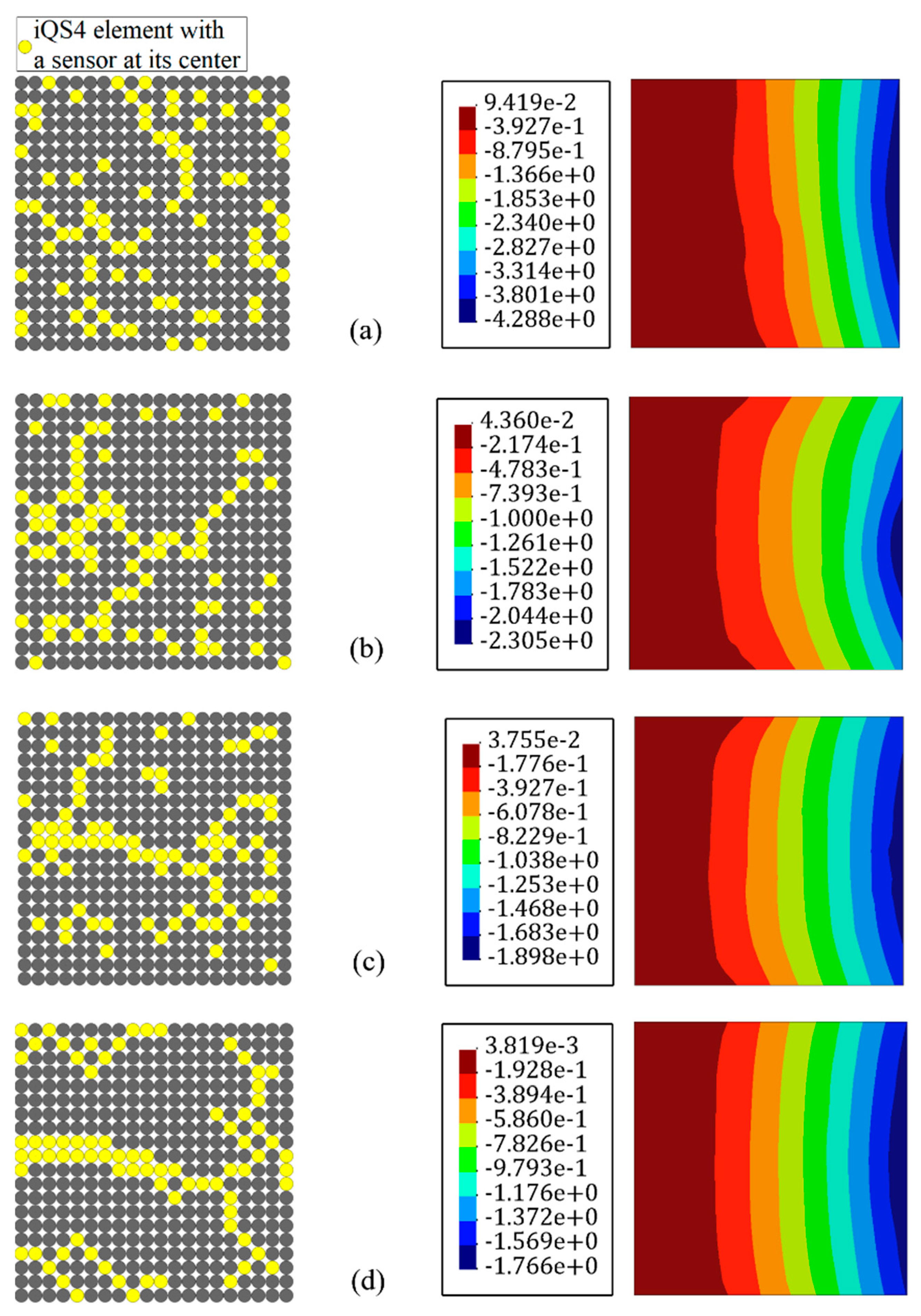
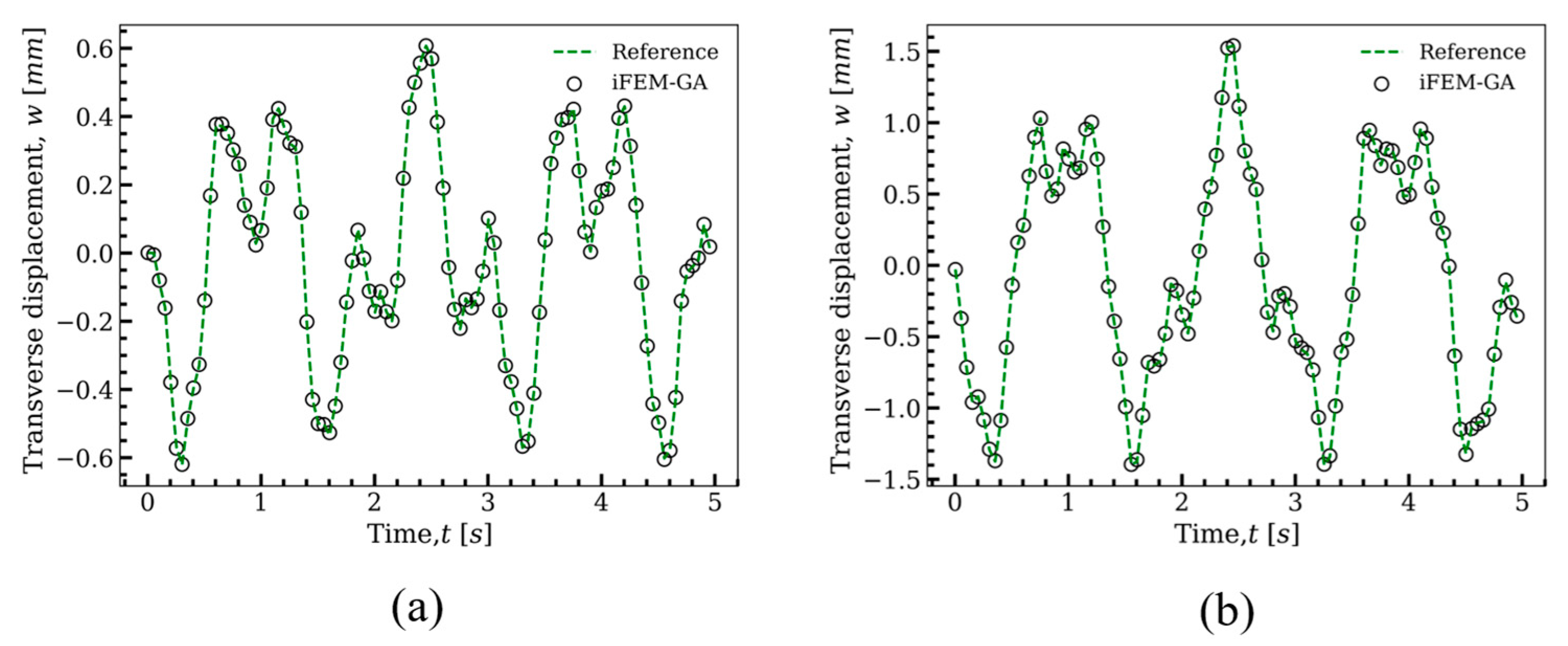
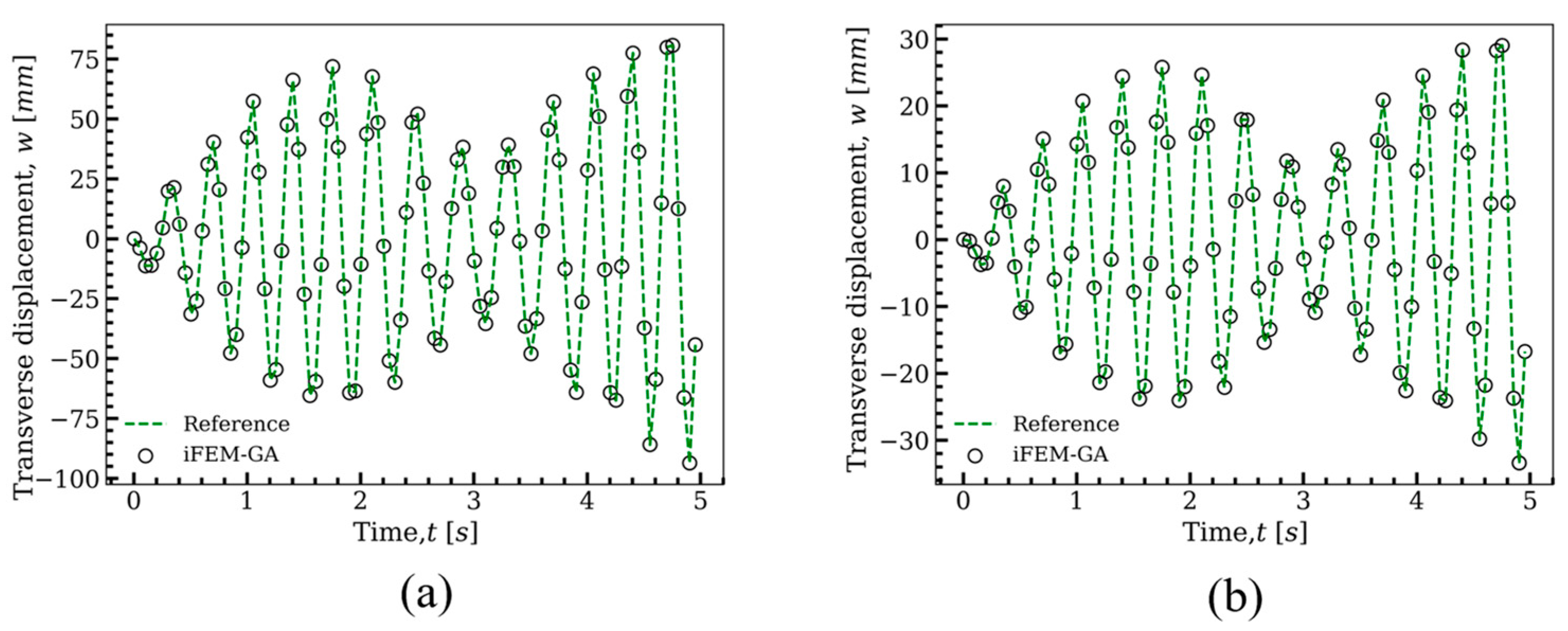
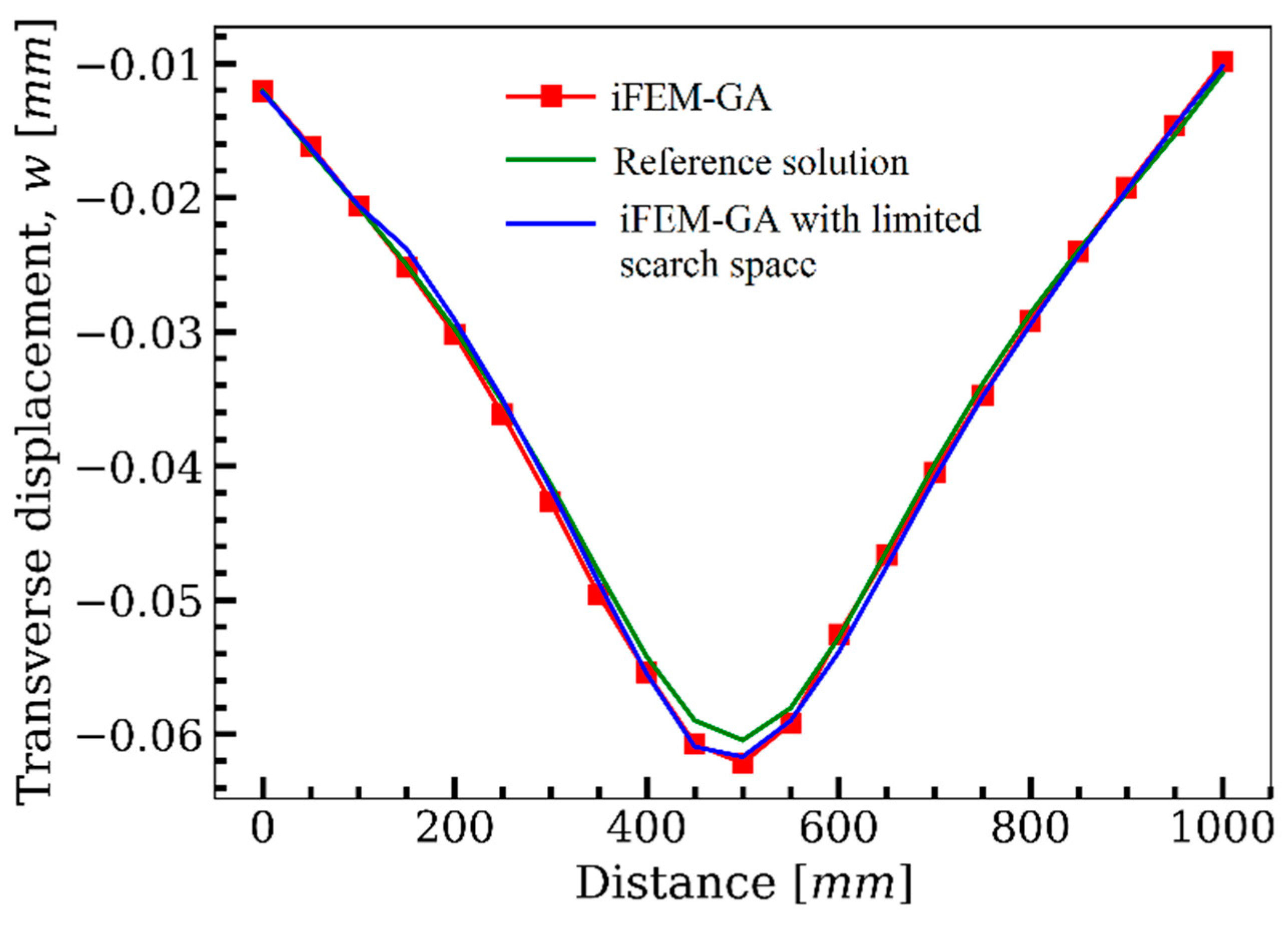
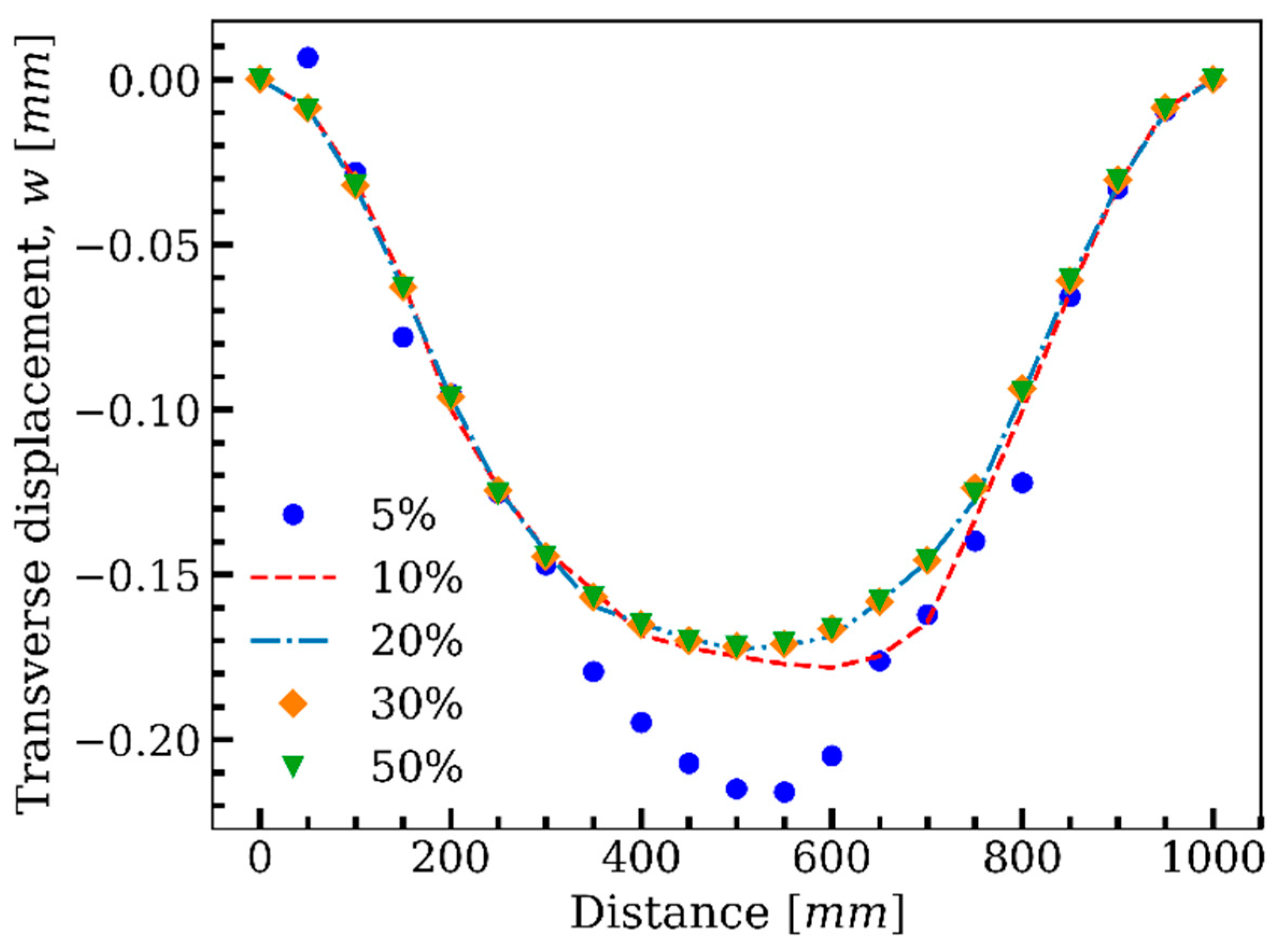
3.1. Cantilever Plate under Static/Dynamic Transverse Loading
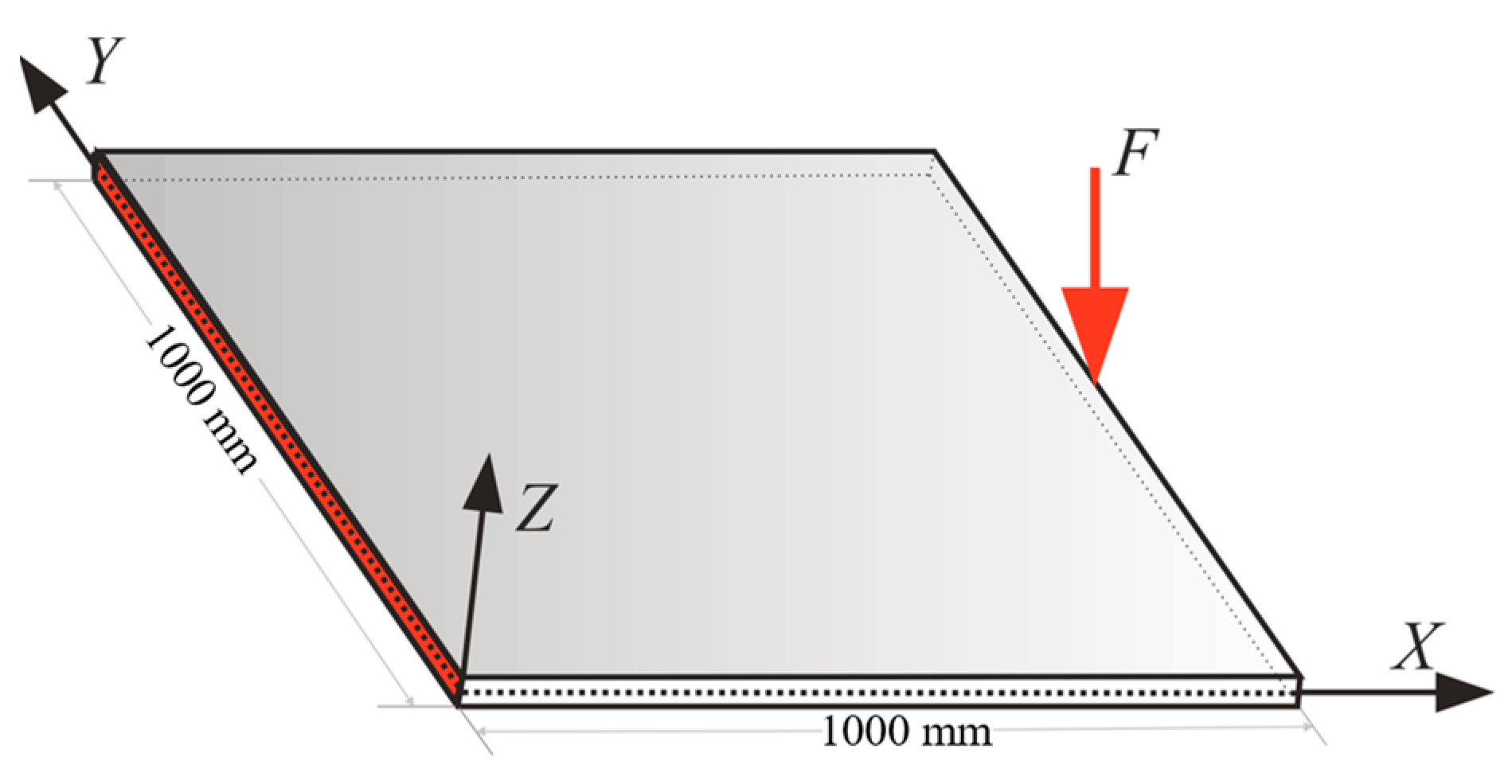
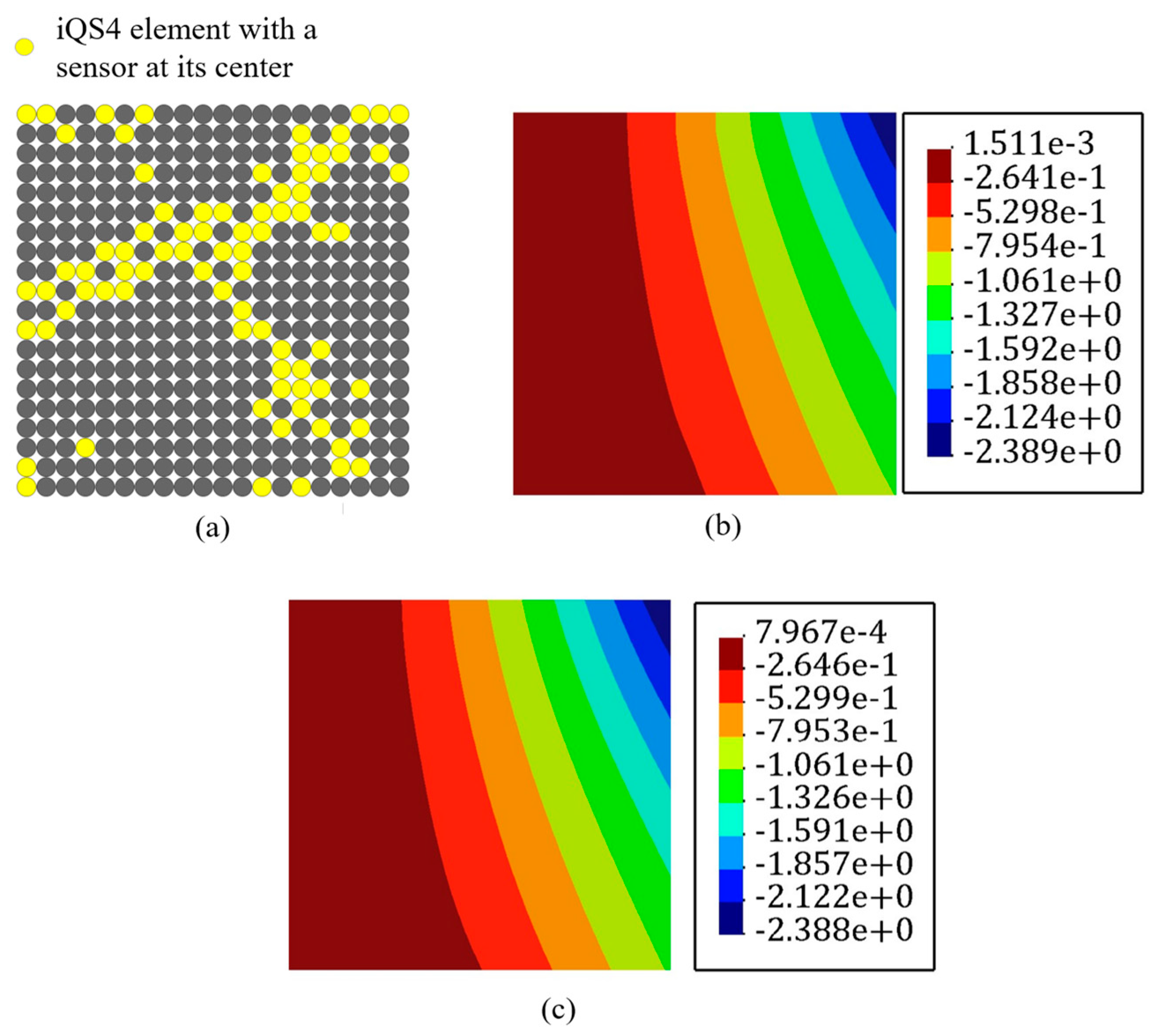
3.2. Cantilever Plate under Concentrated Loading at Its Corner
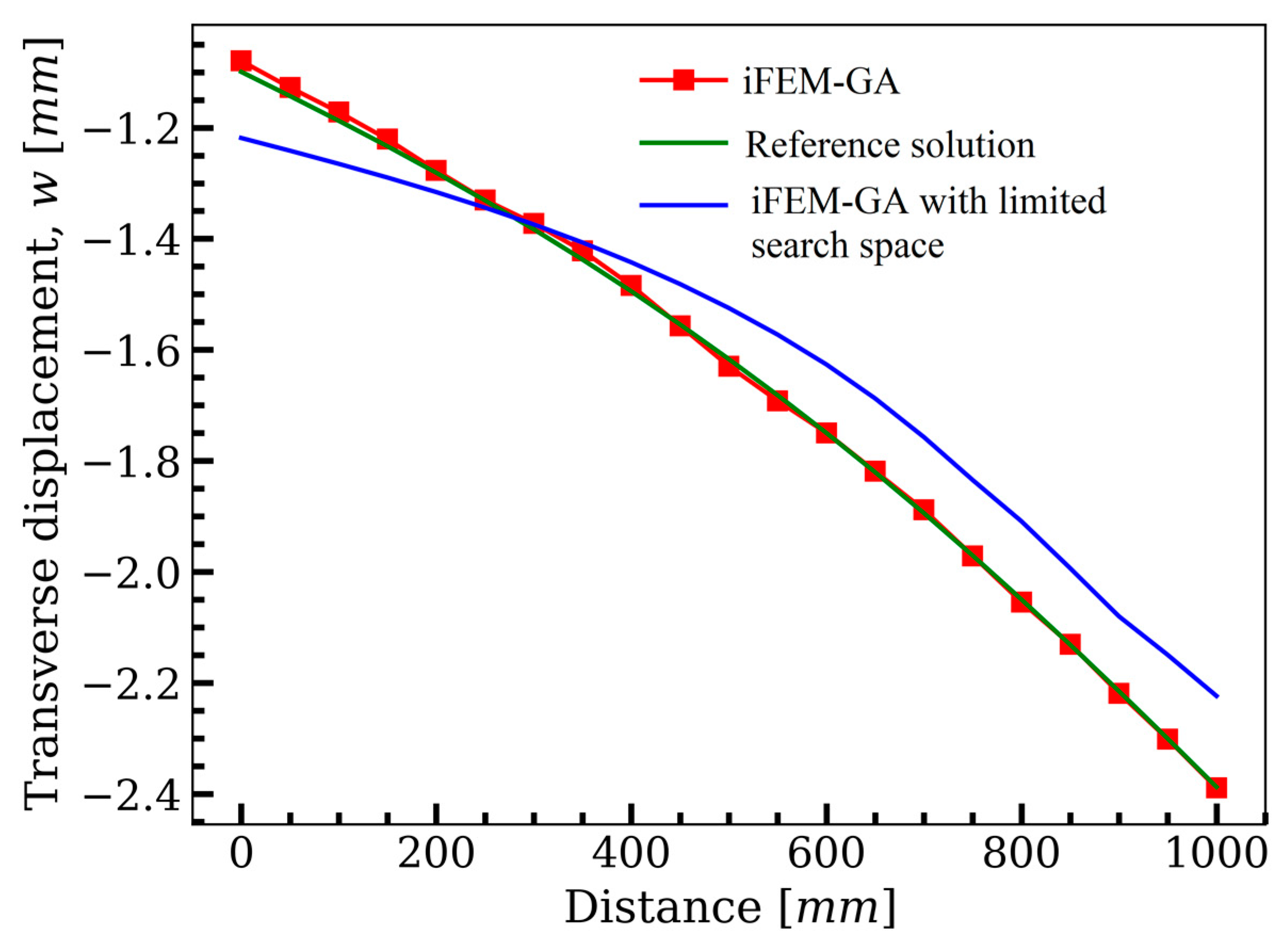
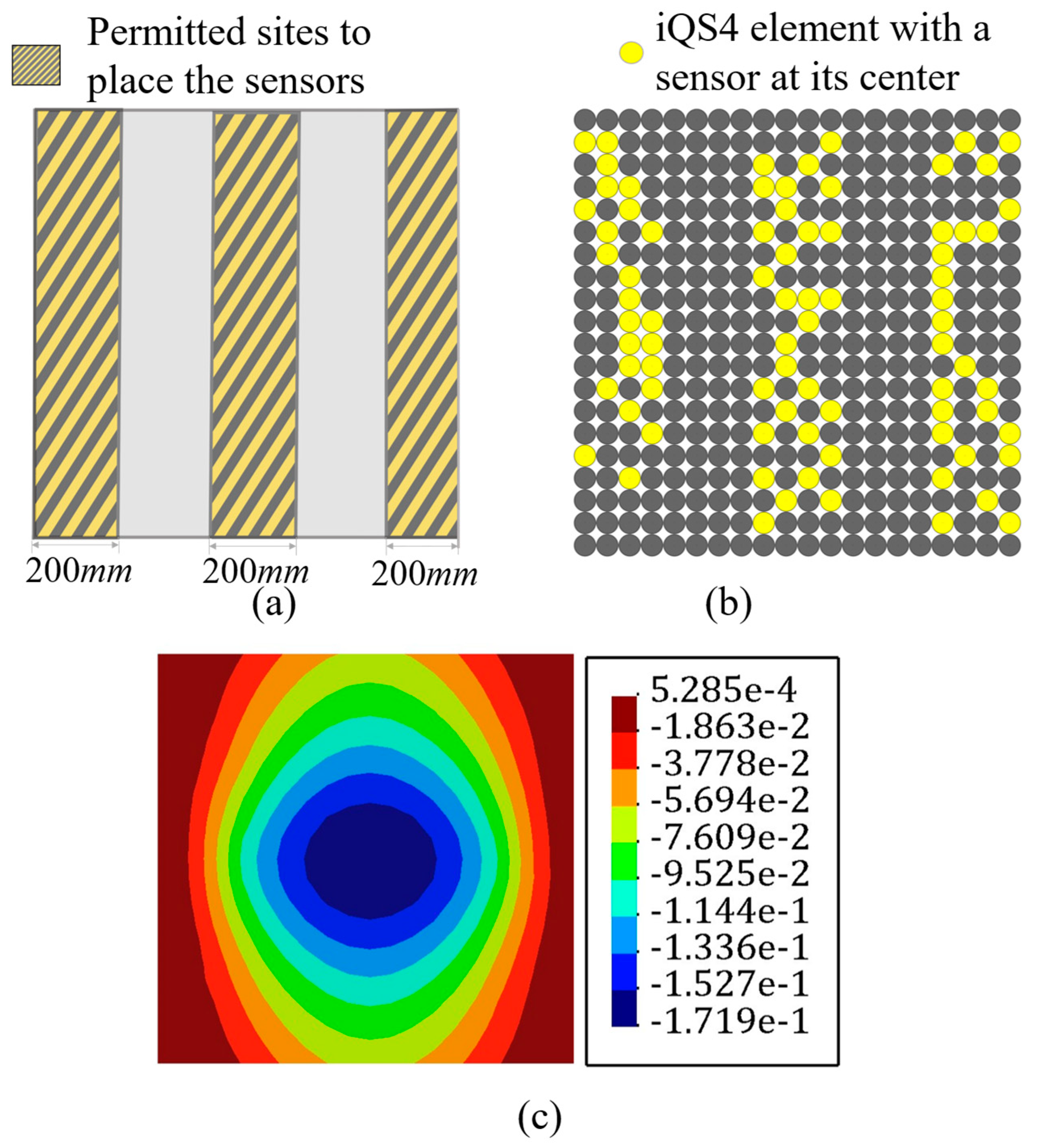
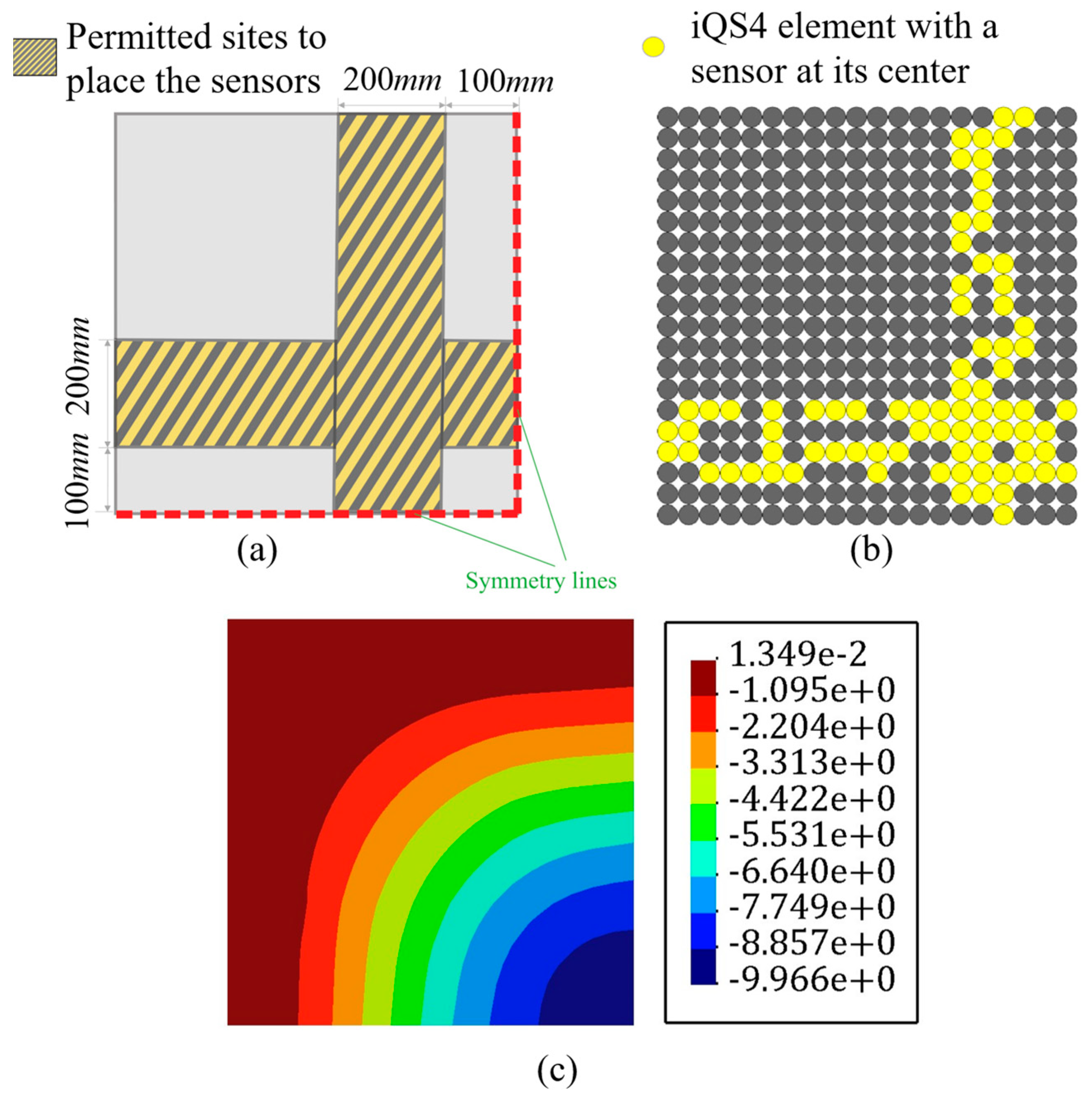
3.3. Partially Clamped Plate under Concentrated Loading at Its Center
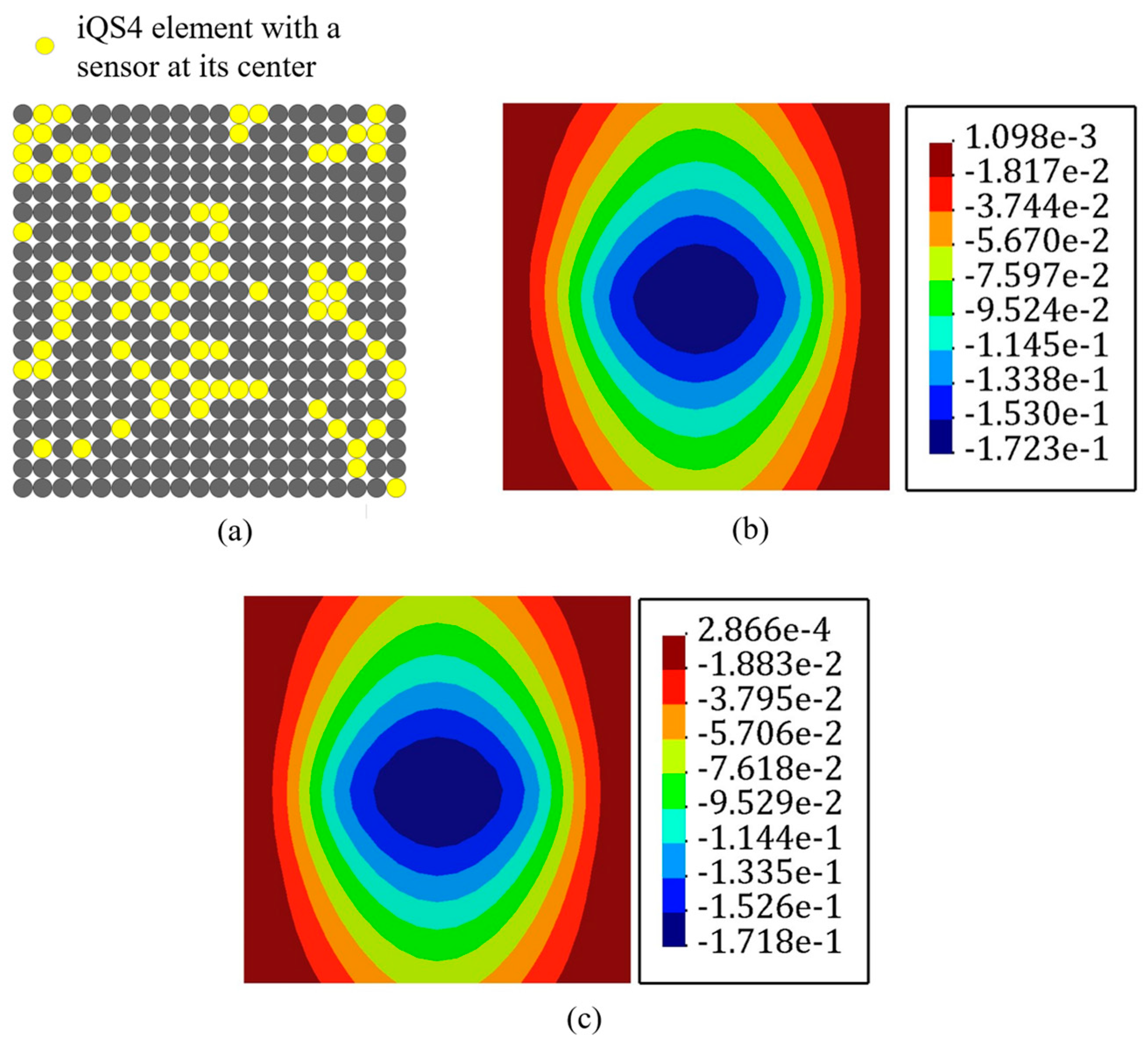
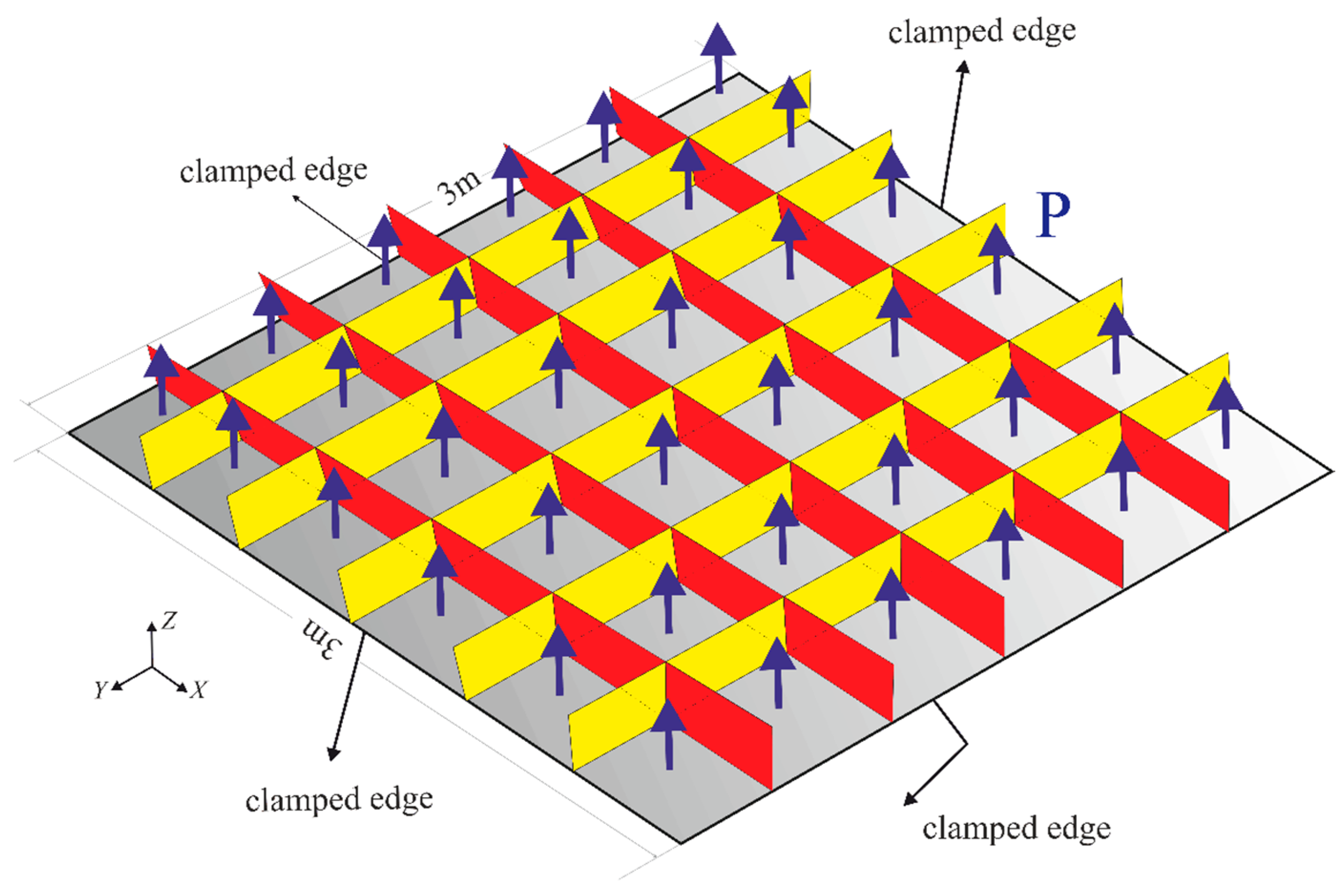
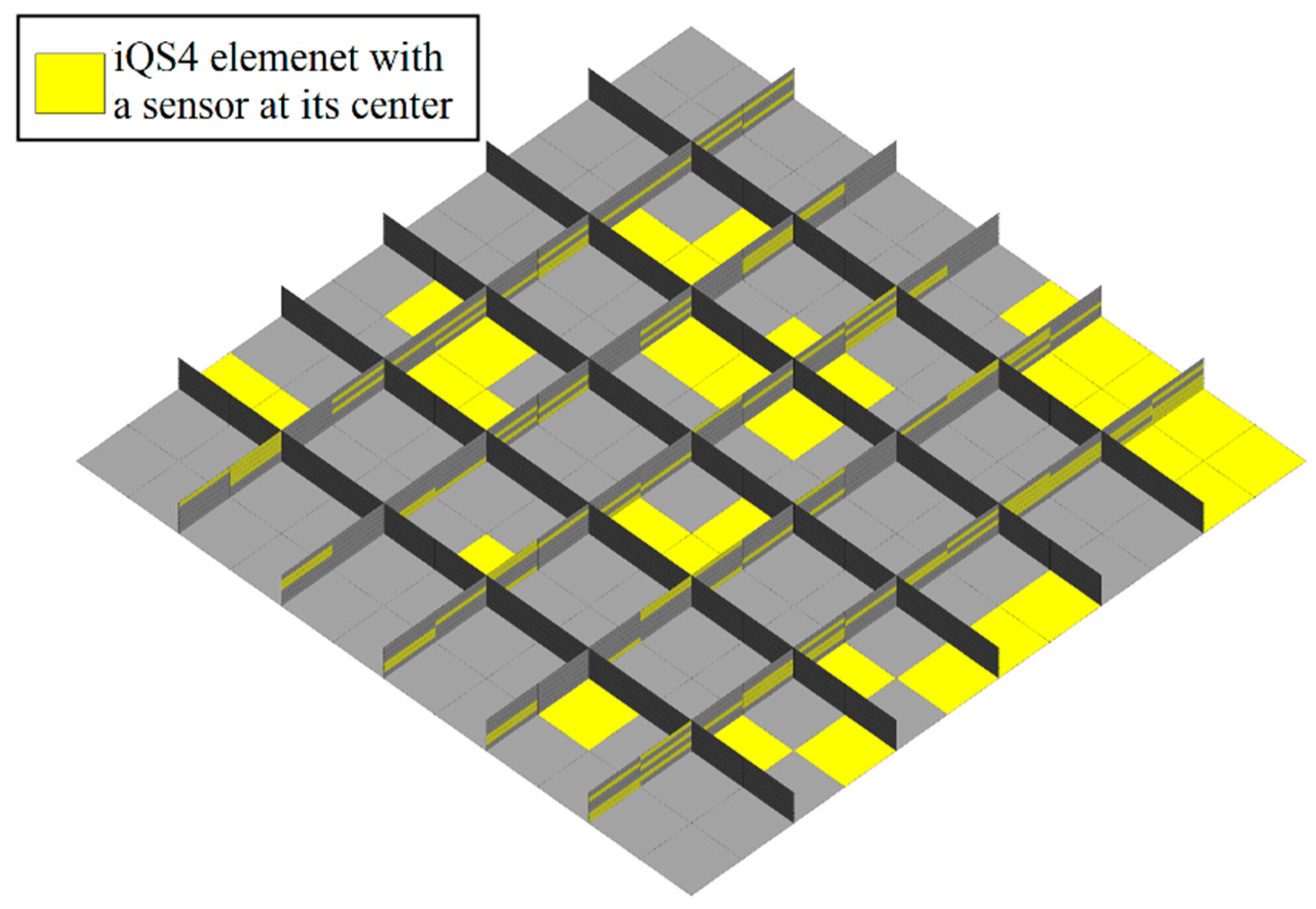
3.4. Fully Clamped Plate under Uniform Pressure
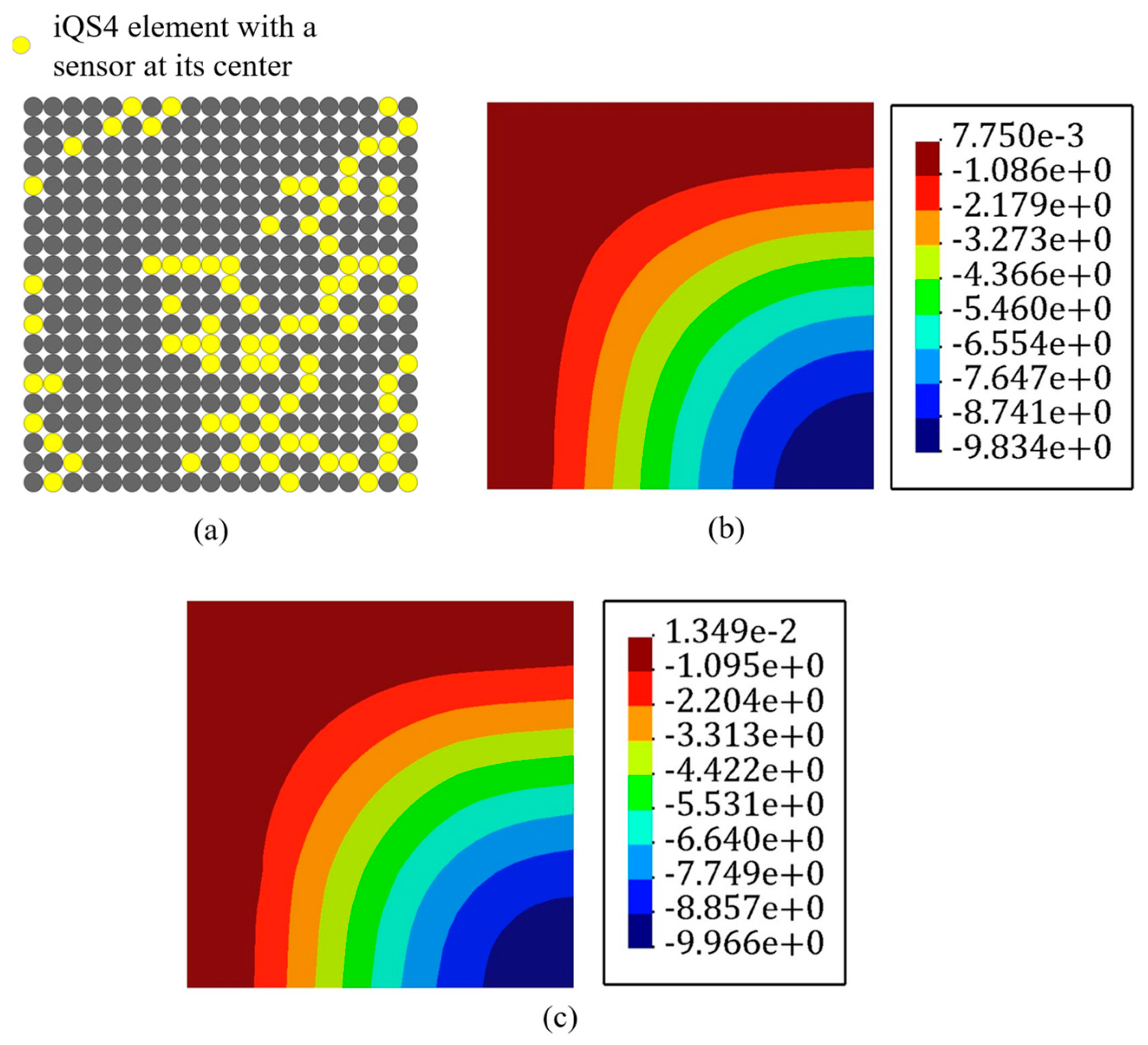
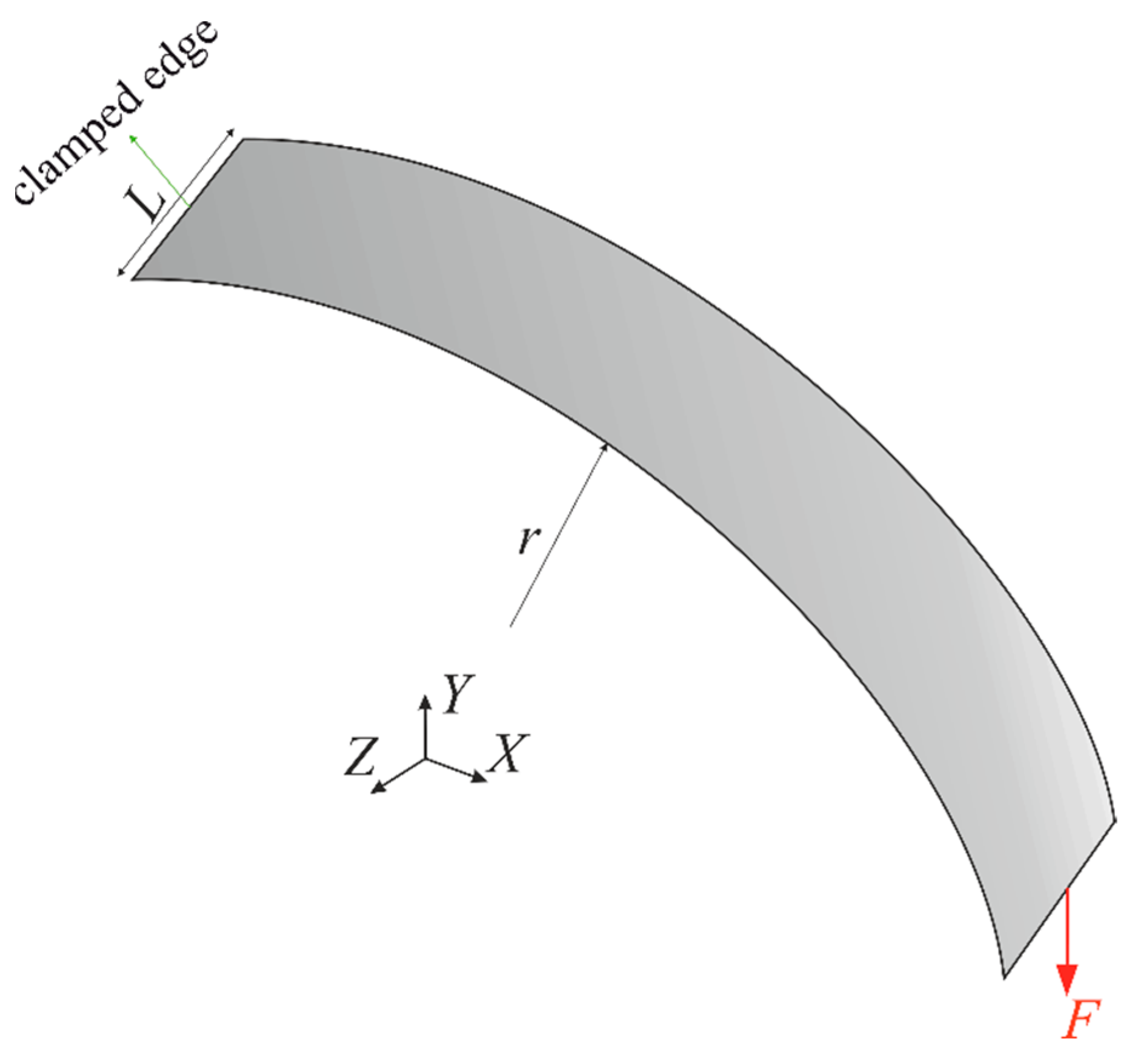
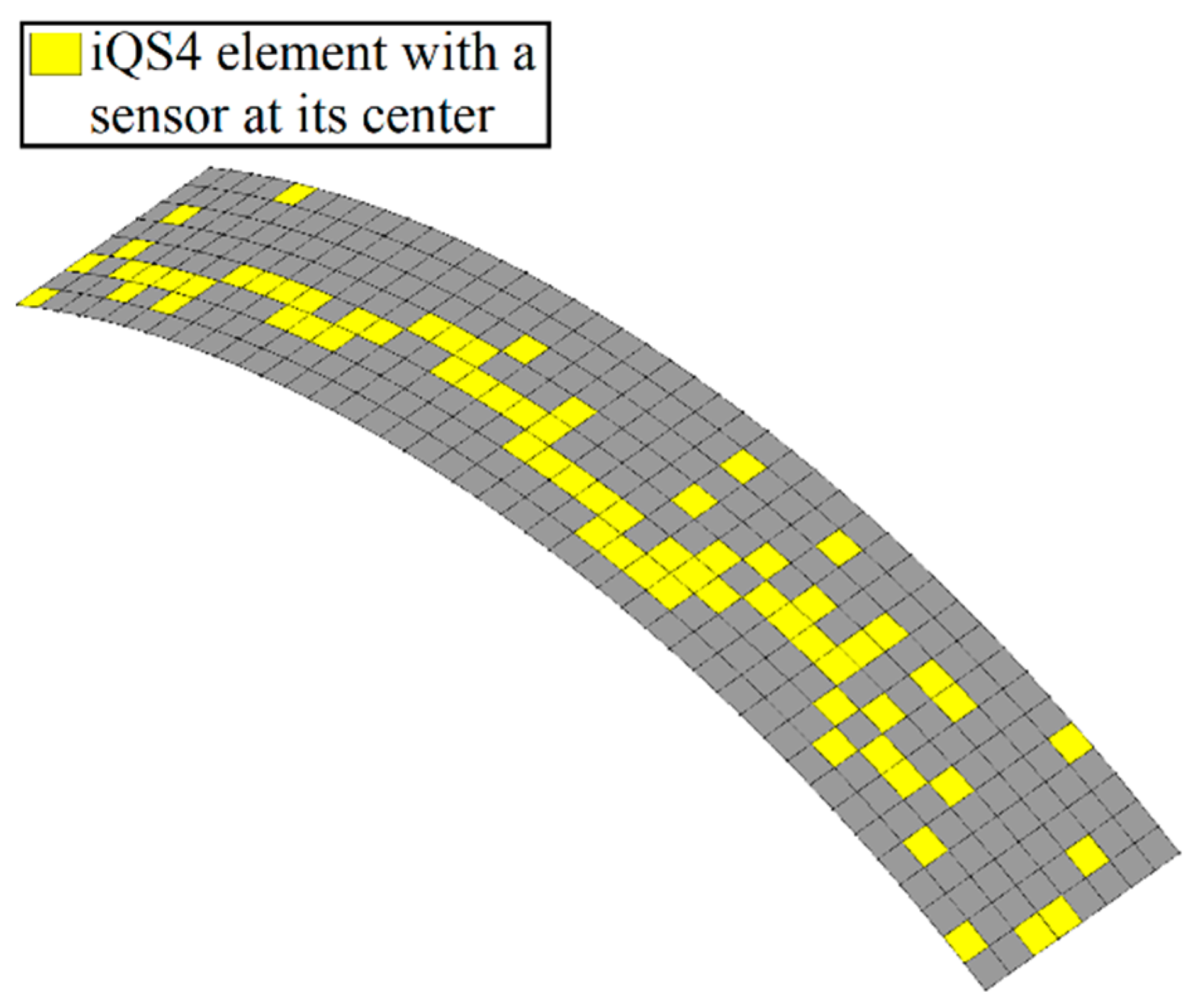
3.5. Stiffened Plate and Curved Shell Structures
4. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Balageas, D.; Fritzen, C.P.; Güemes, A. Structural Health Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2010; Volume 5. [Google Scholar]
- Wild, G.; Pollock, L.; Abdelwahab, A.K.; Murray, J. The Need for Aerospace Structural Health Monitoring: A review of aircraft fatigue accidents. Int. J. Progn. Health Manag. 2021, 24, 12. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Mir-Haidari, S.E.; Behdinan, K. Application and implementation of the bond graph methodology on the structural damage detection and monitoring of aeroengines. Aerosp. Sci. Technol. 2021, 117, 106910. [Google Scholar] [CrossRef]
- Wu, B.; Liu, B.J.; Zheng, J.; Wang, T.; Chen, R.G.; Chen, X.L.; Zhang, K.S.; Zou, Z.Q. Strain-based health monitoring and remaining life prediction of large caliber gun barrel. Measurement 2018, 122, 297–311. [Google Scholar] [CrossRef]
- Saade, M.; Mustapha, S. Assessment of the structural conditions in steel pipeline under various operational conditions—A machine learning approach. Measurement 2020, 166, 108262. [Google Scholar] [CrossRef]
- Fang, F.; Qiu, L.; Yuan, S.; Ren, Y. Dynamic probability modeling-based aircraft structural health monitoring framework under time-varying conditions: Validation in an in-flight test simulated on ground. Aerosp. Sci. Technol. 2019, 95, 105467. [Google Scholar] [CrossRef]
- Gethin, W.R.; Meng, X.L.; Alan, H.D. Integrating a global positioning system and accelerometers to monitor the deflection of bridges. J. Surv. Eng. 2004, 130, 65–72. [Google Scholar]
- Zhang, S.; Liu, B.; He, J. Pipeline deformation monitoring using distributed fiber optical sensor. Measurement 2019, 133, 208–213. [Google Scholar] [CrossRef]
- Brownjohn, J.M.; De Stefano, A.; Xu, Y.L.; Wenzel, H.; Aktan, A.E. Vibration-based monitoring of civil infrastructure: Challenges and successes. J. Civ. Struct. Health Monit. 2011, 1, 79–95. [Google Scholar] [CrossRef]
- Rehman, S.K.; Ibrahim, Z.; Memon, S.A.; Jameel, M. Nondestructive test methods for concrete bridges: A review. Constr. Build. Mater. 2016, 15, 58–86. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibration—Based structural damage identification. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Bengherbia, B.; Zmirli, M.O.; Toubal, A.; Guessoum, A. FPGA-based wireless sensor nodes for vibration monitoring system and fault diagnosis. Measurement 2017, 101, 81–92. [Google Scholar] [CrossRef]
- Kim, H.J.; Jang, B.S.; Du Kim, J. Fatigue-damage prediction for ship and offshore structures under wide-banded non-Gaussian random loadings part I: Approximation of cycle distribution in wide-banded gaussian random processes. Appl. Ocean Res. 2020, 101, 1022. [Google Scholar] [CrossRef]
- Tabrizi, I.E.; Kefal, A.; Zanjani, J.S.; Yildiz, M. Damage growth and failure detection in hybrid fiber composites using experimental in-situ optical strain measurements and smoothing element analysis. Int. J. Damage Mech. 2022, 31, 479–507. [Google Scholar] [CrossRef]
- Kuang, K.S.; Quek, S.T.; Koh, C.G.; Cantwell, W.J.; Scully, P.J. Plastic optical fibre sensors for structural health monitoring: A review of recent progress. J. Sens. 2009, 2009, 312053. [Google Scholar] [CrossRef]
- Lynch, J.P.; Loh, K.J. A summary review of wireless sensors and sensor networks for structural health monitoring. Shock Vib. Dig. 2006, 38, 91–130. [Google Scholar] [CrossRef]
- Mascarenas, D.L.; Todd, M.D.; Park, G.; Farrar, C.R. Development of an impedance-based wireless sensor node for structural health monitoring. Smart Mater. Struct. 2007, 16, 2137. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape sensing methods: Review and experimental comparison on a wing-shaped plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.A.; Kefal, A.; Yildiz, M. A comparative and review study on shape and stress sensing of flat/curved shell geometries using C0-continuous family of iFEM elements. Sensors 2020, 20, 3808. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M. Material and strain sensing uncertainties quantification for the shape sensing of a composite wing box. Mech. Syst. Signal Process. 2021, 160, 107875. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M.; Marzocca, P. External loads identification and shape sensing on an aluminum wing box: An integrated approach. Aerosp. Sci. Technol. 2021, 114, 106. [Google Scholar] [CrossRef]
- Wang, X.; Si, C.; Wang, Z.; Li, Y. Displacement field reconstruction of structures under thermal and mechanical loading environment. Aerosp. Sci. Technol. 2021, 117, 106914. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Wang, J.; Ren, L.; You, R.; Jiang, T.; Jia, Z.; Wang, G.X. Experimental study of pipeline deformation monitoring using the inverse finite element method based on the iBeam3 element. Measurement 2021, 184, 109881. [Google Scholar] [CrossRef]
- Li, M.; Kefal, A.; Cerik, B.C.; Oterkus, E. Dent damage identification in stiffened cylindrical structures using inverse Finite Element Method. Ocean Eng. 2020, 198, 106944. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, L.; Bao, H.; Du, J. Shape sensing of variable cross-section beam using the inverse finite element method and isogeometric analysis. Measurement 2020, 158, 107656. [Google Scholar] [CrossRef]
- Kefal, A.; Tabrizi, I.E.; Yildiz, M.; Tessler, A. A smoothed iFEM approach for efficient shape-sensing applications: Numerical and experimental validation on composite structures. Mech. Syst. Signal Process. 2021, 152, 107486. [Google Scholar] [CrossRef]
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Comparison of strain pre-extrapolation techniques for shape and strain sensing by iFEM of a composite plate subjected to compression buckling. Compos. Struct. 2021, 262, 113587. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A quadrilateral inverse-shell element with drilling degrees of freedom for shape sensing and structural health monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Kefal, A.; Mayang, J.B.; Oterkus, E.; Yildiz, M. Three-dimensional shape and stress monitoring of bulk carriers based on iFEM methodology. Ocean Eng. 2018, 147, 256–267. [Google Scholar] [CrossRef]
- Kefal, A. Structural Health Monitoring of Marine Structures by Using Inverse Finite Element Method. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2015. [Google Scholar]
- Li, M.; Kefal, A.; Oterkus, E.; Oterkus, S. Structural health monitoring of an offshore wind turbine tower using iFEM methodology. Ocean Eng. 2020, 204, 107291. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M. Composite wing box deformed-shape reconstruction based on measured strains: Optimization and comparison of existing approaches. Aerosp. Sci. Technol. 2020, 99, 105758. [Google Scholar] [CrossRef]
- Foss, G.; Haugse, E. Using modal test results to develop strain to displacement transformations. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995; Volume 112. [Google Scholar]
- Ko, W.L.; Richards, W.L.; Tran, V.T. Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures; NASA/TP-2007-214612; NASA: Washington, DC, USA, 2007.
- Cortés, A.; Romate, X.F.; Jiménez-Suárez, A.; Campo, M.; Prolongo, M.G.; Ureña, A.; Prolongo, S.G. 3D printed anti-icing and de-icing system based on CNT/GNP doped epoxy composites with self-curing and structural health monitoring capabilities. Smart Mater. Struct. 2020, 30, 25016. [Google Scholar] [CrossRef]
- Lammering, R.; Gabbert, U.; Sinapius, M.; Schuster, T.; Wierach, P. (Eds.) Lamb-Wave Based Structural Health Monitoring in Polymer Composites; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fu, H.; Khodaei, Z.S.; Aliabadi, M.F. An event-triggered energy-efficient wireless structural health monitoring system for impact detection in composite airframes. IEEE Internet Things J. 2018, 29, 1183–1192. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Tessler, A. Real-time displacement monitoring of a composite stiffened panel subjected to mechanical and thermal loads. Meccanica 2015, 50, 2487–2496. [Google Scholar] [CrossRef]
- Kefal, A.; Tabrizi, I.E.; Tansan, M.; Kisa, E.; Yildiz, M. An experimental implementation of inverse finite element method for real-time shape and strain sensing of composite and sandwich structures. Compos. Struct. 2021, 15, 258. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Di Sciuva, M.; Tessler, A. A novel approach for displacement and stress monitoring of sandwich structures based on the inverse Finite Element Method. Compos. Struct. 2015, 127, 69–76. [Google Scholar] [CrossRef]
- Kefal, A.; Tessler, A.; Oterkus, E. An enhanced inverse finite element method for displacement and stress monitoring of multilayered composite and sandwich structures. Compos. Struct. 2017, 179, 514–540. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. A consistent refinement of first-order shear deformation theory for laminated composite and sandwich plates using improved zigzag kinematics. J. Mech. Mater. Struct. 2010, 5, 341–367. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Shape sensing of 3D frame structures using an inverse finite element method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Roy, R.; Gherlone, M.; Surace, C. A shape sensing methodology for beams with generic cross-sections: Application to airfoil beams. Aerosp. Sci. Technol. 2021, 110, 106484. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Shape sensing of aerospace structures by coupling isogeometric analysis and inverse finite element method. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Grapevine, TX, USA, 9–13 January 2017; p. 427. [Google Scholar]
- Papa, U.; Russo, S.; Lamboglia, A.; Del Core, G.; Iannuzzo, G. Health structure monitoring for the design of an innovative UAS fixed wing through inverse finite element method (iFEM). Aerosp. Sci. Technol. 2017, 69, 439–448. [Google Scholar] [CrossRef]
- Kefal, A.; Yildiz, M. Modeling of sensor placement strategy for shape sensing and structural health monitoring of a wing-shaped sandwich panel using inverse finite element method. Sensors 2017, 17, 2775. [Google Scholar] [CrossRef]
- Kammer, D.C.; Tinker, M.L. Optimal placement of triaxial accelerometers for modal vibration tests. Mech. Syst. Signal Process. 2004, 18, 29–41. [Google Scholar] [CrossRef]
- Kammer, D.C. Sensor placement for on-orbit modal identification and correlation of large space structures. J. Guid. Control. Dyn. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Salama, M.; Rose, T.; Garba, J. Optimal placement of excitations and sensors for verification of large dynamical systems. In Proceedings of the 28th Structures, Structural Dynamics and Materials Conference, Monterey, CA, USA, 6–8 April 1987; p. 782. [Google Scholar]
- Yi, T.H.; Li, H.N.; Gu, M. Optimal sensor placement for structural health monitoring based on multiple optimization strategies. Struct. Des. Tall Spec. Build. 2011, 20, 881–900. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Soman, R.; Malinowski, P. Optimization of sensor placement for structural health monitoring: A review. Struct. Health Monit. 2019, 18, 963–988. [Google Scholar] [CrossRef]
- Yang, W.; Yang, H.; Tang, S. Optimization, and control application of sensor placement in aero servo elastic of UAV. Aerosp. Sci. Technol. 2019, 85, 61–74. [Google Scholar] [CrossRef]
- Kefal, A. An efficient curved inverse-shell element for shape sensing and structural health monitoring of cylindrical marine structures. Ocean Eng. 2019, 188, 106262. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.A.; Tabrizi, I.E.; Kefal, A.; Yildiz, M. A combined experimental/numerical study on deformation sensing of sandwich structures through inverse analysis of pre-extrapolated strain measurements. Measurement 2021, 185, 110031. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Isogeometric iFEM analysis of thin shell structures. Sensors 2020, 20, 2685. [Google Scholar] [CrossRef] [PubMed]
- Roy, R.; Tessler, A.; Surace, C.; Gherlone, M. Shape sensing of plate structures using the inverse finite element method: Investigation of efficient strain-sensor patterns. Sensors 2020, 20, 7049. [Google Scholar] [CrossRef] [PubMed]
- Cook, R.D. Four-node ‘flat’ shell element: Drilling degrees of freedom, membrane-bending coupling, warped geometry, and behavior. Comput. Struct. 1994, 50, 549–555. [Google Scholar] [CrossRef]
- Tessler, A.; Hughes, T.J. An improved treatment of transverse shear in the Mindlin-type four-node quadrilateral element. Comput. Methods Appl. Mech. Eng. 1983, 39, 311–335. [Google Scholar] [CrossRef]
- Bentley, P.J.; Wakefield, J.P. Hierarchical crossover in genetic algorithms. In Proceedings of the 1st On-Line Workshop on Soft Computing (WSC1), Nagoya, Japan, 19–31 August 1996; pp. 37–42. [Google Scholar]
- Liu, W.; Gao, W.C.; Sun, Y.; Xu, M.J. Optimal sensor placement for spatial lattice structure based on genetic algorithms. J. Sound Vib. 2008, 317, 75–89. [Google Scholar] [CrossRef]
- Guo, H.Y.; Zhang, L.; Zhang, L.L.; Zhou, J.X. Optimal placement of sensors for structural health monitoring using improved genetic algorithms. Smart Mater. Struct. 2004, 13, 528. [Google Scholar] [CrossRef]
- Swann, C.; Chattopadhyay, A. Optimization of piezoelectric sensor location for delamination detection in composite laminates. Eng. Optim. 2006, 38, 511–528. [Google Scholar] [CrossRef]








| Individual | Sum of Gene Values, | ||||
|---|---|---|---|---|---|
| … | |||||
| 1 | 1 | 0 | … | 1 | |
| 2 | 0 | 0 | … | 1 | |
| … | … | … | … | … | … |
| 1 | 1 | … | 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghasemzadeh, M.; Kefal, A. Sensor Placement Optimization for Shape Sensing of Plates and Shells Using Genetic Algorithm and Inverse Finite Element Method. Sensors 2022, 22, 9252. https://doi.org/10.3390/s22239252
Ghasemzadeh M, Kefal A. Sensor Placement Optimization for Shape Sensing of Plates and Shells Using Genetic Algorithm and Inverse Finite Element Method. Sensors. 2022; 22(23):9252. https://doi.org/10.3390/s22239252
Chicago/Turabian StyleGhasemzadeh, Maryam, and Adnan Kefal. 2022. "Sensor Placement Optimization for Shape Sensing of Plates and Shells Using Genetic Algorithm and Inverse Finite Element Method" Sensors 22, no. 23: 9252. https://doi.org/10.3390/s22239252
APA StyleGhasemzadeh, M., & Kefal, A. (2022). Sensor Placement Optimization for Shape Sensing of Plates and Shells Using Genetic Algorithm and Inverse Finite Element Method. Sensors, 22(23), 9252. https://doi.org/10.3390/s22239252







