Link-State Aware Hybrid Routing in the Terrestrial–Satellite Integrated Network †
Abstract
1. Introduction
- Link-state aware hybrid routing: Although existing works have already studied the communication link planning according to the network topology information, the intermittent and dynamic nature of the TSE–satellite link selection is still missing. In our work, we propose a link-state aware hybrid routing scheme for data transmission in the dynamic TSIN. The design is under a practical communication scenario that the link connections in satellites and resources are time-varying. By deriving the delay of both inter-satellite and TSE–satellite links, we formulate a hybrid routing problem aimed at minimizing the data transmission delay by optimally selecting the inter-satellite and TSE–satellite links.
- Characterization on TSIN topology: The updating time of the topology structure is assumed to be a fixed time interval in existing models, which introduces significant difficulties in balancing the network overhead and accurate transmission delay. To tackle this issue, we propose a space–time topology graph to represent the data transmission process in dynamic TSIN, where the link resources in both the spatial and temporal dimensions are quantified. In particular, we derive the optimal time updating interval of the topology relationship, with which the effectiveness and accuracy of obtaining the hybrid path can be balanced.
- Decomposition solution: The inter-satellite link and terrestrial–satellite link connection are time-varying and intermittent in TSIN, which makes the optimal data transmission path planning a challenging issue. By exploiting the space–time topology structure, we propose a satellite link selection algorithm to resolve the optimum inter-satellite link connection problem. Then, a hybrid routing algorithm based on a bipartite graph is proposed to determine the optimal TSE–satellite communication link connection, which can solve the subproblems with smaller sizes.
2. Related Work
2.1. Satellite Routing Schemes
2.2. Hybrid Terrestrial–Satellite Routing Schemes
3. System Model
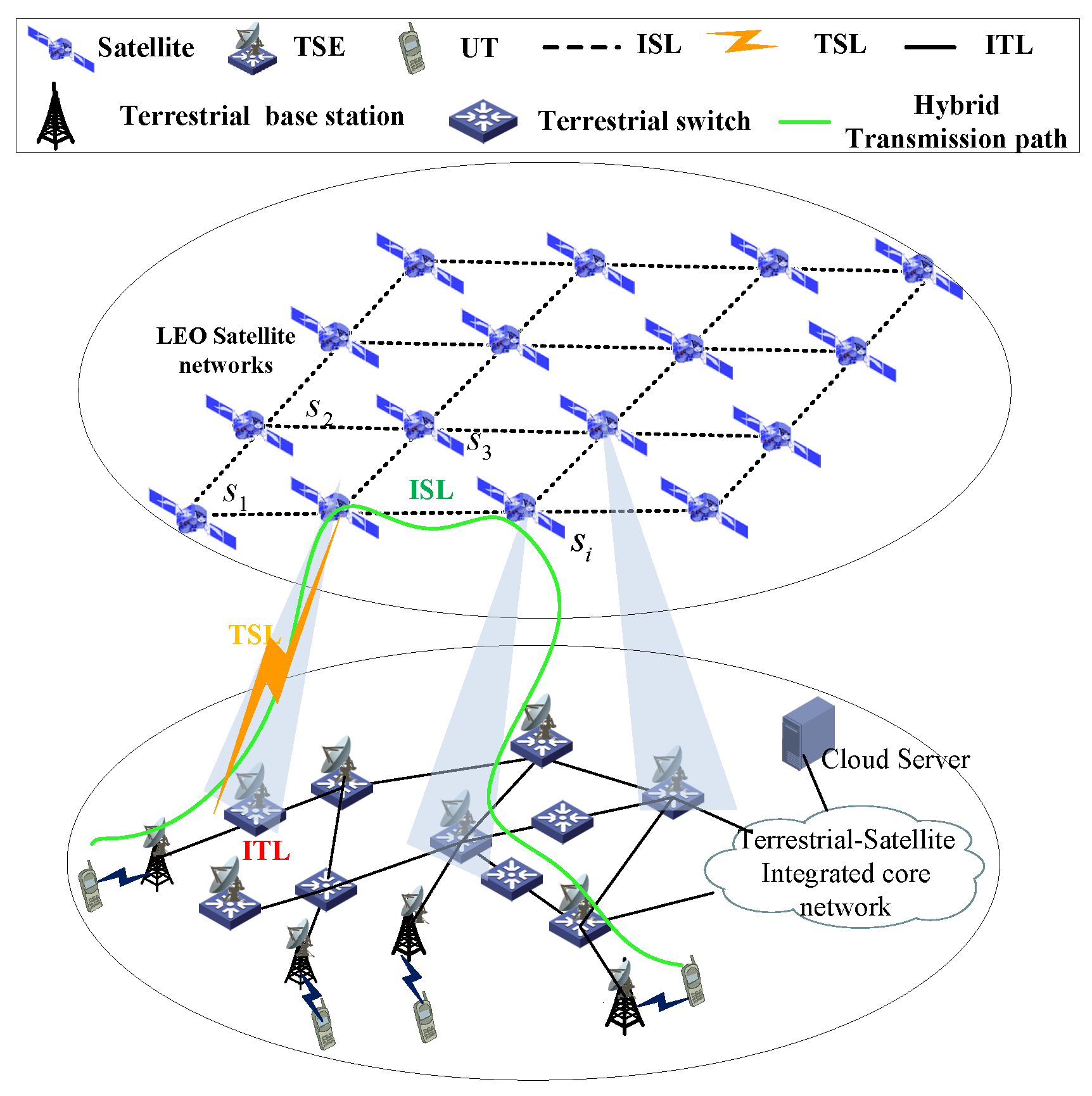
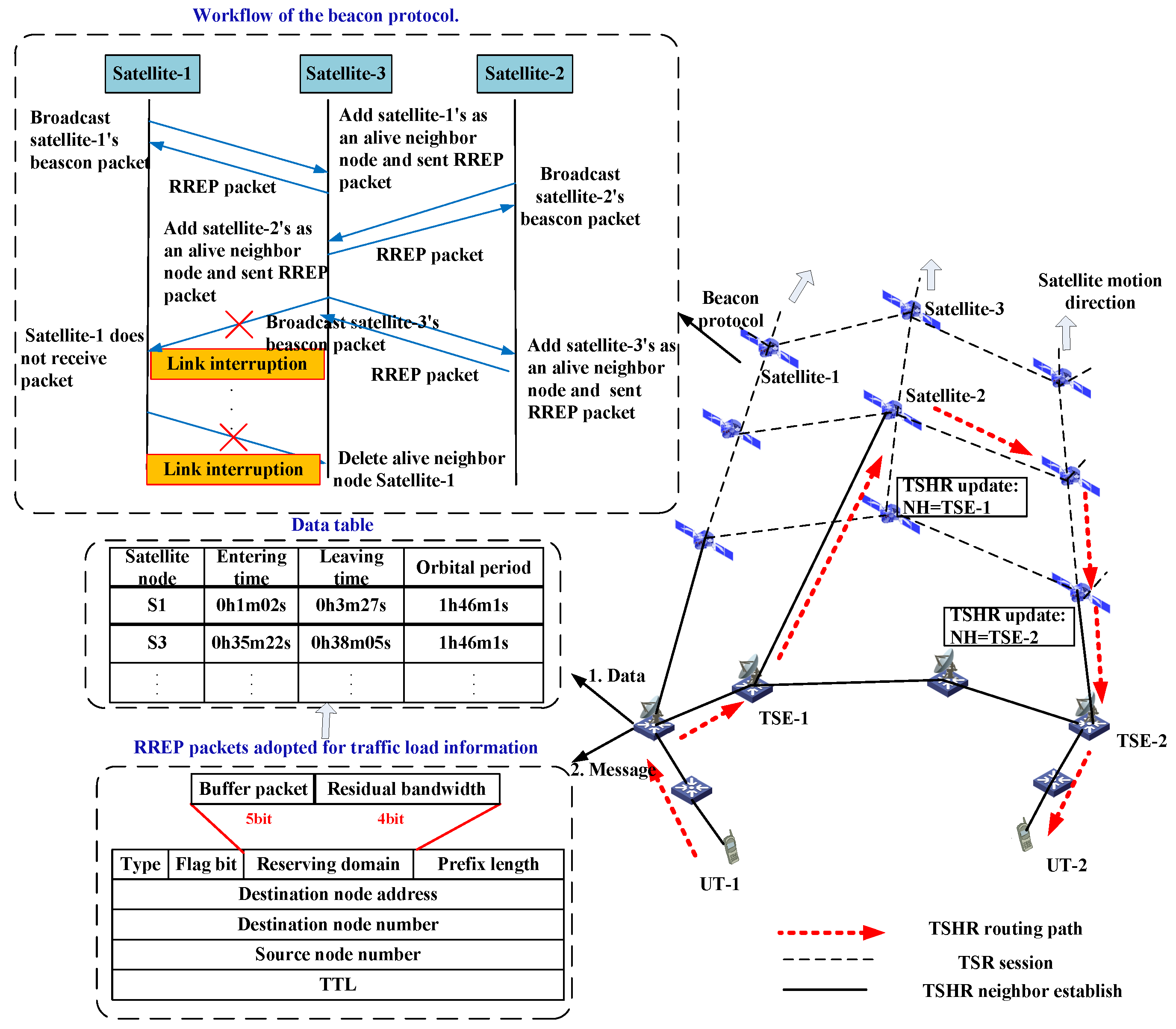
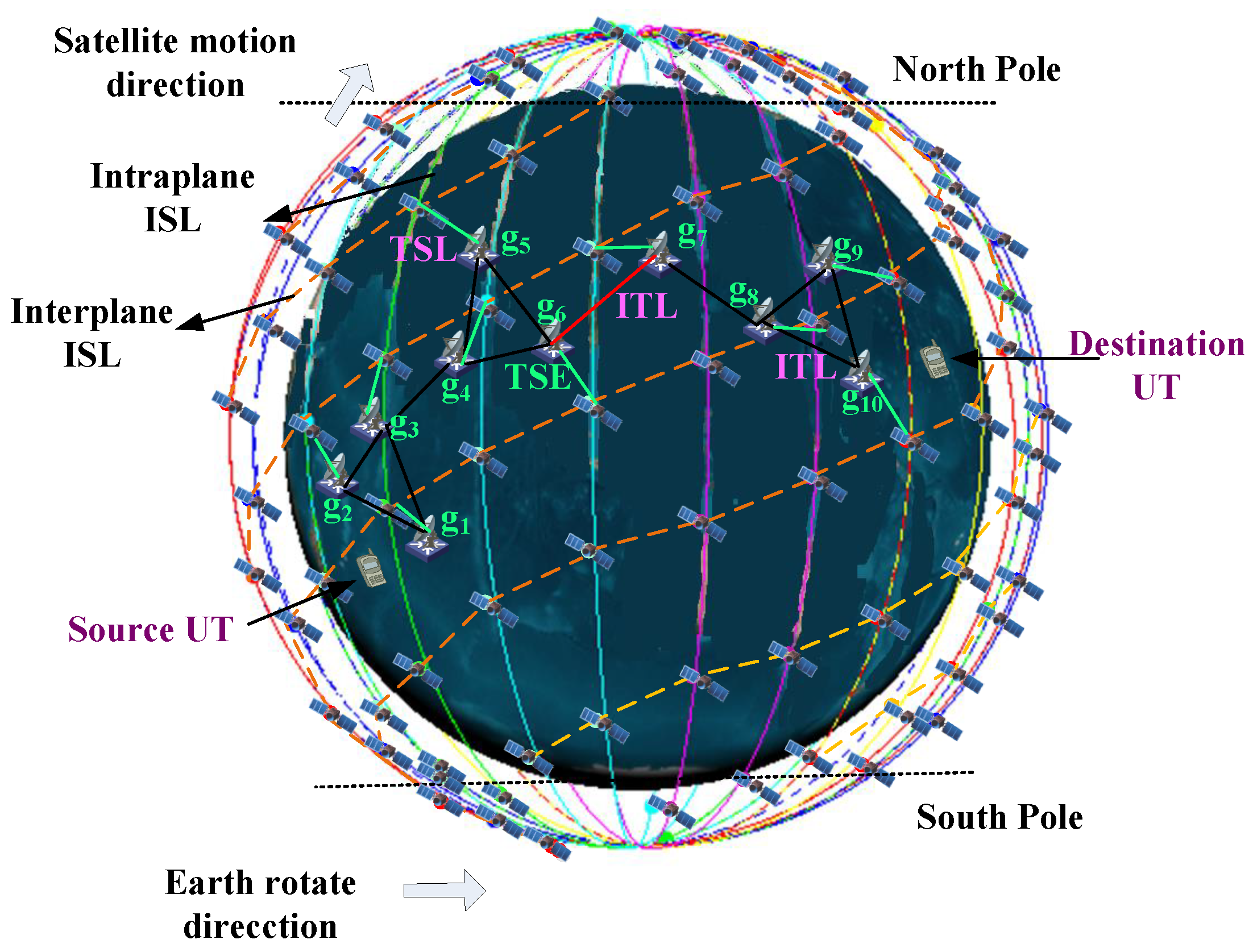
3.1. Scenario Description
- -
- Inter-satellite link (ISL): the link between satellites, the distance of which would change rapidly with the highly moving constellations.
- -
- TSE-satellite link (TSL): the link between a TSE and a satellite. Since a satellite can cover different TSEs for a different time, the TSL is time-varying.
- -
- Inter-terrestrial link (ITL): the link between terrestrial nodes. As the terrestrial network service equipments are usually static, the ITL distance is invariant.
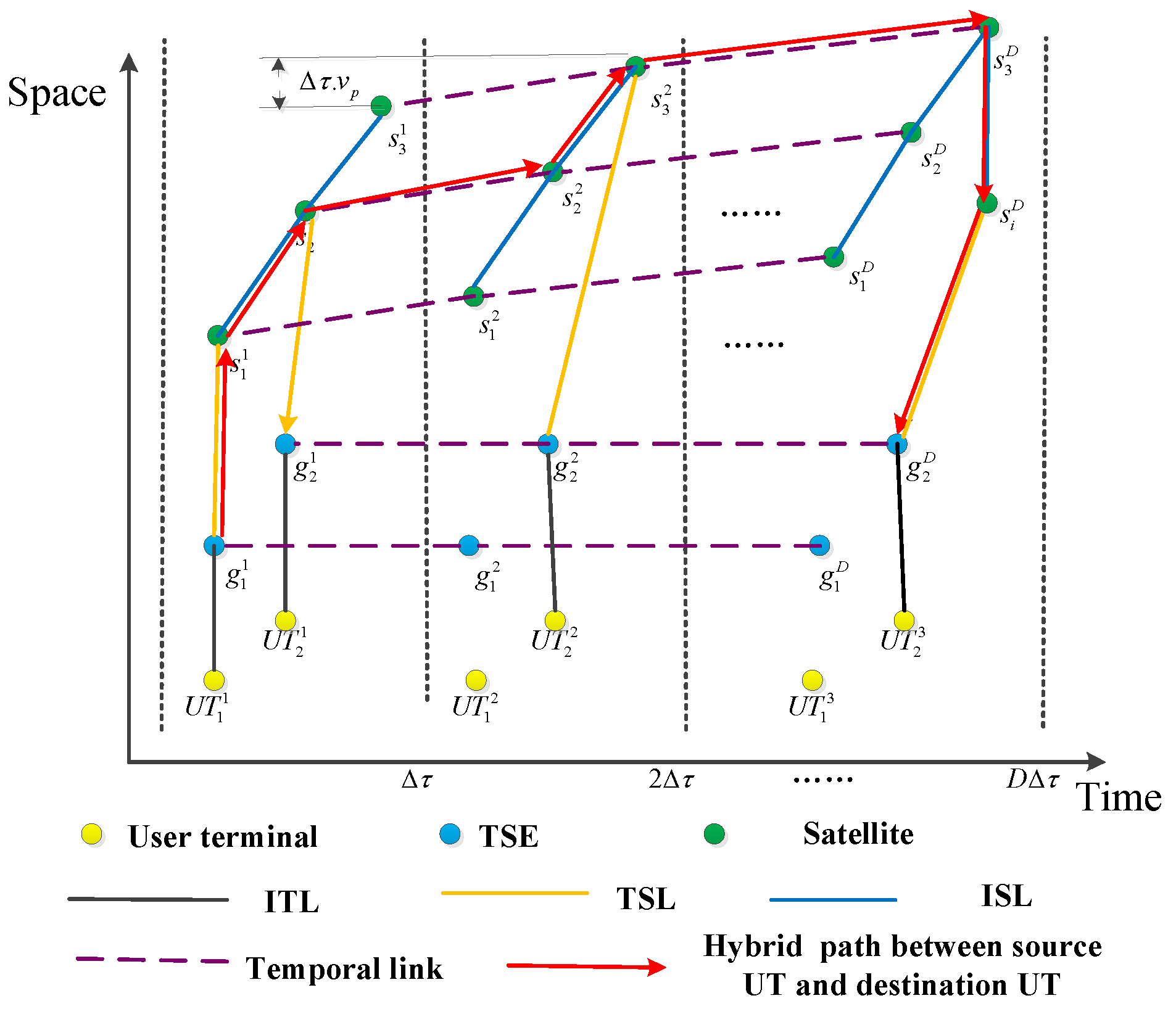
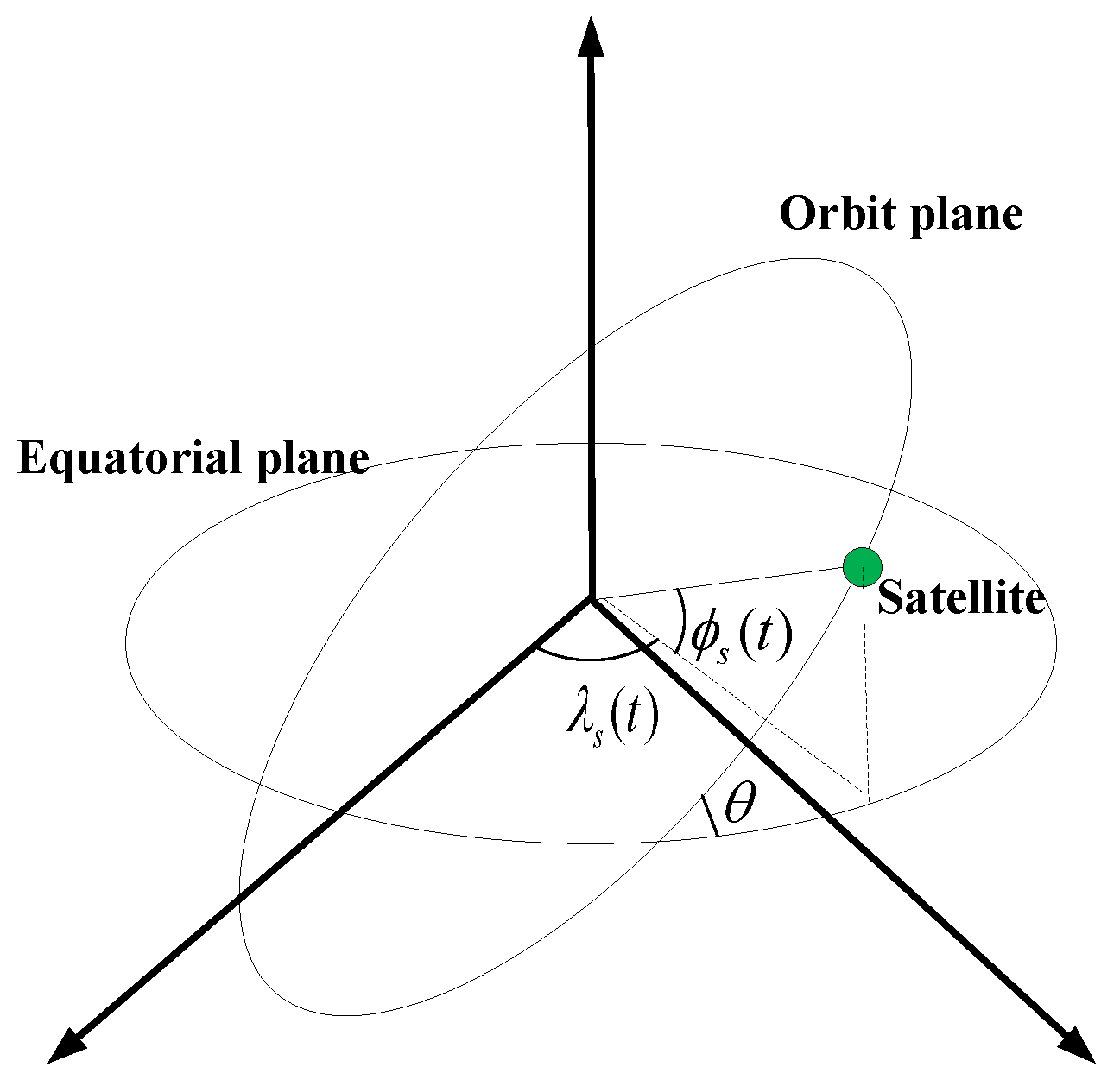
3.2. Space–Time Topology Model
3.3. Problem Formulation
4. Link-State Aware Hybrid Routing Scheme
4.1. Time Interval Optimization
4.2. Link-State Aware Hybrid Routing Algorithm
4.2.1. Time Interval Optimization-Based ISL Selection Algorithm
| Algorithm 1 Time Interval Optimization-based Satellite Routing |
Input: Space-Time graph , source satellite , TTL of data packet, start time t, data packet size Output: Router Table 1:Initialize: Update router table and searched set by executing Algorithm 1 Let source set Set termination time Optimal set 2: If then 3: Return 4: End 5: While do 6: foreach do 7: If then 8: Continue loop in line 6 9: End 10: 11: Neighbor Find all non-empty neighbor set of 12: Update by executing Algorithm 1 13: End for 14: Extract which has minimum delay from 15: Add into 16: Add into 17: Return |
| Algorithm 2 Link Delay Maintenance |
Input: Source satellite , start time t, terminal time , data packet size , neighbor set Output: The optimal set 1:Foreach 2: If then 3: Continue loop in line 1 4: End 5: If 6: Continue loop in line 1 7: End 8: 9: If then 10: , put into ; 11: Replace with ; 12: End 13: End 14: Return |
4.2.2. Hybrid Routing Algorithm Based on Bipartite Graph
| Algorithm 3 KM-based Link Selection |
Input: Bipartite graph, the minimum matching of Output: link selection in t-th 1:Initialize: 2: Foreach do 3: If then 4: , 5: If 6: Continue loop in line 2 7: End 8: If then 9: 10: 11: End 12: End 13: Extract in 14: End 15: Return |
| Algorithm 4 KM-based Link-state Aware Terrestrial-Satellite Hybrid Routing algorithm |
Input:Network topology; Output: Link planning of hybrid routing 1:Initialize: Update by executing Algorithm 2 2: If then 3: Construct bipartite graph of 4: Calculate link metric of according to (24) 5: Calculate the minimum weight match of by using Algorithm3, Extract hybrid path planning in t-th 6: Write in link connection planning 7: Update data volume of link according (25) 8: 9: End 10: Return |
4.3. Complexity Analysis
5. Simulation and Analysis
5.1. Simulation Setup
5.2. Satellite Routing Performance
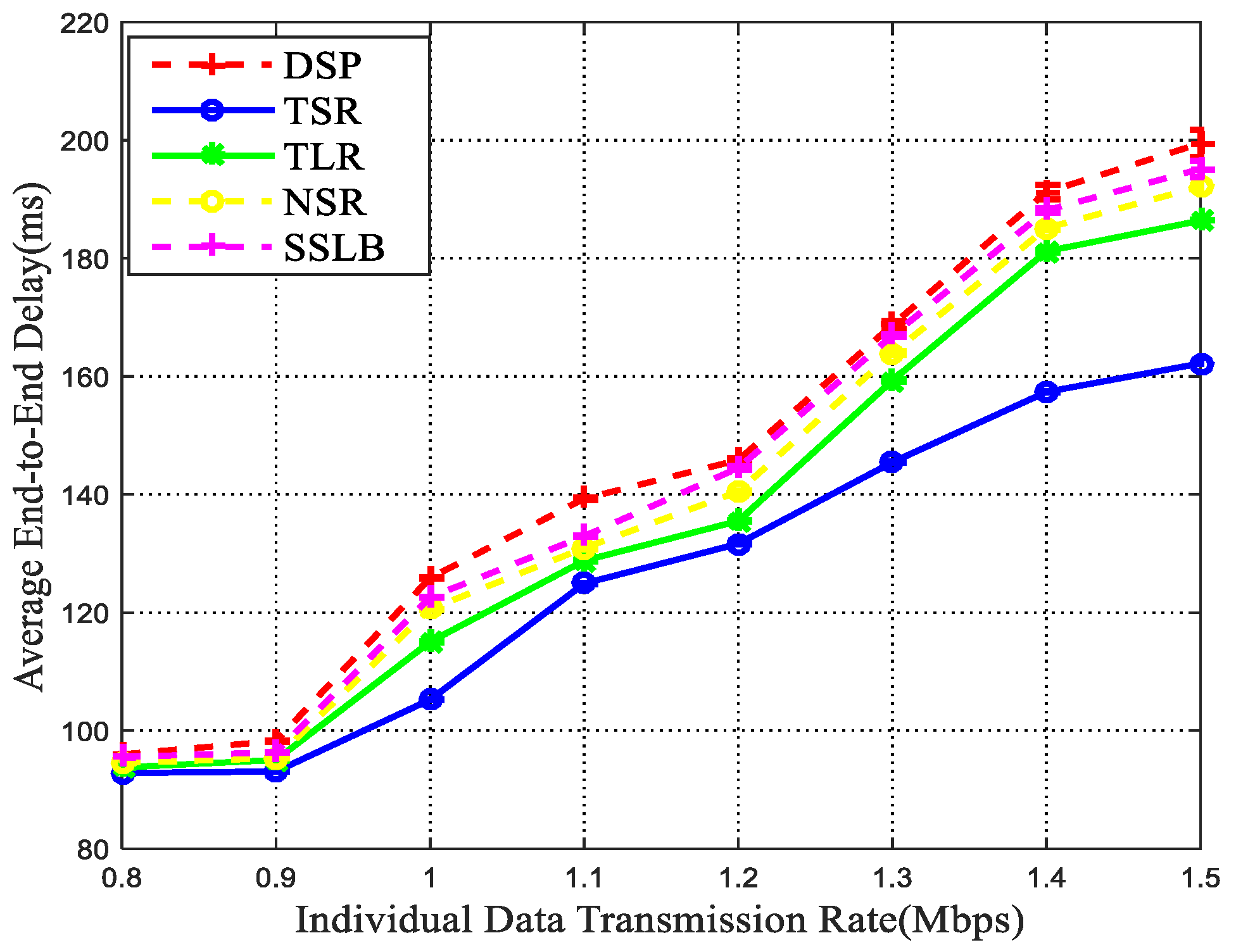
5.2.1. Transmission Delay
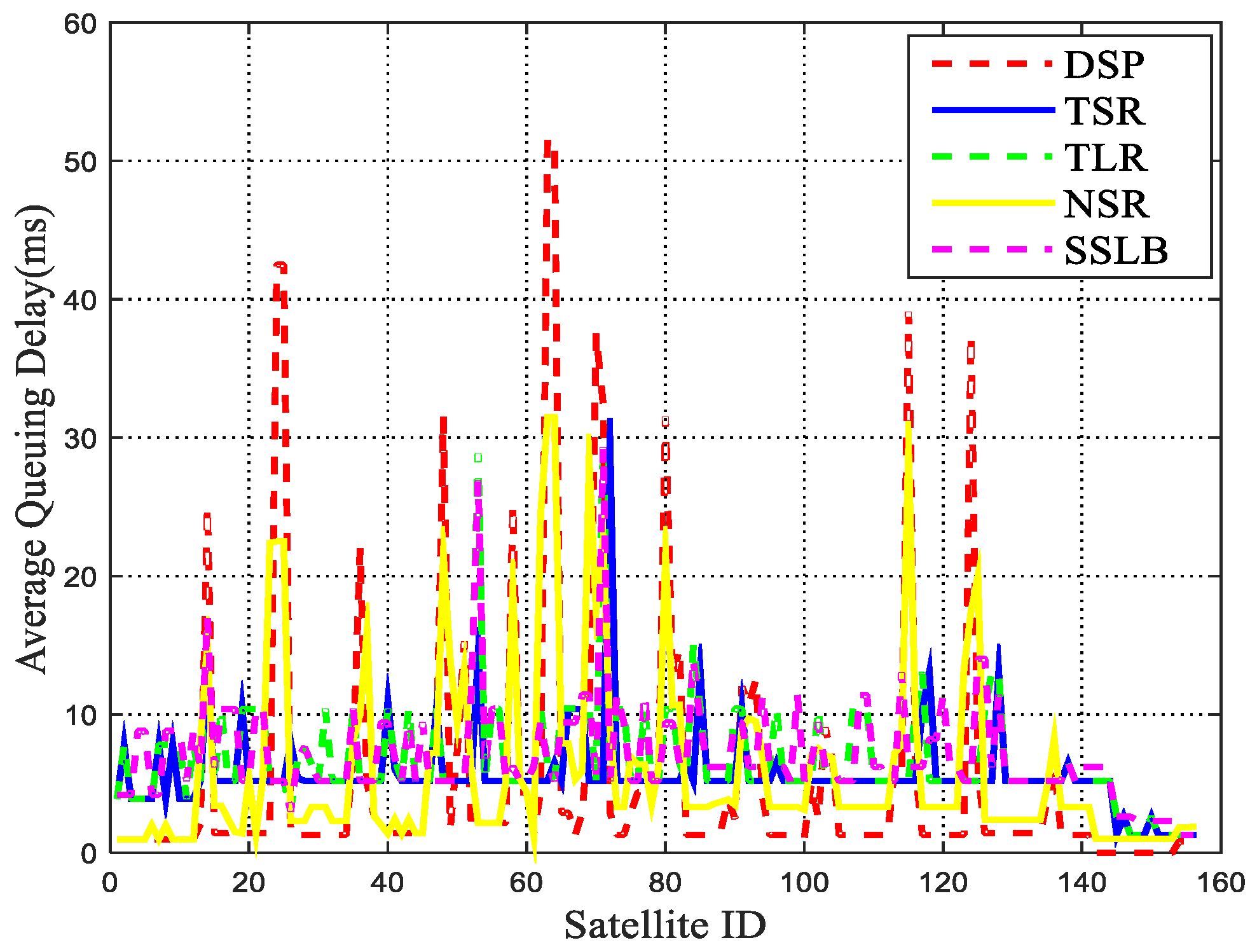
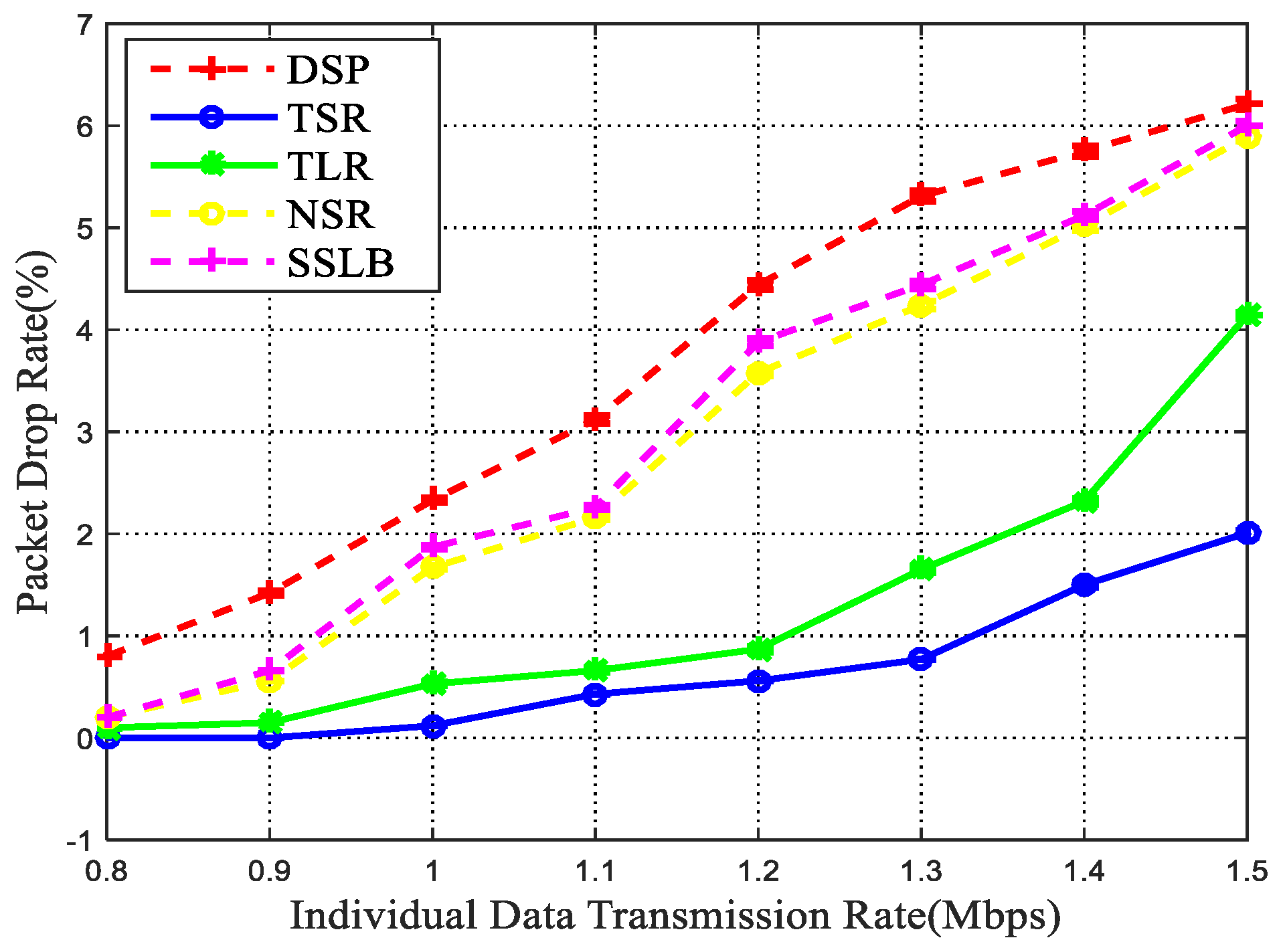
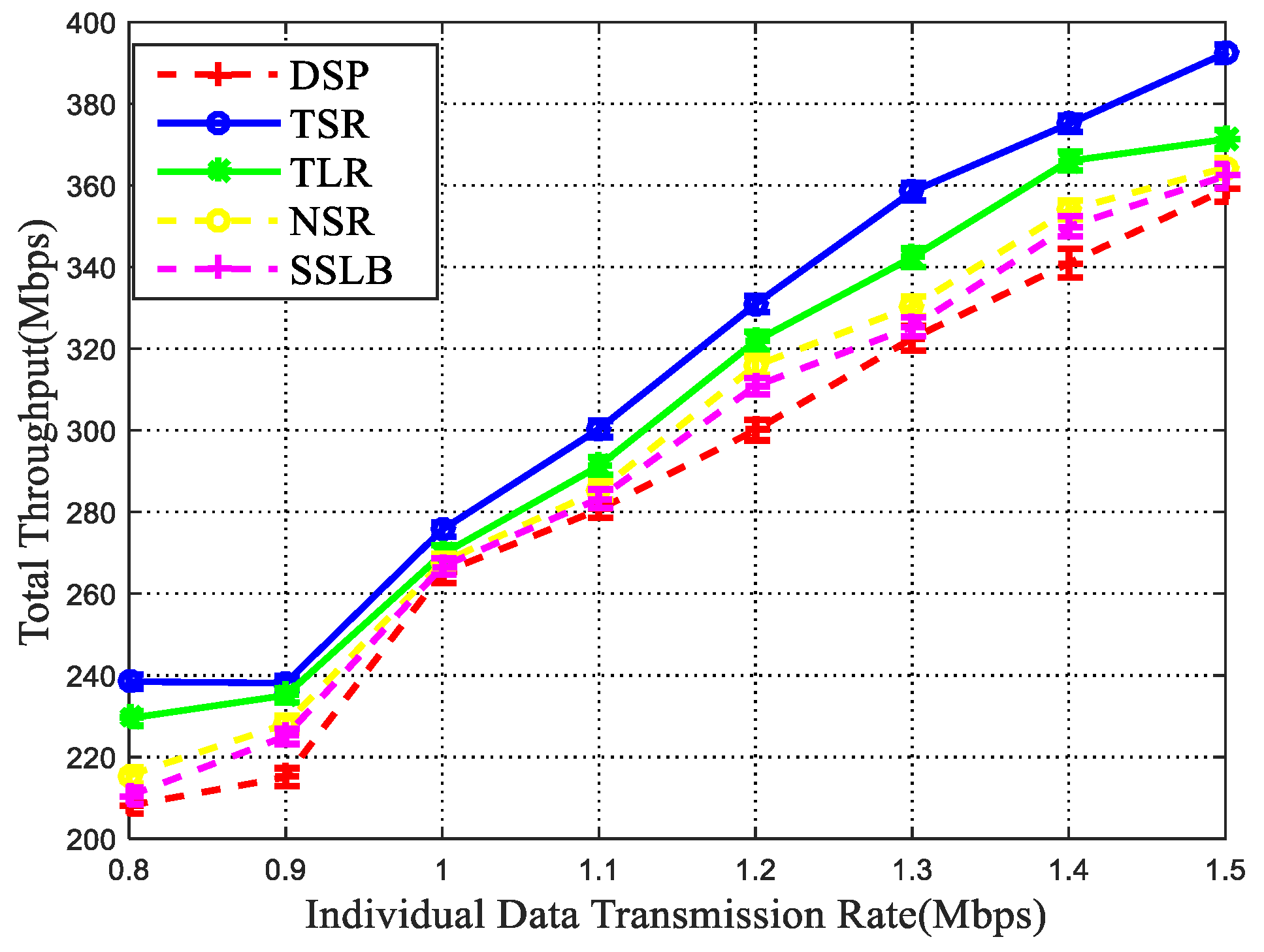
5.2.2. Packet Drop Rate and Network Throughput
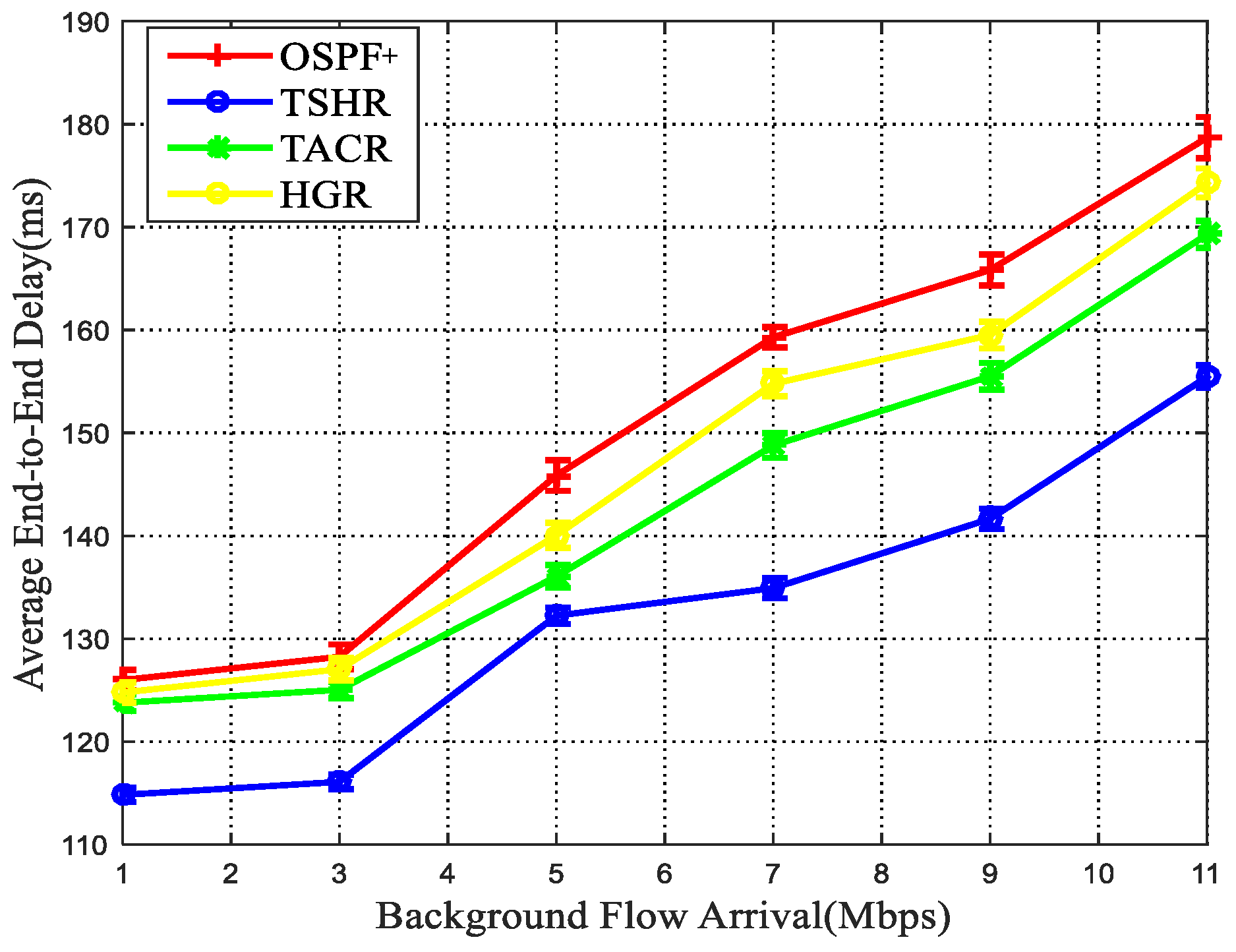
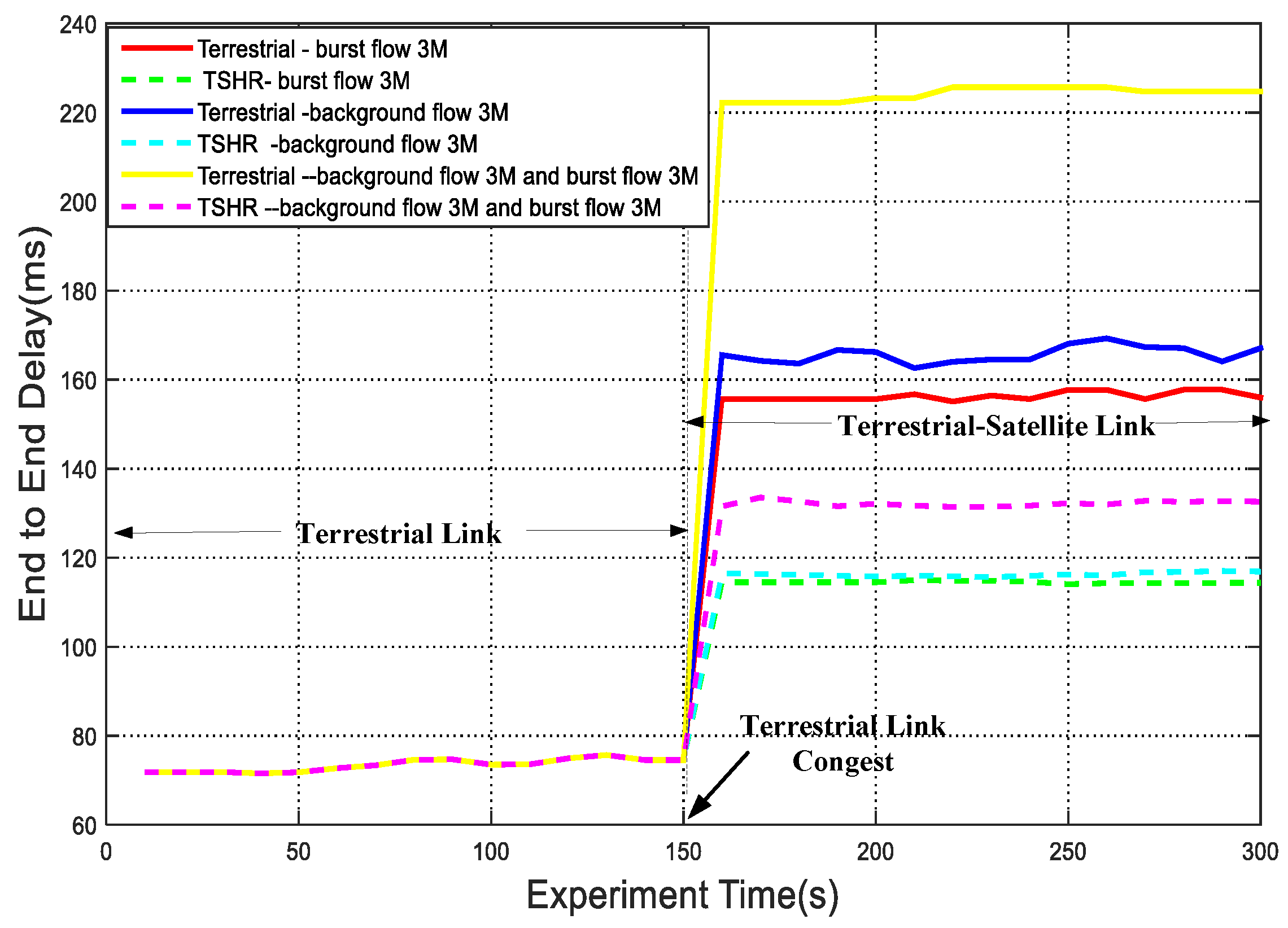
5.3. Terrestrial–Satellite Routing Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhou, C.; Wu, W.; He, H.; Y, P.; Lyu, F.; Cheng, N.; Shen, X. Deep Reinforcement Learning for Delay-Oriented IoT Task Scheduling in Space-Air-Ground Integrated Network. IEEE Trans. Wirel. Commun. 2021, 20, 911–925. [Google Scholar] [CrossRef]
- Chiu, T.; Pang, A.; Chung, W.; Zhang, J. Latency-Driven Fog Cooperation Approach in Fog Radio Access Networks. IEEE Trans. Serv. Comput. 2019, 12, 698–711. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, C.; Wang, J.; Wang, L.; Ren, Y.; Hanzo, L. Multicast Beamforming Optimization in Cloud-Based Heterogeneous Terrestrial and Satellite Networks. IEEE Trans. Veh. Technol. 2020, 69, 1766–1776. [Google Scholar] [CrossRef]
- Bi, Y.; Han, G.; Xu, S.; Wang, X.; Lin, C.; Yu, Z.; Sun, P. Software Defined Space-Terrestrial Integrated Networks: Architecture, Challenges and Solutions. IEEE Netw. Mag. 2019, 33, 22–28. [Google Scholar] [CrossRef]
- Shen, X.; Cheng, N.; Zhou, H.; Lyu, F.; Quan, W.; Shi, W.; Wu, H.; Zhou, C. Space-air-ground integrated networks: Review and prospect. Chin. J. Internet Things 2020, 4, 1–17. [Google Scholar]
- Kato, N.; Fadlullah, Z.M.; Tang, F.; Mao, B.; Tani, S.; Okamura, A.; Liu, J. Optimizing Space-Air-Ground Integrated Networks by Artificial Intelligence. IEEE Wirel. Commun. Mag. 2019, 26, 140–147. [Google Scholar] [CrossRef]
- Xu, H.; Li, D.; Liu, M.; Han, G.; Huang, W.; Xu, C. QoE-driven intelligent handover for user-centric mobile satellite networks. IEEE Trans. Veh. Technol. 2020, 69, 10127–10139. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-Air-Ground Integrated Network: A Survey. IEEE Commun. Surv. Tutorials 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- Khan, M.A.; Kumar, N.; Mohsan, S.A.H.; Khan, W.U.; Nasralla, M.M.; Alsharif, M.H.; Zywiołek, J.; Ullah, I. Swarm of UAVs for Network Management in 6G: A Technical Review. IEEE Trans. Netw. Serv. Manag. 2022. [Google Scholar] [CrossRef]
- Di, B.; Zhang, H.; Song, L.; Li, Y.; Li, G.Y. Ultra-dense LEO: Integrating Terrestrial-Satellite Networks into 5G and Beyond for Data Offloading. IEEE Trans. Wirel. Commun. 2019, 57, 62–69. [Google Scholar] [CrossRef]
- Cheng, N.; Quan, W.; Shi, W.; Wu, H.; Ye, Q.; Zhou, H.; Zhuang, W.; Shen, X.; Bai, B. A Comprehensive Simulation Platform for Space-Air-Ground Integrated Network. IEEE Wirel. Commun. 2020, 27, 178–185. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Y.; Zhao, L.; Kato, N. Joint Placement of Controllers and Gateways in SDN-Enabled 5G-Satellite Integrated Network. IEEE J. Sel. Areas Commun. 2018, 36, 221–232. [Google Scholar] [CrossRef]
- ETSI TS 102 292; Satellite Earth Stations and Systems (SES); Broadband Satellite Multimedia (BSM) Services and Architectures; Functional Architecture for IP Interworking with BSM Networks. ETSI: Sophia Antipolis, France, 2015. Available online: http://www.etsi.org (accessed on 18 March 2015).
- Artiga, X.; Perez-Neira, A.; Baranda, J. Shared Access Satellite-Terrestrial Reconfigurable Backhaul Network Enabled by Smart Antennas at MmWave Band. IEEE Netw. 2018, 32, 46–53. [Google Scholar] [CrossRef]
- Yang, Z.; Li, H.; Wu, Q. Analyzing and optimizing BGP stability in future space-based internet. In Proceedings of the IEEE International Performance Computing and Communications Conference, San Diego, CA, USA, 10–12 December 2017. [Google Scholar]
- Yang, Z.; Li, H.; Wu, Q. Topology discovery sub-layer for integrated terrestrial-satellite network routing schemes. China Commun. 2018, 15, 42–57. [Google Scholar] [CrossRef]
- Xu, M. Intra-domain routing protocol OSPF+ for integrated terrestrial and space networks. J. Tsinghua Univ. (Sci. Technol.) 2017, 57, 12–17. [Google Scholar]
- Hong, S.C.; Kim, B.W.; Chang, G.L. FSA-based link assignment and routing in lowearth orbit satellite networks. IEEE Trans. Veh. Technol. 1998, 47, 1037–1048. [Google Scholar] [CrossRef]
- Korcak, O.; Alagoz, F.; Jamalipour, A. Priority-based adaptive routing in NGEO satellite networks. Int. J. Commun. Syst. 2007, 20, 313–333. [Google Scholar] [CrossRef]
- Ekici, E.; Akyildiz, I.F.; Bender, M.D. A distributed routing algorithm for datagram traffic in leo satellite networks. IEEE/ACM Trans. Netw. 2001, 9, 137–147. [Google Scholar] [CrossRef]
- Li, J.; Lu, H.; Xue, K.; Zhang, Y. Temporal Netgrid Model-Based Dynamic Routing in Large-Scale Small Satellite Networks. IEEE Trans. Veh. Technol. 2019, 68, 6009–6021. [Google Scholar] [CrossRef]
- Rao, Y.; Wang, R.-C. Agent-based load balancing routing for LEO satellite networks. Comput. Netw. 2010, 54, 3187–3195. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, G.; Jin, F.; Jiang, B.; Fu, Y. Agent-based dynamic routing in the packet-switched LEO satellite networks. In Proceedings of the IEEE International Conference Wireless Communication Signal Process, New Orleans, LA, USA, 9–12 March 2015; pp. 1–6. [Google Scholar]
- Taleb, T.; Mashimo, D.; Jamalipour, A. Explicit Load Balancing Technique for NGEO Satellite IP Networks With On-Board Processing Capabilities. IEEE/ACM Trans. Netw. 2009, 17, 281–293. [Google Scholar] [CrossRef]
- Song, G.; Chao, M.; Yang, B.; Zheng, Y. TLR: A traffic-light-based intelligent routing strategy for NGEO satellite IP networks. IEEE Trans. Wirel. Commun. 2014, 13, 3380–3393. [Google Scholar] [CrossRef]
- Liu, J.; Luo, R.; Huang, T. A load balancing routing strategy for LEO satellite network. IEEE Access 2020, 8, 155136–155144. [Google Scholar] [CrossRef]
- Guo, Q.; Gu, R.; Dong, T. SDN-based End-to-end Fragment-aware Routing for Elastic Data Flows in LEO Satellite-Terrestrial Network. IEEE Access 2018, 7, 396–410. [Google Scholar] [CrossRef]
- Li, J.; Xue, K.; Liu, J.; Zhang, Y.; Fang, Y. An ICN/SDN-Based Network Architecture and Efficient Content Retrieval for Future Satellite-Terrestrial Integrated Networks. IEEE Netw. 2020, 34, 188–195. [Google Scholar] [CrossRef]
- Li, T.; Zhou, H.; Luo, H.; Yu, S. SERvICE: A software defined framework for integrated space-terrestrial satellite communication. IEEE Trans. Mob. Comput. 2018, 17, 703–716. [Google Scholar] [CrossRef]
- Ivanov, A.; Tonchev, K.; Poulkov, V.; Manolova, A.; Neshov, N.N. Graph-Based Resource Allocation for Integrated Space and Terrestrial Communications. Sensors 2022, 22, 5778. [Google Scholar] [CrossRef]
- Jiang, W. Graph-based deep learning for communication networks: A survey. Comput. Commun. 2022, 185, 40–54. [Google Scholar] [CrossRef]
- Liu, M.; Li, J.; Lu, H. Routing in small satellite networks: A GNN-based learning approach. arXiv 2021, arXiv:2108.08523. [Google Scholar]
- Wang, H.; Ran, Y.; Zhao, L. GRouting: Dynamic Routing for LEO Satellite Networks with Graph-based Deep Reinforcement Learning. In Proceedings of the 2021 4th International Conference on Hot Information-Centric Networking (HotICN), Nanjing, China, 25–27 November 2021; pp. 123–128. [Google Scholar]
- Lv, S.; Li, H.; Wu, J. Routing Strategy of Integrated Satellite-Terrestrial Network Based on Hyperbolic Geometry. IEEE Access 2020, 8, 113003–113010. [Google Scholar] [CrossRef]
- Li, F.; Chen, S.; Huang, M. Reliable topology design in time-evolving delay-tolerant networks with unreliable links. IEEE Trans. Mob. Comput. 2015, 14, 1301–1314. [Google Scholar] [CrossRef]
- Fraire, J.; Madoery, P.; Finochietto, J. Traffic-aware contact plan design for disruption-tolerant space sensor networks. Ad. Hoc. Netw. 2016, 47, 41–52. [Google Scholar] [CrossRef]
- Zhou, D.; Sheng, M.; Wang, X.; Xu, C.; Liu, R.; Li, J. Mission aware contact plan design in resource-limited small satellite networks. IEEE Trans. Commun. 2017, 65, 2451–2466. [Google Scholar] [CrossRef]
- Zhou, D.; Sheng, M.; Liu, R.; Wang, Y.; Li, J. Channel-aware mission scheduling in broadband data relay satellite networks. IEEE J. Sel. Areas Commun. 2018, 36, 1052–1064. [Google Scholar] [CrossRef]
- Xu, H.; Li, D.; Liu, M.; Han, G.; Huang, W.; Xu, C. A Hybrid Routing Algorithm in Terrestrial-Satellite Integrated Network. In Proceedings of the IEEE International Conference on Communications in China, Chongqing, China, 10–12 August 2020. [Google Scholar]
- Zheng, K.; Liu, F.; Zheng, Q. A graph-based cooperative scheduling scheme for vehicular networks. IEEE Trans. Veh. Technol. 2013, 62, 1450–1458. [Google Scholar] [CrossRef]
- Satellite Tool Kit. 2016. Available online: https://softadvice.informer.com/Satellite_Tool_Kit_10.html (accessed on 3 October 2016).
- Marvi, M.; Aijaz, A.; Khurram, M. On the Use of ON/OFF Traffic Models for Spatio-Temporal Analysis of Wireless Networks. IEEE Commun. Lett. 2019, 23, 1219–1222. [Google Scholar] [CrossRef]
- Mohorcic, M.; Werner, M.; Svigelj, A.; Kandus, G. Adaptive routing for packet-oriented intersatellite link networks: Performance in various traffic scenarios. IEEE Trans. Wirel. Commun. 2002, 1, 808–818. [Google Scholar] [CrossRef]

| Routing Schemes | Core Idea | Limitations | |
|---|---|---|---|
| Satellite routing schemes | Routing algorithm based on virtual topology [18,19] | The system period is divided into equal-length snapshots, and the route of each snapshot is calculated offline | The routing table needs to be frequently synchronized |
| Routing algorithm based on virtual node [20,21] | Virtual nodes are set to represent physical satellites, and the shortest distance route between virtual nodes is calculated | The link congestion and failure would deteriorate throughput performance | |
| Routing algorithm based on load balancing [22,23,24,25,26] | Based on the traffic state information, the route is adjusted dynamically according to the real-time state at intermediate nodes to avoid congestion | The intermittent problem of link connection caused by dynamic topology has not been solved | |
| Hybrid terrestrial -satellite routing schemes | Relay routing [13,14] | Satellites act as relay forwarding nodes, which are interconnected through ground stations | The scalability of satellite networks is limited |
| Extended terrestrial routing [15,17] | Terrestrial routing algorithms are extended to the satellite networks | Dynamic topology leads to frequent path updates | |
| SDN-based routing [27,28,29] | The control center collects the link information of the whole network and calculates the route | The time-varying topology of satellites increases the computation overhead | |
| Graph-based routing [30,31,32,33,34,35,36,37,38] | Communication link planning algorithm is designed according to the scheduled contact graph | The frequent changes of inter-satellite link and terrestrial-satellite link selection is missing | |
| Notations | Definitions |
|---|---|
| S | The set of satellites |
| G | The set of TSEs |
| The set of UTs | |
| D | The total number of time intervals in path plan |
| The duration of each time interval | |
| The directed graph composed of T layers | |
| V | The vertices set of G |
| The links set of G | |
| The links set of spatial link | |
| The links set of temporal link | |
| The distance of link | |
| The transmission speed of radio signal | |
| The capacity of link | |
| The data volume in storage of for during the t-th time interval | |
| The capacity of link for data | |
| The connection state of link | |
| The propagation delay | |
| The queuing delay | |
| The transmission delay | |
| The communication opportunities for UTs to TSE in each time interval | |
| The communication opportunities for satellite to TSE in each time interval | |
| The communication opportunities for satellite to satellite in each time interval | |
| The maximum capacity of | |
| The minimum rate requirement of data transmission |
| Constellation | Iridium | Hongyun |
|---|---|---|
| No. of planes | 6 | 13 |
| No. of satellites per plane | 11 | 12 |
| Orbital inclination | ||
| Orbital height | 788 km | 1000 km |
| Intraplane ISLs length | 4032.9 km | 3790 km |
| Intraplane ISLs propagation delay | 13.5 ms | 12.6 ms |
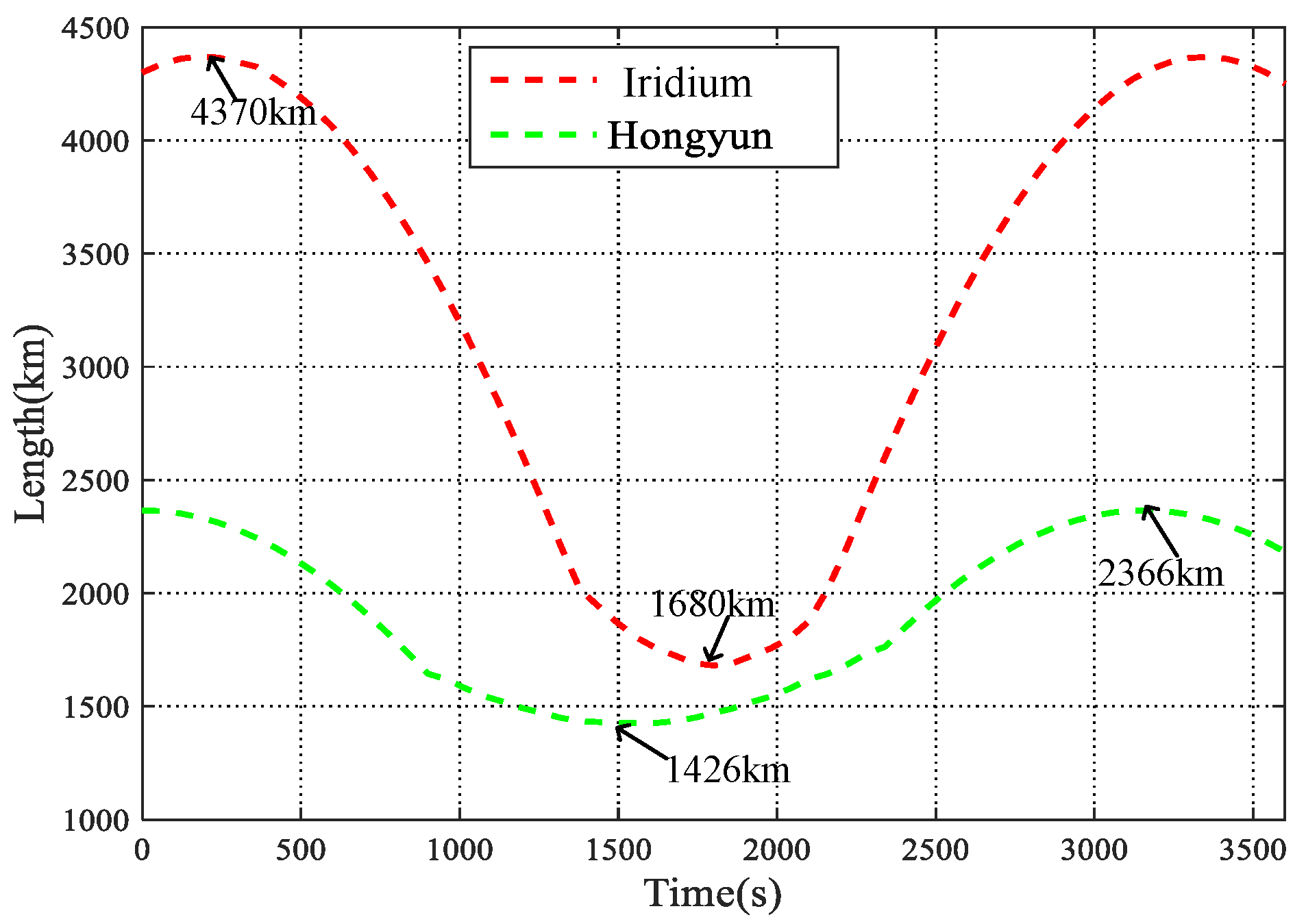
| Longest interplane ISLs distance | 4370 km | 2366 km |
| Longest interplane ISLs propagation delay | 14.5 ms | 7.89 ms |
| Shortest interplane ISLs distance | 1680 km | 1426 km |
| Shortest interplane ISLs propagation delay | 5.6 ms | 4.75 ms |
| Parameters | Values |
|---|---|
| Orbital altitude | 1000 km |
| 87.4 | |
| N | 13 |
| M | 12 |
| Minimum elevation angle | 10 |
| Phase offset between interplane satellites | 360/12/2 = 15 |
| Bandwidth of ISL | 15 Mbps |
| Bandwidth of ground link | 15 Mbps |
| Queue type | FIFO |
| Buffer queue size | 100 packets |
| Packet sizes | 1500 byte |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Shi, Z.; Liu, M.; Zhang, N.; Yan, Y.; Han, G. Link-State Aware Hybrid Routing in the Terrestrial–Satellite Integrated Network. Sensors 2022, 22, 9124. https://doi.org/10.3390/s22239124
Xu H, Shi Z, Liu M, Zhang N, Yan Y, Han G. Link-State Aware Hybrid Routing in the Terrestrial–Satellite Integrated Network. Sensors. 2022; 22(23):9124. https://doi.org/10.3390/s22239124
Chicago/Turabian StyleXu, Huihui, Zhangsong Shi, Mingliu Liu, Ning Zhang, Yanjun Yan, and Guangjie Han. 2022. "Link-State Aware Hybrid Routing in the Terrestrial–Satellite Integrated Network" Sensors 22, no. 23: 9124. https://doi.org/10.3390/s22239124
APA StyleXu, H., Shi, Z., Liu, M., Zhang, N., Yan, Y., & Han, G. (2022). Link-State Aware Hybrid Routing in the Terrestrial–Satellite Integrated Network. Sensors, 22(23), 9124. https://doi.org/10.3390/s22239124










