An Optimization-Based Motion Planner for Car-like Logistics Robots on Narrow Roads
Abstract
:1. Introduction
2. Literature Review
2.1. Researches on Point-to-Point Motion Planning Methods
2.2. Studies on Narrow Road Motion Planning Methods
2.3. Studies on Timed-Elastic-Band Methods
3. Materials and Methods
3.1. Motion Smoothing
3.1.1. Motion Planning Modeling
3.1.2. Jerk Limitation
3.2. Reverse Planning Enhancement
3.3. Obstacle Avoidance Strategy
4. Results and Discussion
4.1. Simulation and Analysis
4.1.1. Trajectory Motion Performance Comparison
4.1.2. Tracking Performance Comparison
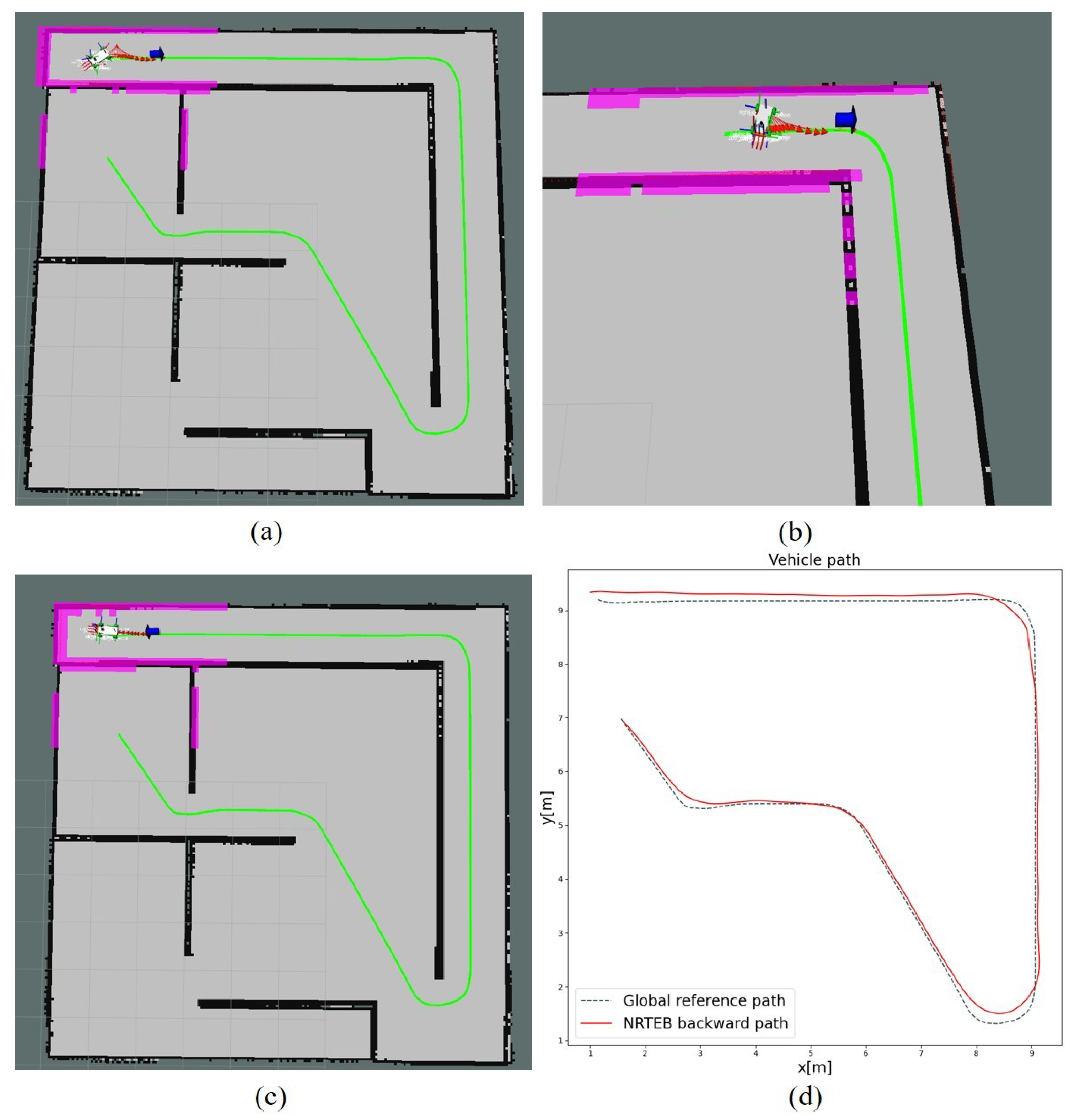
4.1.3. Comparison of Reversing Trajectory
4.2. Realistic Obstacle Avoidance Scenarios
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Algorithm A1 processBackward |
| Input:: the robot current position; : A local path intercepted from the global path; : the global target Output:
|
| Algorithm A2 processObstalcesOnLocalTarget |
| Input:, , l, , , , Output:
|
References
- Pikner, H.; Sell, R.; Karjust, K.; Malayjerdi, E.; Velsker, T. Cyber-physical control system for autonomous logistic robot. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 699–704. [Google Scholar]
- Samaniego, R.; Rodríguez, R.; Vázquez, F.; López, J. Efficient path planing for articulated vehicles in cluttered environments. Sensors 2020, 20, 6821. [Google Scholar] [CrossRef] [PubMed]
- Mohanan, M.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robot. Auton. Syst. 2018, 100, 171–185. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using Kinect-style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef] [Green Version]
- Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Robot. 2019, 4, eaav1488. [Google Scholar] [CrossRef]
- Pan, H.; Guo, C.; Wang, Z. Research for path planning based on improved astart algorithm. In Proceedings of the 2017 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS), Dalian, China, 24–26 July 2017; pp. 225–230. [Google Scholar]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A review of motion planning for highway autonomous driving. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1826–1848. [Google Scholar] [CrossRef] [Green Version]
- Elbanhawi, M.; Simic, M. Sampling-based robot motion planning: A review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Chi, W.; Ding, Z.; Wang, J.; Chen, G.; Sun, L. A Generalized Voronoi Diagram-Based Efficient Heuristic Path Planning Method for RRTs in Mobile Robots. IEEE Trans. Ind. Electron. 2021, 69, 4926–4937. [Google Scholar] [CrossRef]
- Liu, X.; Jing, Q.; Fang, L.; Jin, C.; Zhao, X. The planning of modern logistics park in Jilin city. In Proceedings of the 2011 Chinese Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; pp. 1757–1761. [Google Scholar]
- Guastella, D.C.; Muscato, G. Learning-based methods of perception and navigation for ground vehicles in unstructured environments: A review. Sensors 2020, 21, 73. [Google Scholar] [CrossRef]
- Nowakiewicz, M. MST-Based method for 6DOF rigid body motion planning in narrow passages. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5380–5385. [Google Scholar]
- Wang, Z.; Shen, Y.; Zhang, L.; Zhang, S.; Zhou, Y. Towards Robust Autonomous Coverage Navigation for Carlike Robots. IEEE Robot. Autom. Lett. 2021, 6, 8742–8749. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A review of motion planning techniques for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1135–1145. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Kim, J.S.; Lim, S.S.; Park, K.H. A fast path planning by path graph optimization. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2003, 33, 121–129. [Google Scholar] [CrossRef]
- Ferguson, D.; Howard, T.M.; Likhachev, M. Motion planning in urban environments. J. Field Robot. 2008, 25, 939–960. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-exploring random trees: A new tool for path planning. Mathematics 1998, 98, 303–307. [Google Scholar]
- Karaman, S.; Walter, M.R.; Perez, A.; Frazzoli, E.; Teller, S. Anytime motion planning using the RRT. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1478–1483. [Google Scholar]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Xu, W.; Wei, J.; Dolan, J.M.; Zhao, H.; Zha, H. A real-time motion planner with trajectory optimization for autonomous vehicles. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 2061–2067. [Google Scholar]
- González, D.; Pérez, J.; Lattarulo, R.; Milanés, V.; Nashashibi, F. Continuous curvature planning with obstacle avoidance capabilities in urban scenarios. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1430–1435. [Google Scholar]
- Farouki, R.T. Pythagorean—Hodograph Curves; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Xiong, L.; Fu, Z.; Zeng, D.; Leng, B. An Optimized Trajectory Planner and Motion Controller Framework for Autonomous Driving in Unstructured Environments. Sensors 2021, 21, 4409. [Google Scholar] [CrossRef]
- Fan, H.; Zhu, F.; Liu, C.; Zhang, L.; Zhuang, L.; Li, D.; Zhu, W.; Hu, J.; Li, H.; Kong, Q. Baidu apollo em motion planner. arXiv 2018, arXiv:1807.08048. [Google Scholar]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the ROBOTIK 2012, 7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; pp. 74–79. [Google Scholar]
- Sun, X.; Deng, S.; Tong, B. Trajectory Planning Approach of Mobile Robot Dynamic Obstacle Avoidance with Multiple Constraints. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 829–834. [Google Scholar]
- Wang, J.; Zhang, T.; Ma, N.; Li, Z.; Ma, H.; Meng, F.; Meng, M.Q.H. A survey of learning-based robot motion planning. IET Cyber-Syst. Robot. 2021, 3, 302–314. [Google Scholar] [CrossRef]
- Michalke, T.P.; Gläser, C.; Bürkle, L.; Niewels, F. The narrow road assistant-next generation advanced driver assistance in inner-city. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 2173–2180. [Google Scholar]
- Takamatsu, Y.; Takada, Y.; Kishi, N. A narrow road driving assistance system based on driving style. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 1669–1674. [Google Scholar]
- Sato, T.; Daimon, T.; Kawashima, H.; Kinoshita, M.; Ikeda, A. Fundamental study on human interface of narrow road drive assist system based on drivers’ cognitive process. JSAE Rev. 2003, 24, 189–196. [Google Scholar] [CrossRef]
- Tian, X.; Fu, M.; Yang, Y.; Wang, M.; Liu, D. Local Smooth Path Planning for Turning Around in Narrow Environment. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1924–1929. [Google Scholar]
- Li, B.; Chen, B. An Adaptive Rapidly-Exploring Random Tree. IEEE/CAA J. Autom. Sin. 2021, 9, 283–294. [Google Scholar] [CrossRef]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Timed-elastic-bands for time-optimal point-to-point nonlinear model predictive control. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 3352–3357. [Google Scholar]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Efficient trajectory optimization using a sparse model. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013; pp. 138–143. [Google Scholar]
- Quinlan, S. Real-Time Modification of Collision-Free Paths. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1995. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Integrated online trajectory planning and optimization in distinctive topologies. Robot. Auton. Syst. 2017, 88, 142–153. [Google Scholar] [CrossRef]
- Marin-Plaza, P.; Hussein, A.; Martin, D.; de la Escalera, A. Global and local path planning study in a ROS-based research platform for autonomous vehicles. J. Adv. Transp. 2018, 2018, 6392697. [Google Scholar] [CrossRef]
- Keller, M.; Hoffmann, F.; Hass, C.; Bertram, T.; Seewald, A. Planning of optimal collision avoidance trajectories with timed elastic bands. IFAC Proc. Vol. 2014, 47, 9822–9827. [Google Scholar] [CrossRef]
- Ulbrich, F.; Goehring, D.; Langner, T.; Boroujeni, Z.; Rojas, R. Stable timed elastic bands with loose ends. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 186–192. [Google Scholar]
- Smith, J.S.; Xu, R.; Vela, P. egoTEB: Egocentric, Perception Space Navigation Using Timed-Elastic-Bands. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2703–2709. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Kinodynamic trajectory optimization and control for car-like robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5681–5686. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; p. 5. [Google Scholar]
- Rosmann, C.; Hoffmann, F.; Bertram, T. Online Trajectory Planning in ROS under Kinodynamic Constraints with Timed-Elastic-Bands. In Robot Operating System (ROS); Koubaa, A., Ed.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2017; Volume 707, pp. 231–261. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar]















| Constraint Parameters | Values | Application Scope |
|---|---|---|
| Maximum linear velocity (m/s) | 0.4 | MPC, TEB, NRTEB |
| Maximum angular velocity (m/s) | 0.3 | MPC, TEB, NRTEB |
| Maximum linear acc (m/s) | 0.5 | MPC, TEB, NRTEB |
| Maximum angular acc (rad/s) | 0.5 | MPC, TEB, NRTEB |
| Minimum distance to obstacle (m) | 0.5 | MPC, TEB, NRTEB |
| Maximum linear jerk (m/s) | 0.1 | NRTEB |
| Maximum angular jerk (rad/s) | 0.1 | NRTEB |
| The weight of linear velocity () | 1.0 | TEB, NRTEB |
| The weight of angular vel () | 1.0 | TEB, NRTEB |
| The weight of linear acc () | 1.0 | TEB, NRTEB |
| The weight of angular acc () | 1.0 | TEB, NRTEB |
| The weight of linear jerk () | 1.0 | NRTEB |
| The weight of angular jerk () | 1.0 | NRTEB |
| The weight of states | MPC | |
| The weight of controls | MPC |
| Constraint Parameters | Values |
|---|---|
| Maximum linear velocity (m/s) | 0.5 |
| Maximum angular velocity (m/s) | 0.5 |
| Maximum linear acc (m/s) | 1.0 |
| Maximum angular acc (rad/s) | 1.0 |
| Maximum linear jerk (m/s) | 2.0 |
| Maximum angular jerk (rad/s) | 2.0 |
| Local costmap size (m) | 5 × 5 |
| Local costmap update frequency (Hz) | 10.0 |
| robot footprint size (m) | 0.4 × 0.2 |
| Maximum steering angle (rad) | 0.785 |
| Motion planning frequency (Hz) | 10.0 |
| MPC | TEB | NRTEB | |
|---|---|---|---|
| Path length (m) | 23.186 | 23.507 | 23.644 |
| Average lateral tracking error (m) | 0.094 | 0.062 | 0.071 |
| Min | Max | Average (abs) | ||
|---|---|---|---|---|
| MPC | −1.001 | 1.004 | 0.072 | |
| −2.590 | 1.486 | 0.197 | ||
| T | 0.041 | 488.954 | 154.117 | |
| TEB | −1.092 | 1.090 | 0.146 | |
| −2.331 | 2.797 | 0.251 | ||
| T | 0.045 | 15.508 | 1.488 | |
| NRTEB | −0.295 | 0.309 | 0.065 | |
| −0.562 | 0.738 | 0.070 | ||
| T | 0.050 | 18.920 | 2.069 |
| Components | Product Model |
|---|---|
| IPC | NVIDIA Jetson Xavier NX |
| GNSS | CHCNAV CGI410 |
| LiDAR (front) | RoboSense-RS-LiDAR-16 |
| LiDAR (back) | LEME-02A |
| Camera | Netcan 1080p |
| 4G wireless | QUECTEL |
| Vehicle control unit | self-developed |
| Chassis Parameters | Values |
|---|---|
| Track (m) | 0.60 |
| Wheelbase (m) | 0.98 |
| Maximum steering angle (rad) | 0.52 |
| Minimum turning radius (m) | 1.70 |
| Rated load (kg) | 200 |
| Maximum velocity (m/s) | 2.80 |
| Maximum acceleration (no load) (m/s) | 2.5 |
| Rated acceleration (m/s) | 0.77 |
| Envelope size (m) |
| Planner Parameters | Values |
|---|---|
| 1.0 | |
| 1.0 | |
| l (m) | 1.0 |
| () | 60 |
| Lookahead_dist (m) | 4.0 |
| Maximum linear velocity (forward) (m/s) | 2.50 |
| Maximum linear velocity (backward) (m/s) | 1.50 |
| Maximum angular velocity (rad/s) | 0.50 |
| Maximum acceleration (m/s) | 0.75 |
| Maximum linear jerk (m/s) | 1.0 |
| Maximum angular jerk (rad/s) | 0.5 |
| Minimum turning radius (m) | 1.70 |
| Minimum distance to obstacle (m) | 0.5 |
| Local costmap size (m) | |
| Local costmap update frequency (Hz) | 10.0 |
| Motion planning frequency (Hz) | 10.0 |
| Min | Max | Average (abs) | ||
|---|---|---|---|---|
| TEB | −1.368 | 1.173 | 0.154 | |
| −2.565 | 2.657 | 0.362 | ||
| T | 10.854 | 117.142 | 50.627 | |
| — | — | 217.514 | ||
| NRTEB | −0.274 | 0.298 | 0.062 | |
| −0.575 | 0.743 | 0.071 | ||
| T | 11.947 | 120.620 | 53.613 | |
| — | — | 239.265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Wu, H.; Liu, C.; Jiao, H. An Optimization-Based Motion Planner for Car-like Logistics Robots on Narrow Roads. Sensors 2022, 22, 8948. https://doi.org/10.3390/s22228948
Yu L, Wu H, Liu C, Jiao H. An Optimization-Based Motion Planner for Car-like Logistics Robots on Narrow Roads. Sensors. 2022; 22(22):8948. https://doi.org/10.3390/s22228948
Chicago/Turabian StyleYu, Lingli, Hanzhao Wu, Chongliang Liu, and Hao Jiao. 2022. "An Optimization-Based Motion Planner for Car-like Logistics Robots on Narrow Roads" Sensors 22, no. 22: 8948. https://doi.org/10.3390/s22228948
APA StyleYu, L., Wu, H., Liu, C., & Jiao, H. (2022). An Optimization-Based Motion Planner for Car-like Logistics Robots on Narrow Roads. Sensors, 22(22), 8948. https://doi.org/10.3390/s22228948






