Structural Optimisation and Design of a Cable-Driven Hyper-Redundant Manipulator for Confined Semi-Structured Environments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structural Optimisation of Hyper-Redundant Manipulators
2.2. Optimisation Algorithms
2.3. Kinematics of Hyper Redundant Manipulators
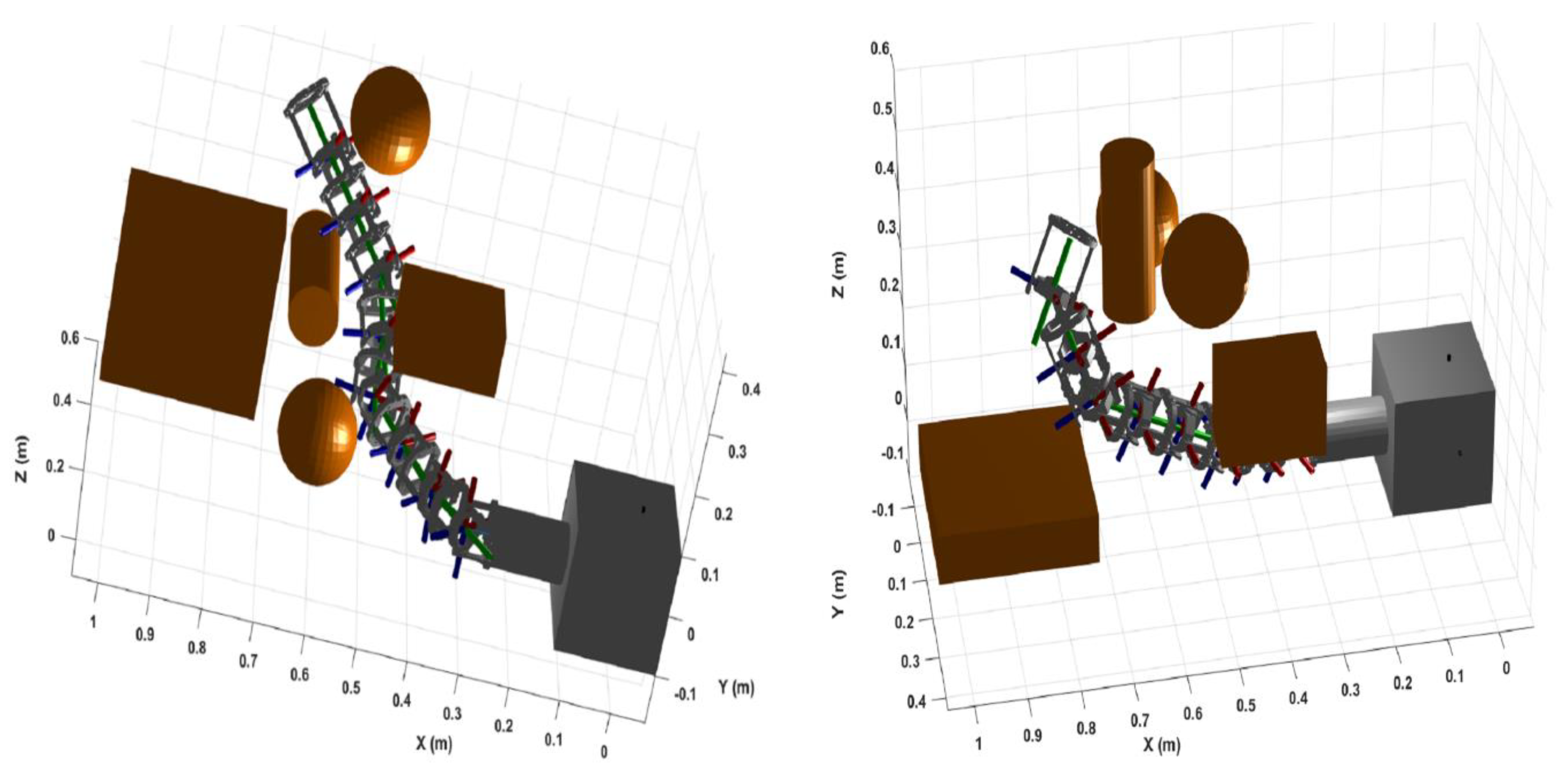
3. Results and Discussion
3.1. Manipulability Optimisation
3.2. Inverse Kinematics (IK) Optimisation
3.3. Results Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nuzzi, R.; Brusasco, L. State of the art of robotic surgery related to vision: Brain and eye applications of newly available devices. Eye Brain 2018, 10, 13–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moghaddam, B.M.; Chhabra, R. On the guidance, navigation and control of in-orbit space robotic missions: A survey and prospective vision. Acta Astronaut. 2021, 184, 70–100. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Al-Khulaidi, R.A.; Akmeliawati, R.; Azlan, N.Z.; Bakr, N.H.A.; Fauzi, N.M. Development of robotic hands of signbot, advanced Malaysian sign-language performing robot. Adv. Robot. Res. 2018, 2, 183. [Google Scholar]
- Kim, M.J.; Chi, H.-L.; Wang, X.; Ding, L. Automation and Robotics in Construction and Civil Engineering. J. Intell. Robot. Syst. 2015, 79, 347–350. [Google Scholar] [CrossRef] [Green Version]
- Oyekan, J.O.; Hutabarat, W.; Tiwari, A.; Grech, R.; Aung, M.H.; Mariani, M.P.; López-Dávalos, L.; Ricaud, T.; Singh, S.; Dupuis, C. The effectiveness of virtual environments in developing collaborative strategies between industrial robots and humans. Robot. Comput.-Integr. Manuf. 2019, 55, 41–54. [Google Scholar] [CrossRef]
- Domae, Y. Recent trends in the research of industrial robots and future outlook. J. Robot. Mechatron. 2019, 31, 57–62. [Google Scholar] [CrossRef]
- Bock, T. The future of construction automation: Technological disruption and the upcoming ubiquity of robotics. Autom. Constr. 2015, 59, 113–121. [Google Scholar] [CrossRef]
- Oesterreich, T.D.; Teuteberg, F. Understanding the implications of digitisation and automation in the context of Industry 4.0: A triangulation approach and elements of a research agenda for the construction industry. Comput. Ind. 2016, 83, 121–139. [Google Scholar] [CrossRef]
- Bac, C.W.; Hemming, J.; van Tuijl, B.A.J.; Barth, R.; Wais, E.; van Henten, E.J. Performance Evaluation of a Harvesting Robot for Sweet Pepper. J. Field Robot. 2017, 34, 1123–1139. [Google Scholar] [CrossRef]
- Kurita, H.; Iida, M.; Cho, W.; Suguri, M. Rice Autonomous Harvesting: Operation Framework. J. Field Robot. 2017, 34, 1084–1099. [Google Scholar] [CrossRef]
- Silwal, A.; Davidson, J.R.; Karkee, M.; Mo, C.; Zhang, Q.; Lewis, K. Design, integration, and field evaluation of a robotic apple harvester. J. Field Robot. 2017, 34, 1140–1159. [Google Scholar] [CrossRef]
- Botterill, T.; Paulin, S.; Green, R.; Williams, S.; Lin, J.; Saxton, V.; Mills, S.; Chen, X.; Corbett-Davies, S. A Robot System for Pruning Grape Vines. J. Field Robot. 2017, 34, 1100–1122. [Google Scholar] [CrossRef]
- Birrell, S.; Hughes, J.; Cai, J.Y.; Iida, F. A field-tested robotic harvesting system for iceberg lettuce. J. Field Robot. 2018, 37, 225–245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Funami, Y.; Kawakura, S.; Tadano, K. Development of a Robotic Arm for Automated Harvesting of Asparagus. Eur. J. Agric. Food Sci. 2020, 2, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Colas, F.; Oth, L.; Siegwart, R.Y. Incremental topological segmentation for semi-structured environments using discretized GVG. Auton. Robot. 2015, 38, 143–160. [Google Scholar] [CrossRef]
- Meng, Y.; Sun, Y.; Chang, W.-S. Optimal trajectory planning of complicated robotic timber joints based on particle swarm optimization and an adaptive genetic algorithm. Constr. Robot. 2021, 5, 131–146. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zhao, X.; Zhao, P.; He, L. Time-optimal trajectory planning of serial manipulator based on adaptive cuckoo search algorithm. J. Mech. Sci. Technol. 2021, 35, 3171–3181. [Google Scholar] [CrossRef]
- Huang, J.; Hu, P.; Wu, K.; Zeng, M. Optimal time-jerk trajectory planning for industrial robots. Mech. Mach. Theory 2018, 121, 530–544. [Google Scholar] [CrossRef]
- Rout, A.; Deepak, B.; Biswal, B.B.; Mahanta, G.B. Trajectory Generation of an Industrial Robot With Constrained Kinematic and Dynamic Variations for Improving Positional Accuracy. Int. J. Appl. Metaheuristic Comput. 2021, 12, 163–179. [Google Scholar] [CrossRef]
- Nho Cho, C.; Jung, H.; Son, J.; Gi Kim, K. A modular control scheme for hyper-redundant robots. Int. J. Adv. Robot. Syst. 2015, 12, 91. [Google Scholar] [CrossRef]
- Siciliano, B.; Khatib, O.; Kröger, T. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 200. [Google Scholar]
- Miteva, L.; Chavdarov, I.; Yovchev, K. Trajectory Planning for Redundant Robotic Manipulators with Constrained Joint Space. In Proceedings of the 2020 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 17–19 September 2020; pp. 1–6. [Google Scholar]
- Tang, L.; Wang, J.; Zheng, Y.; Gu, G.; Zhu, L.; Zhu, X. Design of a cable-driven hyper-redundant robot with experimental validation. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417734458. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Zhang, Y.; Huang, F.; Li, J.; Chen, Z.; Song, W.; Zhu, S.; Gu, J. Design and Kinematic Control of the Cable-Driven Hyper-Redundant Manipulator for Potential Underwater Applications. Appl. Sci. 2019, 9, 1142. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Liu, T.; Li, Y. Kinematics, Dynamics, and Control of a Cable-Driven Hyper-Redundant Manipulator. IEEE/ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Bac, C.W.; van Henten, E.J.; Hemming, J.; Edan, Y. Harvesting Robots for High-value Crops: State-of-the-art Review and Challenges Ahead. J. Field Robot. 2014, 31, 888–911. [Google Scholar] [CrossRef]
- Pierrot, F.; Nabat, V.; Company, O.; Krut, S.; Poignet, P. Optimal Design of a 4-DOF Parallel Manipulator: From Academia to Industry. IEEE Trans. Robot. 2009, 25, 213–224. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, H.; Luo, Z.; Wang, F. Robot mechanical structure optimization design. In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 15–18 December 2007; pp. 1919–1923. [Google Scholar]
- Bjørlykhaug, E.; Egeland, O. Mechanical Design Optimization of a 6DOF Serial Manipulator Using Genetic Algorithm. IEEE Access 2018, 6, 59087–59095. [Google Scholar] [CrossRef]
- Kivelä, T.; Mattila, J.; Puura, J. A generic method to optimize a redundant serial robotic manipulator’s structure. Autom. Constr. 2017, 81, 172–179. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Klein, C.A.; Blaho, B.E. Dexterity Measures for the Design and Control of Kinematically Redundant Manipulators. Int. J. Robot. Res. 1987, 6, 72–83. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; La, H.M.; Luo, X. Manipulability Optimization of Redundant Manipulators Using Dynamic Neural Networks. IEEE Trans. Ind. Electron. 2017, 64, 4710–4720. [Google Scholar] [CrossRef]
- Chandrashekhar, A. Generation of Manipulability Ellipsoids for Different Configurations Using the Yoshikawa’s Manipulability Index and Manipulability Ellipsoid. Int. J. Theor. Appl. Mech. 2017, 12, 623–635. [Google Scholar]
- Dufour, K.; Suleiman, W. On Maximizing Manipulability Index while Solving a Kinematics Task. J. Intell. Robot. Syst. 2020, 100, 3–13. [Google Scholar] [CrossRef]
- Dufour, K.; Suleiman, W. On integrating manipulability index into inverse kinematics solver. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6967–6972. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- MathWorks Fmincon. Available online: https://au.mathworks.com/help/optim/ug/fmincon.html (accessed on 23 July 2020).
- Muthiah, A.; Rajkumar, R. A Comparison of Artificial Bee Colony algorithm and Genetic Algorithm to Minimize the Makespan for Job Shop Scheduling. Procedia Eng. 2014, 97, 1745–1754. [Google Scholar]
- Alqattan, Z.N.M.; Abdullah, R. A Comparison between Artificial Bee Colony and Particle Swarm Optimization Algorithms for Protein Structure Prediction Problem; Springer: Berlin/Heidelberg, Germany, 2013; pp. 331–340. [Google Scholar]
- Rao, R.S.; Narasimham, S.; Ramalingaraju, M. Optimization of Distribution Network Configuration for Loss Reduction Using Artificial Bee Colony Algorithm. Int. J. Electr. Comput. Eng. 2008, 2, 1964–1970. [Google Scholar]
- Marais, W.; Göktoǧan, A. Design and Control of CRAM: A Highly Articulated Cable-driven Remote Access Manipulator for Confined Space Inspection. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA-2017), Sydney, Australia, 11–13 December 2017. [Google Scholar]
- Karaboga, D. Artificial bee colony algorithm. Scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Mohammadi, H.R.; Zsombor-murray, P.J.D.; Angeles, J. The Isotropic Design of Two General Classes of Planar Parallel Manipulators. J. Robot. Syst. 1995, 12, 795–805. [Google Scholar] [CrossRef]
- Hosseini, M.A.; Daniali, H.M. Weighted local conditioning index of a positioning and orienting parallel manipulator. Sci. Iran. 2011, 18, 115–120. [Google Scholar] [CrossRef]
- Marais, W.; Göktoǧan, A. A New Manipulability Measure for the Control of CRAM: A Cable-driven Remote Access Manipulator. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA-2017), Sydney, Australia, 11–13 December 2017. [Google Scholar]















| Joint | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| . . . | . . . | . . . | . . . | . . . |
| Joint Parameters | Manipulability Measures | Inverse Kinematics Optimisation | ||||||
|---|---|---|---|---|---|---|---|---|
| Yoshikawa | LCI | ∆H | ||||||
| Fmincon | ABC | Fmincon | ABC | Fmincon | ABC | Fmincon | ABC | |
| Objective Function Value | 7.4 × 108 | 1.5× 109 | 0.0101 | 0.0107 | 4.3 × 10−4 | 6.8 × 10−4 | 4.14 × 10−6 | 0.46 |
| q1 (deg) | 11.4 | 2.22 | 71 | 90.0 | 79.49 | 24.2 | 30.5 | 35 |
| q2 (deg) | 29.3 | 1 | 12 | 90.0 | 3.67 | 87.1 | 25.6 | 32 |
| q3 (deg) | 0 | 33.6 | −88.7 | −90.0 | 89.91 | 17.8 | 14.6 | 2 |
| q4 (deg) | 9.3 | 8.91 | -84.9 | -20.6 | 61.2 | 90.0 | 17 | 0.3 |
| q5 (deg) | 0 | 5.49 | 35 | 90.0 | 52.3 | 19.5 | 16 | 80 |
| q6 (deg) | 9.2 | 12.6 | 56.8 | 3.83 | 66 | 90.0 | 19 | 16 |
| q7 (deg) | 0 | 2.02 | 46.6 | 89.2 | 34.7 | 83.8 | 54 | 67 |
| q8 (deg) | 12.2 | 1.89 | 80.3 | 21.2 | 65.8 | 73.8 | 13.8 | 61 |
| q9 (deg) | 90 | 90.0 | 17 | 6.3 | 13 | 41.4 | 65.6 | 67 |
| q10 (deg) | 90 | 3.62 | 57.5 | 50.7 | 62 | 22.8 | 78 | 70 |
| q11 (deg) | 9.8 | 0.487 | 39.4 | −90.0 | 35.5 | 33.6 | 70.5 | 14.6 |
| q12 (deg) | 0 | 2.32 | 27.7 | −38.6 | 37 | −90.0 | 71.6 | 0.5 |
| q13 (deg) | 4.7 | 13.3 | 30.8 | 88.9 | 48.4 | 5.19 | 8.8 | 68 |
| q14 (deg) | 0 | 7.36 | 85.18 | 39.5 | 81 | 88.5 | 68 | 38 |
| q15 (deg) | 29 | 38.4 | 10.7 | 90.0 | 27.3 | −90.0 | 37 | 90 |
| q16 (deg) | 90 | 3.27 | 89.67 | 9.72 | 90 | 90.0 | 17 | 90 |
| a (mm) | 120.00 | 150.0 | 100 | 90.0 | 100.0 | 90.1 | 107 | 124 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Khulaidi, R.; Akmeliawati, R.; Grainger, S.; Lu, T.-F. Structural Optimisation and Design of a Cable-Driven Hyper-Redundant Manipulator for Confined Semi-Structured Environments. Sensors 2022, 22, 8632. https://doi.org/10.3390/s22228632
Al-Khulaidi R, Akmeliawati R, Grainger S, Lu T-F. Structural Optimisation and Design of a Cable-Driven Hyper-Redundant Manipulator for Confined Semi-Structured Environments. Sensors. 2022; 22(22):8632. https://doi.org/10.3390/s22228632
Chicago/Turabian StyleAl-Khulaidi, Rami, Rini Akmeliawati, Steven Grainger, and Tien-Fu Lu. 2022. "Structural Optimisation and Design of a Cable-Driven Hyper-Redundant Manipulator for Confined Semi-Structured Environments" Sensors 22, no. 22: 8632. https://doi.org/10.3390/s22228632
APA StyleAl-Khulaidi, R., Akmeliawati, R., Grainger, S., & Lu, T.-F. (2022). Structural Optimisation and Design of a Cable-Driven Hyper-Redundant Manipulator for Confined Semi-Structured Environments. Sensors, 22(22), 8632. https://doi.org/10.3390/s22228632






