0.5 V, nW-Range Universal Filter Based on Multiple-Input Transconductor for Biosignals Processing
Abstract
:1. Introduction
2. Methods
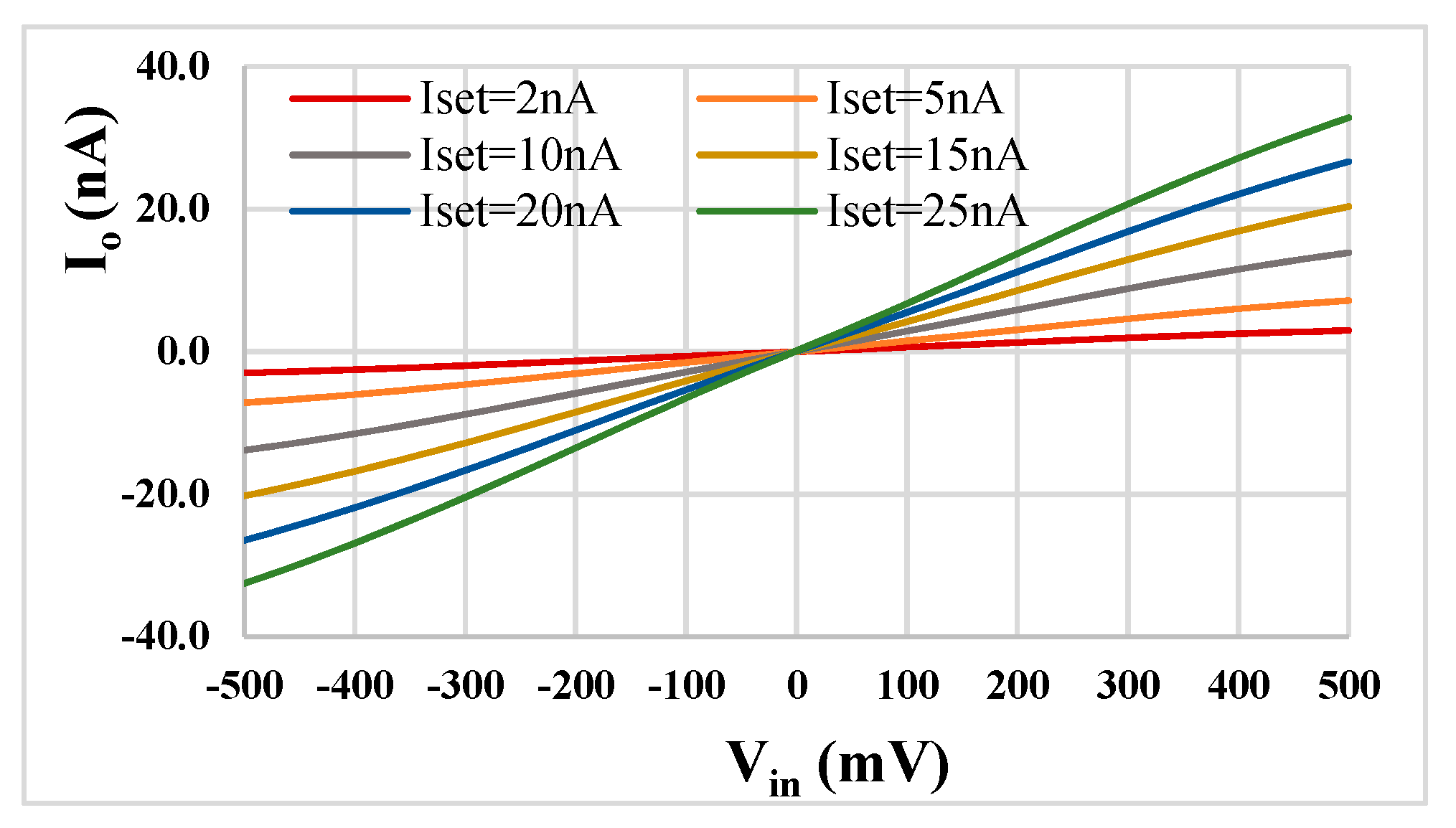
2.1. The Multiple-Input Gm
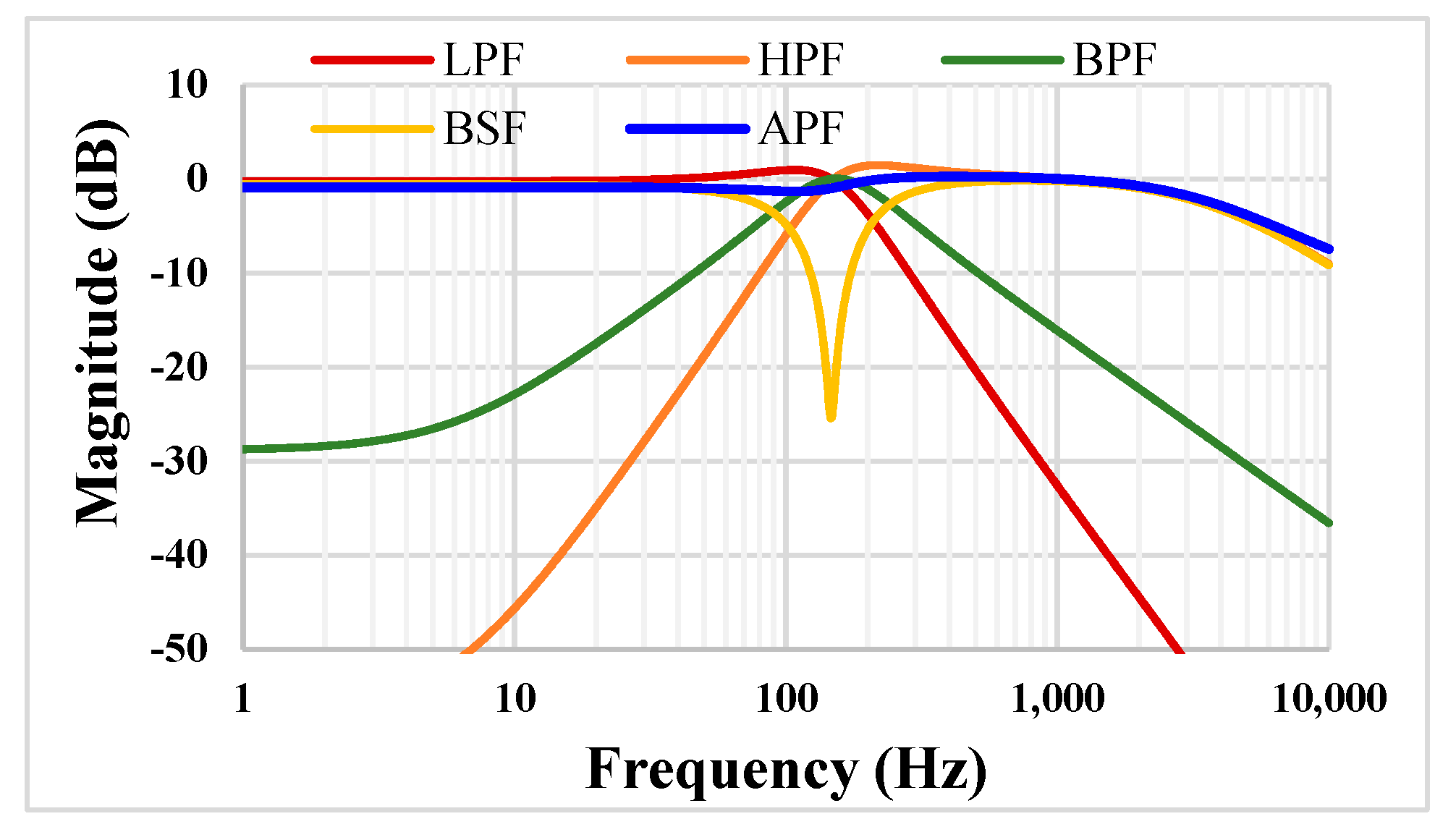
2.2. Universal Filter Design
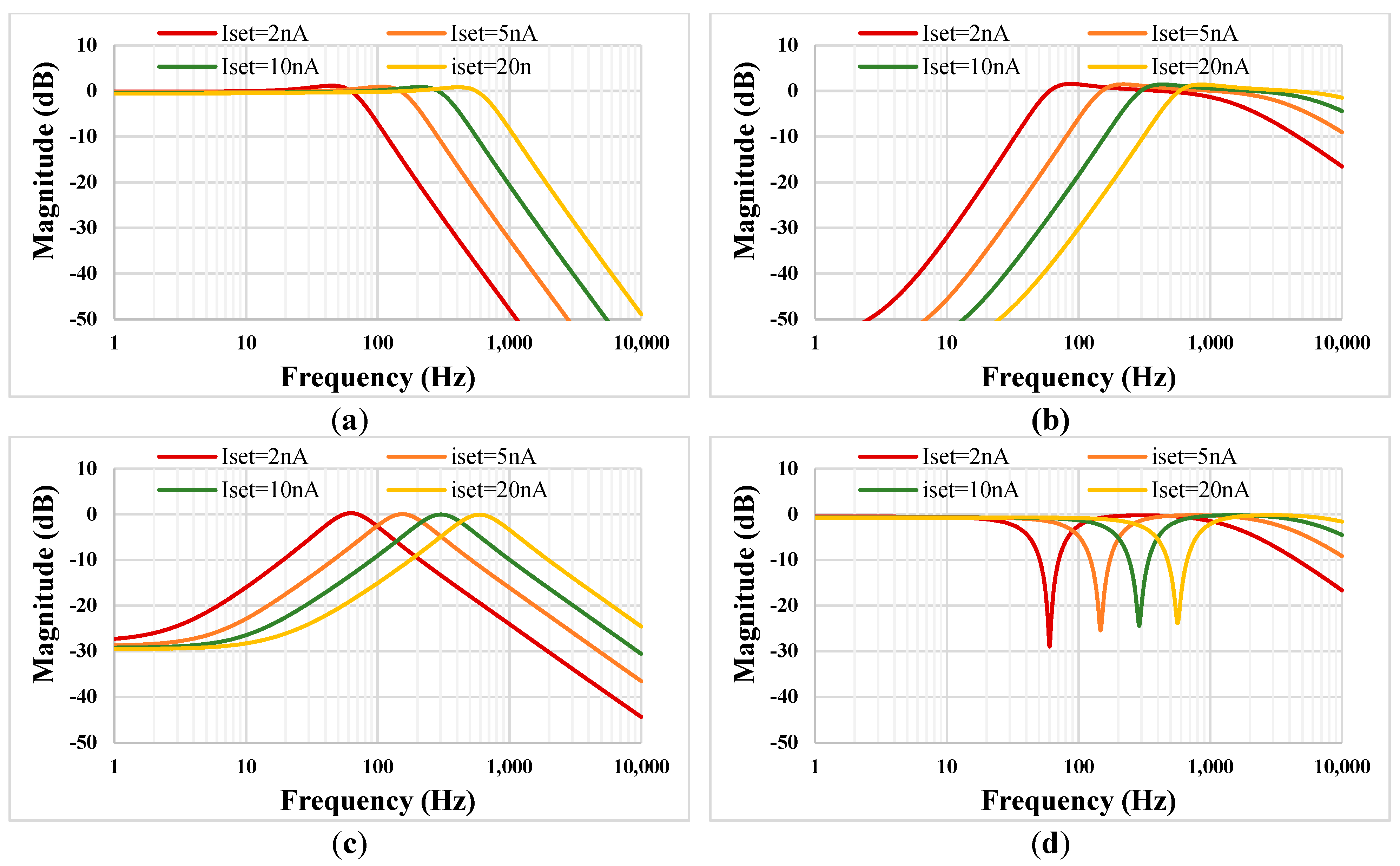
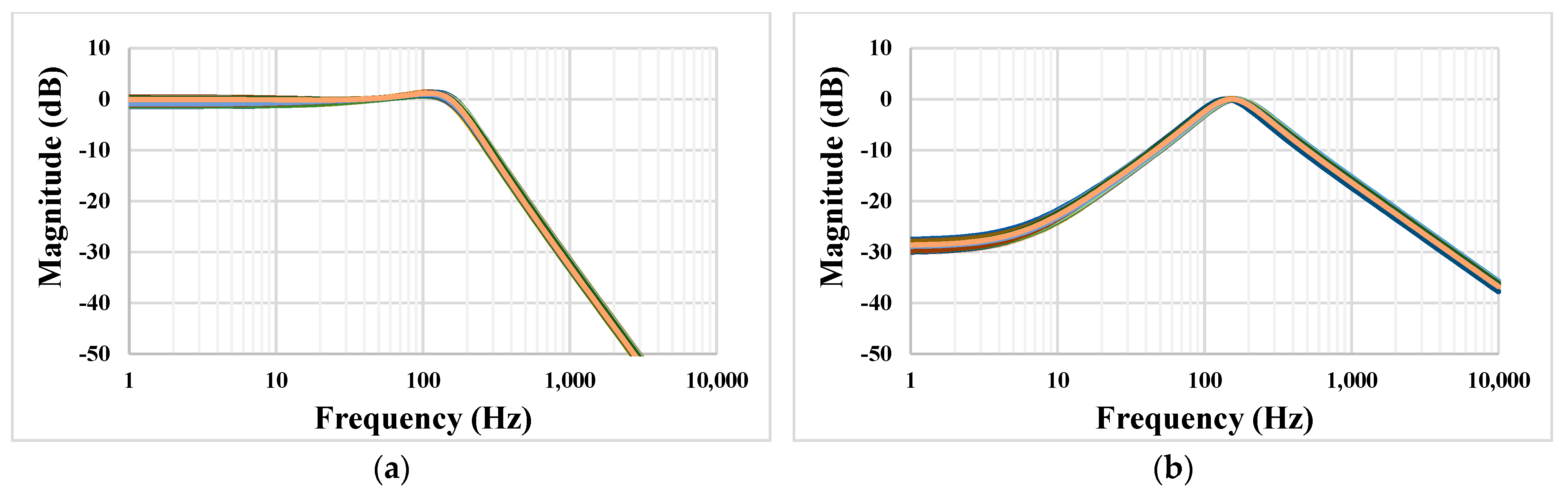
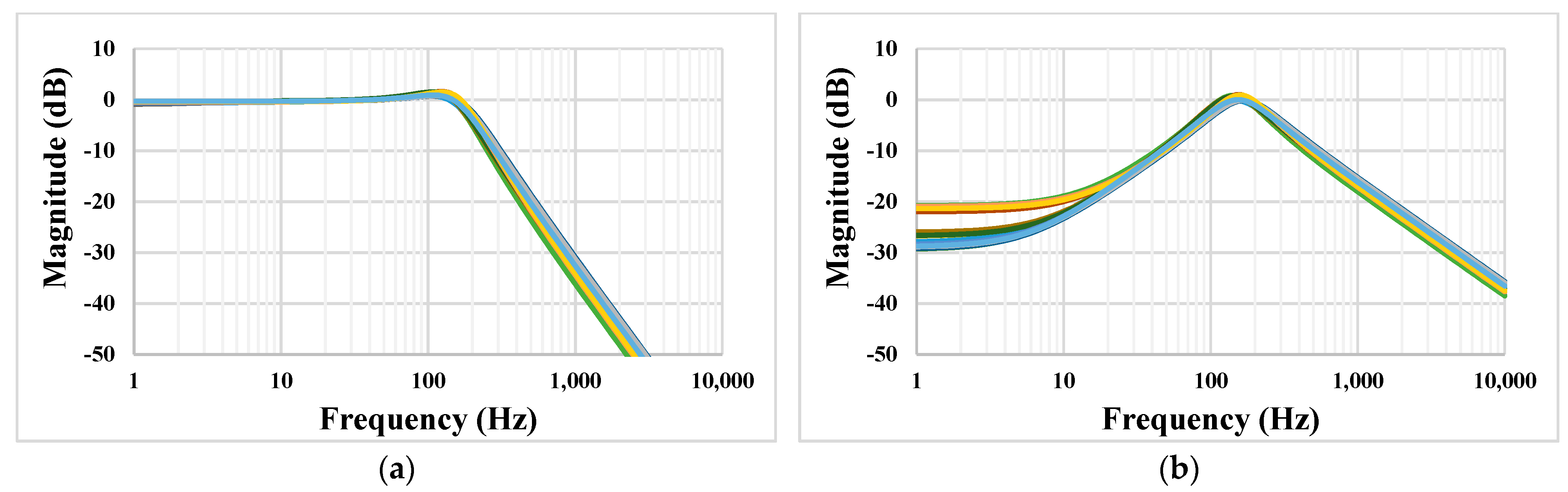
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kwak, J.Y.; Park, S.-Y. Compact Continuous Time Common-Mode Feedback Circuit for Low-Power, Area-Constrained Neural Recording Amplifiers. Electronics 2021, 10, 145. [Google Scholar] [CrossRef]
- Tasneem, N.T.; Mahbub, I. A 2.53 NEF 8-bit 10 kS/s 0.5 μm CMOS Neural Recording Read-Out Circuit with High Linearity for Neuromodulation Implants. Electronics 2021, 10, 590. [Google Scholar] [CrossRef]
- Ballo, A.; Pennisi, S.; Scotti, G. 0.5 V CMOS Inverter-Based Transconductance Amplifier with Quiescent Current Control. J. Low Power Electron. Appl. 2021, 11, 37. [Google Scholar] [CrossRef]
- Nordi, T.M.; Gounella, R.H.; Luppe, M.; Junior, J.N.S.; Fonoff, E.T.; Colombari, E.; Romero, M.A.; Carmo, J.P.P.D. Low-Noise Amplifier for Deep-Brain Stimulation (DBS). Electronics 2022, 11, 939. [Google Scholar] [CrossRef]
- Wyszynski, A.; Schaumann, R. Using multiple-input transconductors to reduce number of components in OTA-C filter design. Electron. Lett. 1992, 28, 217–220. [Google Scholar] [CrossRef]
- Gopinathan, V.; Tsividis, Y.P.; Tan, K.-S.; Hester, R.K. Design considerations for high-frequency continuous-time filters and implementation of an antialiasing filter for digital video. IEEE J. Solid-State Circuits 1990, 25, 1368–1378. [Google Scholar] [CrossRef]
- Mourabit, A.E.; Lu, G.-N.; Pittet, P. Wide-linear-range subthreshold OTA for low-power, low-Voltage, and low-frequency applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1481–1488. [Google Scholar] [CrossRef]
- Munoz, F.; Torralba, A.; Carvajal, R.G.; Tombs, J.; Ramirez-Angulo, J. Floating-gate-based tunable CMOS low-voltage linear transconductor and its application to HF g/sub m/-C filter design. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2001, 48, 106–110. [Google Scholar] [CrossRef]
- Lopez-Martin, A.J.; Ramirez-Angulo, J.; Carvajal, R.G.; Acosta, L. CMOS transconductors with continuous tuning using FGMOS balanced output current scaling. IEEE J. Solid-State Circuits 2008, 43, 1313–1323. [Google Scholar] [CrossRef]
- Rodriguez-Villegas, E. Low Power and Low Voltage Circuit Design with the FGMOS Transistor; The Institution of Engineering and Technology: London, UK, 2006; ISBN 0-86341-617-9/978-086341-617-0. [Google Scholar]
- Rico-Aniles, H.D.; Ramirez-Angulo, J.; Lopez-Martin, A.J.; Carvajal, R.G. 360 nW gate-driven ultra-low voltage CMOS linear transconductor with 1 MHz bandwidth and wide input range. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2332–2336. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Psychalinos, C. Multiple-input bulk-driven MOS transistor for low-voltage low-frequency applications. Circuits Syst. Signal Process. 2019, 38, 2829–2845. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Veldandi, H.; Jaikla, W. Multiple-input bulk-driven quasi-floating-gate MOS transistor for low-voltage low-power integrated circuits. AEU-Int. J. Electron. Commun. 2019, 100, 32–38. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Jaikla, W.; Ranjan, R.K. Comparative performance study of multiple-input bulk-driven and multiple-input bulk-driven quasi-floating-gate DDCCs. AEU-Int. J. Electron. Commun. 2019, 108, 1928. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Tang, K.-T. A 0.5-V multiple-input bulk-driven OTA in 0.18-μm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1739–1747. [Google Scholar] [CrossRef]
- Krummenacher, F.; Joehl, N. A 4-MHz CMOS continuous-time filter with on-chip automatic tuning. IEEE J. Solid-State Circuits 1988, 23, 750–758. [Google Scholar] [CrossRef]
- Furth, P.M.; Andreou, A.G. Linearised differential transconductors in subthreshold CMOS. Electron. Lett. 1995, 31, 545–547. [Google Scholar] [CrossRef] [Green Version]
- Tsividis, Y.P.; McAndrew, C. Operation and Modeling of the MOS Transistor; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Sedra, A.S.; Smith, K.C. Microelectronic Circuit, 4th ed.; Chapter 11; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Psychalinos, C.; Kasimis, C.; Khateb, F. Multiple-input single-output universal biquad filter using single output operational transconductance amplifiers. AEU-Int. J. Electron. Commun. 2018, 93, 360–367. [Google Scholar] [CrossRef]
- Jaikla, W.; Talabthong, P.; Siripongdee, S.; Supavarasuwat, P.; Suwanjan, P.; Chaichana, A. Electronically controlled voltage mode first order multifunction filter using low-voltage low-power bulk-driven OTAs. Microelectron. J. 2019, 91, 22–35. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Voltage Mode Third-Order Universal Filter Using a Single CCII. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020; pp. 160–165. [Google Scholar] [CrossRef]
- Unuk, T.; Yuce, E. A mixed-mode filter with DVCCs and grounded passive components only. AEU-Int. J. Electron. Commun. 2022, 144, 154063. [Google Scholar] [CrossRef]
- Wang, S.-F.; Chen, H.-P.; Ku, Y.; Chen, P.-Y. A CFOA-based voltage-mode multifunction biquadratic filter and a quadrature oscillator using the CFOA-based biquadratic filter. Appl. Sci. 2019, 9, 2304. [Google Scholar] [CrossRef] [Green Version]
- Bhaskar, D.R.; Raj, A.; Senani, R. Three new CFOA-based SIMO-type universal active filter configurations with unrivalled features. AEU-Int. J. Electron. Commun. 2022, 153, 154285. [Google Scholar] [CrossRef]
- Wang, S.-F.; Chen, H.-P.; Ku, Y.; Yang, C.-M. Independently tunable voltage-mode OTA-C biquadratic filter with five inputs and three outputs and its fully-uncoupled quadrature sinusoidal oscillator application. AEU-Int. J. Electron. Commun. 2019, 110, 152822. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T.; Psychalinos, C. Multiple-input universal filter and quadrature oscillator using multiple-input operational transconductance amplifiers. IEEE Access 2021, 9, 56253–56263. [Google Scholar] [CrossRef]
- Namdari, A.; Dolatshahi, M. Design of a low-voltage and low-power, reconfigurable universal OTA-C filter. Analog. Integr. Circuits Signal Process. 2022, 111, 169–188. [Google Scholar] [CrossRef]
- Pevarez-Lozano, H.; Sanchez-Sinencio, E. Minimum parasitic effects biquadratic OTA-C filter architectures. Analog. Integr. Circuits Signal Process. 1991, 1, 297–319. [Google Scholar] [CrossRef]
- Sun, Y.; Fidler, J.K. Synthesis and performance analysis of universal minimum component integrator-based IFLF OTA-grounded capacitor filter. IEE Proc. Circuits Devices Syst. 1996, 143, 107–114. [Google Scholar] [CrossRef]


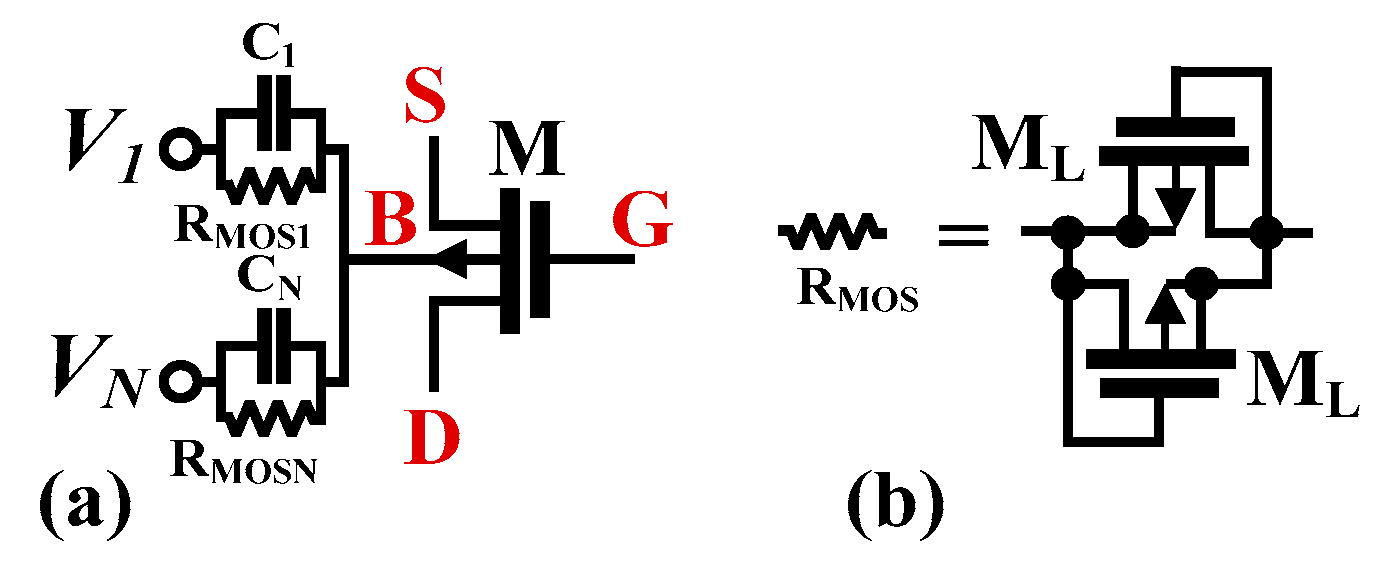





| Filtering Function | Input | Output | |
|---|---|---|---|
| LP | Non-inverting | ||
| Inverting | |||
| BP | Non-inverting | and | |
| Inverting | and | ||
| HP | Non-inverting | ||
| Inverting | |||
| BS | Non-inverting | ||
| Inverting | |||
| AP | Non-inverting | ||
| Inverting | |||
| Device Name | W/L (µm⁄µm) |
|---|---|
| M1, M2, M7–M10, M13 | 2 × 15/1 |
| M3–M6 | 2 × 10/1 |
| M3c–M6c | 10/1 |
| M7c–M10c, M13c, M11, M12 | 15/1 |
| ML | 5/4 |
| This Work | [26] | [27] | [28] | |
|---|---|---|---|---|
| Technology (nm) | 180 | commercial IC | 180 | 180 |
| VDD (V) | 0.5 | ±15 | 1.2 | ±0.3 |
| Power consumption (nW) | 37 | 860 × 106 | 0.96 × 106 | 5770 |
| DR (dB) | 50 | 53.2 | ||
| Fter function | 22 (VM) | 13 (VM) | 22(VM) | 20 (MM) |
| Offer inverting and non-inverting of five standard responses | Yes | No | Yes | No |
| Natural frequency (kHz) | 0.153 | 217 | 1 | 5 |
| Number of active and passive element | 3-OTA, 2-C | 5-OTA, 2-C | 4-OTA, 2-C | 8-OTA, 2-C |
| Total harmonic distortion (%) | 0.33@100 mVpp | 1.93@200 mVpp | 1.67@600 mVpp | <2@200 mVpp |
| 2.41 × 10−12 | - | 78.6 | 1.26 × 10−12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khateb, F.; Kumngern, M.; Kulej, T.; Akbari, M.; Stopjakova, V. 0.5 V, nW-Range Universal Filter Based on Multiple-Input Transconductor for Biosignals Processing. Sensors 2022, 22, 8619. https://doi.org/10.3390/s22228619
Khateb F, Kumngern M, Kulej T, Akbari M, Stopjakova V. 0.5 V, nW-Range Universal Filter Based on Multiple-Input Transconductor for Biosignals Processing. Sensors. 2022; 22(22):8619. https://doi.org/10.3390/s22228619
Chicago/Turabian StyleKhateb, Fabian, Montree Kumngern, Tomasz Kulej, Meysam Akbari, and Viera Stopjakova. 2022. "0.5 V, nW-Range Universal Filter Based on Multiple-Input Transconductor for Biosignals Processing" Sensors 22, no. 22: 8619. https://doi.org/10.3390/s22228619
APA StyleKhateb, F., Kumngern, M., Kulej, T., Akbari, M., & Stopjakova, V. (2022). 0.5 V, nW-Range Universal Filter Based on Multiple-Input Transconductor for Biosignals Processing. Sensors, 22(22), 8619. https://doi.org/10.3390/s22228619








