Small Ultrasound-Based Corrosion Sensor for Intraday Corrosion Rate Estimation
Abstract
1. Introduction
Corrosion Monitoring in Offshore Wind Turbines
2. Theory
2.1. Ultrasound Theory
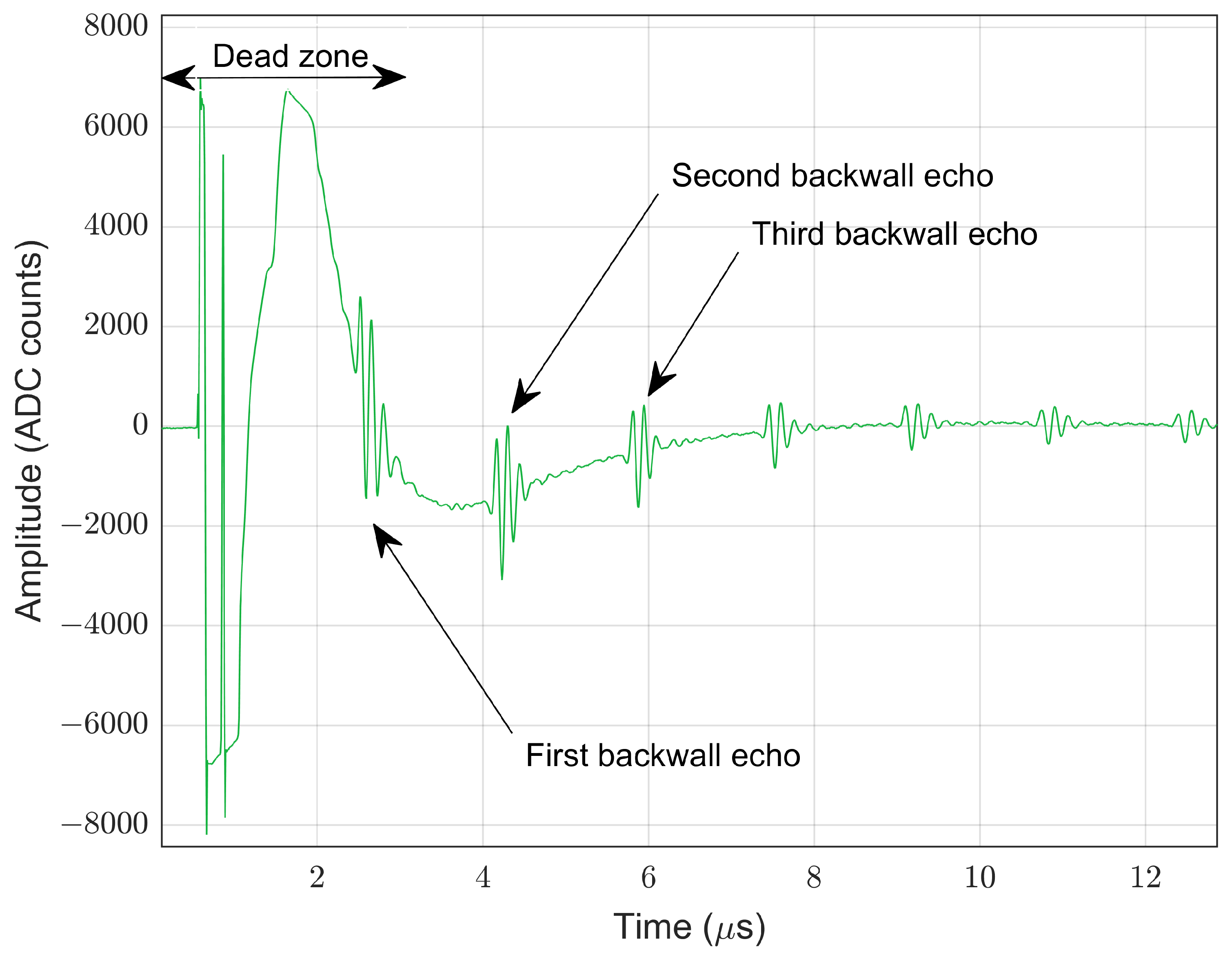
- Mode 1: excitation signal—first back-wall echo.
- Mode 2: near surface—first back-wall echo.
- Mode 3: two successive back-wall echoes.
Estimation of Time of Flight
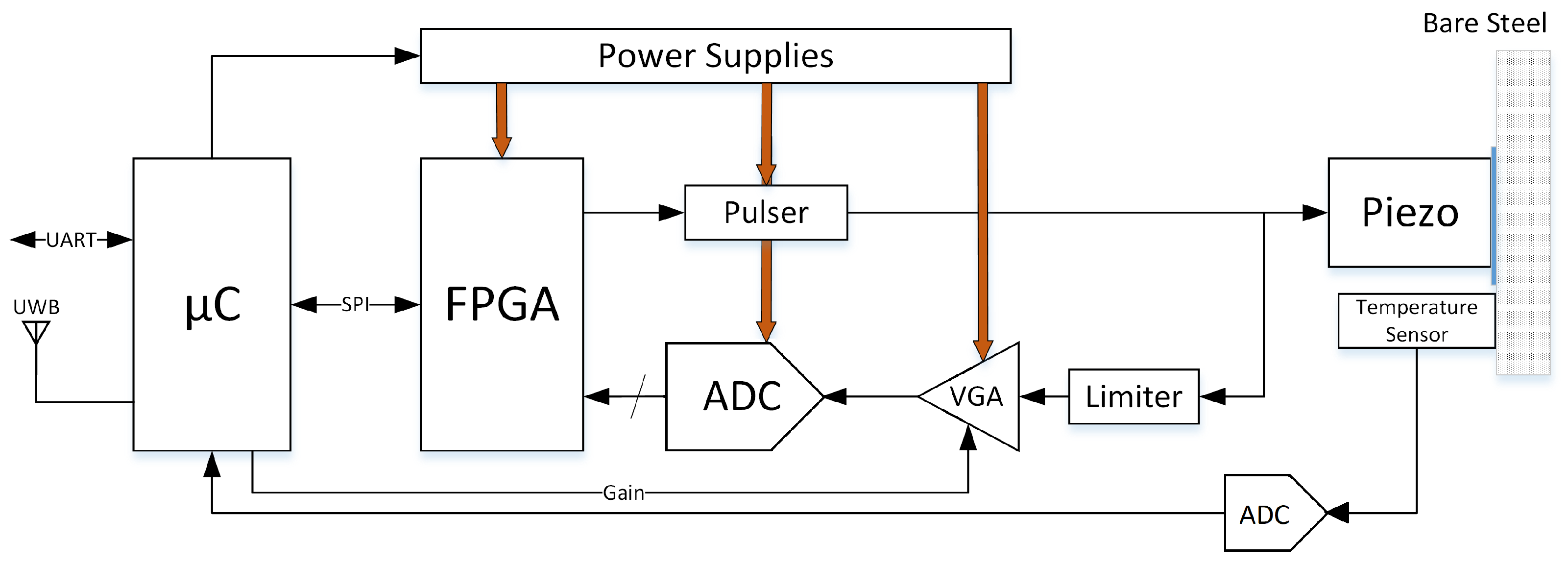
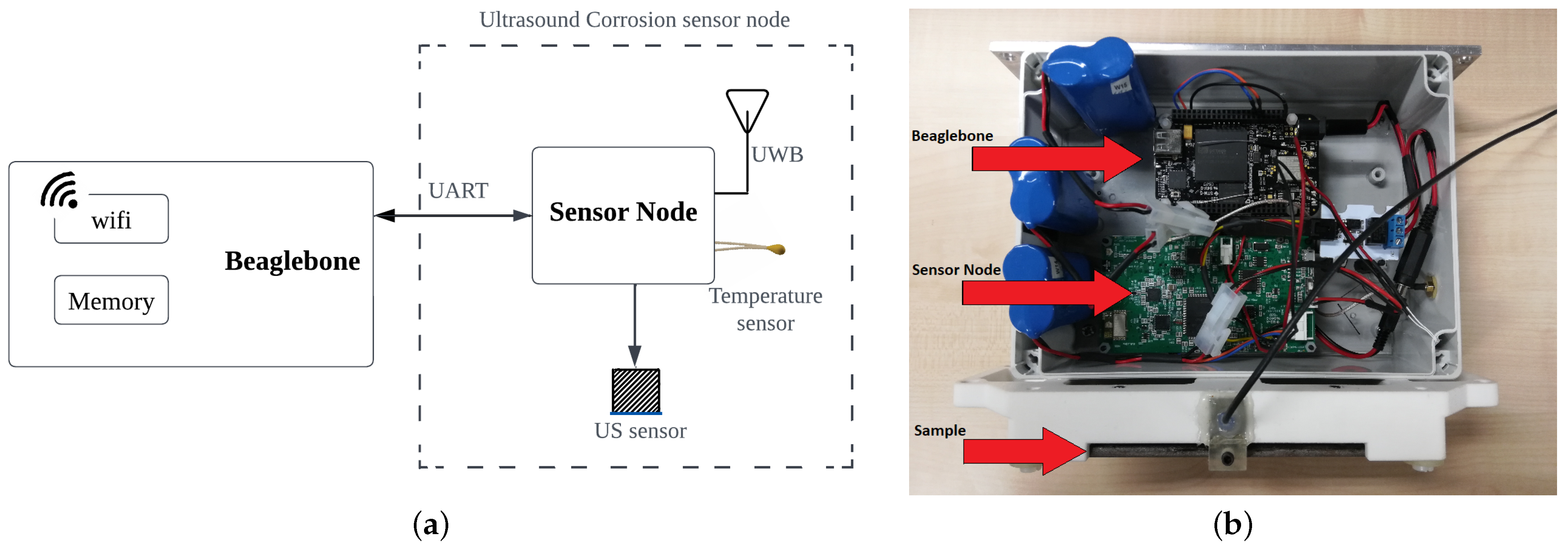
2.2. Description of the Corrosion Sensor
Architecture of the Sensor Node
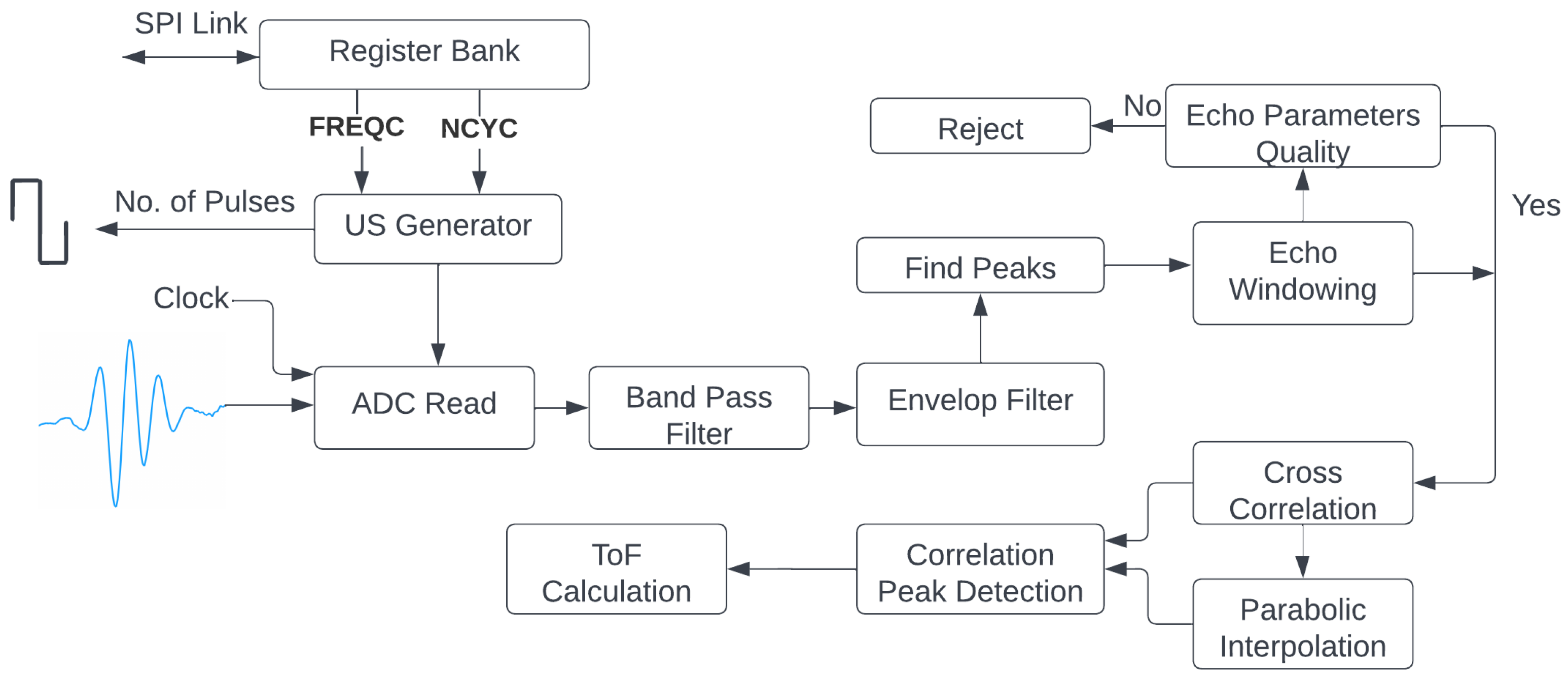
2.3. Algorithm Description of ToF Calculation
2.4. Calculation of Relative Thickness Loss Using ToF
2.4.1. Temperature Experiment
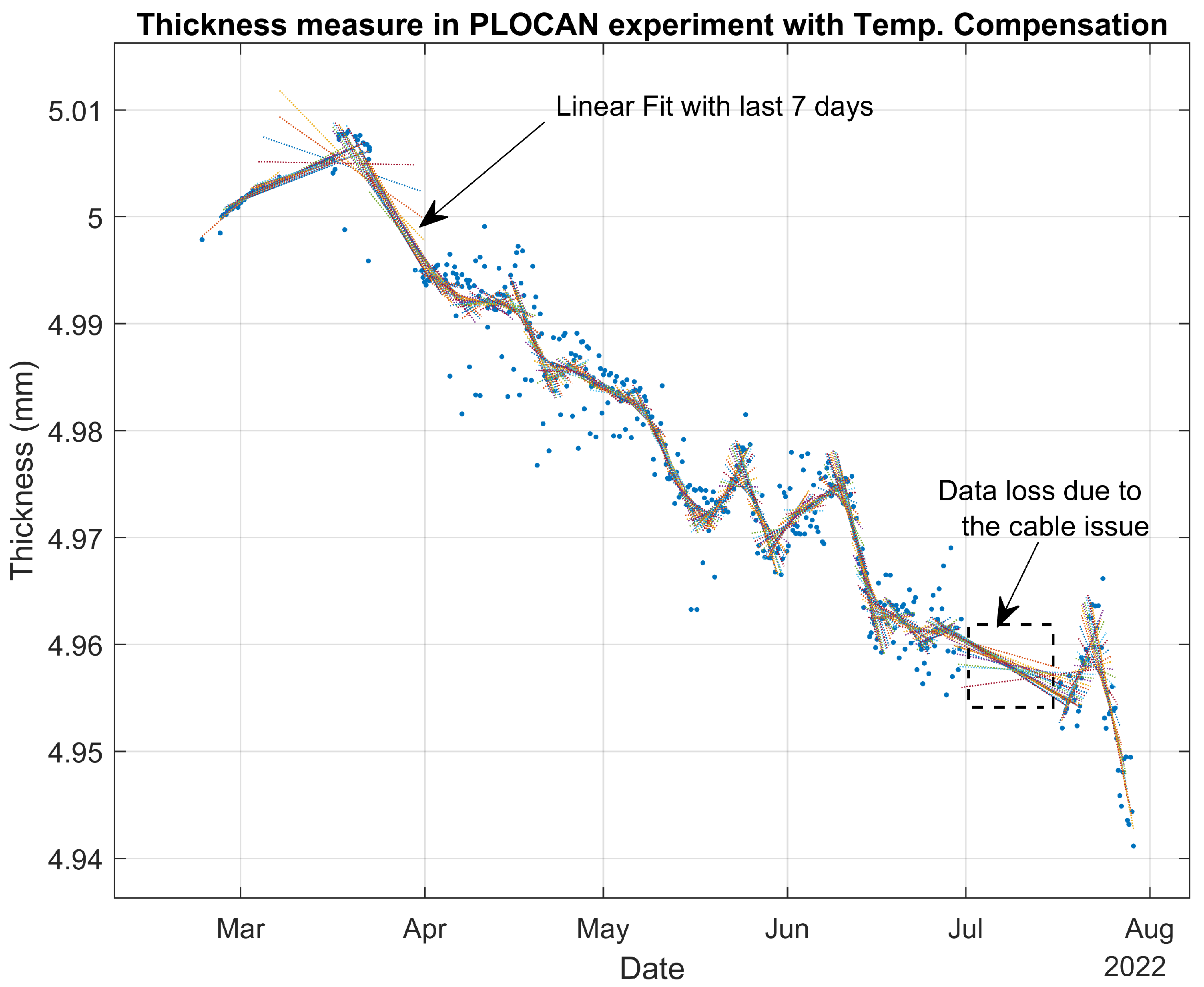
3. Experiment: Evolution of Thickness Loss Due to Corrosion in Real Conditions
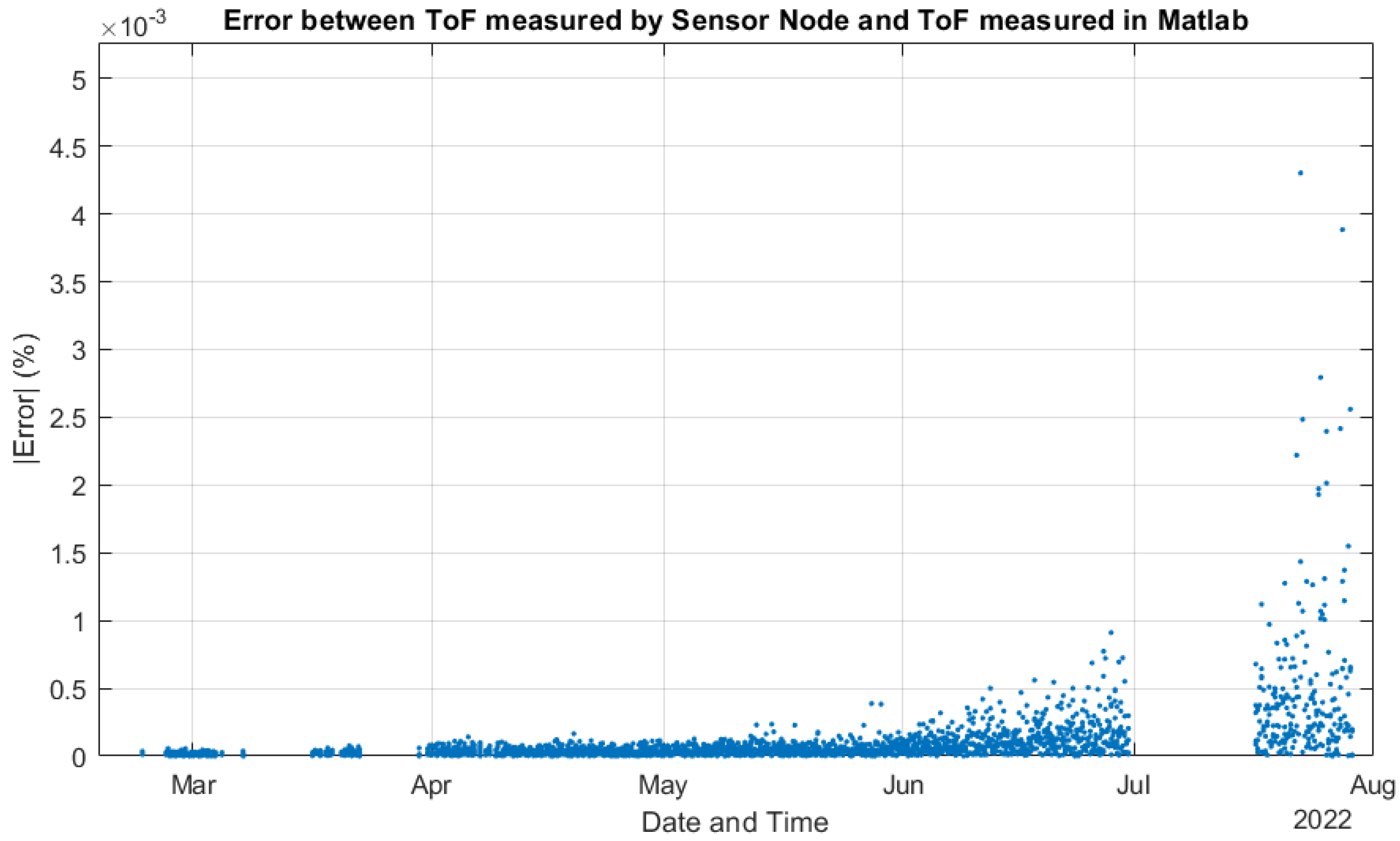
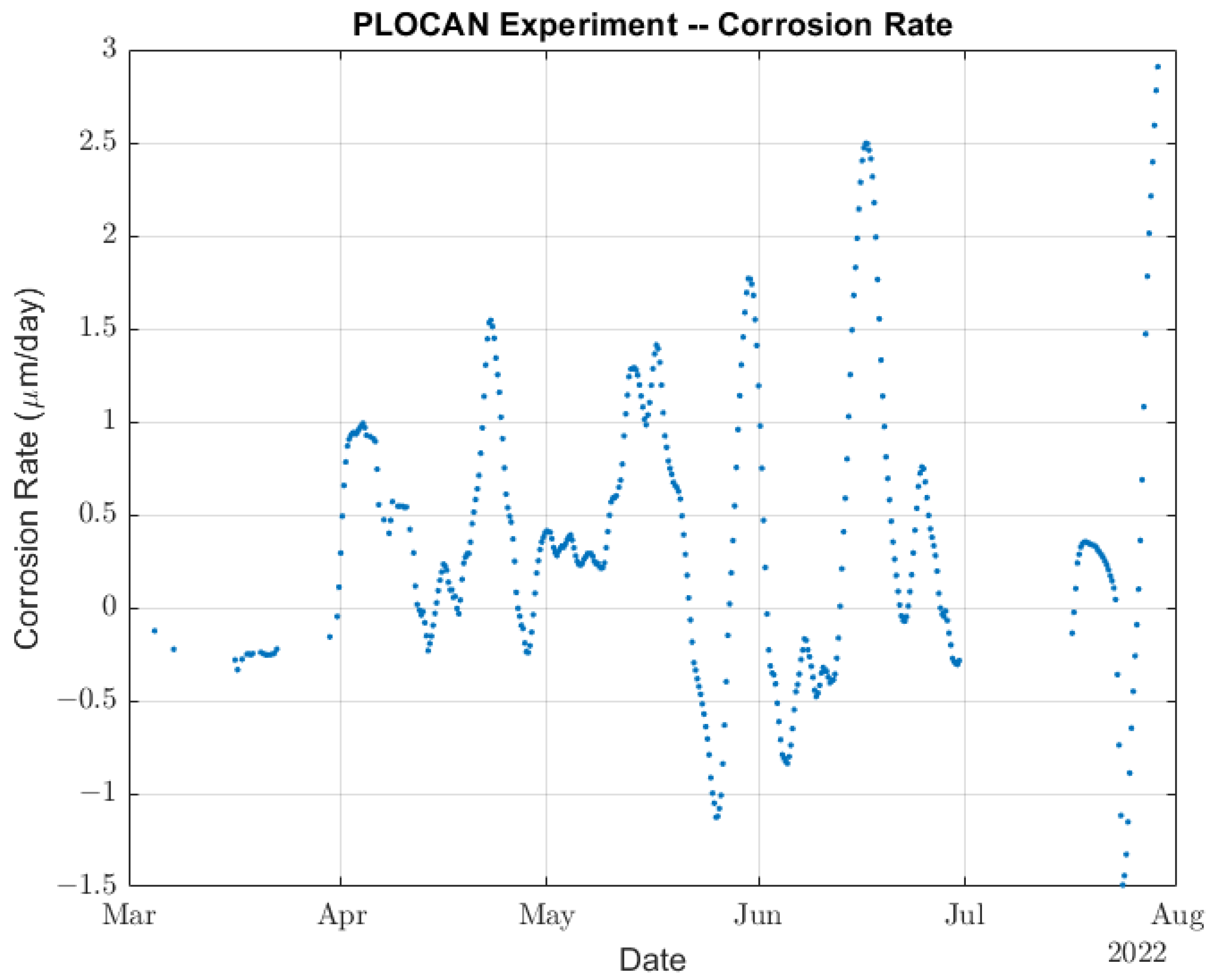
4. Results of the Experiment and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Analog-to-digital converter |
| AFE | Analog front end |
| BP | Bandpass |
| CAPEX | Capital expenditure |
| CCF | Cross-correlation function |
| FPGA | Field-programmable gate array |
| GDP | Gross domestic product |
| I2C | Interintegrated circuit |
| NDT | Nondestructive testing |
| OWTs | Offshore wind turbines |
| RMS | Root mean square |
| SNR | Signal-to-noise ratio |
| SHM | Structural health monitoring |
| SL | Signal level |
| SPI | Serial peripheral interface |
| ToF | Time-of-flight |
| UART | Universal asynchronous receiver and transmitter |
| US | Ultrasound |
| VGA | Variable gain amplifier |
References
- IRENA. Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects by International Renewable Energy Association. 2019. Available online: https://www.irena.org/-/media/files/irena/agency/publication/2019/oct/irena_future_of_wind_2019.pdf (accessed on 7 July 2022).
- The European Offshore Wind Industry: Key Trends and Statistics 2017, Wind Europe. 2018. Available online: https://windeurope.org/about-wind/statistics/offshore/european-offshore-wind-industry-key-trends-statistics-2017/ (accessed on 9 July 2022).
- Zheng, D.; Bose, S. Offshore wind turbine design. In Wind Power Generation and Wind Turbine Design; WIT Press: Southampton, UK, 2010; p. 363. [Google Scholar]
- Márquez, F.P.G.; Jimenez, A.A.; Muñoz, C.Q.G. Non-destructive testing of wind turbines using ultrasonic waves. In Non-Destructive Testing and Condition Monitoring Techniques for Renewable Energy Industrial Assets; Elsevier: Boston, MA, USA, 2020; pp. 91–101. [Google Scholar]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Martinez-Luengo, M.; Kolios, A.; Wang, L. Structural health monitoring of offshore wind turbines: A review through the Statistical Pattern Recognition Paradigm. Renew. Sustain. Energy Rev. 2016, 64, 91–105. [Google Scholar] [CrossRef]
- Smarsly, K.; Hartmann, D.; Law, K.H. An integrated monitoring system for life-cycle management of wind turbines. Int. J. Smart Struct. Syst. 2013, 12, 209–233. [Google Scholar] [CrossRef]
- Igwemezie, V.; Mehmanparast, A.; Kolios, A. Materials selection for XL wind turbine support structures: A corrosion-fatigue perspective. Mar. Struct. 2018, 61, 381–397. [Google Scholar] [CrossRef]
- Koch, G.; Varney, J.; Thompson, N.; Moghissi, O.; Gould, M.; Payer, J. NACE International Impact Report: International Measures of Prevention, Application, and Economics of Corrosion Technologies Study; Technical Report; NACE International: Houston, TX, USA, 2016. [Google Scholar]
- Hossain, M.L.; Abu-Siada, A.; Muyeen, S. Methods for advanced wind turbine condition monitoring and early diagnosis: A literature review. Energies 2018, 11, 1309. [Google Scholar] [CrossRef]
- Price, S.; Figueira, R. Corrosion Protection Systems and Fatigue Corrosion in Offshore Wind Structures: Current Status and Future Perspectives. Coatings 2017, 7, 25. [Google Scholar] [CrossRef]
- Corrosion Classifications for Offshore Wind. Available online: https://www.onropes.co.uk/corrosion-classifications#:~:text=In%20the%20tidal%20and%20splash,yearly%20depending%20on%20the%20location (accessed on 19 August 2022).
- Nassar, N.E.A. Corrosion in marine and offshore steel structures: Classification and overview. Int. J. Adv. Eng. Sci. Appl. 2022, 3, 7–11. [Google Scholar] [CrossRef]
- Khodabux, W.; Causon, P.; Brennan, F. Profiling corrosion rates for offshore wind turbines with depth in the North Sea. Energies 2020, 13, 2518. [Google Scholar] [CrossRef]
- International, N. Techniques for Monitoring Corrosion and Related Parameters in Field Applications; NACE International: Houston, TX, USA, 1999. [Google Scholar]
- Bardal, E.; Drugli, J. Corrosion detection and diagnosis. Mater. Sci. Eng. 2004, 3. [Google Scholar]
- Forsyth, D.S. Non-destructive testing for corrosion. In Corrosion Fatigue and Environmentally Assisted Cracking in Aging Military Vehicles (RTO-AG-AVT-140); NATO: Washington, DC, USA, 2011. [Google Scholar]
- Wright, R.F.; Lu, P.; Devkota, J.; Lu, F.; Ziomek-Moroz, M.; Ohodnicki, P.R. Corrosion sensors for structural health monitoring of oil and natural gas infrastructure: A review. Sensors 2019, 19, 3964. [Google Scholar] [CrossRef]
- Hendee, W.R.; Ritenour, E.R. Medical Imaging Physics; Wiley-Liss, Inc.: New York, NY, USA, 2002; pp. 303–353. [Google Scholar]
- Wróbel, G.; Pawlak, S. A comparison study of the pulseecho and through-transmission ultrasonics in glass/epoxy composites. J. Achiev. Mater. Manuf. Eng. 2007, 22, 51–54. [Google Scholar]
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing; Springer Science & Business Media: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Fowler, K.A.; Elfbaum, G.M.; Smith, K.A.; Nelligan, T.J. Theory and application of precision ultrasonic thickness gauging. Insight 1996, 38, 582–587. [Google Scholar]
- An Introduction to Ultrasonic Transducers for Nondestructive Testing, OLYMPUS. Available online: https://www.olympus-ims.com/en/resources/white-papers/intro-ultrasonic-transducers-ndt-testing/ (accessed on 18 August 2022).
- Rathod, V.T. A review of acoustic impedance matching techniques for piezoelectric sensors and transducers. Sensors 2020, 20, 4051. [Google Scholar] [CrossRef]
- Rathod, V.T. A review of electric impedance matching techniques for piezoelectric sensors, actuators and transducers. Electronics 2019, 8, 169. [Google Scholar] [CrossRef]
- Zou, F.; Cegla, F. High accuracy ultrasonic corrosion monitoring. In CORROSION 2017; OnePetro: New Orleans, LA, USA, 2017. [Google Scholar]
- Queirós, R.; Martins, R.C.; Girao, P.S.; Serra, A.C. A new method for high resolution ultrasonic ranging in air. In Proceedings of the XVIII IMEKO World Congress, Rio de Janeiro, Brazil, 17–22 September 2006; pp. 17–22. [Google Scholar]
- Huang, Y.; Wang, J.S.; Huang, K.; Ho, C.; Huang, J.; Young, M.S. Envelope pulsed ultrasonic distance measurement system based upon amplitude modulation and phase modulation. Rev. Sci. Instruments 2007, 78, 065103. [Google Scholar] [CrossRef]
- Franco, E.E.; Meza, J.M.; Buiochi, F. Measurement of elastic properties of materials by the ultrasonic through-transmission technique. Dyna 2011, 78, 58–64. [Google Scholar]
- Svilainis, L. Review of high resolution time of flight estimation techniques for ultrasonic signals. In Proceedings of the 2013 International Conference NDT, Telford, UK, 10–12 September 2013; pp. 1–12. [Google Scholar]
- Herter, S.; Youssef, S.; Becker, M.M.; Fischer, S.C. Machine Learning Based Preprocessing to Ensure Validity of Cross-Correlated Ultrasound Signals for Time-of-Flight Measurements. J. Nondestruct. Eval. 2021, 40, 1–9. [Google Scholar] [CrossRef]
- Schäfer, M.; Theado, H.; Becker, M.M.; Fischer, S.C. Optimization of the Unambiguity of Cross-Correlated Ultrasonic Signals through Coded Excitation Sequences for Robust Time-of-Flight Measurements. Signals 2021, 2, 366–377. [Google Scholar] [CrossRef]
- Lu, Z. Estimating time-of-flight of multi-superimposed ultrasonic echo signal through envelope. In Proceedings of the 2014 International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 14–16 November 2014; pp. 300–303. [Google Scholar]
- Lu, Z.; Yang, C.; Qin, D.; Luo, Y.; Momayez, M. Estimating ultrasonic time-of-flight through echo signal envelope and modified Gauss Newton method. Measurement 2016, 94, 355–363. [Google Scholar] [CrossRef]
- Thibbotuwa, U.C.; Cortés, A.; Irizar, A. Ultrasound-Based Smart Corrosion Monitoring System for Offshore Wind Turbines. Appl. Sci. 2022, 12, 808. [Google Scholar] [CrossRef]
- Contact Transducers—Olympus-IMS.com. Available online: https://www.olympus-ims.com/en/ultrasonic-transducers/contact-transducers/#!cms[focus]=cmsContent10861 (accessed on 15 November 2021).
- Guisasola, A.; Cortés, A.; Cejudo, J.; da Silva, A.; Losada, M.; Bustamante, P. Reliable and Low-Power Communications System Based on IR-UWB for Offshore Wind Turbines. Electronics 2022, 11, 570. [Google Scholar] [CrossRef]
- Ultra-Tiny, 16-Bit Delta-Sigma ADC with I2C Interface, LTC2451. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/2451fg.pdf (accessed on 25 June 2022).
- GA10K3A1i SERIES II THERMISTORS. Available online: https://il.farnell.com/te-connectivity/ga10k3a1ib/thermistor-ntc-10k/dp/3397780 (accessed on 20 June 2022).
- Cespedes, I.; Huang, Y.; Ophir, J.; Spratt, S. Methods for estimation of subsample time delays of digitized echo signals. Ultrason. Imaging 1995, 17, 142–171. [Google Scholar] [CrossRef]
- Red Pitaya STEMlab 125-14. Available online: https://redpitaya.com/stemlab-125-14/ (accessed on 1 June 2022).
- Structalit® 1028 R. Available online: https://www.panacol.com/panacol/datasheets/structalit/structalit-1028r-english-tds-panacol-adhesive.pdf (accessed on 24 June 2022).
- PX900D A Low Viscosity Unfilled Epoxy Resin System. Available online: https://www.blelektronik.com.pl/wp-content/uploads/2019/07/PX900D.pdf (accessed on 24 June 2022).
- Zou, F.; Cegla, F.B. On quantitative corrosion rate monitoring with ultrasound. J. Electroanal. Chem. 2018, 812, 115–121. [Google Scholar] [CrossRef]
- Technical Discussion: Can Corrosion Deposits on Hidden Face Affect Thickness Reading? Available online: https://www.ndt.net/forum/thread.php?rootID=52247 (accessed on 1 September 2021).

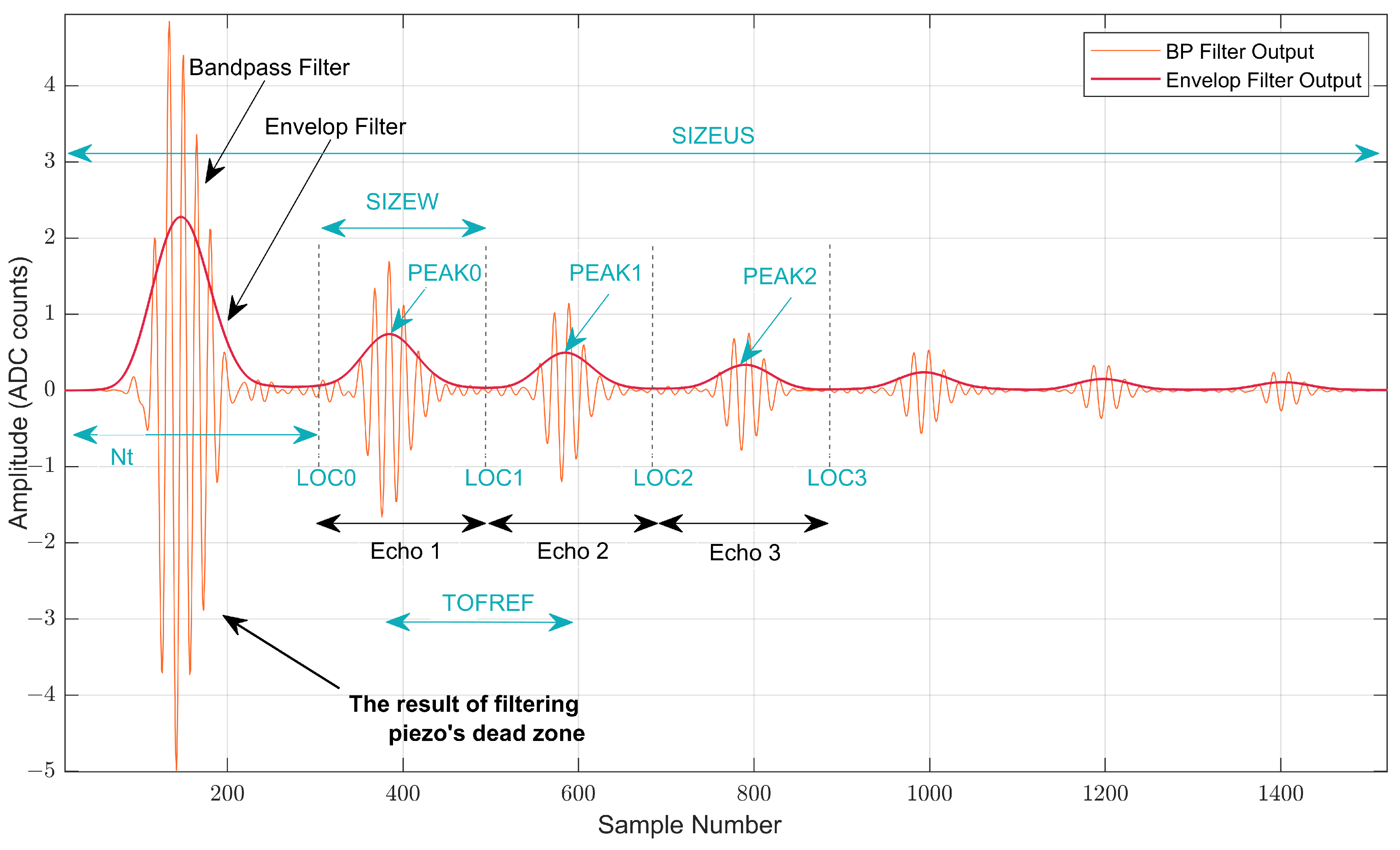







| Parameter Name | Description | Value |
|---|---|---|
| SIZEUS | Number of data samples received from the ADC | 2048 |
| NT | Number of samples that must be trimmed | 0 |
| from the envelop signal to remove | ||
| of the piezo’s dead zone | ||
| FREQC | Number of cycles of the sampling period | 16 |
| to obtain the piezo sensor’s resonance | ||
| frequency | ||
| NCYC | Number of periods of the excitation pulse | 1 |
| TOFREF | Approximate expected value of the ToF in number of samples | 210 |
| SIZEW | Typical echo duration in number of samples | 192 |
| ECHON | First echo to be detected and processed | 2 |
| SIZEWL | Number of cross-correlation samples taken on the | 32 |
| left-hand side of the correlation index 0 | ||
| SIZEXC | Total number of processed cross-correlation samples | 64 |
| Experimental Setup | Value |
|---|---|
| Sample material | S355 |
| Sample thickness | 5 mm |
| Ultrasound probe | V111 (Olympus) |
| Probe diameter of contact | 15 mm |
| Probe nominal element size | 13 mm |
| Adhesive/Couplant | Structalit 1028 R |
| US signal frequency | 7.8 MHz |
| US signal amplitude | 30 V (±15 V) |
| Speed of sound in S355 (long. waves) | 5950 m/s |
| Speed of sound thermal coefficient | °C |
| Thermal expansion coefficient | °C |
| Experimental location in latitude–longitude (decimal degrees) | 27.9920, −15.3686 |
| No. of measurement events per day | 4 (one every 6 h) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thibbotuwa, U.C.; Cortés, A.; Irizar, A. Small Ultrasound-Based Corrosion Sensor for Intraday Corrosion Rate Estimation. Sensors 2022, 22, 8451. https://doi.org/10.3390/s22218451
Thibbotuwa UC, Cortés A, Irizar A. Small Ultrasound-Based Corrosion Sensor for Intraday Corrosion Rate Estimation. Sensors. 2022; 22(21):8451. https://doi.org/10.3390/s22218451
Chicago/Turabian StyleThibbotuwa, Upeksha Chathurani, Ainhoa Cortés, and Andoni Irizar. 2022. "Small Ultrasound-Based Corrosion Sensor for Intraday Corrosion Rate Estimation" Sensors 22, no. 21: 8451. https://doi.org/10.3390/s22218451
APA StyleThibbotuwa, U. C., Cortés, A., & Irizar, A. (2022). Small Ultrasound-Based Corrosion Sensor for Intraday Corrosion Rate Estimation. Sensors, 22(21), 8451. https://doi.org/10.3390/s22218451







