The Effects of Sheet Thickness and Excitation Frequency on Hysteresis Loops of Non-Oriented Electrical Steel
Abstract
1. Introduction
1.1. Basic Information on Non-Oriented Electrical Steels
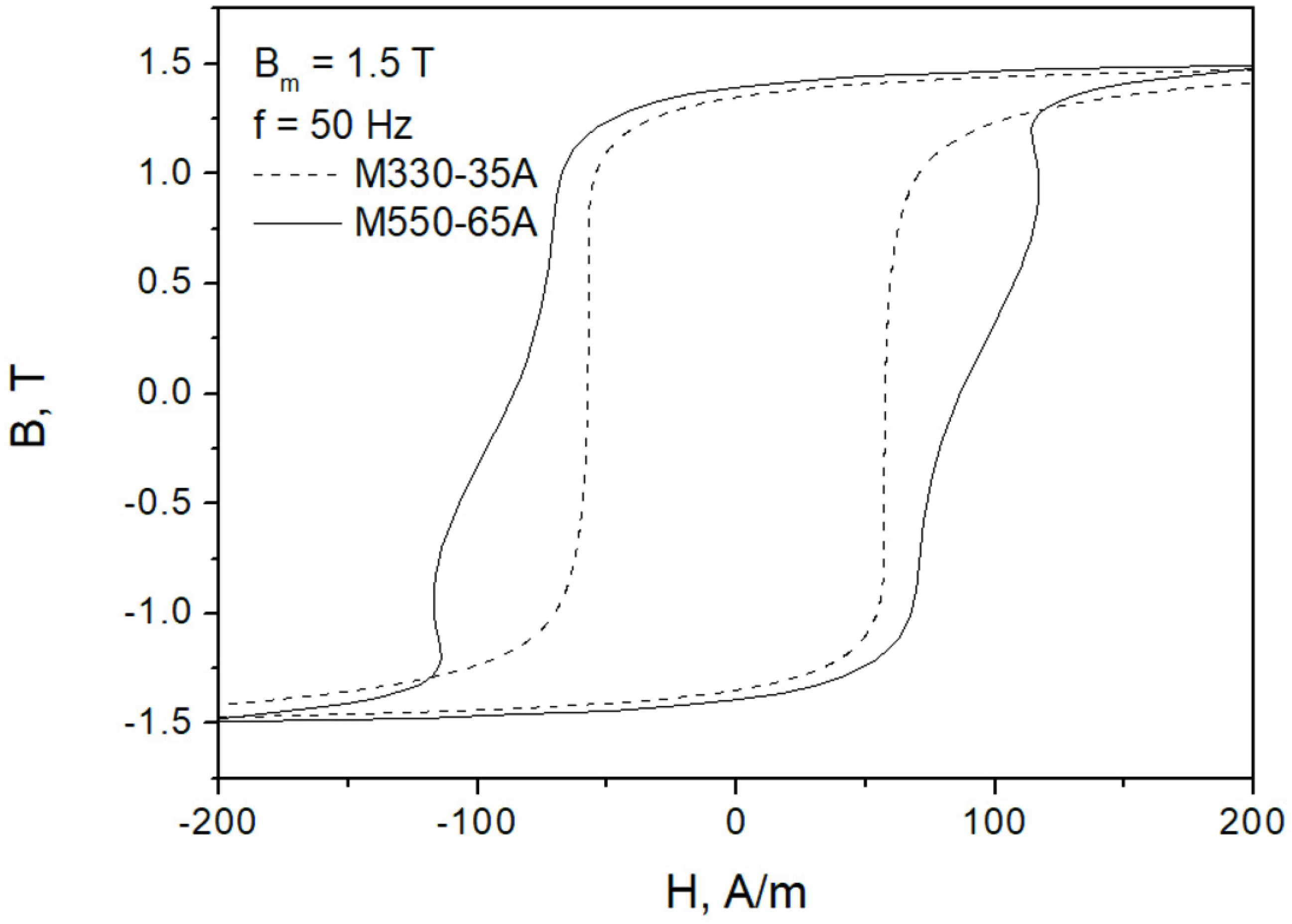
1.2. Basic Information on the Examined Steel Samples and the Measurement Setup
- Frequency range 5–400 Hz, with a resolution Δf = 0.01 Hz and setting accuracy 0.2%;
- Magnetic induction (or polarization) range 0.05–2.0 T, with a resolution ΔB = 0.01 T and setting accuracy 0.1%;
- Admissible deviation of the secondary voltage shape factor from the pure sine signal does not exceed 0.1%. The accuracy of measurements meets the requirements of IEC and DIN (German) standards in the range prescribed by the standards. The guaranteed expanded uncertainty of type B for loss measurements is below 1.5% (for the 0.95 confidence level).
1.3. Problem Statement
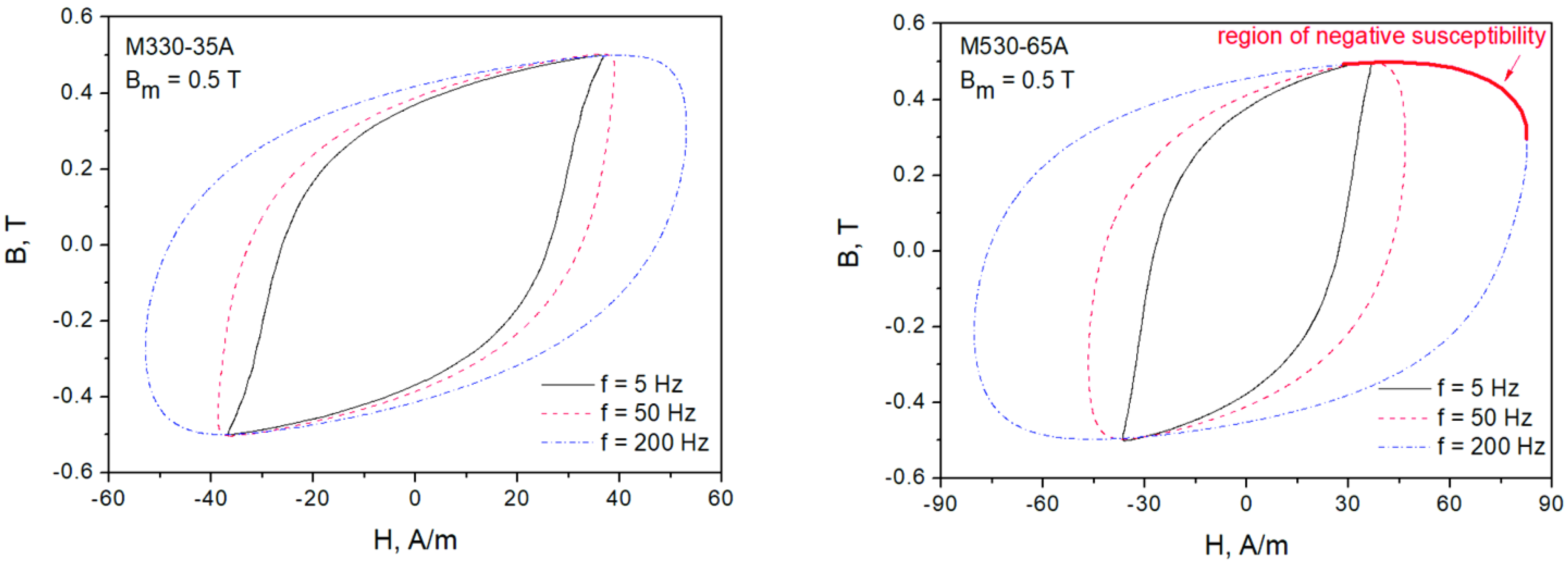
1.3.1. Some Useful Quasi-Static Hysteresis Models and the Mysterious Negative Susceptibility Region Observed for Dynamic Loops
1.3.2. To Separate or Not to Separate? That Is the Question
- According to Occam’s razor principle, the description should be made as simple as possible, and the three-term description has some limitations due to the presence of the “classical” loss term, which in its original form does not account for corrections due to eddy current shielding; therefore, it should be considered as approximate only. Already in 1963 Becker warned against an uncritical use of three-term separation schemes: “…if the losses are being calculated on a model that is not correct, it does not appear fruitful to regard the discrepancy as a third independent component of the total loss” [36].
- The origin of excess loss as related to eddy currents has been put into question by Mayergoyz and Serpico, who regarded the third term as being related rather to the intrinsic nonlinear dynamics underlying bistable/multistable behavior associated with hysteresis [51].
1.3.3. How to Extend a Hysteresis Model to Dynamic Conditions
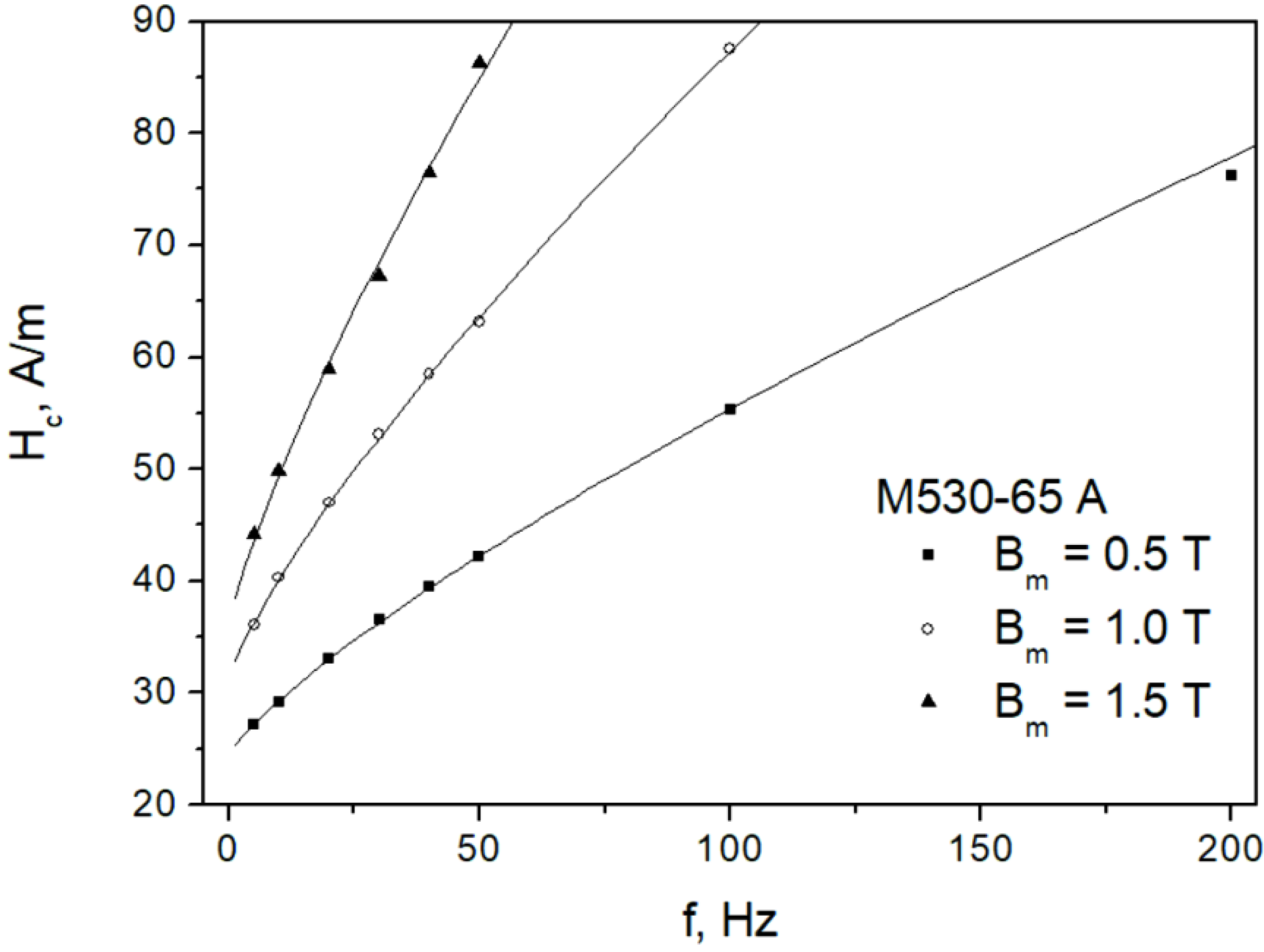
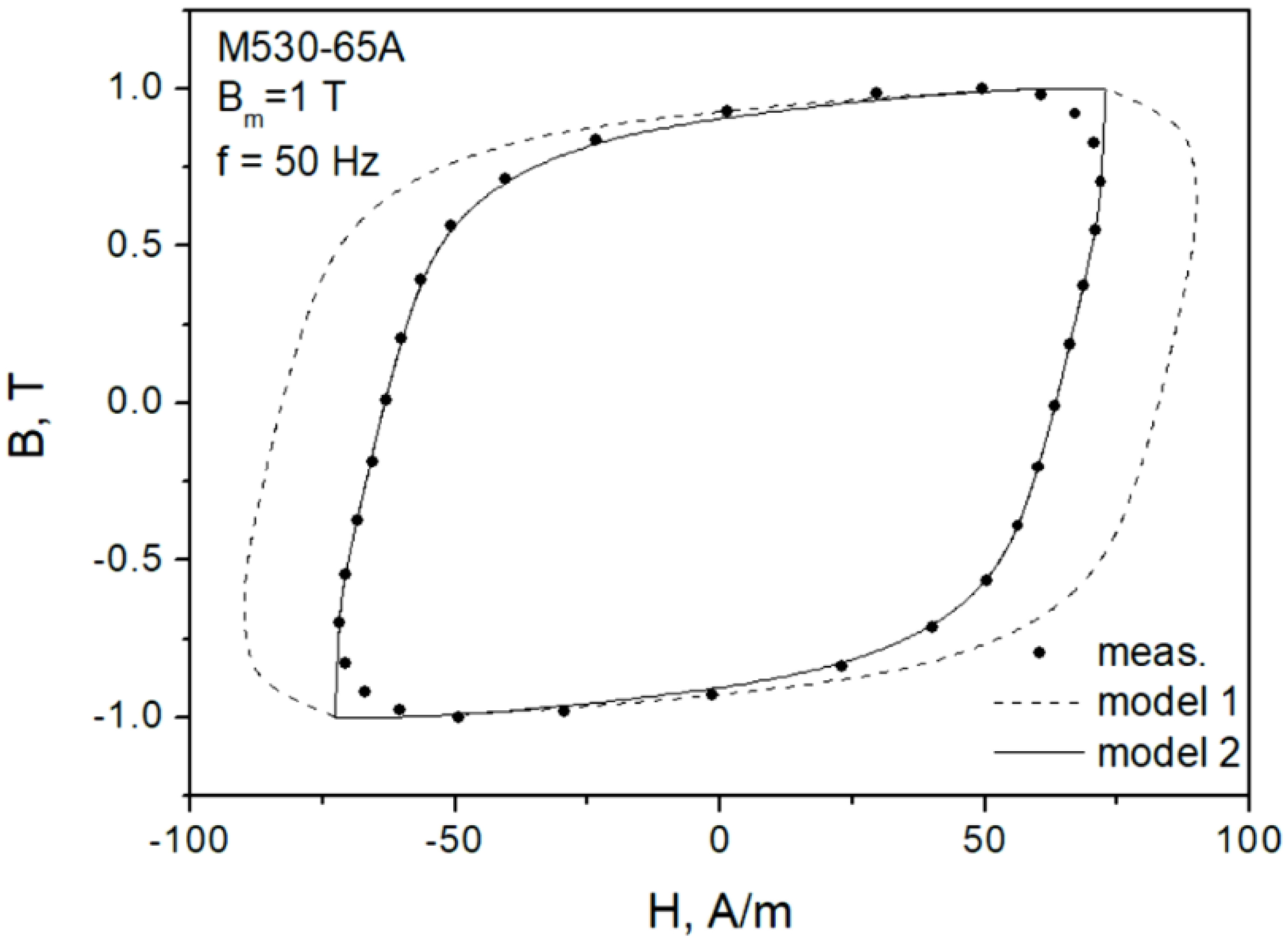
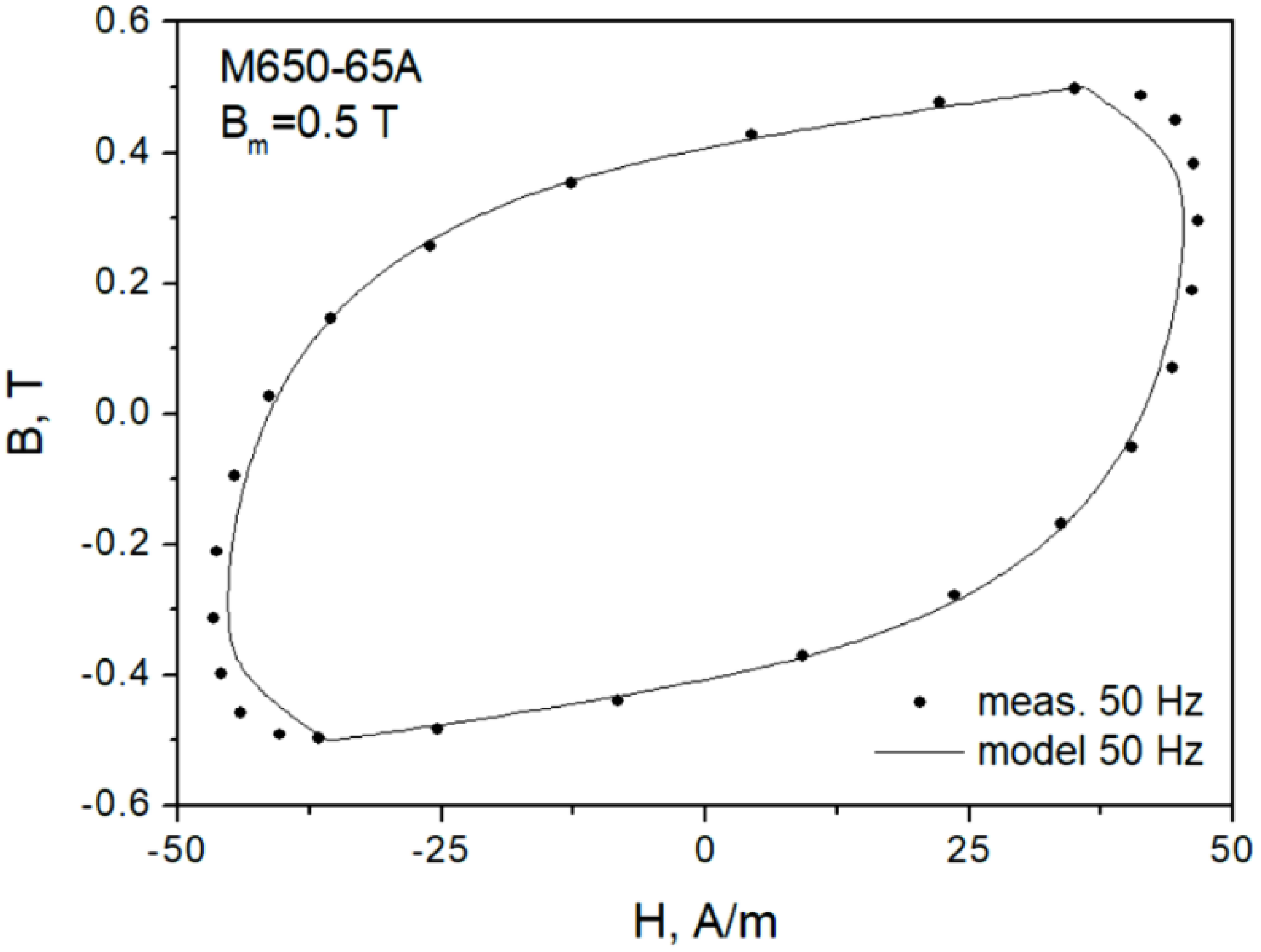
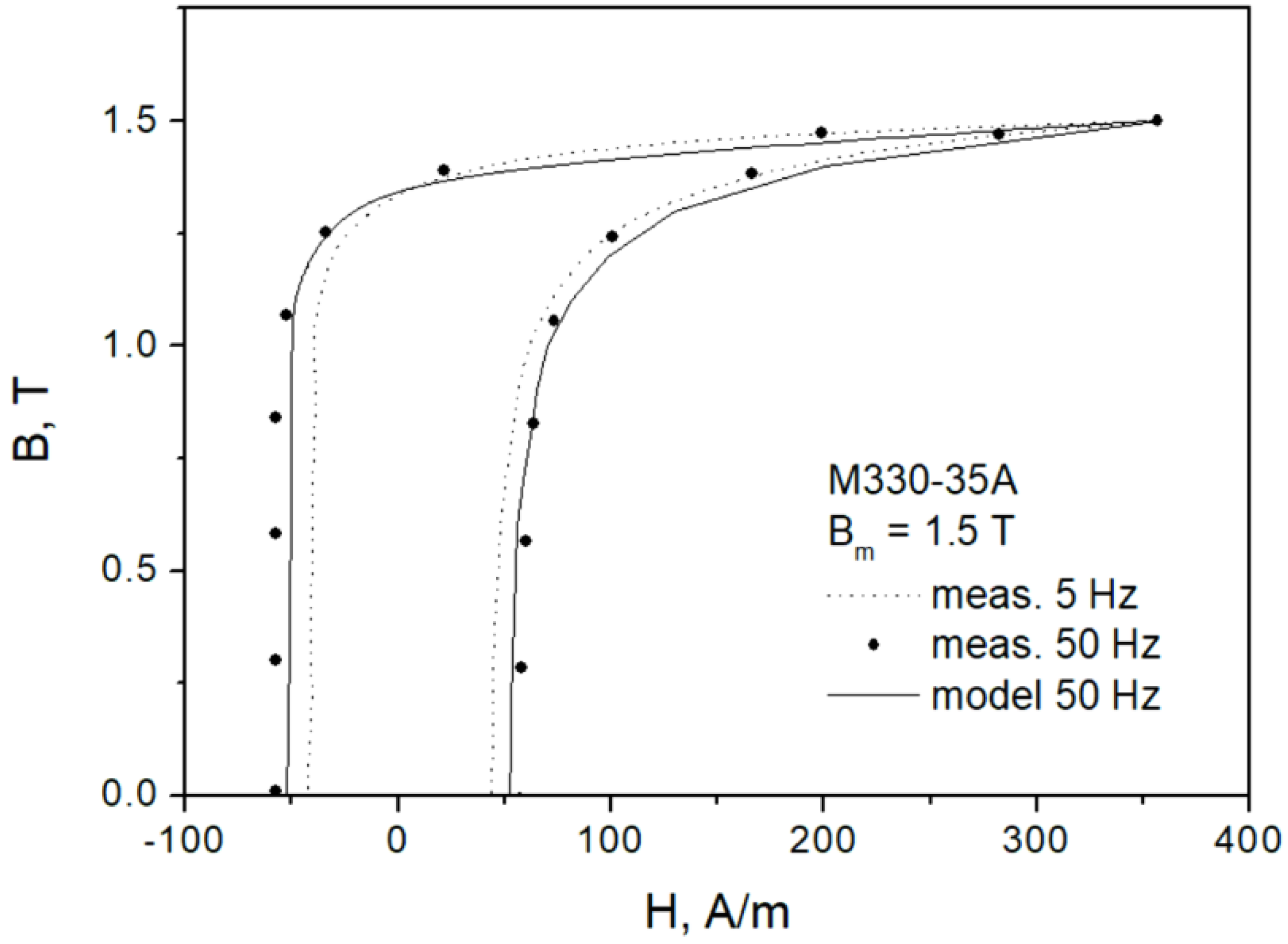
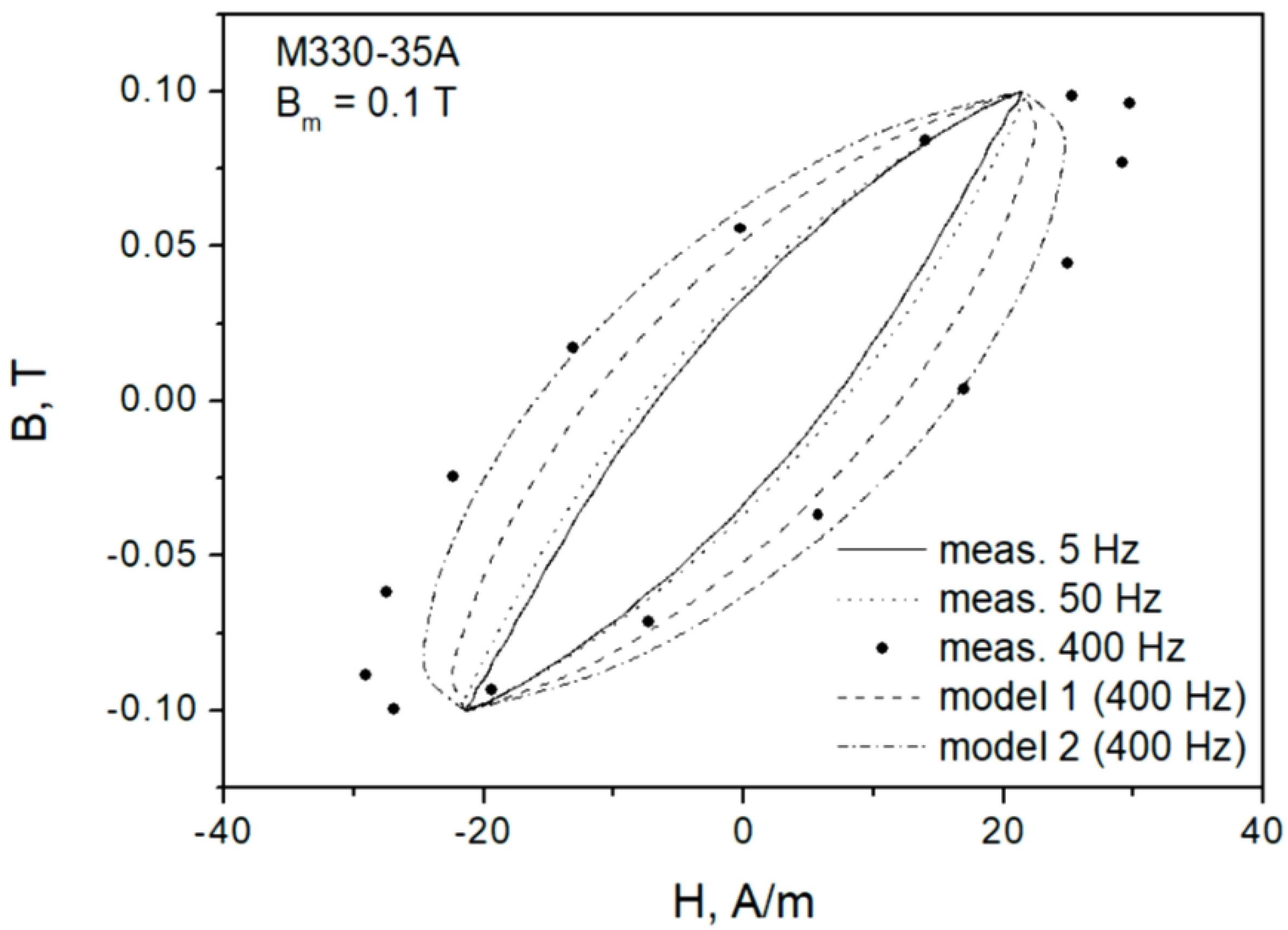
2. Modeling
- We consider the ascending branch of the linear fit to be acceptable, in particular for higher induction levels; however, a more complicated nonlinear dependency might be more appropriate for lower induction levels, in particular for the thick sample;
- The slopes of the fitting lines increase with increasing induction amplitude; this fact is at odds with the constant value assumed in Ref. [59]. The approach considered by Raulet et al. assumed a constant value in the whole sample cross-section regardless of excitation level, which allowed the authors to implement a simple finite-difference scheme for solving the diffusion equation. The measurement results depicted in Figure 4 and Figure 5 prove that the assumption of constant is oversimplified, since the local induction values at each “slice” of the sample (i.e., at different depths) may vary considerably; accordingly, the local values should be updated.
- It is assumed that the quasi-static (or more precisely ) dependence is known for a given amplitude ;
- From the measurements of , we know the value of the fractional exponent needed for subsequent computations;
- If we consider the ascending branch of the hysteresis loop under symmetric excitation, then we notice immediately that varies from to in accordance with , where the “local” time runs from 0 to . Thus, in order to reconstruct the waveform for an increased frequency, we compute for that frequency. Substituting the known quantities into (3), there is just one unknown, namely the normalization constant ; its value is determined from a comparison of measured and modeled magnetization curves at increased frequency;
- The descending branch of the hysteresis loop is determined from the odd symmetry condition, .
3. Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hassani, V.; Tjahjowidodo, T.; Nho Do, T. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Engdahl, G.; Mayergoyz, I.D. Handbook of Giant Magnetostrictive Materials; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Lagoudas, D.C. (Ed.) Shape Memory Alloys. Modeling and Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Shan, X.; Song, H.; Cao, H.; Zhang, L.; Zhao, X.; Fan, J. A Dynamic Hysteresis Model and Nonlinear Control System for a Structure-Integrated Piezoelectric Sensor-Actuator. Sensors 2021, 21, 269. [Google Scholar] [CrossRef]
- Ankener, W.; Böttger, D.; Smaga, M.; Gabi, Y.; Strass, B.; Wolter, B.; Beck, T. Micromagnetic and Microstructural Characterization of Ferromagnetic Steels in Different Heat Treatment Conditions. Sensors 2022, 22, 4428. [Google Scholar] [CrossRef] [PubMed]
- Graham, C.D. Physical origin of losses in conducting ferromagnetic materials (invited). J. Appl. Phys. 1982, 53, 8276–8280. [Google Scholar] [CrossRef]
- Davies, H.A.; Fiorillo, F.; Flohrer, S.; Guenther, H.; Hasegawa, R.; Sievert, J.; Varga, L.K.; Yamaguchi, M. Challenges in optimizing the magnetic properties of bulk soft magnetic materials. J. Magn. Magn. Mater. 2006, 320, 2411–2422. [Google Scholar]
- Available online: https://www.verifiedmarketresearch.com/product/non-grain-oriented-electrical-steel-market/ (accessed on 1 September 2022).
- Silveyra, J.M.; Ferrara, E.; Huber, D.L.; Monson, T.C. Soft magnetic materials for a sustainable and electrified world. Science 2018, 363, eaao0195. [Google Scholar] [CrossRef]
- Moses, A.J. Poznanie Zjawisk w Materiałach Magnetycznych Warunkiem Obniżenia Strat Energii w Magnetowodach Urządzeń Elektromagnetycznych (Knowledge of Phenomena in Magnetic Materials as a Condition for Reduction of Energy Losses in Magnetic Conductors of Electromagnetic Devices—In Polish). Lecture Held at Lublin University of Technology, Poland on the Occasion of Granting the Title “Doctor Honoris Causa” to Professor Antony Moses, Lublin, Poland. 2003. Available online: http://bc.pollub.pl/Content/203/PDF/Profesor%20Moses%20dr%20hc%20PL.pdf (accessed on 1 September 2022).
- European Commission Regulation (EC) No. 640/2009 of 22 July 2009 Implementing Directive 2005/32/EC of the European Parliament and of the Council with Regard to Ecodesign Requirements for Electric Motors. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2009:191:0026:0034:EN:PDF (accessed on 1 September 2022).
- Available online: https://www.rjmeasurement.com.pl/index.php/en/offer/measuring-circuits/116-probka-toroidalna-2 (accessed on 1 September 2022).
- Chwastek, K. Modeling of dynamic hysteresis losses using the Jiles-Atherton approach. Math. Comp. Model. Dyn. Syst. 2009, 15, 95–105. [Google Scholar] [CrossRef]
- Tumański, S. Modern methods of electrical steel testing—A review. Przegląd Elektrotechniczny 2021, 3, 162–167. [Google Scholar] [CrossRef]
- de Souza Dias, M.B.; Landgraf, F.J.G.; Chwastek, K. Modeling the Effect of Compressive Stress on Hysteresis Loop of Grain-Oriented Electrical Steel. Energies 2022, 15, 1128. [Google Scholar] [CrossRef]
- Koltermann, P.I.; Righi, L.A.; Bastos, J.P.A.; Carlson, R.; Sadowski, N.; Batistela, N.J. A modified Jiles method for hysteresis computation including minor loops. Phys. B 2000, 275, 233–237. [Google Scholar] [CrossRef]
- Steentjes, S.; Hameyer, K.; Dolinar, D.; Petrun, M. Iron-loss and magnetic hysteresis under arbitrary waveforms in NO electrical steel: A comparative study of hysteresis models. IEEE Trans. Ind. Electron. 2017, 64, 2511–2520. [Google Scholar] [CrossRef]
- Harrison, R.G. A physical model of spin ferromagnetism. IEEE Trans. Magn. 2003, 39, 950–960. [Google Scholar] [CrossRef]
- Takács, J. A phenomenological mathematical model of hysteresis. Compel 2001, 20, 1002–1015. [Google Scholar] [CrossRef]
- Milovanović, A.M.; Koprivica, B.M. Mathematical model of major hysteresis loop and transient magnetizations. Electromagnetics 2015, 35, 155–166. [Google Scholar] [CrossRef]
- Hamel, M.; Nait Ouslimane, A.; Hocini, F. A study of Jiles-Atherton and the modified arctangent models for the description of dynamic hysteresis curves. Phys. B 2022, 638, 413930. [Google Scholar] [CrossRef]
- Tellinen, J. A simple scalar model for magnetic hysteresis. IEEE Trans. Magn. 1998, 34, 2200–2206. [Google Scholar] [CrossRef]
- Li, Y.; Chen, R.; Cheng, Z.; Zhang, C.; Liu, L. Dynamic hysteresis loops modeling of electrical steel with harmonic components. IEEE Trans. Ind. Appl. 2020, 56, 4804–4811. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Sadowski, N.; Batistela, N.J.; Bastos, J.P.A.; Laioje-Mazenc, M. An inverse Jiles-Atherton model to take into account hysteresis in time-stepping finite-element calculations. IEEE Trans. Magn. 2002, 38, 797–800. [Google Scholar] [CrossRef]
- Baghel, A.P.S.; Kulkarni, S. Dynamic Loss Inclusion in the Jiles–Atherton (JA) Hysteresis Model Using the Original JA Approach and the Field Separation Approach. IEEE Trans. Magn. 2014, 50, 7009004. [Google Scholar] [CrossRef]
- Podberezhnaya, I.; Pavlenko, A. Accounting for dynamic losses in the Jiles-Atherton model of magnetic hysteresis. J. Magn. Magn. Mater. 2020, 513, 167070. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Harrison, R.G.; Chwastek, K. On physical aspects of the Jiles-Atherton hysteresis models. J. Appl. Phys. 2012, 112, 043916. [Google Scholar] [CrossRef]
- Jastrzębski, R.; Chwastek, K. Comparison of macroscopic descriptions of magnetization curves. ITM Web Conf. 2017, 15, 03003. [Google Scholar] [CrossRef]
- Zhu, J.G.; Hui, S.Y.R.; Ramsden, V.S. Discrete modeling of magnetic cores including hysteresis eddy current and anomalous losses. IEE Proc. A 1993, 140, 317–322. [Google Scholar]
- Bernard, Y.; Mendes, E.; Bouillault, F. Dynamic hysteresis modeling based on Preisach model. IEEE Trans. Magn. 2002, 38, 885–888. [Google Scholar] [CrossRef]
- Zakrzewski, K. Wpływ histerezy magnetycznej na podział i rozkład strat mocy w blachach elektrotechnicznych (Influence of hysteresis on power in ferromagnetic steels—In Polish). Rozpr. Elektr. 1971, 17, 431–446. [Google Scholar]
- Bertotti, G. Hysteresis in Magnetism; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- McKeehan, L.W.; Bozorth, R.M. Hysteresis losses and the area of the hysteresis loop. Phys. Rev. 1934, 46, 526. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; IEEE Press: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Becker, J.J. Magnetization changes and losses in conducting ferromagnetic materials. J. Appl. Phys. 1963, 34, 1327–1332. [Google Scholar] [CrossRef]
- Ould Oulali, S.H.; Mohellebi, H.; Hocini, F.; Chaibi, R.; Féliachi, M. Eddy currents and hysteresis losses evaluation using dynamic Preisach model. J. Optoelectr. Adv. Mater. 2008, 10, 1093–1097. Available online: https://old.joam.inoe.ro/index.php?option=magazine&op=view&idu=1367&catid=26 (accessed on 1 September 2022).
- Jastrzębski, R.; Chwastek, K. Modeling frequency dependent effects in the GRUCAD hysteresis model. In Proceedings of the 2017 Progress in Applied Electrical Engineering (PAEE), Kościelisko, Poland, 25–30 June 2017; IEEE Explore: Piscataway, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Chwastek, K. Modeling hysteresis loops in thick steel sheet with the dynamic Takács model. Phys. B 2012, 407, 3632–3634. [Google Scholar] [CrossRef]
- Chwastek, K.; Gozdur, R. Towards a unified approach to hysteresis and micromagnetics modeling: A dynamic extension to the Harrison model. Phys. B 2019, 572, 242–246. [Google Scholar] [CrossRef]
- Petrun, M.; Chwastek, K.; Dolinar, D. Hysteresis curves of a resistance spot welding transformer. Compel 2013, 32, 1404–1416. [Google Scholar] [CrossRef]
- Barranger, J. Hysteresis and Eddy-Current Losses of a Transformer Lamination Viewed as an Application of the Poynting Theorem. NASA Technical Note TN D-3114. 1965. Available online: https://core.ac.uk/download/pdf/80676116.pdf (accessed on 1 September 2022).
- Chwastek, K. AC loss density component in electrical steel sheets. Philos. Mag. Lett. 2010, 90, 809–817. [Google Scholar] [CrossRef]
- de Leon, F.; Qaseer, L.; Cohen, J. AC power from Poynting Theorem: Identification of the power components of magnetic saturating and hysteretic circuits. IEEE Trans. Power Deliv. 2012, 27, 1548–1556. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Comparison of engineering methods of loss prediction in thin ferromagnetic laminations. J. Magn. Magn. Mater. 2008, 320, 2504–2508. [Google Scholar] [CrossRef]
- Jabłoński, P.; Najgebauer, M.; Bereźnicki, M. An Improved Approach to Calculate Eddy Current Loss in Soft Magnetic Materials Based on Measured Hysteresis Loops. Energies 2022, 15, 2869. [Google Scholar] [CrossRef]
- Legg, V.E. Magnetic measurements at low flux densities using the alternating current bridge. Bell Syst. Tech. J. 1936, 15, 39–62. [Google Scholar] [CrossRef]
- Stewart, K.H. Losses in electrical steel. Proc. IEE Part II Power Eng. 1950, 97, 121–125. [Google Scholar] [CrossRef]
- Kowal, D.; Sergeant, P.; Dupré, L.; Vandenbossche, L. Comparison of Iron Loss Models for Electrical Machines With Different Frequency Domain and Time Domain Methods for Excess Loss Prediction. IEEE Trans. Magn. 2015, 51, 6300110. [Google Scholar] [CrossRef]
- Ragusa, C.; Zhao, H.; Appino, C.; Khan, M.; de la Barrière, O.; Fiorillo, F. Loss decomposition in non-oriented steel sheets: The role of the classical losses. IEEE Magn. Lett. 2016, 7, 5106105. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; Serpico, C. Frequency scaling of excess hysteresis losses. IEEE Trans. Magn. 2000, 36, 3192–3194. [Google Scholar] [CrossRef]
- Chua, L.; Stromsoe, K. Mathematical model for dynamic hysteresis loops. Int. J. Eng. Sci. 1971, 9, 435–450. [Google Scholar] [CrossRef]
- Saito, Y.; Saotome, H.; Yamamura, T. A lumped circuit model for a nonlinear inductor exhibiting dynamic hysteresis loops and its application to the electric circuits. Comp. Methods Appl. Mech. Eng. 1983, 38, 185–202. [Google Scholar] [CrossRef]
- Hodgdon, M. Applications of a theory of ferromagnetic hysteresis. IEEE Trans. Magn. 1988, 24, 218–221. [Google Scholar] [CrossRef]
- Krivošik, P. Dynamical losses description in grain-oriented materials. Czechoslov. J. Phys. 2001, 52, A49–A52. [Google Scholar] [CrossRef]
- Song, M.; Yoon, H.; Yang, H.; Koh, C.S. A generalized Chua-type vector hysteresis model for both non-oriented and grain-oriented electrical steel sheets. IEEE Trans. Magn. 2011, 47, 1146–1149. [Google Scholar] [CrossRef]
- Malczyk, R.; Izydorczyk, J. The frequency-dependent Jiles-Atherton hysteresis model. Phys. B 2015, 463, 68–75. [Google Scholar] [CrossRef]
- Zhang, B.; Gupta, B.; Ducharne, B.; Sebald, G.; Uchimoto, T. Dynamic magnetic scalar hysteresis lump model, based on Jiles-Atherton quasi-static hysteresis model extended with dynamic fractional derivatives. IEEE Trans. Magn. 2018, 54, 7301605. [Google Scholar] [CrossRef]
- Raulet, M.-A.; Ducharne, B.; Masson, J.-P.; Bayada, G. The magnetic field diffusion equation including dynamic hysteresis: A linear formulation of the problem. IEEE Trans. Magn. 2004, 40, 872–875. [Google Scholar] [CrossRef]
- Fujiwara, T.; Tahara, R. Eddy current modeling of silicon steel for use on Spice. IEEE Trans. Magn. 1995, 31, 4059–4061. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Dynamic hysteresis modeling. Phys. B 2004, 343, 90–95. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Steentjes, S.; Hameyer, K.; Chwastek, K.; Zurek, S.; Harrison, R.G. Dynamic magnetization models for soft ferromagnetic materials with coarse and fine domain structures. J. Magn. Magn. Mater. 2015, 394, 229–236. [Google Scholar] [CrossRef]
- Dlala, E.; Belahcen, A.; Pippuri, J.; Arkkio, A. Interdependence of hysteresis and eddy-current losses in laminated magnetic cores of electrical machines. IEEE Trans. Magn. 2010, 46, 306–309. [Google Scholar] [CrossRef]
- Pluta, W.A. Some properties of factors of specific total loss components in electrical steel. IEEE Trans. Magn. 2010, 46, 322–325. [Google Scholar] [CrossRef]
- Sowa, M.; Majka, Ł. Ferromagnetic core coil hysteresis modeling using fractional derivatives. Nonlinear Dyn. 2020, 101, 775–793. [Google Scholar] [CrossRef]
- Ducharne, B.; Tsafack, P.; Tene Deffo, Y.A.; Zhang, B.; Sebald, G. Fractional operators for the magnetic dynamic behavior of ferromagnetic specimens: An overview. AIP Adv. 2021, 11, 035309. [Google Scholar] [CrossRef]
- Ducharne, B.; Sebald, G. Fractional derivatives for the core losses prediction: State of the art and beyond. J. Magn. Magn. Mater. 2022, 563, 169961. [Google Scholar] [CrossRef]
- Haller, T.R.; Kramer, J.J. Observation of dynamic domain size variation in a silicon-iron alloy. J. Appl. Phys. 1970, 41, 1034–1035. [Google Scholar] [CrossRef]
- Najgebauer, M. Fractional scaling of magnetic coercivity in electrical steels. Acta Phys. Pol. A 2017, 131, 633–635. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: An engineering approach. IEEE Trans. Magn. 2003, 39, 981–988. [Google Scholar] [CrossRef]
- Ionel, D.M.; Popescu, M.; Dellinger, S.J.; Miller, T.J.E.; Heidemann, R.J.; McGilp, M.I. On the variation with flux and frequency of the core loss coefficients in electrical machines. IEEE Trans. Ind. Appl. 2006, 42, 658–667. [Google Scholar] [CrossRef]
- Lee, P.-K.; Kuo, K.-C.; Wu, C.-J.; Wong, Z.-T.; Yen, J.-Y. Prediction of Iron Losses Using the Modified Steinmetz Equation under the Sinusoidal Waveform. In Proceedings of the 2011 8th Asian Control Conference, Kaohsiung, Taiwan, 15–18 May 2011; Available online: https://ieeexplore.ieee.org/abstract/document/5899136 (accessed on 1 September 2022).
- Novak, G.; Kokošar, J.; Nagode, A.; Steiner Petrovič, D. Core-Loss Prediction for Non-Oriented Electrical Steels Based on the Steinmetz Equation Using Fixed Coefficients with a Wide Frequency Range of Validity. IEEE Trans. Magn. 2015, 51, 2001507. [Google Scholar] [CrossRef]
- Roy, R.; Dalal, A.; Kumar, P. Prediction of high frequency core loss for electrical steel using the data provided by manufacturer. J. Magn. Magn. Mater. 2016, 410, 248–256. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J.; Jiles, D.C. Measurement and Modeling of B–H Loops and Losses of High Silicon Nonoriented Steels. IEEE Trans. Magn. 2006, 42, 3177–3179. [Google Scholar] [CrossRef]
- Baghel, A.P.S.; Gupta, A.; Chwastek, K.; Kulkarni, S.V. Comprehensive modelling of dynamic hysteresis loops in the rolling and transverse directions for transformer laminations. Phys. B 2015, 462, 86–92. [Google Scholar] [CrossRef]
- Broddefalk, A.; Lindenmo, M. Dependence of the power losses of a non-oriented 3% Si-steel on frequency and gauge. J. Magn. Magn. Mater. 2006, 304, e586–e588. [Google Scholar] [CrossRef]






| Application | NO Steel | GO Steel | |||
| Silicon-Less | Low-Silicon | High-Silicon | Conventional | High Permeability | |
| 1. Small motors |  | ||||
| 2. AC motors, medium power |  | ||||
| 3. Welding transformers |  | ||||
| 4. Audio transformers |  | ||||
| 5. Small power transformers |  | ||||
| 6. Big rotating machines |  | ||||
| 7. Alternators and generators, medium power |  | ||||
| 8. Distribution transformers |  | ||||
| 9. Power transformers |  | ||||
| Thickness, mm | Grade Designation | Max. Loss Density, W/kg at f = 50 Hz | Minimal Induction, T | ||
|---|---|---|---|---|---|
| B = 1.5 T | B = 1.0 T | H = 2500 A/m | H = 5000 A/m | ||
| 0.35 mm | M330-35A | 3.30 | 1.30 | 1.49 | 1.60 |
| 0.65 mm | M530-65A | 5.30 | 2.30 | 1.54 | 1.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chwastek, K.R. The Effects of Sheet Thickness and Excitation Frequency on Hysteresis Loops of Non-Oriented Electrical Steel. Sensors 2022, 22, 7873. https://doi.org/10.3390/s22207873
Chwastek KR. The Effects of Sheet Thickness and Excitation Frequency on Hysteresis Loops of Non-Oriented Electrical Steel. Sensors. 2022; 22(20):7873. https://doi.org/10.3390/s22207873
Chicago/Turabian StyleChwastek, Krzysztof Roman. 2022. "The Effects of Sheet Thickness and Excitation Frequency on Hysteresis Loops of Non-Oriented Electrical Steel" Sensors 22, no. 20: 7873. https://doi.org/10.3390/s22207873
APA StyleChwastek, K. R. (2022). The Effects of Sheet Thickness and Excitation Frequency on Hysteresis Loops of Non-Oriented Electrical Steel. Sensors, 22(20), 7873. https://doi.org/10.3390/s22207873







