Flatness Prediction of Cold Rolled Strip Based on Deep Neural Network with Improved Activation Function
Abstract
:1. Introduction
2. Related Theory
2.1. Deep Neural Network
2.2. Type of Activation Function
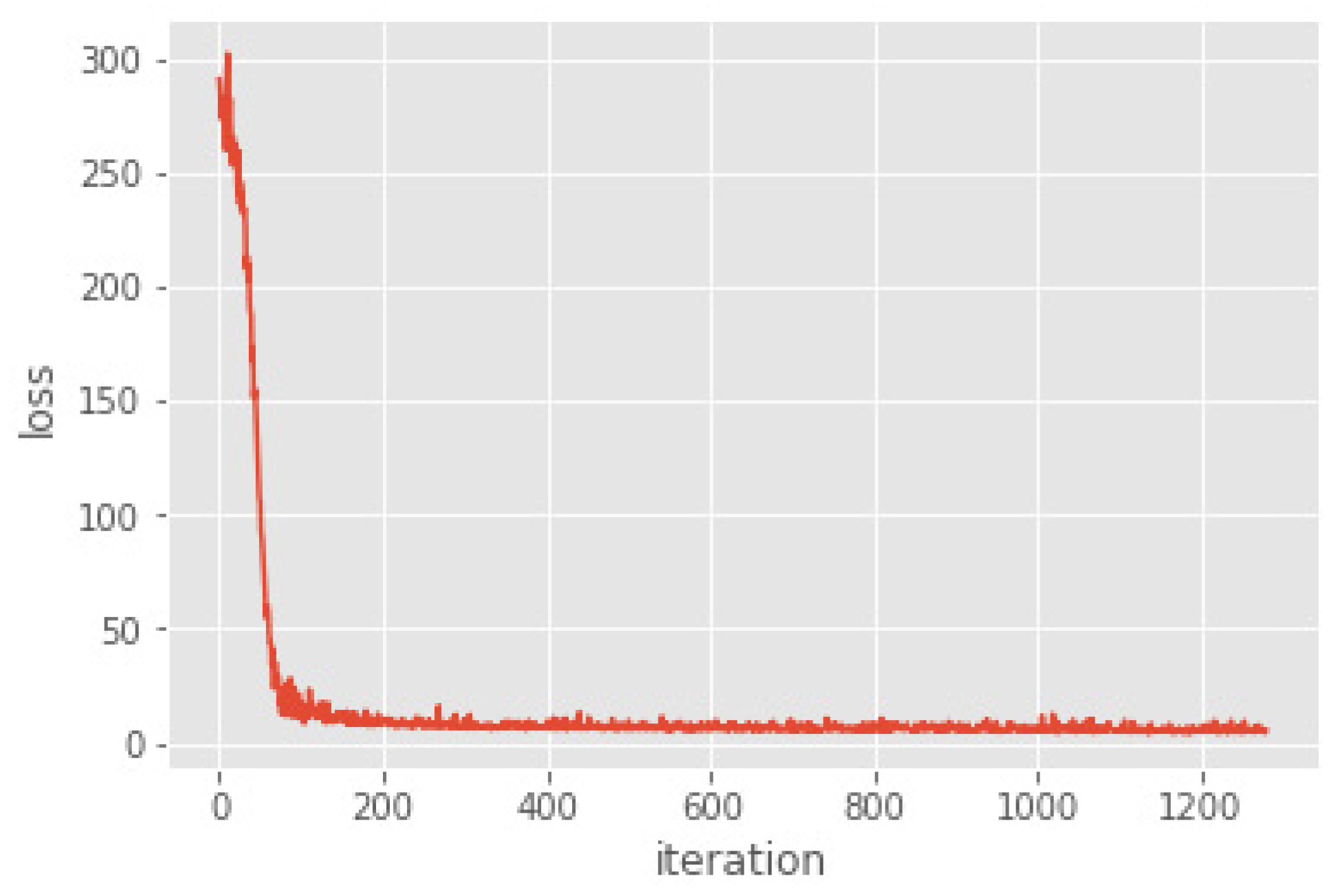
2.3. Loss Function
3. Improved Deep Neural Network
4. Experimental Results and Discussion
4.1. Description of Data
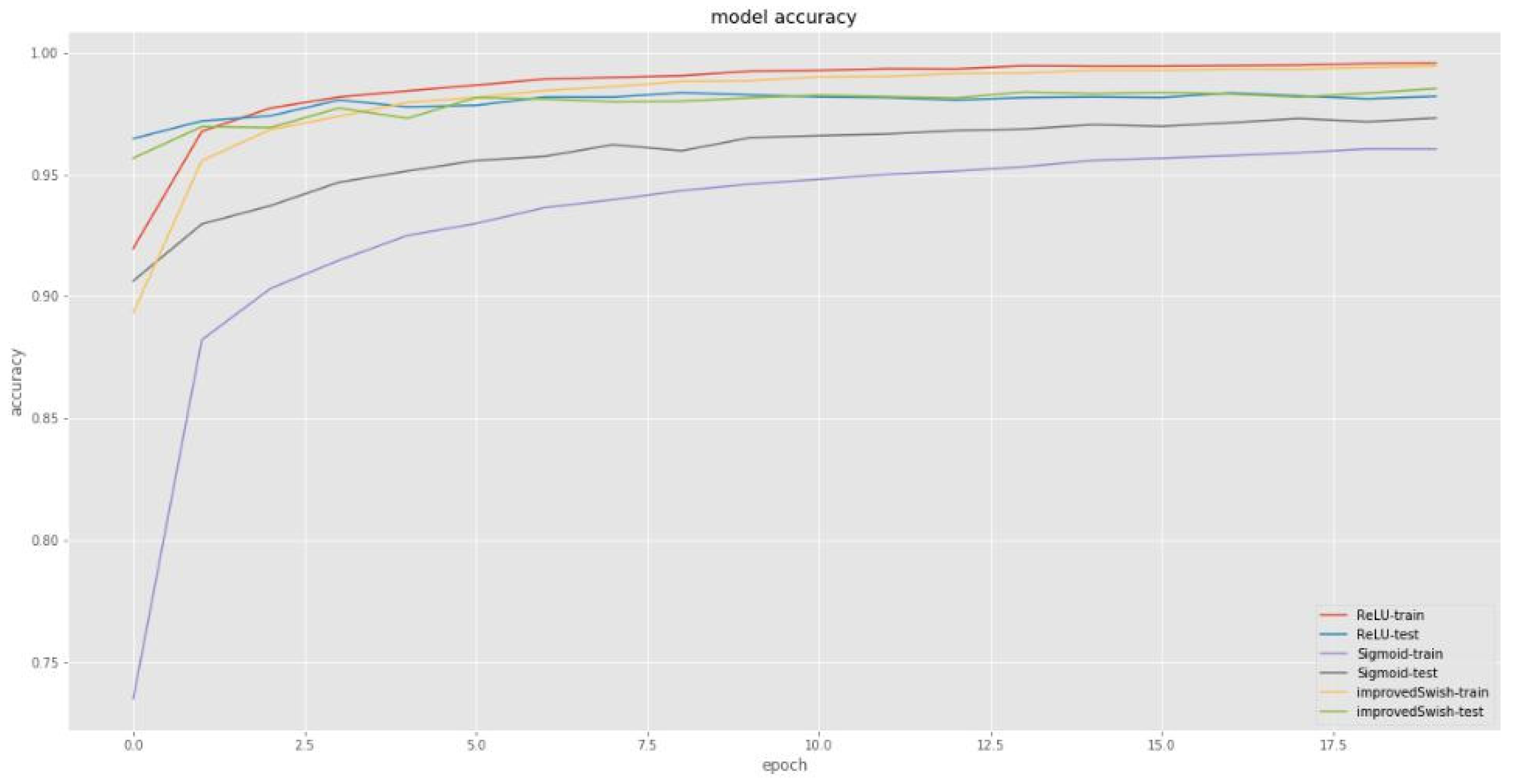
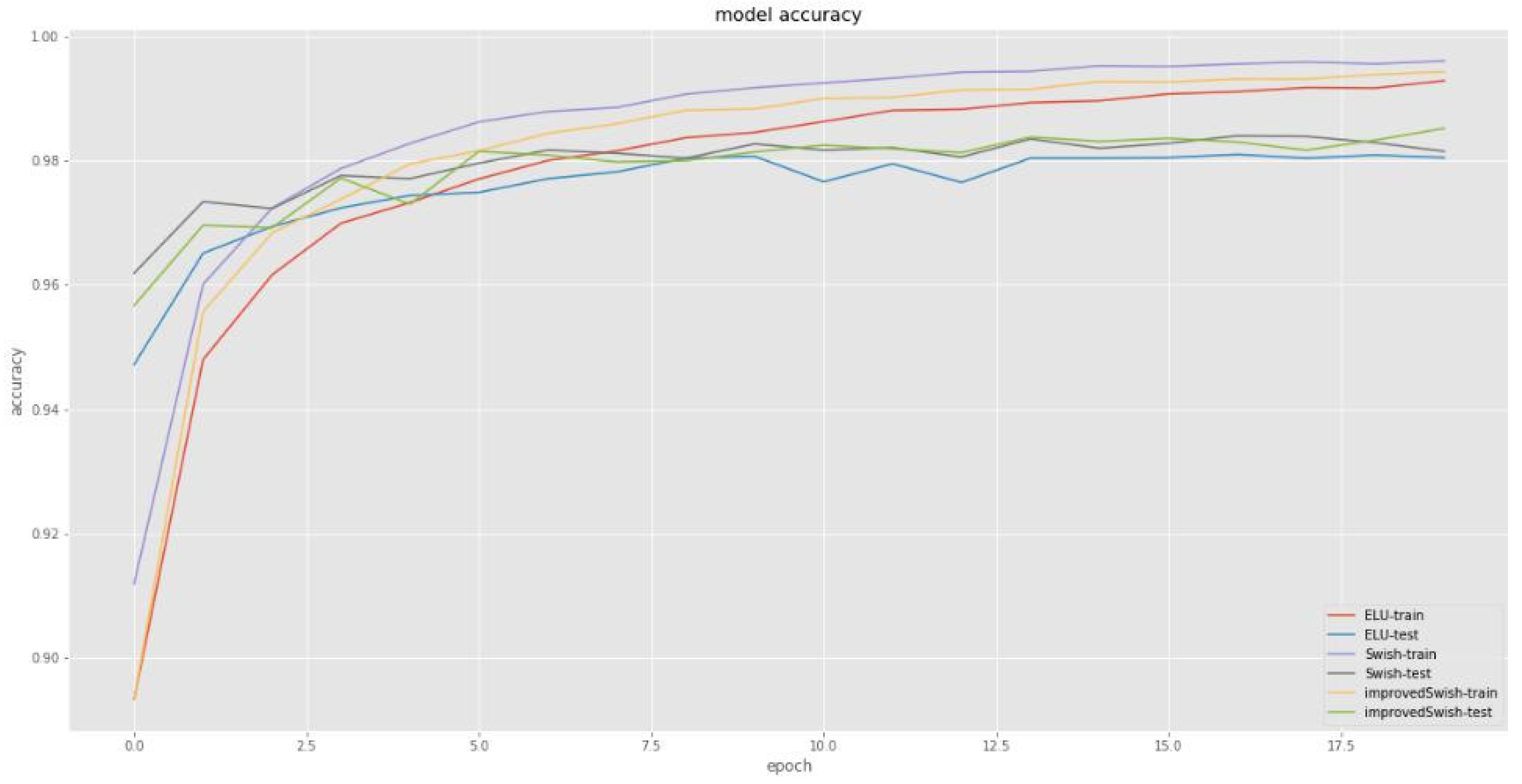
4.2. Experiments Based on MNIST Dataset
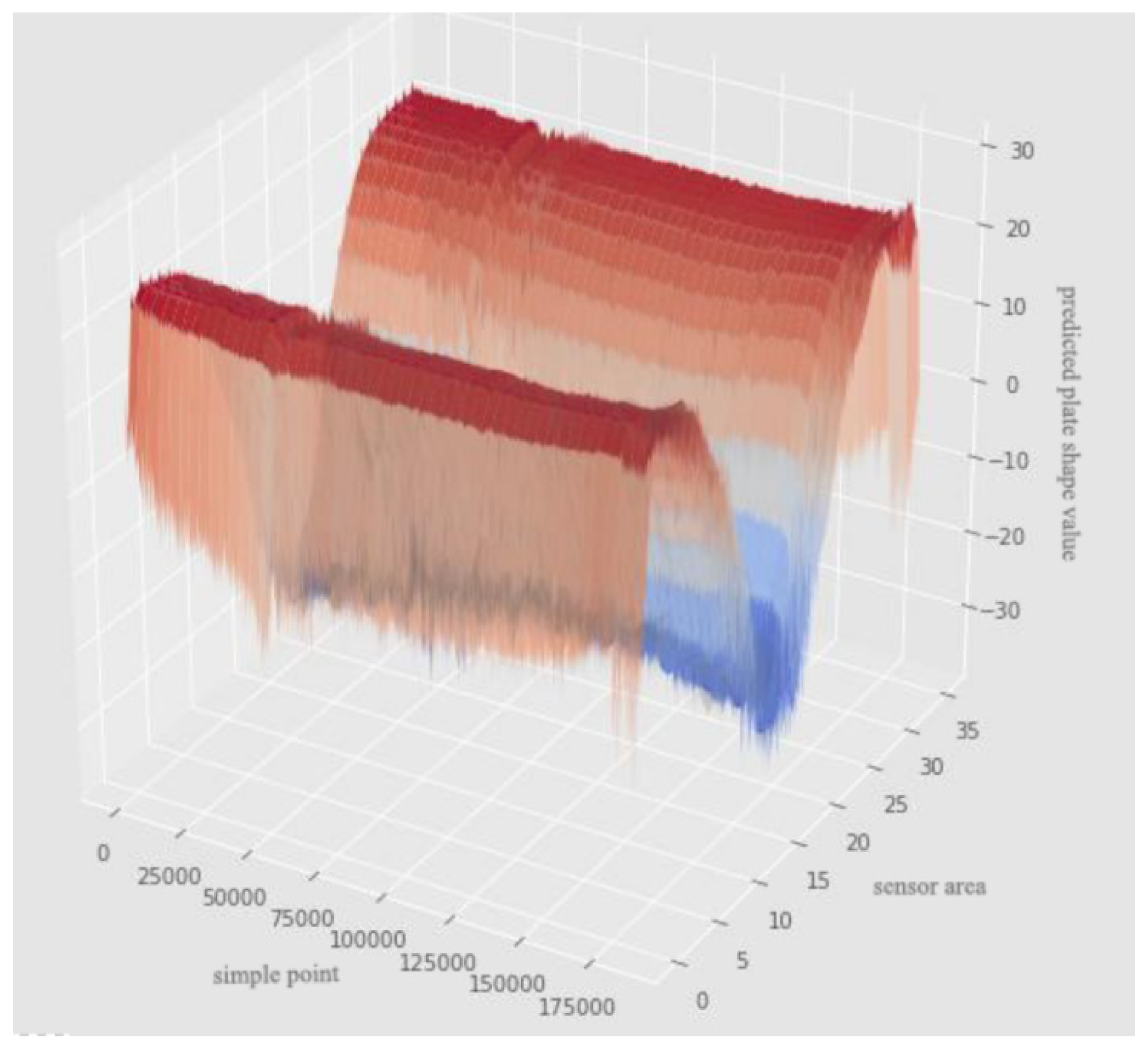
4.3. Flatness Prediction of Cold Rolled Strip
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Non-Convexity of the Loss Function
Appendix B
Global Minimum of the Loss Function
References
- Wang, P. Study and Application of Flatness Control Technology for Cold Rolled Strip. Master’s Thesis, Northeastern University, Shenyang, China, 2011. [Google Scholar]
- Dong, C.; Li, S.; Su, A. Analysis on Shape Defects of Medium and Heavy Plate and Control Measures. Tianjin Metall. 2016, S1, 27–29. [Google Scholar]
- Claire, N. Control of strip flatness in cold rolling. Ironand Steel Eng. 1997, 4, 42–45. [Google Scholar]
- Wang, C.; Zhang, Y.; Zhang, Q. Application of Effect Function in Shape Control of Cold Rolling Mill. Steel Roll. 1999, 4, 28–29. [Google Scholar]
- Chen, E.; Zhang, S.; Xue, T. Study on shape and gauge control system of cold strip mill. J. Plast. Eng. 2016, 23, 92–95. [Google Scholar]
- Liang, X.; Wang, Y.; Zhao, J.; Wang, G. Flatness Feedforward Control Models for Six High Tandem Cold Rolling Mill. Iron Steel 2009, 44, 62–66. [Google Scholar]
- Wang, P.F.; Yan, P.; Liu, H.M.; Zhang, D.H.; Wang, J.S. Actuator Efficiency Adaptive Flatness Control Model and Its Application in 1250 mm Reversible Cold Strip Mill. J. Iron Steel Res. Int. 2013, 20, 13–20. [Google Scholar] [CrossRef]
- Liu, H.; He, H.; Shan, X.; Jiang, G. Flatness Control Based on Dynamic Effective Matrix for Cold Strip Mills. Chin. J. Mech. Eng. 2009, 22, 287–295. [Google Scholar] [CrossRef]
- Liu, J. Research and Development of Flatness Control System in Cold Strip Rolling. Master’s Thesis, Northeastern University, Shenyang, China, 2010. [Google Scholar]
- Zhao, W.; Chen, F.; Huang, H.; Li, D.; Cheng, W. A New Steel Defect Detection Algorithm Based on Deep Learning. Comput. Intell. Neurosci. 2021, 2021, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Wu, J.; Xie, F. Automatic recognition of surface defects for hot-rolled steel strip based on deep attention residual convolutional neural network. Mater. Lett. 2021, 293, 129707. [Google Scholar] [CrossRef]
- Roy, S.; Saini, B.S.; Chakrabarti, D.; Chakraborti, N. Mechanical properties of micro-alloyed steels studied using a evolutionary deep neural network. Mater. Manuf. Process 2020, 35, 611–624. [Google Scholar] [CrossRef]
- Lee, S.Y.; Tama, B.A.; Moon, S.J.; Lee, S. Steel Surface Defect Diagnostics Using Deep Convolutional Neural Network and Class Activation Map. Appl. Sci. 2019, 9, 5449. [Google Scholar] [CrossRef] [Green Version]
- Chun, P.J.; Yamane, T.; Izumi, S.; Kameda, T. Evaluation of Tensile Performance of Steel Members by Analysis of Corroded Steel Surface Using Deep Learning. Metals 2019, 9, 1259. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Bao, Y.; Chen, J.; Zuo, W.; Li, H. Surface fatigue crack identification in steel box girder of bridges by a deep fusion convolutional neural network based on consumer-grade camera images. Struct. Health Monit. 2019, 18, 653–674. [Google Scholar] [CrossRef]
- Grzegorz, P. Multi-Sensor Data Integration Using Deep Learning for Characterization of Defects in Steel Elements. Sensors 2018, 18, 292. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.Y.; Roy, K.; Mares, J.; Sham, C.W.; Chen, B.S.; Lim, J.B.P. Deep learning-based axial capacity prediction for cold-formed steel channel sections using Deep Belief Network. Structures 2021, 33, 2792–2802. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, X.; Liu, L. An Improved VGG19 Transfer Learning Strip Steel Surface Defect Recognition Deep Neural Network Based on Few Samples and Imbalanced Datasets. Appl Sci. 2021, 11, 2606. [Google Scholar] [CrossRef]
- Wu, S.W.; Yang, J.; Cao, G.M. Prediction of the Charpy V-notch impact energy of low carbon steel using a shallow neural network and deep learning. Int. J. Min. Met. Mater. 2021; prepublish. [Google Scholar] [CrossRef]
- Xiao, D.; Wan, L. Remote Sensing Inversion of Saline and Alkaline Land Based on an Improved Seagull Optimization Algorithm and the Two-Hidden-Layer Extreme Learning Machine. Nat. Resour. Res. 2021, 30, 3795–3818. [Google Scholar] [CrossRef]
- Xiao, D.; Le, B.T.; Ha, T.T.L. Iron ore identification method using reflectance spectrometer and a deep neural network framework. Spectrochim. Acta A 2021, 248, 119168. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Roux, N.L.; Vincent, P.; Delalleau, O.; Marcotte, P. Convex Neural Networks. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 123–130. [Google Scholar]



| Activation Function | Formula | Description |
|---|---|---|
| Sigmoid function | The gradient of the Sigmoid function easily falls into the saturation zone in backpropagation. | |
| Tanh function | It has soft saturation and vanishing gradient disadvantages. | |
| ReLU function | As the intensity of the training increases, part of the weight update falls into the hard saturation zone, failing to update. | |
| ELU function | ELU alleviates the vanishing gradient problem. | |
| Swish function | As the amount of data continues to increase, Swish will have better performance. |
| Activation Function | Training Set Loss | Test Set Loss | Training Set Accuracy | Test Set Accuracy |
|---|---|---|---|---|
| Improved Swish activation function | 0.0288 | 0.1088 | 0.9928 | 0.9852 |
| Swish function | 0.0279 | 0.1159 | 0.9933 | 0.9815 |
| ReLU function | 0.029 | 0.1307 | 0.993 | 0.982 |
| ELU function | 0.0308 | 0.1133 | 0.9912 | 0.9802 |
| Sigmoid function | 0.1034 | 0.1066 | 0.9658 | 0.9731 |
| Sensor Area | Predicted Value | True Value | Sensor Area | Predicted Value | True Value | Sensor Area | Predicted Value | True Value |
|---|---|---|---|---|---|---|---|---|
| f939 | −3.299 | −6.014 | f9310 | 20.291 | 20.623 | 9311 | 23.519 | 24.176 |
| f9312 | 23.388 | 23.659 | f9313 | 23.052 | 23.336 | f9314 | 22.456 | 23.036 |
| f9315 | 21.554 | 22.622 | f9316 | 19.862 | 21.321 | f9317 | 17.045 | 18.237 |
| f9318 | 13.198 | 14.230 | f9319 | 8.647 | 9.440 | f9320 | 3.902 | 4.500 |
| f9321 | −1.152 | 0.202 | f9322 | −8.183 | −7.844 | f9323 | −16.903 | −19.211 |
| f9324 | −23.236 | −25.932 | f9325 | −25.180 | −26.736 | f9326 | −25.405 | −25.921 |
| f9327 | −26.771 | −24.859 | f9328 | −27.216 | −25.265 | f9329 | −23.888 | −24.721 |
| f9330 | −16.256 | −17.145 | f9331 | −6.582 | −6.235 | f940 | 1.962 | 2.316 |
| f941 | 8.507 | 8.611 | f942 | 13.305 | 13.130 | f943 | 16.826 | 16.793 |
| f944 | 19.659 | 19.976 | f945 | 21.367 | 21.737 | f946 | 22.339 | 22.387 |
| f947 | 22.915 | 22.913 | f948 | 23.323 | 23.340 | f949 | 23.283 | 23.501 |
| f9410 | 23.124 | 23.366 | f9411 | 17.751 | 17.802 | f9412 | −7.461 | −7.534 |
| MSE of Training Sets | MSE of Test Sets | |
|---|---|---|
| BP | 7.851 | 8.329 |
| DNN | 3.229 | 3.731 |
| Improved DNN | 1.281 | 1.305 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Song, S.; Wang, J.; Balaiti, M.; Song, N.; Li, S. Flatness Prediction of Cold Rolled Strip Based on Deep Neural Network with Improved Activation Function. Sensors 2022, 22, 656. https://doi.org/10.3390/s22020656
Liu J, Song S, Wang J, Balaiti M, Song N, Li S. Flatness Prediction of Cold Rolled Strip Based on Deep Neural Network with Improved Activation Function. Sensors. 2022; 22(2):656. https://doi.org/10.3390/s22020656
Chicago/Turabian StyleLiu, Jingyi, Shuni Song, Jiayi Wang, Maimutimin Balaiti, Nina Song, and Sen Li. 2022. "Flatness Prediction of Cold Rolled Strip Based on Deep Neural Network with Improved Activation Function" Sensors 22, no. 2: 656. https://doi.org/10.3390/s22020656
APA StyleLiu, J., Song, S., Wang, J., Balaiti, M., Song, N., & Li, S. (2022). Flatness Prediction of Cold Rolled Strip Based on Deep Neural Network with Improved Activation Function. Sensors, 22(2), 656. https://doi.org/10.3390/s22020656







