1. Introduction
The aim of Non-Intrusive Load Monitoring (NILM) is to estimate the power consumption on the device level from the aggregated power-consumption signal of a household or a building [
1], while minimizing the number of installed energy meters and thus reducing the wiring harness and improving the retrofitting capabilities [
1,
2]. NILM is defined as a single-channel source-separation task, and the methods that have been proposed in the literature to solve it can be classified into three main categories [
3], namely (i) the pattern-matching (elastic matching) approaches which detect load signatures in the aggregated power-consumption signal by comparing them to a set of reference signatures [
4,
5,
6]; (ii) the source-separation methods, including matrix and tensor factorization as well as sparse coding, which separate base components and activations using numeric solvers [
7,
8,
9]; and (iii) the model-based approaches which are based on machine learning algorithms, usually training one model per device, in order to estimate the power consumption of the loads of interest from the aggregated signal [
10,
11,
12].
In detail, within the last few decades, NILM has been employed in many utility and non-utility applications. As regards the utility applications, energy-consumption reduction for residential [
13,
14] and industrial [
15] areas is the most common application. Furthermore, NILM has been used in energy management of smart-grids to optimize load schedules as well as to increase customers’ satisfaction [
16,
17]. Moreover, NILM has been used to improve load forecasting utilizing specific appliance-usage patterns [
11]. In non-utility applications, NILM has been used for fault detection and diagnostics in both the industrial [
18] and the residential sectors [
19]. Moreover, the privacy-persevering nature of NILM has been used for human behavior monitoring [
20]. Moreover, NILM was evaluated in terms of its ability to extract socio-economic information and consumer behavior [
21].
The recent development of deep machine learning algorithms and the creation of big data collections have resulted in advanced NILM methodologies. NILM methodologies that are based on Deep Neural Networks (DNNs) [
22], Convolutional Neural Networks (CNNs) [
15], Long-Short-Term-Memory (LSTM), and Recurrent Neural Networks (RNNs) are presented in the bibliography [
23]. Specifically, in [
24], the authors presented a causal CNN with gate-dilation optimisation, while, in [
25], the authors proposed a concatenated CNN method for high sampling frequencies. In [
26], the authors presented a bidirectional LSTM approach with forward and backward path optimization and Bayesian optimization of the hyper-parameter. In [
27], the authors proposed the use of RNNs combined with convolutional layers, and, in [
28], the authors presented a NILM method based on deep RNNs. Moreover, recently published work on NILM is focused on the use of Generative Adversarial Networks (GANs) [
29,
30,
31] and on bidirectional Transformers [
32] in order to use self-attention mechanisms to increase the accuracy of NILM [
33], as well as the robustness [
30,
34] of NILM methods. The transfer capability of NILM methods was studied in [
35,
36]. Moreover, the areas of fault detection [
19] and privacy and security-sensitive Information extraction [
3] have been studied.
The above-described approaches utilize either one-dimensional time series as input features [
26,
37] or multivariate time series of several different features, e.g., active power, reactive power, apparent power, and current, as in [
24,
27]. However, CNNs in particular were originally proposed as feature-extraction engines for two-dimensional and three-dimensional inputs, e.g., for image processing [
38]. Therefore, few approaches have investigated the transformation of one-dimensional time series into two-dimensional signal representations while considering the physical nature of the NILM problem, i.e., considering the harmonic content or the relationship between active and reactive power. For example, in [
39], a double-Fourier-integral-based approach for high-frequency energy disaggregation was proposed, and, in [
40], a low-frequency approach based on active and reactive power signatures was proposed. Furthermore, voltage and current signatures were used to convert raw measurements into two-dimensional signatures [
41,
42]. Moreover, in [
43,
44] time series imaging approaches for univariate time series, i.e., when only a single feature is available, were investigated. However, it is not clear which two-dimensional representations have the best disaggregation performance, since, to the best of the authors knowledge, time-series-imaging techniques have not been compared with each other before. Therefore, in this paper, we investigate the NILM performance of two-dimensional signatures utilizing high- and low-frequency data. Furthermore, we compare the two-dimensional representations with previously published approaches using univariate or multivariate features. The contributions are as follows.
Six time-series-imaging (two-dimensional representations) techniques were compared on high- and low-frequency data.
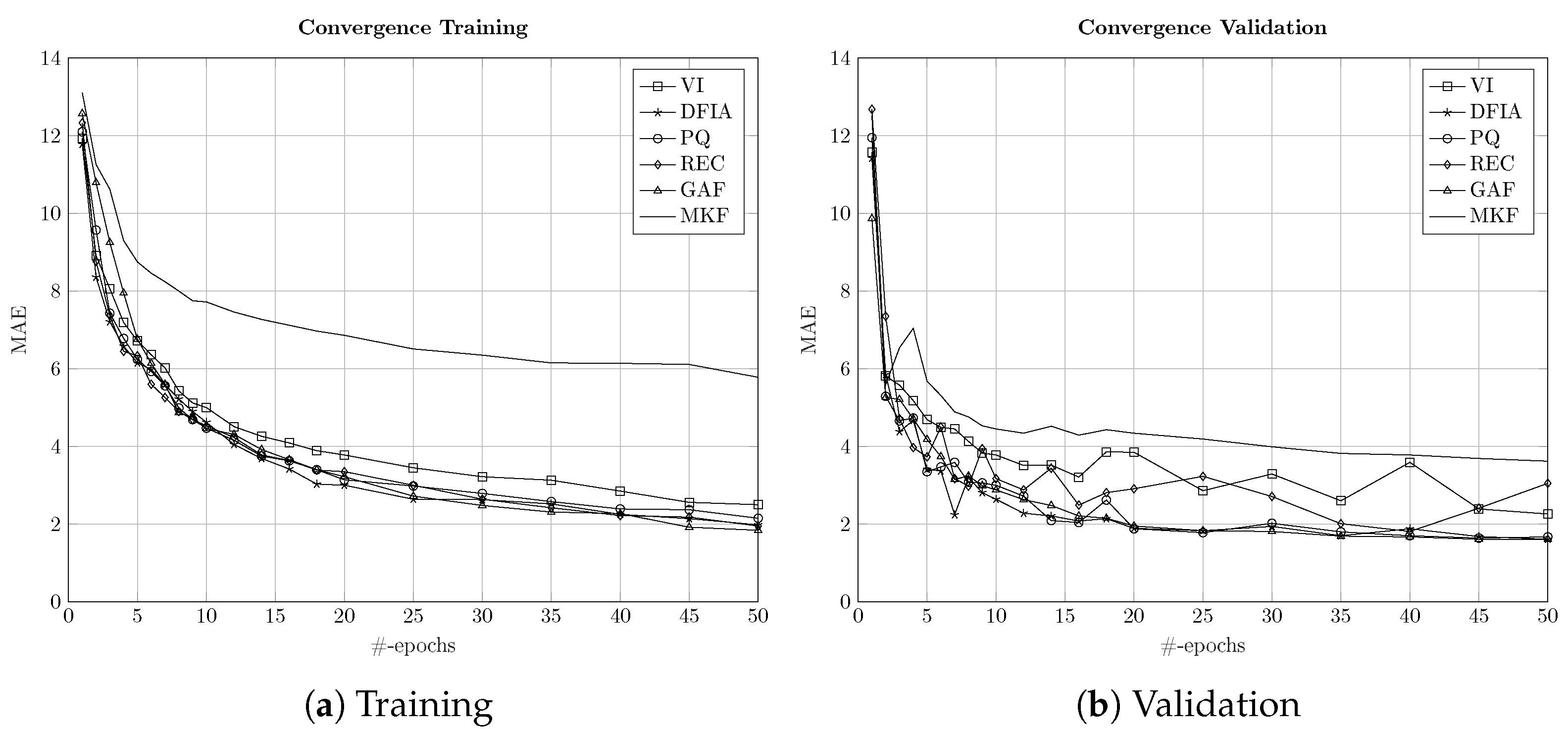
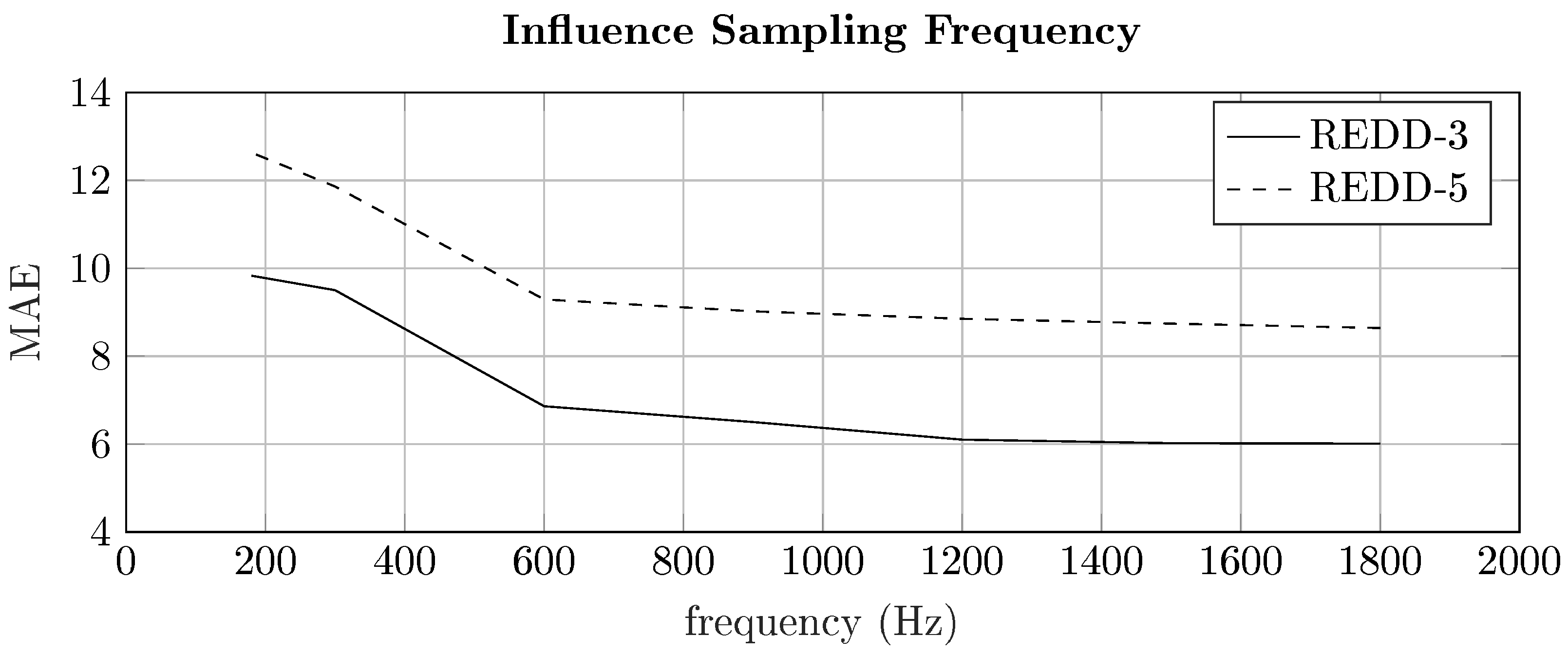
The convergence behavior and the influence on the sampling frequency of the two-dimensional representations were evaluated.
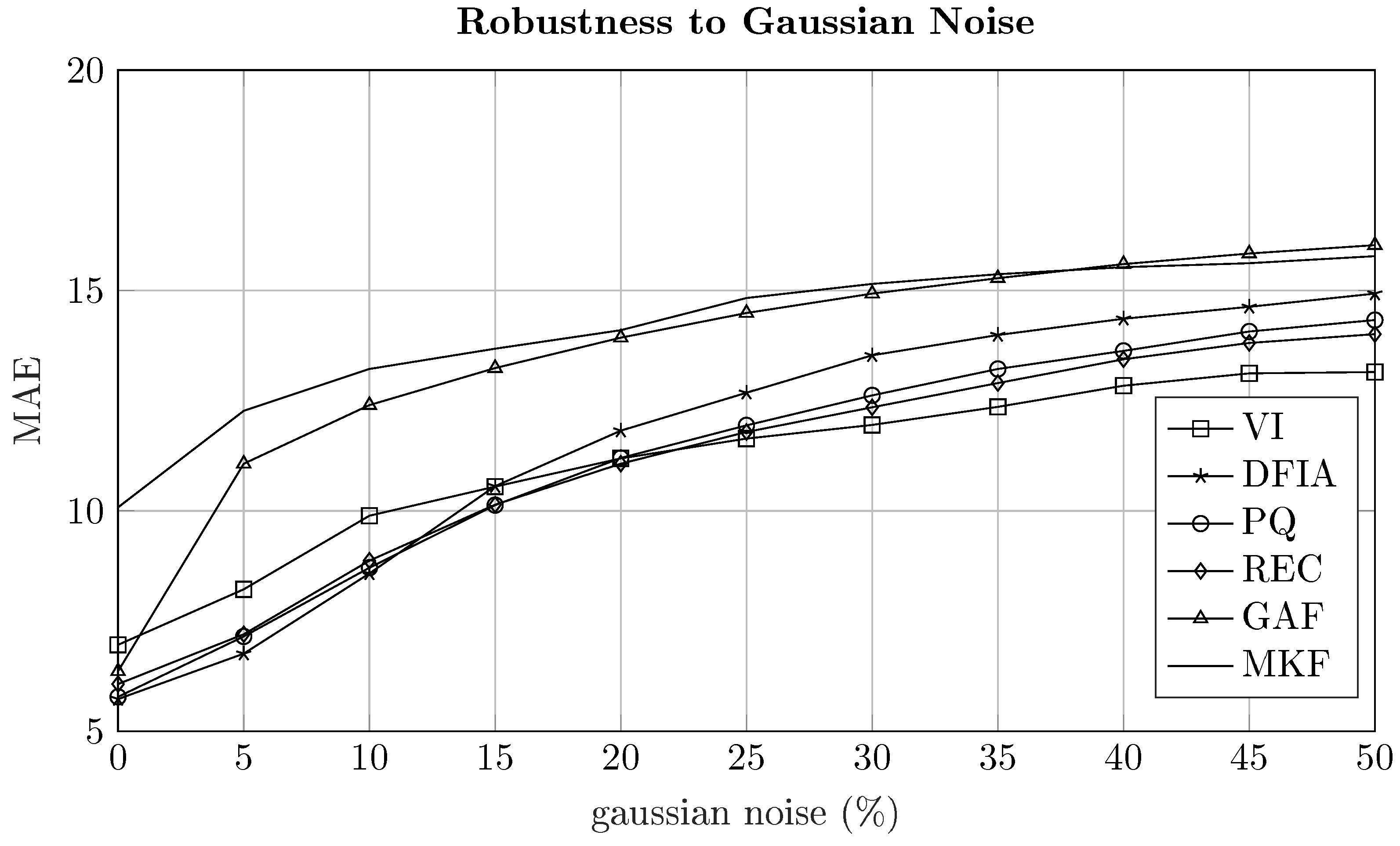
The robustness to noise for the six evaluated time series imaging approaches was evaluated.
The remainder of the paper is structured as follows. In
Section 2, an introduction to time series imaging for energy consumption signals is provided. In
Section 3, the evaluated architecture utilizing two-dimensional representations is presented. In
Section 4, the experimental setup is provided, and the evaluation results are presented in
Section 5. The discussion is provided in
Section 6, while the paper is concluded in
Section 7.
3. NILM Using Two-Dimensional Signal Representations
NILM is defined as the problem of extracting the power consumption on the device level from the aggregated signal measured by one sensor in short-time analysis, i.e., in time-sliding windows. Specifically, given a set of
M-1 known appliances with each of them consuming power
with
, the aggregated power
measured by the sensor is:
where
is the noise generated by one or more unknown device, and
is the aggregation function. In NILM, the goal is to find estimations
,
of the power consumption of each device
m using a disaggregation function
with minimal estimation error, i.e.,
Given that Equation (
9) cannot practically be solved analytically, most NILM approaches perform short-time analysis by segmenting the aggregated signal into frames and then estimating the power consumption of each appliance for every frame. In order to feed the disaggregation function
with more distinctive information, every frame of the active power signal,
(or
for high-frequency data), is usually transferred to a feature representation,
, as discussed in
Section 2. Based on this, the disaggregation problem from Equation (
9) can be reformulated on the frame level using the feature vectors as defined in
Section 2.
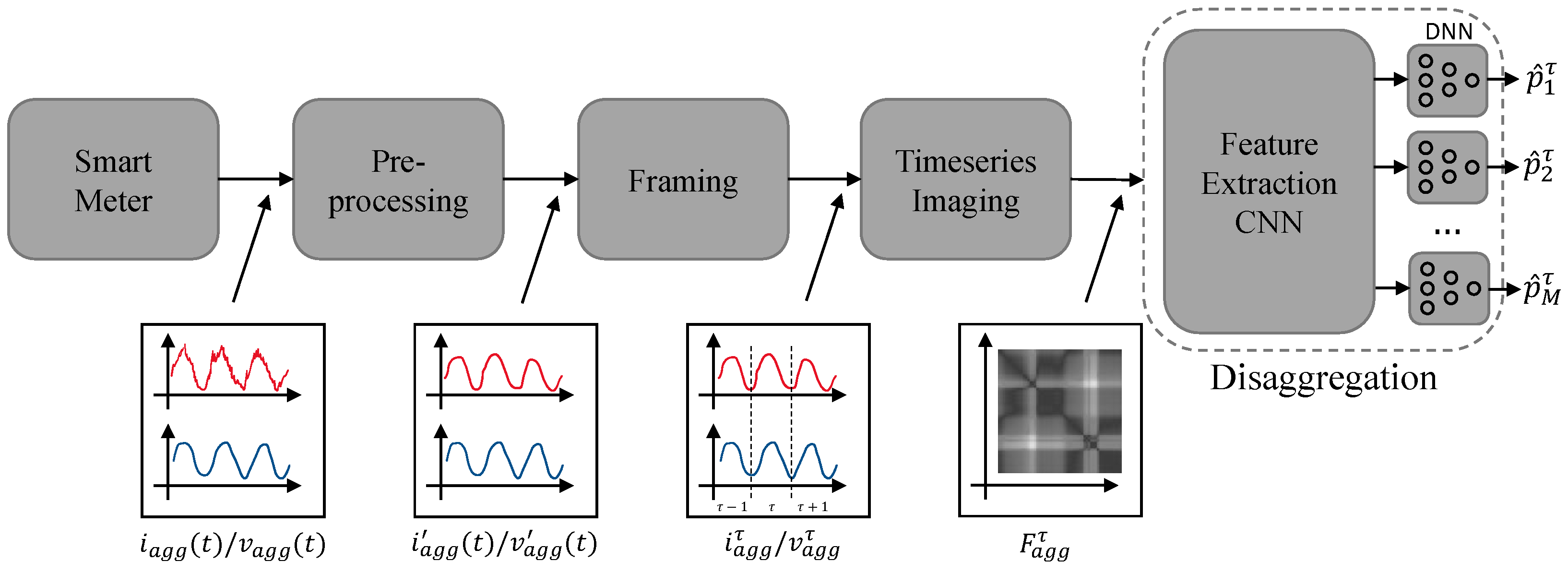
The architecture of the presented NILM method using time series imaging consist of four steps, namely pre-processing, framing, time series imaging (two-dimensional signal representation) as discussed in
Section 2, and disaggregation. The architecture for high-frequency data inputs is illustrated in
Figure 2.
As can be seen in
Figure 2, the raw current (
) and raw voltage (
) signals are initially pre-processed. Pre-processing consists of two steps, namely filtering and down-sampling of the data, resulting in the pre-processed signals
and
. After pre-processing the signals are frame blocked into frames of length
W resulting into the signals
and
. Finally, time series imaging is performed generating the two-dimensional frame representation
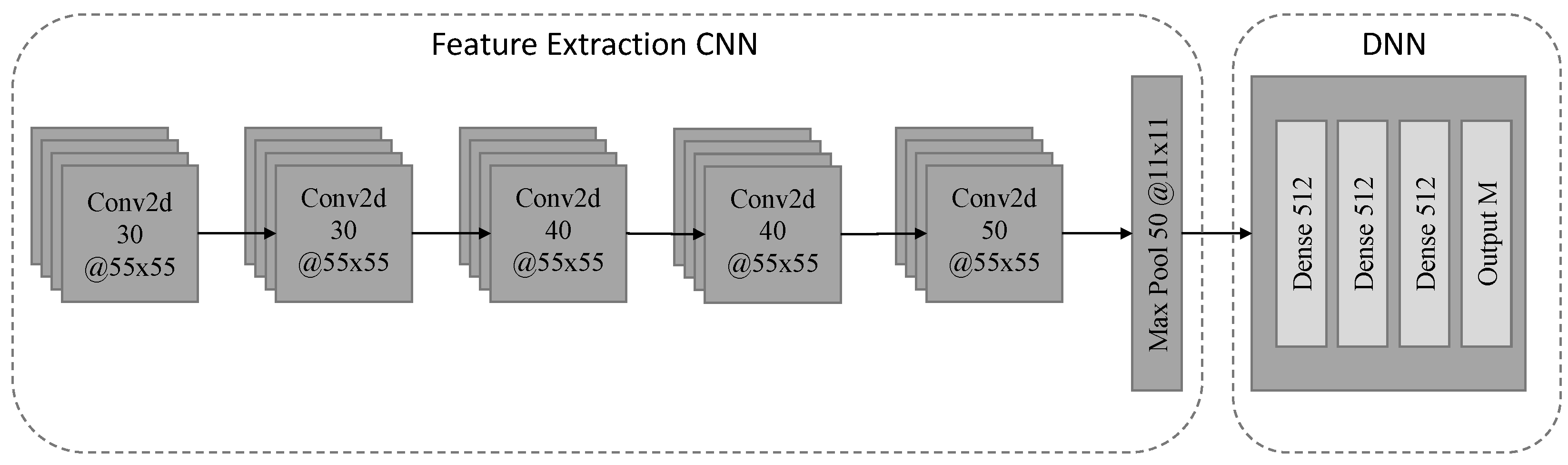
, which is used as input to the disaggregation stage. The disaggregation stage, consisting of a CNN operating as a feature-extraction engine and a DNN estimating the appliance consumption
.
5. Experimental Results
The NILM methodology described in
Section 3 was tested using the experimental setup presented in
Section 4. For the purpose of accurate comparison, performance was tested in terms of estimation accuracy (
), as proposed in [
46].
where
is the estimated power of device
m, with
,
T is the number of disaggregated frames, and
M is the number of disaggregated devices. Furthermore, to compare with previously published approaches, additional accuracy metrics, namely the Mean Absolute Error (MAE) and the normalized Signal Aggregated Error (SAE) are used, which are defined as:
where
denotes the total energy consumption of the appliance
m and
its predicted value. The results for REDD-3 and REDD-5 are tabulated for the six different two-dimensional transformation methods in
Table 4. The results are reported in terms of
, MAE, and SAE using active power as the output feature.
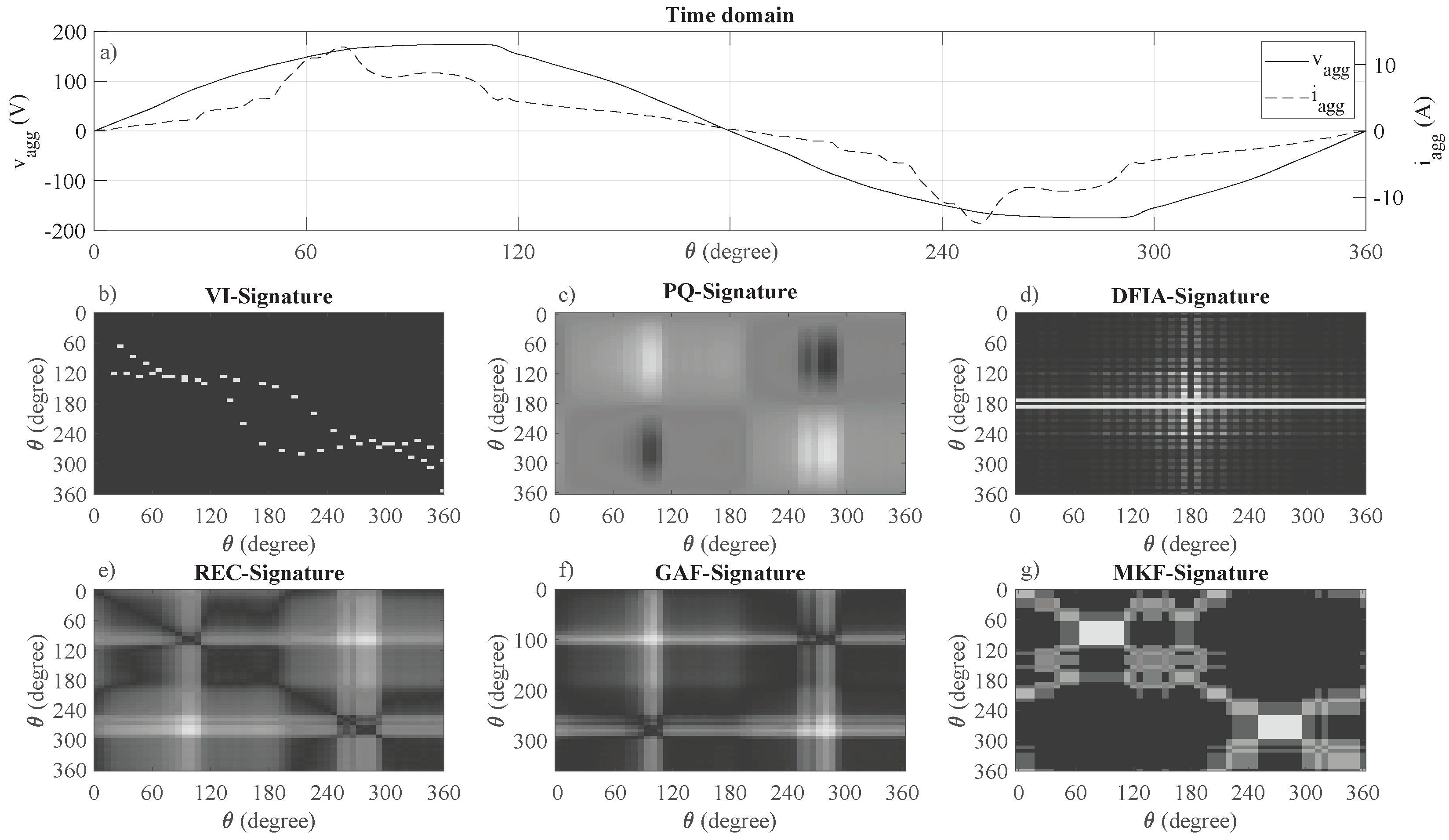
As can be seen in
Table 4, the PQ-transformed signals outperform all other approaches at REDD-3 dataset, while achieving very high performances at the REDD-5 as well. Conversely, MKF is achieving very low performance for all accuracy metrics in both REDD-3 and REDD-5, while REC and GAF are achieving quite similar results for all accuracy metrics and in both datasets. Similarly, the results for AMPds2 are reported for five different two-dimensional transformation methods, since VI trajectories cannot be calculated due to the missing voltage information in the AMPds2 dataset. The results are reported in terms of
, MAE, and SAE using current as output feature and can be found in
Table 5.
As can be seen in
Table 5, once again PQ transformed signals are outperforming all other methods for both deferrable (protocol #3) and all loads (protocol #2), achieving a maximum accuracy of 94.78%. Furthermore, it can also be seen that MKF is reporting the worst performance for all accuracy metrics for both deferrable and all loads. Moreover, it can be seen that the time series imaging methods that are utilizing two input features, e.g., PQ transformed signals or DFIA, are outperforming methods that utilize only univariate input signals, e.g., REC, GAF, and MKF.
To compare the proposed time series imaging methods to previously proposed approaches, the five approaches reporting the best performance on the AMPds2 dataset have been used for comparison and are tabulated in
Table 6. It must be noted that, for the purpose of the direct comparison, the results in
Table 6 have been calculated following the evaluation setups of the corresponding articles, e.g., using only the first year of AMPds2 when comparing to [
10,
24] or using a reduced amount of data (training: 18 August 2012–13 April 2013, testing: 17 May 2013–17 June 2013) when comparing to [
26,
29,
30].
As can be seen in
Table 6, the PQ-transformed signals are outperforming most of the other techniques showing the advantages of utilizing two-dimensional representations in combination with CNNs. Only the WaveNILM [
24] approach using all appliances is performing 0.2% better than the PQ-transformed signals; however, that approach is utilizing four input features (active power, reactive power, apparent power, and current), while the PQ transformation approach is only utilizing two input features (active power and reactive power). Furthermore, when comparing only three appliances as in [
26,
29,
30], the PQ transformation is achieving significantly better performances.
7. Conclusions
A comparison of time series two-dimensional representation methods for energy disaggregation has been presented. In detail, six different time series 2D representation methods for high-frequency data were investigated, and it was shown that PQ transformations outperform other two-dimensional representation-based approaches in almost all investigated evaluation protocols in terms of NILM performance, as well as in terms of run-time. However, when high-noise conditions are considered current and voltage-based signatures (i.e., VI-trajectories) outperform all other approaches showing the highest robustness against increasing levels of noise. Furthermore, it was shown that approaches utilizing both current and voltage time series (such as VI-trajectories, PQ-transforms, or DFIA) are outperforming approaches that rely on univariate data, i.e., the two-dimensional representation that utilize only one time series (such as REC, GAF, or MTF). Moreover, it was shown that utilizing high-frequency data significantly decreases the energy disaggregation error. However, it was also shown that sampling frequencies above 1200 Hz barely show any improvement on the energy disaggregation performance. In general, the results indicate that two-dimensional representations in combination with CNNs are a suitable choice for addressing the energy disaggregation problem. When comparing with previously published methods, it was shown that two-dimensional signatures achieve equal or better performances, while often using fewer features. In the future, the following research directions should be considered. First, an in-depth investigation on sampling frequencies and their influence on appliance specific disaggregation accuracies should be conducted to obtain a better understanding of the impact of certain harmonics on the disaggregation problem. Second, two-dimensional representations (time series imaging) should be combined with transfer learning, utilizing the transfer capability of pre-trained big CNN models mostly used in computer vision tasks.