Application of Adaptive Filtering Based on Variational Mode Decomposition for High-Temperature Electromagnetic Acoustic Transducer Denoising
Abstract
:1. Introduction
2. Basis Theory
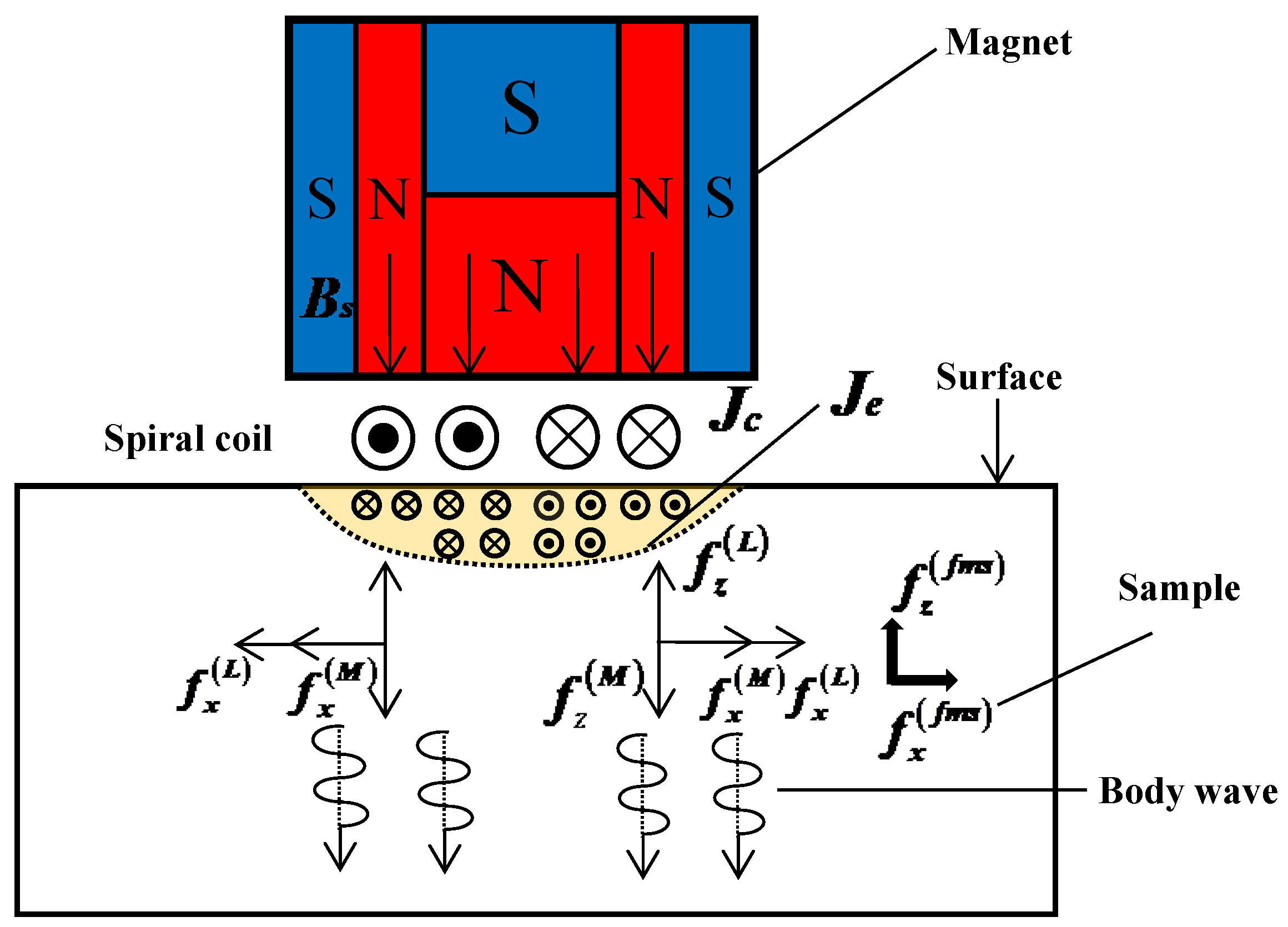
2.1. The Principle of EMAT
2.2. Variational Mode Decomposition (VMD)
- (1)
- Create a variational problem. In the VMD algorithm, the original signal is decomposed into IMF , whose center frequency is . The expression is . Where, is the instantaneous amplitude of , is the phase, and is considered to be a harmonic signal with an amplitude of and a frequency of . To minimize the sum of the estimated bandwidths of each modal function, set up a constrained variational problem as shown below [11]:
- (2)
- Solve the variational problem. The augmented Lagrange function is introduced to transform the constrained problem into an unconstrained problem:
2.3. Wavelet Threshold Denoising (WTD)
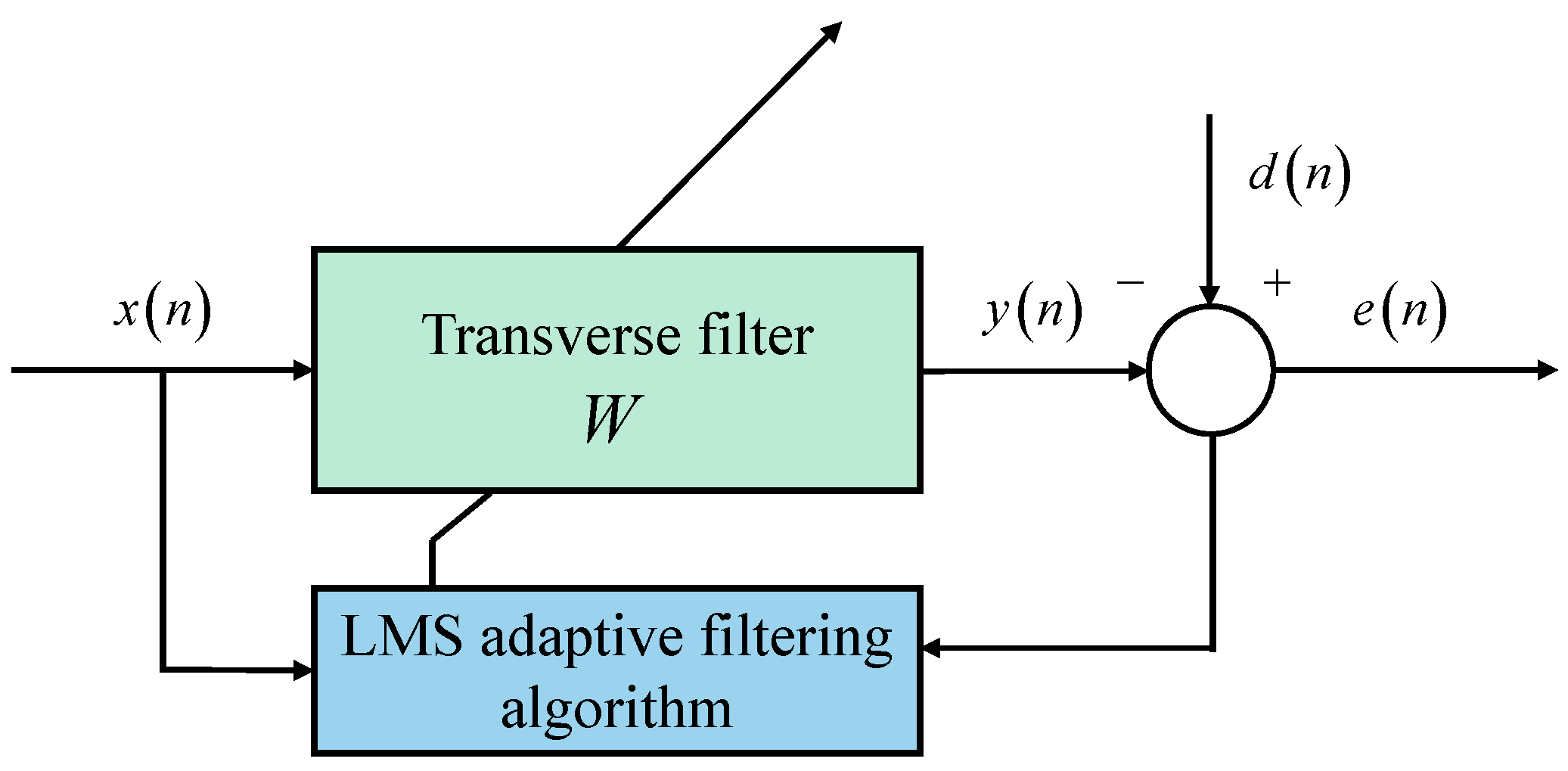
2.4. Least Mean Square Adaptive Filtering
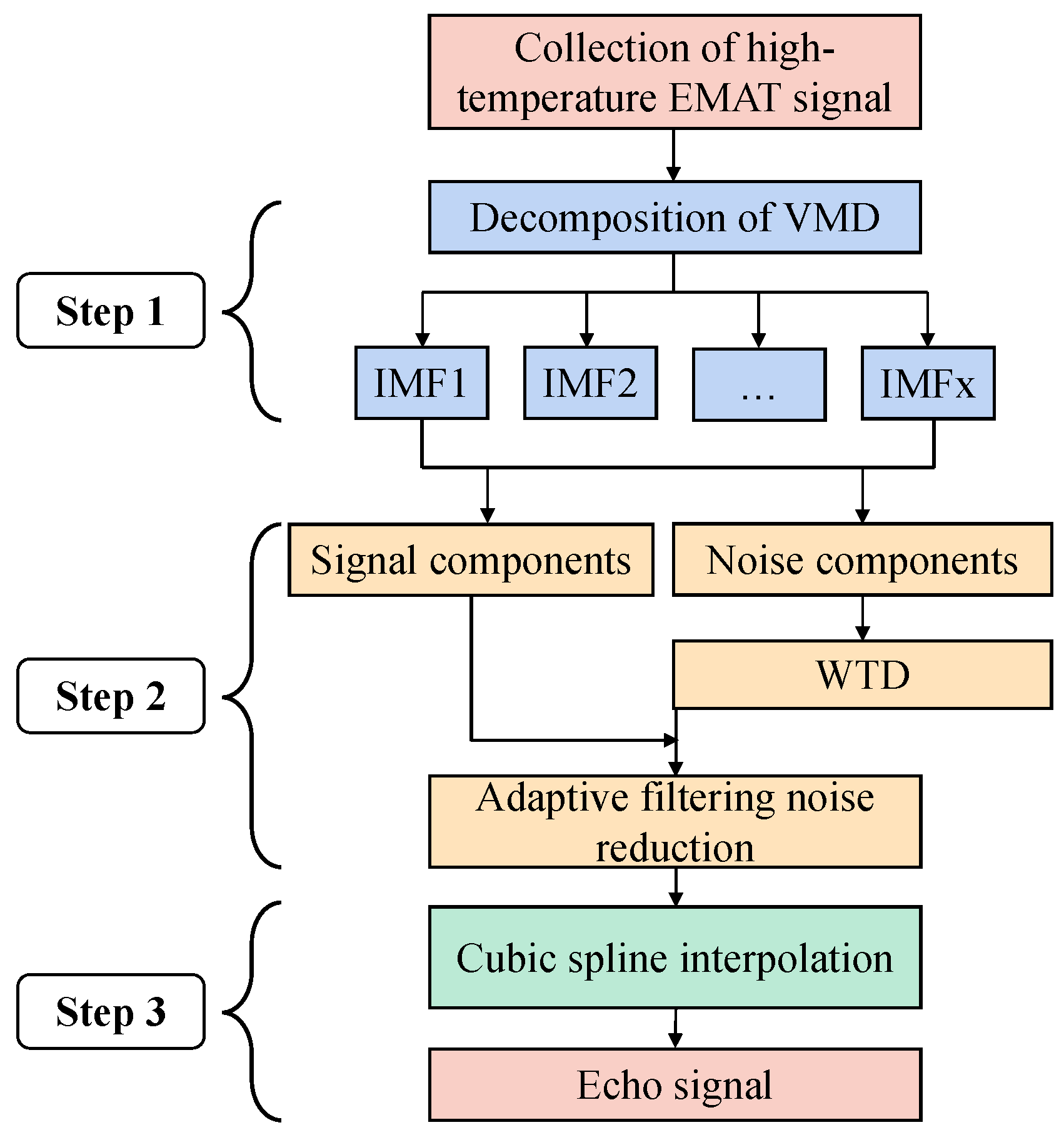
3. Least Mean Square Adaptive Filter Interpolation Denoise Method Based on VMD
4. Experimental Setup
4.1. High-Temperature Experimental Setup
4.2. Thickness Measurement Principle of EMAT
4.3. Parameters Decision
4.4. Signal-to-Noise Ratio Calculation
5. Results Analysis and Discussion
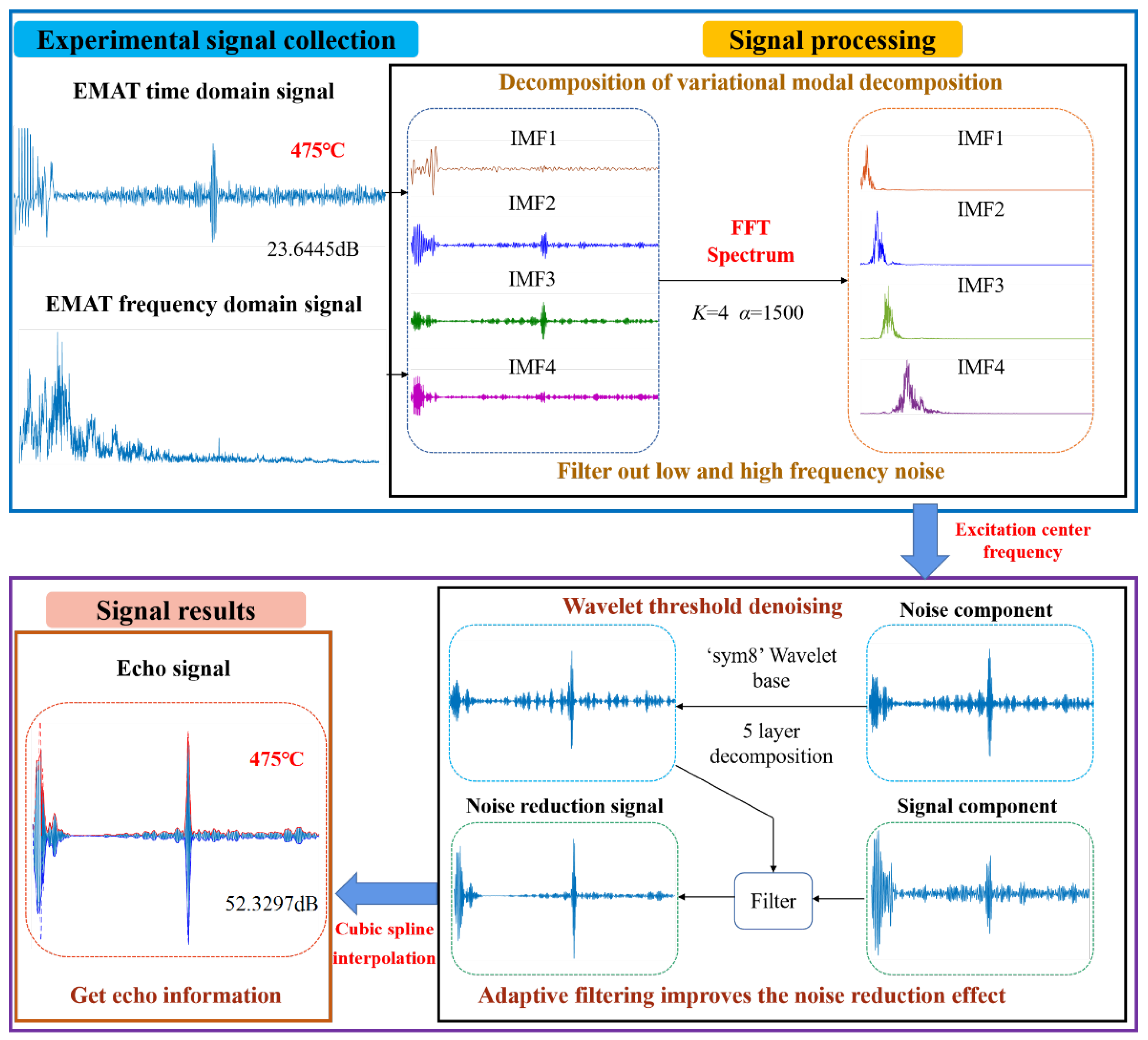
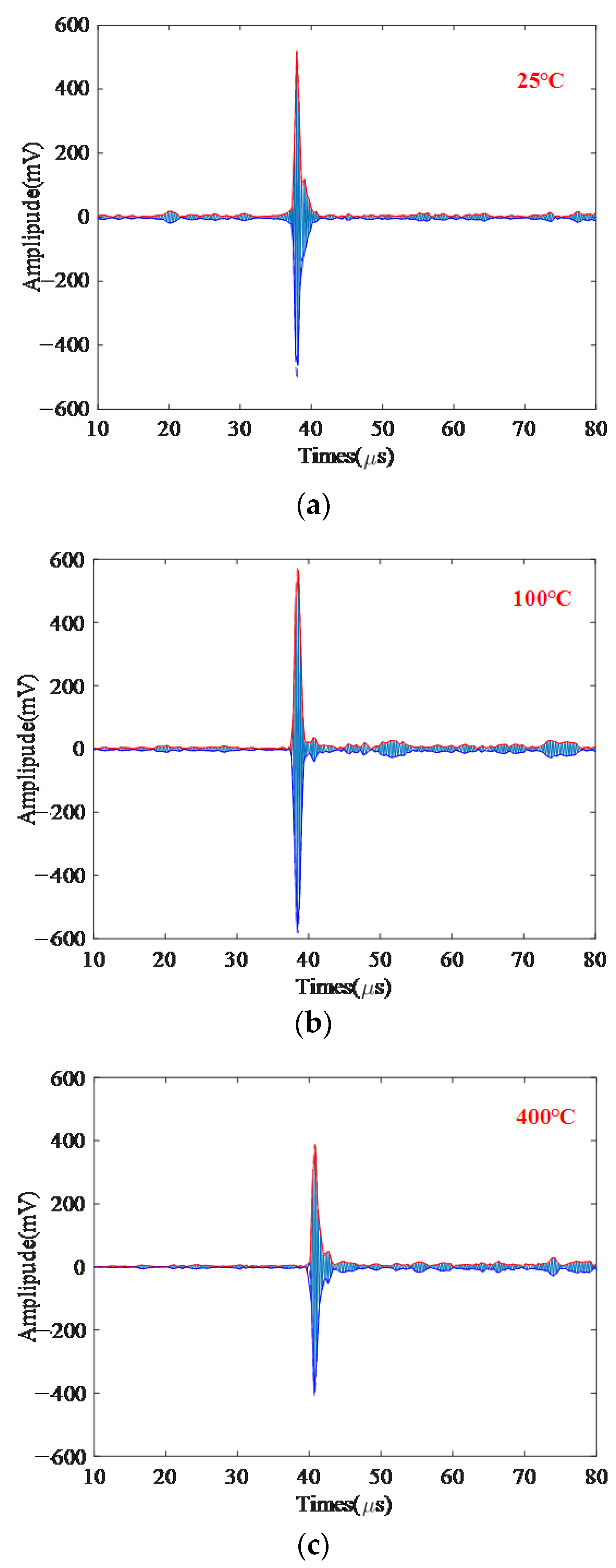
5.1. Signal Processing
5.2. Validation of Proposed Method through Thickness Measurement
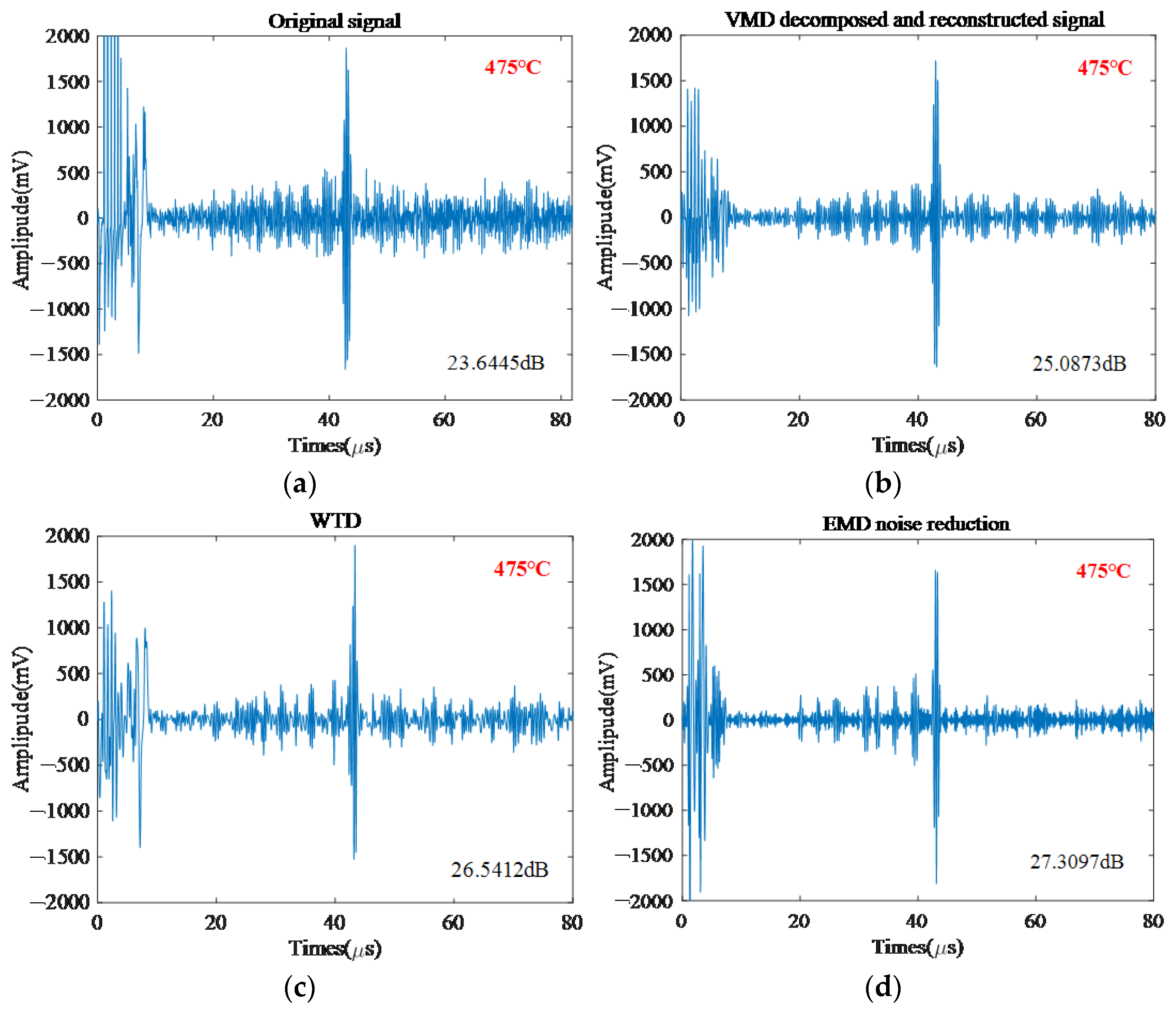
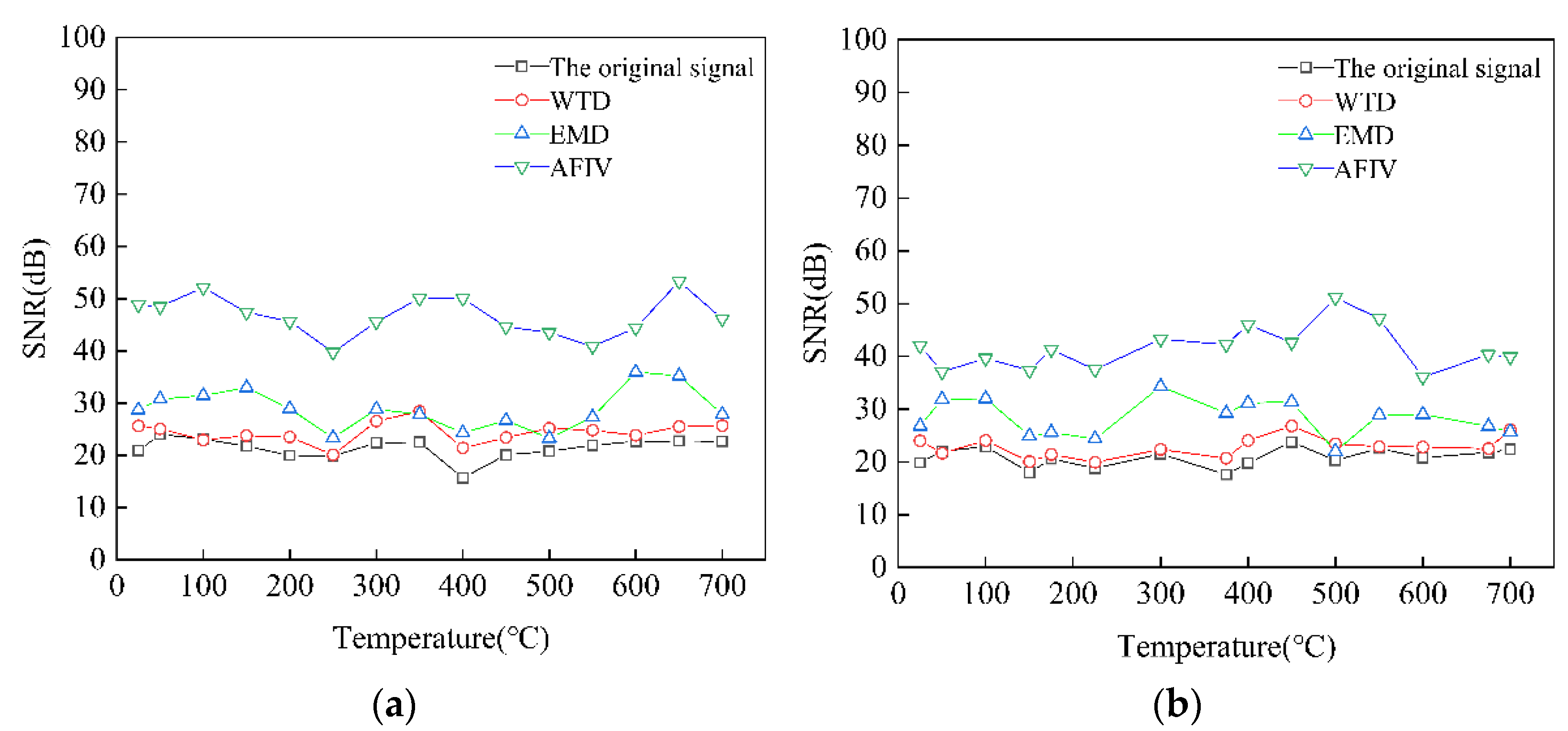
5.3. Comparison with Other Noise Reduction Methods
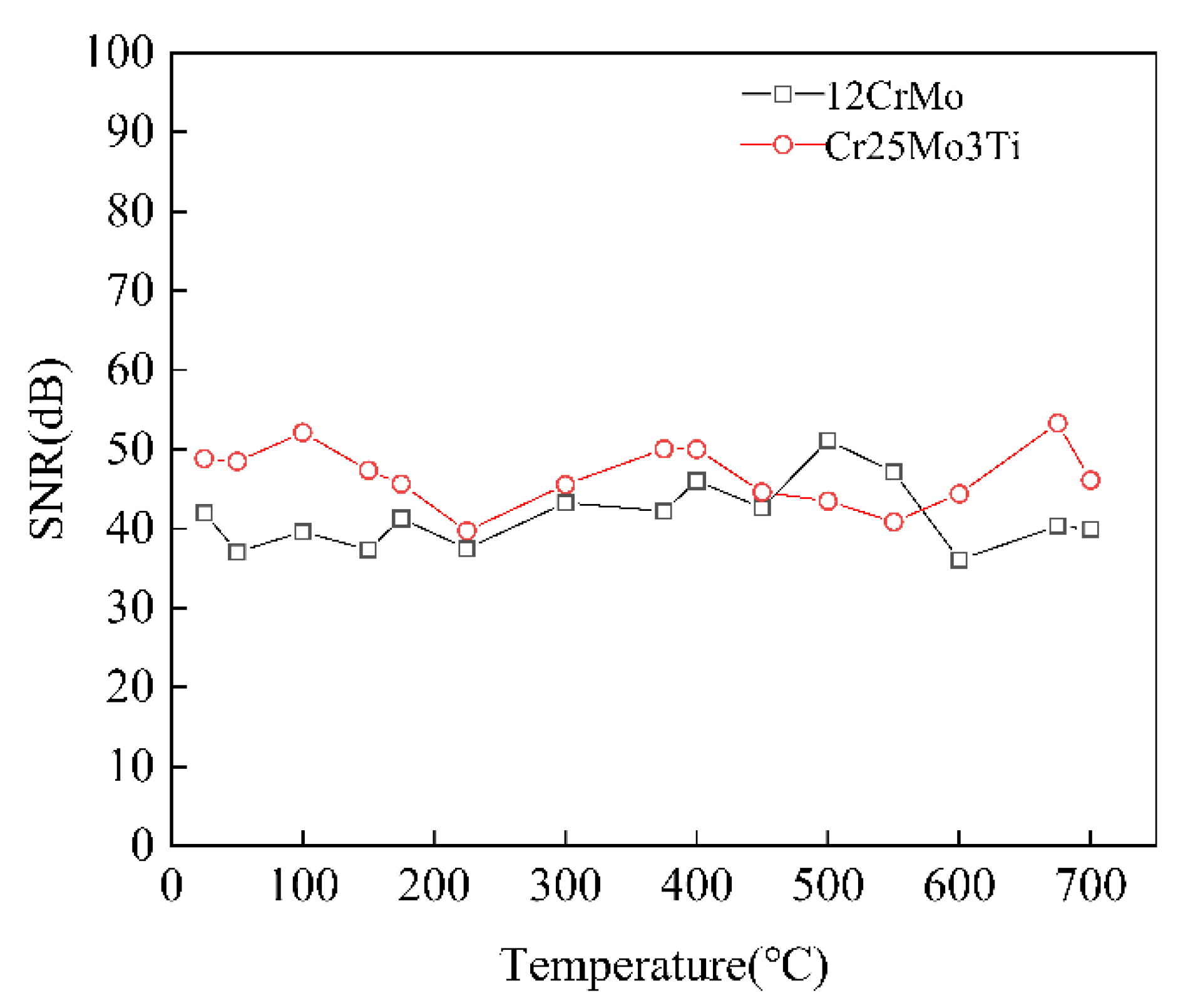
5.4. High-Temperature Robustness of the Proposed Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brizuela, J.; Camacho, J.; Cosarinsky, G.; Iriarte, J.; Cruza, J. Improving elevation resolution in phased-array inspections for NDT. NDT E Int. 2019, 101, 1–16. [Google Scholar] [CrossRef]
- Song, S.; Ni, Y. Ultrasound imaging of pipeline crack based on composite transducer array. Chin. J. Mech. Eng. 2018, 31, 81. [Google Scholar] [CrossRef]
- Baba, A.; Searfass, C.; Tittmann, B. High temperature ultrasonic transducer up to 1000 °C using lithium niobate single crystal. Appl. Phys. Lett. 2010, 97, 2389. [Google Scholar]
- Donoho, D.; Johnstone, I. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Legendre, S.; Goyette, J.; Massicotte, D. Ultrasonic NDE of composite material structures using wavelet coefficients. NDT E Int. 2001, 34, 31–37. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Sun, M.; Shen, Y.; Zhang, W. A wavelet threshold denoising method for ultrasonic signal based on EMD and correlation coefficient analysis. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 3992–3996. [Google Scholar]
- Xu, H.; Xu, C.; Zhou, S. A new ultrasonic guided wave signal processing method for UNDE of laminated composite material. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 2542–2545. [Google Scholar]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, X.; Yuan, J.; Wang, X.; Zeng, Y. The extraction method of laser ultrasonic defect signal based on EEMD. Opt. Commun. 2021, 484, 126570. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Si, D.; Gao, B.; Guo, W.; Yan, Y.; Tian, G.; Yin, Y. Variational mode decomposition linked wavelet method for EMAT denoise with large lift-off effect. NDT E Int. 2019, 107, 102149. [Google Scholar] [CrossRef]
- Abdessalem, B.; Farid, C. Resolution Improvement of Ultrasonic Signals Using Sparse Deconvolution and Variational Mode Decomposition Algorithms. Russ. J. Nondestruct. Test. 2020, 56, 479–489. [Google Scholar] [CrossRef]
- Li, F.; Zhang, B.; Verma, S.; Marfurt, K. Seismic signal denoising using thresholded variational mode decomposition. Explor. Geophys. 2018, 49, 450–461. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, L.; Yan, H.; Bai, Y.; Wang, P. Denoising and base-line drift removal method of MEMS hydrophone signal based on VMD and wavelet threshold processing. IEEE Access 2019, 7, 59913–59922. [Google Scholar] [CrossRef]
- Ram, R.; Mohanty, M.N. Performance analysis of adaptive variational mode decomposition approach for speech enhancement. Int. J. Speech Technol. 2018, 21, 369–381. [Google Scholar] [CrossRef]
- Gu, X.; Chen, C. Rolling bearing fault signal extraction based on stochastic resonance-based denoising and VMD. Int. J. Rotating Mach. 2017, 2017, 3595871. [Google Scholar] [CrossRef]
- Kogia, M.; Gan, T.; Balachandran, W.; Livadas, M.; Kappatos, V.; Szabo, I.; Mohimi, A.; Round, A. High temperature shear horizontal electromagnetic acoustic transducer for guided wave inspection. Sensors 2016, 16, 582–598. [Google Scholar] [CrossRef]
- Shi, W.; Chen, W.; Lu, C.; Cheng, J.; Chen, Y. Application of chirp pulse compression technique to a high-temperature EMAT with a large lift-off. Int. J. Appl. Electromagn. Mech. 2021, 65, 181–196. [Google Scholar]
- Basili, M.; Casini, P.; Morelli, L.; Vestroni, F. Vibration Mitigation of Rail Noise Barriers by Hysteretic Absorbers. J. Appl. Comput. Mech. 2021, 7, 1205–1217. [Google Scholar]
- Tsakonas, E.E.; Sidiropoulos, N.D.; Swami, A. Optimal particle filters for tracking a time-varying harmonic or chirp signal. IEEE Trans. Signal Process. 2008, 56, 4598–4610. [Google Scholar] [CrossRef]
- Lei, Z.; Su, W.; Hu, Q. Multimode Decomposition and Wavelet Threshold Denoising of Mold Level Based on Mutual Information Entropy. Entropy 2019, 21, 202. [Google Scholar] [CrossRef]
- Wei, X.; Feng, G.; Qi, T.; Guo, J.; Li, Z.; Zhao, D.; Li, Z. Reduce the Noise of Transient Electromagnetic Signal Based on the Method of SMA-VMD-WTD. IEEE Sens. J. 2022, 22, 14959–14969. [Google Scholar] [CrossRef]
- Ribichini, R.; Cegla, F.; Nagy, P.B.; Cawley, P. Modelling of electromagnetic acoustic transducers operating on ferromagnetic materials. Am. Inst. Phys. 2010, 1211, 964–971. [Google Scholar]
- Hirao, M.; Ogi, H. EMATs for Science and Industry: Non Contacting Ultrasonic Measurements; Springer: New York, NY, USA, 2003. [Google Scholar]
- Wang, S.; Li, Z.; Li, P.; Liu, X.; Zhai, G. Numerical and experimental evaluation of the receiving performance of meander-line coil EMATs. Nondestruct. Test. Commun. 2014, 29, 269–282. [Google Scholar] [CrossRef]
- Ribichini, R.; Nagy, P.B.; Ogi, H. The impact of magnetostriction on the transduction of normal bias field EMATs. NDT E Int. 2012, 51, 8–15. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Guo, R.; Zhao, J.; Zheng, K.; Xu, J.; Chen, S. Nondestructive testing thickness measurement by laser ultrasound under high temperature. Int. J. Light Electron. Opt. 2018, 172, 1140–1154. [Google Scholar] [CrossRef]
- Lunn, N.; Dixon, S.; Potter, M.D.G. High temperature EMAT design for scanning or fixed point operation on magnetite coated steel. NDT E Int. 2017, 89, 74–80. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Z.; Zhou, J.; Zhang, Z. Study on the Change Law of Transverse Ultrasonic Velocity in a High Temperature Material. Res. Nondestruct. Eval. 2021, 32, 38–57. [Google Scholar] [CrossRef]


| Temperature (°C) | Acoustic Speed [30] (m/s) | Calculated Thickness (mm) | Actual Thickness (mm) | Error (%) |
|---|---|---|---|---|
| 25 | 3246 | 61.122 | 60 | 1.87 |
| 100 | 3122 | 60.223 | 60.975 | 1.23 |
| 200 | 3093 | 59.911 | 60.987 | 1.76 |
| 300 | 3038 | 60.213 | 60.994 | 1.28 |
| 400 | 2940 | 59.917 | 61.001 | 1.77 |
| 500 | 2870 | 60.040 | 61.013 | 1.59 |
| 600 | 2795 | 62.115 | 61.033 | 1.77 |
| 700 | 2656 | 61.805 | 61.062 | 1.21 |
| Denoising Method | VMD | WTD | EMD | AFIV |
|---|---|---|---|---|
| SNR/dB | 25.0873 | 26.5412 | 27.3097 | 52.3297 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Zhou, J.; Liu, Y.; Zhang, J.; Cui, J. Application of Adaptive Filtering Based on Variational Mode Decomposition for High-Temperature Electromagnetic Acoustic Transducer Denoising. Sensors 2022, 22, 7042. https://doi.org/10.3390/s22187042
Zhao S, Zhou J, Liu Y, Zhang J, Cui J. Application of Adaptive Filtering Based on Variational Mode Decomposition for High-Temperature Electromagnetic Acoustic Transducer Denoising. Sensors. 2022; 22(18):7042. https://doi.org/10.3390/s22187042
Chicago/Turabian StyleZhao, Shuaijie, Jinjie Zhou, Yao Liu, Jitang Zhang, and Jie Cui. 2022. "Application of Adaptive Filtering Based on Variational Mode Decomposition for High-Temperature Electromagnetic Acoustic Transducer Denoising" Sensors 22, no. 18: 7042. https://doi.org/10.3390/s22187042
APA StyleZhao, S., Zhou, J., Liu, Y., Zhang, J., & Cui, J. (2022). Application of Adaptive Filtering Based on Variational Mode Decomposition for High-Temperature Electromagnetic Acoustic Transducer Denoising. Sensors, 22(18), 7042. https://doi.org/10.3390/s22187042







