Accuracy Assessment of the 2D-FFT Method Based on Peak Detection of the Spectrum Magnitude at the Particular Frequencies Using the Lamb Wave Signals
Abstract
:1. Introduction
- (1)
- Development of an algorithm of the signal-processing method.
- (2)
- Mathematical modeling of the dispersion curve segments. The purpose is to identify the capabilities of the most accurate reconstructed segments and determine the uncertainty components associated with the model errors.
- (3)
- Experimental setup and verification of the results.
- (4)
- Determination of input and output parameters, which affect the final method accuracy. Optimization of the selected uncertainty components for uncertainty quantification in high-dispersion and non-dispersion zones of phase-velocity dispersion curves of the A0 and S0 modes.
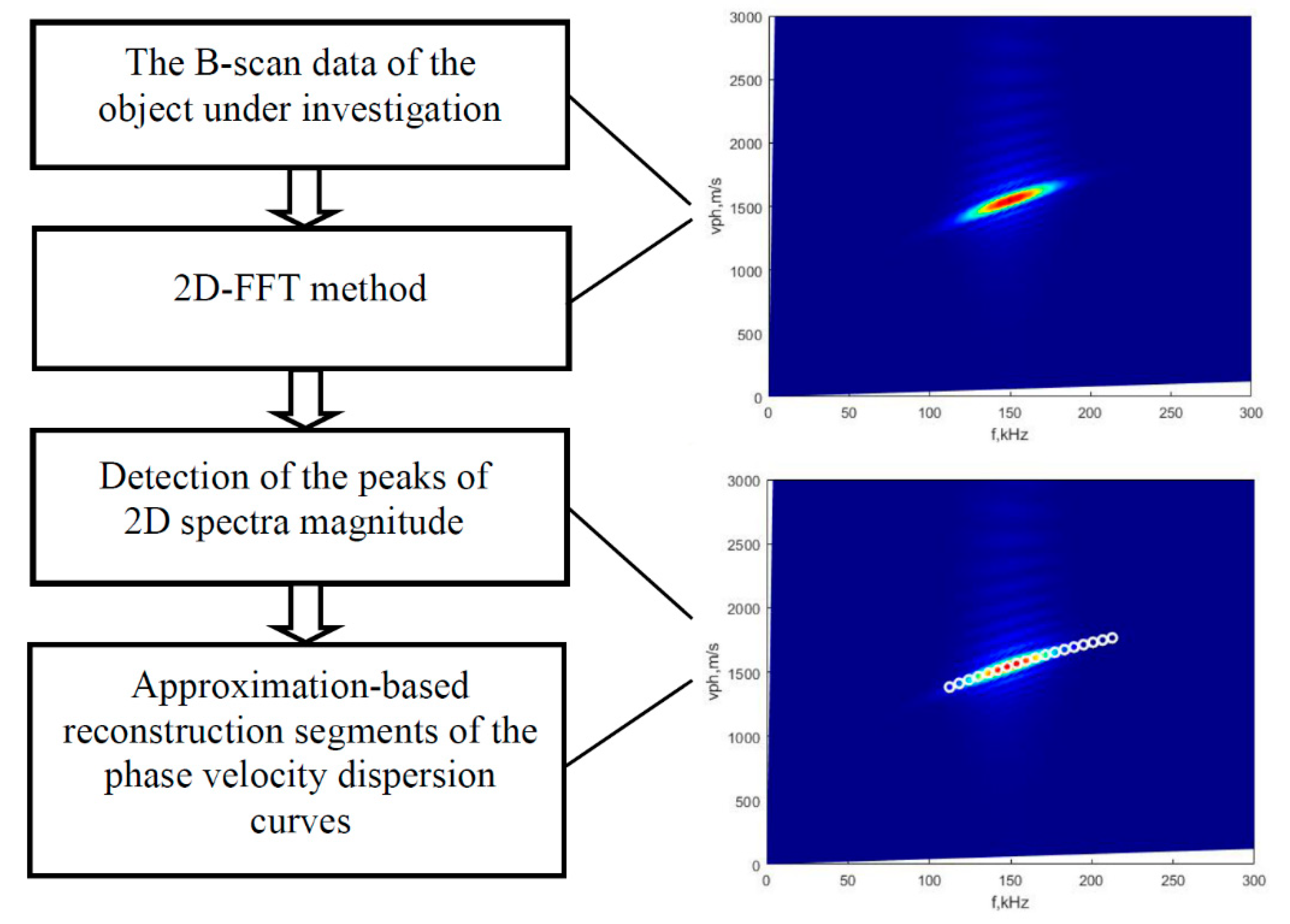
2. The Technique of Peak Detection of the Spectrum Magnitude
- I.
- Application of the 2D-FFT method for analysis of the B-scan data. Since the 2D-FFT method is well-known, the mathematical equations are not given, but the segment of the A0 mode phase-velocity curve obtained by this method is displayed in Figure 1.
- II.
- Detection of 2D spectrum magnitude peaks includes the following steps:
- Selecting the frequency bandwidth (from f1 up to f2).
- Estimating the phase velocity of Lamb wave modes from the 2D-FFT image and applying the peak detection of 2D spectrum magnitude at maximum energy and particular frequencies (within the selected frequency bandwidth).
- The second-order polynomial approximation is applied in order to reduce the influence of scattering effects of detected peaks of phase velocity due to the presence of blurred shapes of 2D spectrum magnitude.
3. The Object Mathematical Simulation and Numerical Verification of the 2D-FFT Method
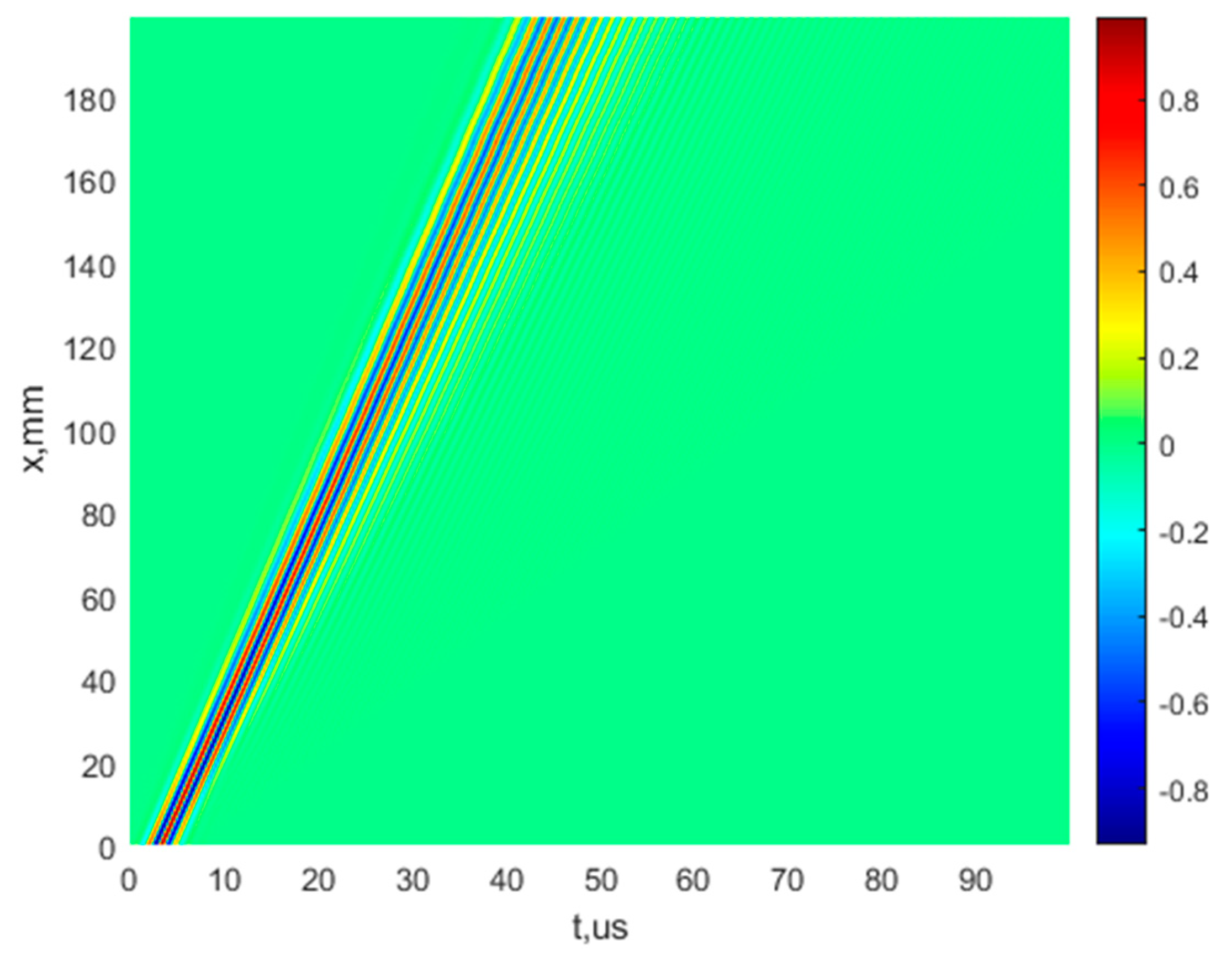
3.1. The Object Mathematical Simulation
3.2. Mathematical Verification of the Method
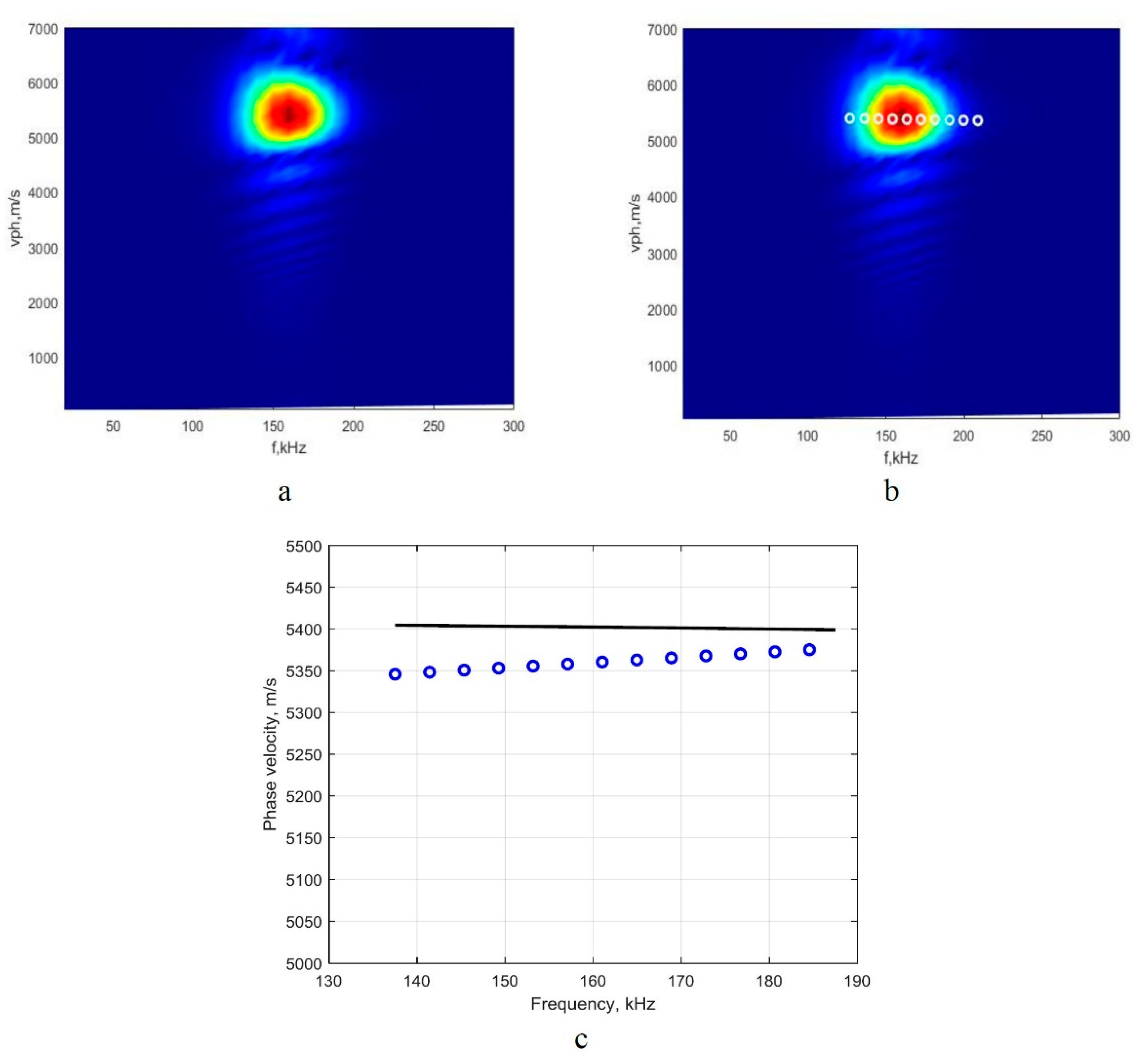
3.2.1. Investigation of the A0 Mode
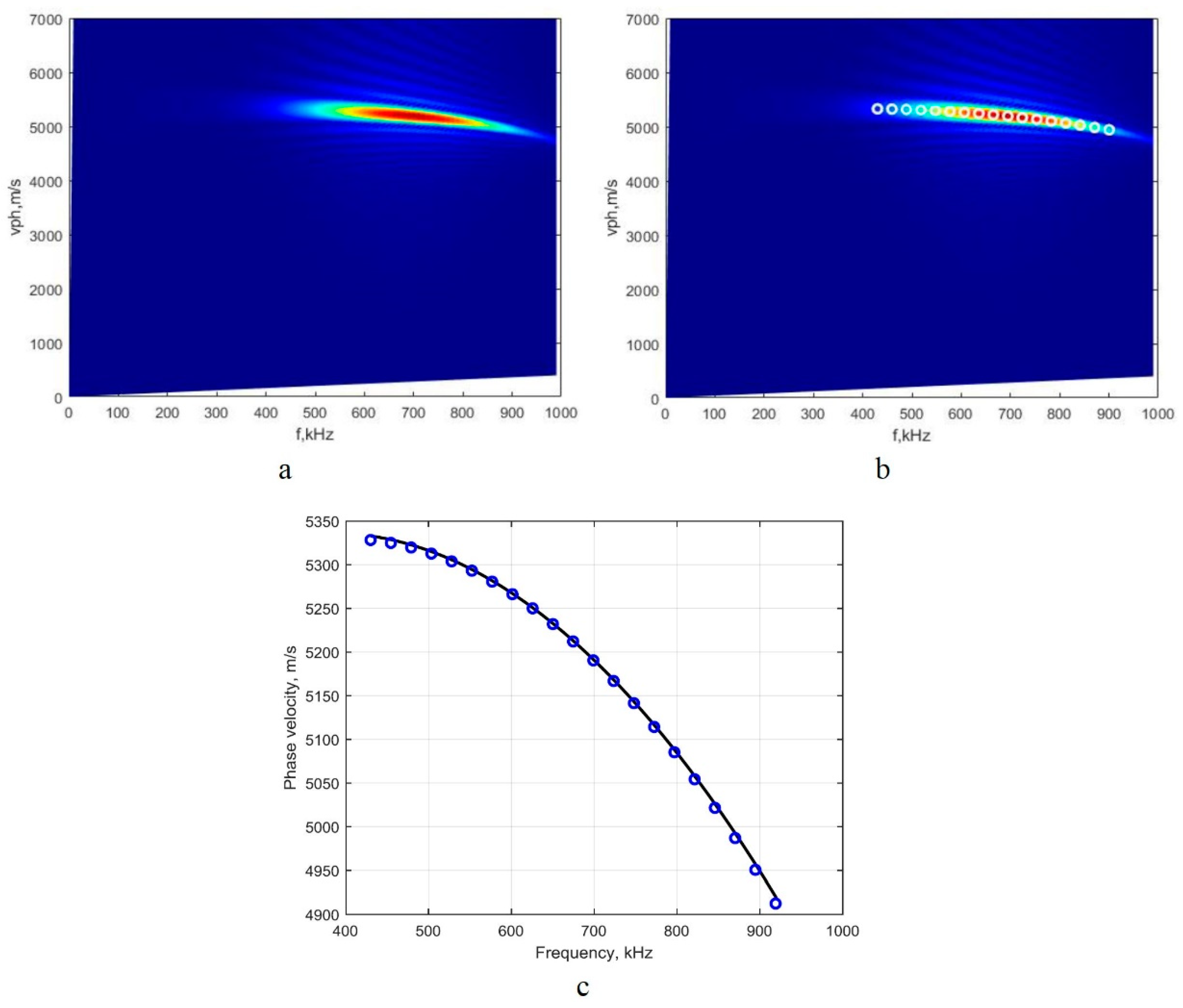
3.2.2. Examining the S0 Mode
4. Experimental Verification
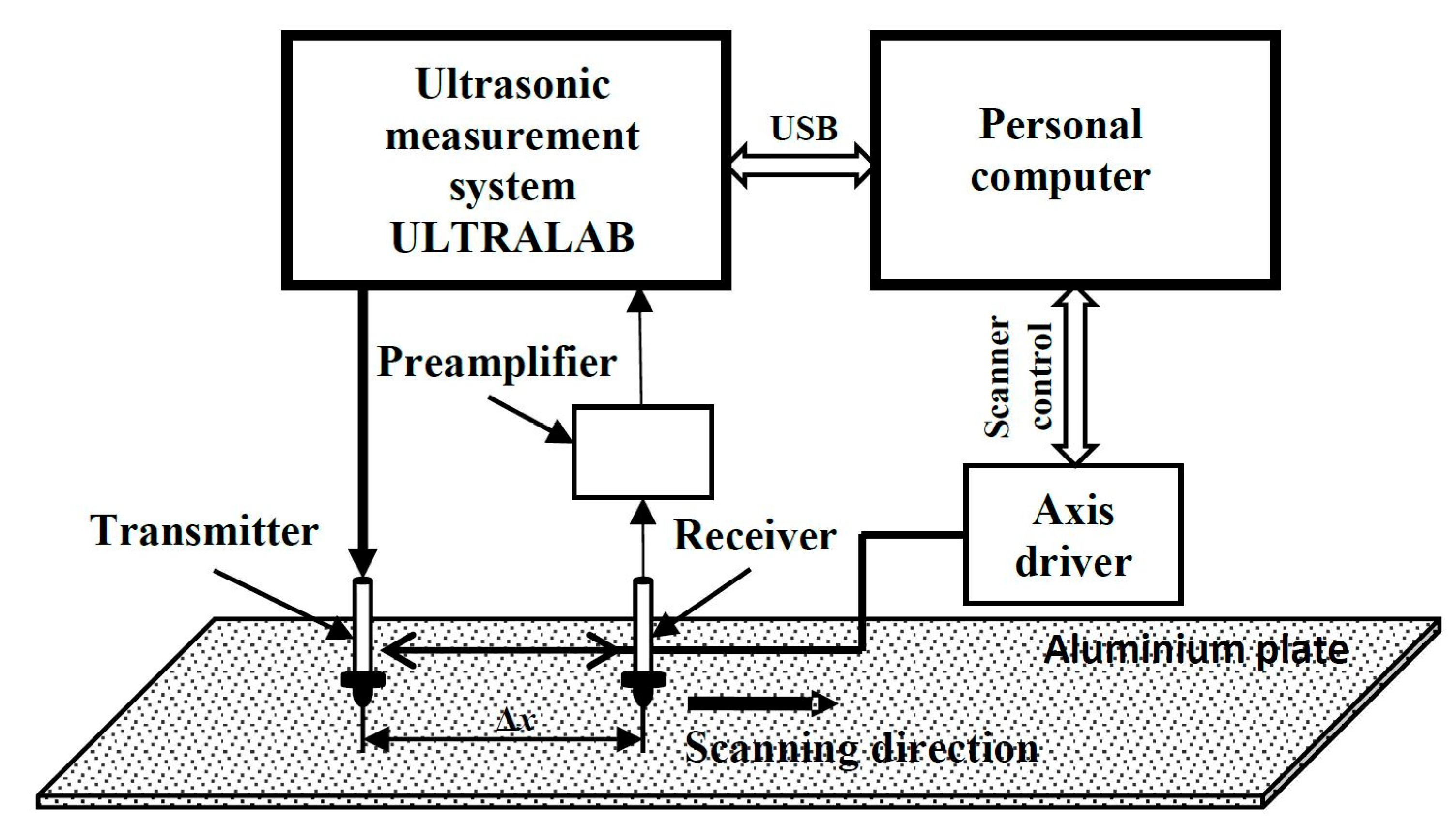
4.1. Description of the Experimental Setup
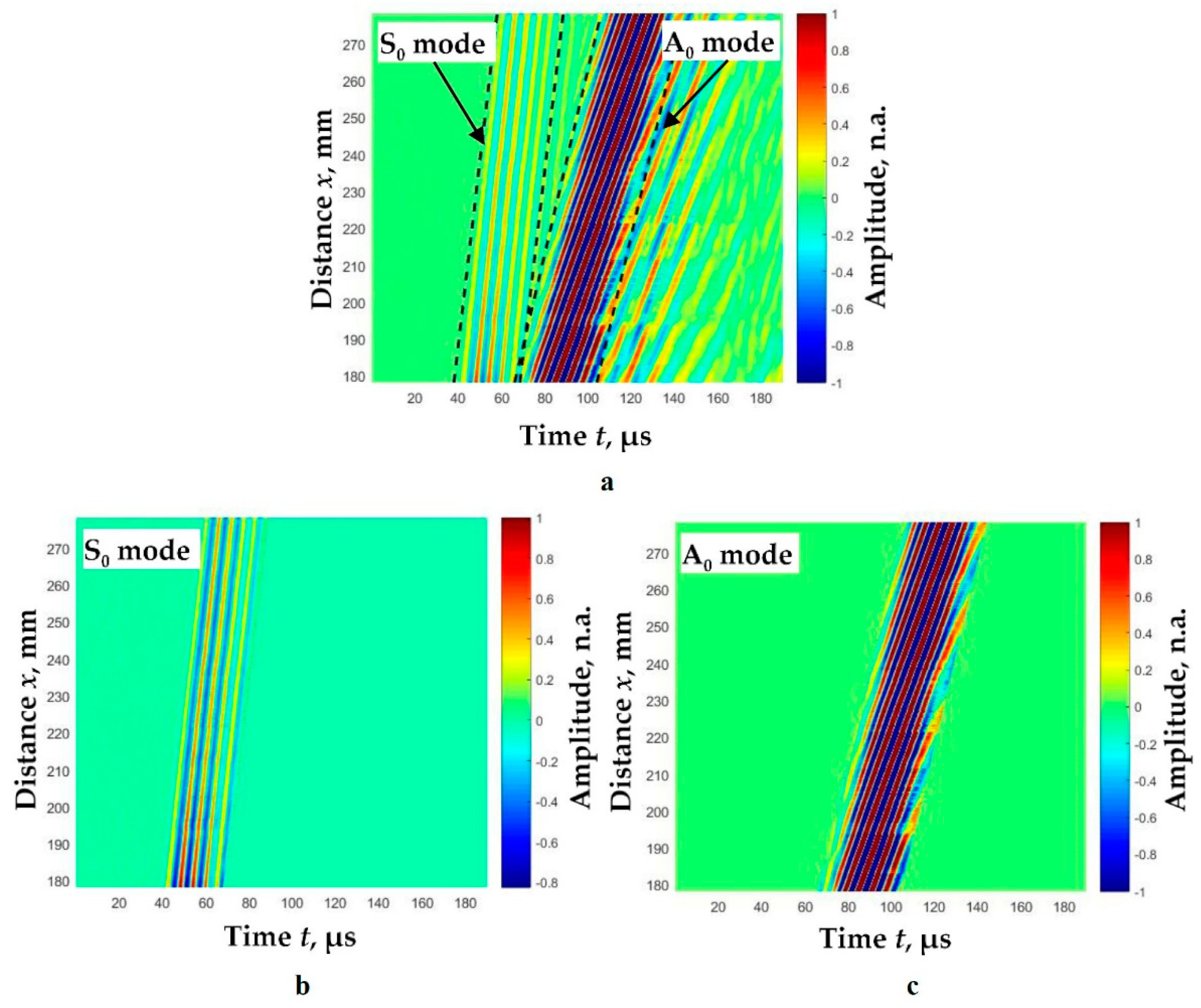
4.2. Experimental Verification of the Analyzed Method
5. Analysis of Uncertainties
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. J. Acoust. Soc. Am. 1991, 89, 1159–1168. [Google Scholar] [CrossRef]
- Ma, Z.; Yu, L. Lamb wave imaging with actuator network for damage quantification in aluminum plate structures. J. Intell. Mater. Syst. Struct. 2021, 32, 182–195. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, K.; Ta, D. High-resolution Lamb waves dispersion curves estimation and elastic property inversion. Ultrasonics 2021, 115, 106427. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Haider, M.F. Propagating, evanescent, and complex wavenumber guided waves in high-performance composites. Materials 2019, 12, 269. [Google Scholar] [CrossRef]
- Nishino, H.; Tanaka, T.; Yoshida, K.; Takatsubo, J. Simultaneous measurement of the phase and group velocities of Lamb waves in a laser-generation based imaging method. Ultrasonics 2012, 52, 530–535. [Google Scholar] [CrossRef] [PubMed]
- Campeiro, L.M.; Budoya, D.E.; Baptista, F.G. Lamb wave inspection using piezoelectric diaphragms: An initial feasibility study. Sens. Actuators A Phys. 2021, 331, 112859. [Google Scholar] [CrossRef]
- Wilcox, P.; Lowe, M.; Cawley, P. Effect of dispersion on long-range inspection using ultrasonic guided waves. NDT E Int. 2001, 34, 1–9. [Google Scholar] [CrossRef]
- Yu, T.H. Plate waves scattering analysis and active damage detection. Sensors 2021, 21, 5458. [Google Scholar] [CrossRef] [PubMed]
- Frank Pai, P.; Deng, H.; Sundaresan, M.J. Time-frequency characterization of lamb waves for material evaluation and damage inspection of plates. Mech. Syst. Signal Process. 2015, 62, 183–206. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, Y.; Tu, X.; Lu, J.; Li, F. Dispersion curve analysis method for Lamb wave mode separation. Struct. Health Monit. 2020, 19, 1590–1601. [Google Scholar] [CrossRef]
- Moreau, L.; Lachaud, C.; Théry, R.; Predoi, M.V.; Marsan, D.; Larose, E.; Weiss, J.; Montagnat, M. Monitoring ice thickness and elastic properties from the measurement of leaky guided waves: A laboratory experiment. J. Acoust. Soc. Am. 2017, 142, 2873. [Google Scholar] [CrossRef] [PubMed]
- Raišutis, R.; Tiwari, K.A.; Žukauskas, E.; Tumšys, O.; Draudvilienė, L. A novel defect estimation approach in wind turbine blades based on phase velocity variation of ultrasonic guided waves. Sensors 2021, 21, 4879. [Google Scholar] [CrossRef] [PubMed]
- Draudvilienė, L.; Tumšys, O.; Raišutis, R. Reconstruction of lamb wave dispersion curves in different objects using signals measured at two different distances. Materials 2021, 14, 6990. [Google Scholar] [CrossRef] [PubMed]
- Draudviliene, L.; Meskuotiene, A. The methodology for the reliability evaluation of the signal processing methods used for the dispersion estimation of Lamb waves. IEEE Trans. Instrum. Meas. 2021, 71, 1–7. [Google Scholar] [CrossRef]
- Sankaran, K.K.; Perez, R.; Jata, K.V. Effects of pitting corrosion on the fatigue behavior of aluminum alloy 7075-T6: Modeling and experimental studies. Mater. Sci. Eng. A 2001, 297, 223–229. [Google Scholar] [CrossRef]
- Pavlakovic, B.; Lowe, M.J.S. Disperse User’s Manual; Non-Destructive Testing Laboratory Department of Mechanical Engineering Imperial College London: London, UK, 2013; p. 207. Available online: https://www.scribd.com/document/410429651/disperse-manual-pdf (accessed on 15 April 2022).
- He, P. Simulation of ultrasound pulse propagation in lossy media obeying a frequency power law. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Draudviliene, L.; Meskuotiene, A.; Mazeika, L.; Raisutis, R. Assessment of quantitative and qualitative characteristics of ultrasonic guided wave phase velocity measurement technique. J. Nondestruct. Eval. 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Vladišauskas, A.; Šliteris, R.; Raišutis, R.; Seniūnas, G.; Žukauskas, E. Contact ultrasonic transducers for mechanical scanning systems. Ultragarsas Ultrasound 2010, 65, 30–35. [Google Scholar]
- Kacker, R.N. Measurement uncertainty and its connection with true value in the GUM versus JCGM documents. Measurement 2018, 127, 525–532. [Google Scholar] [CrossRef]
- Huang, H. Comparison of three approaches for computing measurement uncertainties. Measurement 2020, 163, 107923. [Google Scholar] [CrossRef]
- Couto, P.G.; Damasceno, J.C.; Oliveira, S.D.; Chan, W.K. Monte Carlo simulations applied to uncertainty in measurement. In Theory and Applications of Monte Carlo Simulations, 1st ed.; InTech: London, UK, 2013; Chapter 2; pp. 27–51. [Google Scholar] [CrossRef] [Green Version]





| 1.68 | 3.28 | 0.12 |
| Frequency, kHz | |||
|---|---|---|---|
| 160 | 29.1 | 5.79 | 0.54 |
| 700 | 2.61 | 1.87 | 0.05 |
| Velocity, m/s | Mean Absolute Error | Mean Relative Error | |
|---|---|---|---|
| A0 mode | |||
| 1590 | 9.85 | 1.67 | 0.62 |
| S0 mode | |||
| 5315 | −86.84 | 34.77 | 1.61 |
| Object Parameter xi | Parameter Change Δxi | Velocity Change ΔFxi, m/s | Sensitivity Coefficient Wxi |
|---|---|---|---|
| ρ = 2780 kg/m3 | Δρ = 556 kg/m3 | A0 mode | |
| 110 | |||
| S0 mode | |||
| 640 | |||
| υ = 0.3435 | Δυ = 0.0687 | A0 mode | |
| 14 | 200 m/s | ||
| S0 mode | |||
| 122 | 170 m/s | ||
| E = 71.787 GPa | ΔE = 14.357 GPa | A0 mode | |
| 105 | |||
| S0 mode | |||
| 572 | |||
| d = 2 mm | Δd = 1.6 mm | A0 mode | |
| 137 | |||
| S0 mode | |||
| 3 | |||
| Quantity | Value | Standard Uncertainty | Distribution | Sensitivity Coefficient | Uncertainty Contribution |
|---|---|---|---|---|---|
| 9.85 m/s | 1.67 m/s | normal | 1.0 | 1.7 m/s | |
| 0.0 m/s | 3.28 m/s | normal | 1.0 | 3.3 m/s | |
| 0.0 m/s | 1.2 m/s | normal | 1.0 | 1.2 m/s | |
| 0.0 m | 28.9 × 10−6 m | rectangular | 600 × 103 s−1 | 17 m/s | |
| 0.0 m | 289 × 10−6 m | rectangular | 34 × 103 s−1 | 9.9 m/s | |
| 0.0 kg/m3 | 0.289 kg/m3 | rectangular | 0.06 m/s | ||
| 0.0 m | 28.9 × 10−6 | rectangular | 200 m/s | 5.9 × 10−3 m/s | |
| 0.0 GPa | 289 × 10−6 GPa | rectangular | 2.1 × 10−3 m/s | ||
| 1599.8 m/s | 20.3 m/s | ||||
| Result value: | Expanded uncertainty: | Coverage factor: | Coverage: | ||
| 1600 m/s | 41 m/s | 2.00 | 95% (normal) | ||
| Quantity | Value | Standard Uncertainty | Distribution | Sensitivity Coefficient | Uncertainty Contribution |
|---|---|---|---|---|---|
| −86.8 m/s | 34.8 m/s | normal | 1.0 | 35 m/s | |
| 0.0 m/s | 5.79 m/s | normal | 1.0 | 5.8 m/s | |
| 0.0 m/s | 19.1 m/s | normal | 1.0 | 19 m/s | |
| 0.0 m | 28.9 × 10−6 m | rectangular | 600 × 103 s−1 | 17 m/s | |
| 0.0 m | 289 × 10−6 m | rectangular | 7500 s−1 | 2.2 m/s | |
| 0.0 kg/m3 | 0.289 kg/m3 | rectangular | 0.33 m/s | ||
| 0.0 m | 28.9 × 10−6 | rectangular | 1700 m/s | 0.05 m/s | |
| 0.0 GPa | 289 × 10−6 GPa | rectangular | 0.01 m/s | ||
| 5315.2 m/s | 43.7 m/s | ||||
| Result value: | Expanded uncertainty: | Coverage factor: | Coverage: | ||
| 5315 m/s | 87 m/s | 2.00 | 95% (normal) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Draudvilienė, L.; Meškuotienė, A.; Raišutis, R.; Tumšys, O.; Surgautė, L. Accuracy Assessment of the 2D-FFT Method Based on Peak Detection of the Spectrum Magnitude at the Particular Frequencies Using the Lamb Wave Signals. Sensors 2022, 22, 6750. https://doi.org/10.3390/s22186750
Draudvilienė L, Meškuotienė A, Raišutis R, Tumšys O, Surgautė L. Accuracy Assessment of the 2D-FFT Method Based on Peak Detection of the Spectrum Magnitude at the Particular Frequencies Using the Lamb Wave Signals. Sensors. 2022; 22(18):6750. https://doi.org/10.3390/s22186750
Chicago/Turabian StyleDraudvilienė, Lina, Asta Meškuotienė, Renaldas Raišutis, Olgirdas Tumšys, and Lina Surgautė. 2022. "Accuracy Assessment of the 2D-FFT Method Based on Peak Detection of the Spectrum Magnitude at the Particular Frequencies Using the Lamb Wave Signals" Sensors 22, no. 18: 6750. https://doi.org/10.3390/s22186750
APA StyleDraudvilienė, L., Meškuotienė, A., Raišutis, R., Tumšys, O., & Surgautė, L. (2022). Accuracy Assessment of the 2D-FFT Method Based on Peak Detection of the Spectrum Magnitude at the Particular Frequencies Using the Lamb Wave Signals. Sensors, 22(18), 6750. https://doi.org/10.3390/s22186750






