Multi-Modal Learning-Based Equipment Fault Prediction in the Internet of Things
Abstract
:1. Introduction
- We make the first attempt to launch an multi-modal learning algorithm on equipment fault prediction in the Internet of Things.
- We design a series of strategies to improve the accuracy of equipment fault prediction, use different methods to deal with different quality of detection data, and improve the robustness of fault prediction algorithm by adding noise to high-quality monitoring data.
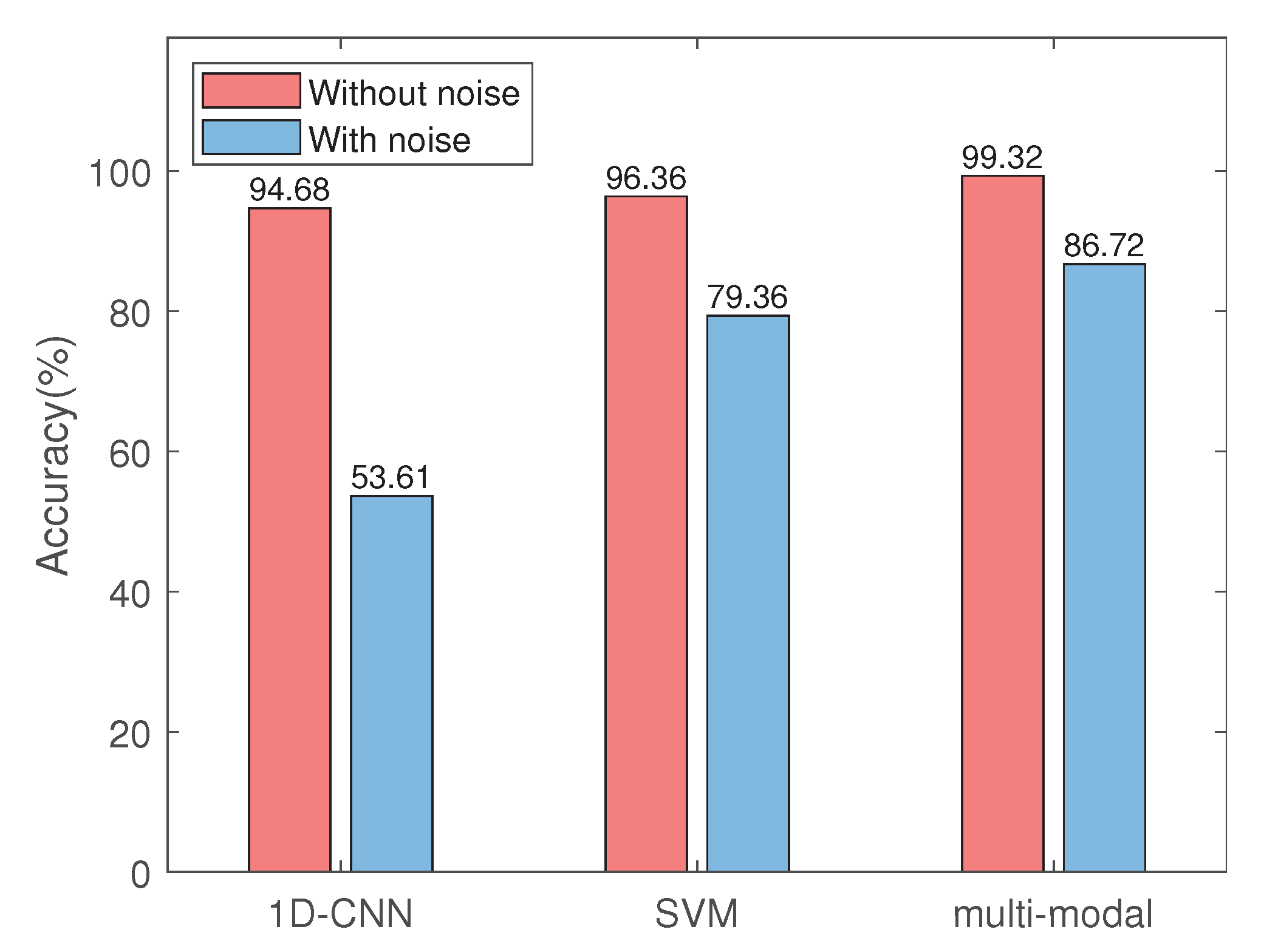
- We evaluate the performance of our proposed multi-modal learning algorithm on the CWRU bearing dataset. Compared with the traditional feature concatenation method, the prediction accuracy of the proposed multi-modal learning algorithm can be improved by up to 7.42%.
2. Related Work
3. System Model and the Target Problem
3.1. System Model
3.2. The Target Problem
3.2.1. Pre-Experiments and Our Observations
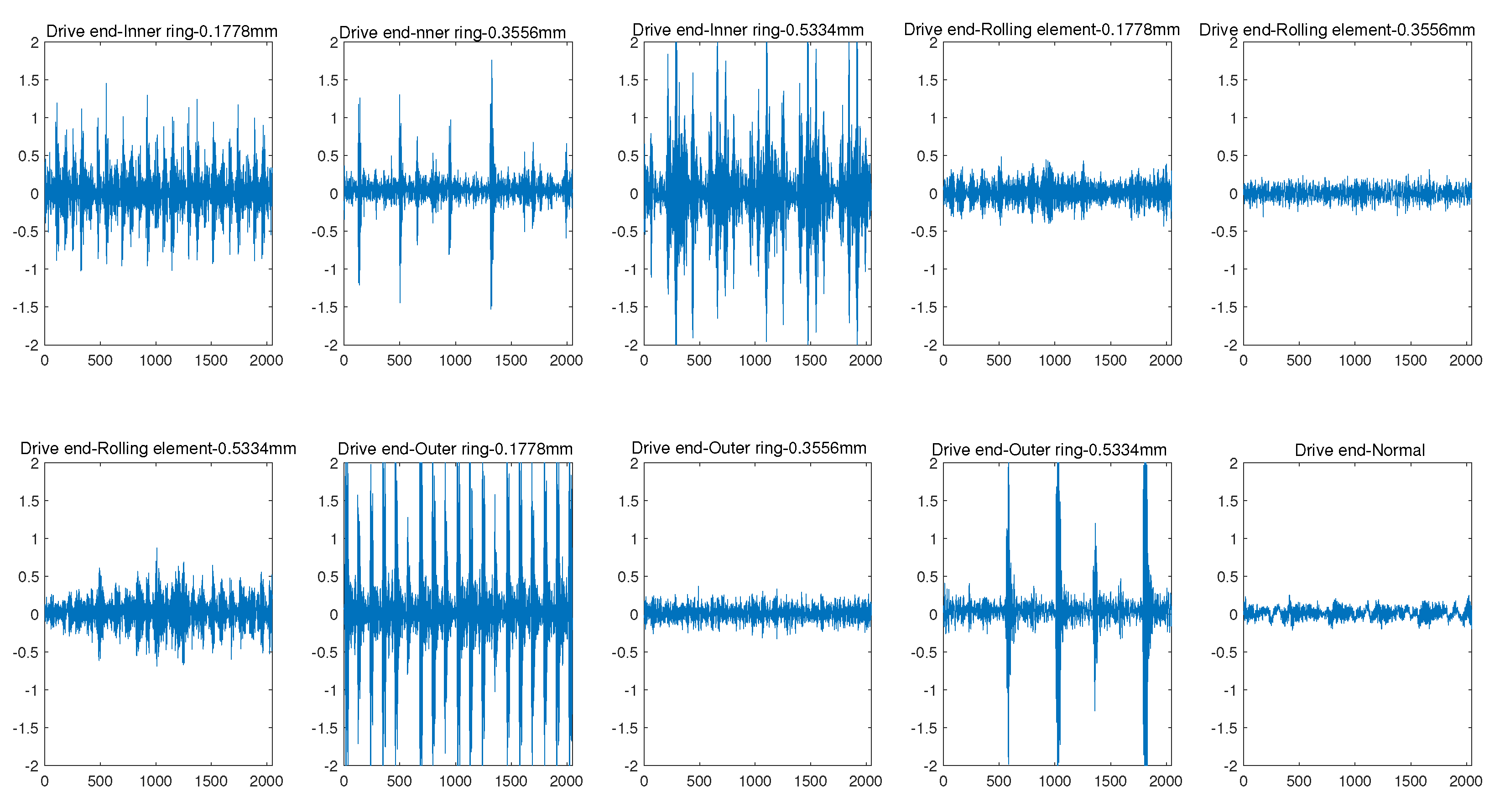
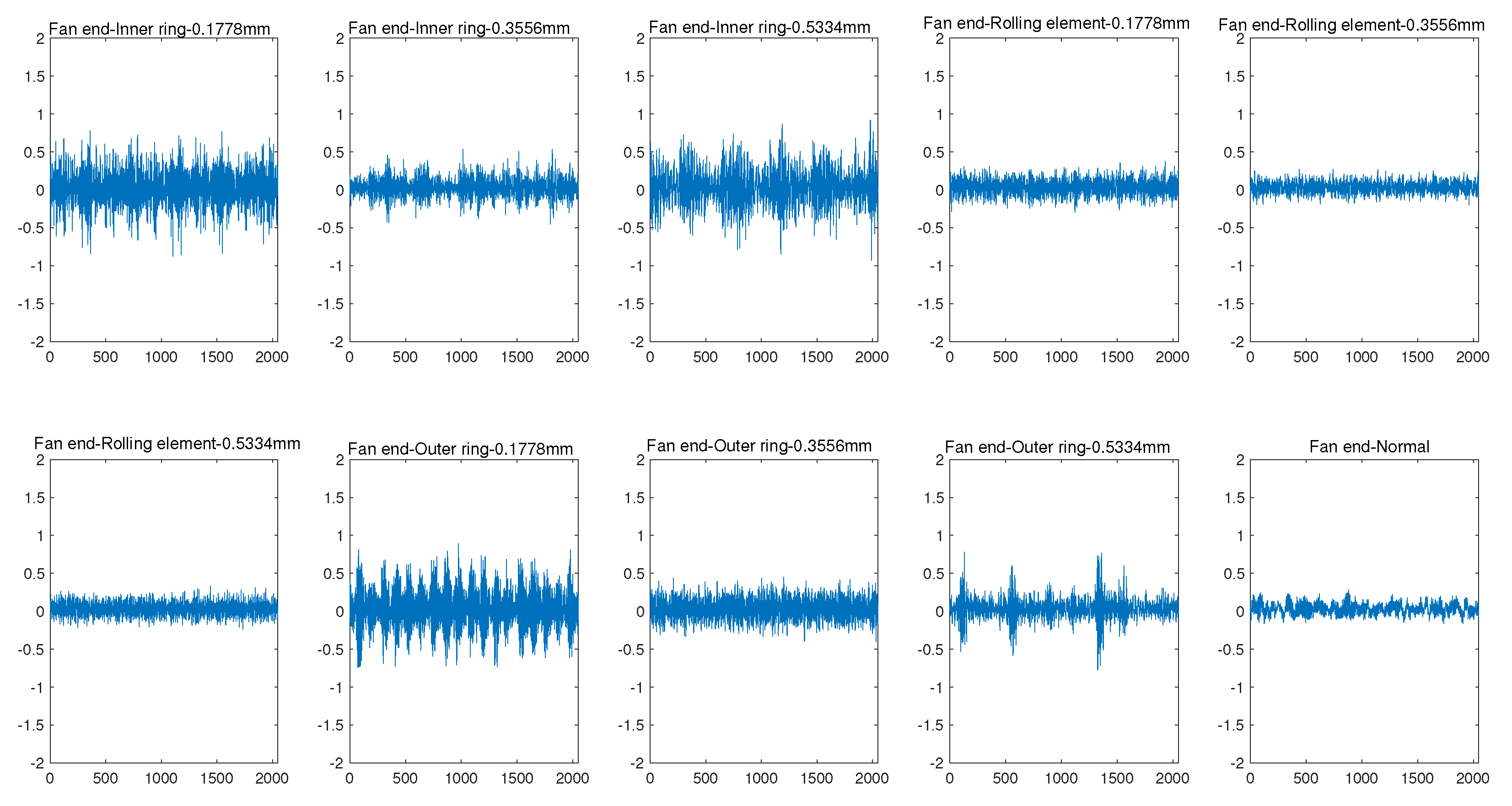
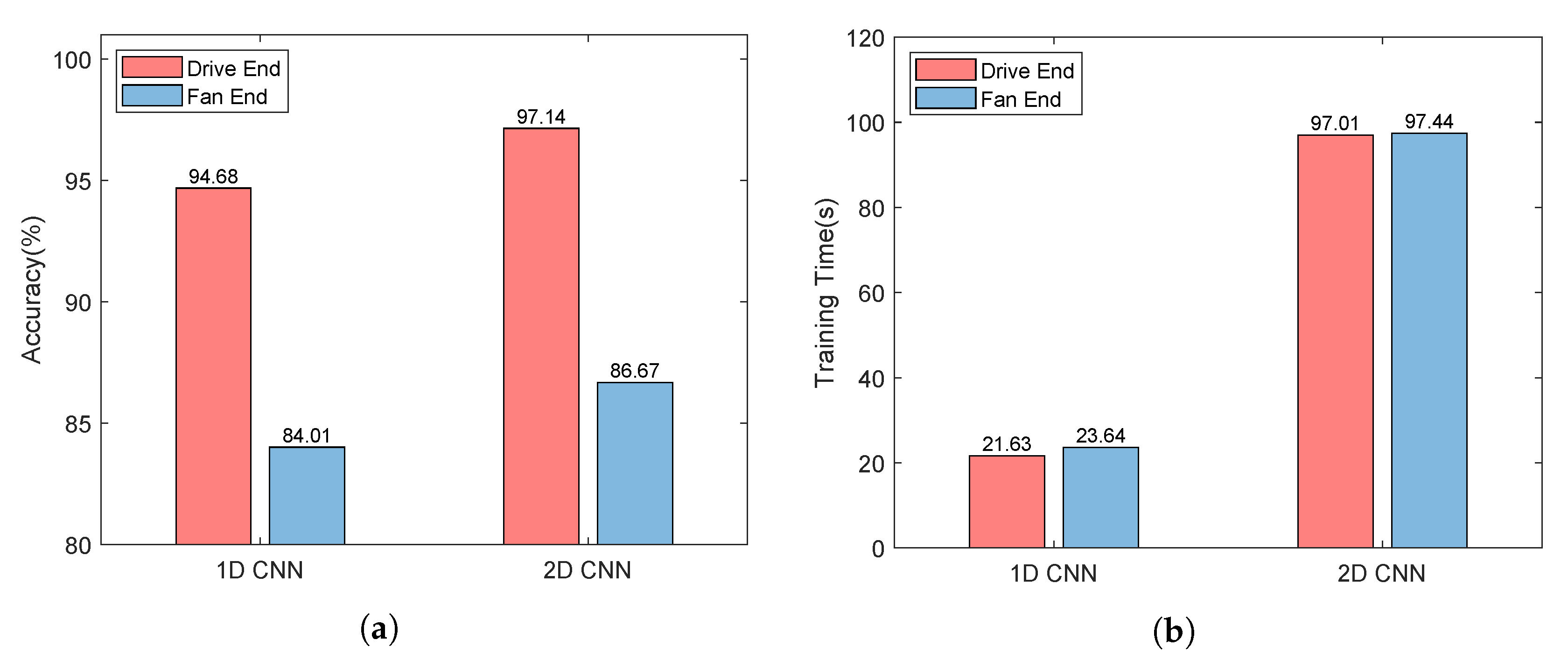
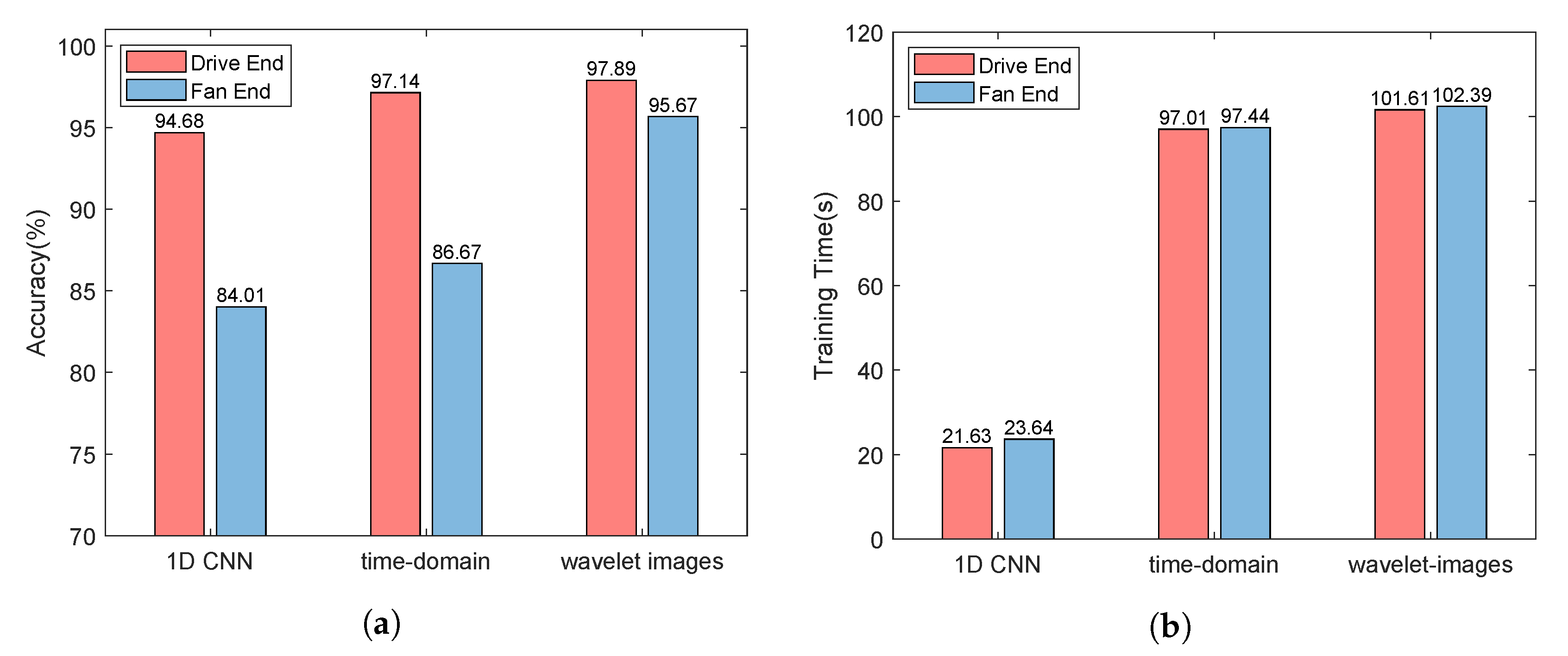
- As shown in Figure 3a, the monitoring data collected by the sensor at the drive end can always provide better performance whether 1D CNN or 2D CNN is used. Using 1D CNN, the prediction accuracy of fault prediction based on driver data can be improved by up to 10.67%. The evidence reinforces that the data collected by different sensors have different contributions to the accuracy of fault diagnosis and prediction. Thus, we distinguish between low-quality monitoring data and high-quality monitoring data.
- As shown in Figure 3a, for each type of monitoring data, compared with 1D CNN, 2D CNN can provide better performance thanks to its better learning ability. Using 2D CNN, the accuracy of fault prediction based on driver data can be improved by 2.46%, and the accuracy of fault prediction based on fan data can be improved by 2.66%. Combined with Figure 3b, the accuracy of fault prediction is improved by about 2.5%, while the training time increases by more than three times. Using 2D CNN, the training time based on driver data increases from 21.63 s to 97.01 s, and the training time based on driver data is increased from 23.64 s to 97.44 s. Therefore, it is necessary to tradeoff the prediction accuracy and the running time.
- The 2D CNN does help improve the accuracy of fault prediction. As shown in Figure 3a, the accuracy of using 2D CNN for two types of sensor data is higher than that of using 1D CNN. For the monitoring data collected by the sensor at the driver end, the prediction accuracy can reach 94.68% using ID CNN. For the monitoring data collected by the fan end sensor, even if 2D CNN is used, the prediction accuracy is only 86.67%. It can be seen that the monitoring data collected by each sensor has different contributions to the performance of fault prediction. Moreover, the performance of the monitoring data collected by the fan end sensor in fault prediction is not satisfactory, thus, its processing technology needs to be further optimized.
3.2.2. The Target Problem
4. The Proposed Equipment Fault Prediction Framework
4.1. Preprocessing and Feature Extraction
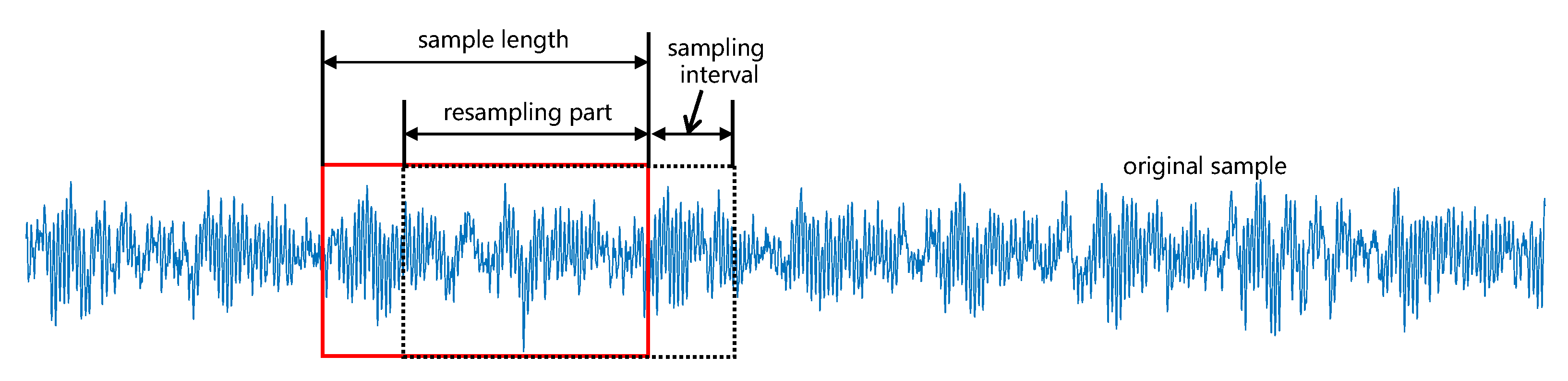
4.1.1. Preprocessing
4.1.2. Feature Extraction
4.1.3. The Loss Function
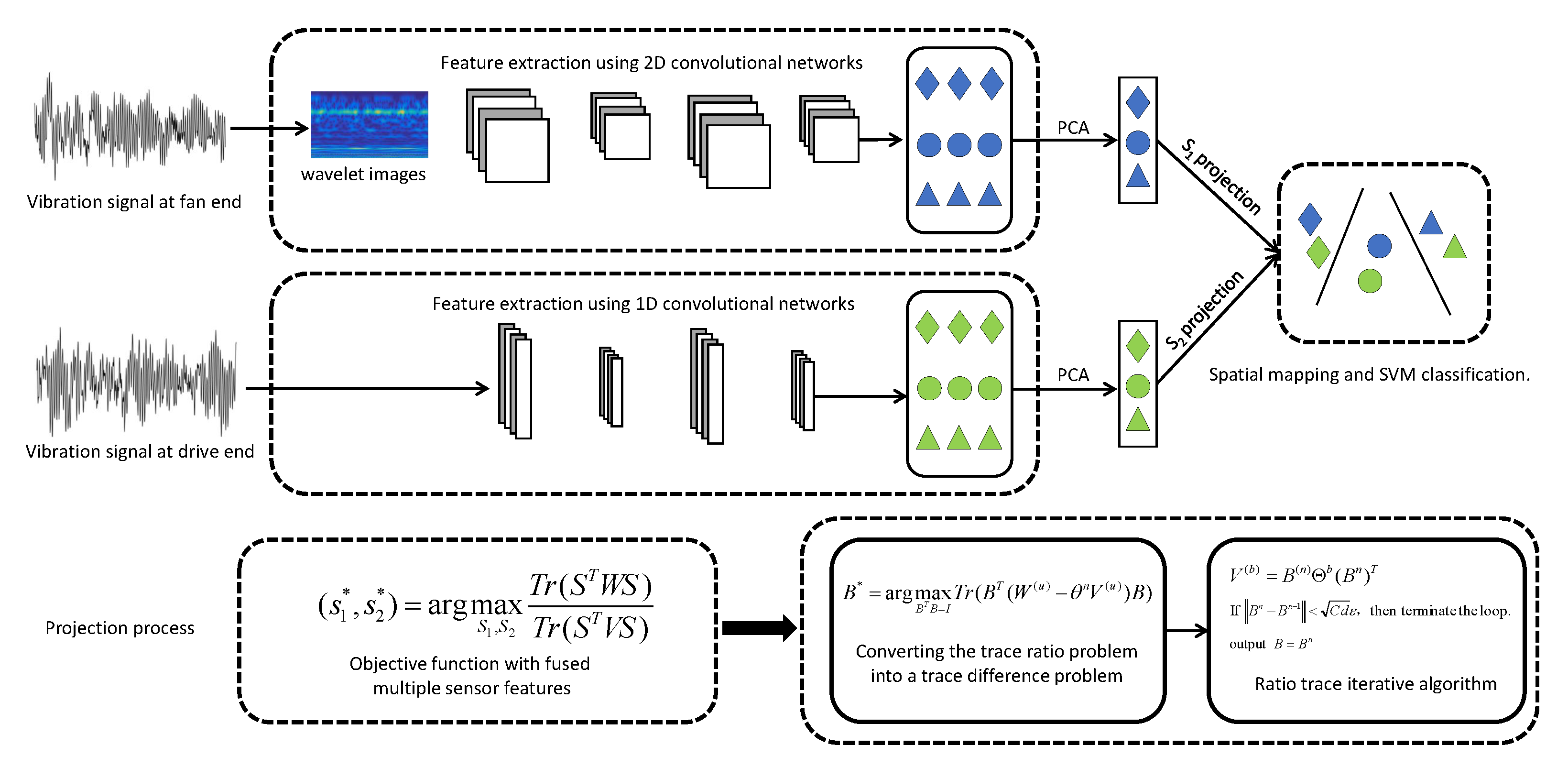
4.2. Multi-Modal Learning Algorithm
4.3. Global Optimum Solution Based on Eigenvalue Decomposition
- Initialize to any column orthogonal matrix.
- Calculate iteratively as follows:
- Construct the trace difference problem as follows:
- Solve the trace difference problem based on eigenvalue decomposition method as follows:where is the th largest eigenvalue of , is the corresponding eigenvector of .
- Reconstruct the projection matrix to maintain orthogonality: Let , d is the rank of low-latitude feature, and perform singular value decomposition on . The projection matrix can be updated as follows:
- The termination criterion for iteration: if , Then the iteration ends, .
| Algorithm 1 Multi-modal Learning Algorithm |
|
5. Experiment Evaluation
5.1. Dataset and Data Preprocessing
5.2. Baselines
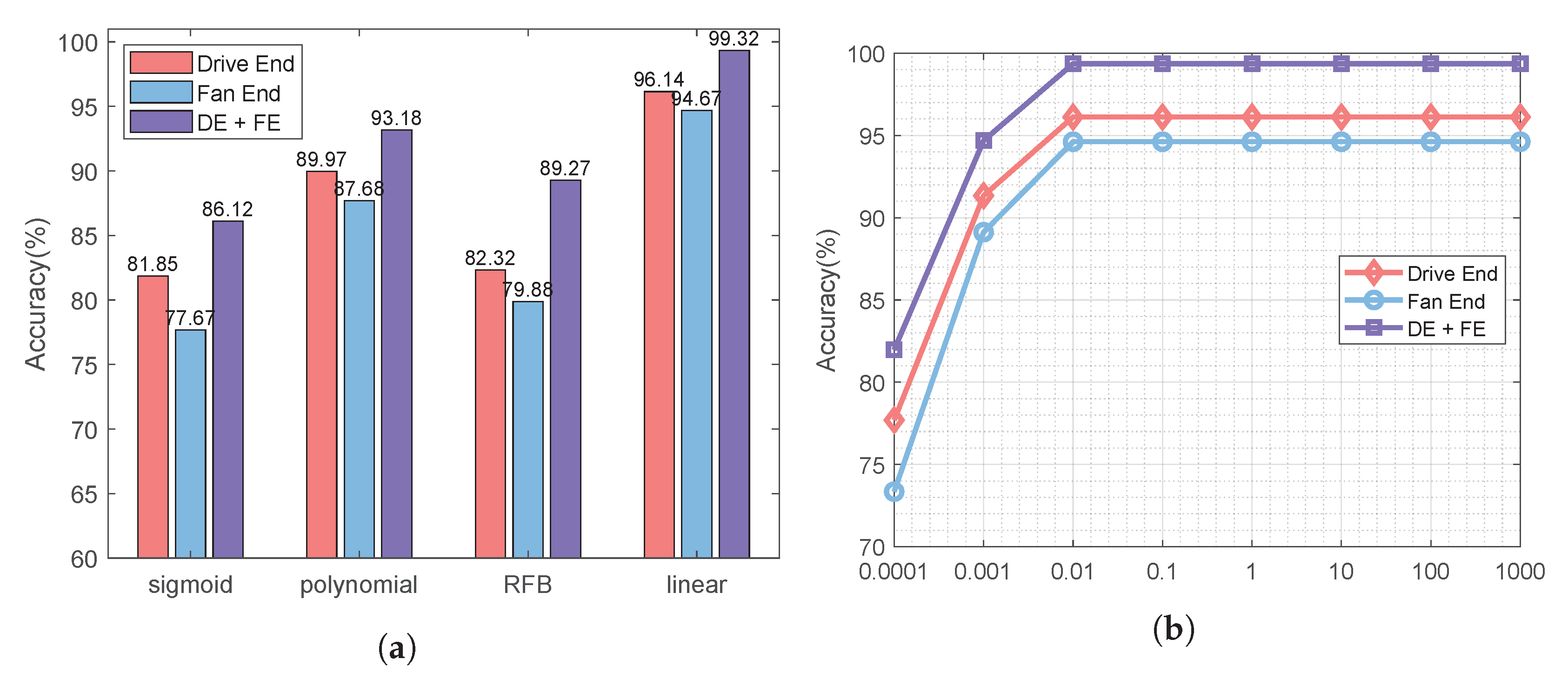
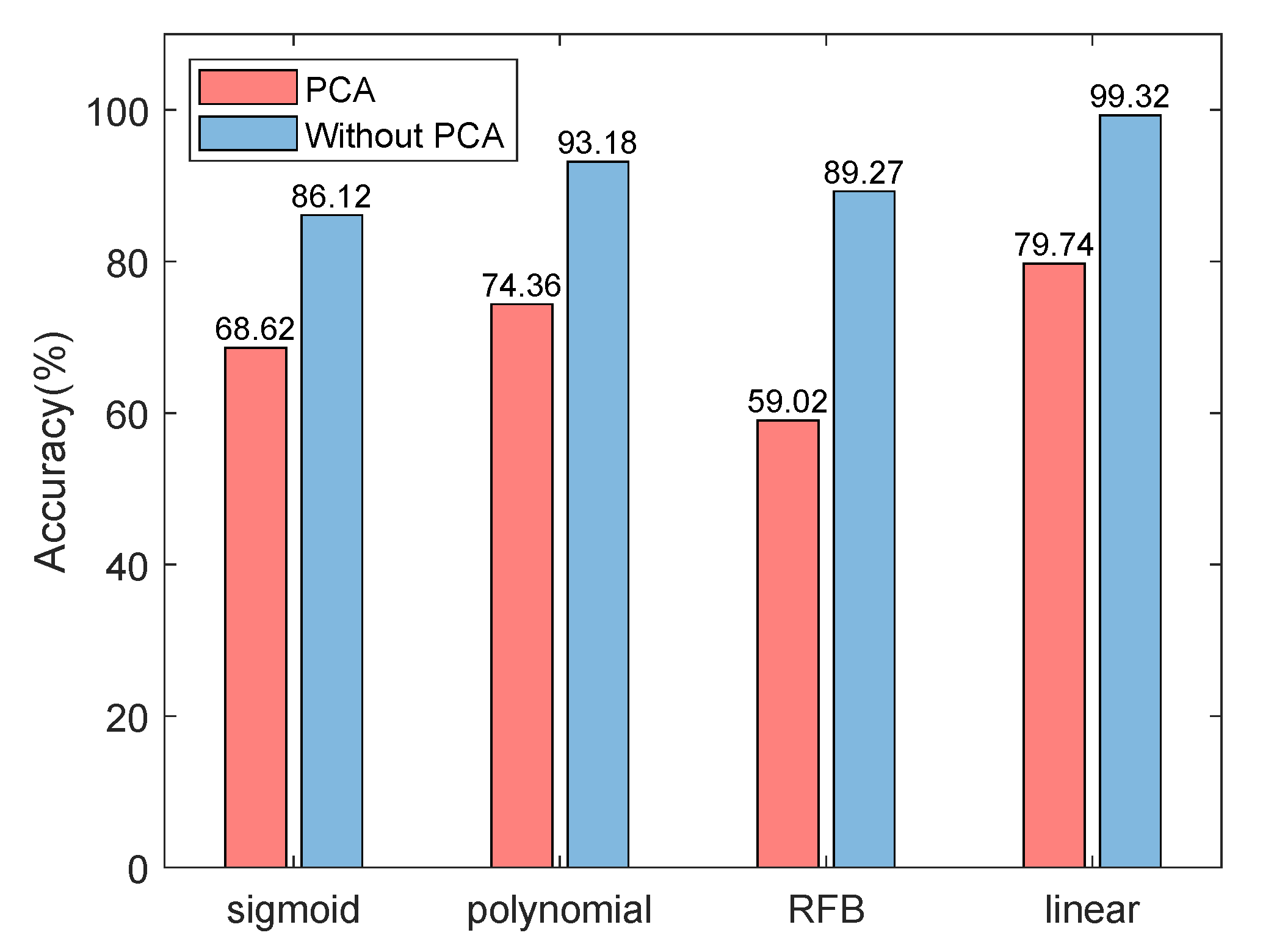
5.3. Performance Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GMA | Generalized Multiview Analysis |
| MvDA | Multi-view Discriminant Analysis |
| CWRU | Case Western Reserve University |
| CNN | Linear dichroism |
| SVM | Support Vector Machine |
| SNR | Signal-Noise Radio |
| PCA | Principal Component Analysis |
| SDIAE | Stacked Discriminat Information-based Auto-Encoder |
| VAEGAN-DRA | Variational Autoencoding Generative Adversarial Networks with Deep Regret Analysis |
| SNN | Spiking Neural Network |
| SIRCNN | Stacked Inverted Residual Convolution Neural Network |
References
- James, A.T.; Gandhi, O.; Deshmukh, S. Fault Diagnosis of Automobile Systems Using Fault Tree based on Digraph Modeling. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 494–508. [Google Scholar] [CrossRef]
- Bhakta, K.; Sikder, N.; Al Nahid, A.; Islam, M.M. Fault Diagnosis of Induction Motor Bearing Using Cepstrum-based Preprocessing and Ensemble Learning Algorithm. In Proceedings of the International Conference on Electrical, Computer and Communication Engineering (ECCE 2019), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar]
- Sohaib, M.; Kim, J.M. Data Driven Leakage Detection and Classification of a Boiler Tube. Appl. Sci. 2019, 9, 2450. [Google Scholar] [CrossRef]
- An, L.; Chen, X.; Yang, S.; Li, X. Person Re-identification by Multi-hypergraph Fusion. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2763–2774. [Google Scholar] [CrossRef]
- Sharma, A.; Kumar, A.; Daume, H.; Jacobs, D.W. Generalized Multiview Analysis: A Discriminative Latent Space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2160–2167. [Google Scholar]
- Kan, M.; Shan, S.; Zhang, H.; Lao, S.; Chen, X. Multi-view Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Hmida, F.B.; Khémiri, K.; Ragot, J.; Gossa, M. Three-stage Kalman Filter for State and Fault Estimation of Linear Stochastic Systems with Unknown Inputs. J. Frankl. Inst. 2012, 349, 2369–2388. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K.; Lee, T.H. Fault Diagnosis and Fault-tolerant Control in Linear Drives Using the Kalman Filter. IEEE Trans. Ind. Electron. 2012, 59, 4285–4292. [Google Scholar] [CrossRef]
- Shah, D.S.; Patel, V.N. A Review of Dynamic Modeling and Fault Identifications Methods for Rolling Element Bearing. Procedia Technol. 2014, 14, 447–456. [Google Scholar] [CrossRef]
- Benmoussa, S.; Bouamama, B.O.; Merzouki, R. Bond Graph Approach for Plant Fault Detection and Isolation: Application to Intelligent Autonomous Vehicle. IEEE Trans. Autom. Sci. Eng. 2013, 11, 585–593. [Google Scholar] [CrossRef]
- Jaise, J.; Ajay Kumar, N.; Shanmugam, N.S.; Sankaranarayanasamy, K.; Ramesh, T. Power System: A Reliability Assessment Using FTA. Int. J. Syst. Assur. Eng. Manag. 2013, 4, 78–85. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D. Rolling Bearing Fault Diagnostic Method based on VMD-AR Model and Random Forest Classifier. Shock Vib. 2016, 2016, 5132046. [Google Scholar] [CrossRef] [Green Version]
- Borghesani, P.; Pennacchi, P.; Randall, R.; Sawalhi, N.; Ricci, R. Application of Cepstrum Pre-whitening for the Diagnosis of Bearing Faults under Variable Speed Conditions. Mech. Syst. Signal Process. 2013, 36, 370–384. [Google Scholar] [CrossRef]
- Cocconcelli, M.; Zimroz, R.; Rubini, R.; Bartelmus, W. STFT based Approach for Ball Bearing Fault Detection in a Varying Speed Motor. In Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2012; pp. 41–50. [Google Scholar]
- Wang, X.; He, Q. Machinery Fault Signal Reconstruction Using Time-Frequency Manifold. In Engineering Asset Management-Systems, Professional Practices and Certification; Springer: Cham, Switzerland, 2015; pp. 777–787. [Google Scholar]
- Cheng, Y.; Yuan, H.; Liu, H.; Lu, C. Fault Diagnosis for Rolling Bearing based on SIFT-KPCA and SVM. Eng. Comput. 2017, 34, 53–65. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Time-frequency Analysis and Support Vector Machine in Automatic Detection of Defect from Vibration Signal of Centrifugal Pump. Measurement 2017, 108, 119–133. [Google Scholar] [CrossRef]
- Abbasi, A.R.; Mahmoudi, M.R.; Avazzadeh, Z. Diagnosis and Clustering of Power Transformer Winding Fault Types by Cross-correlation and Clustering Analysis of FRA Results. IET Gener. Transm. Distrib. 2018, 12, 4301–4309. [Google Scholar] [CrossRef]
- Kim, K.H.; Lee, H.S.; Jeong, H.M.; Kim, H.S.; Park, J.H. A Study on Fault Diagnosis of Boiler Tube Leakage based on Neural Network using Data Mining Technique in the Thermal Power Plant. Trans. Korean Inst. Electr. Eng. 2017, 66, 1445–1453. [Google Scholar]
- Zilong, Z.; Wei, Q. Intelligent Fault Diagnosis of Rolling Bearing Using One-dimensional Multi-scale Deep Convolutional Neural Network Based Health State Classification. In Proceedings of the IEEE 15th International Conference on Networking, Sensing and Control (ICNSC 2018), Zhuhai, China, 27–29 March 2018; pp. 1–6. [Google Scholar]
- Qian, W.; Li, S.; Wang, J.; An, Z.; Jiang, X. An Intelligent Fault Diagnosis Framework for Raw Vibration Signals: Adaptive Overlapping Convolutional Neural Network. Meas. Sci. Technol. 2018, 29, 095009. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Sun, C.; Chen, X. Intelligent Bearing Fault Diagnosis Using Multi-head Attention-based CNN. Procedia Manuf. 2020, 49, 112–118. [Google Scholar] [CrossRef]
- Eren, L.; Ince, T.; Kiranyaz, S. A Generic Intelligent Bearing Fault Diagnosis System Using Compact Adaptive 1D CNN Classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, H.; Wu, Z.; Li, X. Rolling Bearing Fault Diagnosis Using Variational Autoencoding Generative Adversarial Networks with Deep Regret Analysis. Measurement 2021, 168, 108371. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liu, Y.; Zhang, D.; Liang, X. A New Deep Auto-encoder Method with Fusing Discriminant Information for Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2021, 150, 107233. [Google Scholar] [CrossRef]
- Wang, L. Support Vector Machines: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 177. [Google Scholar]
- Zuo, L.; Zhang, L.; Zhang, Z.H.; Luo, X.L.; Liu, Y. A Spiking Neural Network-based Approach to Bearing Fault Diagnosis. J. Manuf. Syst. 2021, 61, 714–724. [Google Scholar] [CrossRef]
- Yao, D.; Liu, H.; Yang, J.; Li, X. A Lightweight Neural Network with Strong Robustness for Bearing Fault Diagnosis. Measurement 2020, 159, 107756. [Google Scholar] [CrossRef]
| Name of the Layers | Parameter Settings |
|---|---|
| 1. Input layer | The size of the input image is 64 × 64 × 3, and perfroming zerocenter normalization. |
| 2. Convolution layer | The number and size of convolution kernel are 8 and 5 × 5; step is [1,1]; filled as same. |
| 3. Batch processing layer | batch normalization |
| 4. Activation function layer | Relu |
| 5. Pooling layer | max pooling; size is 2 × 2; setp is [2,2]; filled as 0. |
| 6. Convolution layer | The number and size of convolution kernel are 16 and 5 × 5; step is [1,1]; filled as same. |
| 7. Batch processing layer | batch normalization |
| 8. Activation function layer | Relu |
| 9. Pooling layer | max pooling; size is 2 × 2; setp is [2,2]; filled as 0. |
| 10. Full connection layer | 4096 |
| Name of the Layers | Parameter Settings |
|---|---|
| 1. Input layer | The size of the vibration signal is 1 × 1024, and perfroming zerocenter normalization. |
| 2. Convolution layer | The number and size of convolution kernel are 8 and 1 × 1024; step is [1,1]; filled as same. |
| 3. Pooling layer | max pooling; size is 1 × 512; filled as same. |
| 4. Convolution layer | The number and size of convolution kernel are 16 and 1 × 512; step is [1,1]; filled as same. |
| 5. Pooling layer | max pooling; size is 1 × 256; filled as same. |
| 6. Full connection layer | 4096 |
| Notation | Definition |
|---|---|
| I | the number of equipment failures |
| J | the number of types of sensors |
| K | the number of samples per sensor |
| Z | the number of features extracted |
| the feature extracted from the monitoring data | |
| the power of noise | |
| the useful power of the signal | |
| o | the noise to be added to each sample |
| D | the multi-modal monitoring dataset |
| F | the projected samples |
| the within-class scatter matrix | |
| the between-class scatter matrix | |
| S | the set of sensor mapping matrix |
| block matrices | |
| the feature dimension of the j-th sensor | |
| B | the projection matrix |
| SVM | SDIAE | VAEGAN-DRA | SNN | SIGCNN | OURS | |
|---|---|---|---|---|---|---|
| Drive End | 92.64% | 97.83% | 98.17% | 98.23% | 98.93% | 99.32% |
| Fan End | 83.97% | 89.34% | 86.07% | 91.67% | 93.93% | |
| Drive End (adding noise) | 61.88% | 71.94% | 68.62% | 82.62% | 88.67% | 86.78% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, X.; Zhang, B.; Liu, C.; Gui, Z.; Yin, X. Multi-Modal Learning-Based Equipment Fault Prediction in the Internet of Things. Sensors 2022, 22, 6722. https://doi.org/10.3390/s22186722
Nan X, Zhang B, Liu C, Gui Z, Yin X. Multi-Modal Learning-Based Equipment Fault Prediction in the Internet of Things. Sensors. 2022; 22(18):6722. https://doi.org/10.3390/s22186722
Chicago/Turabian StyleNan, Xin, Bo Zhang, Changyou Liu, Zhenwen Gui, and Xiaoyan Yin. 2022. "Multi-Modal Learning-Based Equipment Fault Prediction in the Internet of Things" Sensors 22, no. 18: 6722. https://doi.org/10.3390/s22186722
APA StyleNan, X., Zhang, B., Liu, C., Gui, Z., & Yin, X. (2022). Multi-Modal Learning-Based Equipment Fault Prediction in the Internet of Things. Sensors, 22(18), 6722. https://doi.org/10.3390/s22186722






