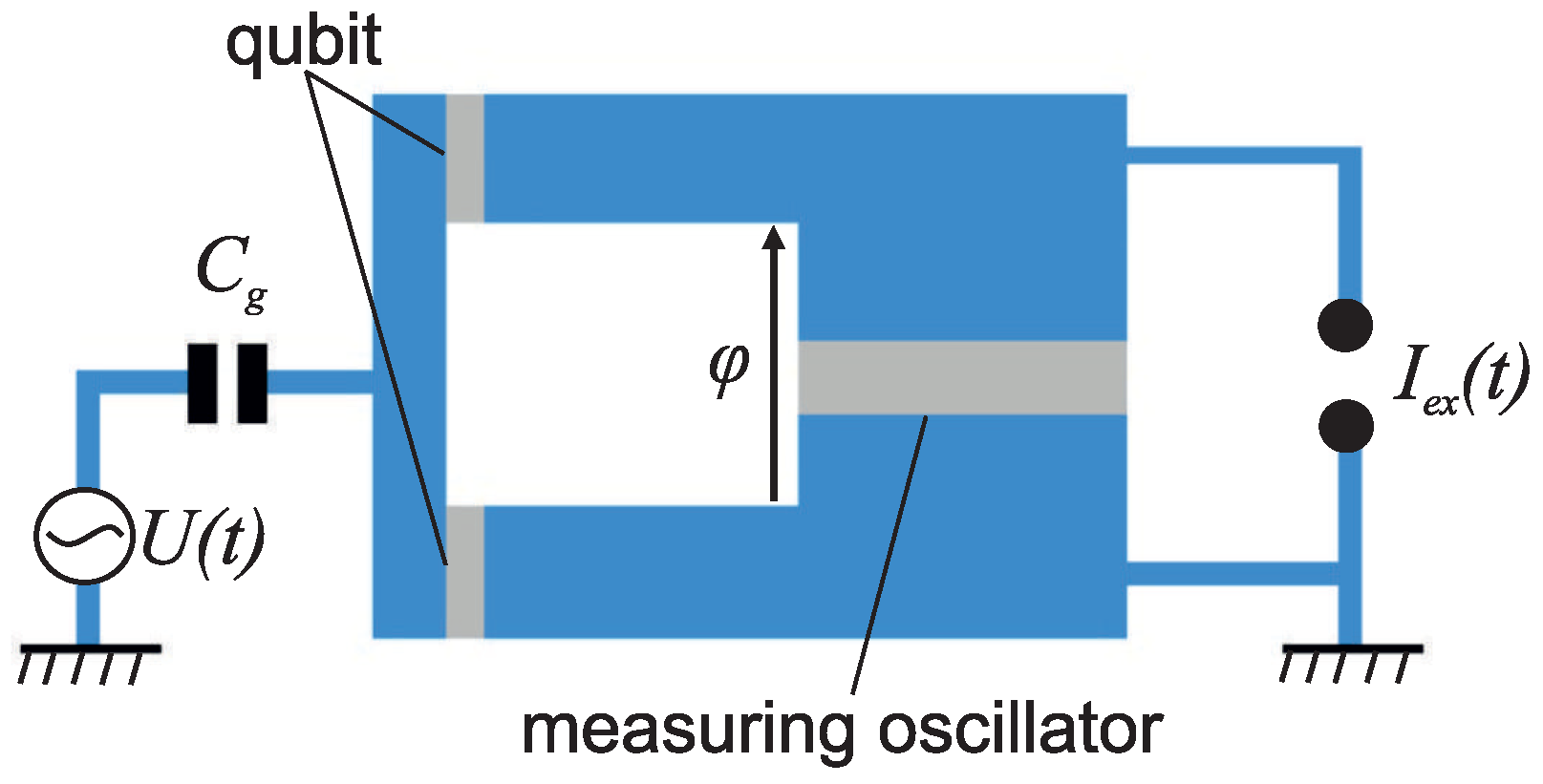
3. The Main Idea: Measuring a Qubit with a High-Q Nonlinear Oscillator
It is well known that a nonlinear oscillator (
3) driven by a periodic external current
and operating in a weak nonlinear regime can be in two dynamic equilibrium states with different amplitudes and phases [
36]. Let us briefly describe the change in the phase portrait of the oscillator during its interaction with a qubit.
In the slowly varying amplitude approximation [
38,
39], the dynamic equilibrium states correspond to stable equilibrium points on the phase plane, separated by a separatrix. In the weakly nonlinear regime, the Hamiltonian for the new slowly varying variables
(see
Appendix A) is given as
where
is the natural frequency of the measuring oscillator,
is the nonlinearity parameter and
is the driving force amplitude. For numerical calculations, we will use the parameter values close to the experimental ones [
16,
24]:
The resulting Hamiltonian (
5) is time-independent, and the corresponding quasienergy surface is shown in
Figure 2a.
L and
R symbols denote the left and right stable focuses, which are in the corresponding extrema of the quasienergy surface, and the letters
denote the saddle point characterizing the separatrix.
For a certain range of initial conditions located inside the lobes of the separatrix and under weak dissipation (large resonator quality factor
Q), the deterministic process of capture into one of the equilibrium points occurs. Another capture scenario takes place when initial conditions are given outside the separatrix. In this case, the oscillator is captured into either the
L focus or the
R focus randomly. As shown in [
39], the capture probability is determined by the area that sweeps out by the separatrix in phase space around the region that corresponds to the considered equilibrium point. The result obtained is described by the well-known Arnold formula [
40]:
where
and
are the areas of the separatrix lobes. As can be seen from (
7), the capture probability does not depend on specific initial conditions outside the separatrix.
The idea of the proposed measurement method: the coupling of the measuring nonlinear oscillator with the qubit induces a dependence of the capture probability into one of the equilibrium points (for example, in the right one–) on the qubit state. Since the two stable oscillations of the measuring oscillator differ from each other in phase, the probabilities and can be measured experimentally.
Note that the phase difference for two stable oscillations in a measuring circuit has recently been widely used for dispersive quantum measurements [
13,
17,
22,
23,
24], where the switching probability between the two stable processes is measured, rather than the capture probability. These methods show the highest discrimination power in the case when one of the stable oscillations disappears at the operating value of the amplitude
f and the frequency
of the external force for one qubit basis state. However, in the range of parameters, when there are two stable oscillations for both qubit basis states, the discrimination power of the measuring oscillator with high quality factor (several hundreds) will be extremely low. The method proposed in this paper makes it possible to carry out dispersive measurements of qubits in this parameters range, refusing to scan by the amplitude of the drive current.
To begin with, we will assume that when the control field
the qubit may be in one of the basis states with quantum number
(which is determined by the eigenvalue of the Pauli matrix
). Then the oscillator Hamiltonian reduces to two independent Hamiltonians
corresponding to the ground
and the excited
qubit states (“pseudospin” polarization), which are obtained from Equation (
5) by replacing
and
. Since the qubit state affects the natural frequency and the nonlinearity of the measuring oscillator, it also changes the separatrix in phase space, as shown in
Figure 2b. The stable oscillations of the nonlinear oscillator in the slowly varying amplitude approximation, corresponding to the points
L and
R in
Figure 2a, can be characterized by the amplitude
A and the phase
, which are found for different polarization as
, where
and
correspond to the coordinates of
L or
R equilibrium points in
Figure 2a for each qubit basis state. The oscillation phase for the left equilibrium point is
, for the right equilibrium point is
.
Figure 2c,d shows the dependences of the amplitudes and phases of stable oscillations of the measuring oscillator on the external force frequency at the quality factor of
, from which the operating frequency range is clearly visible.
Due to the fact that the proposed measurement method is based on measuring the phase difference of various stable oscillations of the measuring oscillator
(see
Figure 2d), it is necessary that such a difference be much larger than the phase perturbation
introduced due to the different qubit states (
).
Figure 3a shows that such a condition is not satisfied at a low Q-factor in the parameters range considered. In addition, we note that when measuring the results of quantum single-qubit operations, it is necessary to carry out multiple measurements and collect statistics (capture probabilities) to achieve the required precision. To estimate the number of single measurements, we analyzed the influence of the control current parameters on the efficiency,
, of separating qubit states with different quantum number
. Each qubit basis state will be characterized by the capture probability of the measuring oscillator into one of the equilibrium points (for example, into the right one)
. Then the separation efficiency can be defined as
.
Figure 3b shows the dependence of this quantity on various parameters of the drive current of the measuring oscillator. It can be seen that for any frequency
, there is an optimal amplitude
f. Based on the analysis of
Figure 3b, the optimal parameters of the drive current (
6) were chosen.
We stress again, that the key element in the proposed measurement method is the passage of the separatrix in phase space by the system. This is equivalent to the passage of separatrix energy on the quasi-energy surface (
Figure 2a). Near this energy the quasi-classical description is broken [
41], and the temperature is assumed to be sufficiently low
K; therefore, a quantum description of the system is necessary. In terms of the creation and, annihilation operators for the measuring oscillator, and for the time when the control field has already been turned off,
, the Hamiltonian of the system can be written as [
16]
with the commutation relation
.
In the rotating wave approximation (
Appendix A), the system Hamiltonian becomes time-independent:
The quasistationary states
of the system are determined by the equation:
As in the classical case for
in the Equation (
9), there are formally two subsystems corresponding to two qubit states. These subsystems evolve independently and are characterized by different Hamiltonians
:
Then instead of (
10) we can write:
The Hilbert space of two-component basis functions splits into two independent subspaces with bases and , respectively. These basis functions can be easily found by numerical methods.
The case
was investigated in [
39], where dissipation was taken into account and it was shown that for a quantum system with two attractors (which can be considered as an analogue of potential wells), the quantum Arnold formula for the capture probabilities in the attractors can be obtained. In the semiclassical approximation, the generalized formula follows from the Bohr-Sommerfeld quantization condition, according to which the area swept by the trajectory of a particle moving in a potential well is proportional to the number of levels in the well. When the number of levels near the separatrix energy is much less than the number of levels related to the left or right equilibrium points, we can get a simple analogy that the ratio between the areas of separatrix lobes in (
7) is determined by the number of levels.
It can be seen from (
9) and (
11), that the interaction (
) of the oscillator with the qubit leads to the splitting of the levels into two series corresponding to different polarizations of the qubit. At the same time, the probability of capture into series of doubling attractors will also depend on the polarization of the qubit. It means that the Josephson oscillator can operate as a sensor of quantum systems. In the next section, the selective characteristics of the proposed sensor will be analyzed in more detail.
4. The Measurement Procedure for Superpositions of Basis Qubit States
Here we consider the dynamics of the qubit coupled with the measuring nonlinear oscillator, paying special attention to its potential as a sensor for measuring superposition states of the qubit. We take into consideration the measuring oscillator dynamics in mesoscopic (quantum) mode of operation in order to minimize back action (the influence of the sensor on the qubit states).
Our original scheme, see
Figure 4, for measuring qubit states has three stages: (1) qubit state initialization based on microwave technique; (2) preparation of the sensor state (output outside the separatrix); (3) readout of qubit states by the nonlinear oscillator. In the following, we will discuss each stage in detail.
Qubit state preparation. At the initial moment,
, we believe that the system of “qubit + nonlinear sensor” is initialized near their ground states (
Figure 4a). The state of the this system is factorized
, where
is the initial state of the measuring oscillator, and
=
is the initial qubit state. Then the process of preparation (recording) is carried out qubit states using the control field
, see the diagram in
Figure 4b. Neglecting the relaxation processes during qubit preparation, the evolution of the system (
8) can be found by solving the nonstationary Schrödinger equation.
Since the qubit continuously interacts with the measuring oscillator, it is necessary to analyze the influence of this interaction on the qubit (back action effect). To do this, we define the fidelity,
F, of preparing qubit states by the Rabi pulse, according to [
42]:
where
is the reduced density operator for the qubit subsystem at the end of the Rabi pulse at the initial state of the qubit
, and
is the density matrix of the qubit after the pulse, but without taking into account the connection with the oscillator
. The summation in (
13) occurs over the six initial states of the qubit
:
,
,
and
. It is obvious that the fidelity,
F, depends not only on the parameters of the qubit control field, but also on the initial state of the measuring oscillator due to the connection of subsystems, which inevitably gives rise to entanglement of their states.
The von Neumann entropy (an entanglement measure of subsystems) was calculated:
where
. Note that the entanglement of the system is determined only by the length of the Bloch vector
[
43].
Figure 5 shows the results of the numerical calculation of the infidelity
and the von Neumann entropy
S for different the
-pulse amplitude and initial states of the measuring oscillator averaged over the Pauli eigenstates. It can be seen from the analysis of this figure that the infidelity,
, decreases with increasing
-pulse amplitude
. This can be explained by the fact that the duration of the
-pulse decreases with increasing amplitude
, and, consequently, the interaction time of the qubit with the measuring oscillator also decreases. However, we are limited by the range of operating control pulse amplitudes, for which we can neglect leakage since the quantum system leaves the two-level qubit subspace. Note also that in
Figure 5a there is a clear local minimum near the value
; at this pulse amplitude the Rabi frequency is equal to the natural measuring oscillator frequency. Qualitatively similar behavior was also observed for the von Neumann entropy.
Another important result is that
and
S grow with an increase in the occupation number of the initial state of the measuring oscillator, see series of curves in
Figure 5. Therefore that effective control (with minimal back action effect) of the qubit by pulses is possible only when the measuring oscillator is in a superposition of states with a small value of the occupation number
n. Note that the acceptable fidelity of performing single qubit operations (
) at the optimal amplitude
is achieved for the measuring oscillator initial states, at which
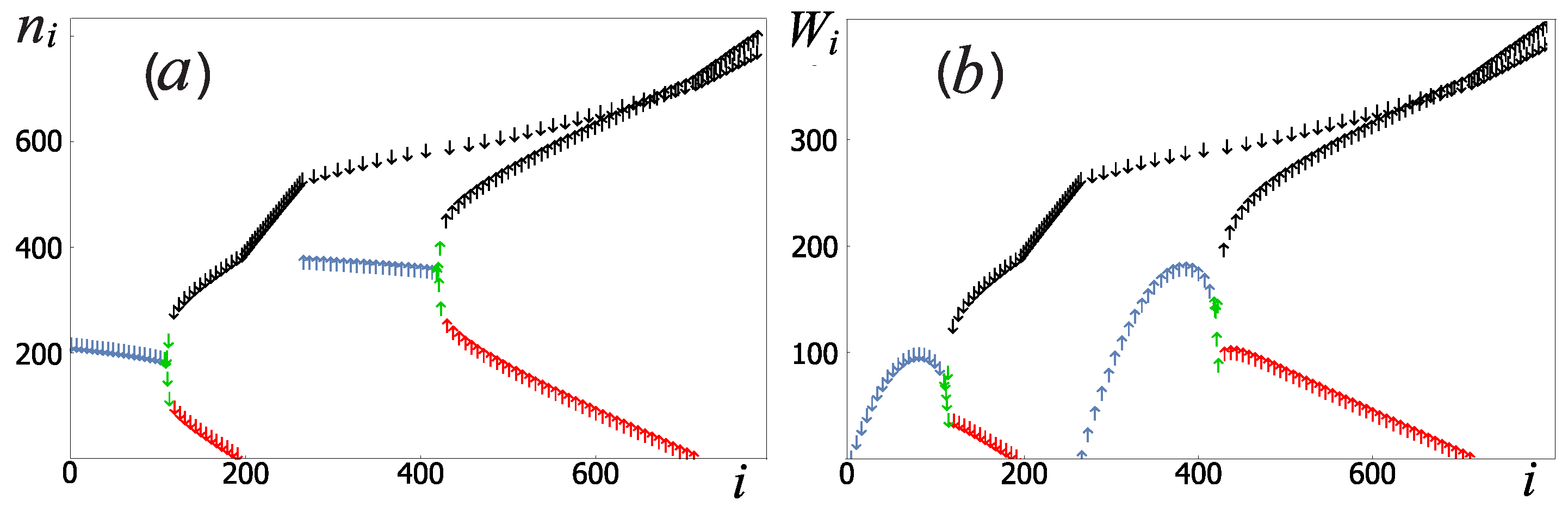
. Analyzing the average occupation number of the measuring oscillator for each system level number, see
Figure 6a, one can see that the necessary oscillator states (
) are close to the level corresponding to the right equilibrium point for each qubit basis state (red color in
Figure 6a). The initialization of the measuring oscillator to these levels can be realized, for example, by adiabatically slow switching on of the drive current, since at
there is only the right equilibrium point. In the classics, this case corresponds to the fact that the area
in the Formula (
7), related to the left equilibrium point, vanishes.
Preparation of the sensor state. After the qubit preparation, it is necessary to excite the oscillator to levels corresponding to the classical region outside the separatrix (indicated in black in
Figure 6a). A schematic representation of this process is shown on the
Figure 4c. One way of such excitation is to use an additional short modulating pulse with a carrier frequency
equal to the frequency of the drive current [
44]. The total external current will be written as
, where
. This pulse does not change the expectation value
of the qubit, since at this stage the action of the qubit control pulse ended
, and
. The sequence of applying signals to the qubit and the sensor is shown in
Figure 7a. Note that in the classical consideration, the process of capturing the measuring oscillator into one of the equilibrium points is considered to be completed immediately after the system enters the region in the phase space inside the separatrix. In this case, the process of transition between the regions of the separatrix belonging to different equilibrium points is impossible. In the quantum case, levels that are close to the energy corresponding to the classical separatrix cannot be strictly assigned to one of the equilibrium points due to the tunneling effect [
39], but as one moves away from the separatrix energy, some levels are more and more localized near the classical equilibrium points. If there are sufficiently many such levels, then for levels that are far from the separatrix energy, the tunneling effect becomes negligible. Due to this, in the process of relaxation, transitions between groups of levels related to different equilibrium points can be neglected.
Figure 7b–d shows the results of numerical simulation of the qubit initialization by a
-pulse and excitation of the measuring oscillator by the modulated current pulse
. At the initial time,
Figure 7b, the system was in the state
, where the oscillator wave function
corresponds to the right equilibrium point with a small average occupation number (red color in
Figure 6a). Usually, in order to create a superposition state of a qubit, they tend to reduce the impact of the measuring device on the qubit during the recording process. In our case, this would be possible if the qubit-oscillator coupling parameter
. In this case, the wave function of the entire system can be factorized, and the qubit wave function takes the form:
, where the amplitudes depend on the Rabi-frequency and pulse duration. As is well known, the complex parameters
and
determine the angles that define the orientation of the vector
on the Bloch sphere. The probability that the z-projection of vector
has a positive value (in other words, the population of the lower level) is equal to
, the negative projection and the population of the upper level are equal
.
If there is a coupling between the qubit and the oscillator,
, after the end of the
-pulse at the time
,
Figure 7c, the system is in the superposition state, which already consists of the group of levels belonging to the right equilibrium point for different qubit basis states (two narrow red peaks in
Figure 7c). The subsequent excitation of the measuring oscillator leads to the fact that the system at the time
(see
Figure 7d) is in the superposition of levels corresponding to the classical region on the phase space outside the separatrix with different qubit basis states
, which corresponds to the black arrows in
Figure 6a and
Figure 7b–d. For the chosen typical parameters (
6), the initialization time of the coupled system (qubit+sensor) is
ns.
Readout of qubit states by the nonlinear oscillator. Further, we assume that the process of qubit preparation and excitation of the measuring oscillator has ended by the time
, then the general wave function is obtained as
Since the proposed method is based on measuring the capture probability of the oscillator by the groups of red and blue levels during process of dissipation (see
Figure 4d), it is necessary to take into account the connection with the environment. We find it convenient to work in the quasi-stationary basis (
10). In the case when transition rates between different levels of the system are much bigger than relaxation rates, the secular approximation is valid and we can average all rapidly oscillating terms. Note that for this approximation, off-diagonal elements do not affect the evolution of diagonal elements [
45]. This makes it possible to pass to the dissipation model based on the master Equation (
A10), see
Appendix B. The diagonal part of the system density matrix is given by
where
and
. The probability of finding the qubit in the ground state is defined as
, where the summation occurs over all levels
j of the oscillator, and the probability of finding the qubit in the excited state is
, and there is the normalization condition:
The capture probabilities of the measuring oscillator into dynamic equilibrium positions
and
correspond to the probabilities of the system being at the blue and red levels, respectively, in
Figure 6a. Before reaching these groups of levels, the system from the prepared state (
Figure 7d) dissipates and inevitably passes through levels lying near the separatrix energy (
Figure 4d). Then, similarly to the classical case, the probability of being captured in the process of relaxation into one of the equilibrium positions does not depend on the particular prepared state [
39]. It is important that the probability of leaving the level
i per unit time
is maximum for levels outside the separatrix energy (black arrows in
Figure 6b). In this case, the value of
decreases as it approaches the level corresponding to the classical equilibrium point (red arrows in
Figure 6b). Due to this, the high relaxation rate outside the separatrix energy levels allows us to approximately find the characteristic measurement time of the qubit state as
, where
is the number of any level near the separatrix (shown in green in
Figure 6b). In the case when the qubit energy relaxation time
is much longer than the measurement process time (
), transitions between levels with different qubit states can be considered impossible, then the system of differential Equation (
A10) splits into two independent subsystems:
where in Equation (
18) the summation occurs only over levels with the qubit state
, and in Equation (
19)–over levels with the qubit state
. Since the ratio of the capture probabilities into the left and right equilibrium points with the same qubit polarization does not depend on the values of
and
, the capture probability of the measuring oscillator into the right equilibrium point for the prepared qubit state is
where
is the capture probability of the measuring oscillator into the right equilibrium point with the qubit initialized to the ground state,
– to the excited state. Using Equations (
17) and (
20) we can get the desired probability of finding the qubit in the ground state:
Thus, by measuring the
value of the Josephson oscillator, it becomes possible to measure the qubit populations in the prepared state. In this case, the values
and
can be determined during the calibration of the measuring oscillator for various states of the qubit with the quantum number
. To determine the capture probability of the oscillator into the right equilibrium point
, it is necessary, as in the experiments [
14,
16,
17,
23], to measure the phase difference between the reflected and the applied signal
. The frequentist probability of this phase difference corresponding to
R branches in
Figure 2d will determine the desired probability
. Note that the proposed method does not require changes in the experimental technique.
Figure 8 shows the simulation of the measurement process at
, as a result of which the system (
Figure 7d) dissipates due to the connection with the bosonic thermostat, passing into a mixed state consisting of groups of levels belonging to different levels of the measuring oscillator and with different qubit states.
Figure 8a–c shows the population probabilities of the system levels
at different times, which were obtained by numerically solving (
A10). In numerical calculations,
is used as the unit of time. As can be seen from
Figure 8a–c, in the process of evolution, a redistribution takes place among the levels in the system. After passing through the group of levels corresponding to the separatrix energy (marked in green), the qubit states are separated (in the time
∼
). Since the probabilities
and
will not change during the further evolution of the system even if the coherence of the qubit states is broken, the measuring oscillator can function as a memory device. Note that the different positions of the Lorentzian peaks in
Figure 8c are related to the level numbering; in the coordinate representation, the centers of these peaks will be close to each other due to the small coupling coefficient of qubit and oscillator [
33]. Using the value of the quality factor of the measuring oscillator Q, one can obtain an estimate of the measurement time
∼
, which gives
∼100 ns for Q∼100, according to [
46]. Therefore, we get that the system initialization process (qubit and measuring oscillator) and the measurement process is
∼150 ns, which according to [
2] is much less than typical relaxation and dephasing times in the systems we are studying.
To determine the probability of the
capturing, it is necessary to sum the probabilities
of the entire group of levels (red arrows in
Figure 8a–c) at time
related to the right equilibrium point for different qubit states.
Figure 8d shows the dependence of
on time for various pulses. It can be seen that this capture probability reaches a constant value after the system passes through a group of levels lying near the separatrix energy in the process of relaxation. It follows from the analysis that using the proposed scheme of the initialization (
Figure 7) and the measurement (
Figure 8a–c), according to (
21) it is possible to determine the probabilities of finding the qubit in the basic states. Neglecting the back action, the
value, in substance, determines the distance indicated by the gray arrow in
Figure 8d. So, for example, for the
-pulse with the chosen parameters of the systems, we found that the probability of finding the qubit in the ground state is
. The difference of this probability from
is due to the influence of the measuring oscillator on the qubit during initialization (back action effect), when the states of the subsystems were being entangled.