Research on Nonlinear Compensation of the MEMS Gyroscope under Tiny Angular Velocity
Abstract
:1. Introduction
- The traditional compensation method: Refers to the IEEE standard format guide [16,17], where the relationship between the input and output angular velocity of the MEMS gyroscope is established, and the optimal relationship is found by polynomial fitting [18,19,20], so as to realize the nonlinear error compensation. However, the performance of polynomial fitting depends on the accuracy of the compensation model and the repeatability of the system output, which is not universal.
- Virtual Coriolis force-based nonlinear compensation method: With a specific resonator structure (force rebalance comb), the MEMS gyroscope outputs an equivalent angular velocity signal by applying an electrical excitation signal and then compensates for the nonlinearity of the MEMS gyroscope according to the output [21,22]. However, the additional vibration introduced by the virtual Coriolis force method, which is coupled to the gyroscope sensitive end, results in additional nonlinear errors.
- Artificial intelligence algorithm: The output model of the MEMS gyroscope was established by using fuzzy logic [23] and neural networks [24]. When the input angular velocity is −60°/s to 60°/s and the interval is 3°/s, the nonlinear error of the MEMS gyroscope is about 140 ppm. However, artificial intelligence algorithms require a large number of samples to train.
- In-run compensation method: The sources of MEMS gyroscope nonlinear error were investigated, and a nonlinear error correction method that does not require system calibration or data fitting was proposed, which can be applied to resonant gyroscopes in amplitude-modulated (AM) mode in general [25,26]. When the input angular velocity is ±0.1°/s, ±0.2°/s, ±0.5°/s, ±1°/s, and ±2°/s, the compensation method is verified.
2. The Output Model of the MEMS Gyroscope under Tiny Angular Velocity
2.1. Nonlinear Analysis of the MEMS Gyroscope
2.2. Establishment of MEMS Gyroscope Output Model
3. Compensation Method
3.1. The Traditional Polynomial Compensation Method
3.2. The Adaptive Fourier Series Compensation Method (AFCM)
4. Experiments and Results
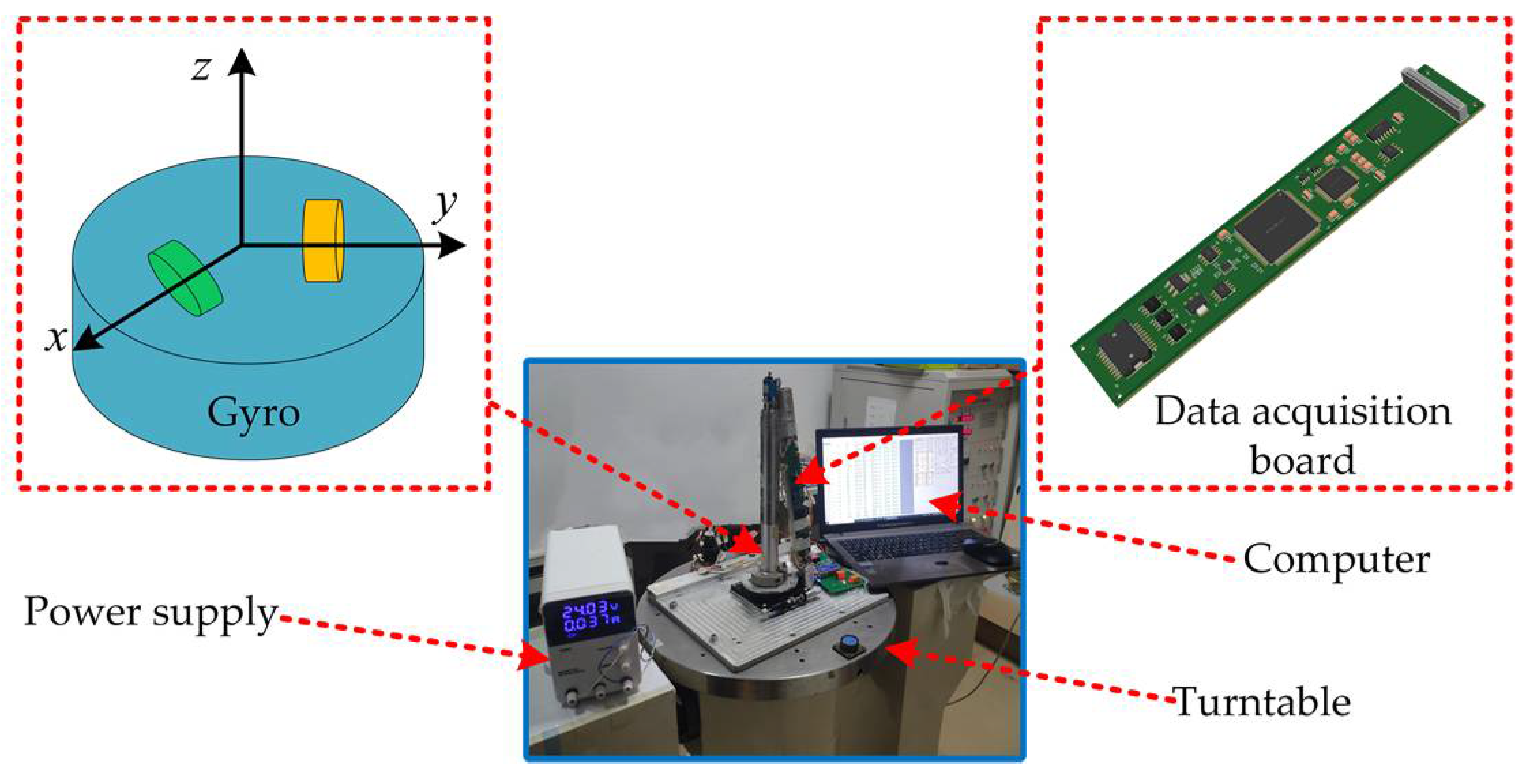
4.1. Experiment Setup
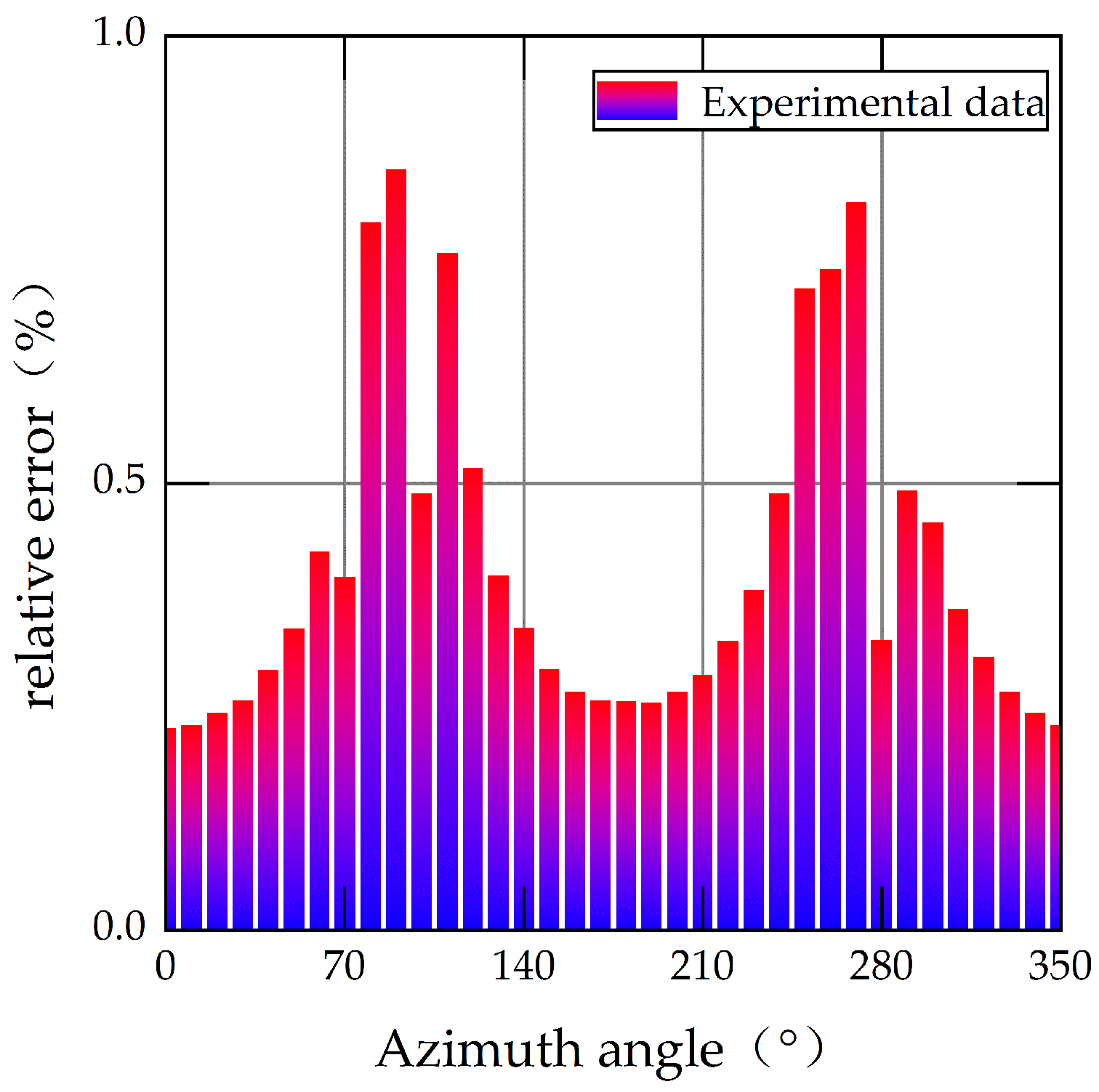
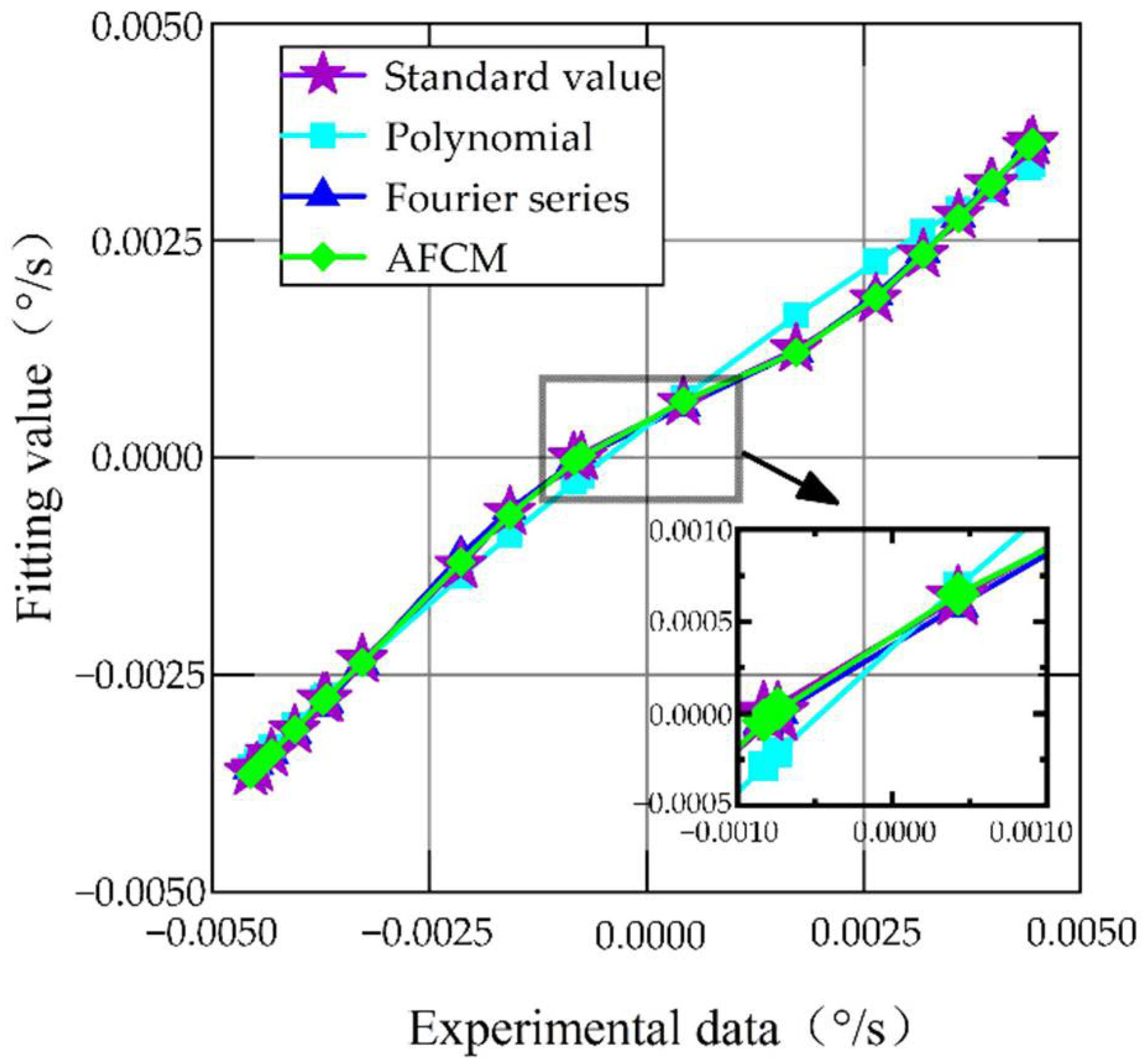
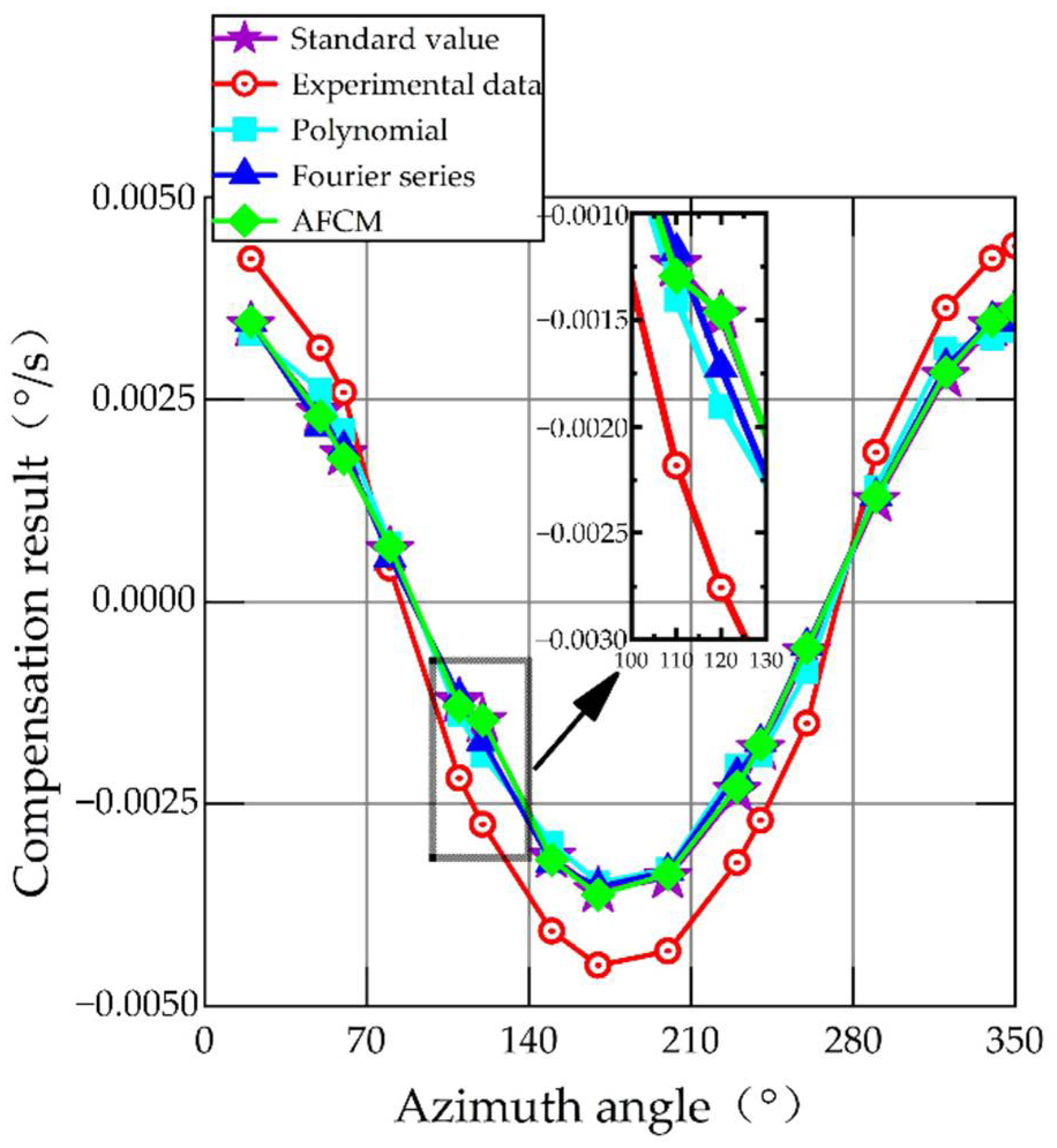
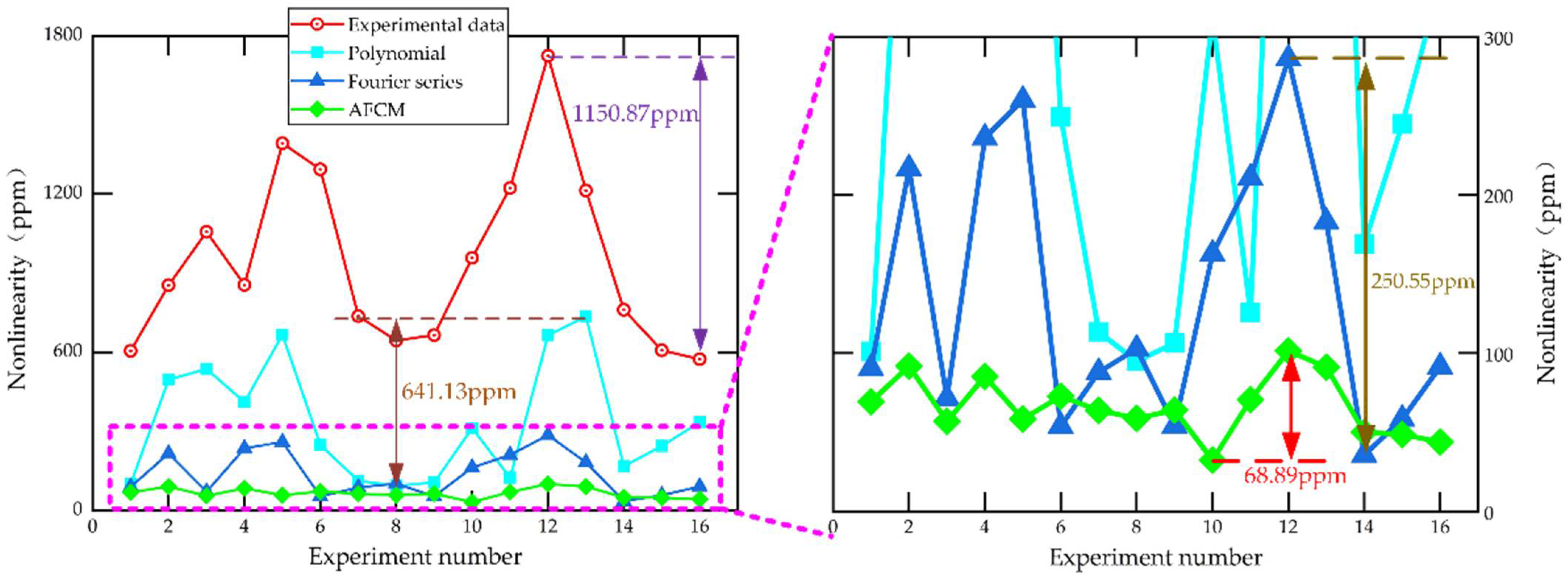
4.2. Analysis of Compensation Results for MEMS Gyroscope
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carratu, M.; Dello Iacono, S.; Hoang, M.L.; Pietrosanto, A. Energy characterization of attitude algorithms. In Proceedings of the 17th IEEE International Conference on Industrial Informatics, INDIN19 Proceedings, Helsinki-Espoo, Finland, 22–25 July 2019; pp. 1585–1590. [Google Scholar]
- Li, Y.; Georgy, J.; Niu, X.; Li, Q.; El-Sheimy, N. Autonomous Calibration of MEMS Gyros in Consumer Portable Devices. IEEE Sens. J. 2015, 15, 4062–4072. [Google Scholar] [CrossRef]
- Feng, R.; Bahari, J.; Jones, J.D.; Leung, A.M. MEMS thermal gyroscope with self-compensation of the linear acceleration effect. Sens. Actuators A Phys. 2013, 203, 413–420. [Google Scholar] [CrossRef]
- Zhang, B.; Chu, H.; Sun, T.; Guo, L. Thermal calibration of a tri-axial MEMS gyroscope based on Parameter-Interpolation method. Sens. Actuators A Phys. 2017, 261, 103–116. [Google Scholar] [CrossRef]
- El-Diasty, M.; El-Rabbany, A.; Pagiatakis, S. Temperature variation effects on stochastic characteristics for low-cost MEMS-based inertial sensor error. Meas. Sci. Technol. 2007, 18, 3321–3328. [Google Scholar] [CrossRef]
- Quinchia, A.G.; Falco, G.; Falletti, E.; Dovis, F.; Ferrer, C. A Comparison between Different Error Modeling of MEMS Applied to GPS/INS Integrated Systems. Sensors 2013, 13, 9549–9588. [Google Scholar] [CrossRef]
- Su, W.P.; Hao, Y.S.; Li, Q.C. ARMA-AKF Model of MEMS Gyro Rotation Data Random Drift compensation. Appl. Mech. Mater. 2013, 321, 549–552. [Google Scholar] [CrossRef]
- Gao, D.Y.; Li, A.; Fu, J.; Zhang, R.C. A MEMS random error analysis method fused with genetic algorithm. Proc. SPIE. 2018, 10835, 1083510. [Google Scholar]
- IEEE Std 1431-2004; IEEE Standard Specifification Format Guide and Test Procedure for Coriolis Vibratory Gyros. IEEE: Piscataway, NJ, USA, 2004; pp. 1–78.
- Zhang, P.; Zhan, X.; Zhang, X.; Zheng, L. Error characteristics analysis and calibration testing for MEMS IMU gyroscope. Aerosp. Syst. 2019, 2, 97–104. [Google Scholar] [CrossRef]
- Luo, J.; Wang, Z.; Shen, C.; Kuijper, A.; Wen, Z.; Liu, S. Modeling and Implementation of Multi-Position Non-Continuous Rotation Gyroscope North Finder. Sensors 2016, 16, 1513. [Google Scholar] [CrossRef]
- Huttner, F.; Kalkkuhl, J.; Reger, J. Offset and Misalignment Estimation for the Online Calibration of an MEMS-IMU Using FIR-Filter Modulating Functions. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 1427–1433. [Google Scholar]
- Jia, Y.; Li, S.; Qin, Y.; Cheng, R. Error Analysis and Compensation of MEMS Rotation Modulation Inertial Navigation System. IEEE Sens. J. 2018, 18, 2023–2030. [Google Scholar] [CrossRef]
- Aydemir, A.G.; Saranlı, A. Characterization and calibration of MEMS inertial sensors for state and parameter estimation applications. Measurement 2012, 45, 1210–1225. [Google Scholar] [CrossRef]
- Hu, Z.; Gallacher, B.J. Effects of Nonlinearity on the Angular Drift Error of an Electrostatic MEMS Rate Integrating Gyroscope. IEEE Sens. J. 2019, 19, 10271–10280. [Google Scholar] [CrossRef]
- IEEE Std 529-1980; Supplement for Strapdown Applications to IEEE Standard Specification Format Guide and Test Procedure for Single-Degree-of-Freedom Rate-Integrating Gyros. IEEE: Piscataway, NJ, USA, 1981; pp. 1–24.
- IEEE Std 647-2006 (Revision of IEEE Std 647-1995); IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros. IEEE: Piscataway, NJ, USA, 2006; pp. 1–96.
- Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Compensation of drifts in high -Q MEMS gyroscopes using temperature self-sensing. Sens. Actuators A: Phys. 2013, 201, 517–524. [Google Scholar] [CrossRef]
- Liu, C.Z.; Wang, X.J.; Tang, Q.J. Error analysis and compensation research of scale factor for MEMS gyroscope. Proc. SPIE. 2014, 9301, 93010R. [Google Scholar]
- Yang, H.; Zhou, B.; Wang, L.; Xing, H.; Zhang, R. A novel tri-axial MEMS gyroscope calibration method over a full temperature range. Sensors 2018, 18, 3004. [Google Scholar] [CrossRef]
- Zhang, J.M.; He, C.H.; Liu, Y.X.; Liu, D.C.; Zhao, Q.C.; Yang, Z.C.; Yan, G.Z. A novel scale factor calibration method for a MEMS gyroscope based on virtual coriolis force. In Proceedings of the 10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Xi’an, China, 7–11 April 2015; pp. 58–62. [Google Scholar]
- Wang, M.; Cao, H.L.; Shen, C.; Chai, J. A novel self-calibration method and experiment of MEMS gyroscope based on virtual coriolis force. Micromachines 2018, 9, 328. [Google Scholar] [CrossRef]
- Li, J.L.; Du, M.; Fang, J.C. Fuzzy modeling and compensation of scale factor for MEMS gyroscope. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Changsha, China, 18–20 December 2010; Volume 1, pp. 766–771. [Google Scholar]
- Zhu, C.H.; Cai, S.; Yang, Y.F.; Xu, W.; Shen, H.H.; Chu, H.R. A Combined Method for MEMS Gyroscope Error Compensation Using a Long Short-Term Memory Network and Kalman Filter in Random Vibration Environments. Sensors 2021, 21, 1181. [Google Scholar] [CrossRef]
- Norouzpour-Shirazi, A.; Ayazi, F. A dual-mode actuation and sensing scheme for in-run calibration of bias and scale factor errors in axisymmetric resonant gyroscopes. IEEE Sens. J. 2018, 18, 1993–2005. [Google Scholar] [CrossRef]
- Jia, J.; Ding, X.K.; Qin, Z.C.; Ruan, Z.H.; Li, H.S. In-Run Scale Factor Compensation for MEMS Gyroscope Without Calibration and Fitting. IEEE Sensors J. 2021, 21, 7316–7325. [Google Scholar] [CrossRef]
- Casinovi, G.; Norouzpour-Shirazi, A.; Dalal, M.; Ayazi, F. Gyroscope sensing and self-calibration architecture based on signal phase shift. Sens. Actuators A Phys. 2016, 241, 1–11. [Google Scholar] [CrossRef]
- Leland, R.P. Mechanical-thermal noise in MEMS gyroscopes. IEEE Sens. J. 2005, 5, 493–500. [Google Scholar] [CrossRef]
- Ding, X.; Jia, J.; Gao, Y.; Li, H. Mechanical and electrical noise in sense channel of MEMS vibratory gyroscopes. Sensors 2017, 17, 2306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohd-Yasin, F.; Nagel, D.J.; Korman, C.E. Noise in MEMS. Meas. Sci. Technol. 2010, 21, 012001. [Google Scholar] [CrossRef]
- Nan, C.Z.; Zhou, J.H.; Chen, W.Y. The application of adaptive theory in MEMS gyro error compensation. Proc. SPIE. 2018, 10847, 108470G. [Google Scholar]
- Zhang, Y.S.; Yang, T. Modeling and compensation of MEMS gyroscope output data based on support vector machine. Measurement 2012, 45, 922–926. [Google Scholar] [CrossRef]
- Lu, J.Z.; Liang, S.F.; Yang, Y.Q. A novel method of calibrating a MEMS inertial reference unit on a turntable under limited working conditions. Meas. Sci. Technol. 2017, 28, 105018. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, B.; Song, M.; Hou, B.; Xing, H.; Zhang, R. A Novel MEMS Gyro North Finder Design Based on the Rotation Modulation Technique. Sensors 2017, 17, 973. [Google Scholar] [CrossRef]
- Fontanella, R.; Accardo, D.; Lo Moriello, R.S. MEMS gyros temperature calibration through artifificial neural networks. Sens. A Phys. 2018, 279, 553–565. [Google Scholar] [CrossRef]
- Guo, X.; Sun, C.; Wang, P.; Huang, L. A hybrid method for MEMS gyroscope signal error compensation. Sens. Rev. 2018, 38, 517–525. [Google Scholar] [CrossRef]
- Araghi, G.; Landry, R.J. Temperature compensation model of MEMS inertial sensors based on neural network. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 301–309. [Google Scholar]




| Working Temperature | Supply Voltage | Working Current | Bandwidth |
| −40 °C~+150 °C | 5 V ± 0.1 V (DC) | ≤300 mA | ≥12 Hz |
| Measuring Range | Zero-Bias Stability | Bias Repeatability | Resolution |
| ±100° | ≤0.3°/h | ≤0.5°/h | ≤0.1°/h |
| Azimuth Angle (°) | Raw Data (°/s) | Polynomial (°/s) | Fourier Series (°/s) | AFCM (°/s) |
|---|---|---|---|---|
| 20 | 0.000826439 | −6.89415 × 10−5 | 6.1758 × 10−5 | 4.72656 × 10−5 |
| 50 | 0.000798303 | 0.000231583 | −0.000101278 | −4.28319 × 10−5 |
| 60 | 0.00076815 | 0.000194944 | 2.59435 × 10−5 | −2.06786 × 10−5 |
| 80 | −0.000215985 | 5.19142 × 10−5 | −2.97954 × 10−5 | 1.07552 × 10−5 |
| 110 | −0.000692641 | −0.000165493 | 6.46396 × 10−5 | −1.45021 × 10−5 |
| 120 | −0.00094015 | −9.06175 × 10−5 | 1.95771 × 10−5 | −2.64337 × 10−5 |
| 150 | −0.000927123 | 7.13357 × 10−5 | −5.54034 × 10−5 | −4.01626 × 10−5 |
| 170 | −0.000921504 | 0.000067901 | 7.34738 × 10−5 | −4.20862 × 10−5 |
| 200 | −0.000908439 | 7.25774 × 10−5 | 3.69618 × 10−5 | 4.3723 × 10−5 |
| 230 | −0.000894303 | 0.000145932 | 7.60111 × 10−5 | 1.51402 × 10−5 |
| 240 | −0.00088915 | −4.56297 × 10−5 | 7.65545 × 10−5 | 2.56077 × 10−5 |
| 260 | −0.000435326 | −8.371 × 10−5 | 3.61233 × 10−5 | 1.27842 × 10−5 |
| 290 | 0.000603201 | 0.00018294 | 4.55104 × 10−5 | 2.26422 × 10−5 |
| 320 | 0.000846424 | 9.39976 × 10−5 | 1.98744 × 10−5 | 2.78241 × 10−5 |
| 340 | 0.000829439 | −0.000167173 | 3.98373 × 10−5 | 3.31562 × 10−5 |
| 350 | 0.000821504 | −0.000239669 | −6.54447 × 10−5 | 3.14372 × 10−5 |
| Average (°/s) | −8.31975 × 10−5 | 1.57433 × 10−5 | 2.02715 × 10−5 | 5.22753 × 10−6 |
| STD (°/s) | 0.000815143 | 0.000142305 | 5.4609 × 10−5 | 3.1414 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, C.; Guo, D.; Zhang, L.; Wang, T. Research on Nonlinear Compensation of the MEMS Gyroscope under Tiny Angular Velocity. Sensors 2022, 22, 6577. https://doi.org/10.3390/s22176577
Ren C, Guo D, Zhang L, Wang T. Research on Nonlinear Compensation of the MEMS Gyroscope under Tiny Angular Velocity. Sensors. 2022; 22(17):6577. https://doi.org/10.3390/s22176577
Chicago/Turabian StyleRen, Chunhua, Dongning Guo, Lu Zhang, and Tianhe Wang. 2022. "Research on Nonlinear Compensation of the MEMS Gyroscope under Tiny Angular Velocity" Sensors 22, no. 17: 6577. https://doi.org/10.3390/s22176577
APA StyleRen, C., Guo, D., Zhang, L., & Wang, T. (2022). Research on Nonlinear Compensation of the MEMS Gyroscope under Tiny Angular Velocity. Sensors, 22(17), 6577. https://doi.org/10.3390/s22176577








