Low-Complexity Joint 3D Super-Resolution Estimation of Range Velocity and Angle of Multi-Targets Based on FMCW Radar
Abstract
:1. Introduction
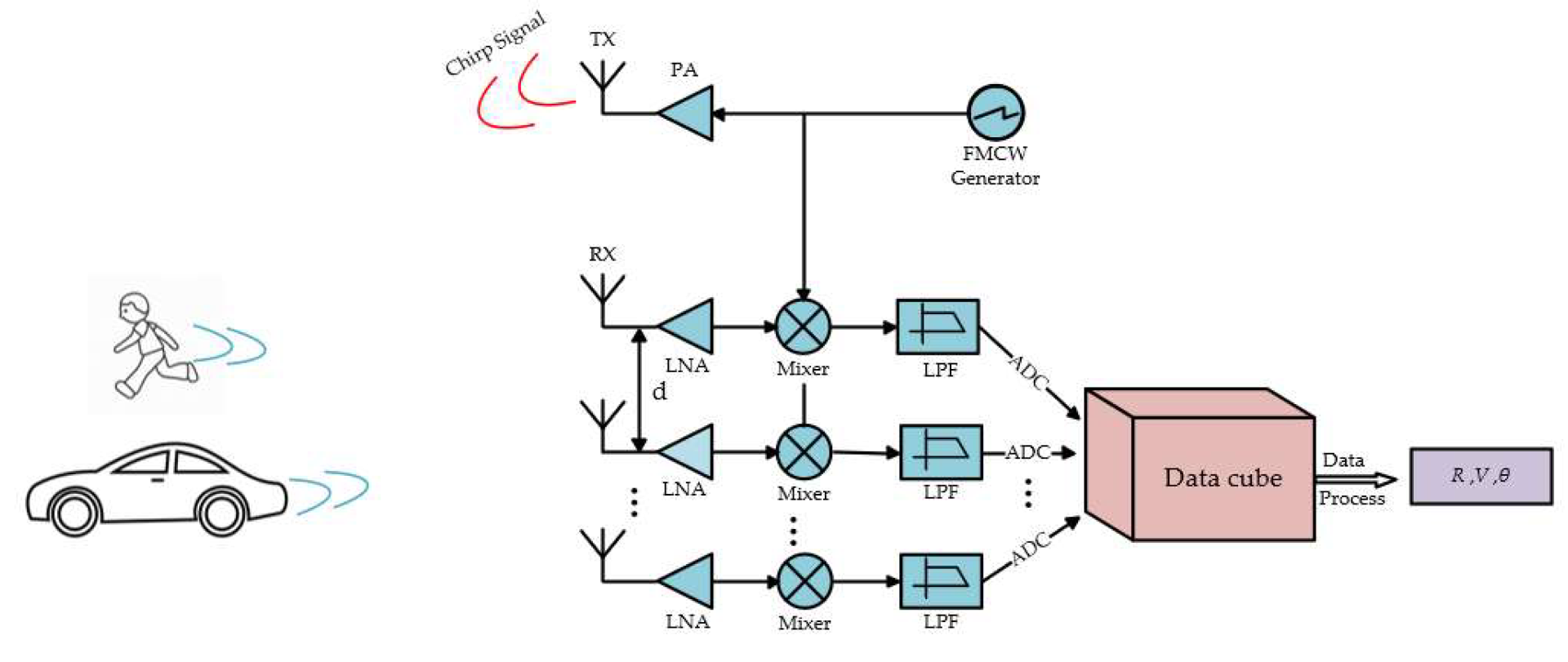
2. Signal Model
3. The Proposed Low-Complexity Super-Resolution Algorithm
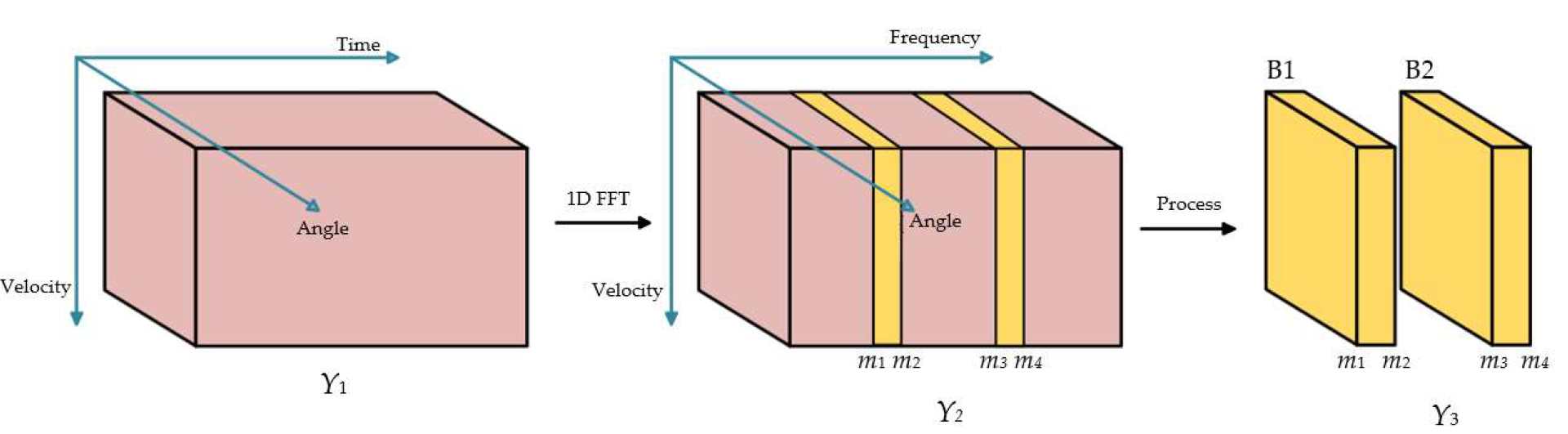
3.1. Targets-Located Blocks Selection
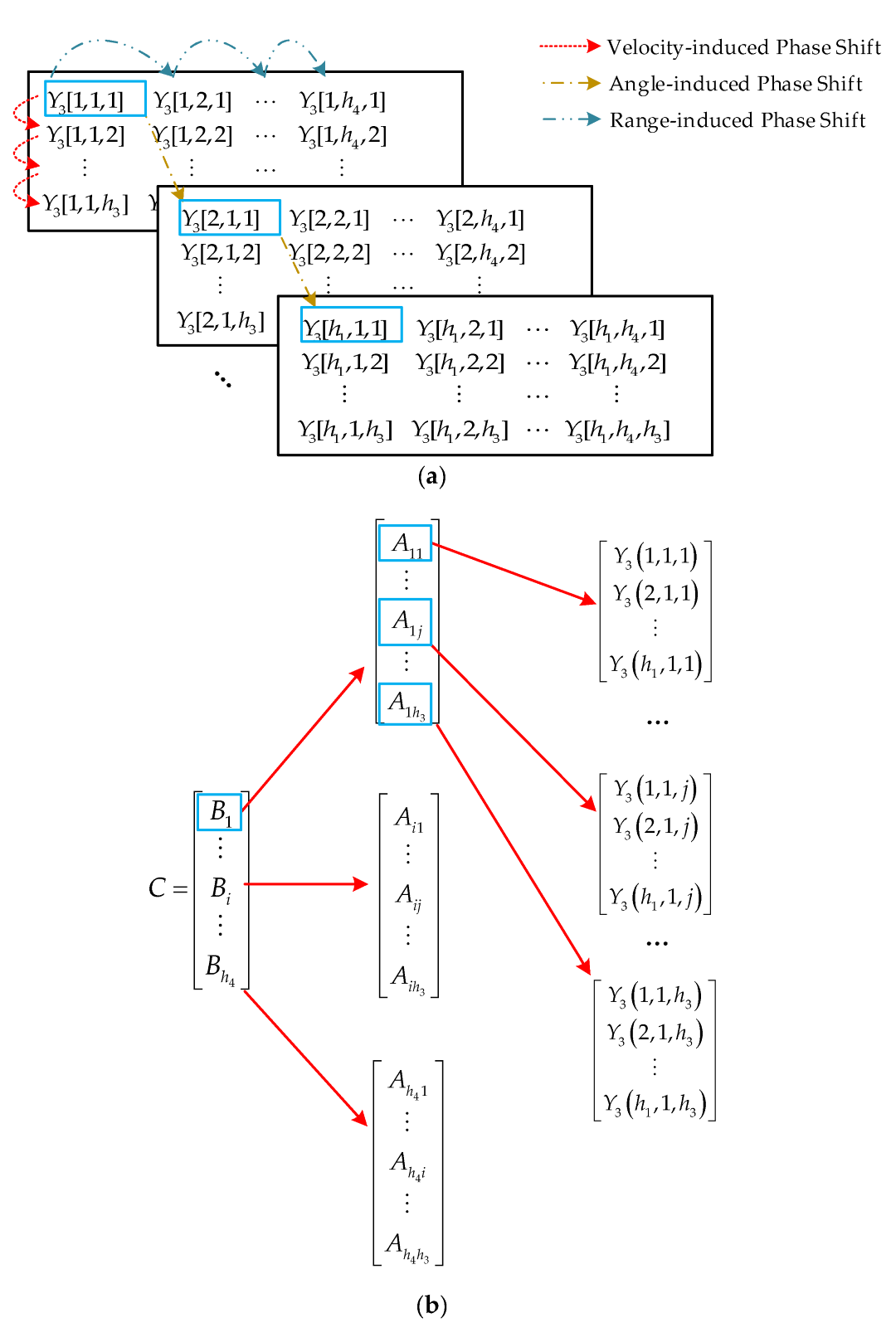
3.2. Decorrelation Processing
3.3. Low Complexity Joint 3D Estimation of Range-Velocity-Angle
4. Experimental Results and Performance Analysis
4.1. Simulation Experiment
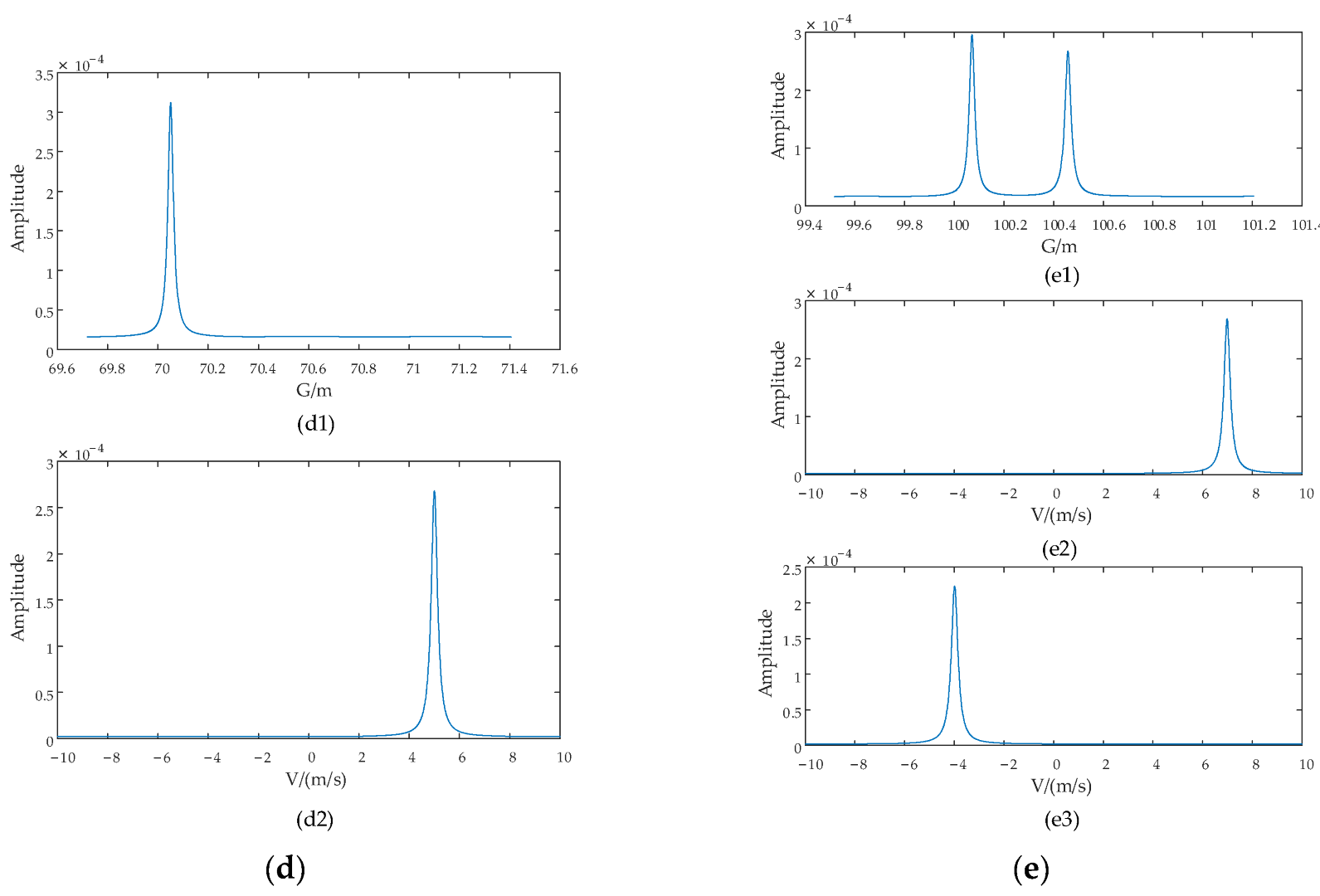
4.1.1. Detection Simulation
4.1.2. Algorithm Accuracy
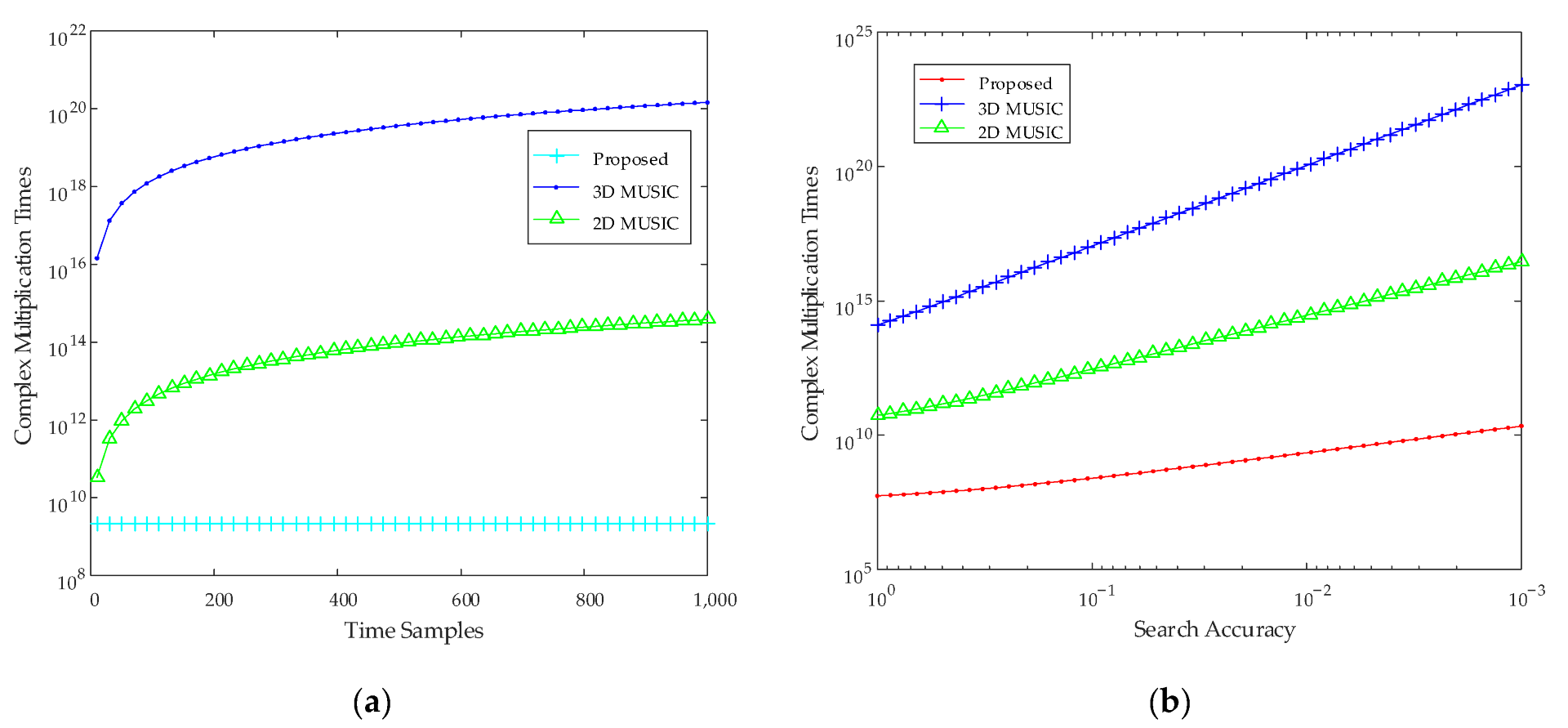
4.1.3. Complexity Analysis
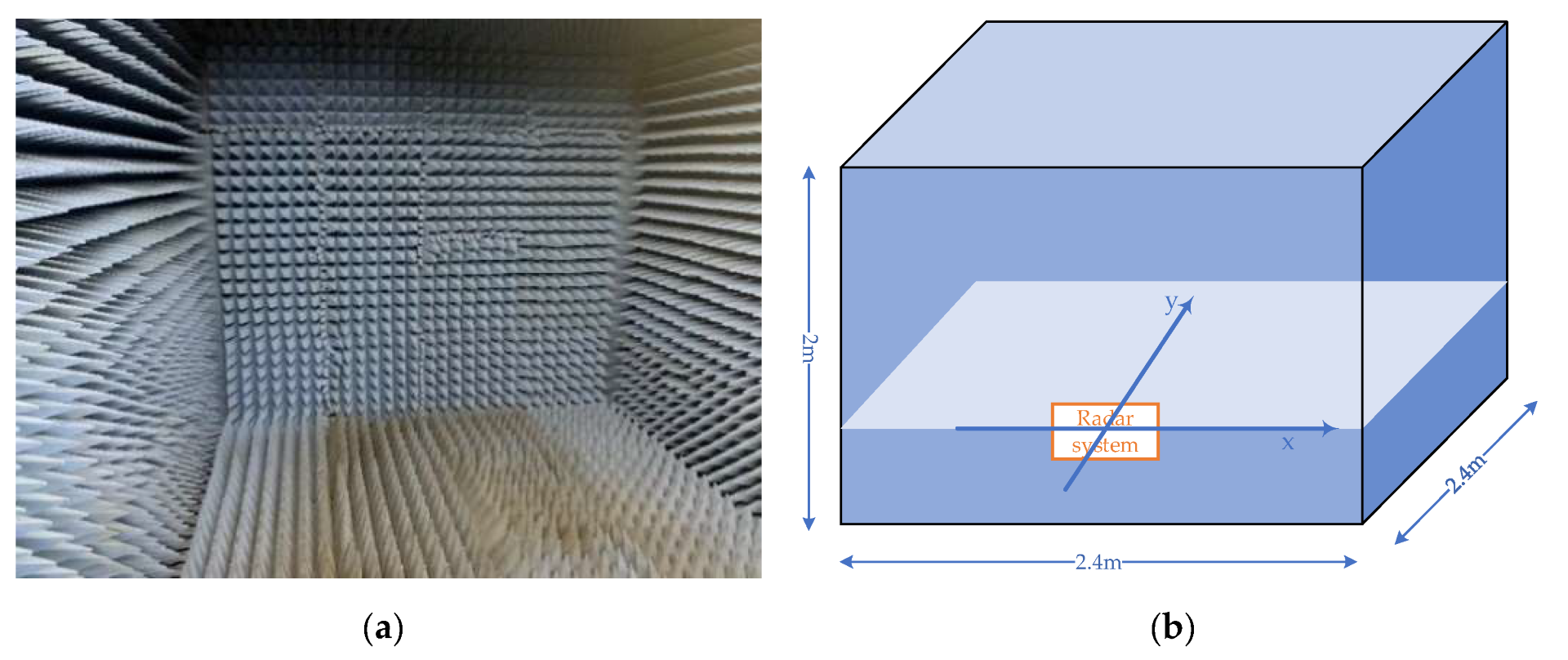
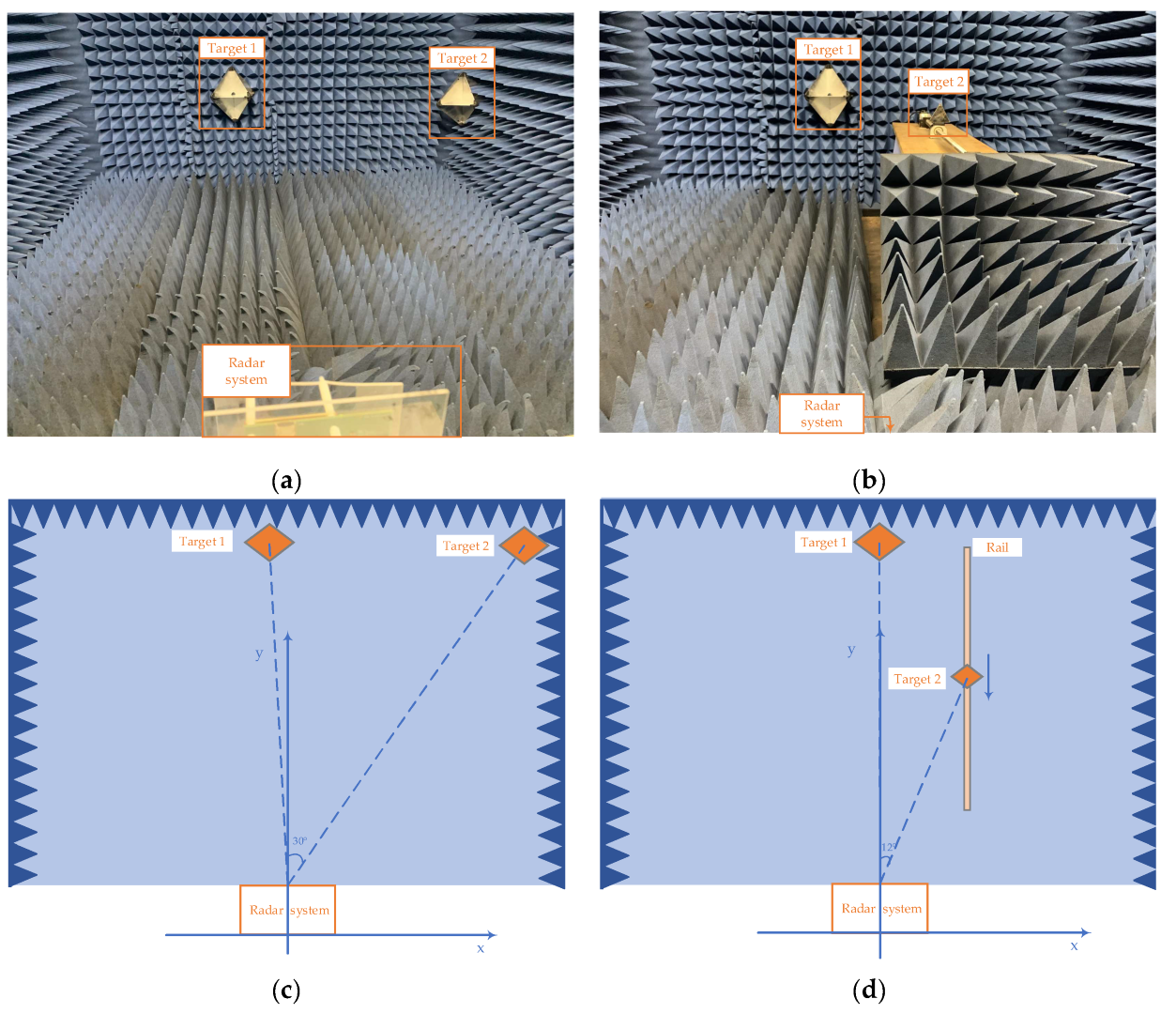
4.2. Actual Experiment
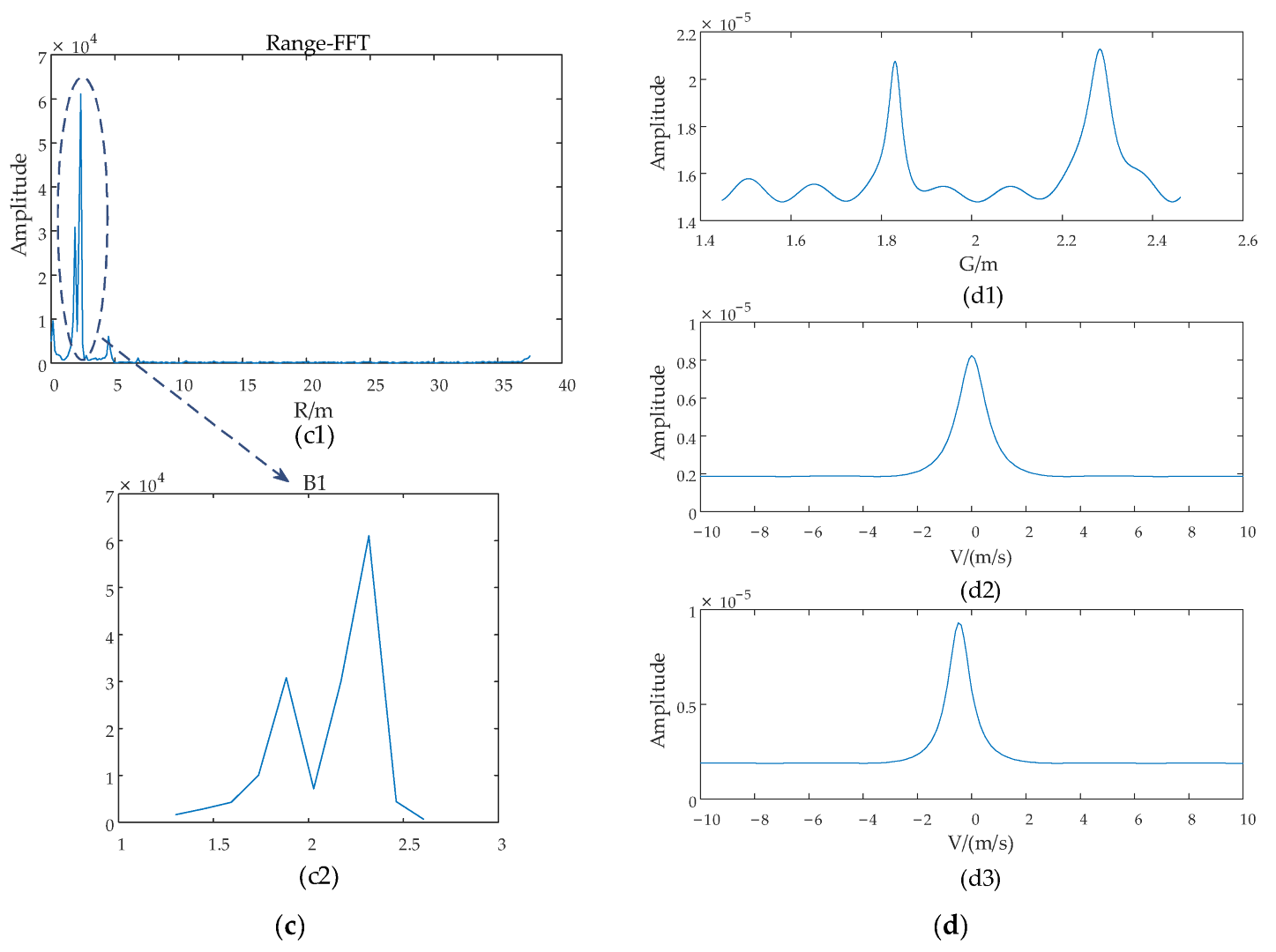
4.2.1. Corner Reflector Detection
4.2.2. Irregular-Shape Target Detection and 2D Imaging
4.2.3. Targets Detection in Outdoor Environment
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Lee, S.; Jung, Y.; Lee, M.; Lee, W. Compressive Sensing-Based SAR Image Reconstruction from Sparse Radar Sensor Data Acquisition in Automotive FMCW Radar System. Sensors 2021, 21, 7283. [Google Scholar] [CrossRef] [PubMed]
- Son, Y.-S.; Sung, H.-K.; Heo, S.W. Automotive Frequency Modulated Continuous Wave Radar Interference Reduction Using Per-Vehicle Chirp Sequences. Sensors 2018, 18, 2831. [Google Scholar] [CrossRef] [PubMed]
- Passafiume, M.; Rojhani, N.; Collodi, G.; Cidronali, A. Modeling Small UAV Micro-Doppler Signature Using Millimeter-Wave FMCW Radar. Electronics 2021, 10, 747. [Google Scholar] [CrossRef]
- Coluccia, A.; Parisi, G.; Fascista, A. Detection and Classification of Multirotor Drones in Radar Sensor Networks: A Review. Sensors 2020, 20, 4172. [Google Scholar] [CrossRef] [PubMed]
- Turppa, E.; Kortelainen, J.M.; Antropov, O.; Kiuru, T. Vital Sign Monitoring Using FMCW Radar in Various Sleeping Scenarios. Sensors 2020, 20, 6505. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Zhao, L.; Mohan, M.P.; Jimeno, J.; Siyal, M.Y.; Alphones, A.; Karim, M.F. mm-Wave Radar-Based Vital Signs Monitoring and Arrhythmia Detection Using Machine Learning. Sensors 2022, 22, 3106. [Google Scholar] [CrossRef] [PubMed]
- Antolinos, E.; García-Rial, F.; Hernández, C.; Montesano, D.; Llorente, J.I.G.; Grajal, J. Cardiopulmonary Activity Monitoring Using Millimeter Wave Radars. Remote Sens. 2020, 12, 2265. [Google Scholar] [CrossRef]
- Hyun, E.; Lee, J.H. A Method for Multi-target Range and Velocity Detection in Automotive FMCW Radar. In Proceedings of the 12th International IEEE Conference on Intelligent Transportation System, St. Louis, MO, USA, 4–7 October 2009; pp. 7–11. [Google Scholar]
- Sediono, W.; Sediono, W. Method of measuring Doppler shift of moving targets using FMCW maritime radar. In Proceedings of the 2013 IEEE International Conference on Teaching, Assessment and Learning for Engineering (TALE), Bali, Indonesia, 26–29 August 2013; pp. 378–381. [Google Scholar] [CrossRef]
- Winkler, V. Range Doppler detection for automotive FMCW radar. In Proceedings of the 4th IEEE European Radar Conference, Munich, Germany, 10–12 October 2007; pp. 166–169. [Google Scholar]
- Manokhin, G.O.; Erdyneev, Z.T.; Geltser, A.A.; Monastyrev, E.A. MUSIC-based algorithm for range-azimuth FMCW radar data processing without estimating number of targets. In Proceedings of the 2015 IEEE 15th Mediterranean Microwave Symposium (MMS), Lecce, Italy, 30 November–2 December 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. In Proceedings of the RADC Spectral Estimation Workshop; Saxpy Computer Corporation: Pleasanton, CA, USA, 1979; pp. 243–258. [Google Scholar]
- Zhou, L.; Zhao, Y.-J.; Cui, H. High resolution wideband DOA estimation based on modified MUSIC algorithm. In Proceedings of the 2008 International Conference on Information and Automation, Changsha, China, 20–23 June 2008; pp. 20–22. [Google Scholar] [CrossRef]
- Iizuka, T.; Toriumi, Y.; Ishiyama, F.; Kato, J. Root-MUSIC Based Power Estimation Method with Super-Resolution FMCW Radar. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 1027–1030. [Google Scholar] [CrossRef]
- Hwang, H.K.; Zekeriva Alivazicioglu, Z.; Yakovlev, A. Direction of arrival estimation using a root-MUSIC algorithm. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists, Hong Kong, China, 19–21 March 2008; Volume II. [Google Scholar]
- Lemma, A.; van der Veen, A.-J.; Deprettere, E. Analysis of joint angle-frequency estimation using ESPRIT. IEEE Trans. Signal Process. 2003, 51, 1264–1283. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Gurcan, Y.; Yarovoy, A. Super-resolution algorithm for joint range-azimuth-Doppler estimation in automotive radars. In Proceedings of the 2017 European Radar Conference (EURAD), Nuremberg, Germany, 11–13 October 2017; pp. 73–76. [Google Scholar] [CrossRef]
- Porozantzidou, M.G.; Chryssomallis, M.T. Azimuth and elevation angles estimation using 2-D MUSIC algorithm with an L-shape antenna. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, Y.; Wang, W.-Q.; Li, G.; Yang, J.; Ge, Y. 2-D DOA estimation of multiple signals based on sparse L-shaped array. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016; pp. 1014–1015. [Google Scholar]
- Belfiori, F.; van Rossum, W.; Hoogeboom, P. Application of 2D MUSIC algorithm to range-azimuth FMCW radar data. In Proceedings of the 2012 9th European Radar Conference, Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 242–245. [Google Scholar]
- Seo, J.; Lee, J.; Park, J.; Kim, H.; You, S. Distributed Two-Dimensional MUSIC for Joint Range and Angle Estimation with Distributed FMCW MIMO Radars. Sensors 2021, 21, 7618. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, S.; Kuptsov, V.; Badenko, V.; Fedotov, A. An Elaborated Signal Model for Simultaneous Range and Vector Velocity Estimation in FMCW Radar. Sensors 2020, 20, 5860. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; He, J.; Yu, W. A Computationally Efficient Scheme for FMCW Radar Detection and Parameter Estimation. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of Departure (DOD) and Direction of Arrival (DOA) Estimation in MIMO Radar with Reduced-Dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Beizuo, Z.; Xiong, X.; Xiaofei, Z. DOA and Polarization Estimation with Reduced-Dimensional MUSIC Algorithm for L-shaped Electromagnetic Vector Sensor Array. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019; pp. 61–64. [Google Scholar] [CrossRef]
- Fang, W.-H.; Fang, L.-D. Joint Angle and Range Estimation With Signal Clustering in FMCW Radar. IEEE Sens. J. 2019, 20, 1882–1892. [Google Scholar] [CrossRef]
- Zhao, E.; Zhang, F.; Zhang, D.; Pan, S. Three-dimensional Multiple Signal Classification (3D-MUSIC) for Super-resolution FMCW Radar Detection. In Proceedings of the 2019 IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Wisudawan, H.N.; Ariananda, D.D.; Hidayat, R. 3-D MUSIC Spectrum Reconstruction for Joint Azimuth-Elevation-Frequency Band Estimation. In Proceedings of the 2020 54th Asilomar Conference on Signals, Systems, and Computers, Virtual, 1–4 November 2020; pp. 1250–1254. [Google Scholar] [CrossRef]
- Pillai, S.; Kwon, B. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal. Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Nam, H.; Li, Y.-C.; Choi, B.; Oh, D. 3D-Subspace-Based Auto-Paired Azimuth Angle, Elevation Angle, and Range Estimation for 24G FMCW Radar with an L-Shaped Array. Sensors 2018, 18, 1113. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.-C.; Oh, D.; Kim, S.; Chong, J.-W. Dual Channel S-Band Frequency Modulated Continuous Wave Through-Wall Radar Imaging. Sensors 2018, 18, 311. [Google Scholar] [CrossRef] [PubMed]
- Schoor, M.; Yang, B. Subspace based DOA estimation in the presence of correlated signals and model errors. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009. [Google Scholar]
- Chen, Y.-M. On spatial smoothing for two-dimensional direction-of-arrival estimation of coherent signals. IEEE Trans. Signal Process. 1997, 45, 1689–1696. [Google Scholar] [CrossRef]
- Wang, H.; Liu, K.R. 2-D spatial smoothing for multipath coherent signal separation. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 391–405. [Google Scholar] [CrossRef] [Green Version]









| Target Number | |||
|---|---|---|---|
| 1 | 29.9976 m | −2.9965 m/s | −20.1844° |
| 2 | 50.0114 m | 4.087 m/s | 34.2881° |
| 3 | 50.0857 m | 5.8879 m/s | 20.7431° |
| 4 | 69.9981 m | 5.0175 m/s | 40.2631° |
| 5 | 100.0015 m | 6.9885 m/s | −29.9204° |
| 6 | 100.5007 m | −3.987 m/s | 29.9461° |
| Target 1 | Target 2 | |
|---|---|---|
| Experiment 1 | [2.312 m, 0 m/s, −4°] | [2.403 m, 0 m/s, 30°] |
| Experiment 2 | [2.295 m, 0 m/s, 0°] | [1.832 m, −0.5 m/s, 12°] |
| Target No. | ||||
|---|---|---|---|---|
| Experiment 1 | 1 | 2.2987 m | 0 m/s | −2.8483° |
| 2 | 2.4447 m | 0 m/s | 28.1479° | |
| Experiment 2 | 1 | 2.2834 m | 0 m/s | −0.26748° |
| 2 | 1.8321 m | −0.5 m/s | 11.7486° |
| 3D-FFT | 3D-MUSIC | The Proposed Algorithm | |
|---|---|---|---|
| Experiment 1 | 0.1115 s | 3days | 1.4936 s |
| Experiment 2 | 0.1123 s | 3days | 1.5018 s |
| R | V | θ | |
|---|---|---|---|
| Experiment 1 | 0.0273 m | 0 m/s | 1.4913° |
| Experiment 2 | 0.0721 m | 0.0630 m/s | 0.8776° |
| Target No. | ||||
|---|---|---|---|---|
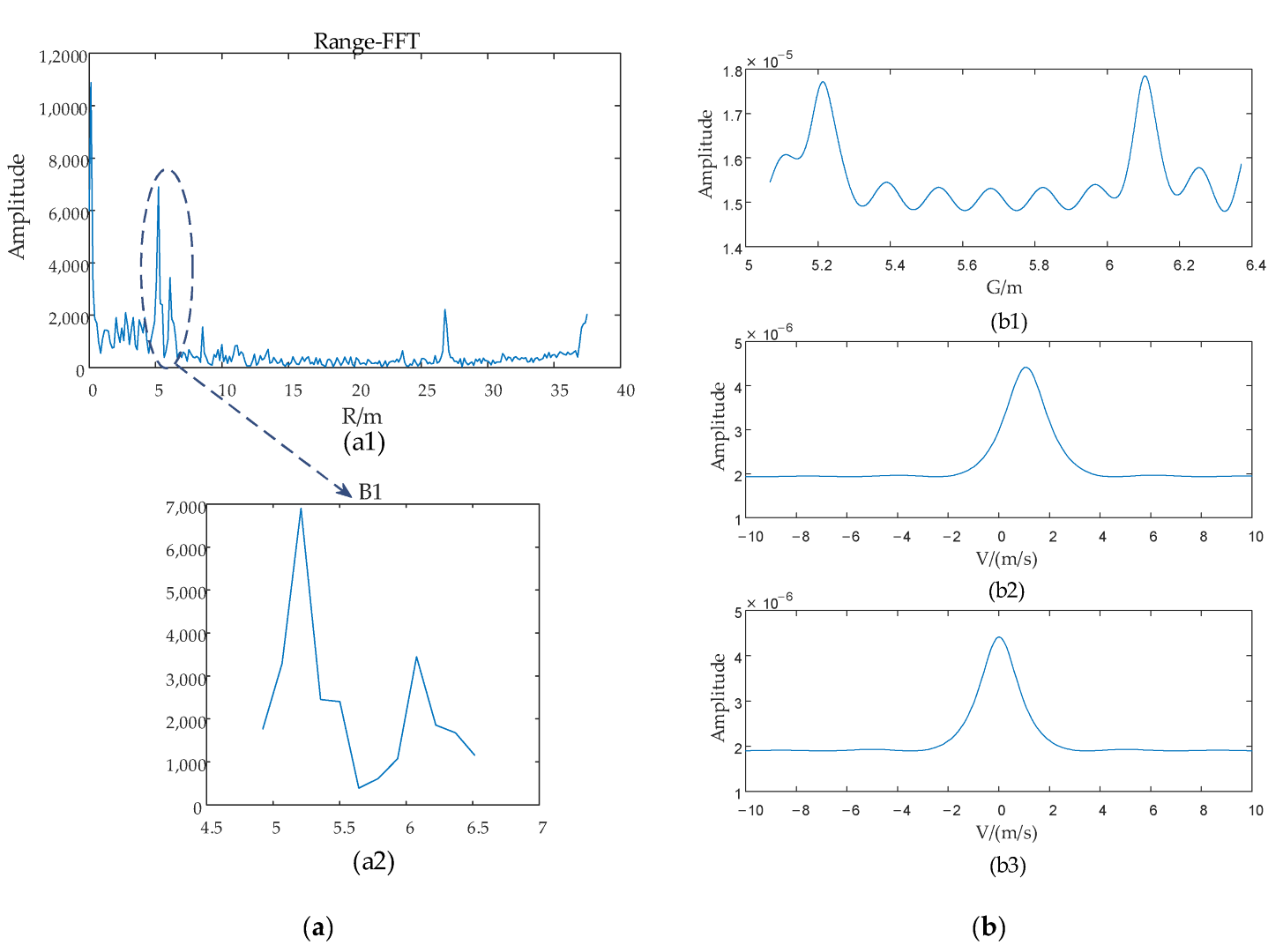
| Experiment 4 | 1 | 6.0998 m | 1.1 m/s | −16.3641° |
| 2 | 5.2129 m | 0 m/s | −2.1378° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Long, Q.; Wu, Z.; Zhou, Z. Low-Complexity Joint 3D Super-Resolution Estimation of Range Velocity and Angle of Multi-Targets Based on FMCW Radar. Sensors 2022, 22, 6474. https://doi.org/10.3390/s22176474
Li Y, Long Q, Wu Z, Zhou Z. Low-Complexity Joint 3D Super-Resolution Estimation of Range Velocity and Angle of Multi-Targets Based on FMCW Radar. Sensors. 2022; 22(17):6474. https://doi.org/10.3390/s22176474
Chicago/Turabian StyleLi, Yingchun, Qi Long, Zhongjie Wu, and Zhiquan Zhou. 2022. "Low-Complexity Joint 3D Super-Resolution Estimation of Range Velocity and Angle of Multi-Targets Based on FMCW Radar" Sensors 22, no. 17: 6474. https://doi.org/10.3390/s22176474
APA StyleLi, Y., Long, Q., Wu, Z., & Zhou, Z. (2022). Low-Complexity Joint 3D Super-Resolution Estimation of Range Velocity and Angle of Multi-Targets Based on FMCW Radar. Sensors, 22(17), 6474. https://doi.org/10.3390/s22176474




