ST-CRMF: Compensated Residual Matrix Factorization with Spatial-Temporal Regularization for Graph-Based Time Series Forecasting
Abstract
:1. Introduction
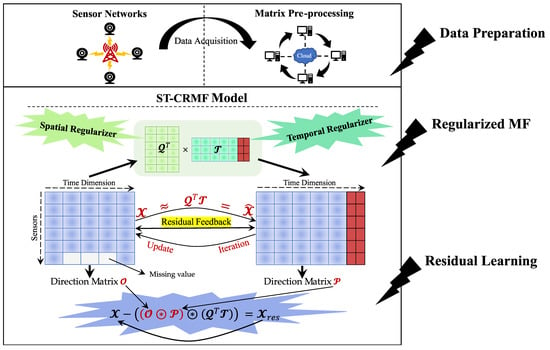
- We propose a novel forecasting model entitled ST-CRMF for depth extraction of the non-linear spatial-temporal dependencies within historical time series and its residuals, where the spatial-temporal regularizers and bi-directional residual structure greatly augment model performance.
- Apart from accurately predicting future traffic sequences, the ST-CRM can deal with incomplete traffic datasets and proves its predictive effectiveness in various missing cases.
- We empirically demonstrate the superiority of the ST-CRMF model on real-world traffic datasets (i.e., Seattle-Loop and METR-LA). The experimental results confirm that the proposed ST-CRMF model achieves satisfactory results for several pre-defined prediction lengths.
2. Related Work
2.1. Traditional Multivariate Time Series Forecasting
2.2. Deep Learning for Traffic Time Series Forecasting
2.3. Spatial-Temporal Modeling Using Incomplete Dataset
3. Methodology
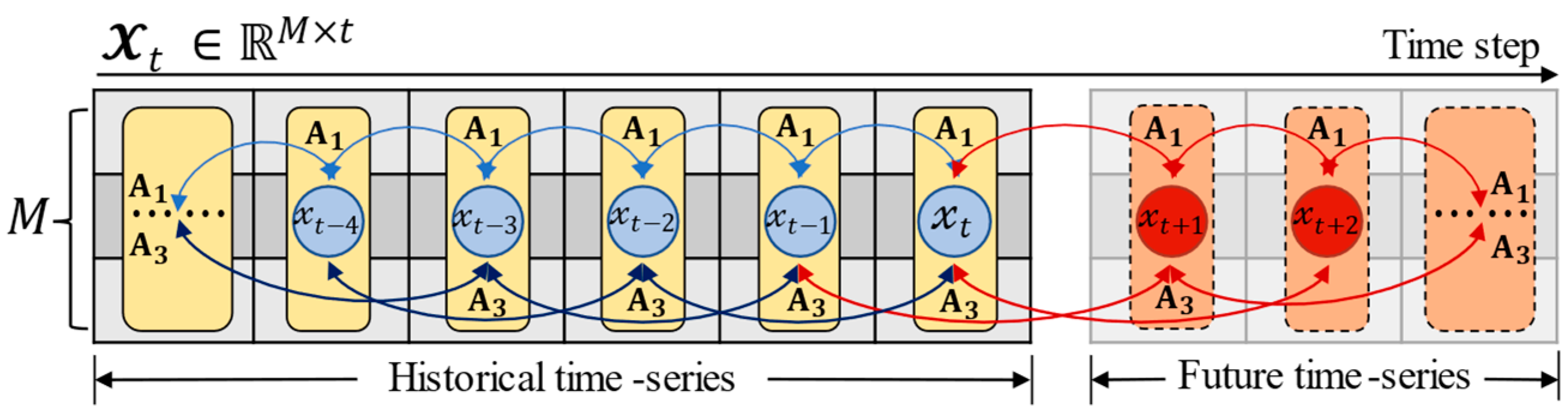
3.1. Preliminaries
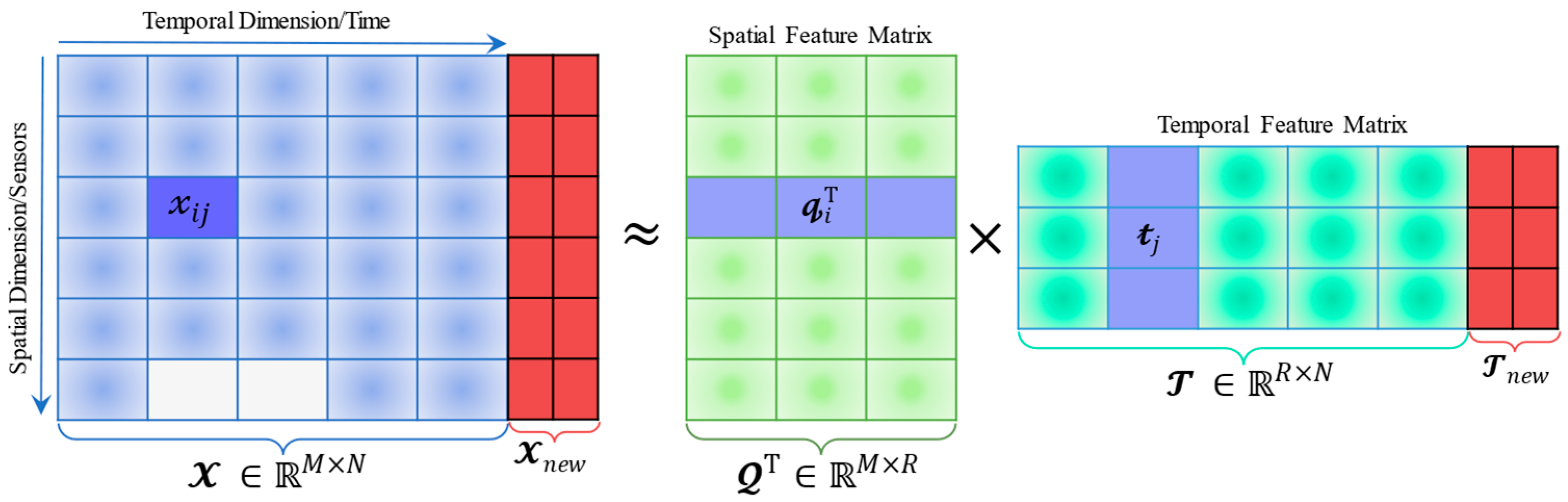
3.2. Spatial-Temporal Matrix Factorization
3.2.1. Matrix Factorization Description
3.2.2. Regularized Spatial-Temporal Matrices Modeling
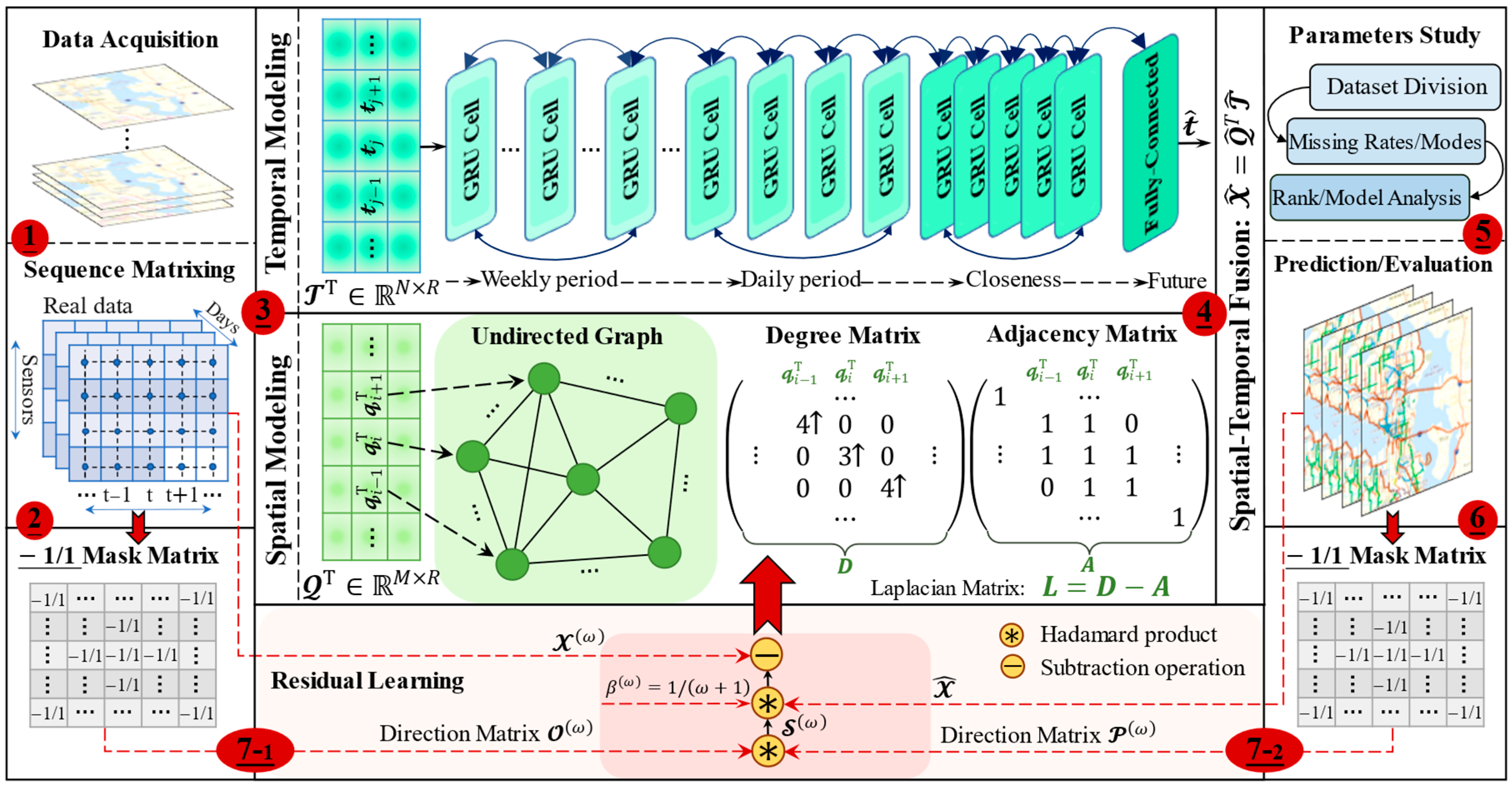
3.3. Overall Architecture of the ST-CRMF Model
3.3.1. Model Implementation
3.3.2. Compensated Residual Learning
3.4. Pseudo-Code of the ST-CRMF Model
| Algorithm 1: Training Procedure of ST-CRMF Model |
| Input: Graph network Feature matrix ; Rank ; Missing rates/scenarios; Maximum iteration . Output: Learned ST-CRMF model; Factor matrices and forecasted/repaired ; Future sequence. 1. Initialize all trainable parameters in ST-CRMF. 2. For to do 3. Compute and update of by the ALS solution in Equation (14): 5. Update the training parameters in GRN regularizer by back-propagation with batch gradient descent. 6. Compute the and the residual matrix by Equation (20), and have it replaced : 8. Until met model stop criteria. 9. Repair the possible missing values in and then update it. 10. Rolling forecast of the future time series by Equation (18). |
4. Experiment Study
4.1. Datasets Description
4.2. Experimental Settings
4.2.1. Baseline Models
- (1)
- STGCN: Spatio-Temporal Graph Convolutional Network employs Chebyshev GCN and gated CNN for capturing the dynamics of spatial and temporal dependencies, respectively [2];
- (2)
- AGCRN: Adaptive Graph Convolutional Recurrent Network captures the node-specific spatial and temporal correlations in traffic time series automatically without a pre-defined graph [3];
- (3)
- Graph-WaveNet: Graph WaveNet integrates the diffusion graph convolutions with dilated casual convolution (called WaveNet) to capture the spatial-temporal dependencies simultaneously [4];
- (4)
- PGCN: Progressive Graph Convolutional Network combines the gated activation unit and the dilated causal convolution to extract the temporal feature in traffic data [26];
- (5)
- DGCRN: Dynamic Graph Convolutional Recurrent Network indicates that their dynamic graph can cooperate effectively with pre-defined graph while improving the prediction performance [33];
- (6)
- GMAN: Graph Multi-Attention Network utilizes a variety of types of purely attention modules to learn complex spatial-temporal dependencies [34];
- (7)
- GATs-GAN: The model incorporates Graph Attention Networks and Generative Adversarial Network to learn the node features and achieve the traffic state derivation [37];
- (8)
- MRA-BGCN: Multi-Range Attentive Bicomponent Graph Convolutional Network uses the edge-wise graph construction, attention mechanism, and so on for traffic prediction [38].
4.2.2. Measures of Model Effectiveness
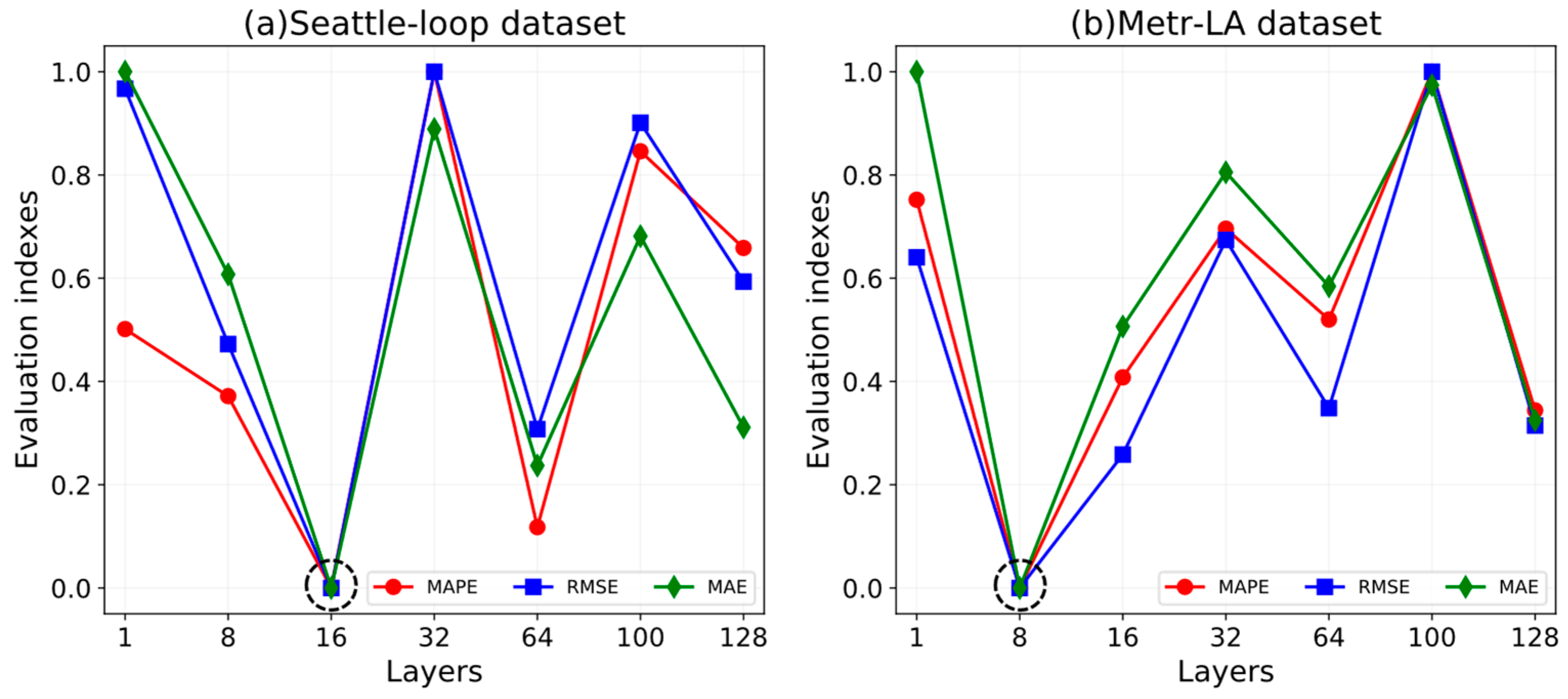
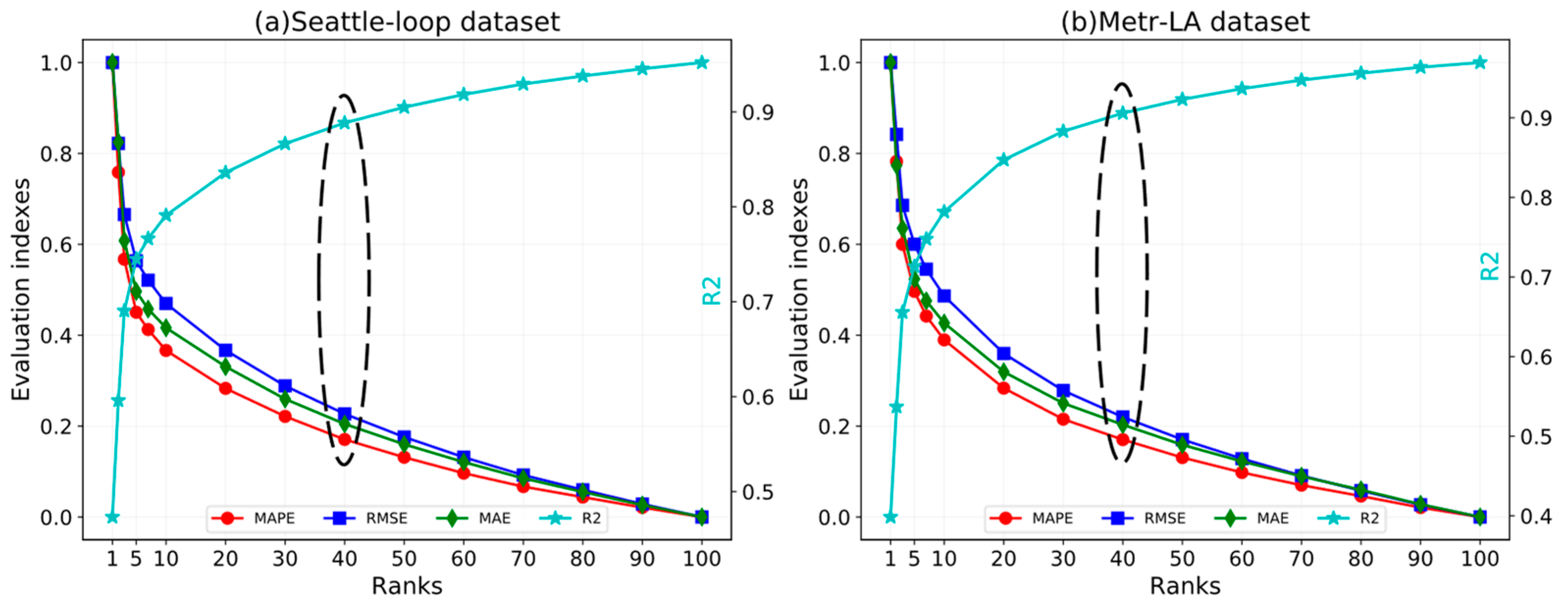
4.2.3. Parameters Study
4.3. Effect of Key Parameters on the ST-CRMF Model
4.4. Empirical Results and Analysis
4.4.1. Comparison with Baselines for 5-/15-/30-min Forecasting
4.4.2. Comparison with Baselines for 15-/30-/60-min Forecasting
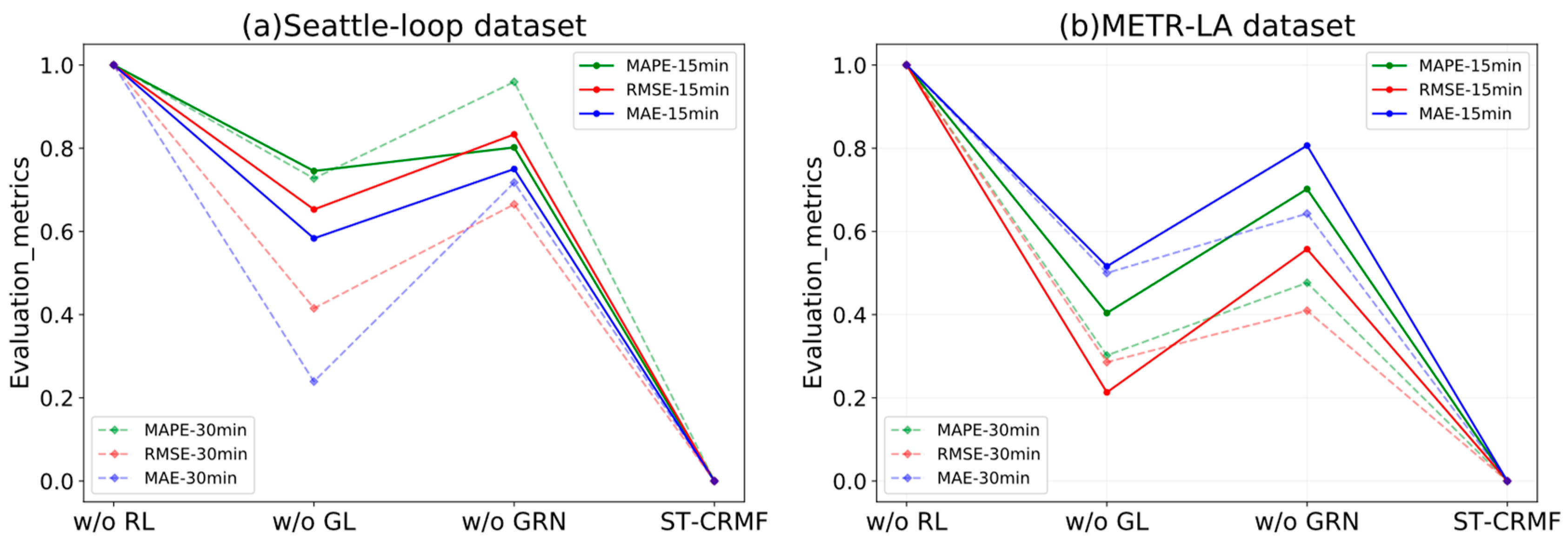
4.5. Ablation Study
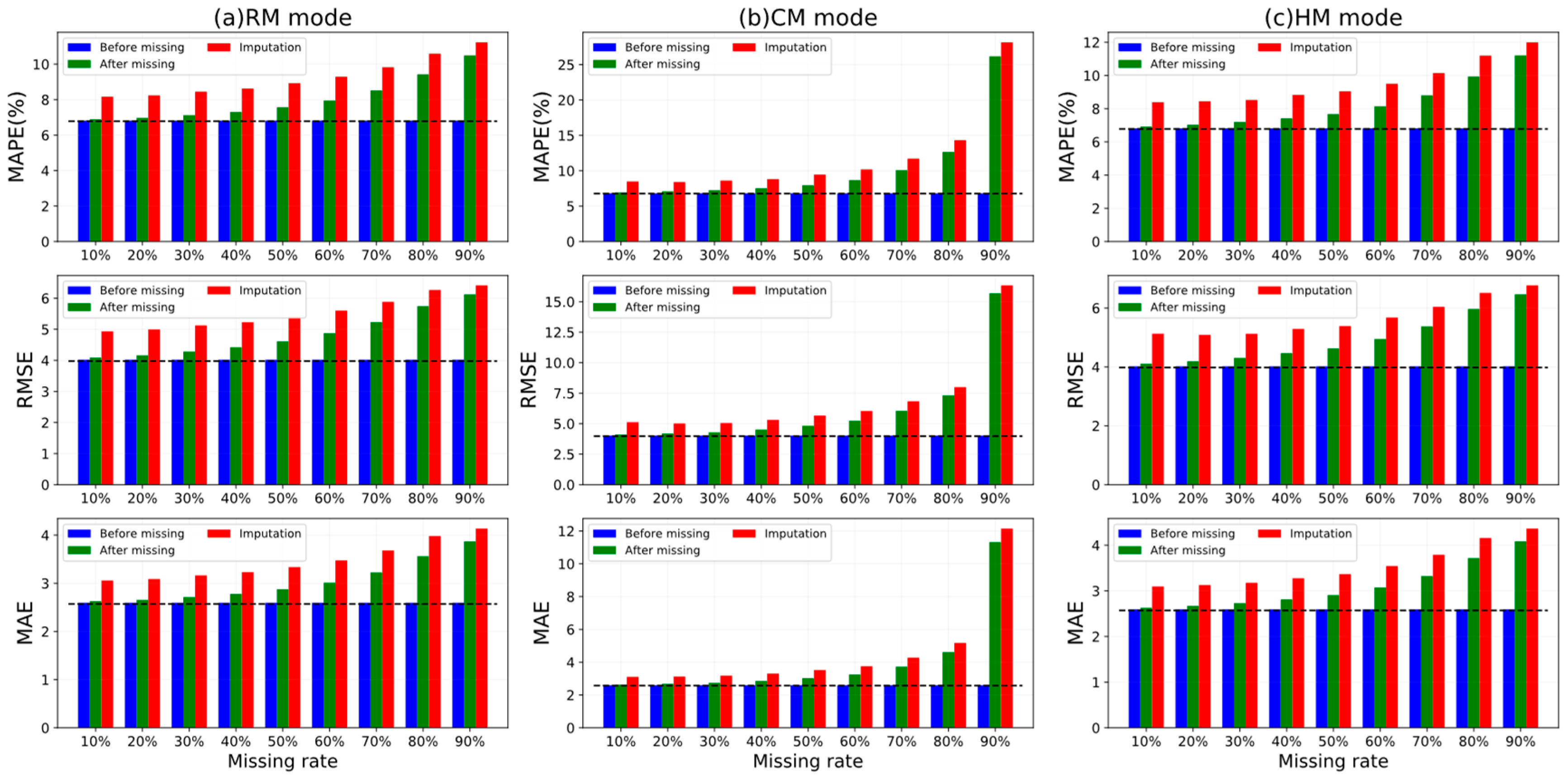
4.6. Model Robustness Analysis
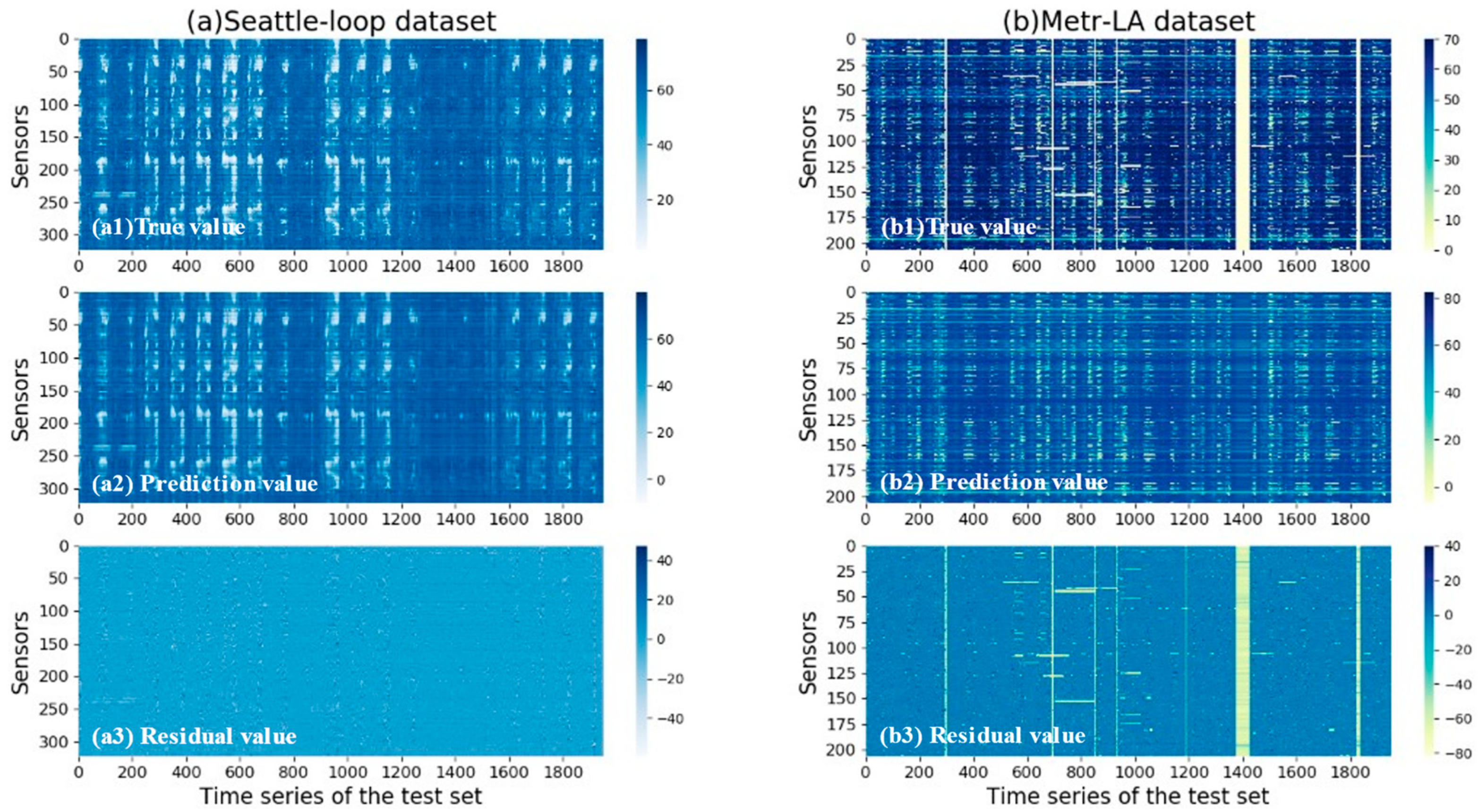
4.7. Prediction Visualization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Z.H.; Pan, S.R.; Long, G.D.; Jiang, J.; Chang, X.J.; Zhang, C.G. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, California, CA, USA, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Yu, B.; Yin, H.T.; Zhu, Z.X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar] [CrossRef]
- Bai, L.; Yao, L.; Li, C.; Wang, X.Z.; Wang, C. Adaptive graph convolutional recurrent network for traffic forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17804–17815. [Google Scholar]
- Wu, Z.H.; Pan, S.R.; Long, G.D.; Jiang, J.; Zhang, C.Q. Graph wavenet for deep spatial-temporal graph modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar] [CrossRef]
- Li, J.L.; Xu, L.H.; Li, R.N.; Wu, P.; Huang, Z.L. Deep spatial-temporal bi-directional residual optimisation based on tensor decomposition for traffic data imputation on urban road network. Appl. Intell. 2022, 52, 11363–11381. [Google Scholar] [CrossRef]
- Yin, X.Y.; Wu, G.Z.; Wei, J.Z.; Shen, Y.M.; Qi, H.; Yin, B.C. Deep learning on traffic prediction: Methods, analysis and future directions. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4927–4943. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.J.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef] [Green Version]
- Alsolami, B.; Mehmood, R.; Albeshri, A. Hybrid statistical and machine learning methods for road traffic prediction: A review and tutorial. In Smart Infrastructure and Applications; Springer: Cham, Switzerland, 2020; pp. 115–133. [Google Scholar]
- Ye, J.X.; Zhao, J.J.; Ye, K.J.; Xu, C.Z. How to build a graph-based deep learning architecture in traffic domain: A survey. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3904–3924. [Google Scholar] [CrossRef]
- Cui, Z.Y.; Ke, R.M.; Pu, Z.Y.; Wang, Y.H. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Gao, C.X.; Zhang, N.; Li, Y.R.; Bian, F.; Wan, H.Y. Self-attention-based time-variant neural networks for multi-step time series forecasting. Neural Comput. Appl. 2022, 34, 8737–8754. [Google Scholar] [CrossRef]
- Wang, H.W.; Peng, Z.R.; Wang, D.S.; Meng, Y.; Wu, T.L.; Sun, W.L.; Lu, Q.C. Evaluation and prediction of transportation resilience under extreme weather events: A diffusion graph convolutional approach. Transp. Res. Part C Emerg. Technol. 2020, 115, 102619. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Zhao, P.; Zheng, C.; Chen, X. A Graph-Based Temporal Attention Framework for Multi-Sensor Traffic Flow Forecasting. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7743–7758. [Google Scholar] [CrossRef]
- Pan, Z.Y.; Liang, Y.X.; Wang, W.F.; Yu, Y.; Zheng, Y.; Zhang, J.B. Urban traffic prediction from spatio-temporal data using deep meta learning. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1720–1730. [Google Scholar]
- Zhang, J.B.; Zheng, Y.; Qi, D.K. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the Thirty-first AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1655–1661. [Google Scholar]
- Chen, F.L.; Chen, Z.Q.; Biswas, S.; Lei, S.; Ramakrishnan, N.; Lu, C.T. Graph convolutional networks with kalman filtering for traffic prediction. In Proceedings of the 28th International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2020; pp. 135–138. [Google Scholar]
- Chen, X.Y.; Sun, L.J. Bayesian temporal factorization for multidimensional time series prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Rao, N.; Yu, H.F.; Ravikumar, P.K.; Dhillon, I.S. Collaborative filtering with graph information: Consistency and scalable methods. Adv. Neural Inf. Process. 2015, 28, 2099–2107. [Google Scholar]
- Chen, X.Y.; He, Z.C.; Sun, L.J. A Bayesian tensor decomposition approach for spatiotemporal traffic data imputation. Transp. Res. Part C Emerg. Technol. 2019, 98, 73–84. [Google Scholar] [CrossRef]
- Laña, I.; Olabarrieta, I.I.; Vélez, M.; Del Ser, J. On the imputation of missing data for road traffic forecasting: New insights and novel techniques. Transp. Res. Part C Emerg. Technol. 2018, 90, 18–33. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Cook, A.R. Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Techniques; Transportation Research Board: Washington, DC, USA, 1979; pp. 1–9. [Google Scholar]
- Williams, B.M.; Hoel, L.A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.F.; Rao, N.; Dhillon, I.S. Temporal regularized matrix factorization for high-dimensional time series prediction. Adv. Neural Inf. Process. Syst. 2016, 29, 847–855. [Google Scholar]
- Zhang, L.Z.; Alharbe, N.R.; Luo, G.C.; Yao, Z.Y.; Li, Y. A hybrid forecasting framework based on support vector regression with a modified genetic algorithm and a random forest for traffic flow prediction. Tsinghua Sci. Technol. 2018, 23, 479–492. [Google Scholar] [CrossRef]
- Li, C.; Xu, P. Application on traffic flow prediction of machine learning in intelligent transportation. Neural Comput. Appl. 2021, 33, 613–624. [Google Scholar] [CrossRef]
- Shin, Y.; Yoon, Y.J. PGCN: Progressive Graph Convolutional Networks for Spatial-Temporal Traffic Forecasting. arXiv 2022, arXiv:2202.08982. [Google Scholar] [CrossRef]
- Kong, X.Y.; Zhang, J.; Wei, X.; Xing, W.W.; Lu, W. Adaptive spatial-temporal graph attention networks for traffic flow forecasting. Appl. Intell. 2022, 52, 4300–4316. [Google Scholar] [CrossRef]
- Zhang, K.L.; Xie, C.Y.; Wang, Y.J.; Ángel, S.M.; Nguyen, T.M.T.; Zhao, Q.D.; Li, Q. Hybrid short-term traffic forecasting architecture and mechanisms for reservation-based Cooperative ITS. J. Syst. Archit. 2021, 117, 102101. [Google Scholar] [CrossRef]
- Lv, Y.S.; Duan, Y.J.; Kang, W.W.; Li, Z.X.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Ma, X.L.; Zhong, H.Y.; Li, Y.; Ma, J.Y.; Cui, Z.Y.; Wang, Y.H. Forecasting transportation network speed using deep capsule networks with nested LSTM models. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4813–4824. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.L.; Lu, W.Q.; Qin, L.Q.; Li, M.; Shao, Z.Z. Short-term prediction of lane-level traffic speeds: A fusion deep learning model. Transp. Res. Part C Emerg. Technol. 2019, 106, 1–16. [Google Scholar] [CrossRef]
- Fang, S.; Pan, X.B.; Xiang, S.M.; Pan, C.H. Meta-msnet: Meta-learning based multi-source data fusion for traffic flow prediction. IEEE Signal Process. Lett. 2021, 28, 6–10. [Google Scholar] [CrossRef]
- Li, F.X.; Feng, J.; Yan, H.; Jin, G.Y.; Yang, F.; Sun, F.N.; Jin, D.P.; Li, Y. Dynamic graph convolutional recurrent network for traffic prediction: Benchmark and solution. ACM Trans. Knowl. Discov. Data 2021, 1156–4681. [Google Scholar] [CrossRef]
- Zheng, C.P.; Fan, X.L.; Wang, C.; Qi, J.Z. Gman: A graph multi-attention network for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 1234–1241. [Google Scholar]
- Ren, P.; Chen, X.Y.; Sun, L.J.; Sun, H. Incremental Bayesian matrix/tensor learning for structural monitoring data imputation and response forecasting. Mech. Syst. Signal Process. 2021, 158, 107734. [Google Scholar] [CrossRef]
- Chen, X.Y.; Lei, M.Y.; Saunier, N.; Sun, L.J. Low-rank autoregressive tensor completion for spatiotemporal traffic data imputation. IEEE Trans. Intell. Transp. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Xu, D.W.; Lin, Z.Q.; Zhou, L.; Li, H.J.; Niu, B. A GATs-GAN framework for road traffic states forecasting. Transp. B Transp. Dyn. 2022, 10, 718–730. [Google Scholar] [CrossRef]
- Chen, W.Q.; Chen, L.; Xie, Y.; Cao, W.; Gao, Y.S.; Feng, X.J. Multi-range attentive bicomponent graph convolutional network for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 3529–3536. [Google Scholar]
- Li, J.L.; Sun, L.J.; Li, Y.S.; Lu, Y.C.; Pan, X.Y.; Zhang, X.L.; Song, Z.W. Rapid prediction of acid detergent fiber content in corn stover based on NIR-spectroscopy technology. Optik 2019, 180, 34–45. [Google Scholar] [CrossRef]
- Li, J.L.; Sun, L.J.; Li, R.N. Nondestructive detection of frying times for soybean oil by NIR-spectroscopy technology with Adaboost-SVM (RBF). Optik 2020, 206, 164248. [Google Scholar] [CrossRef]
- Huang, Z.L.; Xu, L.H.; Lin, Y.J. Multi-stage pedestrian positioning using filtered WiFi scanner data in an urban road environment. Sensors 2020, 20, 3259. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Huang, Z.L.; Pian, Y.Z.; Xu, L.H.; Li, J.L.; Chen, K.X. A combined deep learning method with attention-based LSTM model for short-term traffic speed forecasting. J. Adv. Transp. 2020, 2020, 8863724. [Google Scholar] [CrossRef]

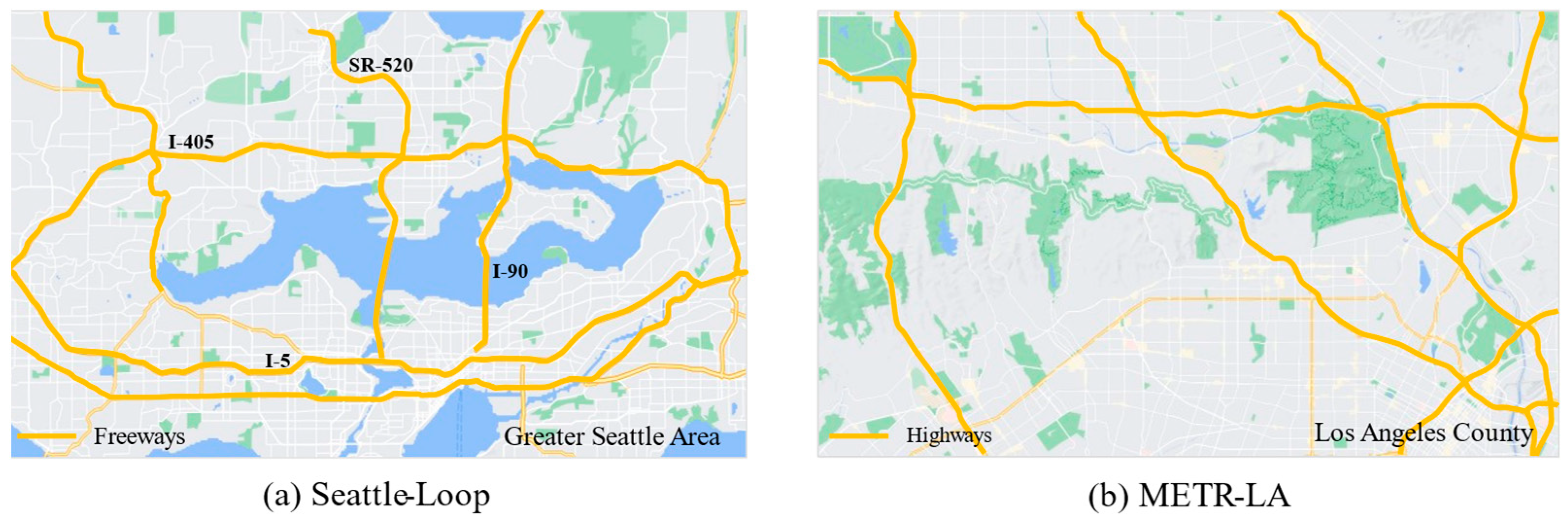

| Datasets | Seattle-Loop (S) | METR-LA (M) | |
|---|---|---|---|
| Information | |||
| Location | The Greater Seattle Area | The Los Angeles County | |
| No. of sensors | 323 | 207 | |
| Time scope | 31 December 2015 | 30 June 2012 | |
| Time granularity | 5 min | 5 min | |
| Period step | 288 (60/5 × 24) | 288 (60/5 × 24) | |
| Timestamps | 105120 | 34272 | |
| Sources (https://github.com) | /zhiyongc/Seattle-Loop-Data (accessed on 2 July 2018) | /liyaguang/DCRNN (accessed on 2 October 2018) | |
| Results | Dataset (S) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5-min | 15-min | 30-min | ||||||||
| Models | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | |
| GRN [12] | 8.74 | 4.92 | 3.24 | 9.67 | 5.39 | 3.48 | 10.23 | 5.76 | 3.63 | |
| LSTM [10] | 8.17 | 4.70 | 3.09 | 8.88 | 5.15 | 3.28 | 9.80 | 5.67 | 3.55 | |
| T-GCN [7] | 6.74 | 4.65 | 3.02 | 8.52 | 5.12 | 3.18 | 10.80 | 6.06 | 3.74 | |
| GMAN [34] | / | / | / | 8.15 | 4.86 | 2.97 | 9.97 | 5.71 | 3.34 | |
| PGCN [26] | / | / | / | 7.56 | 4.80 | 2.85 | 9.46 | 5.80 | 3.28 | |
| GATs-GAN [37] | 6.38 | 3.85 | 2.65 | 7.63 | 4.56 | 2.97 | 8.89 | 5.19 | 3.46 | |
| Graph-WaveNet [4] | / | / | / | 8.35 | 5.11 | 3.10 | 10.83 | 6.37 | 3.68 | |
| ST-CRMF (Ours) | 6.81 | 4.02 | 2.59 | 7.39 | 4.45 | 2.80 | 8.63 | 5.04 | 3.25 | |
| Results | Dataset (M) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 15-min | 30-min | 60-min | ||||||||
| Models | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | |
| ARIMA [21] | 9.60 | 8.21 | 3.99 | 12.70 | 10.45 | 5.15 | 17.40 | 13.23 | 6.90 | |
| STGCN [2] | 7.62 | 5.74 | 2.88 | 9.57 | 7.24 | 3.47 | 12.70 | 9.40 | 4.59 | |
| AGCRN [3] | 7.70 | 5.58 | 2.87 | 9.00 | 6.58 | 3.23 | 10.38 | 7.51 | 3.62 | |
| GMAN [34] | 7.41 | 5.55 | 2.80 | 8.73 | 6.49 | 3.12 | 10.07 | 7.35 | 3.44 | |
| DGCRN [33] | 6.63 | 5.01 | 2.62 | 8.02 | 6.05 | 2.99 | 9.73 | 7.19 | 3.44 | |
| MRA-BGCN [38] | 6.80 | 5.12 | 2.67 | 8.30 | 6.17 | 3.06 | 10.00 | 7.30 | 3.49 | |
| Graph-WaveNet [4] | 6.90 | 5.15 | 2.69 | 8.37 | 6.22 | 3.07 | 10.01 | 7.37 | 3.53 | |
| ST-CRMF (Ours) | 6.43 | 5.05 | 2.52 | 7.87 | 5.94 | 2.85 | 9.65 | 7.10 | 3.38 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wu, P.; Li, R.; Pian, Y.; Huang, Z.; Xu, L.; Li, X. ST-CRMF: Compensated Residual Matrix Factorization with Spatial-Temporal Regularization for Graph-Based Time Series Forecasting. Sensors 2022, 22, 5877. https://doi.org/10.3390/s22155877
Li J, Wu P, Li R, Pian Y, Huang Z, Xu L, Li X. ST-CRMF: Compensated Residual Matrix Factorization with Spatial-Temporal Regularization for Graph-Based Time Series Forecasting. Sensors. 2022; 22(15):5877. https://doi.org/10.3390/s22155877
Chicago/Turabian StyleLi, Jinlong, Pan Wu, Ruonan Li, Yuzhuang Pian, Zilin Huang, Lunhui Xu, and Xiaochen Li. 2022. "ST-CRMF: Compensated Residual Matrix Factorization with Spatial-Temporal Regularization for Graph-Based Time Series Forecasting" Sensors 22, no. 15: 5877. https://doi.org/10.3390/s22155877
APA StyleLi, J., Wu, P., Li, R., Pian, Y., Huang, Z., Xu, L., & Li, X. (2022). ST-CRMF: Compensated Residual Matrix Factorization with Spatial-Temporal Regularization for Graph-Based Time Series Forecasting. Sensors, 22(15), 5877. https://doi.org/10.3390/s22155877