Semi-Supervised Domain Adaptation for Multi-Label Classification on Nonintrusive Load Monitoring
Abstract
:1. Introduction
- We conduct the first classification study in the domain adaptation field for NILM;
- We show performance improvements by incorporating robust feature information distillation techniques based on the teacher–student structure into domain adaptation;
- The decision boundaries are refined through PL-based domain stabilization.
2. Related Work
2.1. Nonintrusive Load Monitoring
2.2. Domain Adaptation
3. Semi-Supervised Domain Adaptation for Multi-Label Classification on Non-Intrusive Load Monitoring
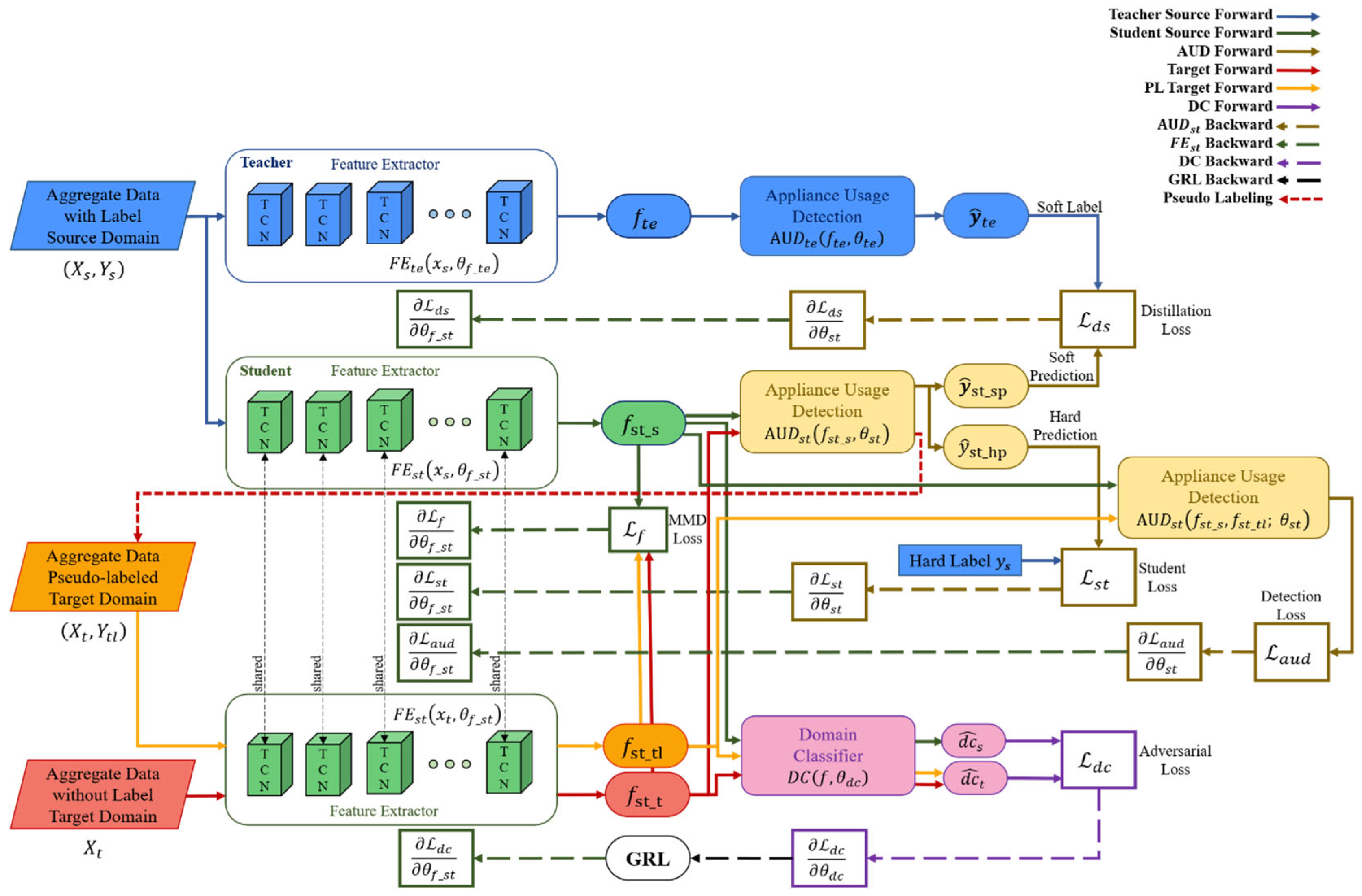
3.1. Network Architecture
- (1)
- Knowledge distillation: knowledge is distilled using a TCN feature extraction-based teacher–student network to receive robust domain-independent features of source data. TCN is an extended time-series data modeling structure in CNN. It provides better performance than typical time-series deep learning models such as LSTM because it has a much longer and more effective memory without a gate mechanism. The TCN consists of several residual blocks, and this block consists of a dilated casual convolution operation O. For input and filter , at point is defined by Equation (3).where is the dilated factor, is -dilated convolution, k is the filter size, and is the past value. However, as the network depth increases, performance decreases rapidly due to overfitting. However, as the network depth increases, performance decreases quickly due to overfitting. Resnet’s key concept, namely, residual mapping, can solve this problem. The TCN residual block includes two layers of dilated casual convolution based on the ReLU activation function, weighted normalization, and dropout. The 1 × 1 convolution layer on the TCN ensures that the input and output are the same size. The output of the transformation of the time series data in the TCN dual block is added to the identity mapping of the input and expressed as follows:where means the set of parameters of the network. It has already been demonstrated that this concept of residual block improves network performance by learning modifications to identity mapping rather than overall transformations. Based on this, it is possible to build a deep TCN network by stacking multiple TCN residual blocks. Assuming that is the input of the -th block, the network forward propagation from the I-th block to the -th block can then be formulated as follows:where, is -th block, is the parameter set of the -th block. Therefore, the feature extractor of the TN is defined as follows:where the number of layers is , is source data, is the parameter set of TN, is source data, is the parameter set of block in the TN. Additionally, the feature extractor of SN can be defined as follows:where is the number of layers, is the parameter set of SN, is the parameter set of block in SN. Based on extracted from Equation (6), the TN must extract soft label information for transferring knowledge to the SN through appliance usage detection, which consists of a fully connected layer. The output of the TN is defined as follows:where refers to the TN, is a predicted classification label of in the TN, is a temperature parameter, a function with a temperature parameter. is the parameter set of , is the elements of output vector of , refers to element, is the number of elements of the output vector. Maximize the benefits of soft label values for knowledge distillation by using temperature parameters to prevent information loss in output. The estimated soft label is compared to the soft prediction of SN and is used as a distillation loss in network training. is obtained as follows:where refers to SN, is a predicted classification label of in the SN and a soft prediction value of SN, is the parameter set of , and is the i-th element of the output vector of The classification performance of SN should be evaluated along with knowledge distillation. The performance can be evaluated by comparing the hard prediction of SN with the ground truth of the source domain data. is obtained as follows:where is a predicted classification label of in the SN and is used as a hard prediction value of SN. In Equation (10), the temperature parameter is not used.
- (2)
- Robust domain adaptation: domain adaptation is performed with robust features extracted with knowledge distillation to obtain domain-independent features. Domain adaptation consists of the following three stages: feature extractor, domain classifier, and appliance usage detection. First, a feature extractor of SN is used. A feature extractor of the source data and an of the target data share a parameter set. Models learned with only source data are difficult to express with target data. To adapt the target domain data representation to , the model learns the feature distribution difference between the two domains using MMD and minimizes it. The MMD distance is obtained as follows:where is a feature space mapping function that turns the original feature space into the reproducing kernel Hilbert space H. Further descriptions of the kernel are given in the following subsection. The domain classifier learns by setting the ground truth values of the source domain data and the target domain data , respectively, to separate the domain-independent features from the feature extractor. has an output for source domain data and an output for target domain data. The two outputs are defined as follows:where is the source domain feature, is the target domain feature and is the parameter set of DC. and values between 0 and 1. can obtain domain-independent features from by learning that the source and target domains cannot be classified. Appliance usage detection uses the of SN. verifies classification performance using source data as input domain-independent features. The prediction of device usage detection can be obtained using Equation (10). In network inference, prediction of the target domain may be obtained using Equation (14).where is the prediction of target data. Detection performance for target domain data is evaluated by comparing with ground truth of target domain data.
- (3)
- Domain stabilization: The target domain data is pseudo-labeled with to enhance the data, thereby stabilizing the domain and improving the performance of the network. First, the feature of the target domain data is input to the . If is obtained through Equation (14), PL is generated as a prediction value having the highest probability among values. However, if the probability is lower than the threshold, the data is not pseudo-labeled. The threshold is obtained experimentally. Domain stabilization consists of three steps, such as feature extraction and domain classifier. Appliance usage detection uses the following three types of data: source data (, ), pseudo-labeled target data (, ), and unlabeled target data . For feature extraction, , and are output through . DC has no change in the domain, , and are classified as inputs, as in Equations (12) and (13). The appliance usage detection performs .
3.2. Network Losses
- (1)
- Knowledge distillation loss: As shown in Figure 1, the knowledge distillation phase loss is the sum of the distillation loss and student loss . is to include the difference in the classification results of the TN and the SN in the loss. is defined as follows:where is the cross-entropy loss and is the learning rate. The cross-entropy loss is calculated about teacher and student output. If the classification results of the teacher and the student are the same and distillation is good, takes a small value. Additionally, means the cross-entropy loss of the classification of SN. is defined as follows:Even in a network with relatively fewer parameters than in the TN, is also reduced when is smaller, so it shows good feature extraction and classification performance.
- (2)
- Feature distribution difference loss: As shown in Figure 1, the feature distribution difference loss is MMD Loss [44] . estimates the difference between the feature distribution of the source domain data and the feature distribution of the target domain data through MMD. is generally defined as follows:For the mapping function of Equation (17), we use kernel tricks because computational resources are required too much to obtain all the moments. We utilize the Gaussian kernel as shown in Equation (18).where g is the Gaussian kernel. In the Equation (18), Taylor’s development of the exponential develops as in Equation (19).Since Equation (19) contains all the moments for x, we use the Gaussian kernel. Gis derived as Equation (20).When Equation (15) is organized using Equation (20), is re-formulated as shown in Equation (21).
- (3)
- Domain classification loss: As shown in Figure 1, the domain classification loss is related to and . is modeled so that the source domain and the target domain cannot be distinguished. To minimize the distribution difference between and , the loss of should be maximized. Using and of , cross-entropy loss as a binary classifier-based can be obtained as Equation (22).where, is the sample number of mini-batch.
- (4)
- Appliance usage detection loss: as shown in Figure 1, the appliance usage detection loss uses in the domain adaptation phase and in the robust domain adaptation phase. Since both losses are applied to the same , the same loss equation is formularized as in Equations (23) and (24).Each neural network is learned by differentiating loss with corresponding weights, as shown in the dotted line in Figure 1.
3.3. Training Strategy
| Algorithm 1: Parameter optimization procedure of the proposed method. |
| Input with M total samples, respectively. Output # Knowledge Distillation Phase for m = 0 to epochs do for n to minibatch do #Foward propagation Teacher: , Student: , , , #Back propagation end for end for # Domain Adaptation Phase for m = 0 to epochs do for n to minibatch do #Foward propagation Source: Target: , #Back propagation end for end for # Robust Domain Adaptation Phase #Pseudo labeling , for m = 0 to epochs do for n to minibatch do #Foward propagation Source: Target: , Pseudo Target: #Back propagation end for end for |
4. Experiments
4.1. Data Preparation
4.1.1. Dataset
4.1.2. Data Preprocessing
4.2. Experimental Setup
4.2.1. Implementation Configuration
4.2.2. Ablation Study Methods
- Baseline: Typical domain adaptation method with BiLSTM-based feature extractors;
- TCN-DA: Domain adaptation method with TCN-based feature extractor;
- gkMMD-DA: Domain adaptation method with Gaussian kernel trick-based MMD Loss in baseline;
- TS-DA: A domain adaptation method for extracting features based on the robust knowledge distillation of the teacher–student structure. The feature extractor of SN used BiLSTM, such as the baseline, and the feature extractor of TN used BiLSTM, which is four times the size of the student;
- PL-DA: How to perform domain optimization with pseudo labeling on baseline method
4.2.3. Evaluation Metrics
4.3. Case Studies and Discussions
4.3.1. Domain Adaptation within the Same Dataset
4.3.2. Domain Adaptation between Different Datasets
4.3.3. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gherheș, V.; Fărcașiu, M.A. Sustainable Behavior among Romanian Students: A Perspective on Electricity Consumption in Households. Sustainability 2021, 13, 9357. [Google Scholar] [CrossRef]
- Somchai, B.; Boonyang, P. Non-intrusive appliances load monitoring (nilm) for energy conservation in household with low sampling rate. Procedia Comput. Sci. 2016, 86, 172–175. [Google Scholar]
- Nur Farahin, E.; Md Pauzi, A.; Yusri, H.M. RETRACTED: A review disaggregation method in Non-intrusive Appliance Load Monitoring. Renew. Sustain. Energy Rev. 2016, 66, 163–173. [Google Scholar]
- Shikha, S.; Angshul, M. Deep sparse coding for non–intrusive load monitoring. IEEE Trans. Smart Grid 2017, 9, 4669–4678. [Google Scholar]
- Cominola, A.; Giuliani, M.; Piga, D.; Castelletti, A.; Rizzoli, A.E. A hybrid signature-based iterative disaggregation algorithm for non-intrusive load monitoring. Appl. Energy 2017, 185, 331–344. [Google Scholar] [CrossRef]
- Shi, X.; Ming, H.; Shakkottai, S.; Xie, L.; Yao, J. Nonintrusive load monitoring in residential households with low-resolution data. Appl. Energy 2019, 252, 113283. [Google Scholar] [CrossRef]
- Georgia, E.; Lina, S.; Vladimir, S. Power Disaggregation of Domestic Smart Meter Readings Using Dynamic Time warping. In Proceedings of the 2014 6th International Symposium on Communications, Control and Signal Processing (ISCCSP), Athens, Greece, 21–23 May 2014; IEEE: Manhattan, NY, USA, 2014; pp. 36–39. [Google Scholar]
- Yu-Hsiu, L.; Men-Shen, T. Non-intrusive load monitoring by novel neuro-fuzzy classification considering uncertainties. IEEE Trans. Smart Grid 2014, 5, 2376–2384. [Google Scholar]
- Kanghang, H.; He, K.; Stankovic, L.; Liao, J.; Stankovic, V. Non-intrusive load disaggregation using graph signal processing. IEEE Trans. Smart Grid 2016, 9, 1739–1747. [Google Scholar]
- Hart, G.W. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, J.; Li, W.; Gulliver, T.A.; Li, S. Semisupervised multilabel deep learning based nonintrusive load monitoring in smart grids. IEEE Trans. Ind. Inform. 2019, 16, 6892–6902. [Google Scholar] [CrossRef]
- Sagar, V.; Shikha, S.; Angshul, M. Multi-label LSTM autoencoder for non-intrusive appliance load monitoring. Electr. Power Syst. Res. 2021, 199, 107414. [Google Scholar]
- Hyeontaek, H.; Sanggil, K. Nonintrusive Load Monitoring using a LSTM with Feedback Structure. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar]
- Da Silva Nolasco, L.; Lazzaretti, A.E.; Mulinari, B.M. DeepDFML-NILM: A New CNN-Based Architecture for Detection, Feature Extraction and Multi-Label Classification in NILM Signals. IEEE Sens. J. 2021, 22, 501–509. [Google Scholar] [CrossRef]
- Christoforos, N.; Dimitris, V. On time series representations for multi-label NILM. Neural Comput. Appl. 2020, 32, 17275–17290. [Google Scholar]
- Patrick, H.; Calatroni, A.; Rumsch, A.; Paice, A. Review on deep neural networks applied to low-frequency nilm. Energies 2021, 14, 2390. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Improving nonintrusive load monitoring efficiency via a hybrid programing method. IEEE Trans. Ind. Inform. 2016, 12, 2148–2157. [Google Scholar] [CrossRef]
- Basu, K.; Debusschere, V.; Douzal-Chouakria, A.; Bacha, S. Time series distance-based methods for non-intrusive load monitoring in residential buildings. Energy Build. 2015, 96, 109–117. [Google Scholar] [CrossRef]
- Yaroslav, G.; Lempitsky, V. Unsupervised Domain Adaptation by Backpropagation. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1180–1189. [Google Scholar]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Unsupervised domain adaptation with residual transfer networks. Adv. Neural Inf. Processing Syst. 2016, 29, 136–144. [Google Scholar]
- Liu, Y.; Zhong, L.; Qiu, J.; Lu, J.; Wang, W. Unsupervised domain adaptation for nonintrusive load monitoring via adversarial and joint adaptation network. IEEE Trans. Ind. Inform. 2021, 18, 266–277. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Liang, H. Deep Domain Adaptation for Non-Intrusive Load Monitoring Based on a Knowledge Transfer Learning Network. IEEE Trans. Smart Grid 2021, 13, 280–292. [Google Scholar] [CrossRef]
- Suzuki, K.; Inagaki, S.; Suzuki, T.; Nakamura, H.; Ito, K. Nonintrusive Appliance Load Monitoring Based on Integer Programming. In Proceedings of the 2008 SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; IEEE: Manhattan, NY, USA, 2008; pp. 2742–2747. [Google Scholar]
- Michael, B.; Jürgen, V. Nonintrusive appliance load monitoring based on an optical sensor. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; IEEE: Manhattan, NY, USA, 2003; Volume 4, p. 8. [Google Scholar]
- Arend, B.J.; Xiaohua, X.; Jiangfeng, Z. Active Power Residential Non-Intrusive Appliance Load Monitoring System. In Proceedings of the AFRICON 2009, Nairobi, Kenya, 23–25 September 2009; IEEE: Manhattan, NY, USA, 2009; pp. 1–6. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2010, 22, 199–210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mei, W.; Weihong, D. Deep visual domain adaptation: A survey. Neurocomputing 2018, 312, 135–153. [Google Scholar]
- Isobe, T.; Jia, X.; Chen, S.; He, J.; Shi, Y.; Liu, J.; Lu, H.; Wang, S. Multi-Target Domain Adaptation with Collaborative Consistency Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8187–8196. [Google Scholar]
- Yuang, L.; Wei, Z.; Jun, W. Source-Free Domain Adaptation for Semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1215–1224. [Google Scholar]
- Guoqiang, W.; Lan, C.; Zeng, W.; Chen, Z. Metaalign: Coordinating Domain Alignment and Classification for Unsupervised Domain Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 16643–16653. [Google Scholar]
- Zechen, B.; Wang, Z.; Wang, J.; Hu, D.; Ding, E. Unsupervised Multi-Source Domain Adaptation for Person Re-Identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12914–12923. [Google Scholar]
- Jingjing, L.; Jing, M.; Su, H.; Lu, K.; Zhu, L.; Shen, H.T. Faster domain adaptation networks. IEEE Trans. Knowl. Data Eng. 2021, 1. [Google Scholar] [CrossRef]
- Dongdong, W.; Han, T.; Chu, F.; Zuo, M.J. Weighted domain adaptation networks for machinery fault diagnosis. Mech. Syst. Signal Processing 2021, 158, 107744. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Zhang, N.; Saenko, K.; Darrell, T. Deep domain confusion: Maximizing for domain invariance. arXiv 2014, arXiv:1412.3474. [Google Scholar]
- Hao, W.; Wang, W.; Zhang, C.; Xu, F. Cross-Domain Metric Learning Based on Information Theory. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Juntao, H.; Hongsheng, Q. Unsupervised Domain Adaptation with Multi-kernel MMD. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; IEEE: Manhattan, NY, USA, 2021; pp. 8576–8581. [Google Scholar]
- Zhang, W.; Zhang, X.; Lan, L.; Luo, Z. Maximum mean and covariance discrepancy for unsupervised domain adaptation. Neural Processing Lett. 2020, 51, 347–366. [Google Scholar] [CrossRef]
- Wen, Z.; Wu, W. Discriminative Joint Probability Maximum Mean Discrepancy (DJP-MMD) for Domain Adaptation. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; IEEE: Manhattan, NY, USA, 2020; pp. 1–8. [Google Scholar]
- Mingsheng, L.; Zhu, H.; Wang, J.; Jordan, M.I. Deep Transfer Learning with Joint Adaptation Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2208–2217. [Google Scholar]
- Wan, N.; Zhang, C.; Chen, Q.; Li, H.; Liu, X.; Wei, X. MDDA: A Multi-scene Recognition Model with Multi-dimensional Domain Adaptation. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–10 May 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1245–1250. [Google Scholar]
- Wang, L.; Mao, S.; Wilamowski, B.M.; Nelms, R.M. Pre-trained models for non-intrusive appliance load monitoring. IEEE Trans. Green Commun. Netw. 2021, 6, 56–68. [Google Scholar] [CrossRef]
- Shaojie, B.; Zico, K.J.; Koltun, V.K. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Geoffrey, H.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Xin, Y.; Chaofeng, H.; Lifeng, S. Two-Stream Federated Learning: Reduce the Communication Costs. In Proceedings of the 2018 IEEE Visual Communications and Image Processing (VCIP), Taichung, Taiwan, 9–12 December 2018; IEEE: Manhattan, NY, USA, 2018; pp. 1–4. [Google Scholar]
- Kelly, J.K.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [Green Version]
- Zico, K.J.; Johnson, M.J. Redd: A public data set for energy disaggregation research. In Proceedings of the Workshop on Data Mining Applications in Sustainability (SIGKDD), San Diego, CA, USA, 21 August 2011; pp. 59–62. [Google Scholar]
- Linge, S.; Langtangen, H.P. Programming for Computations-Python: A Gentle Introduction to Numerical Simulations with Python 3.6; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Processing Syst. 2019, 32, 8024–8035. [Google Scholar]

| UK-DALE | REDD | |||||||
|---|---|---|---|---|---|---|---|---|
| House 1 | House 2 | House 1 | House 3 | |||||
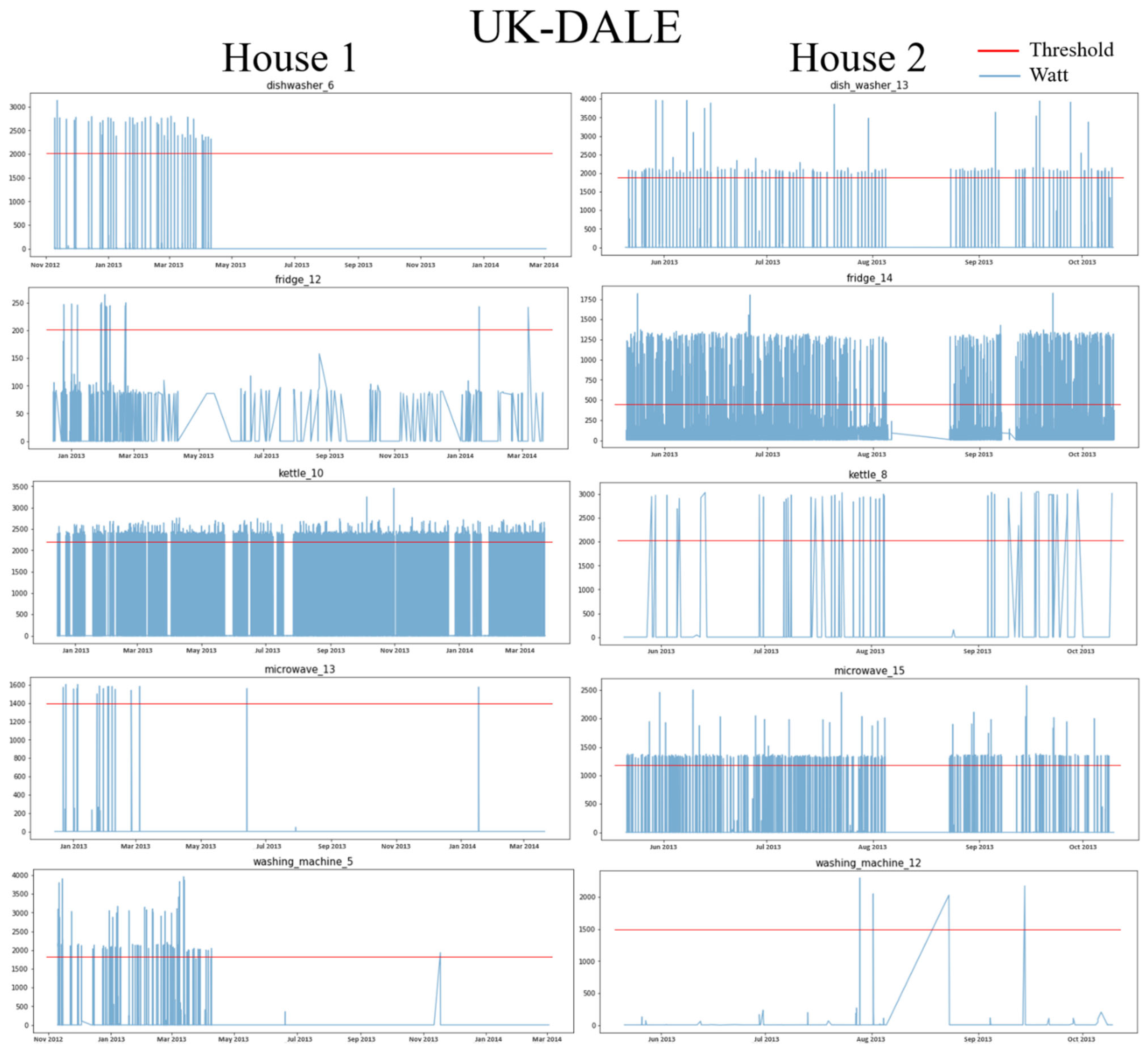
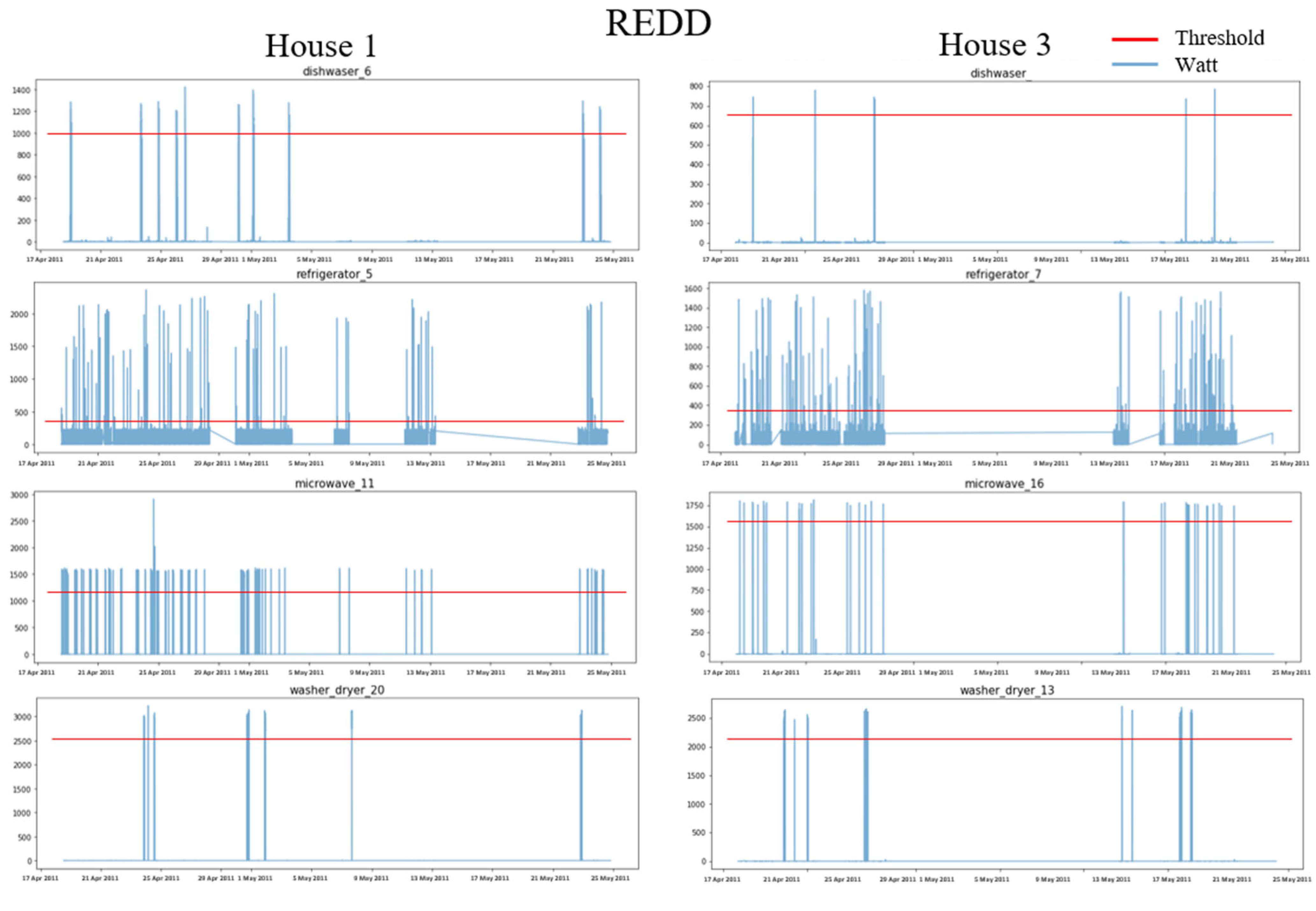
| Appliance | Threshold | The Number of ON Event | Threshold | The Number of ON Event | Threshold | The Number of ON Event | Threshold | The Number of ON Event |
| DW | 2000 | 4431 | 1800 | 3236 | 1000 | 6712 | 650 | 2934 |
| FG | 250 | 2441 | 400 | 5291 | 400 | 2944 | 350 | 3344 |
| KT | 2200 | 4495 | 2000 | 1694 | - | - | - | - |
| MV | 1400 | 1242 | 1200 | 4218 | 1200 | 4809 | 1600 | 1327 |
| WM | 1800 | 4980 | 1500 | 1524 | 2500 | 4796 | 2200 | 5764 |
| Parameter Description | Value |
|---|---|
| Number of TCN blocks | 8 (TN) |
| 5 (SN) | |
| Number of filters in each TCN block | 128 (TN) |
| 64 (SN) | |
| Filter size | 3 |
| Number of fully connected layers | 5 (TN) |
| 3 (SN) | |
| 2 (Domain Classifier) | |
| Dilation factor | |
| Activation function | ReLU |
| Dropout probability | 0.1 |
| Number of maximum epochs | 200 |
| Number of minimum early stopping epochs | 4 |
| Mini-batch size | 512 |
| Learning rate | 3 × 10−3 |
| Appliance | Method | UK-DALE | REDD | ||
|---|---|---|---|---|---|
| DW | Baseline | 0.781 | 0.805 | ||
| TCN-DA | 0.832 | 0.827 | |||
| gkMMD-DA | 0.778 | 0.793 | |||
| TS-DA | 0.812 | 0.826 | |||
| PL-DA | 0.787 | 0.811 | |||
| Ours | 0.822 | 0.832 | |||
| Improvement | 5.25% | 3.35% | |||
| FG | Baseline | 0.833 | 0.834 | 0.817 | 0.818 |
| TCN-DA | 0.842 | 0.841 | 0.829 | 0.840 | |
| gkMMD-DA | 0.837 | 0.836 | 0.819 | 0.819 | |
| TS-DA | 0.850 | 0.853 | 0.824 | 0.827 | |
| PL-DA | 0.834 | 0.845 | 0.818 | 0.819 | |
| Ours | 0.875 | 0.872 | 0.843 | 0.852 | |
| Improvement | 5.04% | 4.56% | 3.18% | 4.16% | |
| KT | Baseline | 0.761 | 0.832 | ||
| TCN-DA | 0.811 | 0.839 | |||
| gkMMD-DA | 0.753 | 0.820 | |||
| TS-DA | 0.807 | 0.835 | |||
| PL-DA | 0.770 | 0.833 | |||
| Ours | 0.817 | 0.868 | |||
| Improvement | 7.36% | 4.33% | |||
| MV | Baseline | 0.742 | 0.791 | 0.793 | 0.790 |
| TCN-DA | 0.751 | 0.798 | 0.806 | 0.721 | |
| gkMMD-DA | 0.746 | 0.795 | 0.797 | 0.774 | |
| TS-DA | 0.753 | 0.803 | 0.804 | 0.798 | |
| PL-DA | 0.744 | 0.796 | 0.794 | 0.793 | |
| Ours | 0.774 | 0.812 | 0.814 | 0.818 | |
| Improvement | 4.31% | 2.65% | 2.65% | 3.54% | |
| WM | Baseline | 0.615 | 0.611 | 0.841 | 0.782 |
| TCN-DA | 0.725 | 0.708 | 0.844 | 0.799 | |
| gkMMD-DA | 0.623 | 0.625 | 0.842 | 0.786 | |
| TS-DA | 0.668 | 0.653 | 0.832 | 0.783 | |
| PL-DA | 0.623 | 0.615 | 0.843 | 0.783 | |
| Ours | 0.736 | 0.713 | 0.870 | 0.832 | |
| Improvement | 19.67% | 16.69% | 3.45% | 6.39% | |
| Appliance | UK-DALE | REDD | ||
|---|---|---|---|---|
| DW | 0.823 | 0.828 | ||
| FG | 0.857 | 0.854 | 0.834 | 0.847 |
| KT | 0.813 | 0.841 | ||
| MV | 0.762 | 0.805 | 0.809 | 0.764 |
| WM | 0.730 | 0.709 | 0.852 | 0.815 |
| Appliance | Method | ||
|---|---|---|---|
| DW | Baseline | 0.741 | 0.712 |
| TCN-DA | 0.779 | 0.737 | |
| gkMMD-DA | 0.736 | 0.713 | |
| TS-DA | 0.770 | 0.745 | |
| PL-DA | 0.747 | 0.714 | |
| Ours | 0.778 | 0.747 | |
| Improvement | 4.99% | 4.92% | |
| FG | Baseline | 0.786 | 0.764 |
| TCN-DA | 0.794 | 0.787 | |
| gkMMD-DA | 0.787 | 0.769 | |
| TS-DA | 0.800 | 0.772 | |
| PL-DA | 0.787 | 0.770 | |
| Ours | 0.821 | 0.797 | |
| Improvement | 4.45% | 4.32% | |
| MV | Baseline | 0.719 | 0.739 |
| TCN-DA | 0.726 | 0.716 | |
| gkMMD-DA | 0.719 | 0.746 | |
| TS-DA | 0.729 | 0.749 | |
| PL-DA | 0.717 | 0.743 | |
| Ours | 0.742 | 0.763 | |
| Improvement | 3.2% | 3.25% | |
| WM | Baseline | 0.563 | 0.758 |
| TCN-DA | 0.669 | 0.773 | |
| gkMMD-DA | 0.573 | 0.766 | |
| TS-DA | 0.610 | 0.758 | |
| PL-DA | 0.568 | 0.763 | |
| Ours | 0.672 | 0.769 | |
| Improvement | 19.36% | 1.45% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hur, C.-H.; Lee, H.-E.; Kim, Y.-J.; Kang, S.-G. Semi-Supervised Domain Adaptation for Multi-Label Classification on Nonintrusive Load Monitoring. Sensors 2022, 22, 5838. https://doi.org/10.3390/s22155838
Hur C-H, Lee H-E, Kim Y-J, Kang S-G. Semi-Supervised Domain Adaptation for Multi-Label Classification on Nonintrusive Load Monitoring. Sensors. 2022; 22(15):5838. https://doi.org/10.3390/s22155838
Chicago/Turabian StyleHur, Cheong-Hwan, Han-Eum Lee, Young-Joo Kim, and Sang-Gil Kang. 2022. "Semi-Supervised Domain Adaptation for Multi-Label Classification on Nonintrusive Load Monitoring" Sensors 22, no. 15: 5838. https://doi.org/10.3390/s22155838
APA StyleHur, C.-H., Lee, H.-E., Kim, Y.-J., & Kang, S.-G. (2022). Semi-Supervised Domain Adaptation for Multi-Label Classification on Nonintrusive Load Monitoring. Sensors, 22(15), 5838. https://doi.org/10.3390/s22155838





