Quantitative Analysis Using Consecutive Time Window for Unobtrusive Atrial Fibrillation Detection Based on Ballistocardiogram Signal
Abstract
1. Introduction
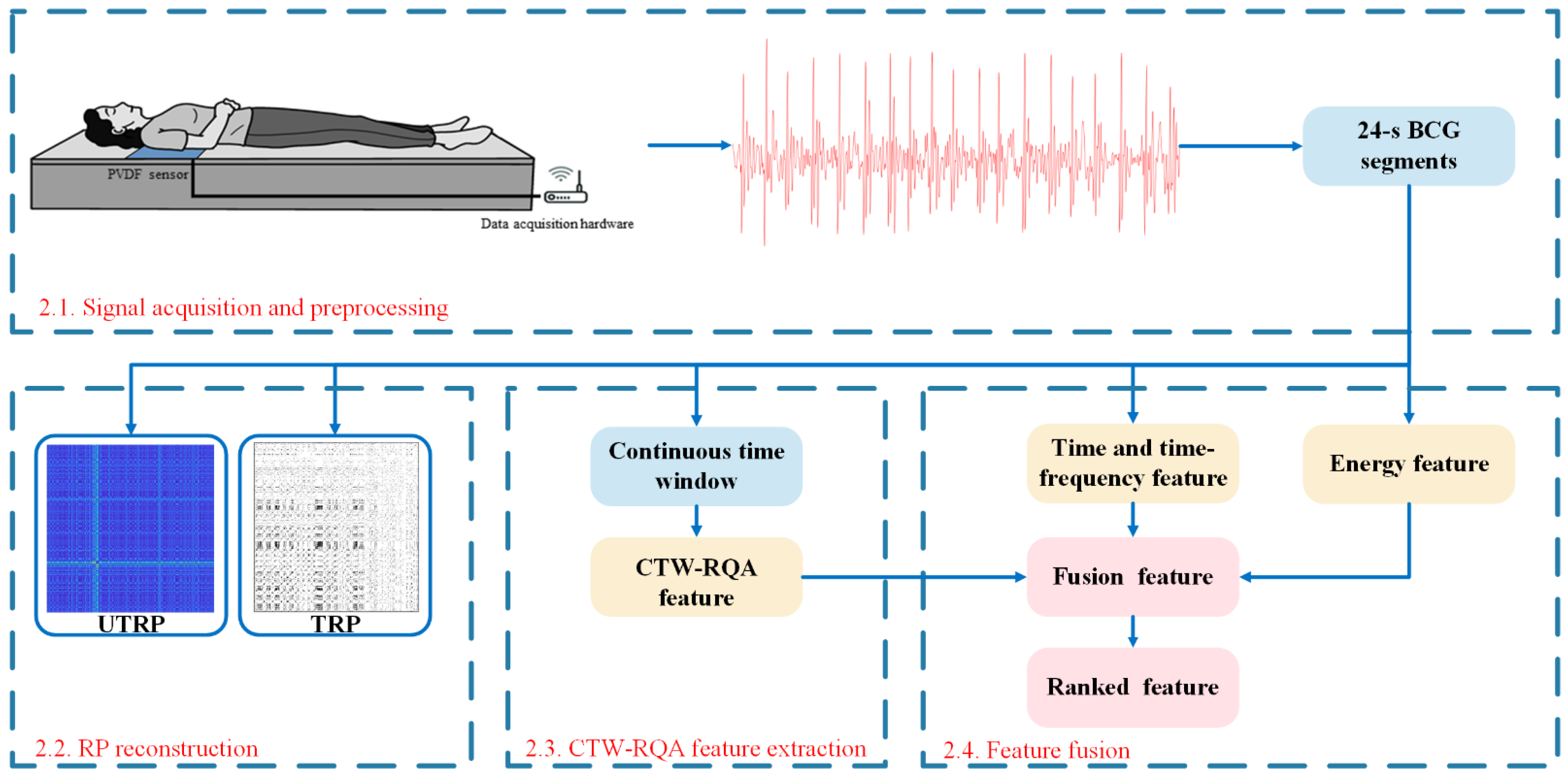
2. Methods
2.1. Signal Acquisition and Preprocessing
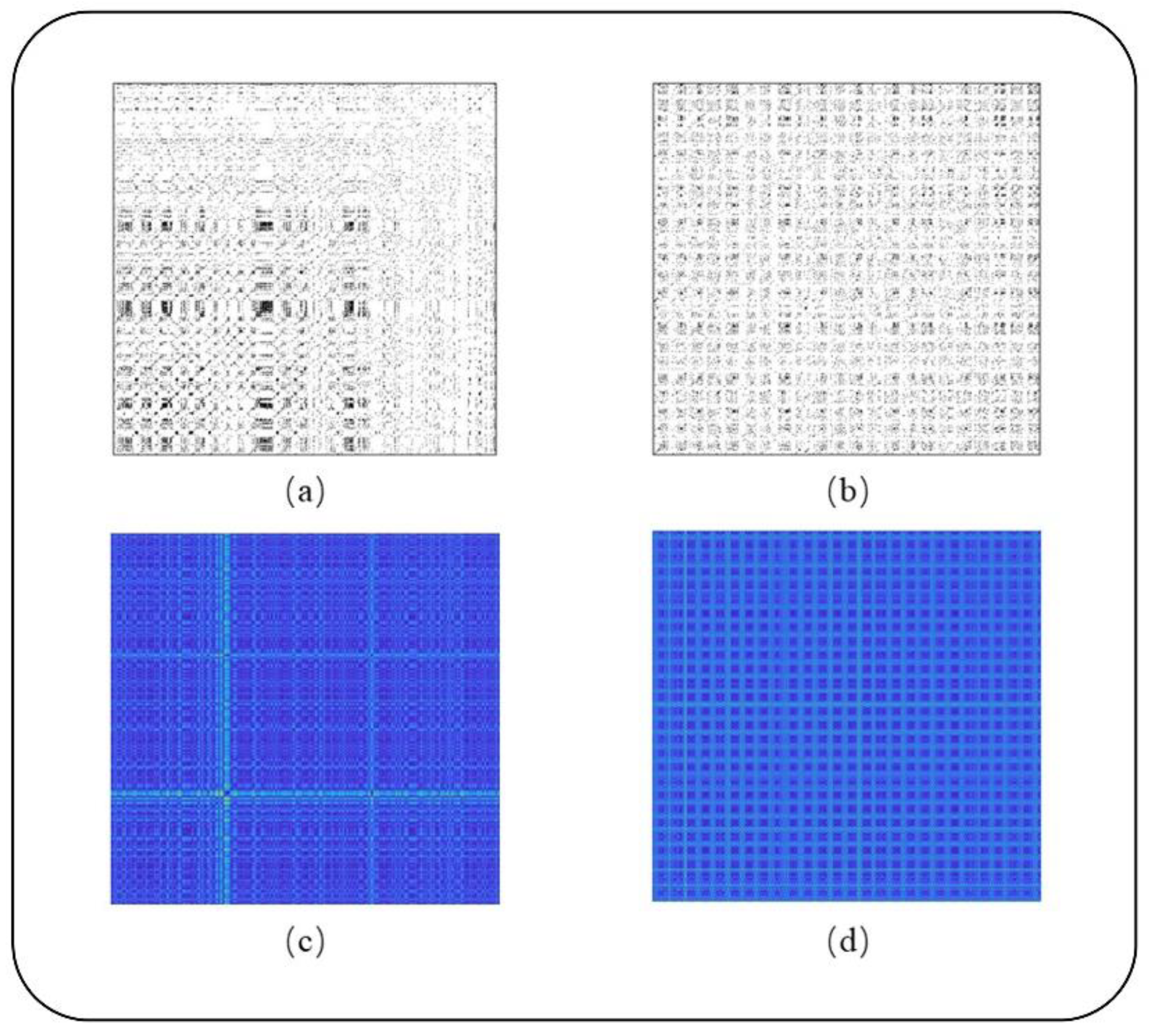
2.2. RP Reconstruction
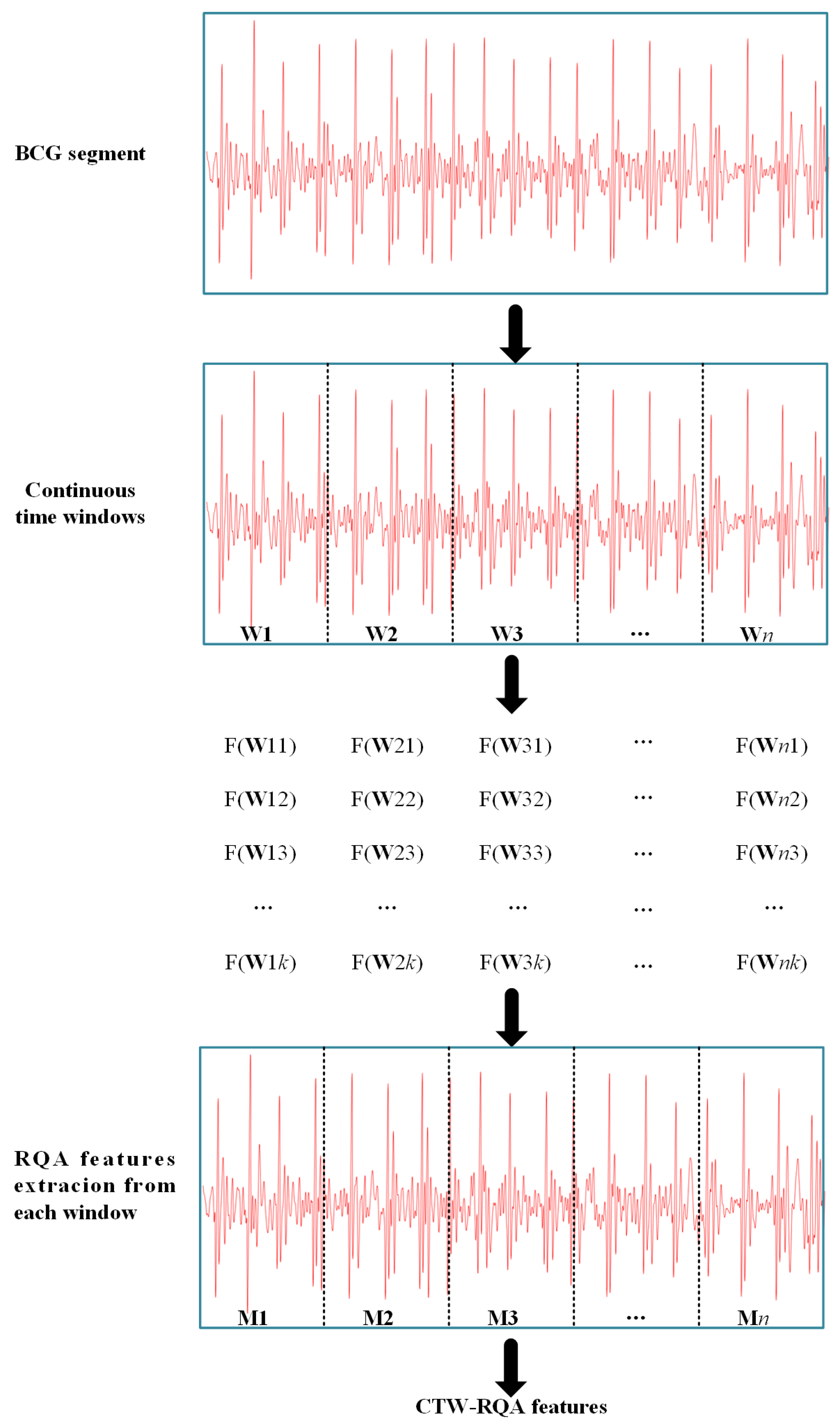
2.3. CTW–RQA Feature Extraction
2.4. Feature Fusion
2.4.1. Time and Time-Frequency Features and Energy Feature Extraction
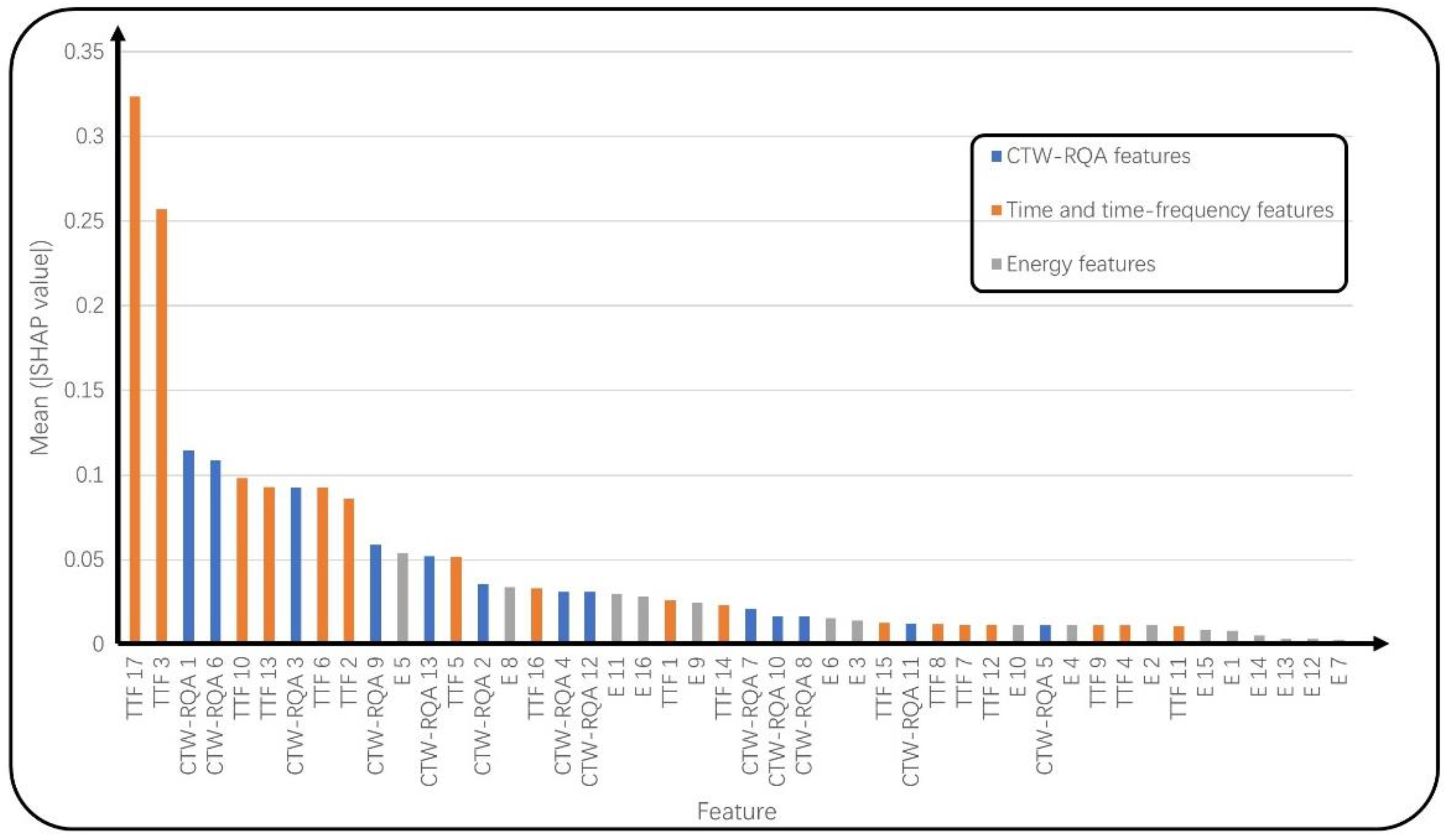
2.4.2. Feature Ranking and Selection
2.4.3. Fusion Feature Extraction
3. Results
3.1. AF Detection Based on the RP Diagram
3.2. AF Detection Based on CTW–RQA Features
3.3. AF Detection Based on Time and Time-Frequency Features and Energy Features
3.4. AF Detection Based on Fusion Features
3.5. AF Detection Based on Ranked Features
4. Discussion
4.1. Effects of RP and RQA
4.2. Effect of the Proposed CTW–RQA Features
4.3. Effect of Fusion Features and Ranked Features
4.4. Comparison with Existing Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 56.38 | 59.41 | 40.25 | 72.50 |
| NB | 62.88 | 66.78 | 51.25 | 74.50 |
| ENS | 77.88 | 80.38 | 73.75 | 82.00 |
| RF | 83.50 | 85.64 | 80.50 | 86.50 |
| DT | 79.63 | 79.70 | 79.50 | 79.75 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 56.50 | 65.52 | 36.19 | 78.95 |
| NB | 69.38 | 69.15 | 75.24 | 62.89 |
| ENS | 75.75 | 78.54 | 74.05 | 77.63 |
| RF | 81.75 | 83.74 | 80.95 | 82.63 |
| DT | 72.25 | 72.92 | 75.00 | 69.21 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 59.25 | 65.56 | 43.17 | 76.15 |
| NB | 56.63 | 54.21 | 99.02 | 12.05 |
| ENS | 81.25 | 80.95 | 82.93 | 79.49 |
| RF | 89.38 | 90.52 | 88.54 | 90.26 |
| DT | 78.88 | 78.76 | 80.49 | 77.18 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 63.13 | 67.52 | 47.31 | 78.24 |
| NB | 61.13 | 55.85 | 97.70 | 26.16 |
| ENS | 82.13 | 81.47 | 82.10 | 82.15 |
| RF | 86.13 | 86.46 | 84.91 | 87.29 |
| DT | 79.75 | 78.70 | 80.31 | 79.22 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 65.88 | 69.21 | 53.73 | 77.37 |
| NB | 71.63 | 85.22 | 50.39 | 91.73 |
| ENS | 84.38 | 83.33 | 84.83 | 83.94 |
| RF | 87.63 | 85.89 | 89.20 | 86.13 |
| DT | 79.38 | 76.79 | 82.52 | 76.40 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 58.38 | 59.00 | 50.76 | 65.76 |
| NB | 72.13 | 68.31 | 80.96 | 63.55 |
| ENS | 75.50 | 74.03 | 77.41 | 73.65 |
| RF | 78.50 | 77.89 | 78.68 | 78.33 |
| DT | 73.63 | 72.82 | 74.11 | 73.15 |
References
- Miyasaka, Y.; Barnes, M.E.; Gersh, B.J.; Cha, S.S.; Bailey, K.R.; Abhayaratna, W.P.; Seward, J.B.; Tsang, T.S. Secular trends in incidence of atrial fibrillation in Olmsted County, Minnesota, 1980 to 2000, and implications on the projections for future prevalence. Circulation 2006, 114, 119–125. [Google Scholar] [CrossRef]
- Go, A.S.; Hylek, E.M.; Phillips, K.A.; Chang, Y.; Henault, L.E.; Selby, J.V.; Singer, D.E. Prevalence of diagnosed atrial fibrillation in adults: National implications for rhythm management and stroke prevention: The AnTicoagulation and Risk Factors in Atrial Fibrillation (ATRIA) Study. Jama 2001, 285, 2370–2375. [Google Scholar] [CrossRef]
- Kirchhof, P. The future of atrial fibrillation management: Integrated care and stratified therapy. Lancet 2017, 390, 1873–1887. [Google Scholar] [CrossRef]
- Benjamin, E.J.; Muntner, P.; Alonso, A.; Bittencourt, M.S.; Callaway, C.W.; Carson, A.P.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Das, S.R.; et al. American Heart Association Council on Epidemiology and Prevention Statistics Committee and Stroke Statistics Subcommittee. Heart Disease and Stroke Statistics-2019 Update: A Report From the American Heart Association. Circulation 2019, 139, e56–e528. [Google Scholar] [CrossRef]
- Ladavich, S.; Ghoraani, B. Rate-independent detection of atrial fibrillation by statistical modeling of atrial activity. Biomed. Signal Process. Control 2015, 18, 274–281. [Google Scholar] [CrossRef]
- Ledezma, C.A.; Zhou, X.; Rodríguez, B.; Tan, P.; Diaz-Zuccarini, V. A modeling and machine learning approach to ECG feature engineering for the detection of ischemia using pseudo-ECG. PLoS ONE 2019, 14, e0220294. [Google Scholar] [CrossRef]
- Sepulveda-Suescun, J.P.; Murillo-Escobar, J.; Urda-Benitez, R.D.; Orrego-Metaute, D.A.; Orozco-Duque, A. Atrial fibrillation detection through heart rate variability using a machine learning approach and Poincare plot features. In Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, CO, USA, 26–28 October 2016; Springer: Berlin/Heidelberg, Germany, 2017; pp. 565–568. [Google Scholar]
- Dash, S.; Chon, K.H.; Lu, S.; Raeder, E.A. Automatic real time detection of atrial fibrillation. Ann. Biomed. Eng. 2009, 37, 1701–1709. [Google Scholar] [CrossRef]
- Guidoboni, G.; Sala, L.; Enayati, M.; Sacco, R.; Szopos, M.; Keller, J.M.; Popescu, M.; Despins, L.; Huxley, V.H.; Skubic, M. Cardiovascular function and ballistocardiogram: A relationship interpreted via mathematical modeling. IEEE Trans. Biomed. Eng. 2019, 66, 2906–2917. [Google Scholar] [CrossRef]
- Etemadi, M.; Inan, O.T. Wearable ballistocardiogram and seismocardiogram systems for health and performance. J. Appl. Physiol. 2018, 124, 452–461. [Google Scholar] [CrossRef]
- di Rienzo, M.; Meriggi, P.; Rizzo, F.; Vaini, E.; Faini, A.; Merati, G.; Parati, G.; Castiglioni, P. A Wearable system for the seismocardiogram assessment in daily life conditions. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4263–4266. [Google Scholar]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef]
- Rajput, J.S.; Sharma, M.; Kumar, T.S.; Acharya, U.R. Automated detection of hypertension using continuous wavelet transform and a deep neural network with Ballistocardiography signals. Int. J. Environ. Res. Public Health. 2022, 19, 4014. [Google Scholar] [CrossRef]
- Han, X.; Wu, X.; Wang, J.; Li, H.; Cao, K.; Cao, H.; Zhong, K.; Yang, X. The latest progress and development trend in the research of ballistocardiography (BCG) and seismocardiogram (SCG) in the field of health care. Appl. Sci. 2021, 11, 8896. [Google Scholar] [CrossRef]
- Kim, C.S.; Ober, S.L.; McMurtry, M.S.; Finegan, B.A.; Inan, O.T.; Mukkamala, R.; Hahn, J.O. Ballistocardiogram: Mechanism and potential for unobtrusive cardiovascular health monitoring. Sci. Rep. 2016, 6, 31297. [Google Scholar] [CrossRef]
- Jiang, F.; Zhou, Y.; Ling, T.; Zhang, Y.; Zhu, Z. Recent Research for Unobtrusive Atrial Fibrillation Detection Methods Based on Cardiac Dynamics Signals: A Survey. Sensors 2021, 21, 3814. [Google Scholar] [CrossRef]
- Brueser, C.; Diesel, J.; Zink, M.D.; Winter, S.; Schauerte, P.; Leonhardt, S. Automatic detection of atrial fibrillation in cardiac vibration signals. IEEE J. Biomed. Health Inform. 2012, 17, 162–171. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, B.; Xu, L.; Fang, P.; Hu, J. Automatic detection of atrial fibrillation from ballistocardiogram (BCG) using wavelet features and machine learning. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4322–4325. [Google Scholar]
- Wen, X.; Huang, Y.; Wu, X.; Zhang, B. A feasible feature extraction method for atrial fibrillation detection from BCG. IEEE J. Biomed. Health Inform. 2019, 24, 1093–1103. [Google Scholar] [CrossRef]
- Jiang, F.; Hong, C.; Cheng, T.; Wang, H.; Xu, B.; Zhang, B. Attention-based multi-scale features fusion for un obtrusive atrial fibrillation detection using ballistocardiogram signal. BioMedical Eng. OnLine 2021, 20, 12. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. World Sci. Ser. Nonlinear Sci. Ser. A 1995, 16, 441–446. [Google Scholar]
- Garcia-Ochoa, E. Recurrence plots: A new methodology for electrochemical noise signal analysis. J. Electroanal. Chem. 2020, 114092, 864. [Google Scholar] [CrossRef]
- Sun, R.; Wang, Y. Predicting termination of atrial fibrillation based on the structure and quantification of the recurrence plot. Med. Eng. Phys. 2008, 30, 1105–1111. [Google Scholar] [CrossRef]
- Mathunjwa, B.M.; Lin, Y.T.; Lin, C.H.; Abbod, M.F.; Shieh, J.S. ECG arrhythmia classification by using a recurrence plot and convolutional neural network. Biomed. Signal Processing Control 2021, 64, 102262. [Google Scholar] [CrossRef]
- Chen, S.T.; Chou, C.Y.; Tseng, L.H. Recurrence Plot Analysis of HRV for Exposure to Low-Frequency Noise. Advanced Materials Research; Trans Tech Publication Ltd.: Freienbach, Switzerland, 2014; Volume 1044, pp. 1251–1257. [Google Scholar]
- Panula, T.; Hurnanen, T.; Tuominen, J.; Kaisti, M.; Koskinen, J.; Pänkäälä, M.; Koivisto, T. A Wearable Sensor Node for Detecting Atrial Fibrillation Using Real-Time Digital Signal Processing. In Proceedings of the 2018 25th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 681–684. [Google Scholar]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Su, F.; Dong, H. Prediction of ECG Signal Based on TS Fuzzy Model of Phase Space Reconstruction. In Proceedings of the 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Quanzhou, China, 19–21 October 2019; pp. 1–6. [Google Scholar]
- Matassini, L.; Kantz, H.; Hołyst, J.; Hegger, R. Optimizing of recurrence plots for noise reduction. Phys. Rev. E 2002, 65, 021102. [Google Scholar] [CrossRef]
- Schinkel, S.; Dimigen, O.; Marwan, N. Selection of recurrence threshold for signal detection. Eur. Phys. J. Spec. Top. 2008, 164, 45–53. [Google Scholar] [CrossRef]
- Marwan, N. A historical review of recurrence plots. Eur. Phys. J. Spec. Top. 2008, 164, 3–12. [Google Scholar] [CrossRef]
- Gu, Q.; Li, Z.; Jia, W. Generalized Fisher score for feature selection. In Proceedings of the Twenty-Seventh Conference on Uncertainty in Artificial Intelligence (UAI’11), Barcelona, Spain, 14–17 July 2011; AUAI Press: Arlington, VA, USA, 2011; pp. 266–273. [Google Scholar]
- Ikram, S.T.; Cherukuri, A.K. Intrusion detection model using fusion of chi-square feature selection and multi class SVM. J. King Saud Univ.-Comput. Inf. Sci. 2017, 29, 462–472. [Google Scholar]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Chen, J.; Yuan, S.; Lv, D.; Xiang, Y. A Novel Self-learning Feature Selection Approach Based on Feature Attributions. Expert Syst. Appl. 2021, 183, 115219. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.D.; Pintelas, P.E. Machine learning: A review of classification and combining techniques. Artif. Intell. Rev. 2006, 26, 159–190. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Aloys, S.; Paul, B.; Ralf, P. Robust reconstruction of a signal from its unthresholded recurrence plot subject to disturbances. Phys. Lett. A 2017, 381, 604–615. [Google Scholar]
- Zhao, Z.; Zhang, Y.; Comert, Z.; Deng, Y. Computer-Aided Diagnosis System of Fetal Hypoxia Incorporating Recurrence Plot with Convolutional Neural Network. Front. Physiol. 2019, 10, 255. [Google Scholar] [CrossRef]
- Li, X.; Bi, G. Systematic analysis of uncertainty principles of the local polynomial Fourier transform. EURASIP J. Adv. Signal Process. 2014, 181. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature Selection. ACM Comput. Surv. 2018, 50, 1–45. [Google Scholar] [CrossRef]
- Inui, T.; Kohno, H.; Kawasaki, Y.; Matsuura, K.; Ueda, H.; Tamura, Y.; Watanabe, M.; Inage, Y.; Yakita, Y.; Wakabayashi, Y.; et al. Use of a smart watch for early detection of paroxysmal atrial fibrillation: Validation study. JMIR Cardio 2020, 4, 14857. [Google Scholar] [CrossRef]
- Rajakariar, K.; Koshy, A.N.; Sajeev, J.K.; Nair, S.; Roberts, L.; Teh, A.W. Accuracy of a smartwatch based single-lead electrocardiogram device in detection of atrial fibrillation. Heart 2020, 106, 665–670. [Google Scholar] [CrossRef]
- Shao, M.; Zhou, Z.; Bin, G.; Bai, Y.; Wu, S. A wearable electrocardiogram telemonitoring system for atrial fibrillation detection. Sensors 2020, 20, 606. [Google Scholar] [CrossRef]
- Xiong, Z.; Stiles, M.K.; Gillis, A.M.; Zhao, J. Enhancing the detection of atrial fibrillation from wearable sensors with neural style transfer and convolutional recurrent networks. Comput. Biol. Med. 2022, 146, e105551. [Google Scholar] [CrossRef]
- Jung, S.; Lee, H.A.; Kang, I.S.; Shin, S.H.; Chang, Y.; Woo, S.D.; Park, M.S.; Kim, Y.D.; Nam, H.S.; Heo, J.H.; et al. Clinical implications of atrial fibrillation detection using wearable devices in patients with cryptogenic stroke (CANDLE-AF) trial: Design and rationale. Front. Cardiovasc. Med. 2022, 9, e837958. [Google Scholar] [CrossRef]
- Fukuma, N.; Hasumi, E.; Fujiu, K.; Waki, K.; Toyooka, T.; Komuro, I.; Ohe, K. Feasibility of a T-shirt-type wearable electrocardiography monitor for detection of covert atrial fibrillation in young healthy adults. Sci. Rep. 2019, 9, 11768. [Google Scholar] [CrossRef]
- Bonomi, A.G.; Schipper, F.; Eerikäinen, L.M.; Margarito, J.; Aarts, R.M.; Babaeizadeh, S.; Morree, H.M.; Dekker, L. Atrial fibrillation detection using photo-plethysmography and acceleration data at the wrist. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 277–280. [Google Scholar]
- Bonomi, A.G.; Schipper, F.; Eerikäinen, L.M.; Margarito, J.; van Dinther, R.; Muesch, G.; Morree, H.M.; Aarts, R.M.; Babaeizadeh, S.; McManusand, D.D.; et al. Atrial fibrillation detection using a novel cardiac ambulatory monitor based on photo-plethysmography at the wrist. J. Am. Heart Assoc. 2018, 7, e009351. [Google Scholar] [CrossRef]
- Eerikäinen, L.M.; Bonomi, A.G.; Schipper, F.; Dekker, L.R.; de Morree, H.M.; Vullings, R.; Aarts, R.M. Detecting atrial fibrillation and atrial flutter in daily life using photoplethysmography data. IEEE J. Biomed. Health Inform. 2019, 24, 1610–1618. [Google Scholar] [CrossRef]
- Krivoshei, L.; Weber, S.; Burkard, T.; Maseli, A.; Brasier, N.; Kühne, M.; Conen, D.; Huebner, T.; Seeck, A.; Eckstein, J. Smart detection of atrial fibrillation. EP Europace 2017, 19, 753–757. [Google Scholar] [CrossRef]
- Estrella-Gallego, A.; Vazquez-Briseno, M.; Nieto-Hipolito, J.I.; Gutierrez-Lopez, E.; Sanchez-Lopez, J.D.; García-Berumen, A.; Rivera-Rodriguez, R. Monitoring atrial fibrillation using PPG signals and a smartphone. Int. J. Online Biomed. Eng. 2020, 16, 60–74. [Google Scholar] [CrossRef]
- Couderc, J.P.; Kyal, S.; Mestha, L.K.; Xu, B.; Peterson, D.R.; Xia, X.; Hall, B. Detection of atrial fibrillation using contactless facial video monitoring. Heart Rhythm 2015, 12, 195–201. [Google Scholar] [CrossRef]
- Duncker, D.; Ding, W.Y.; Etheridge, S.; Noseworthy, P.A.; Veltmann, C.; Yao, X.; Bunch, T.J.; Gupta, D. Smart wearables for cardiac monitoring—real-world use beyond atrial fibrillation. Sensors 2021, 21, 2539. [Google Scholar] [CrossRef]
- Nazarian, S.; Lam, K.; Darzi, A.; Ashrafian, H. Diagnostic accuracy of smartwatches for the detection of cardiac arrhythmia: Systematic review and meta-analysis. J. Med. Internet Res. 2021, 23, e28974. [Google Scholar] [CrossRef]



| Symbols | Measure | Definition |
|---|---|---|
| RQA 1 | Recurrence rate (RR) | |
| RQA 2 | Determinism (DET) | |
| RQA 3 | Laminarity (LAM) | |
| RQA 4 | Ratio (RATIO) | |
| RQA 5 | Averaged diagonal line length (L) | |
| RQA 6 | Trapping time (TT) | |
| RQA 7 | Longest diagonal line () | |
| RQA 8 | Longest vertical line () | |
| RQA 9 | Divergence (DIV) | |
| RQA 10 | Entropy (ENTR) | |
| RQA 11 | ) | |
| RQA 12 | Clustering coefficient (CLUST) | |
| RQA 13 | Longest white vertical line () |
| Symbols | Measure | Definition |
|---|---|---|
| TTF1 | Standard Deviation | |
| TTF2 | Skewness | |
| TTF3 | Kurtosis | |
| TTF4 | Range | |
| TTF5 | ||
| TTF6 | ||
| TTF7 | ||
| TTF8 | ||
| TTF9 | ||
| TTF10 | ||
| TTF11 | ||
| TTF12 | ||
| TTF13 | ||
| TTF14 | ||
| TTF15 | ||
| TTF16 | Harmonic Drama Frequency | |
| TTF17 | Kurtosis of Continuous Time Energy Spectral Density |
| Symbols | Definition |
|---|---|
| E1 | |
| E2 | |
| E3 | |
| E4 | |
| E5 | |
| E6 | |
| E7 | |
| E8 | |
| E9 | |
| E10 | |
| E11 | |
| E12 | |
| E13 | |
| E14 | |
| E15 | |
| E16 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| TRP | 56.13 | 73.50 | 38.75 | 59.38 |
| UTRP | 73.25 | 78.75 | 67.75 | 76.12 |
| Features | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| RQA | 83.50 | 85.64 | 80.50 | 86.50 |
| 4 s CTW–RQA (n = 6) | 81.75 | 83.74 | 80.95 | 82.63 |
| 8 s CTW–RQA (n = 3) | 89.38 | 90.52 | 88.54 | 90.26 |
| 12 s CTW–RQA (n = 2) | 86.13 | 86.46 | 84.91 | 87.29 |
| Features | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| Without CWT | 87.63 | 85.89 | 89.20 | 86.13 |
| 4 s CTW (n = 6) | 79.73 | 69.21 | 53.73 | 77.37 |
| 8 s CTW (n = 3) | 84.63 | 85.22 | 50.39 | 91.73 |
| 12 s CTW (n = 2) | 85.38 | 83.33 | 84.83 | 83.94 |
| Features | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| Without CWT | 78.50 | 77.89 | 78.68 | 78.33 |
| 4 s CTW (n = 6) | 68.15 | 65.52 | 36.19 | 78.95 |
| 8 s CTW (n = 3) | 74.63 | 69.15 | 75.24 | 62.89 |
| 12 s CTW (n = 2) | 76.78 | 78.54 | 74.05 | 77.63 |
| Fisher Score | MRMR (×10−3) | Chi-Square Test | Mean (|SHAP Value|) (×10−2) | |
|---|---|---|---|---|
| RQA 1 | 26.7275 | 15.6968 | 86.1661 | 9.16 |
| RQA 2 | 0.0069 | 36.1666 | 76.7835 | 5.83 |
| RQA 3 | 0.0614 | 26.1460 | 109.6421 | 9.26 |
| RQA 4 | 0.0067 | 7.4060 | 79.8617 | 4.03 |
| RQA 5 | 0.0025 | 7.5923 | 126.0331 | 0.75 |
| RQA 6 | 0.0117 | 9.2184 | 69.9101 | 7.84 |
| RQA 7 | 0.0437 | 5.9155 | 108.9972 | 1.38 |
| RQA 8 | 0.0515 | 14.0229 | 63.5000 | 2.99 |
| RQA 9 | 0.0445 | 8.5346 | 83.1469 | 1.31 |
| RQA 10 | 0.0136 | 14.6556 | 114.1749 | 1.69 |
| RQA 11 | 0.0463 | 24.4646 | 102.5003 | 2.02 |
| RQA 12 | 0.0282 | 6.8314 | 95.5515 | 3.84 |
| RQA 13 | 0.0282 | 16.0161 | 118.5287 | 2.12 |
| Method | ACC | PRE | SEN | SPE |
|---|---|---|---|---|
| KNN | 58.13 | 84.07 | 23.06 | 95.36 |
| NB | 81.63 | 85.52 | 77.42 | 86.08 |
| ENS | 91.75 | 95.29 | 88.35 | 95.36 |
| RF | 95.63 | 95.84 | 95.63 | 95.62 |
| DT | 84.50 | 85.82 | 83.74 | 85.31 |
| Method | Top 13 | Top 16 | Top 17 |
|---|---|---|---|
| Fisher’s coefficient | 91.25% | 89.63% | 90.88% |
| MRMR | 92.88% | 93.13% | 93.63% |
| Chi-square test | 95.25% | 95.25% | 95.38% |
| SHAP value | 93.75% | 94.13% | 94.63% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, T.; Jiang, F.; Li, Q.; Zeng, J.; Zhang, B. Quantitative Analysis Using Consecutive Time Window for Unobtrusive Atrial Fibrillation Detection Based on Ballistocardiogram Signal. Sensors 2022, 22, 5516. https://doi.org/10.3390/s22155516
Cheng T, Jiang F, Li Q, Zeng J, Zhang B. Quantitative Analysis Using Consecutive Time Window for Unobtrusive Atrial Fibrillation Detection Based on Ballistocardiogram Signal. Sensors. 2022; 22(15):5516. https://doi.org/10.3390/s22155516
Chicago/Turabian StyleCheng, Tianqing, Fangfang Jiang, Qing Li, Jitao Zeng, and Biyong Zhang. 2022. "Quantitative Analysis Using Consecutive Time Window for Unobtrusive Atrial Fibrillation Detection Based on Ballistocardiogram Signal" Sensors 22, no. 15: 5516. https://doi.org/10.3390/s22155516
APA StyleCheng, T., Jiang, F., Li, Q., Zeng, J., & Zhang, B. (2022). Quantitative Analysis Using Consecutive Time Window for Unobtrusive Atrial Fibrillation Detection Based on Ballistocardiogram Signal. Sensors, 22(15), 5516. https://doi.org/10.3390/s22155516






