1. Introduction
A microfluidic chip, or a
Lab-on-a-Chip (LoC), is a device that performs lab operations on a microscale through a set of fluid manipulations. A prominent and established kind of LoCs are pressure-driven and channel-based devices [
1] in which fluids are flowing through a configuration of channels with a scale in the order of micrometers or, in some cases, even nanometers (note that alternative LoCs, e.g., based on paper-based microfluidics [
2] or
electrowetting on dielectric (EWOD, [
3]) exist but are not considered in this work). The advantage of working on this scale is that less chemical components are required and chemical reactions usually take less time [
4]. However, the design and fabrication of corresponding devices is still a time-consuming and tedious process: channels must be appropriately dimensioned, pressure and flow rates must be accordingly adjusted, and even the slightest changes may completely change the behavior.
Simulations are an essential tool in this process as they can offer an early evaluation of the behavior of a design—even in the absence of a fabricated prototype. To this end, a huge variety of complementary simulation approaches have been introduced in the past [
5,
6,
7]. They operate on different abstraction levels, i.e., simplifications of the real-world physics to model the respectively needed physical phenomena.
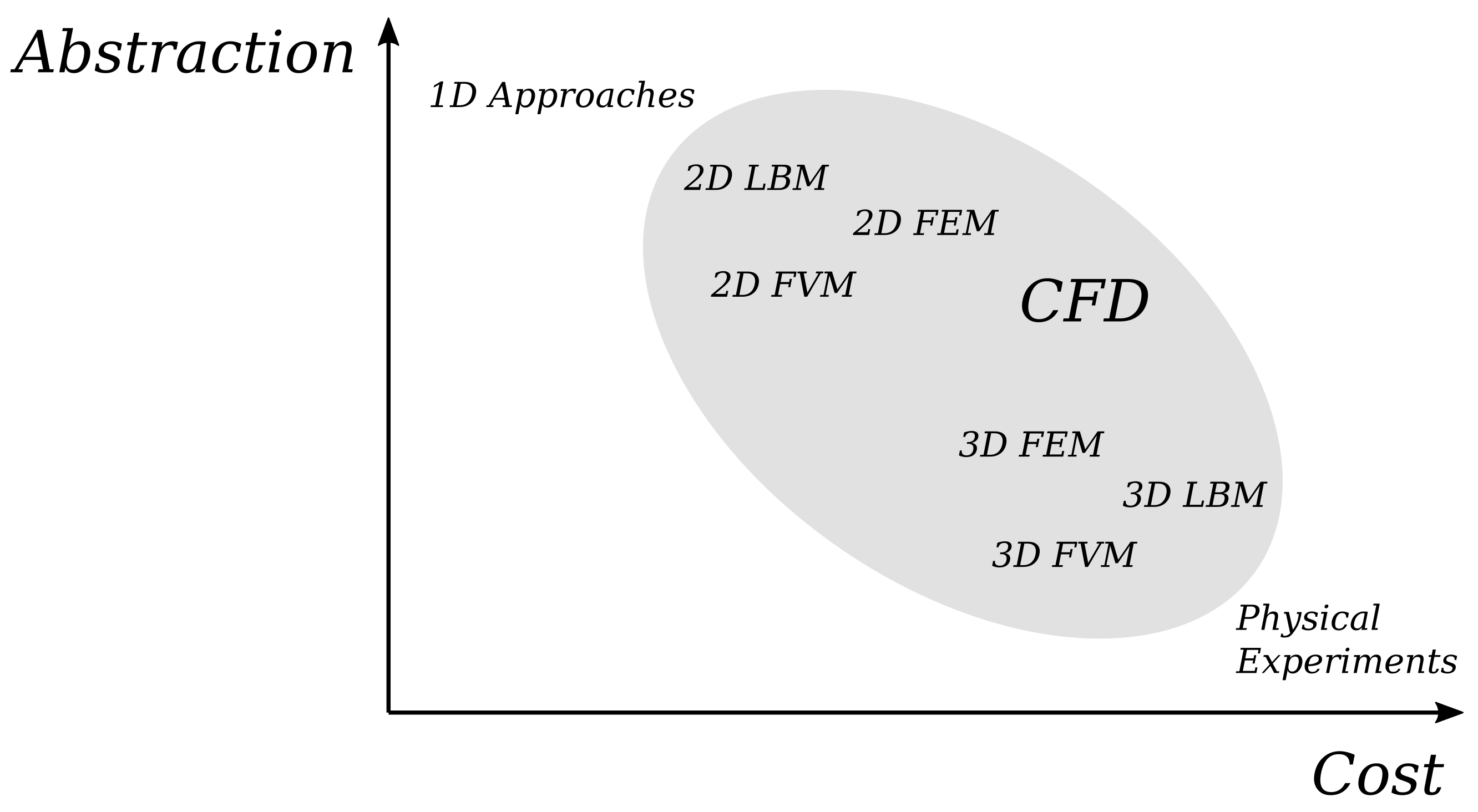
Figure 1 provides a rough overview of simulation approaches on the abstraction-cost scale. Examples of approaches on a high abstraction level are 1D approaches as introduced and used, e.g., in [
5,
8]. These approaches are usually based on analytical solutions of simplified problems and the computational effort scales linearly with the mesh refinement (i.e., the computational complexity of these approaches is
, where
n is the amount of data points along one dimension of the problem geometry). Approaches on a lower abstraction level rely on
Computational Fluid Dynamics(CFD, [
9]) and, more precisely, on methods such as the
Finite Volume Method (FVM, [
9,
10]), and the
Lattice-Boltzmann Method (LBM, [
11,
12]). These can be further divided into 2D and 3D approaches, i.e., into methods considering a 2-dimensional and a 3-dimensional space, and, hence, scale in a quadratic (
) and cubic (
) fashion, respectively. Evaluations and case studies such as conducted in [
8] illustrate the potential and showcased how the use of simulations can reduce the design time of an LoC substantially (in some of those studies, design time reductions from an entire month to a single day have been observed).
However, simulations are not perfect and, although helpful, do not necessarily reflect the real-world behavior (i.e., the ground truth). In fact, depending on the considered case, the used simulation approach, the made assumptions and configurations, etc., different behavior of a given design may be concluded from a simulation run. The FVM approach alone can give different simulation results, depending on, e.g., the spatial and temporal discretization, the quality of the mesh, or even the obtained order of spatial accuracy for higher-order schemes [
10]. A review done in [
13] provides a broad overview of possible methods within the FVM approach to model the interface of a multiphase flow only; and a case study done in [
14] showcases that, for a single simulation approach (FVM), even the chosen tool can significantly influence the required computational time and simulated results. The same can be said for other CFD methods, such as the LBM. Despite this broad spectrum of available simulation approaches for microfluidics, most designers and researchers often only adopt a single simulation approach for their microfluidic simulations [
15,
16,
17,
18,
19,
20]. Moreover, conducting these simulations may be computationally expensive—with simulations on lower abstraction levels easily taking days or even weeks to complete [
14] while, in contrast, simulations on higher abstraction levels might be faster but may not provide the desired accuracy. Not knowing the spectrum and capabilities of the single simulation methods at the different abstractions levels makes it hard, if not impossible, to properly trade-off the desired quality of the possible results against the computational effort needed to generate them.
In this work, we aim at shedding light into this by providing (1) an overview of different and complementary simulation methods as well as (2) a case study of their performance for microfluidic designs (note that the scope of this work is to raise the awareness and discuss the potential of simulation and, hence, does not include experimental data obtained from physically produced microfluidic devices). To this end, we consider three typical and representative use cases of pressure-driven and channel-based microfluidic devices (namely the non-Newtonian flow in a channel, the mixing of two fluids in a channel, and the behavior of droplets in channels; covered in more detail in
Section 2). For each of those use cases, its corresponding representation according to the 1D, 2D, and 3D abstraction level is considered. Based on that, we review representative simulation methods (covered in
Section 3) and describe how the considered use cases can be properly simulated with them (covered in
Section 4). Results of those simulations (covered in
Section 5) are discussed and showcase the benefits, but also the pitfalls, of simulations at different abstraction levels.
By this, this case study certainly does not claim to comprehensively cover the problem or to allow for generic conclusions about what simulation method and abstraction level performs best for what use case. However, the reviews, results, and discussions provided in this paper certainly raise awareness of the spectrum of available solutions and its applicability with respect to computational efforts vs. quality. More precisely, this work provides (besides others) the following main insights:
Simulations at high abstraction levels come with less computational costs than simulations at lower abstraction levels. While not surprising at all, this is, to the best of our knowledge, the first case study that investigates the performance of simulations and quantifies the computational cost for microfluidic devices at different abstraction levels.
Applying more computational efforts does not always yield a better simulation quality. In fact, we show that for certain use cases, applying a (computationally more expensive) lower abstraction does not significantly improve the accuracy of the results. Insights like those enable the designers or researcher to properly trade-off the available approaches and to save a lot of simulation time without a severe less of quality.
The choice of the applied simulator should reflect the need of the designer or researcher. If, e.g., droplets are considered and the end-user is only interested in the position of them, the 1D abstraction level might be sufficient (providing a very fast solution). If, instead, also the integrity or the deformation of the droplet is of interest, the more accurate but also much slower 2D/3D approach might be needed. Again, insights which equip the designers or researcher to choose the right solution for the task.
For some use cases, simulations provide inconclusive results. This shows that, although simulations really can help in many use cases, they might not always be the “ground-truth”. After all, they do not reflect the real world in a perfect fashion but heavily rely on the underlying models and assumptions. Being aware of that and the complementary approaches helps designers and researchers to constantly reflect when a certain simulation can be trusted and, in case of contradicting results, which simulation approach most likely covered the real world best.
Overall, this case study certainly does not aim to establish a ground truth for simulation of microfluidic devices (after all, the fabrication and evaluation of actual prototypes are still needed for that). However, it offers an overview and several insights for what simulation approaches can be utilized today when designing corresponding devices (and for what they cannot be utilized yet).
2. Considered Use Cases
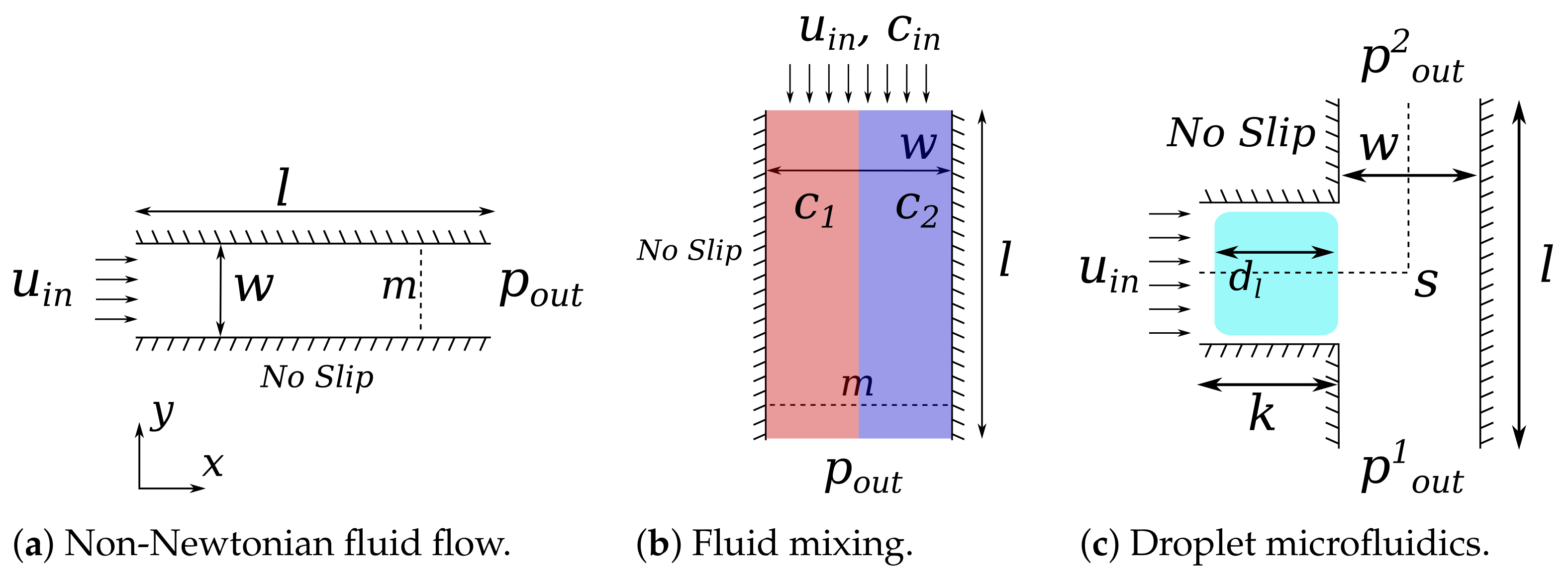
The goal of this work is to provide an overview and evaluation of the performance of different and complementary approaches for the simulation of fluidic behavior in pressure-driven channel-based microfluidic devices. To this end, a representative set of use cases (covering different phenomena in fluid physics) is key. In this section, we introduce the use cases that have been considered in our case study, namely non-Newtonian fluid flow, fluid mixing, and droplet microfluidics, as well as motivate their importance in the field of microfluidics. All of them rely on the flow of a fluid through a rectangular channel which is reviewed first. Afterwards, each use case is described.
2.1. Fluid Flow through a Channel
The flow of a fluid through a channel is obviously the basis for any simulation of a channel-based microfluidic device. The corresponding physics can be analytically described through the Hagen–Poiseuille law defined by
where
r is the radius and
l is the length of the channel,
is the applied pressure difference,
is the viscosity of the fluid, and
Q describes the mass flow rate. However, this law can only be applied if
cylindrical channels are considered; while, in microfluidics, channels usually have a
rectangular shape. Accordingly, the Hagen–Poiseuille law needs to be modified. More precisely, for a rectangular channel with width
w and height
h, the mass flow rate is given by [
21]
Here, the summation can be truncated after the second term, with a truncation error of
. The mass flow rate can be used to get the average flow velocity of the fluid. However, inside a channel, the flow velocity is not equal everywhere. The fluid is stagnant at the walls, and the largest fluid velocity is found furthest away from the channel walls, in the middle of the channel. This is due to the shear stress, which occurs because molecules stick to each other and pull each other; creating horizontal layers of fluid flowing at different speeds, in a laminar fashion. The viscosity of a fluid describes the resistance to the rate of deformation. The distribution of flow velocity along the cross-section of a channel is described by the flow profile.
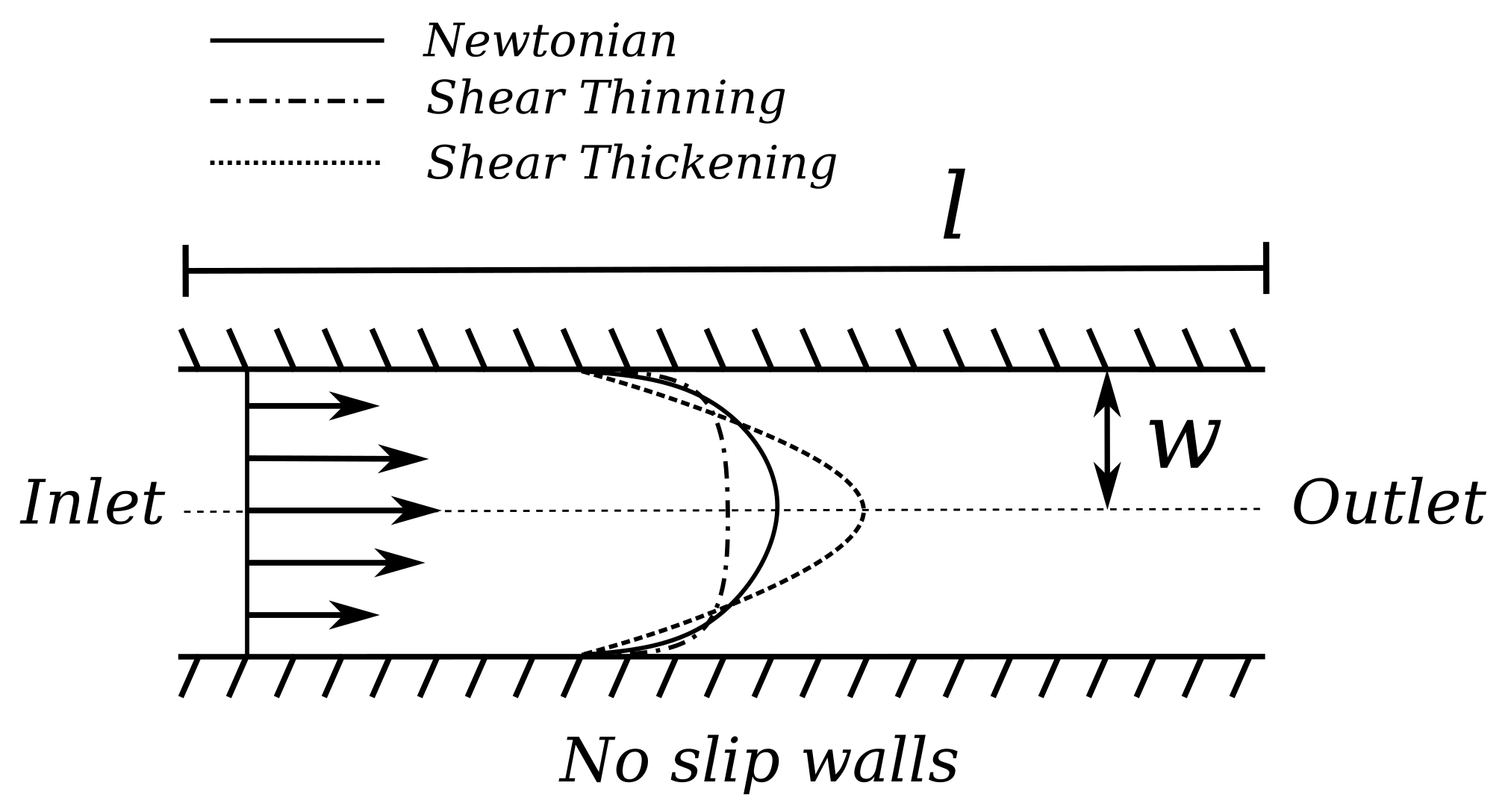
Example 1. For a Newtonian fluid (a fluid in which the viscosity of the fluid depends linearly on the shear strain rate, e.g., rate of deformation) such as water, the flow profile is parabolic. In Figure 2, this is shown by the solid line. More precisely, Figure 2 shows the flow in a channel flowing from the left to the right, with a channel length l and a channel width w, as well as walls on the top and bottom. The arrows on the left indicate the inflow velocity at the inlet, following the Newtonian flow profile. Based on the considerations so far, we can analyze flows for channel-based microfluidic devices. However, this only covers the main basic case. As soon as further issues beyond a simple channel flow are considered (such as the use cases considered in this work), purely relying on Equation (
2) is insufficient. An additional analysis is required which is covered next.
2.2. Non-Newtonian Fluid Flow
Thus far, we assumed a fluid flow behaving in a Newtonian fashion, i.e., the fluid viscosity linearly depends on the shear strain rate. The shear strain rate of a fluid describes its shear deformation, resulting from external forces, with respect to time. A fluid’s viscosity can thus be said to be a measure of its resistance against deformation. For real world problems, the corresponding fluids cannot always be assumed to behave in a Newtonian fashion. In particular in applications, e.g., from the food industry, material science, and in the medical field, fluids frequently show a nonlinear relation between the viscosity and the rate of deformation and, hence, show non-Newtonian properties [
22]. Accordingly, this constitutes a good representative case for the evaluations conducted in this work.
Example 2. Examples of non-Newtonian fluids are shear-thinning or shear-thickening fluids, i.e., the fluid viscosity decreases or increases with increased shear strain rate, respectively. The dashed lines in Figure 2 indicate the corresponding flow profiles for shear-thinning and shear-thickening fluids. Here, it is obvious how for, e.g., shear-thinning fluids, the rate of deformation of the fluid near the wall is significantly high; causing the flow to have a more uniform flow speed in the center region of the flow channel. Shear-thickening fluids will get a sharper flow profile, due to the higher resistance against deformation of the fluid. The flow profile for non-Newtonian fluids can be described by using rheological models, such as the power-law [
23], the Casson model [
24], and the Carreau–Yasuda model [
25,
26]. In this case study, we will model the shear-thinning behavior of blood in a rectangular channel, using the Carreau–Yasuda model. This model gives the effective viscosity
as a function of shear strain rate
as
Here,
and
are the viscosity at zero and infinite strain rate, respectively,
is the relaxation time, and
n and
a are power indices. These parameters are fluid-dependent and we will use the following values for blood (which are in line with experimental data [
27]):
Because microfluidic devices only need a very small amount of specimen to perform tests, compared to regular labs, it is attractive to apply them in the medical field, where specimen fluid is often limited. This use case was chosen due to its relevance for the application of LoCs in the medical field, but it can easily be adapted to other non-Newtonian fluid problems by changing the fluid parameters or the problem domain accordingly.
2.3. Fluid Mixing
In this use case, we address the mixing properties of two miscible fluids. Mixing of two or more miscible fluids is a common operation in (bio-)chemistry, and in microfluidics it can be used to, e.g., generate a stream of liquid with predefined concentrations [
28]. Mixing is usually induced through stirring, and fluids predominantly mix through convection. For LoCs, however, this is not the case. Due to the laminar nature of flow in microfluidic channels, the mixing operation of two or more fluids depends on the diffusive properties of the fluids, rather than convective transport properties.
The diffusion distance
d of molecules depends on the diffusion coefficient
and flow time
t, and is given by [
29]
Diffusion is a very slow transport mechanism, and even in microchannels, it can take up to several minutes to achieve full mixing, which requires relatively long flow channels [
29]. Mixing can be induced through active mixing methods, such as using actuators [
30], peristaltic pumps [
31], or electro-kinetics [
32]. In this case study, however, we will focus on the passive mixing properties of two fluids in a meandering channel. Meandering channels provide enough mixing time for fluids flowing at a certain speed, whilst not taking up too much area on a microfluidic chip.
Example 3. Figure 3 shows an example of passive mixing in a meandering channel (this Figure was authorized for reprinting). On the left, we have two inlets containing fluids of different colors. The mixing mechanism within the meandering channel is illustrated here. It can be seen that the laminarity of the flow causes very little mixing between the two colored streams, and a lot of LoC area is required to accommodate, e.g., meandering channels. The dimensioning of such channels highly depends on the mixing properties of the fluids. The mixing of fluids with different concentrations or content is a fundamental (bio-)chemical lab operation. Therefore, reliable and fast predictions of mixing properties are of utmost importance for LoC design, making this use case relevant for our case study.
2.4. Droplet Microfluidics
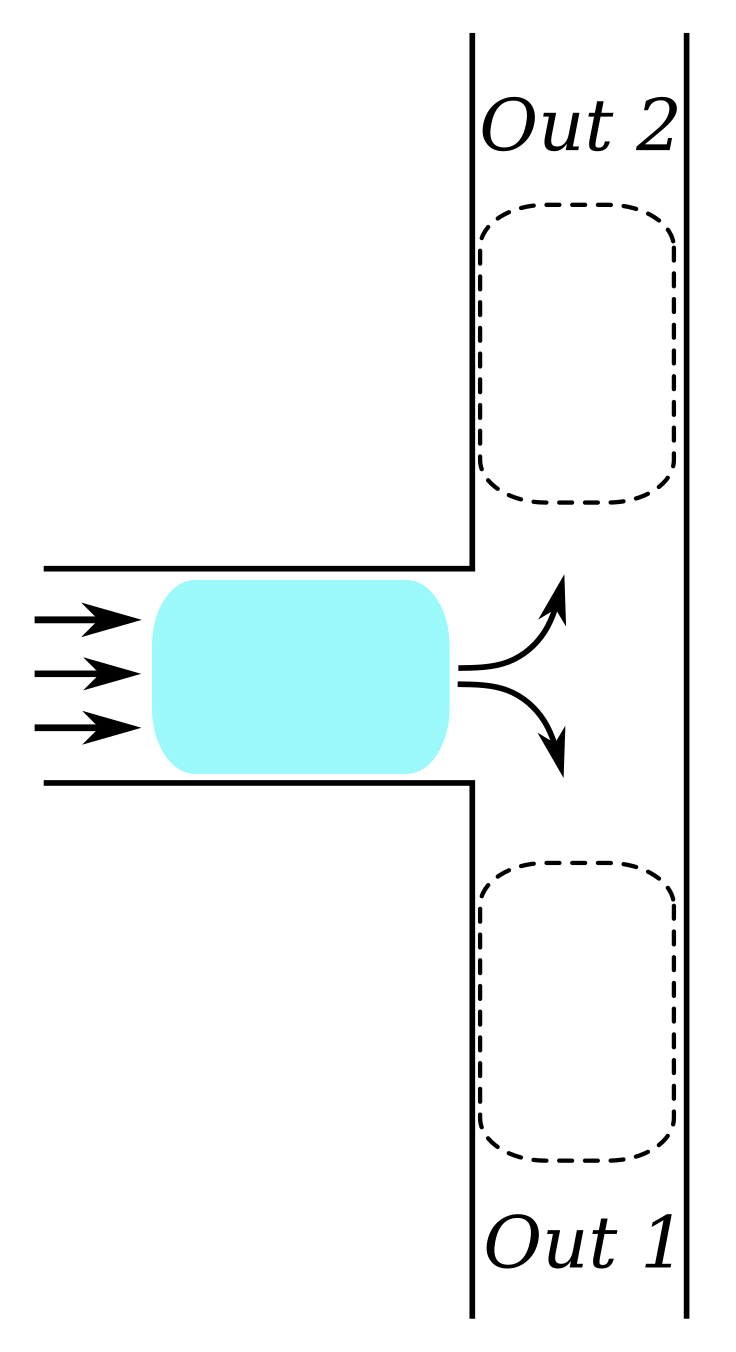
Finally, we consider the droplet microfluidics use case in which the fluid flowing through the channel acts as a carrier fluid for another injected (immiscible) fluid; leading to the formation of droplets which are transported by the carrier fluid. This leads to a two-phase microfluidic system. A network of channels allows the droplet to take different paths. This system can be used to transport bio-chemical assays to the desired location on the chip.
Example 4. An example of how microfluidic droplets can take different paths is illustrated using Figure 4. Here, a colored droplet is shown, flowing in from the left, heading towards a bifurcation (T-junction). At the bifurcation, the droplet can either flow to the top or to the bottom. Provided that the droplet does not split, it will choose the path which constitutes the highest total pressure difference, i.e., the path with the lowest hydraulic resistance. Combined with the flow speed, the pressure difference of a channel can be expressed as a resistance. The hydraulic resistance of a channel is given by
Droplet paths can be predicted relatively easily using the laws described in
Section 2.1, the hydraulic resistance of channels, and analogous methods from electrical engineering such as Kirchoff’s law [
5].
However, droplet deformations depend on the surface tension, which can be described for droplets using
where
and
are the pressures of the carrier fluid and droplet, respectively,
r is the radius of the droplet, and
is the surface tension coefficient of the two liquids and depends on the temperature. The prediction of whether a droplet splits or not needs the analysis of the surface tension of the droplet. In this use case, we consider a droplet flowing through a bifurcation, as in
Figure 4, by which stresses are applied to the droplet surface to observe whether splitting occurs.
Droplet microfluidics provides the basics for several microfluidics applications such as single cell analysis [
22], high throughput PCR [
33], and material science [
22], and is, hence, a relevant use case.
5. Obtained Results and Discussion
Eventually, this section summarizes all results obtained by the case study described above and draws corresponding conclusions from them. Following the structure of all sections above, each case is discussed separately in the following.
5.1. Non-Newtonian Fluid Flow
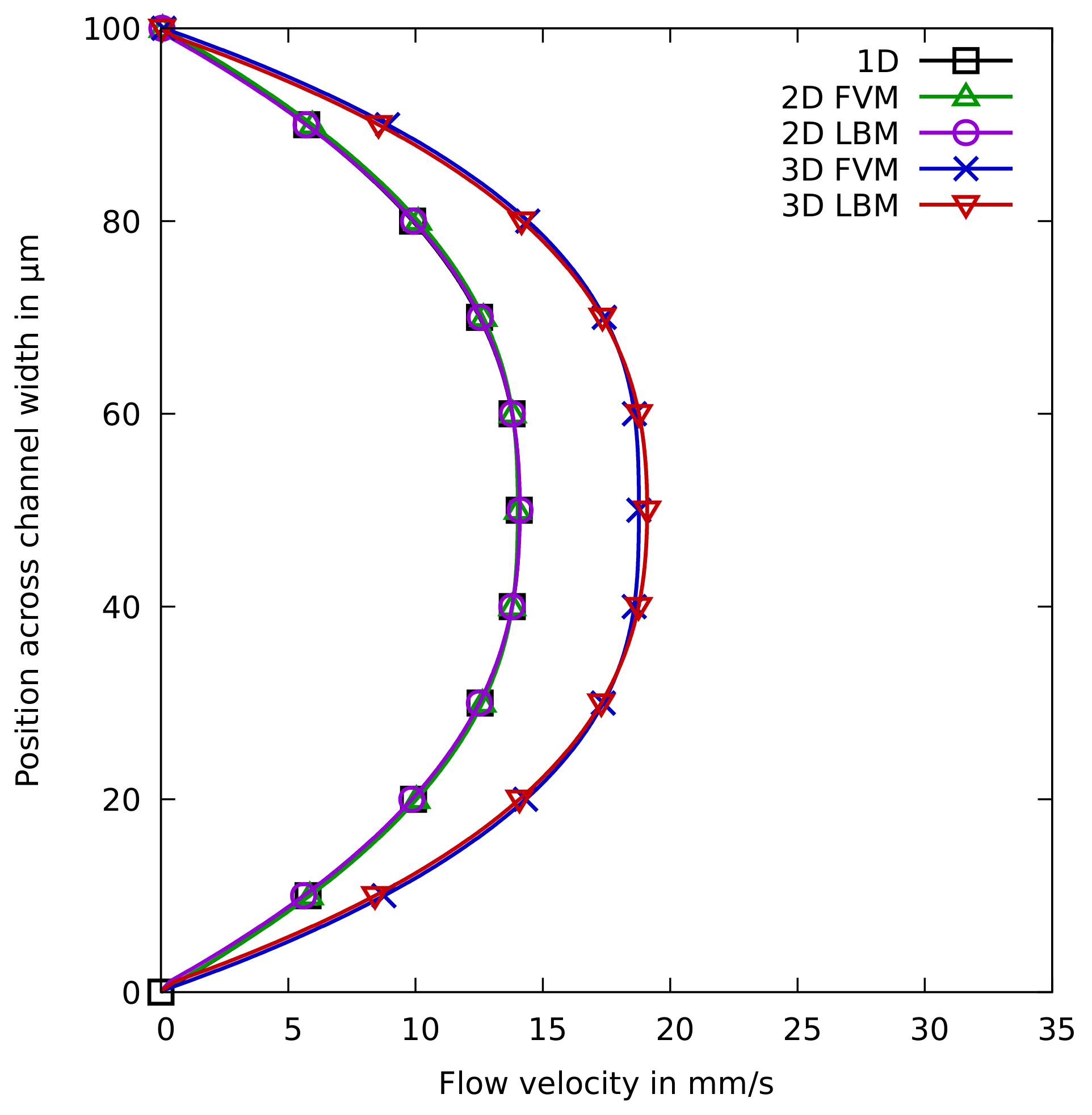
The resulting flow profiles are probably the most relevant results generated by the simulators for this use case. Correspondingly obtained results are given in
Figure 7 for all simulation approaches. The flow profile is taken along the width of the channel at the measurement line
m in
Figure 6a. On the
x-axis, the velocity of the stream is given in
and, on the
y-axis, the position along the width of the channel is given in
m. The correspondingly needed runtimes in CPU seconds and required memory in MB are summarized in
Table 1. For the 1D approach, no runtimes/memory requirements are reported since all simulations can be completed in negligible time (i.e., less than a second).
The plots clearly show that the results from the 1D and the 2D approaches are rather close to each other—indicating a similar quality for both of them. Considering that the 1D approach requires almost no computational efforts (while the 2D approaches may take some minutes), this provides a clear indication to choose the former over the latter for straight channel use cases. If 3D is considered, different results are obtained, i.e., the maximum velocity of the 3D simulations is significantly higher than that of the 2D simulations. This is to be expected, as the inlet flow speed is set equal for all simulations, and the 3D simulations have the wall effect of four walls instead of only two walls—resulting in a higher maximum velocity, because the fluid is being “squeezed” through a tinier gap. However, this higher precision comes at a larger computational cost: In case of FVM, the runtime even increases by a factor of almost 165; in case of LBM by a factor of about 71.
Overall, this allows for the conclusions that, if a rough approximation is sufficient for the end-user’s needs, the 1D simulation certainly delivers that at almost no computational costs. If instead very precise results are needed, the end-user probably should take the extra mile and use the 3D simulation (despite its computational costs). In this example, the 2D simulations hardly provide any further benefits compared to the 1D approach, however, one should keep in mind that the 2D approach can also be used for more complex two-dimensional flow problems. There is no significant difference in the computational cost, between the FVM and LBM approaches, and both give adequate results for this use case.
5.2. Fluid Mixing
The mixing performances are probably the most relevant results generated by the simulators for this use case. This is quantified using the
Absolute Mixing Index (AMI) as given by [
51], i.e.,
where
represents the concentration of fluid A coming in on the left, normalized on a scale from 0 to 1. The average value of
over all
N data points is given by
.
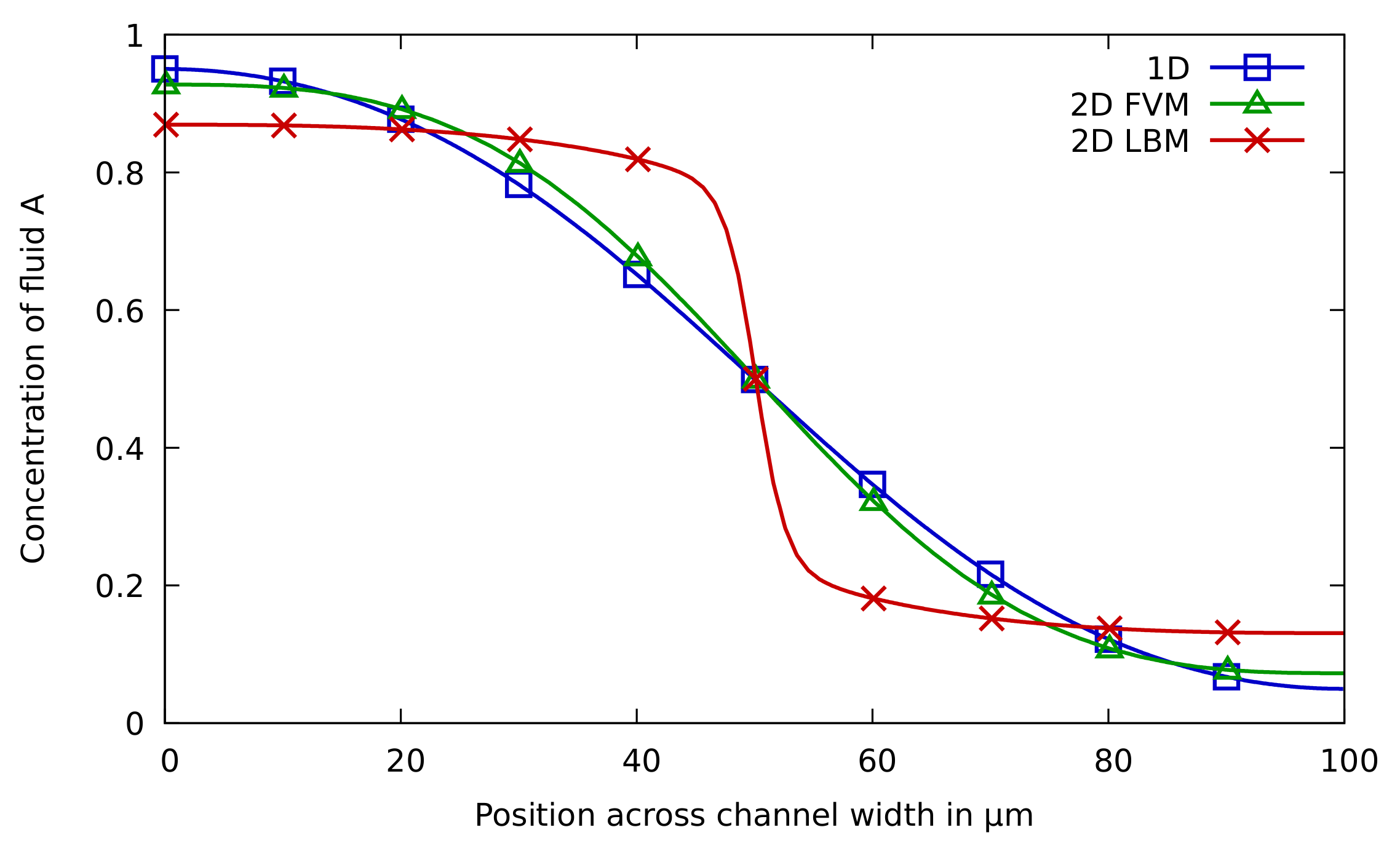
The results for the mixing use case taken at cross-section
m in
Figure 6b are summarized in
Figure 8 and
Figure 9. The results of the 1D and 2D approaches are shown in
Figure 8, where the
x-axis denotes the position along the channel width and the
y-axis denotes the concentration of fluid A. The concentration of fluid A as obtained by the 3D FVM and 3D LBM approaches is given in
Figure 9a,b, respectively. Here, completely red means a 100% concentration of fluid A and completely blue means a 100% concentration of fluid B. The correspondingly acquired AMI values, needed runtimes, and memory requirements are provided in
Table 2. Again, for the 1D approach, no runtimes are reported since all simulations can be completed in negligible time (i.e., less than a second).
For this use case, the simulation results are much more inconclusive. In fact, there obviously is a huge difference between the results obtained by the FVM method and the LBM method. Since we considered a straight channel during the mixing, the 1D simulation (relying on an analytical solution that is exact in this case) does provide a ground truth—verifying that the results obtained by FVM are correct, while the results obtained by LBM are far off. This does not mean that the LBM approach cannot be used for miscible flow simulation, but it does indicate that the Shan–Chen multiphase method is probably not the best method for this use case.
As for runtime performance, the 1D solution obviously is the best option again. Considering that, for this scenario, this even provides a ground truth, it obviously is the best choice in general. However, this only holds for straight channels. As soon as, e.g., a meandering channel is considered, the 1D approach is not exact anymore, and designers or researchers must rely on CFD methods (and need to accept the longer runtimes). Then, the previously reported results can be seen as an indication that, having the option between the described methods, FVM seems to lead to better results. However, a physical prototype might be needed to give a decisive answer to which approach indeed provides the best quality. Overall, these differences clearly show that just trusting a single simulation engine can easily be misleading and may serve the impression that simulations always give the end-users accurate results. Using different schemes, leading to different results, may increase awareness that simulations are not always perfect, and should be critically reflected upon.
5.3. Droplet Microfluidics
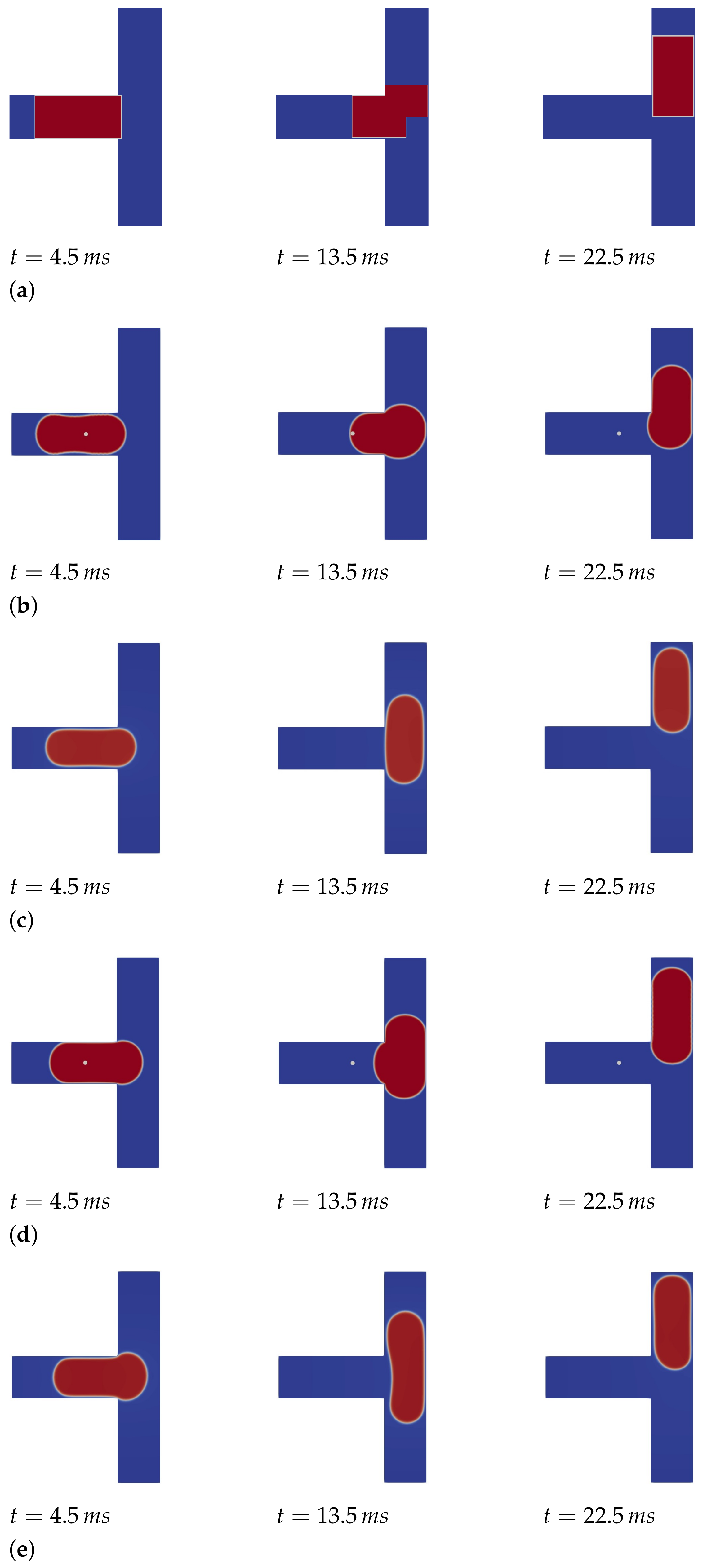
Finally, the positions and possible deformations of the droplets are probably the most relevant results generated by the simulators for this use case. Correspondingly obtained results are summarized in
Figure 10 for the 1D, 2D, and 3D approaches. More precisely, for each case, the position and the shape of the droplet is shown (denoted as red entity) for three timestamps. Note that, since the 1D approach is incapable of simulating the shape of the droplet, its position is simply denoted in terms of a block-like entity in
Figure 10a. The correspondingly needed runtimes and memory requirements are provided in
Table 3. Here, no runtimes are reported for the 1D approach since all simulations can be completed in negligible time (i.e., less than a second).
The results for this use case perfectly show the trade-off between quality and computational effort. In fact, the results from the 1D approach (generated in almost no time), provide rather accurate positions (in fact, the position of the droplet is almost identical in 1D, 2D, and 3D). Hence, if the end-user is just interested in the positions of droplets, 1D certainly is the way to go. However, one still has to be careful for the slight difference that is observable between the 1D and 3D approaches. In fact, these differences might accumulate for more complex channel configurations.
If also deformation (or stability) of the droplet is considered, then the 1D approach is not suitable at all and the end-user has to opt for 2D, or even 3D, approaches. This obviously comes at a substantially higher computational cost, but it seems that a 2D approach already comes with an acceptable accuracy, i.e., it might not always be necessary to spend the substantially larger runtime required for 3D approaches. In fact, although the droplet seems to have a lower velocity in the 2D approaches, all 2D and 3D approaches agree that the droplet does not break. If a designer or researcher wishes to have more detailed information on the droplet deformation, care should again be taken, as it is clear that none of the approaches really agree on how the droplet deforms.
6. Conclusions
In this work, we considered the simulation of pressure-driven and channel-based microfluidic devices at different levels of abstraction. To this end, we considered three representative use cases, namely the non-Newtonian flow in a channel, the mixing of two fluids in a channel, and the behavior of droplets in channels. The case study and the obtained results clearly show that simulations are certainly not perfect but frequently provide insights that can aid and improve the design process. At the same time, the case study shows that the broad spectrum of simulation approaches leads to different performances with respect to accuracy and required compute time.
Table 4 provides a color-coded overview of the correspondingly obtained “take-home messages” for each use case (columns) and abstraction level (rows). Here, green denotes the best possible option (e.g., simulating a non-Newtonian fluid flow in a rectangular channel is best conducted using the 1D abstraction as it provides precise results in negligible runtime), while red denotes an option which should be avoided (e.g., simulating a fluid mixing process within a straight channel in 2D or 3D takes too much time, and does not yield much extra information in return) or which is not applicable at all (e.g., splitting and deformations in droplet microfluidics cannot be simulated at all in 1D). Orange denotes options which could be useful, but usually involve a trade-off (e.g., simulating deformations in droplet microfluidics in 2D may not provide perfect accuracy but, considering the much less runtime compared to 3D, may provide an acceptable compromise).
Overall, this clearly shows that designers and researchers should be aware of the available solutions and accordingly trade-off these performances with their respective needs. With this, we believe that this work provides a contribution towards increasing the awareness and the understanding of the potential of simulation for microfluidic devices.
Future work certainly should focus on improving the accuracy and reliability of the simulation results—particularly towards avoiding contradictory or inconclusive results. This could be accounted for through the introduction of an error margin that allows for a bigger solution space—increasing the chance that the ground-truth is considered. This error margin could lead designers towards more robust designs of microfluidic devices. Additionally, a better understanding about computational efforts vs. quality of simulations at the different abstraction levels (as fostered through this work) may pave the way towards hybrid solutions, i.e., a combination of simulation approaches where the overall design is simulated at high abstractions (fast, but less accurate) and corner case components are simulated at lower abstractions (slower, but for smaller parts and with better accuracy). For all these endeavors, the insights gained through this case study provide a good basis.