Quadcopter UAVs Extended States/Disturbance Observer-Based Nonlinear Robust Backstepping Control
Abstract
:1. Introduction
- (i)
- The proposed algorithm overcomes the drawbacks of previous methods in the requirement of full state measurement. The ESDO is able to estimate the velocity state of the vehicle once this parameter cannot be directly measured. Thus, the implementation cost for data acquisition may be reduced and the influence of high measurement noise generated from the velocity sensor is also alleviated.
- (ii)
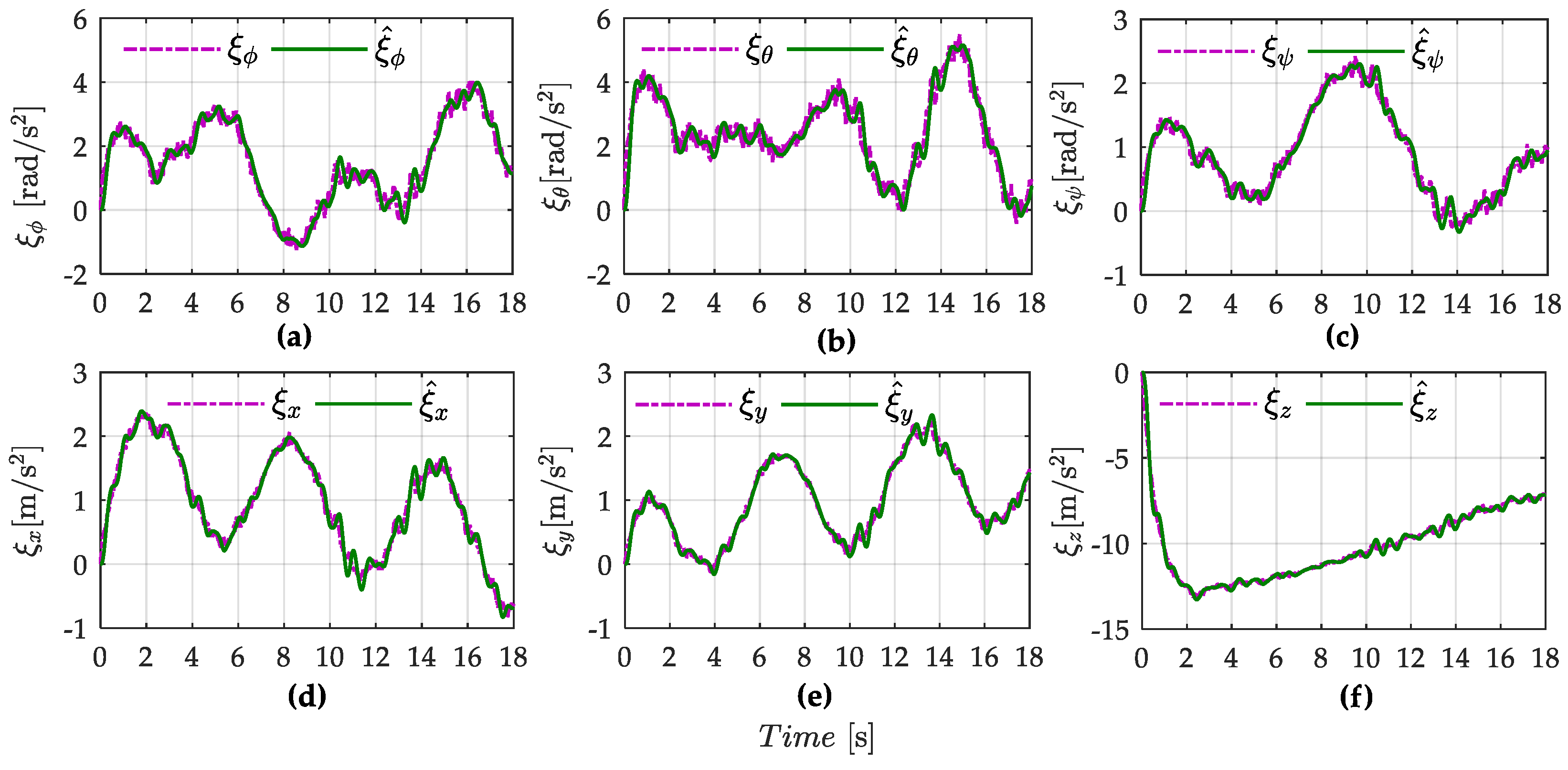
- The unmeasured velocity states and lumped perturbations are estimated by the presented ESDO integrating with advantages of the recursive structure of the backstepping technique, the convergence of tracking errors is always guaranteed.
- (iii)
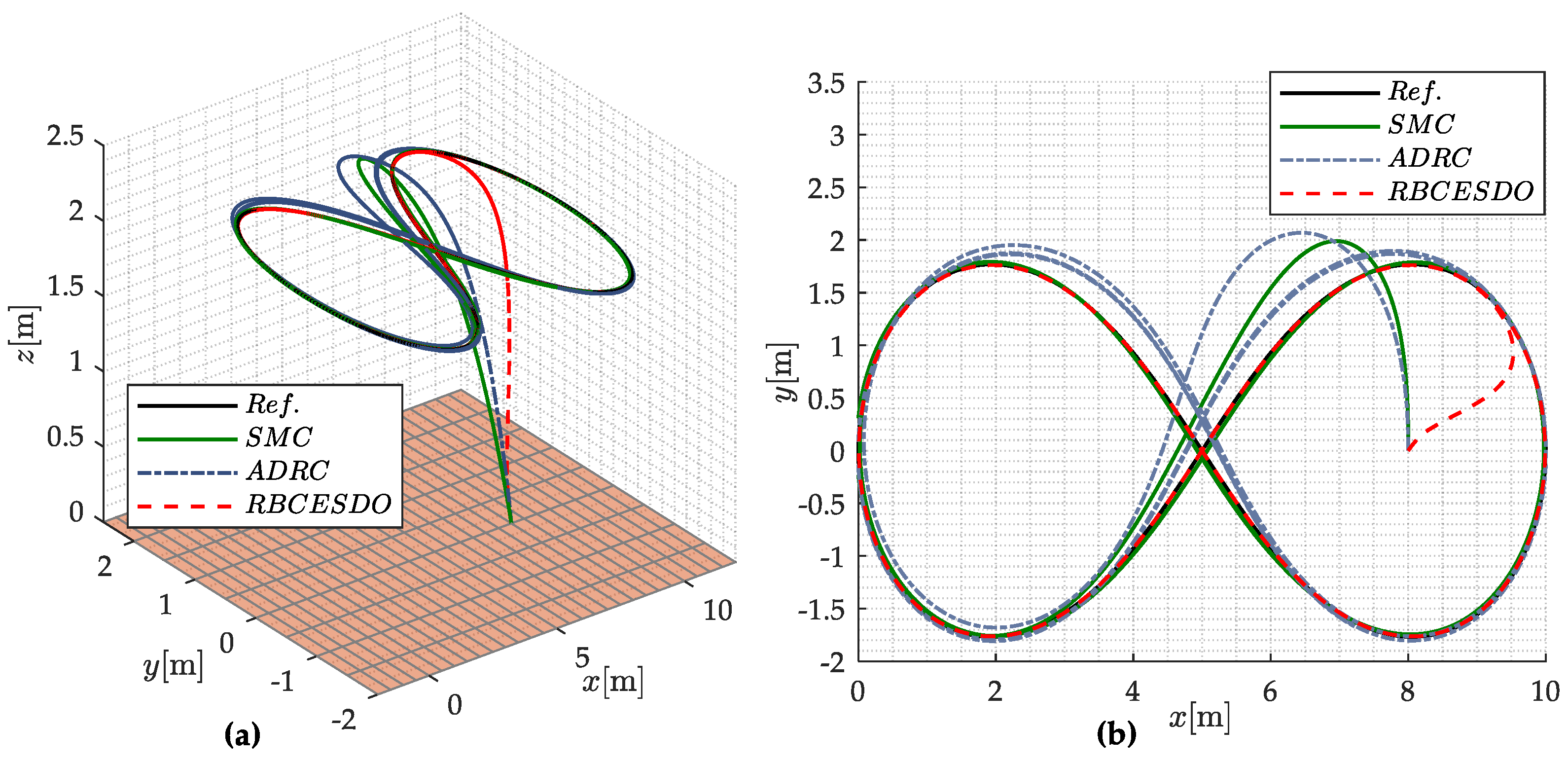
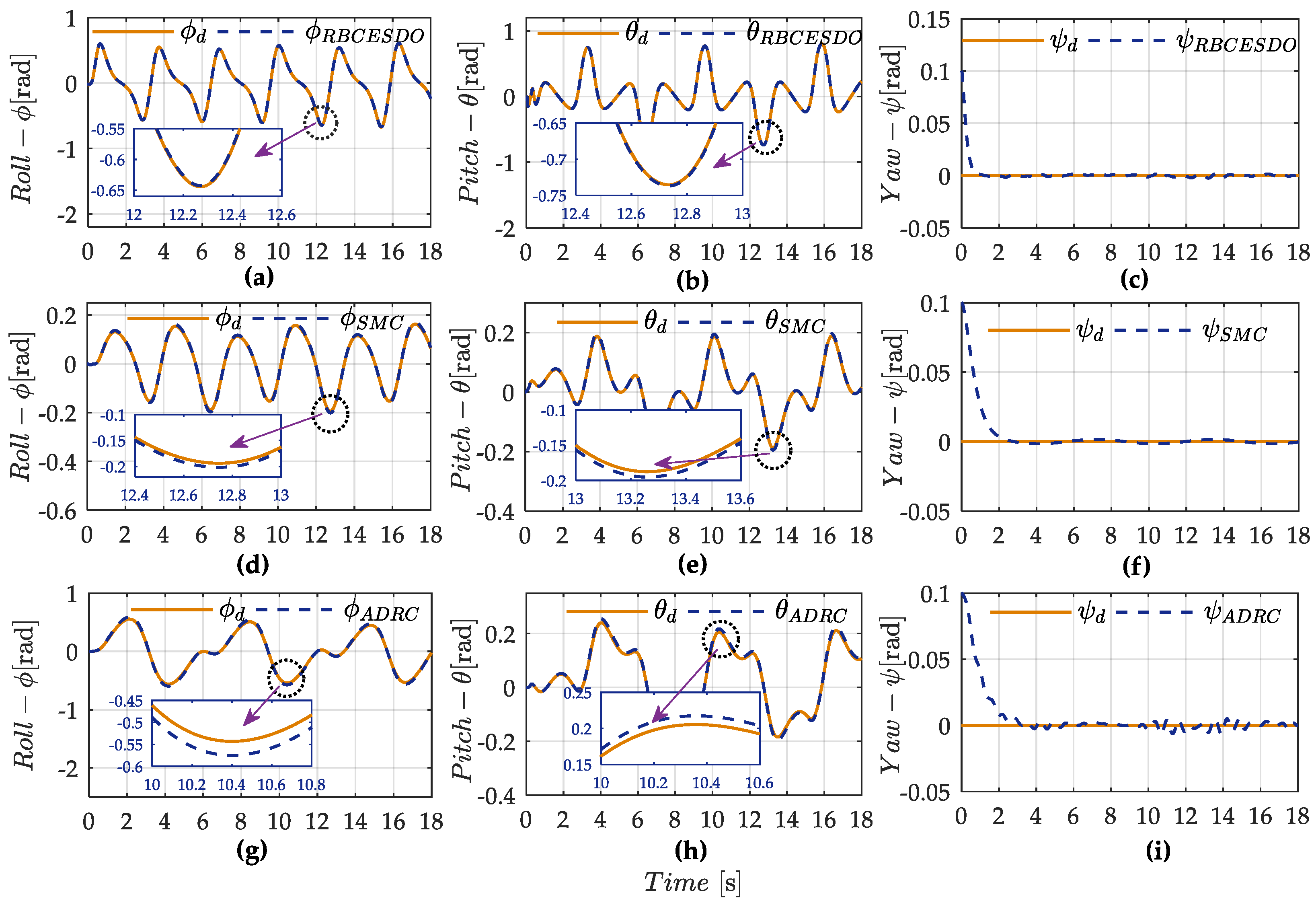
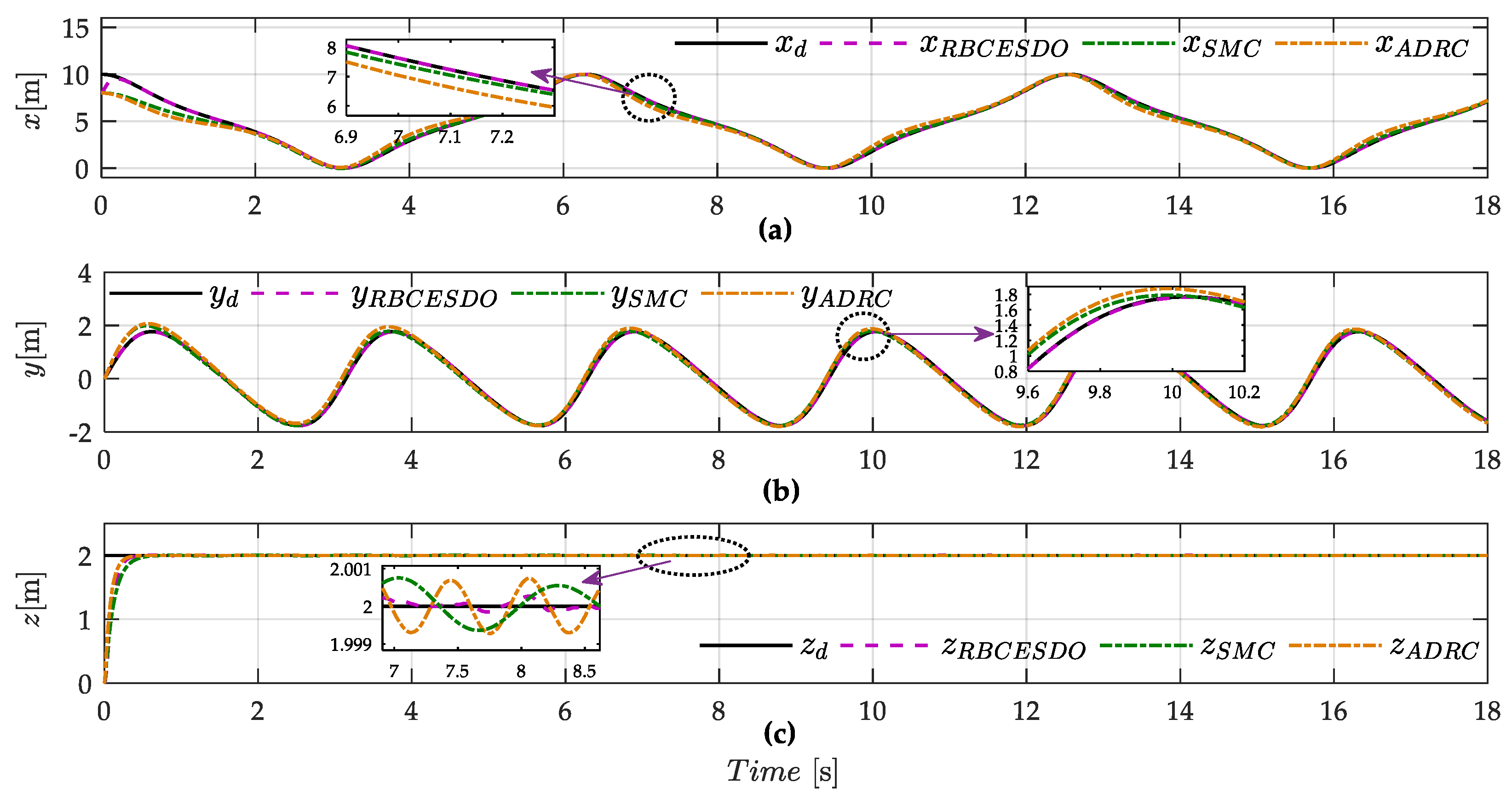
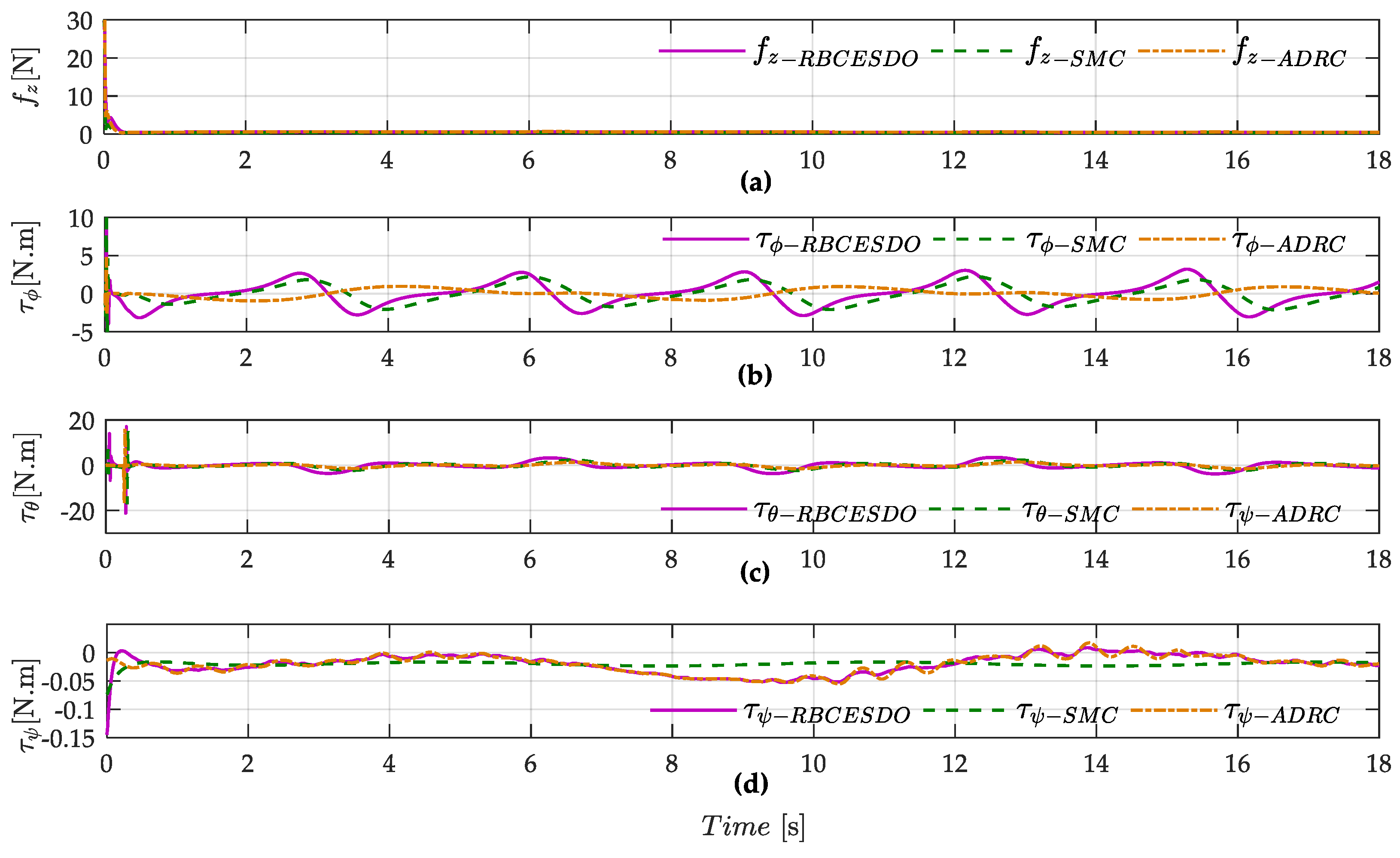
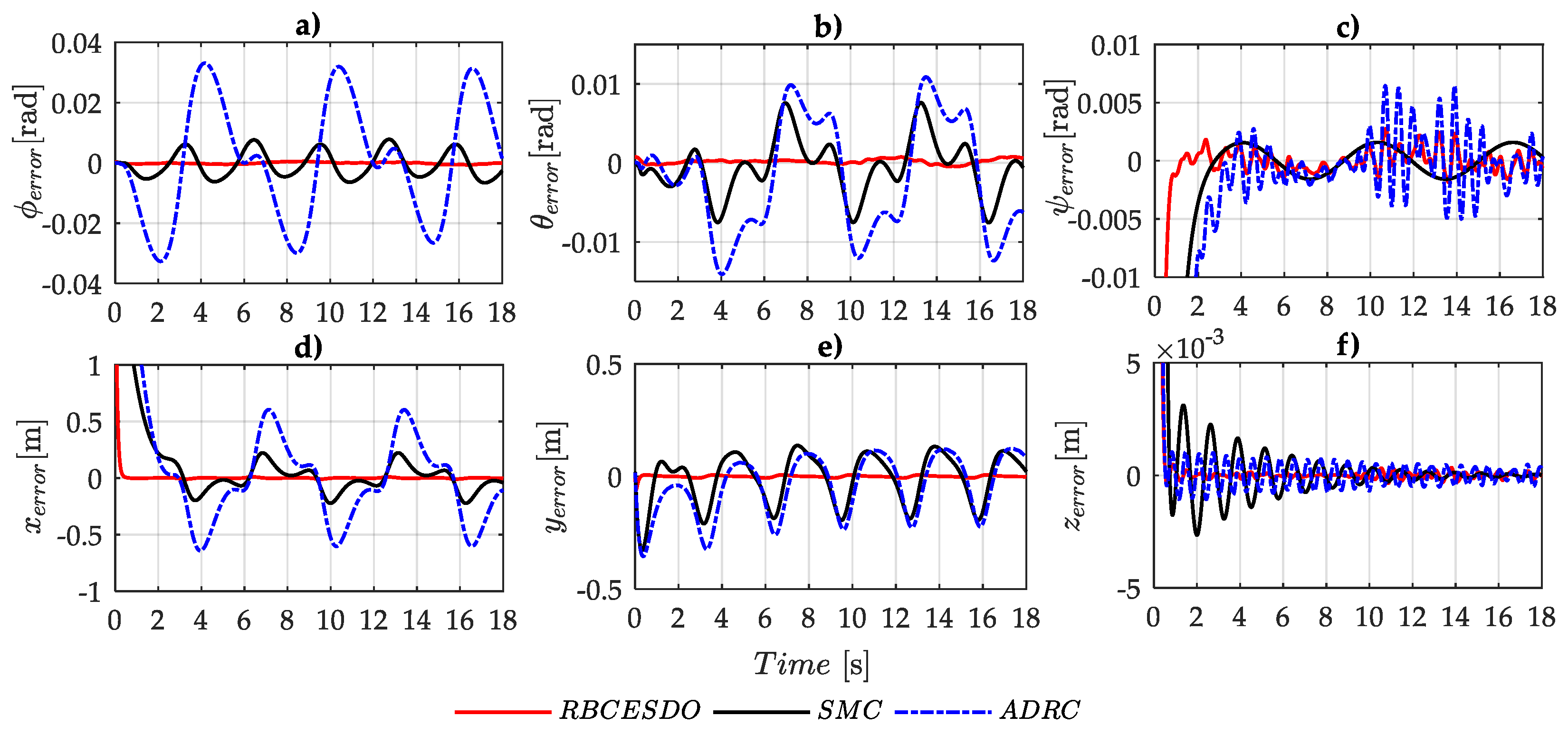
- The numerical simulation is fully executed in both attitude and position control mode; these performance results are compared with other existing control methods to confirm the strict stability and efficiency of the presented control scheme in both the convergence error and anti-disturbance capacity.
- (iv)
- Finally, unlike the existing methods, the upper bounds of the uncertainties and/or external disturbances are not demanded during the steps of designing the proposed control scheme.
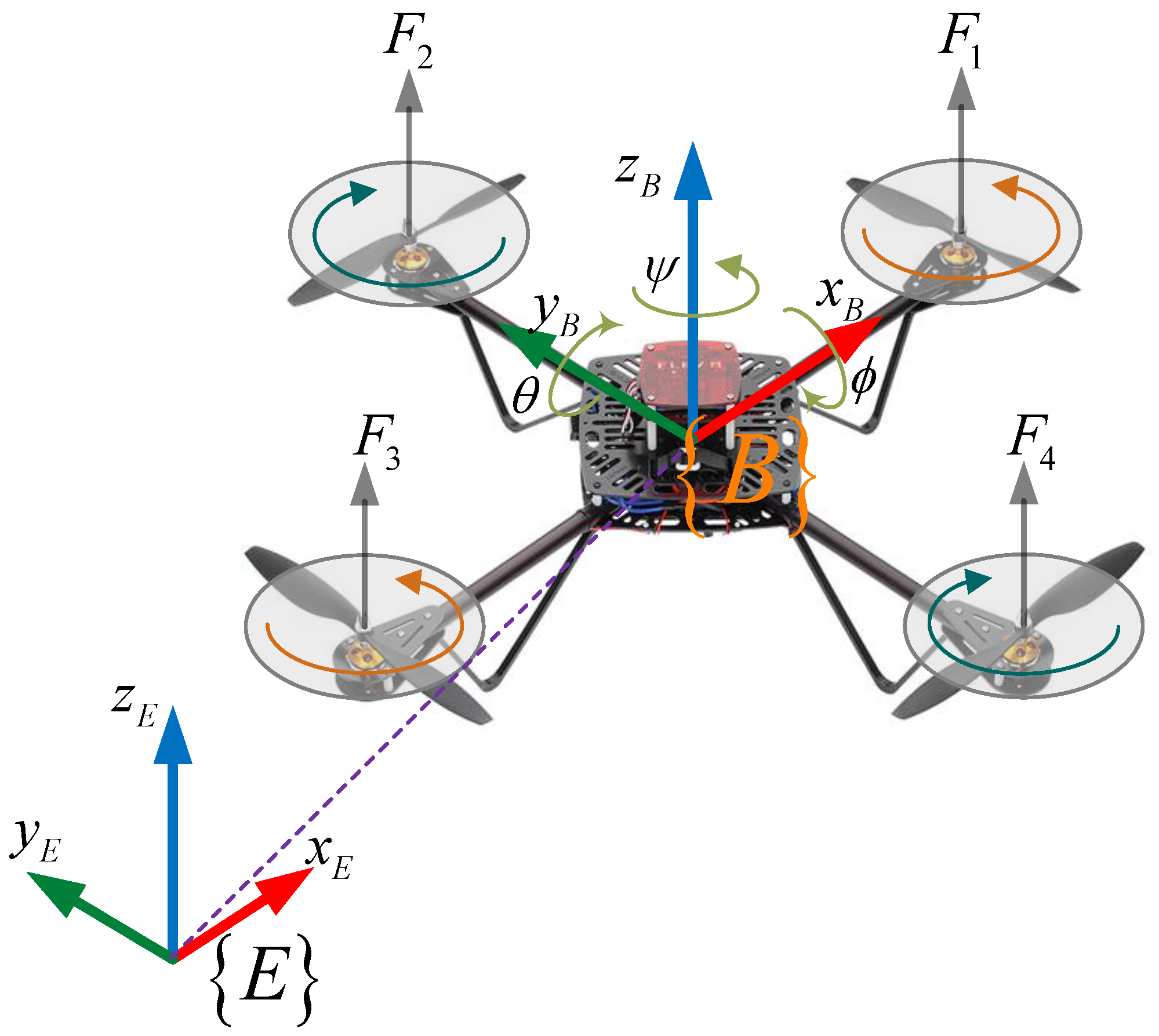
2. Mathematical Model and Problem Description
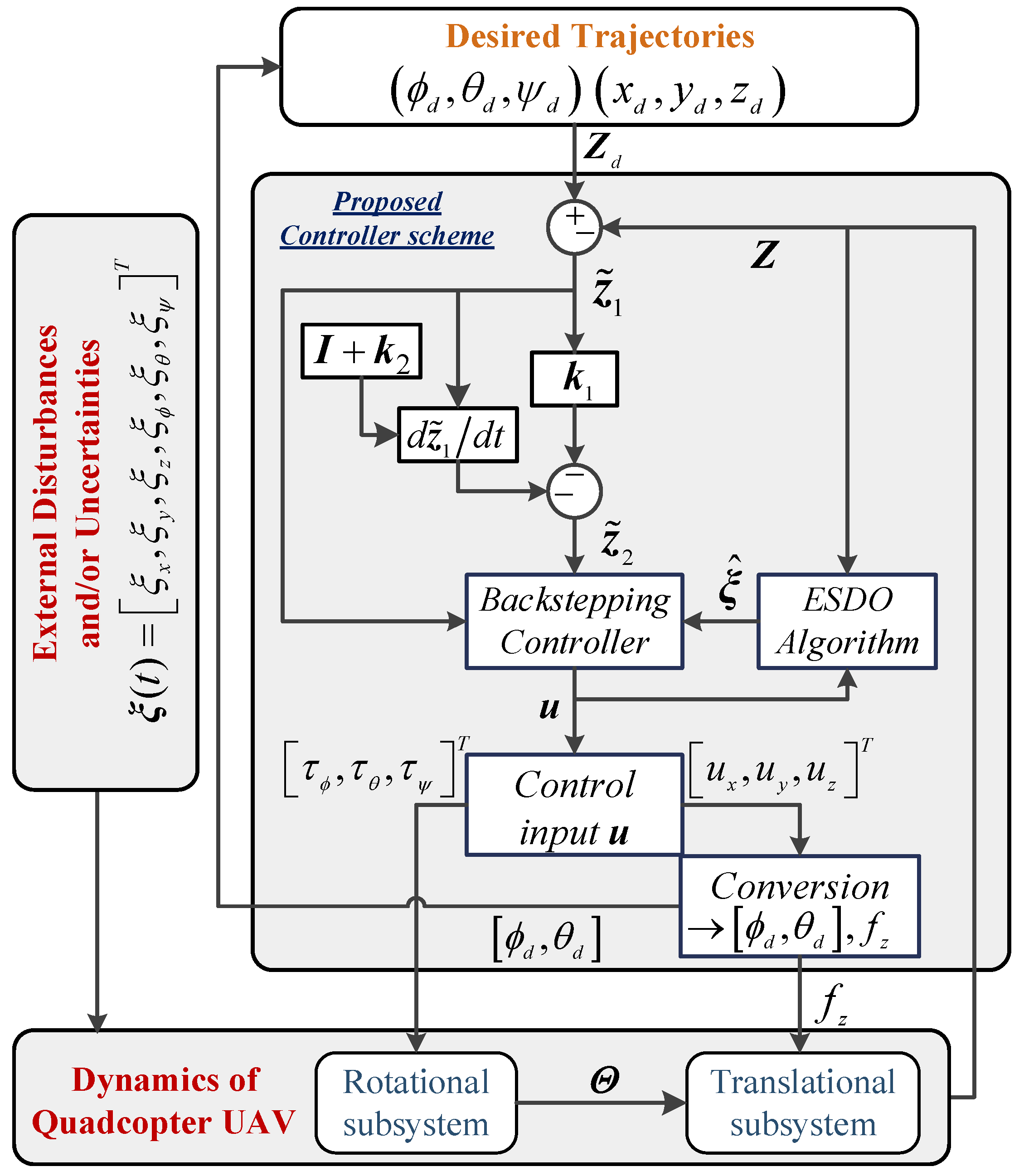
3. Robust Backstepping Control-Based ESDO
3.1. Extended State/Disturbance Observer (ESDO)
3.2. Robust Backstepping Controller Design
3.3. Stability Analysis of the Proposed Robust Backstepping Controller
4. Simulation Results and Discussions
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hao, L.; Wang, X.; Zhong, Y. Quaternion-Based Robust Attitude Control for Uncertain Robotic Quadrotors. IEEE Trans. Ind. Inform. 2015, 11, 406–415. [Google Scholar]
- Martinez Leon, A.S.; Rukavitsyn, A.N.; Jatsun, S.F. UAV Airframe Topology Optimization. In Proceedings of the 6th International Conference on Industrial Engineering (ICIE 2020), Sochi, Russia, 17–21 May 2020; ICIE 2021, Lecture Notes in Mechanical Engineering. Springer: Cham, Germany, 2021. [Google Scholar] [CrossRef]
- Yan, C.; Fu, L.; Zhang, J.; Wang, J. A comprehensive Survey on UAV Communication Channel Modelling. IEEE Access 2019, 7, 107769–107792. [Google Scholar] [CrossRef]
- Hu, S.; Wu, Q.; Wang, X. Energy Management and Trajectory Optimization for UAV-Enabled Legitimate Monitoring Systems. IEEE Trans. Wirel. Commun. 2021, 20, 142–155. [Google Scholar] [CrossRef]
- Zuo, Z. Trajectory tracking control design with command filtered compensation for a quadrotor. Control Theory Appl. IET 2010, 4, 2343–2355. [Google Scholar] [CrossRef]
- Rinaldi, F.; Chiesa, S.; Quagliotti, F. Linear quadratic control for quadrotors UAVs dynamics and formation flight. J. Intell. Robot. Syst. 2013, 70, 203–220. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. Robust nonlinear control for path tracking of a quad-rotor helicopter. Asian J. Control 2015, 17, 142–156. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernández-González, O.; Valencia-Palomo, G.; López-Estrada, F.R.; Rodríguez-Mata, A.E.; Garrido, J. Filtered observer-based ida-pbc control for trajectory tracking of a quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Ricardo, P.A.; Javier, M.V. Adaptive control for quadcopter trajectory tracking with accurate parameterization. IEEE Access 2019, 7, 2169–3536. [Google Scholar]
- Li, C.; Zhang, Y.; Li, P. Full control of a quadrotor using parameter-scheduled backstepping method: Implementation and experimental tests. Nonlinear Dyn. 2017, 89, 1259–1278. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/ nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude and position experimental studies. Control Theory Appl. IET 2012, 6, 1812–1827. [Google Scholar] [CrossRef] [Green Version]
- Thanh, H.L.N.N.; Hong, S.K. Quadcopter robust adaptive second order sliding mode control based on PID sliding surface. IEEE Access 2018, 6, 66850–66860. [Google Scholar] [CrossRef]
- Ha, L.N.N.T.; Hong, S.K. Robust dynamic sliding mode control-based PID-super twisting algorithm and disturbance observer for second-order nonlinear systems: Application to UAVs. Electronics 2019, 8, 760. [Google Scholar] [CrossRef] [Green Version]
- Zheng, E.H.; Xiong, J.J.; Luo, J.L. Second order sliding mode control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Cao, D.; Yang, J. High-order sliding mode observer-based trajectory tracking control for a quadcopter UAV with uncertain dynamics. Nonlinear Dyn. 2020, 102, 2583–2596. [Google Scholar] [CrossRef]
- Gong, X.; Hou, Z.C.; Zhao, C.J.; Bai, Y.; Tian, Y.T. Adaptive backstepping sliding mode trajectory tracking control for a quadrotor. Int. J. Autom. Comput. 2012, 9, 555–560. [Google Scholar] [CrossRef]
- Rodriguez, H.R.; Vega, V.P.; Orta, A.S.; Salazar, O.G. Robust backstepping control based on integral sliding mode for tracking of quadrotors. J. Intell. Robot. Syst. 2014, 73, 51–66. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S. Adaptive sliding mode control for finite-time stability of quad-rotor UAVs with parametric uncertainties. ISA Trans. 2018, 72, 1–14. [Google Scholar] [CrossRef]
- Yin, Y.; Niu, H.; Liu, X. Adaptive neural network sliding mode control for quad tilt rotor aircraft. Complexity 2017, 2017, 7104708. [Google Scholar] [CrossRef] [Green Version]
- Labbadi, M.; Cherkaoui, M. Adaptive fractional-order nonsingular fast terminal sliding mode based robust tracking control of quadrotor UAV with gaussian random disturbances and uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2265–2277. [Google Scholar] [CrossRef]
- Lei, X.; Guo, K.; Ge, S.S. Disturbance observer-based control of small unmanned aerial rotorcraft. Math. Probl. Eng. 2013, 2013, 464938. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer-based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef] [Green Version]
- Xu, B. Composite learning finite-time control with application to quadrotors. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1806–1815. [Google Scholar] [CrossRef]
- Wang, F.; Gao, H.; Wang, K.; Zhou, C.; Zong, Q.; Hua, C. Disturbance observer-based finite-time control design for a quadcopter UAV with external disturbance. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 834–847. [Google Scholar] [CrossRef]
- Derbel, N.; Ghommam, J.; Zhu, Q. Applications of Sliding Mode Control; Springer: Singapore, 2017. [Google Scholar]
- Chen, F.; Lei, W.; Zhang, K.; Tao, G.; Jang, B. A novel nonlinear resilient control for a quadcopter UAV via backstepping control and nonlinear disturbance observer. Nonlinear Dyn 2016, 85, 1281–1295. [Google Scholar] [CrossRef]
- Thanh, H.L.N.N.; Hong, S.K. An extended multi-surface sliding control for matched/mismatched uncertain nonlinear systems through a lumped disturbance estimator. IEEE Access 2020, 8, 91468–91475. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R. Antisaturation command filtered backstepping control-based disturbance rejection for a quadarotor UAV. IEEE Trans. Circuits Syst. II Express Briefs. 2021, 68, 3577–3581. [Google Scholar] [CrossRef]
- Fu, C.; Hong, W.; Lu, H.; Zhang, L.; Guo, X.; Tian, Y. Adaptive robust backstepping attitude control for a multi-rotor unmanned aerial vehicle with time-varying output constraints. Aerosp. Sci. Technol. 2018, 78, 593–603. [Google Scholar] [CrossRef]
- Das, A.; Lewis, F.; Subbarao, K. Backstepping approach for controlling a quadrotor using Lagrange form dynamics. J. Intell. Robot. Syst. 2009, 56, 127–151. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Zheng, S.; Dong, S.; Sun, G. Fixed-time disturbance observer-based robust fault-tolerant tracking control for uncertain quadrotor UAV subject to input delay. Nonlinear Dyn. 2022, 107, 2363–2390. [Google Scholar] [CrossRef]
- Shao, X.; Liu, J.; Wang, H. Robust back-stepping output feedback trajectory tracking for quadrotors via extended state observer and sigmoid tracking differentiator. Mech. Syst. Signal Proc. 2018, 104, 631–647. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust backstepping sliding mode control and observer-based fault estimation for a quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Zheng, F.; Zhen, Z.; Gong, H. Observer-based backstepping longitudinal control for carrier-based UAV with actuator faults. J. Syst. Eng. Electron. 2017, 28, 322–377. [Google Scholar]
- He, M.; He, J. Extended state observer-based robust backstepping sliding mode control for a small-size helicopter. IEEE Access 2018, 6, 33480–33488. [Google Scholar] [CrossRef]
- Shao, X.; Liu, J.; Cao, H.; Shen, C.; Wang, H. Robust dynamic surface trajectory tracking control for a quadcopter UAV via extended state observer. Int. J. Robust Nonlinear Control 2018, 28, 2700–2719. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Petros, A.; Sun, J. Robust Adaptive Control; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
| Symbol | Descriptions | Value and Unit |
|---|---|---|
| Total mass of the vehicle | ||
| Arm length of quadcopter UAV frame | ||
| Inertial moment of a rotor | ||
| Inertial moment around x-axis | ||
| Inertial moment around y-axis | ||
| Inertial moment around z-axis | ||
| Thrust coefficient | ||
| Drag coefficient |
| Parameter | Descriptions | Value |
|---|---|---|
| Observer gain of matrix | ||
| Observer gain of matrix | ||
| Controller gain | ||
| Controller gain | ||
| Controller gain | ||
| Initial state value |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thanh, H.L.N.N.; Huynh, T.T.; Vu, M.T.; Mung, N.X.; Phi, N.N.; Hong, S.K.; Vu, T.N.L. Quadcopter UAVs Extended States/Disturbance Observer-Based Nonlinear Robust Backstepping Control. Sensors 2022, 22, 5082. https://doi.org/10.3390/s22145082
Thanh HLNN, Huynh TT, Vu MT, Mung NX, Phi NN, Hong SK, Vu TNL. Quadcopter UAVs Extended States/Disturbance Observer-Based Nonlinear Robust Backstepping Control. Sensors. 2022; 22(14):5082. https://doi.org/10.3390/s22145082
Chicago/Turabian StyleThanh, Ha Le Nhu Ngoc, Tuan Tu Huynh, Mai The Vu, Nguyen Xuan Mung, Nguyen Ngoc Phi, Sung Kyung Hong, and Truong Nguyen Luan Vu. 2022. "Quadcopter UAVs Extended States/Disturbance Observer-Based Nonlinear Robust Backstepping Control" Sensors 22, no. 14: 5082. https://doi.org/10.3390/s22145082
APA StyleThanh, H. L. N. N., Huynh, T. T., Vu, M. T., Mung, N. X., Phi, N. N., Hong, S. K., & Vu, T. N. L. (2022). Quadcopter UAVs Extended States/Disturbance Observer-Based Nonlinear Robust Backstepping Control. Sensors, 22(14), 5082. https://doi.org/10.3390/s22145082











