Defense against Adversarial Swarms with Parameter Uncertainty
Abstract
:1. Introduction
2. Modeling Adverserial Swarms
2.1. Cooperative Swarm Models
- collision avoidance between swarm members;
- alignment forces between neighboring swarm members;
- stabilizing forces.
2.1.1. Example Model 1: Virtual Body Artificial Potential
2.1.2. Example Model 2: Reynolds Boid Model
2.2. Adversarial Swarm Models
Example Attrition Model: Single-Shot Destruction
3. Problem Formulation
3.1. Uncertain Parameter Optimal Control
3.2. Computational Efficiency
4. Consistency of Dual Variables
5. Numerical Example
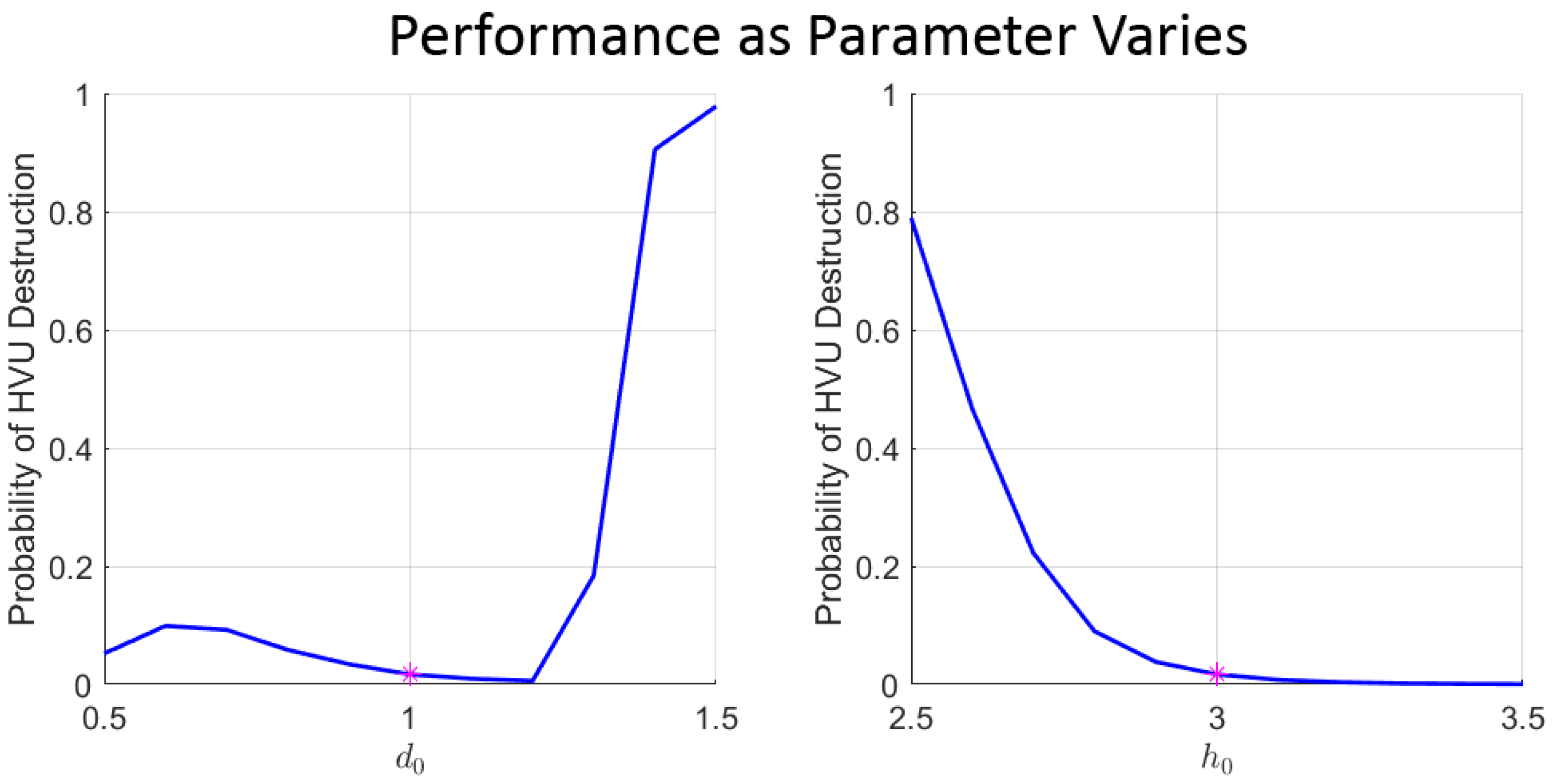
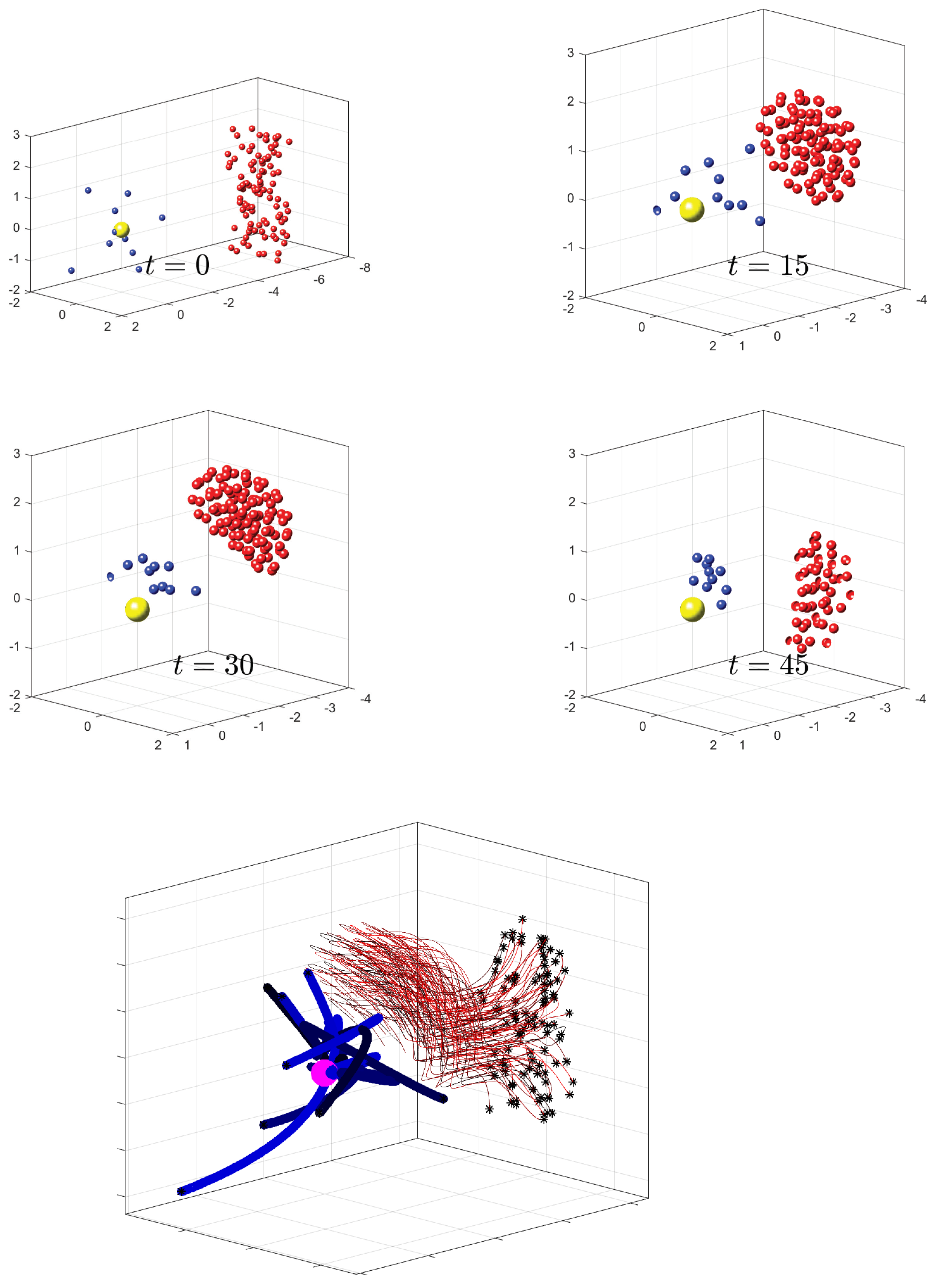
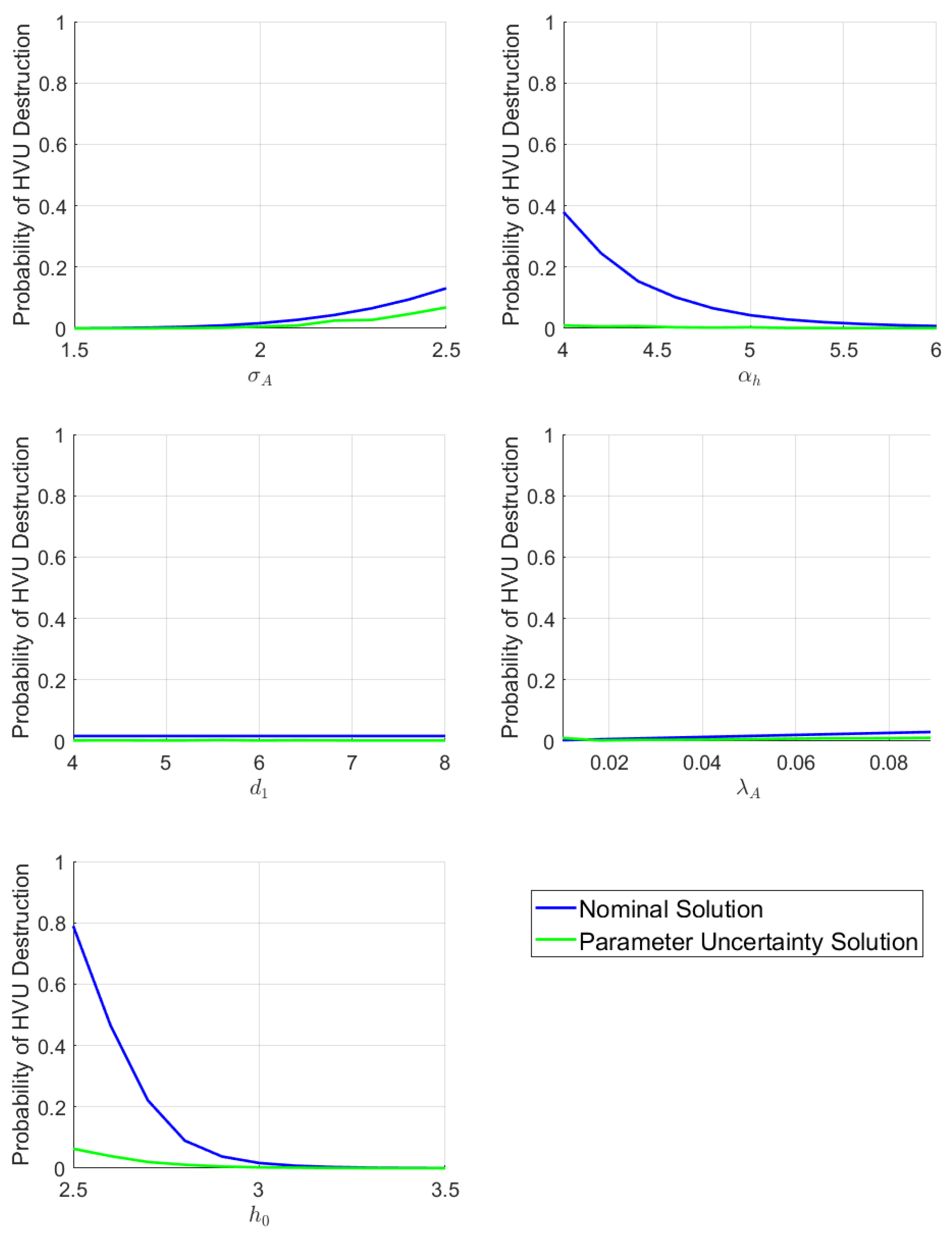
5.1. Example Model 1: Virtual Body Artificial Potential
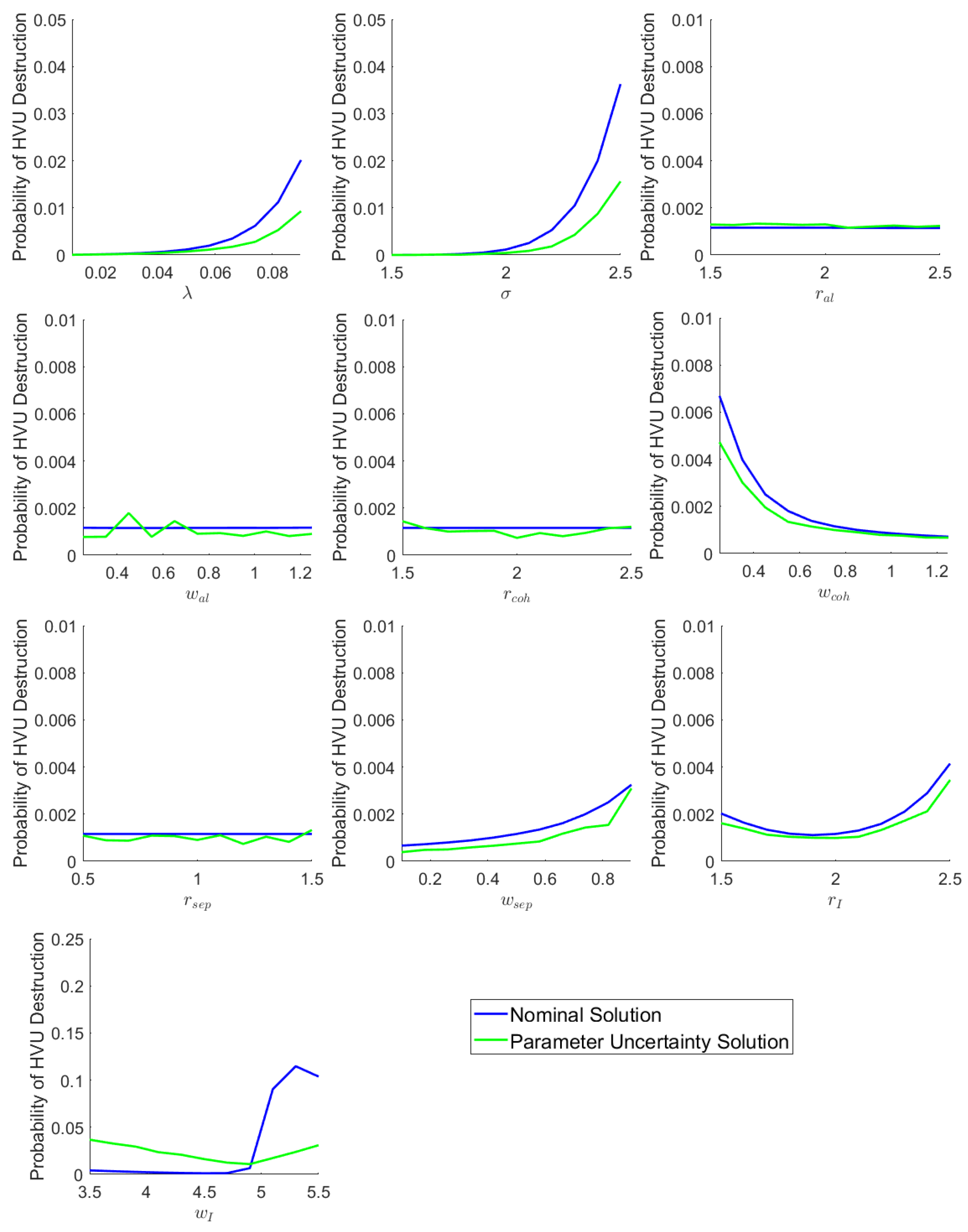
5.2. Example Model 2: Reynolds Boid Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Assumptions and Definitions
Appendix B. Main Theorem Proof
References
- Walton, C.; Gong, Q.; Kaminer, I.; Royset, J.O. Optimal Motion Planning for Searching for Uncertain Targets. IFAC Proc. Vol. 2014, 47, 8977–8982. [Google Scholar] [CrossRef] [Green Version]
- Gong, Q.; Kang, W.; Walton, C.; Kaminer, I.; Park, H. Partial Observability Analysis of an Adversarial Swarm Model. J. Guid. Control. Dyn. 2020, 43, 250–261. [Google Scholar] [CrossRef]
- Phelps, C.; Gong, Q.; Royset, J.O.; Walton, C.; Kaminer, I. Consistent approximation of a nonlinear optimal control problem with uncertain parameters. Automatica 2014, 50, 2987–2997. [Google Scholar] [CrossRef] [Green Version]
- Walton, C.; Kaminer, I.; Gong, Q. Consistent numerical methods for state and control constrained trajectory optimisation with parameter dependency. Int. J. Control 2021, 94, 2564–2574. [Google Scholar] [CrossRef]
- Weinan, E.; Han, J.; Li, Q. A mean-field optimal control formulation of deep learning. arXiv 2018, arXiv:1807.01083. [Google Scholar]
- Walton, C.; Phelps, C.; Gong, Q.; Kaminer, I. A Numerical Algorithm for Optimal Control of Systems with Parameter Uncertainty. IFAC-PapersOnLine 2016, 49, 468–475. [Google Scholar] [CrossRef]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef] [Green Version]
- Mehmood, U.; Paoletti, N.; Phan, D.; Grosu, R.; Lin, S.; Stoller, S.D.; Tiwari, A.; Yang, J.; Smolka, S.A. Declarative vs rule-based control for flocking dynamics. In Proceedings of the 33rd Annual ACM Symposium on Applied Computing, Pau, France, 9–13 April 2018; pp. 816–823. [Google Scholar]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar]
- Mavrovouniotis, M.; Li, C.; Yang, S. A survey of swarm intelligence for dynamic optimization: Algorithms and applications. J. Swarm Evol. Comput. 2017, 33, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Leonard, N.E.; Fiorelli, E. Virtual leaders, artificial potentials and coordinated control of groups. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No. 01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 3, pp. 2968–2973. [Google Scholar]
- Ogren, P.; Fiorelli, E.; Leonard, N.E. Cooperative control of mobile sensor networks: Adaptive gradient climbing in a distributed environment. IEEE Trans. Autom. Control 2004, 49, 1292–1302. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, C.W. Flocks, Herds and Schools: A Distributed Behavioral Model; ACM: New York, NY, USA, 1987; Volume 21. [Google Scholar]
- Haque, M.; Rahmani, A.; Egerstedt, M. A hybrid, multi-agent model of foraging bottlenose dolphins. IFAC Proc. Vol. 2009, 42, 262–267. [Google Scholar] [CrossRef] [Green Version]
- Strömbom, D.; Mann, R.P.; Wilson, A.M.; Hailes, S.; Morton, A.J.; Sumpter, D.J.; King, A.J. Solving the shepherding problem: Heuristics for herding autonomous, interacting agents. J. R. Soc. Interface 2014, 11, 20140719. [Google Scholar] [CrossRef] [PubMed]
- Pierson, A.; Schwager, M. Bio-inspired non-cooperative multi-robot herding. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1843–1849. [Google Scholar]
- Paranjape, A.A.; Chung, S.J.; Kim, K.; Shim, D.H. Robotic herding of a flock of birds using an unmanned aerial vehicle. IEEE Trans. Robot. 2018, 34, 901–915. [Google Scholar] [CrossRef] [Green Version]
- Kolon, C.; Schwartz, I.B. The Dynamics of Interacting Swarms. arXiv 2018, arXiv:1803.08817. [Google Scholar]
- Szwaykowska, K.; Schwartz, I.B.; Romero, L.M.y.T.; Heckman, C.R.; Mox, D.; Hsieh, M.A. Collective motion patterns of swarms with delay coupling: Theory and experiment. Phys. Rev. E 2016, 93, 032307. [Google Scholar] [CrossRef] [Green Version]
- Walton, C.; Lambrianides, P.; Kaminer, I.; Royset, J.; Gong, Q. Optimal motion planning in rapid-fire combat situations with attacker uncertainty. Nav. Res. Logist. 2018, 65, 101–119. [Google Scholar] [CrossRef]
- Ruths, J.; Li, J.S. Optimal Control of Inhomogeneous Ensembles. Trans. Autom. Control 2012, 57, 2012–2032. [Google Scholar] [CrossRef] [Green Version]
- Hager, W.W. Runge-Kutta Methods in optimal control and the transformed adjoint system. Numer. Math. 2000, 87, 247–282. [Google Scholar] [CrossRef]
- Gong, Q.; Ross, I.M.; Kang, W.; Fahroo, F. Connections Between the Covector Mapping Theorem and Convergence of Pseudospectral Methods for Optimal Control. Comput. Optim. Appl. 2008, 41, 307–335. [Google Scholar] [CrossRef] [Green Version]
- Gabasov, R.; Kirillova, F.M. The Maximum Principle in Optimal Control Theory; Publishing House Nauka i Tekhnika: Minsk, Belarus, 1974. (In Russian) [Google Scholar]
- Hartl, R.F.; Sethi, S.P.; Vickson, R.G. A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 1995, 37, 181–218. [Google Scholar] [CrossRef]
- Nakamura-Zimmerer, T.; Gong, Q.; Kang, W. Adaptive Deep Learning for High-Dimensional Hamilton–Jacobi–Bellman Equations. SIAM J. Sci. Comput. 2021, 43, A1221–A1247. [Google Scholar] [CrossRef]


| Parameter | Value | Meaning |
|---|---|---|
| 45 | final time | |
| 5 | tracking coefficient | |
| K | 10 | number of defenders |
| interaction parameter | ||
| 2 | defender weapon intensity | |
| 2 | defender weapon range | |
| N | 100 | number of attackers |
| 5 | dissipative force |
| Parameter | Nominal | Range | Meaning |
|---|---|---|---|
| [0.1, 0.9] | control gain | ||
| 1 | [0.5, 1.5] | lower range limit | |
| 6 | [4, 8] | upper range limit | |
| [0.01, 0.09] | weapon intensity | ||
| 2 | [1.5. 2.5] | weapon range | |
| 6 | [5, 7] | herding intensity | |
| 3 | [2, 4] | herding range |
| Parameter | Nominal | Range | Meaning |
|---|---|---|---|
| [0.01, 0.09] | weapon intensity | ||
| 2 | [1.5, 2.5] | weapon range | |
| 2 | [1.5, 2.5] | alignment range | |
| [0.25, 1.25] | alignment intensity | ||
| 2 | [1.5, 2.5] | cohesion range | |
| [0.25, 1.25] | cohesion intensity | ||
| 1 | [0.5, 1.5] | separation range | |
| [0.1, 0.9] | separation intensity | ||
| 2 | [1.5, 2.5] | herding range | |
| [3.5, 5.5] | herding intensity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walton, C.; Kaminer, I.; Gong, Q.; Clark, A.H.; Tsatsanifos, T. Defense against Adversarial Swarms with Parameter Uncertainty. Sensors 2022, 22, 4773. https://doi.org/10.3390/s22134773
Walton C, Kaminer I, Gong Q, Clark AH, Tsatsanifos T. Defense against Adversarial Swarms with Parameter Uncertainty. Sensors. 2022; 22(13):4773. https://doi.org/10.3390/s22134773
Chicago/Turabian StyleWalton, Claire, Isaac Kaminer, Qi Gong, Abram H. Clark, and Theodoros Tsatsanifos. 2022. "Defense against Adversarial Swarms with Parameter Uncertainty" Sensors 22, no. 13: 4773. https://doi.org/10.3390/s22134773
APA StyleWalton, C., Kaminer, I., Gong, Q., Clark, A. H., & Tsatsanifos, T. (2022). Defense against Adversarial Swarms with Parameter Uncertainty. Sensors, 22(13), 4773. https://doi.org/10.3390/s22134773







