FPGA-Based Processor for Continual Capacitive-Coupling Impedance Spectroscopy and Circuit Parameter Estimation
Abstract
:1. Introduction
- The architecture of the proposed FPGA-based processor based on CIS and parameter estimation in the CR circuit model that can be measured in real-time were shown;
- The measurement accuracy of the proposed FPGA-based processor was confirmed;
- We show that continual impedance estimation in real-time is possible using the proposed FPGA-based processor.
2. Materials and Systems
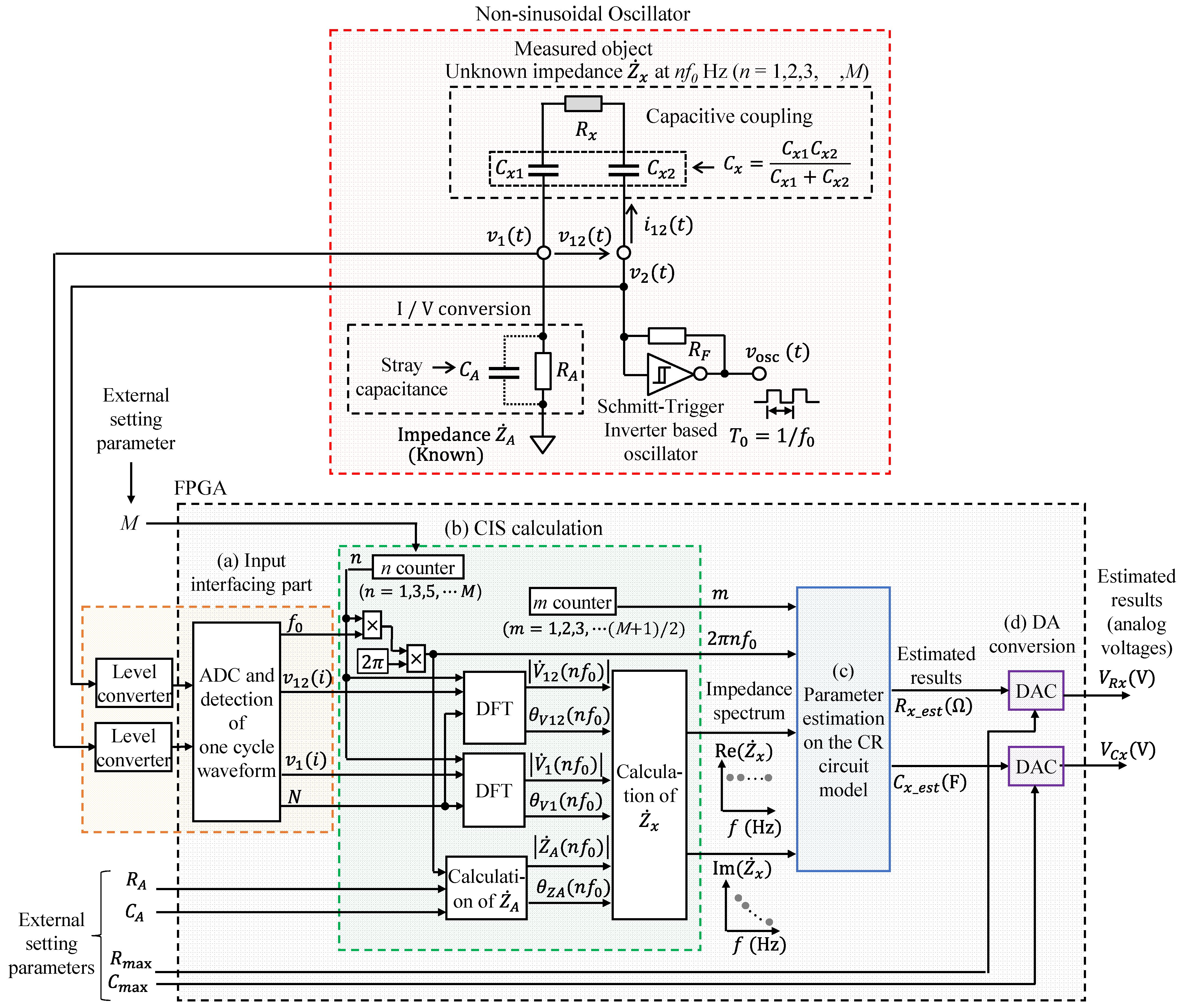
2.1. Overview of the Proposed FPGA-Based Processor and CIS Method
2.2. Architecture of the Proposed FPGA-Based Processor for CIS and the Parameter Estimation on the CR Circuit Model
- (a)
- Input interfacing part;
- (b)
- CIS calculation;
- (c)
- Parameter estimation on the CR circuit model;
- (d)
- Digital-to-analog (DA) conversion.
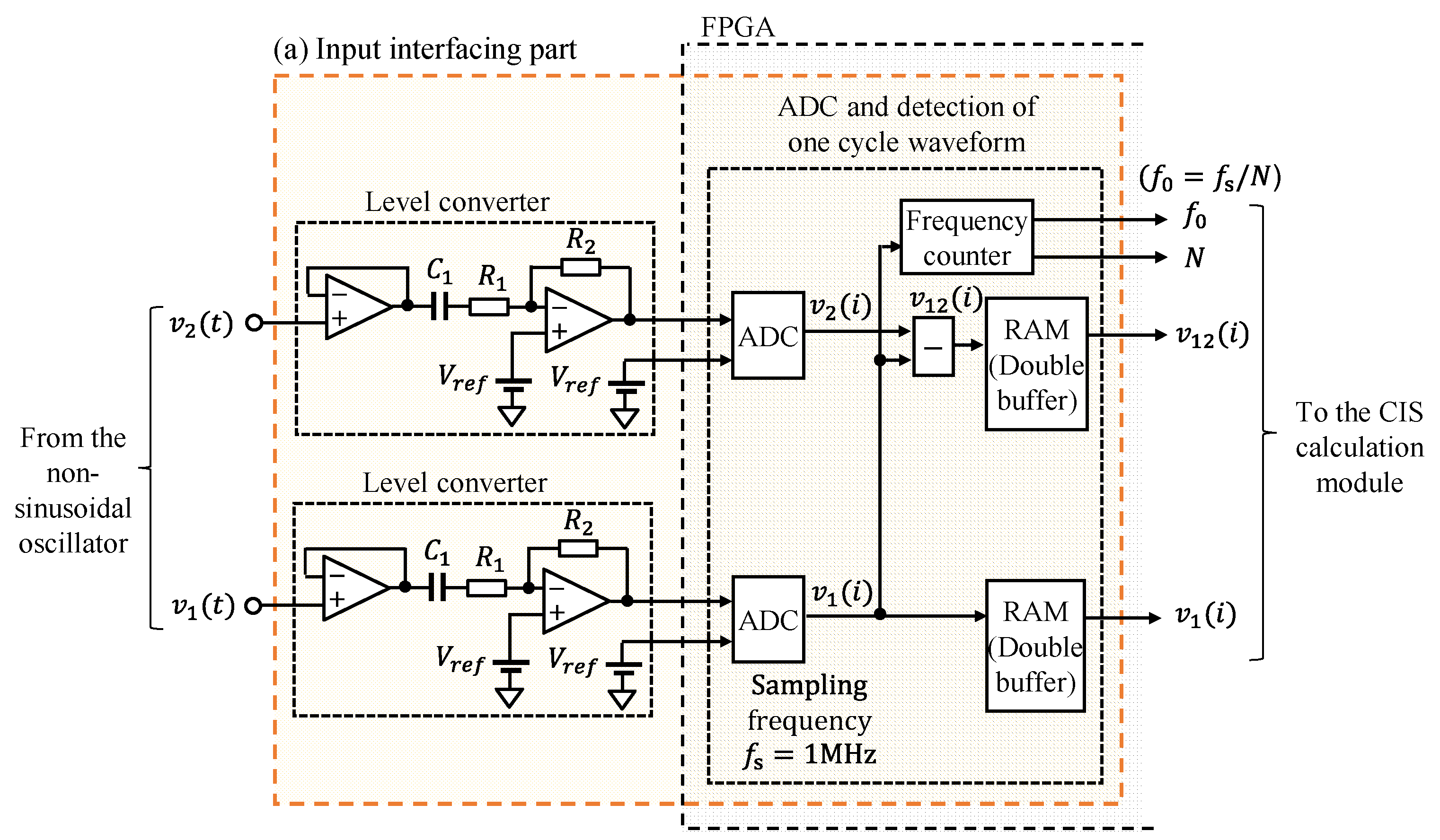
2.2.1. Input Interfacing Part
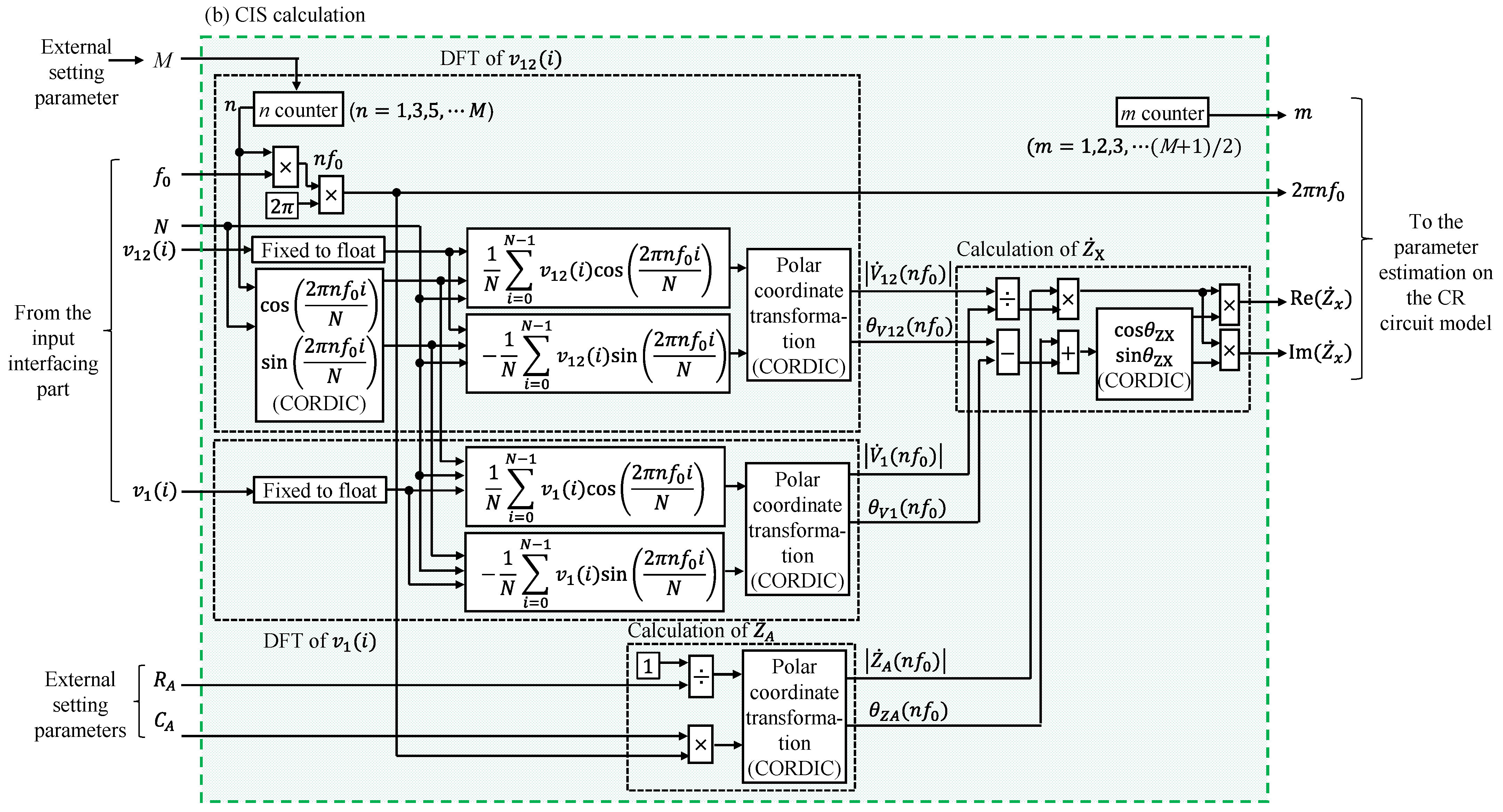
2.2.2. CIS Calculation
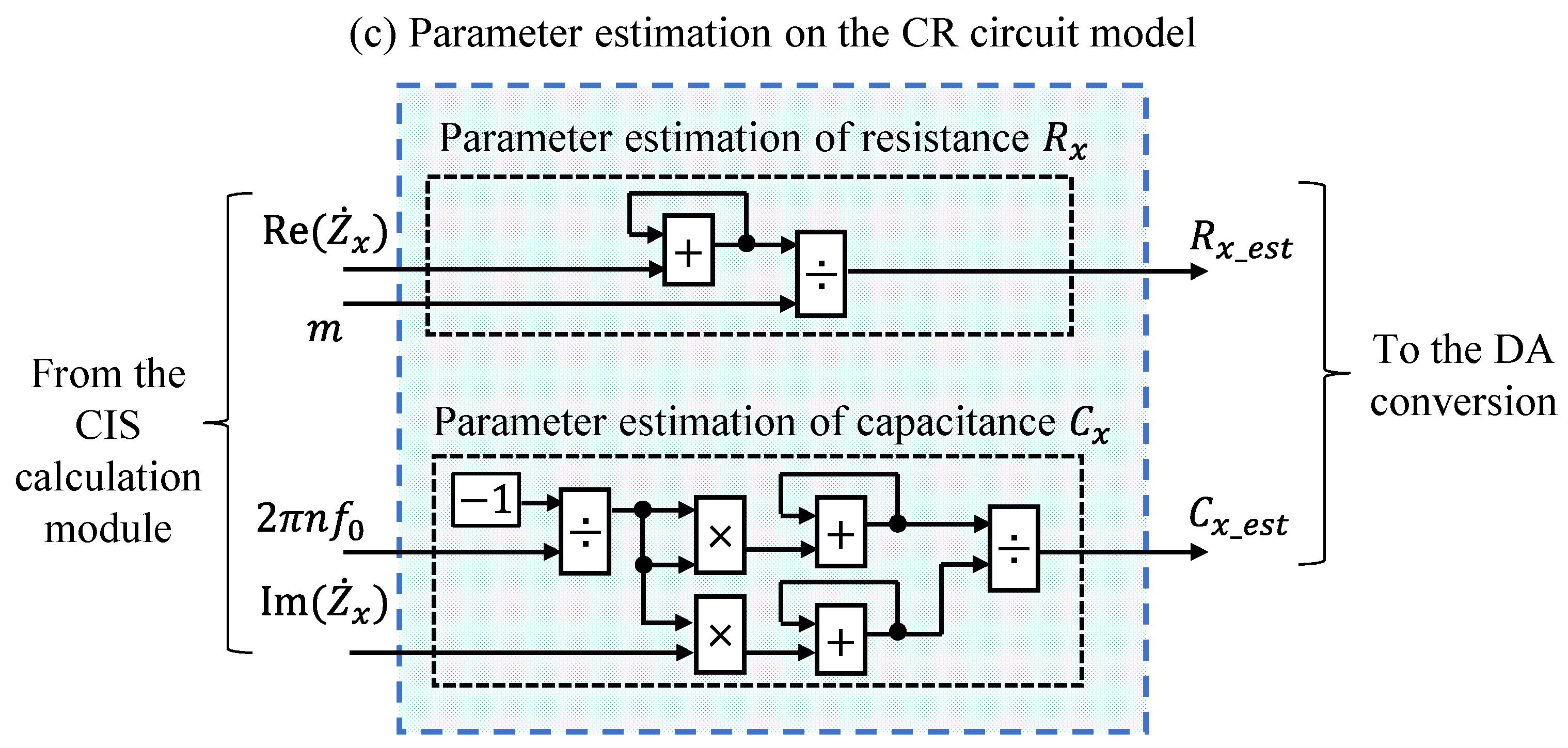
2.2.3. Parameter Estimation on CR Circuit Model Based on the Least-Squares Method
2.2.4. DA Conversion
2.3. Execution Time of the Proposed FPGA-Based Processor
3. System Evaluation Method
3.1. Calculation Method of the Execution Times and Other Environments for Comparison
3.2. Measuring Methods of Fixed Resistors and Capacitors
3.3. Measuring Method of CdS Photocell for Time-Varying Impedance Measurement
4. Results
4.1. Result of the Comparison of Execution Times
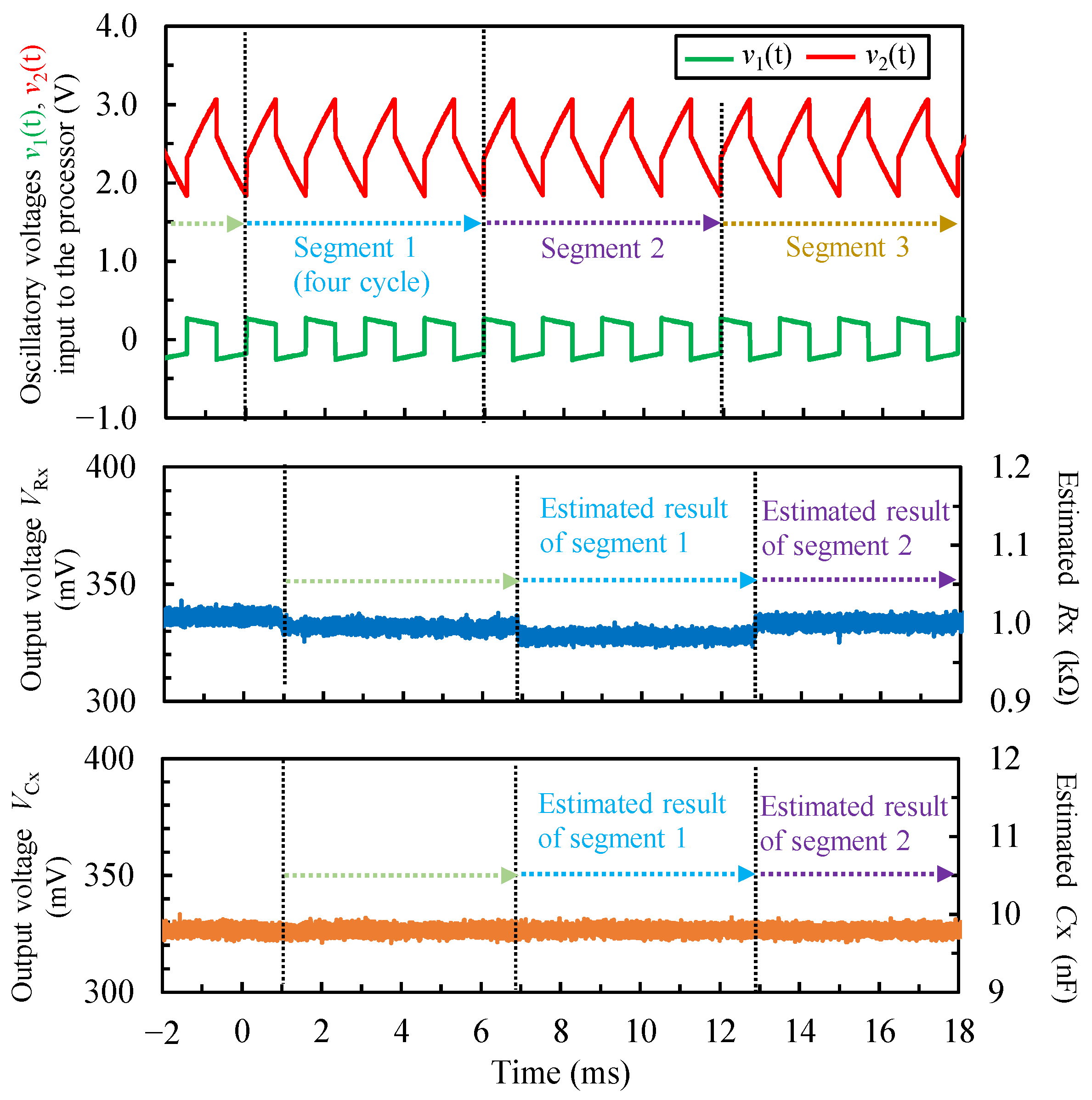
4.2. Measurement Results of Fixed Resistors and Capacitors
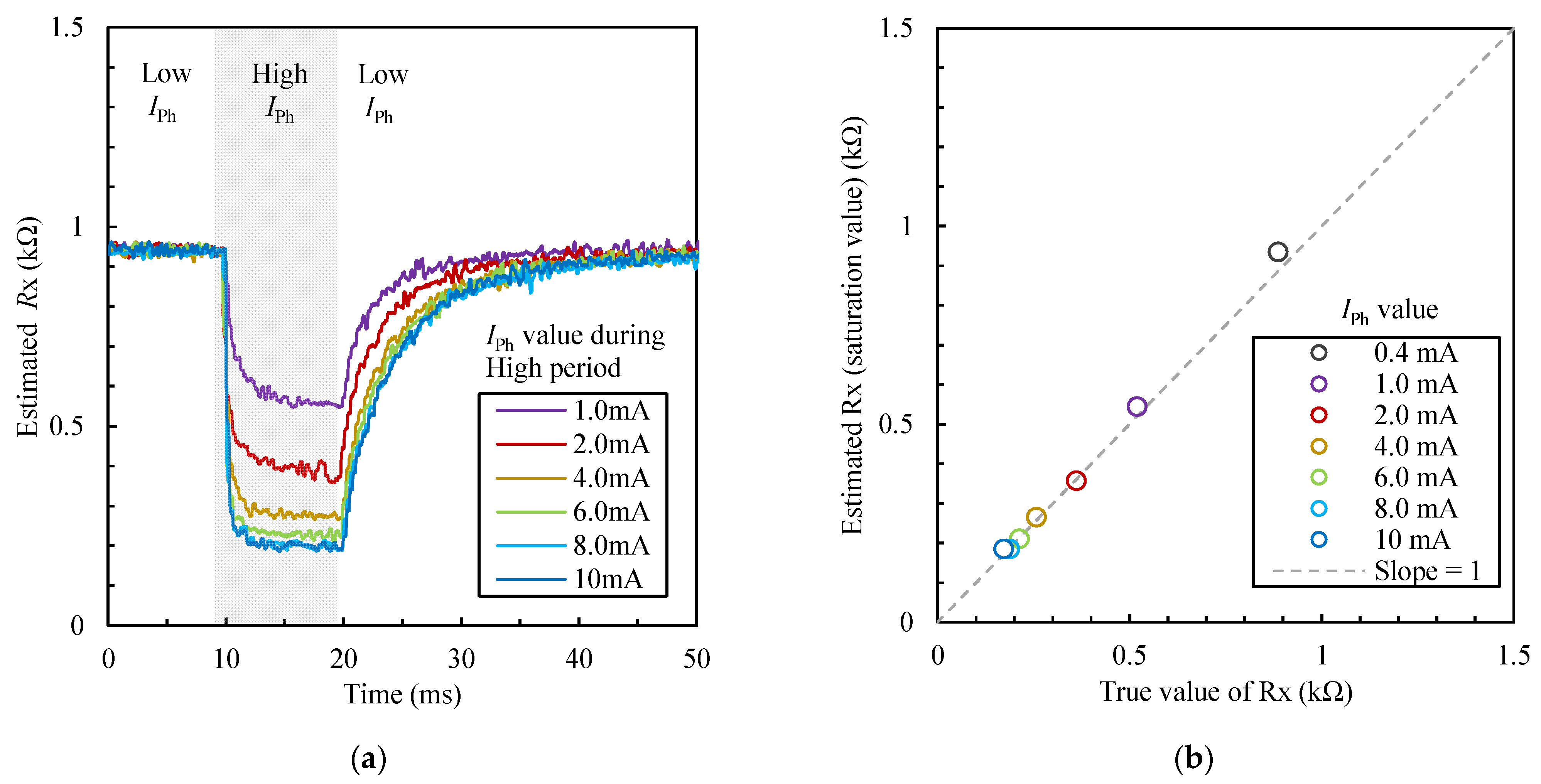
4.3. Measurement Results of CdS Photocell
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grossi, M.; Riccò, B. Electrical impedance spectroscopy (EIS) for biological analysis and food characterization: A review. J. Sens. Sens. Syst. 2017, 6, 303–325. [Google Scholar] [CrossRef]
- Zappen, H.; Ringbeck, F.; Sauer, D.U. Application of Time-Resolved Multi-Sine Impedance Spectroscopy for Lithium-Ion Battery Characterization. Batteries 2018, 4, 64. [Google Scholar] [CrossRef]
- Orlikowski, J.; Ryl, J.; Jarzynka, M.; Krakowiak, S.; Darowicki, K. Instantaneous Impedance Monitoring of Aluminum Alloy 7075 Corrosion in Borate Buffer with Admixed Chloride Ions. Corrosion 2015, 71, 828–838. [Google Scholar] [CrossRef]
- Bar-On, L.; Shacham-Diamand, Y. On the Interpretation of Four Point Impedance Spectroscopy of Plant Dehydration Monitoring. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 482–492. [Google Scholar] [CrossRef]
- Piccoli, A.; Rossi, B.; Pillon, L.; Bucciante, G. A new method for monitoring body fluid variation by bioimpedance analysis: The RXc graph. Kidney Int. 1994, 46, 534–539. [Google Scholar] [CrossRef]
- Nwosu, A.C.; Mayland, C.R.; Mason, S.; Cox, T.F.; Varro, A.; Ellershaw, J. The association of hydration status with physical signs, symptoms and survival in advanced cancer—The use of bioelectrical impedance vector analysis (BIVA) technology to evaluate fluid volume in palliative care: An observational study. PLoS ONE 2016, 11, e0163114. [Google Scholar] [CrossRef]
- Da Fonseca, R.D.; Santos, P.R.; Monteiro, M.S.; Fernandes, L.A.; Campos, A.H.; Borges, D.L.; Rosa, S.D.S.R.F. Parametric evaluation of impedance curve in radiofrequency ablation: A quantitative description of the asymmetry and dynamic variation of impedance in bovine ex vivo model. PLoS ONE 2021, 16, e0245145. [Google Scholar] [CrossRef]
- Li, X.; Qin, Z.; Fu, H.; Li, T.; Peng, R.; Li, Z.; Rini, J.M.; Liu, X. Enhancing the performance of paper-based electrochemical impedance spectroscopy nanobiosensors: An experimental approach. Biosens. Bioelectron. 2020, 177, 112672. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Z.; Wang, Y.; Lin, J. A portable impedance detector of interdigitated array microelectrode for rapid detection of avian influenza virus. In Computer and Computing Technologies in Agriculture VIII. CCTA 2014. IFIP Advances in Information and Communication Technology; Li, D., Chen, Y., Eds.; Springer: Cham, Switzerland, 2015; Volume 452. [Google Scholar]
- Ma, H.; Wallbank, R.W.R.; Chaji, R.; Li, J.; Suzuki, Y.; Jiggins, C.; Nathan, A. An impedance-based integrated biosensor for suspended DNA characterization. Sci. Rep. 2013, 3, 2730. [Google Scholar] [CrossRef]
- Van Grinsven, B.; Vandenryt, T.; Duchateau, S.; Gaulke, A.; Grieten, L.; Thoelen, R.; Ingebrandt, S.; De Ceuninck, W.; Wagner, P. Customized impedance spectroscopy device as possible sensor platform for biosensor applications. Phys. Status Solidi (A) 2010, 207, 919–923. [Google Scholar] [CrossRef]
- Dheman, K.S.; Mayer, P.; Magno, M.; Schuerle, S. Wireless, Artefact Aware Impedance Sensor Node for Continuous Bio-Impedance Monitoring. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1122–1134. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Jafar, R. Cuffless blood pressure monitoring from an array of wrist bio-impedance sensors using subject-specific regression models: Proof of concept. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1723–1735. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Hall, D.A.; Jafari, R. Pulse Wave Modeling Using Bio-Impedance Simulation Platform Based on a 3D Time-Varying Circuit Model. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 143–158. [Google Scholar] [CrossRef] [PubMed]
- Barber, D.C.; Brown, B.H. Applied potential tomography. J. Phys. E 1984, 17, 723–733. [Google Scholar] [CrossRef]
- Wu, Y.; Hanzaee, F.F.; Jiang, D.; Bayford, R.H.; Demosthenous, A. Electrical Impedance Tomography for Biomedical Applications: Circuits and Systems Review. IEEE Open J. Circuits Syst. 2021, 2, 380–397. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, D.; Habibollahi, M.; Almarri, N.; Demosthenous, A. Time Stamp—A Novel Time-to-Digital Demodulation Method for Bioimpedance Implant Applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 997–1007. [Google Scholar] [CrossRef]
- Hedayatipour, A.; Aslanzadeh, S.; Hesari, S.H.; Haque, M.A.; McFarlane, N. A Wearable CMOS Impedance to Frequency Sensing System for Non-Invasive Impedance Measurements. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1108–1121. [Google Scholar] [CrossRef]
- Analog Devices, AD5933 Data Sheet Rev. F. Available online: https://www.analog.com/en/products/ad5933.html (accessed on 1 May 2022).
- Piasecki, T.; Chabowski, K.; Nitsch, K. Design, calibration and tests of versatile low frequency impedance analyser based on ARM microcontroller. Measurement 2016, 91, 155–161. [Google Scholar] [CrossRef]
- Cabrera-López, J.J.; Velasco-Medina, J.; Denis, E.R.; Calderón, J.F.B.; Guevara, O.J.G. Bioimpedance measurement using mixed-signal embedded system. In Proceedings of the 2016 IEEE 7th Latin American Symposium on Circuits & Systems (LASCAS), Florianopolis, Brazil, 28 February–2 March 2016; pp. 335–338. [Google Scholar]
- Priidel, E.; Pesti, K.; Min, M.; Ojarand, J.; Martens, O. FPGA-based 16-bit 20 MHz device for the inductive measurement of electrical bio-impedance. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Manickam, A.; Chevalier, A.; McDermott, M.; Ellington, A.D.; Hassibi, A. A CMOS Electrochemical Impedance Spectroscopy (EIS) Biosensor Array. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 379–390. [Google Scholar] [CrossRef]
- Cheon, S.-I.; Kweon, S.-J.; Kim, Y.; Koo, J.; Ha, S.; Je, M. An Impedance Readout IC with Ratio-Based Measurement Techniques for Electrical Impedance Spectroscopy. Sensors 2022, 22, 1563. [Google Scholar] [CrossRef]
- Rao, A.; Murphy, E.K.; Halter, R.J.; Odame, K.M. A 1 MHz Miniaturized Electrical Impedance Tomography System for Prostate Imaging. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 787–799. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Wang, G.; Li, Y.; Zeng, L.; Li, H.; Gao, Y.; Ma, Y.; Lian, Y.; Heng, C.H. A 13-channel 1.53-mW 11.28-mm2 electrical impedance tomography SoC based on frequency division multiplexing for lung physiological imaging. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 938–949. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Jiang, D.; Bardill, A.; Bayford, R.; Demosthenous, A. A 122 fps, 1 MHz Bandwidth Multi-Frequency Wearable EIT Belt Featuring Novel Active Electrode Architecture for Neonatal Thorax Vital Sign Monitoring. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Hao, Z.; Wu, X.; Wang, X. An optimal Electrical Impedance Tomography drive pattern for human-computer interaction applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Rosa, B.M.G.; Yang, G.-Z. Bladder Volume Monitoring Using Electrical Impedance Tomography with Simultaneous Multi-Tone Tissue Stimulation and DFT-Based Impedance Calculation Inside an FPGA. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 775–786. [Google Scholar] [CrossRef] [PubMed]
- Strodthoff, N.; Strodthoff, C.; Becher, T.; Weiler, N.; Frerichs, I. Inferring Respiratory and Circulatory Parameters from Electrical Impedance Tomography with Deep Recurrent Models. IEEE J. Biomed. Health Inform. 2021, 25, 3105–3111. [Google Scholar] [CrossRef]
- Takhti, M.; Odame, K. Structured Design Methodology to Achieve a High SNR Electrical Impedance Tomography. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 364–375. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Ueno, A. Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study. Sensors 2020, 20, 6392. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Ogawa, E.; Ueno, A. Short-Time Impedance Spectroscopy Using a Mode-Switching Nonsinusoidal Oscillator: Applicability to Biological Tissues and Continuous Measurement. Sensors 2021, 21, 6951. [Google Scholar] [CrossRef]
- Huerta-Nuñez, L.F.E.; Gutierrez-Iglesias, G.; Martinez-Cuazitl, A.; Mata-Miranda, M.M.; Alvarez-Jiménez, V.D.; Sánchez-Monroy, V.; Golberg, A.; González-Díaz, C.A. A biosensor capable of identifying low quantities of breast cancer cells by electrical impedance spectroscopy. Sci. Rep. 2019, 9, 6419. [Google Scholar] [CrossRef]




| Symbol | Meaning |
|---|---|
| Rx | Unknown resistance of the measurement object. |
| Cx1 | Unknown capacitance 1 of capacitive coupling to the measurement object. |
| Cx2 | Unknown capacitance 2 of capacitive coupling to the measurement object. |
| Cx | Unknown capacitance caused by capacitive coupling. Combined capacitance of Cx1 and Cx2. Cx = Cx1 Cx2/(Cx1 + Cx2). |
| Unknown impedance of measurement object and capacitance caused by capacitive coupling. Combined impedance of Rx and Cx. | |
| RA | Known resistance for I/V conversion. A resistance for calibration and converting the current flowing through the measurement object into a voltage . |
| CA | Stray capacitance generated in parallel with RA. |
| Known impedance. Combined impedance of RA and CA. | |
| Nonsinusoidal oscillation waveform generated by capacitive coupling to the measurement object. Voltage applied to . | |
| Nonsinusoidal oscillation waveform generated by capacitive coupling to the measurement object. | |
| Excited voltage to the measurement object. . | |
| Current flowing through the measurement object. | |
| Complex voltage of Complex number indication of . | |
| Complex voltage of Complex number indication of . | |
| Complex current of Complex number indication of . | |
| f | Frequency. |
| f0 | Fundamental frequency of nonsinusoidal oscillation waveform. |
| T0 | Period of fundamental frequency f0. T0 = 1/f0. |
| n | Integer number. |
| Complex voltages at frequency nf0. | |
| Complex voltages at frequency nf0. | |
| Real part of . | |
| Imaginary part of . | |
| Real part of . | |
| Imaginary part of . | |
| Amplitude spectrum of . | |
| Phase spectrum of . | |
| Amplitude spectrum of . | |
| Phase spectrum of . | |
| Amplitude spectrum of . | |
| Phase spectrum of . | |
| Real part of . Real part of the impedance of the measurement object. | |
| Imaginary part of . Imaginary part of the impedance of the measurement object. | |
| fs | Sampling frequency of ADC. |
| N | Number of oscillation waveform samples at f0. |
| M | Upper limit order of fundamental frequency harmonics. |
| Rx_est | Estimated Rx by least-squares method. |
| Cx_est | Estimated Cx by least-squares method. |
| JRx | Constant minimized by the least-squares method for Rx. |
| JCx | Constant minimized by the least-squares method for Cx. |
| u | Constant with 1/Cx replaced. |
| m | Number of vector elements. m = (M + 1)/2. |
| Real part vectors of IS at nf0 (n = 1, 3, 5, …, M). One row m column vector. | |
| Imaginary part vectors of IS at nf0 (n = 1, 3, 5, …, M). One row m column vector. | |
| Real parts of the basis vector at nf0 (n = 1, 3, 5, …, M). M row one column vector. | |
| Imaginary parts of the basis vector at nf0 (n = 1, 3, 5, …, M). m row one column vector. | |
| VRx | Processor output voltage of Rx. Estimated Rx (Rx_est) converted to voltage. |
| VCx | Processor output voltage of Cx. Estimated Cx (Cx_est) converted to voltage. |
| Q | Quantization bits of Rx_est and Cx_est. |
| Vmax | Maximum output voltage of the FPGA board. |
| Rmax | Maximum value of measurable resistance. |
| Cmax | Maximum value of measurable capacitance. |
| RLPF | Resistance of LPF used in the DA converter. |
| CLPF | Capacitance of LPF used in the DA converter. |
| Execution time of the proposed FPGA-based processor. | |
| Reciprocal of operating frequency of FPGA. |
| Item | PC | Raspberry Pi 4 Model B |
|---|---|---|
| CPU | Intel Core i7-1165G7@2.80 GHz, 1.69 GHz | Broadcom 2711 4-core ARM Cortex-A72@1.5 GHz |
| RAM | 16 GB | 8 GB |
| SSD | 512 GB | – |
| OS | Windows 10 Home | Raspbian OS |
| C compiler | Visual Studio 2019 | GCC |
| FPGA Resources | Available (Z-7020, xc7z020clg400-1) | Utilization |
|---|---|---|
| Look up table (LUT) | 53,200 | 38,896 (73.1%) |
| LUT RAM | 17,400 | 939 (5.4%) |
| Flip flop | 106,400 | 56,011 (52.6%) |
| Block RAM | 140 | 16.5 (11.8%) |
| DSP | 220 | 72 (32.7%) |
| Environments | Execution Time (ms) | Ratio | |
|---|---|---|---|
| FPGA-based proposed processor @150 MHz | 0.153 | 1 | |
| PC (C, Single thread) @2.8 GHz, 1.69 GHz | Minimum | 0.217 | 1.41 |
| Mean ± S.D. | 0.263 ± 0.029 | 1.71 | |
| Maximum | 0.310 | 2.02 | |
| Raspberry Pi 4 (C, Single thread) @1.5 GHz | Minimum | 1.047 | 6.8 |
| Mean ± S.D. | 2.551 ± 0.622 | 16.6 | |
| Maximum | 3.193 | 20.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsukahara, A.; Yamaguchi, T.; Tanaka, Y.; Ueno, A. FPGA-Based Processor for Continual Capacitive-Coupling Impedance Spectroscopy and Circuit Parameter Estimation. Sensors 2022, 22, 4406. https://doi.org/10.3390/s22124406
Tsukahara A, Yamaguchi T, Tanaka Y, Ueno A. FPGA-Based Processor for Continual Capacitive-Coupling Impedance Spectroscopy and Circuit Parameter Estimation. Sensors. 2022; 22(12):4406. https://doi.org/10.3390/s22124406
Chicago/Turabian StyleTsukahara, Akihiko, Tomiharu Yamaguchi, Yuho Tanaka, and Akinori Ueno. 2022. "FPGA-Based Processor for Continual Capacitive-Coupling Impedance Spectroscopy and Circuit Parameter Estimation" Sensors 22, no. 12: 4406. https://doi.org/10.3390/s22124406
APA StyleTsukahara, A., Yamaguchi, T., Tanaka, Y., & Ueno, A. (2022). FPGA-Based Processor for Continual Capacitive-Coupling Impedance Spectroscopy and Circuit Parameter Estimation. Sensors, 22(12), 4406. https://doi.org/10.3390/s22124406






