Using Conventional Cameras as Sensors for Estimating Confidence Intervals for the Speed of Vessels from Single Images
Abstract
:1. Introduction
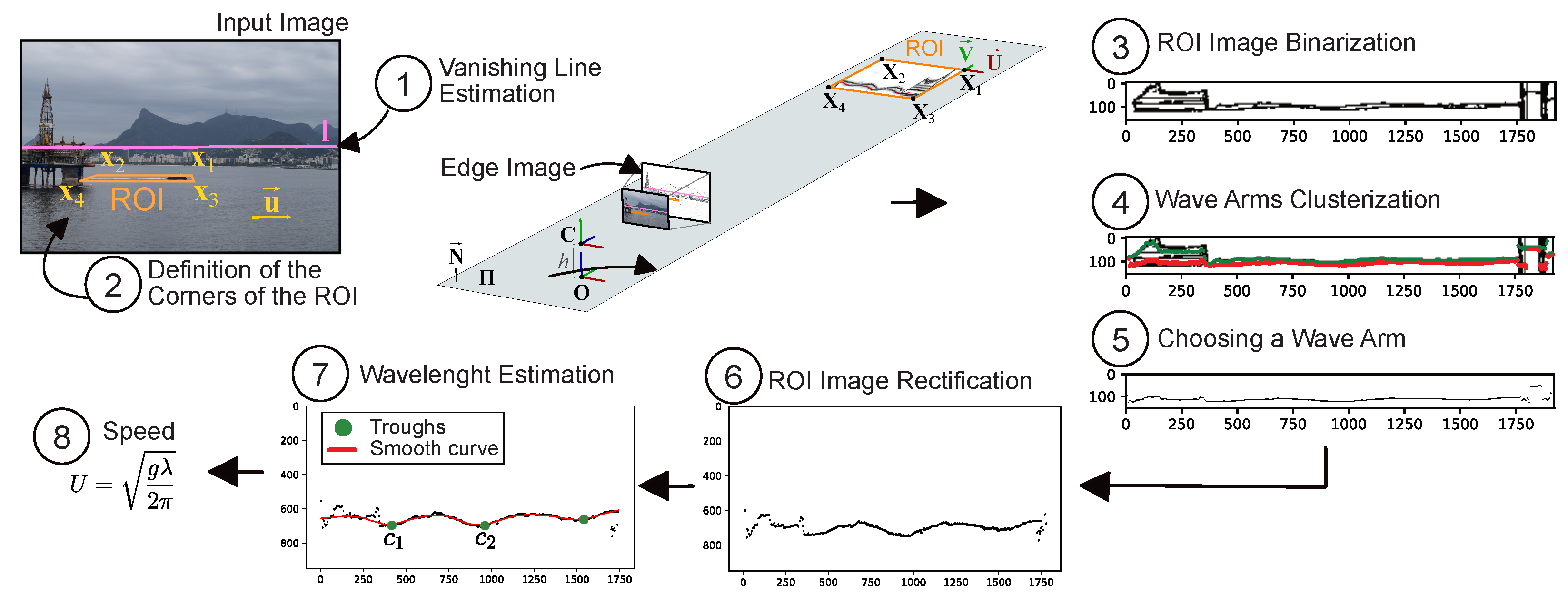
2. Computing Vessel Speed
2.1. Vanishing Line Estimation
2.2. Definition of the Corners of the ROI
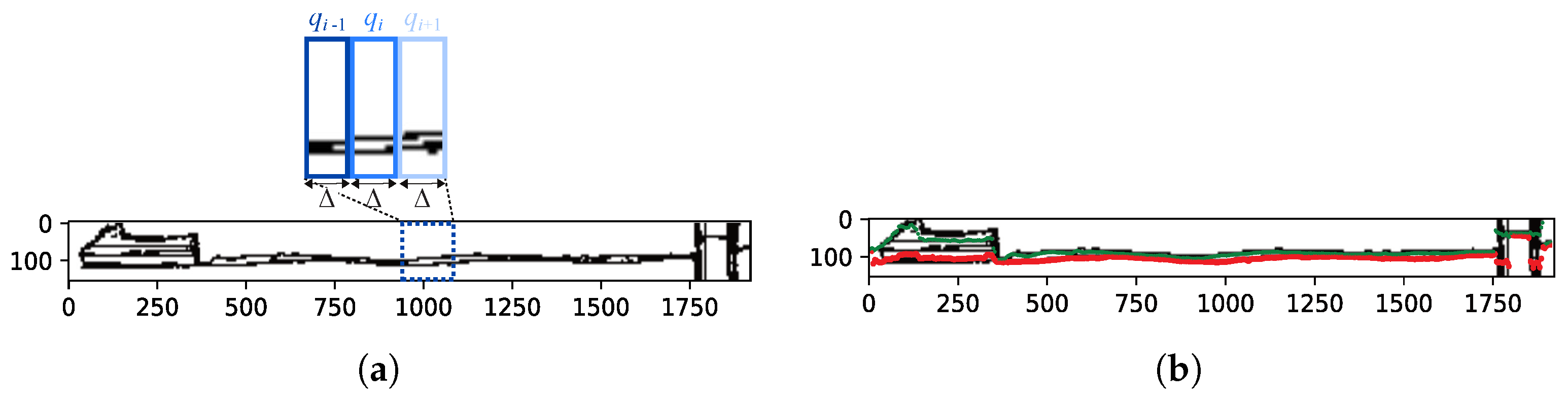
2.3. Finding the Wave Arms
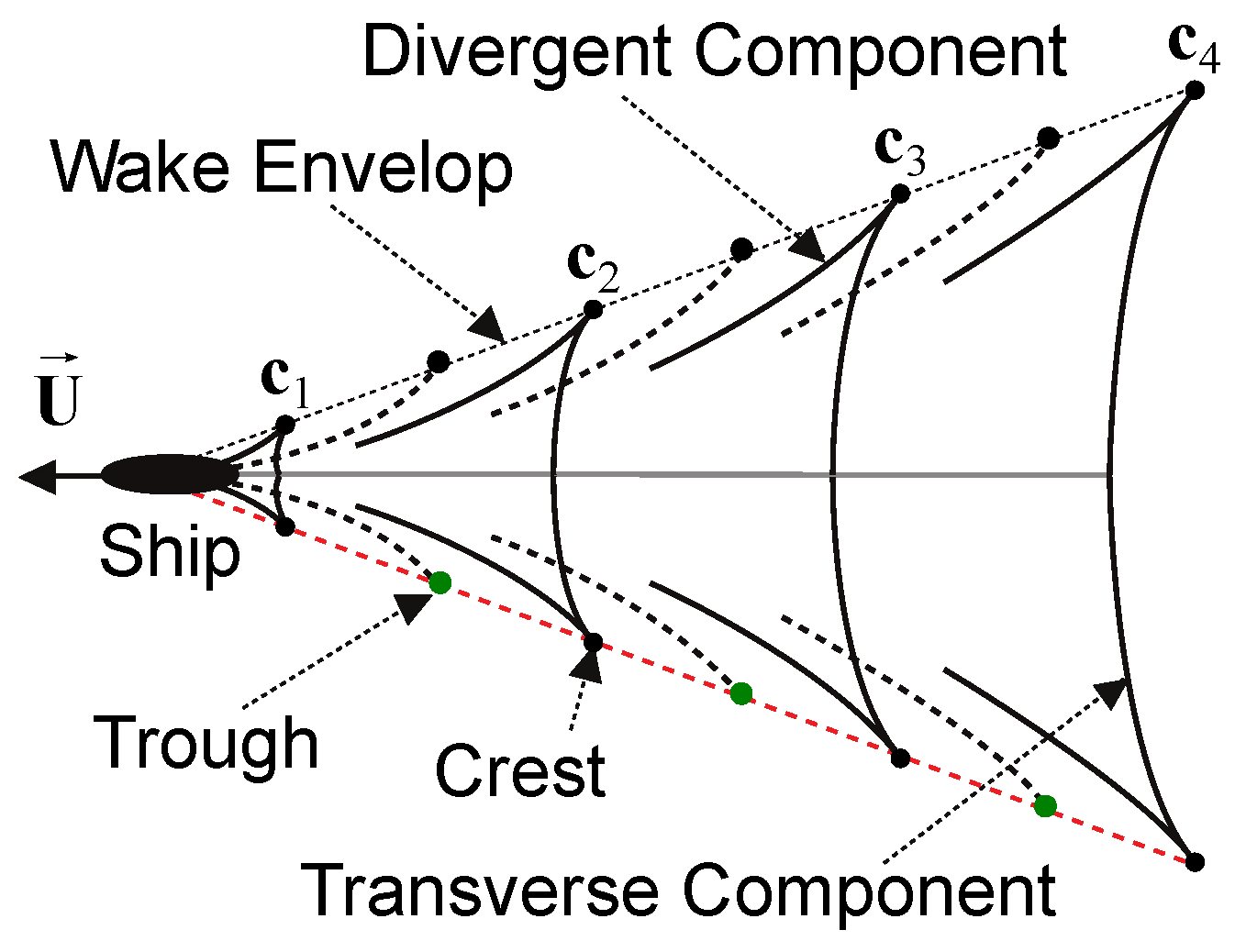
2.4. Wavelength and Speed Estimation
2.4.1. ROI Image Rectification
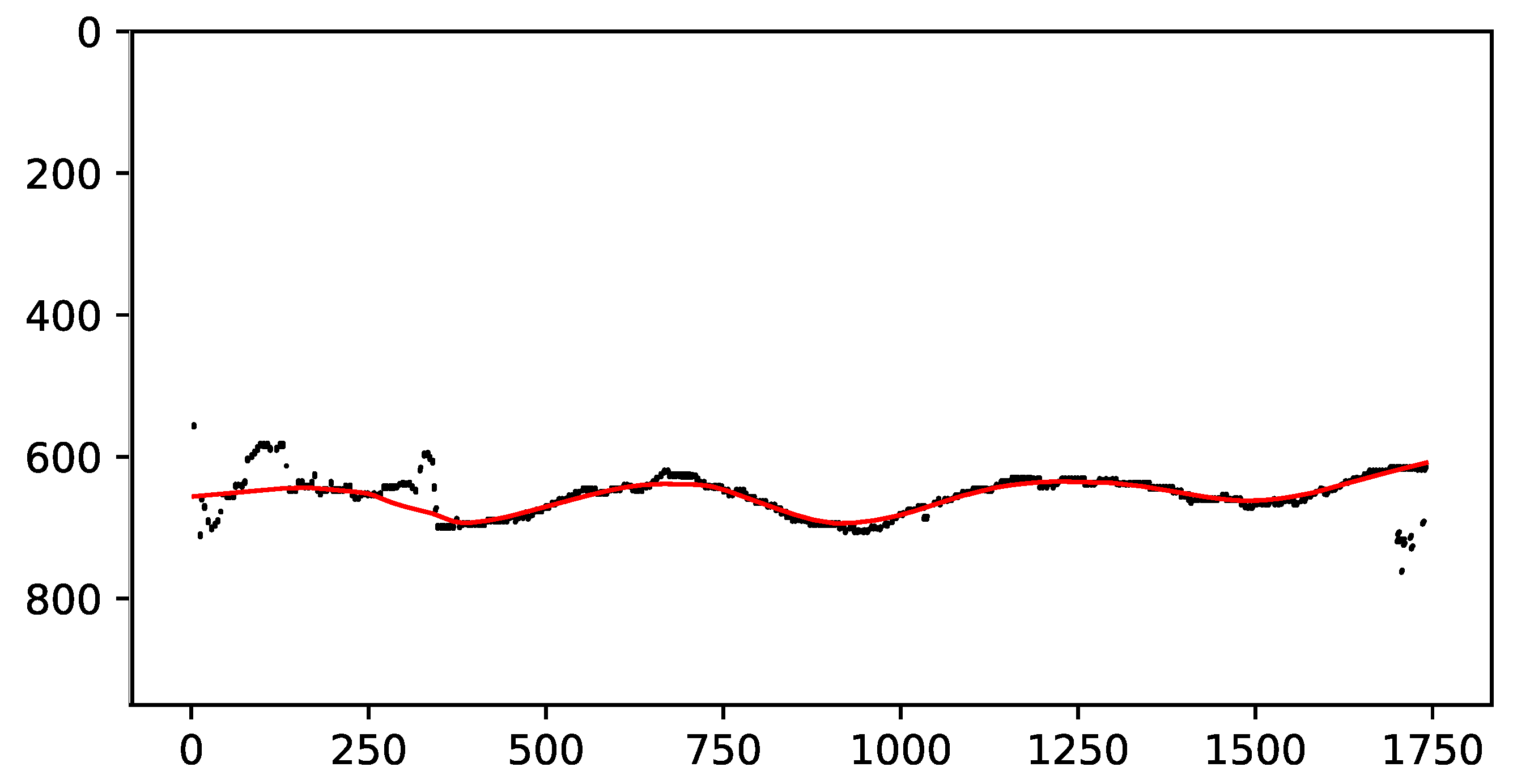
2.4.2. Curve Fitting
2.4.3. Wavelength Estimation
- When the vessel went to the right in the input image , the curve maximum and minimum corresponded to the troughs and crests of the wave arm;
- When the vessel went to the left in the input image , the curve maximum and minimum corresponded to the crests and troughs of the wave arm.
2.4.4. Vessel Speed Estimation
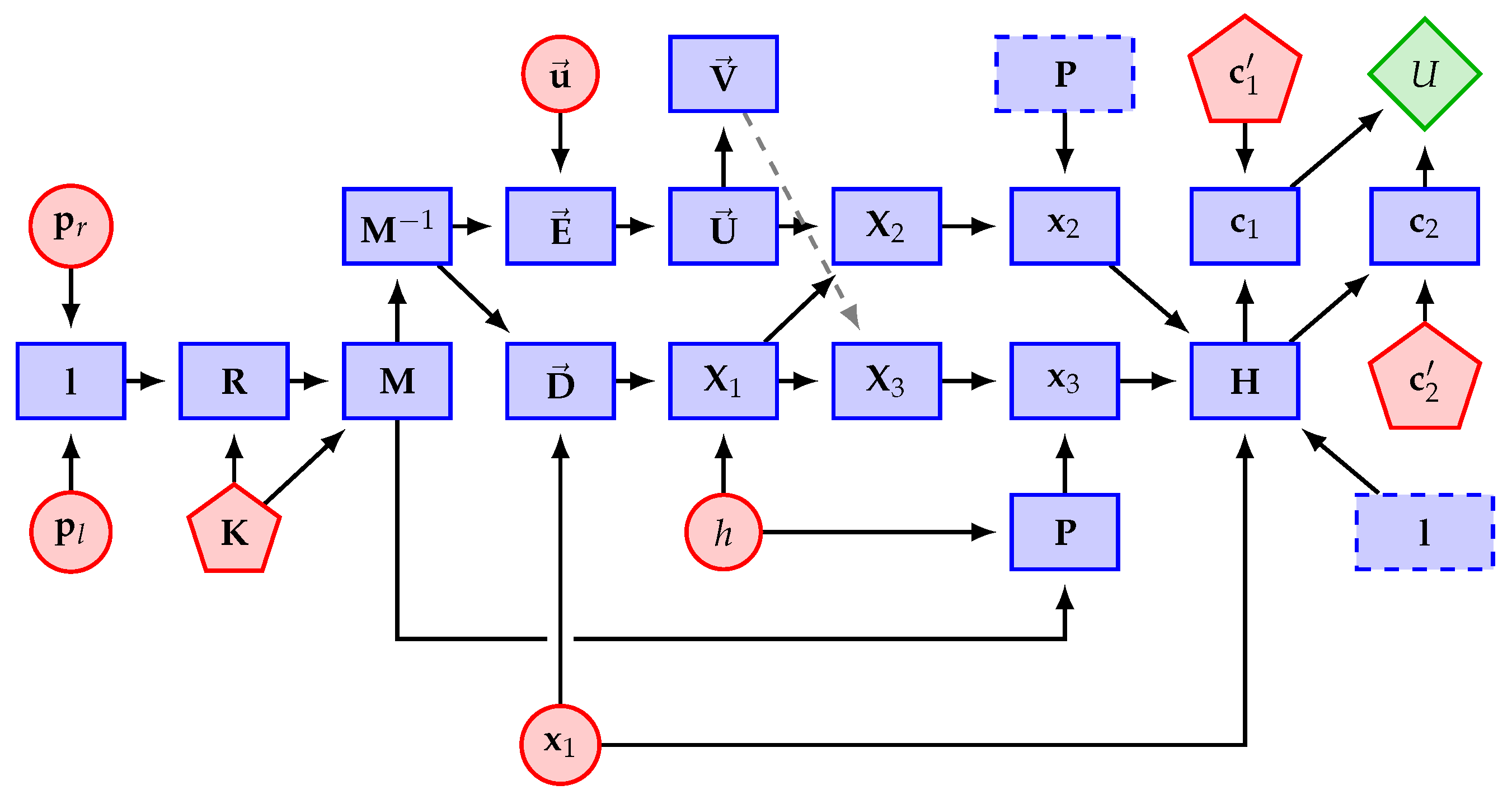
3. First-Order Error Propagation
- , : The y axis coordinates of the endpoints and of the vanishing line that are estimated for the mean water plane, respectively (Section 2.1);
- , : The coordinates of the corner of the ROI in the input image ;
- : The angle that defines the direction of the vessel in the input image ;
- , , , : The set of heights that is used in (2) to calculate the camera height h above the sea level in meters;
- , , , , , : The homogeneous coordinates of two adjacent troughs of the wave arm that is closest to the camera, i.e., points and that were used in (7), but represented by pixel coordinates in . These variables are not taken as sources of uncertainty because their rectified counterparts ( and ) naturally include the uncertainty that is propagated from other variables (see Appendix A for details);
- , , , , : The intrinsic parameters that define the camera calibration matrix . They are the focal length in terms of pixel dimensions in the x and y directions, skew, and the coordinates of the principal point in terms of pixel dimensions, respectively [17]. Recall from Section 2.2 that we extracted metadata from the input image file to compute . In this work, we assumed that the intrinsic parameters of the camera were constant values since it was observed that they do not usually have much influence on the uncertainty of image-based measurements [25].
4. Experiments and Results
- , : The standard deviations of and were estimated using:where is the mean value of the differences between the y coordinates that were observed on endpoints that were returned by HLW and the endpoints of vanishing lines that were manually identified by us in a dataset comprising images, which led to and pixels;
- , : We also used the experimental samples to set and pixels. The samples were obtained by repeatedly selecting the first corner of the ROI in the chosen image to serve as a reference. The standard deviations for the and coordinates were calculated using (12) for the coordinates of the selected points;
- : The same reference image was used to indicate the orientation of a vessel, which produced angular samples that were used to compute radians;
- , , , : The standard deviations of the tripod height and the floor height were empirically set to and m, respectively, by assuming a conservative uncertainty for the measurement of those input variables. We used Google Maps to measure the ground height and set its uncertainty to m based on the variations we observed in this tool. We estimated m by applying (12) to a set of average tidal heights that were computed from observations in [27,28,29].
4.1. Analysis of Relative Error
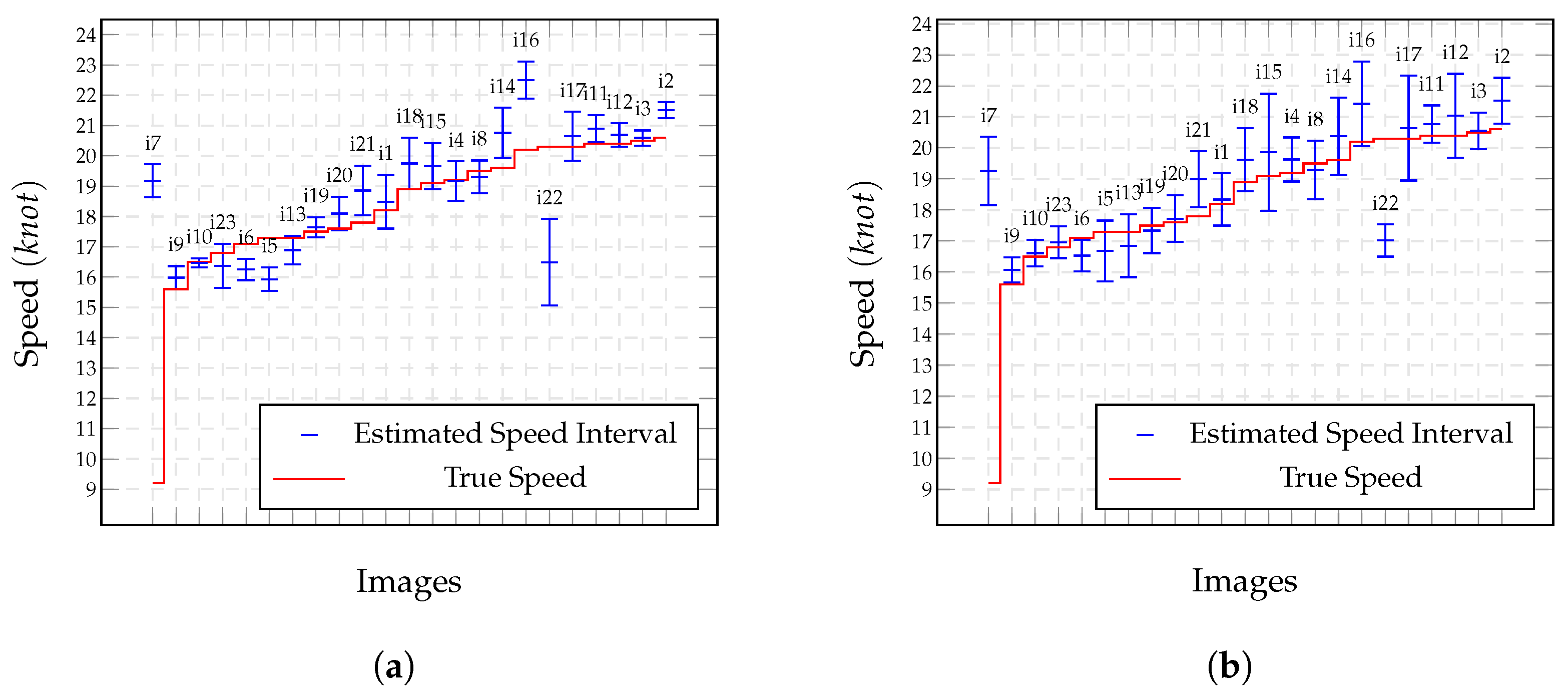
4.2. Analysis of Confidence Intervals Estimated Using the Samples
4.3. Analysis of Confidence Intervals Estimated Using Error Propagation
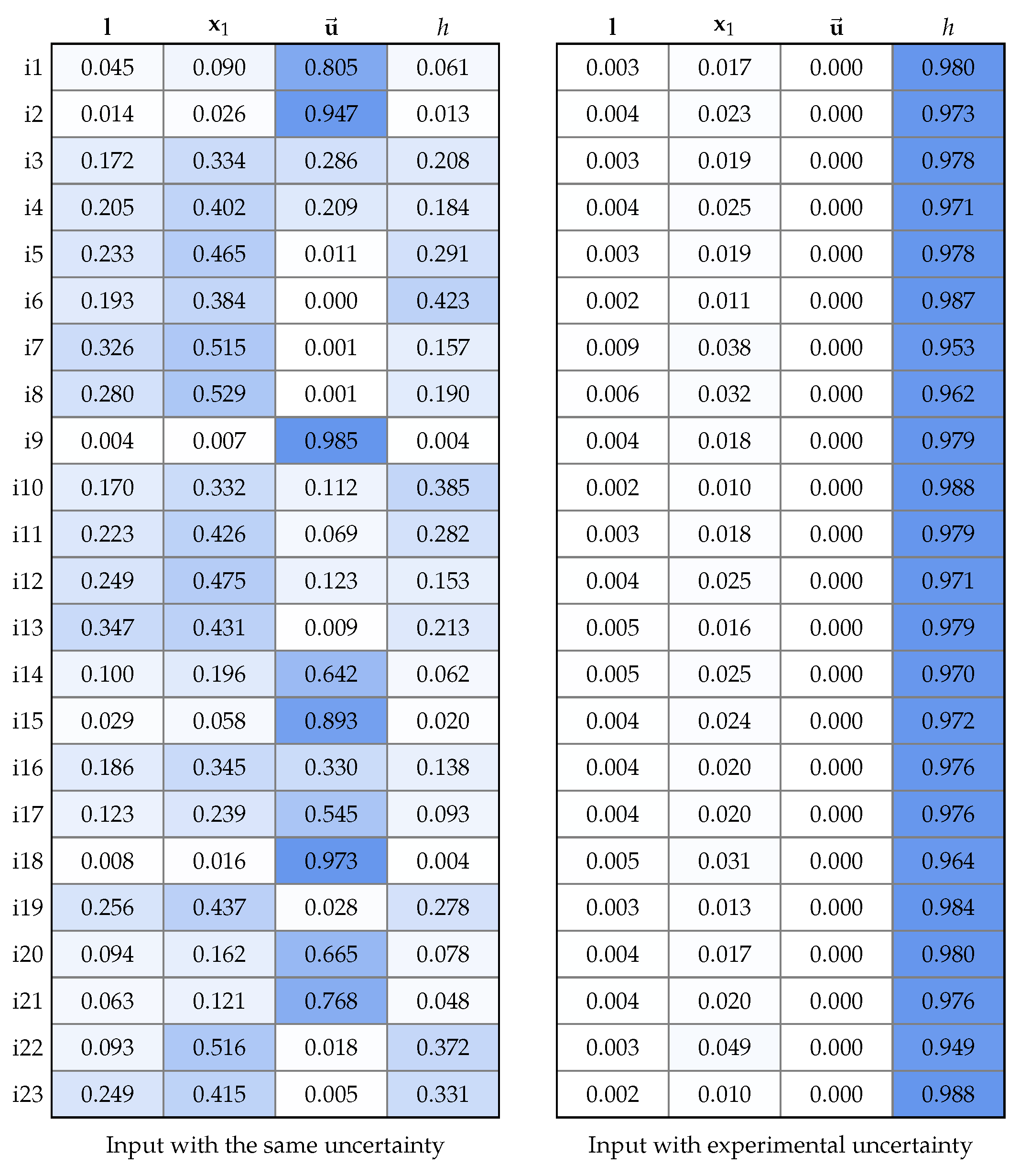
4.4. Impact of the Uncertainty of Each Input Variable
4.5. Resilience to Variations in Resolution
4.6. Resilience to Variations in JPG Compression Rate
5. Conclusions and Future Works
- Lighting conditions affect edge detection and the detection of wave arms. In our experiments, we had no problems in daylight, but it was not always possible to process images that were captured at dawn or dusk and our solution cannot be applied at night. The same applies to rain and fog;
- Due to geographical restrictions in our experiments, we used images of the port and starboard of vessels that were traveling in the left and right directions in front of the camera and moving along a linear course at a (supposedly) constant speed. However, we believe that our approach is robust to variations in camera orientation since it was possible to see the troughs in the wake, even at the grazing angle;
- As demonstrated in our experiments, well-defined capillary wakes due to wind and, possibly, those generated by nearby vessels may affect the Kelvin wake pattern. However, we believe that this is a problem that could be overcome by the detection of crossing wakes;
- Since this method is to be applied to single images, the use of video could provide dozens of independent measurements per second, which could be combined to reduce error or eliminate spurious estimates;
- Although we did not try this in our experiments, pre-processing the images to increase contrast could help in the detection of the wakes of slower vessels.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Partial Derivatives for Error Propagation
- Take the coordinates of the troughs in the rectified ROI;
- Map them onto using the inverse homography , thereby obtaining and :
- Consider that and are variables without uncertainty (see the pentagons in Figure 5);
- Transport the uncertainty that are propagated on onto and by mapping and back to the rectified ROI using:
References
- Hand, M. Autonomous Shipping: Are We Being Blinded by Technology? 2019. Available online: https://www.seatrade-maritime.com/asia/autonomous-shipping-are-we-being-blinded-technology (accessed on 12 December 2020).
- Hellenic Shipping News Worldwide. Autonomous Shipping: Trends and Innovators in a Growing Industry. 2020. Available online: https://www.nasdaq.com/articles/autonomous-shipping%3A-trends-and-innovators-in-a-growing-industry-2020-02-18 (accessed on 12 December 2020).
- Li, Q.; Wang, C.; Li, X.; Wen, C. FeatFlow: Learning geometric features for 3D motion estimation. Pattern Recognit. 2021, 111, 107574. [Google Scholar] [CrossRef]
- Wawrzyniak, N.; Hyla, T.; Popik, A. Vessel detection and tracking method based on video surveillance. Sensors 2019, 19, 5230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panico, A.; Graziano, M.D.; Renga, A. SAR-based vessel velocity estimation from partially imaged Kelvin Pattern. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 2067–2071. [Google Scholar] [CrossRef]
- Wang, C.; Shen, P.; Li, X.; Zhu, J.; Li, Z. A novel vessel velocity estimation method using dual-platform TerraSAR-X and TanDEM-X full polarimetric SAR data in pursuit monostatic mode. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6130–6144. [Google Scholar] [CrossRef]
- Huang, S.; Liu, D.; Gao, G.; Guo, X. A novel method for speckle noise reduction and ship target detection in SAR images. Pattern Recognit. 2009, 42, 1533–1542. [Google Scholar] [CrossRef]
- Guo, H.; Yang, X.; Wang, N.; Gao, X. A CenterNet++ model for ship detection in SAR images. Pattern Recognit. 2021, 112, 107787. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, J.; Qin, Y. A novel technique for ship wake detection from optical images. Remote Sens. Environ. 2021, 258, 112375. [Google Scholar] [CrossRef]
- Broggi, A.; Cerri, P.; Grisleri, P.; Paterlini, M. Boat speed monitoring using artificial vision. In Image Analysis and Processing—ICIAP 2009, Proceedings of the 15th International Conference, Vietri sul Mare, Italy, 8–11 September 2009; Springer: Berlin/Heidelberg, Germany, 2019; pp. 327–336. [Google Scholar]
- Tan, S.; Piepmeier, J.A.; Kriebel, D.L. A computer vision system for monitoring vessel motion in conjunction with vessel wake measurements. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 4–7 November 2012; pp. 1830–1834. [Google Scholar]
- Peng, J.; Wang, T.; Lin, W.; Wang, J.; See, J.; Wen, S.; Ding, E. TPM: Multiple object tracking with tracklet-plane matching. Pattern Recognit. 2020, 102, 107480. [Google Scholar] [CrossRef]
- Huillca, J.L.; Fernandes, L.A.F. Computing vessel velocity from single perspective projection images. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 325–329. [Google Scholar]
- Thomson, W. On ship waves. Proc. Inst. Mech. Eng. 1887, 38, 409–434. [Google Scholar] [CrossRef]
- Newman, J.N. The inverse ship-wave problem. In Proceedings of the Sixth International Workshop on Water Waves and Floating Bodies, Falmouth, MA, USA, 14–17 April 1991; pp. 193–197. [Google Scholar]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Workman, S.; Zhai, M.; Jacobs, N. Horizon lines in the wild. arXiv 2016, arXiv:1604.02129. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Breitinger, A.; Clua, E.; Fernandes, L.A.F. An Augmented Reality Periscope for Submarines with Extended Visual Classification. Sensors 2021, 21, 7624. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cheng, M.M.; Hu, X.; Bian, J.; Zhang, L.; Bai, X.; Tang, J. Richer convolutional features for edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1939–1946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Wilcox, R. The regression smoother LOWESS: A confidence band that allows heteroscedasticity and has some specified simultaneous probability coverage. J. Mod. Appl. Stat. Methods 2017, 16, 29–38. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Fernandes, L.A.F.; Oliveira, M.; Silva, R. Uncertainty propagation: Avoiding the expensive sampling process for real-time image-based measurements. Comput. Stat. Data Anl. 2008, 52, 3852–3876. [Google Scholar] [CrossRef]
- Nikon. User’s Manual Nikon D3300. Available online: https://downloadcenter.nikonimglib.com/pt/products/21/D3300.html (accessed on 12 December 2020).
- Tábuas de Maré. Available online: https://www.marinha.mil.br/chm/tabuas-de-mare (accessed on 18 November 2019).
- Tábua de Marés e SOLUNARES de Pescaria. Available online: https://tabuademares.com (accessed on 18 November 2019).
- TidesChart: Check the Tide Anywhere in World. Available online: https://pt.tideschart.com (accessed on 18 November 2019).
- FURUNO, S.A. FAR-21x7 Series Brochure. Available online: https://www.furuno.com/files/Brochure/236/upload/far-21x7.pdf (accessed on 12 December 2020).
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality. Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML, JCGM 100:2008, GUM 1995 with Minor Corrections; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008. [Google Scholar]
- Papadopoulo, T.; Lourakis, M.I.A. Estimating the Jacobian of the Singular Value Decomposition. In Computer Vision—ECCV 2000, Proceedings of the 6th European Conference on Computer Vision, Dublin, Ireland, 26 June–1 July 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 554–570. [Google Scholar]


| Notation | Meaning |
|---|---|
| Input and edge image, respectively | |
| Water plane | |
| The i-th point in image space under homogeneous coordinates | |
| The i-th point in world space under homogeneous coordinates | |
| Coordinates of point in image space | |
| Coordinates of point in world space | |
| Vector encoding the vanishing line in image space | |
| Vector in image space under homogeneous coordinates | |
| Vector in world space under homogeneous coordinates | |
| An matrix | |
| Inverse of a matrix | |
| Transpose of a matrix |
| Image | Vessel | Time (hh:mm) | Weather | Tide (Meters) | Speed | Error | Results of [13] | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Name | U | |||||||||
| i1 | Fenix | 10:09 | Cloudy | 0.30 | 18.2 | 18.339 | 0.139 | 0.008 | 17.234 | 0.053 | |
| i2 | Apolo | 10:12 | Cloudy | 0.30 | 20.6 | 21.533 | 0.933 | 0.045 | 25.467 | 0.236 | |
| i3 | Apolo | 10:13 | Cloudy | 0.30 | 20.5 | 20.609 | 0.109 | 0.005 | 26.629 | 0.299 | |
| i4 | Neptuno | 10:19 | Cloudy | 0.50 | 19.2 | 19.434 | 0.234 | 0.012 | 21.788 | 0.135 | |
| i5 | Neptuno | 10:21 | Cloudy | 0.50 | 17.3 | 16.683 | 0.617 | 0.036 | 20.346 | 0.176 | |
| i6 | Neptuno | 10:22 | Cloudy | 0.50 | 17.1 | 16.530 | 0.570 | 0.033 | 27.785 | 0.625 | |
| i7 | Escander Amazonas | 10:28 | Cloudy | 0.60 | 09.2 | 19.262 | 10.062 | 1.094 | 17.326 | 0.883 | |
| i8 | Missing | 10:39 | Cloudy | 0.70 | 19.5 | 19.288 | 0.212 | 0.011 | 26.036 | 0.335 | |
| i9 | Fenix | 10:41 | Cloudy | 0.70 | 15.6 | 15.984 | 0.384 | 0.025 | 18.231 | 0.169 | |
| i10 | Fenix | 10:43 | Cloudy | 0.70 | 16.5 | 16.611 | 0.111 | 0.007 | 20.133 | 0.220 | |
| i11 | Missing | 11:08 | Cloudy | 0.50 | 20.4 | 20.771 | 0.371 | 0.018 | 26.436 | 0.296 | |
| i12 | Missing | 11:09 | Cloudy | 0.50 | 20.4 | 20.543 | 0.143 | 0.007 | 23.863 | 0.170 | |
| i13 | Missing | 11:12 | Cloudy | 0.50 | 17.3 | 16.846 | 0.454 | 0.026 | 23.259 | 0.344 | |
| i14 | Zeus | 11:42 | Cloudy | 0.70 | 19.6 | 20.533 | 0.933 | 0.048 | 26.982 | 0.377 | |
| i15 | Neptuno | 11:43 | Cloudy | 0.70 | 19.1 | 19.861 | 0.761 | 0.040 | 19.407 | 0.016 | |
| i16 | Neptuno | 12:10 | Cloudy | 0.90 | 20.2 | 22.120 | 1.920 | 0.095 | 25.951 | 0.285 | |
| i17 | Missing | 12:13 | Cloudy | 0.90 | 20.3 | 20.638 | 0.338 | 0.017 | 22.254 | 0.096 | |
| i18 | Zeus | 16:12 | Scattered storm | 1.10 | 18.9 | 19.617 | 0.717 | 0.038 | 22.086 | 0.169 | |
| i19 | Zeus | 16:50 | Partly cloudy | 0.70 | 17.5 | 17.342 | 0.158 | 0.009 | 22.249 | 0.271 | |
| i20 | Zeus | 16:51 | Partly cloudy | 0.70 | 17.6 | 17.808 | 0.208 | 0.012 | 19.947 | 0.133 | |
| i21 | Zeus | 16:51 | Partly cloudy | 0.70 | 17.8 | 18.947 | 1.147 | 0.064 | 25.107 | 0.410 | |
| i22 | Missing | 17:01 | Partly cloudy | 0.70 | 20.3 | 16.490 | 3.810 | 0.188 | 23.448 | 0.155 | |
| i23 | Zeus | 17:21 | Partly cloudy | 0.50 | 16.8 | 16.084 | 0.716 | 0.043 | 21.008 | 0.251 | |
| Image | Speed | Relative Error | |||||
|---|---|---|---|---|---|---|---|
| i1 | 18.2 | 18.34 | 18.75 | – | 0.01 | 0.03 | – |
| i2 | 20.6 | 21.53 | 22.39 | 21.82 | 0.05 | 0.09 | 0.06 |
| i3 | 20.5 | 20.61 | 23.53 | 13.64 | 0.01 | 0.15 | 0.33 |
| i4 | 19.2 | 19.43 | 20.71 | 19.36 | 0.01 | 0.08 | 0.01 |
| i5 | 17.3 | 16.68 | 19.10 | 13.96 | 0.04 | 0.10 | 0.19 |
| i6 | 17.1 | 16.53 | 17.93 | 17.86 | 0.03 | 0.05 | 0.04 |
| i7 | 09.2 | 19.26 | – | – | 1.09 | – | – |
| i8 | 19.5 | 19.29 | 19.30 | 21.75 | 0.01 | 0.01 | 0.12 |
| i9 | 15.6 | 15.98 | 19.38 | – | 0.02 | 0.24 | – |
| i10 | 16.5 | 16.61 | 16.15 | 15.38 | 0.01 | 0.02 | 0.07 |
| i11 | 20.4 | 20.77 | 22.24 | 6.40 | 0.02 | 0.09 | 0.69 |
| i12 | 20.4 | 20.54 | 13.32 | 10.45 | 0.01 | 0.35 | 0.49 |
| i13 | 17.3 | 16.85 | 18.78 | – | 0.03 | 0.09 | – |
| i14 | 19.6 | 20.53 | 19.50 | – | 0.05 | 0.01 | – |
| i15 | 19.1 | 19.86 | 11.08 | – | 0.04 | 0.42 | – |
| i16 | 20.2 | 22.12 | 20.09 | – | 0.10 | 0.01 | – |
| i17 | 20.3 | 20.64 | 18.95 | – | 0.02 | 0.07 | – |
| i18 | 18.9 | 19.62 | 22.07 | 14.48 | 0.04 | 0.17 | 0.23 |
| i19 | 17.5 | 17.34 | 21.46 | 18.58 | 0.01 | 0.23 | 0.06 |
| i20 | 17.6 | 17.81 | 19.24 | 10.54 | 0.01 | 0.09 | 0.40 |
| i21 | 17.8 | 18.95 | – | – | 0.06 | – | – |
| i22 | 20.3 | 16.49 | 10.22 | 14.99 | 0.19 | 0.50 | 0.26 |
| i23 | 16.8 | 16.08 | 17.09 | – | 0.04 | 0.02 | – |
| Image | Speed () | Relative Error | |||||||
|---|---|---|---|---|---|---|---|---|---|
| i1 | 18.2 | 18.34 | 18.21 | 18.21 | 18.21 | 0.0077 | 0.0005 | 0.0005 | 0.0005 |
| i2 | 20.6 | 21.52 | 21.48 | 21.48 | 21.48 | 0.0447 | 0.0427 | 0.0427 | 0.0427 |
| i3 | 20.5 | 20.55 | 20.52 | 20.42 | 20.00 | 0.0024 | 0.0010 | 0.0039 | 0.0244 |
| i4 | 19.2 | 19.63 | 19.93 | 19.93 | 20.27 | 0.0224 | 0.0380 | 0.0380 | 0.0557 |
| i5 | 17.3 | 16.68 | 16.34 | 16.34 | 16.34 | 0.0358 | 0.0555 | 0.0555 | 0.0555 |
| i6 | 17.1 | 16.53 | 16.54 | 16.54 | 16.54 | 0.0333 | 0.0327 | 0.0327 | 0.0327 |
| i7 | 9.2 | 19.26 | 19.32 | 19.32 | 19.12 | 1.0935 | 1.1000 | 1.1000 | 1.0783 |
| i8 | 19.5 | 19.29 | 19.28 | 19.28 | 19.28 | 0.0108 | 0.0113 | 0.0113 | 0.0113 |
| i9 | 15.6 | 16.07 | 16.09 | 16.09 | 16.09 | 0.0301 | 0.0314 | 0.0314 | 0.0314 |
| i10 | 16.5 | 16.61 | 16.55 | 16.55 | 16.55 | 0.0067 | 0.0030 | 0.0030 | 0.0030 |
| i11 | 20.4 | 20.77 | 20.83 | 20.83 | 20.83 | 0.0181 | 0.0211 | 0.0211 | 0.0211 |
| i12 | 20.4 | 21.04 | 21.10 | 21.10 | 21.03 | 0.0314 | 0.0343 | 0.0343 | 0.0309 |
| i13 | 17.3 | 16.85 | 16.82 | 16.00 | 15.99 | 0.0260 | 0.0277 | 0.0751 | 0.0757 |
| i14 | 19.6 | 20.38 | 20.17 | 20.21 | 20.21 | 0.0398 | 0.0291 | 0.0311 | 0.0311 |
| i15 | 19.1 | 19.86 | 19.70 | 19.73 | 19.70 | 0.0398 | 0.0314 | 0.0330 | 0.0314 |
| i16 | 20.2 | 21.42 | 21.22 | 21.76 | 21.22 | 0.0604 | 0.0505 | 0.0772 | 0.0505 |
| i17 | 20.3 | 20.64 | 20.62 | 20.54 | 20.82 | 0.0167 | 0.0158 | 0.0118 | 0.0256 |
| i18 | 18.9 | 19.62 | 20.29 | 20.80 | 20.61 | 0.0381 | 0.0735 | 0.1005 | 0.0905 |
| i19 | 17.5 | 17.34 | 17.40 | 17.40 | 17.40 | 0.0091 | 0.0057 | 0.0057 | 0.0057 |
| i20 | 17.6 | 17.72 | 16.95 | 17.87 | 17.12 | 0.0068 | 0.0369 | 0.0153 | 0.0273 |
| i21 | 17.8 | 18.99 | 18.36 | 18.36 | 18.36 | 0.0669 | 0.0315 | 0.0315 | 0.0315 |
| i22 | 20.3 | 17.02 | 17.25 | 17.25 | 6.80 | 0.1616 | 0.1502 | 0.1502 | 0.6650 |
| i23 | 16.8 | 16.96 | 16.99 | 16.99 | 16.99 | 0.0095 | 0.0113 | 0.0113 | 0.0113 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huillca, J.L.; Fernandes, L.A.F. Using Conventional Cameras as Sensors for Estimating Confidence Intervals for the Speed of Vessels from Single Images. Sensors 2022, 22, 4213. https://doi.org/10.3390/s22114213
Huillca JL, Fernandes LAF. Using Conventional Cameras as Sensors for Estimating Confidence Intervals for the Speed of Vessels from Single Images. Sensors. 2022; 22(11):4213. https://doi.org/10.3390/s22114213
Chicago/Turabian StyleHuillca, Jose L., and Leandro A. F. Fernandes. 2022. "Using Conventional Cameras as Sensors for Estimating Confidence Intervals for the Speed of Vessels from Single Images" Sensors 22, no. 11: 4213. https://doi.org/10.3390/s22114213
APA StyleHuillca, J. L., & Fernandes, L. A. F. (2022). Using Conventional Cameras as Sensors for Estimating Confidence Intervals for the Speed of Vessels from Single Images. Sensors, 22(11), 4213. https://doi.org/10.3390/s22114213







