Ultrasound Sensing Using Packaged Microsphere Cavity in the Underwater Environment
Abstract
1. Introduction
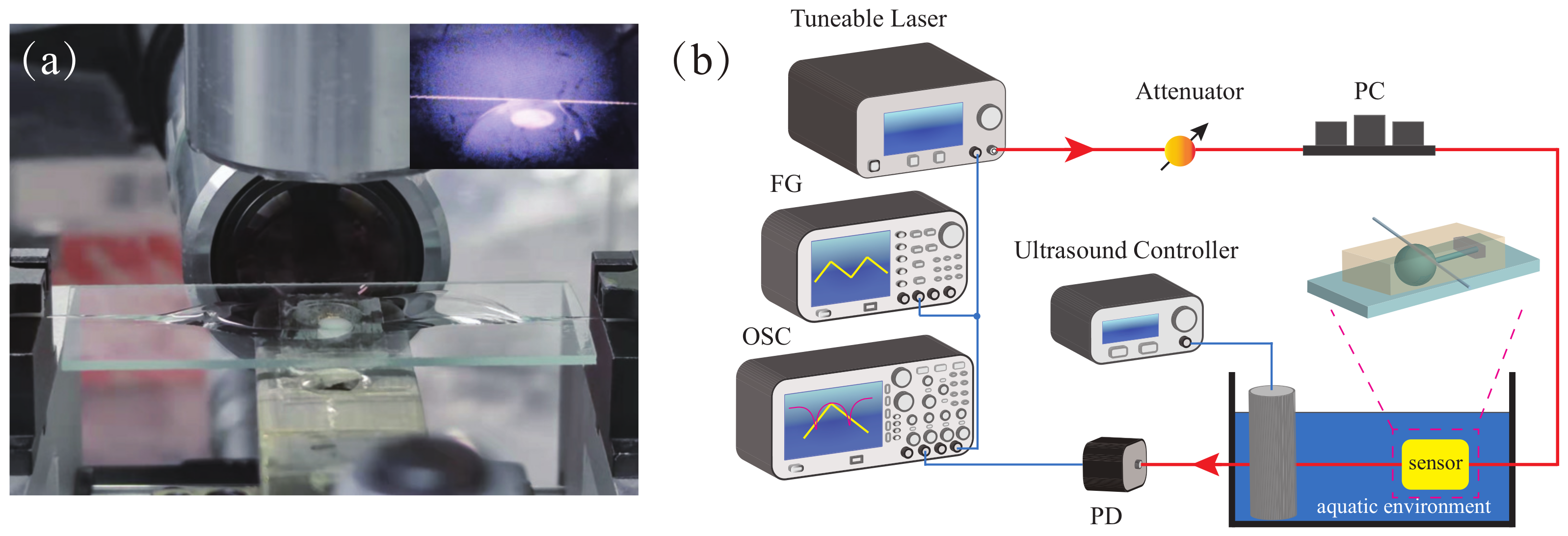
2. Experiment Methods
2.1. Fabrication of Microsphere Ultrasound Sensors
2.2. Experimental Setup
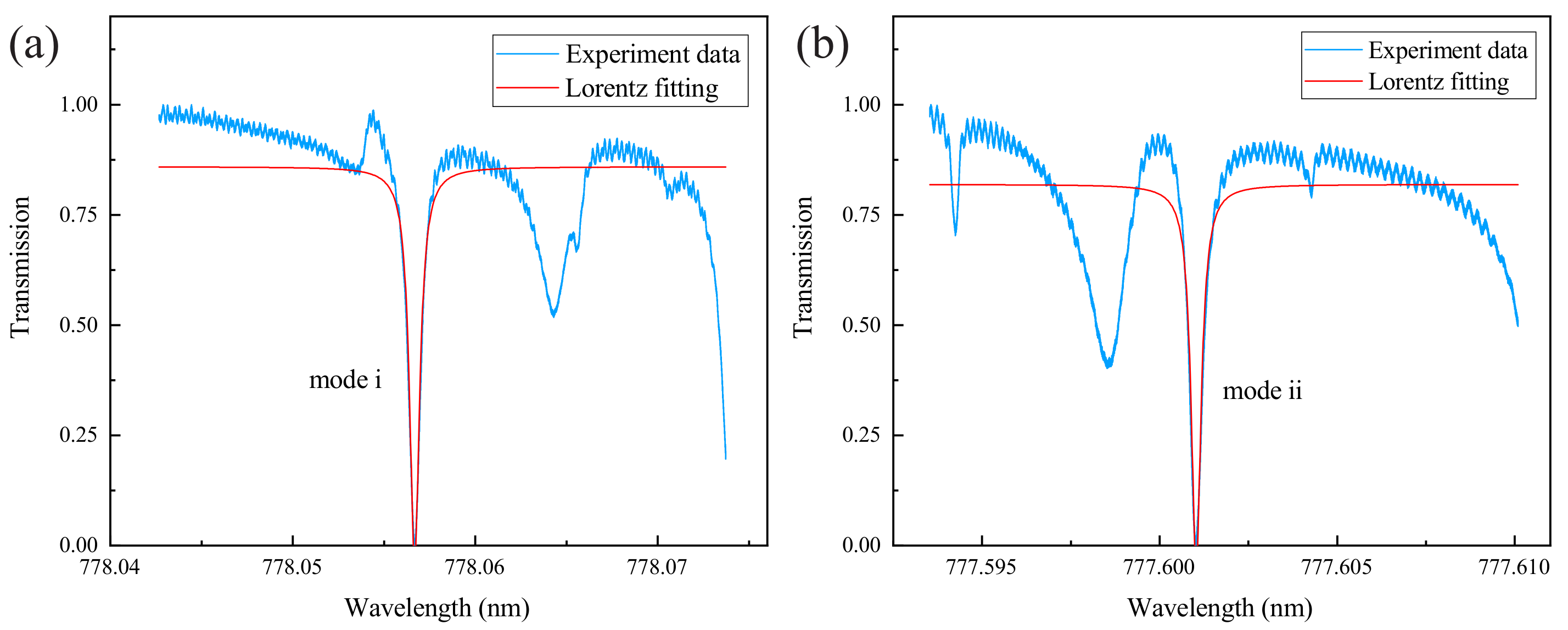
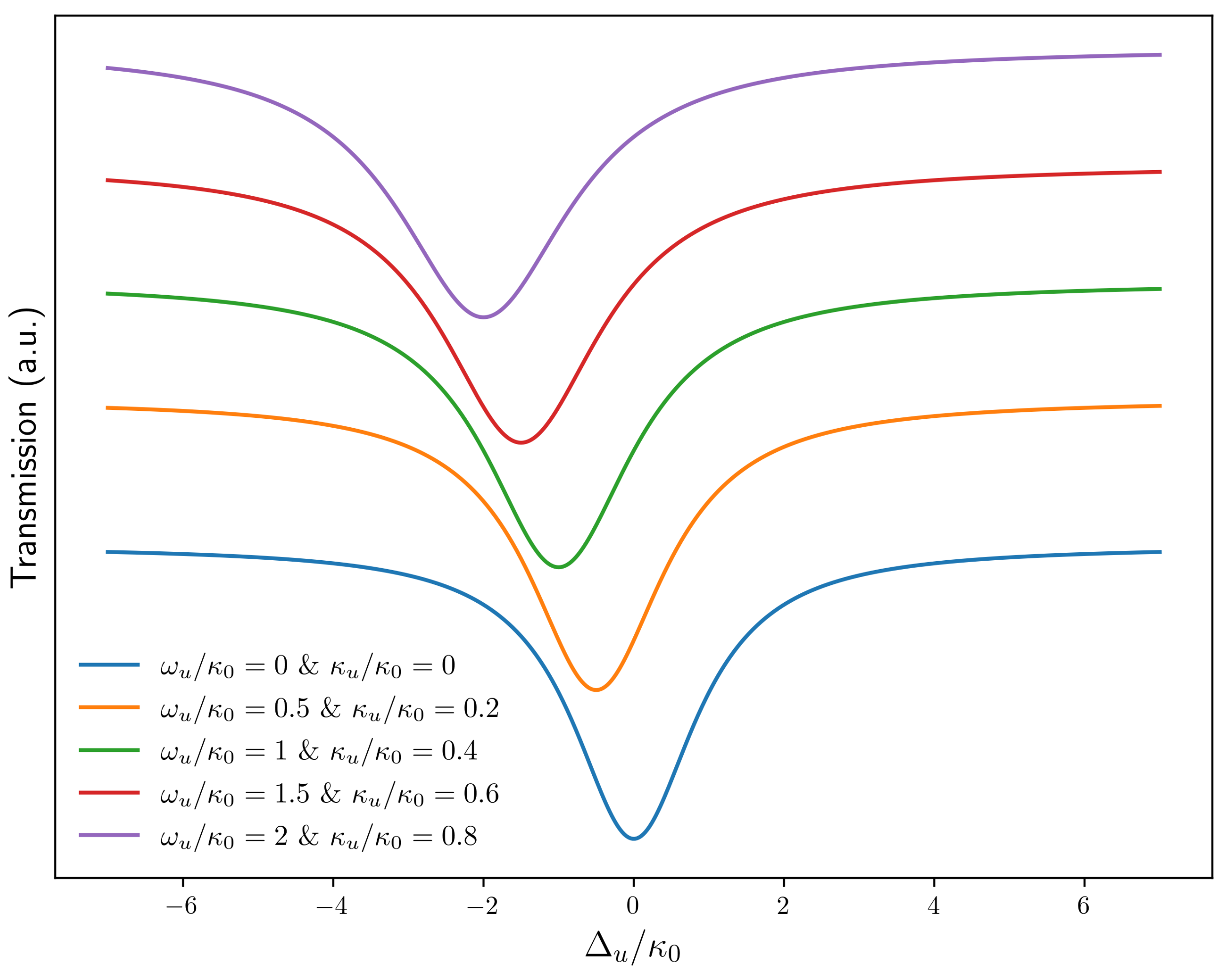
3. Phenomenological Theoretical Model
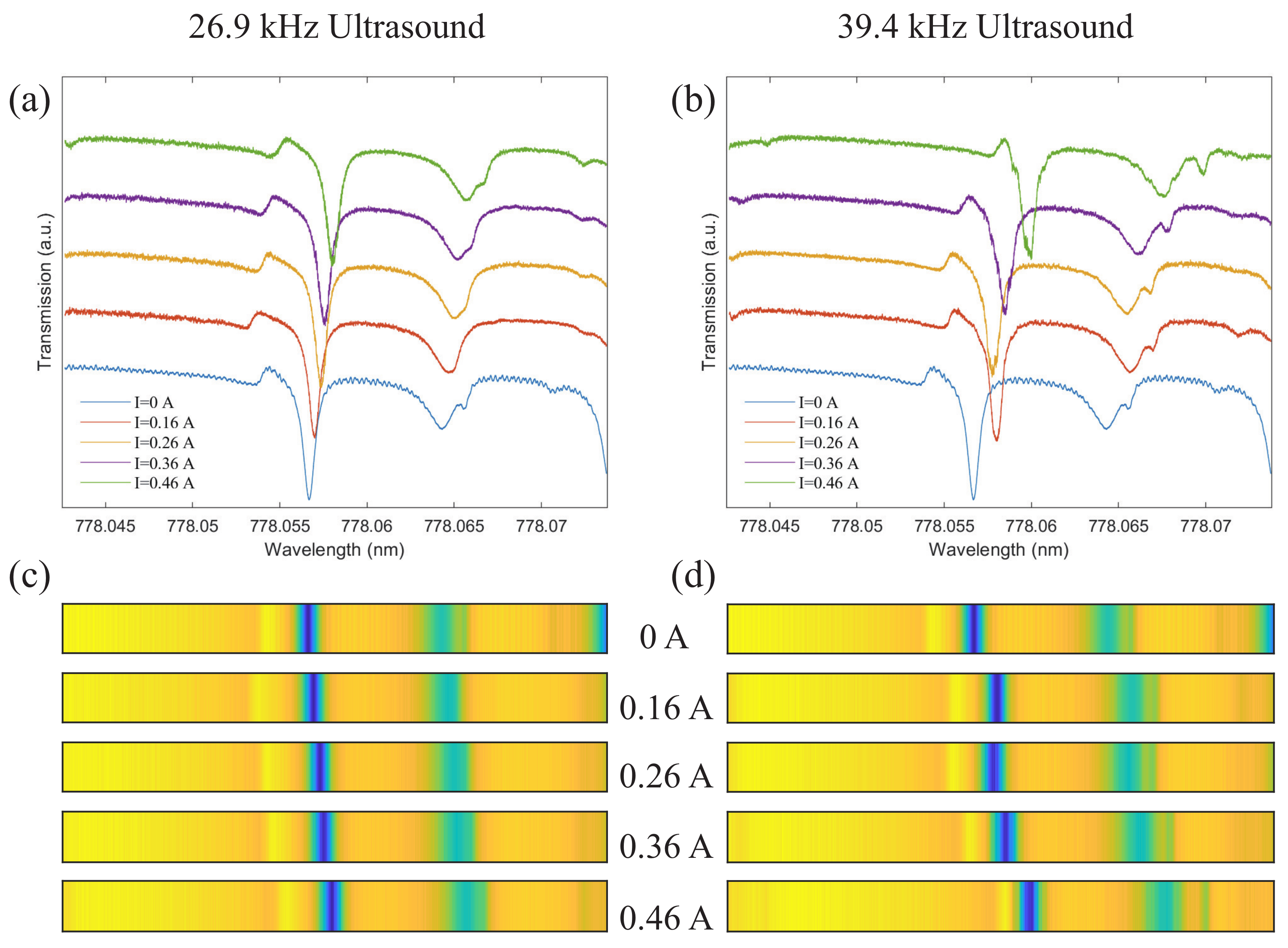
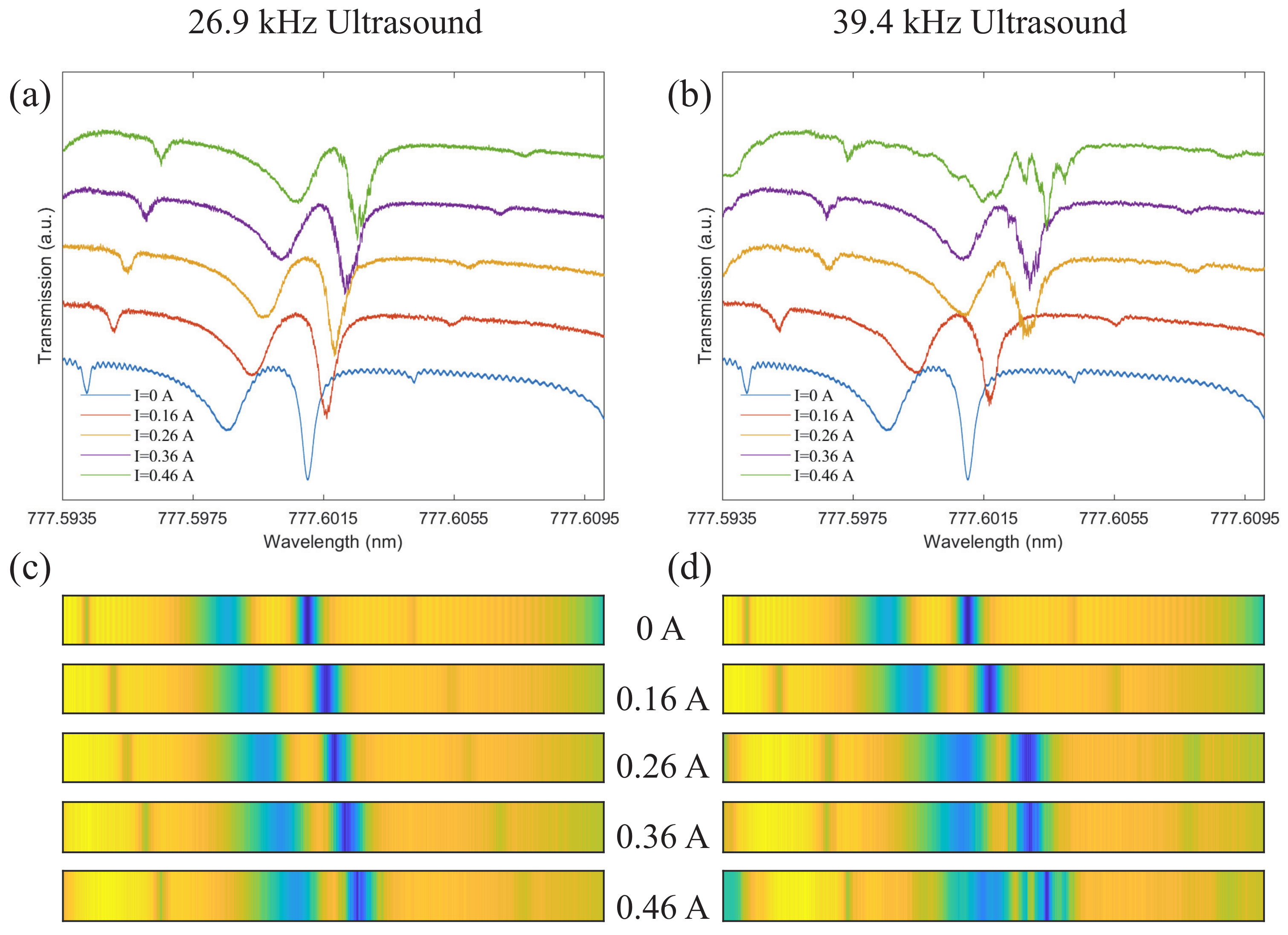
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Ling, T.; Chen, S.L.; Guo, L.J. Ultrabroad Bandwidth and Highly Sensitive Optical Ultrasonic Detector for Photoacoustic Imaging. ACS Photonics 2014, 1, 1093–1098. [Google Scholar] [CrossRef]
- Mitragotri, S. Healing sound: The use of ultrasound in drug delivery and other therapeutic applications. Nat. Rev. Drug Discov. 2005, 4, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Bobkova, S.; Shaw, A.; Gavrilov, L.; Khokhlova, V.; Hand, J. Feasibility of HIFU tissue ablation in the presence of ribs using a 2D random phased array. AIP Conf. Proc. 2010, 1215, 27–30. [Google Scholar] [CrossRef]
- Zhmud, V.A.; Kondratiev, N.O.; Kuznetsov, K.A.; Trubin, V.G.; Dimitrov, L.V. Application of ultrasonic sensor for measuring distances in robotics. J. Phys. Conf. Ser. 2018, 1015, 032189. [Google Scholar] [CrossRef]
- Carullo, A.; Parvis, M. An ultrasonic sensor for distance measurement in automotive applications. IEEE Sens. J. 2001, 1, 143. [Google Scholar] [CrossRef]
- Kolkman, R.G.; Blomme, E.; Cool, T.; Bilcke, M.; van Leeuwen, T.G.; Steenbergen, W.; Grimbergen, K.A.; den Heeten, G.J. Feasibility of noncontact piezoelectric detection of photoacoustic signals in tissue-mimicking phantoms. J. Biomed. Opt. 2010, 15, 1–4. [Google Scholar] [CrossRef][Green Version]
- Nan, H.; Boyle, K.C.; Apte, N.; Aliroteh, M.S.; Bhuyan, A.; Nikoozadeh, A.; Khuri-Yakub, B.T.; Arbabian, A. Non-contact thermoacoustic detection of embedded targets using airborne-capacitive micromachined ultrasonic transducers. Appl. Phys. Lett. 2015, 106, 084101. [Google Scholar] [CrossRef]
- Deán-Ben, X.L.; Pang, G.A.; Montero de Espinosa, F.; Razansky, D. Non-contact optoacoustic imaging with focused air-coupled transducers. Appl. Phys. Lett. 2015, 107, 051105. [Google Scholar] [CrossRef]
- Han, C.; Zhao, C.; Ding, H.; Chen, C. Spherical microcavity-based membrane-free Fizeau interferometric acoustic sensor. Opt. Lett. 2019, 44, 3677–3680. [Google Scholar] [CrossRef]
- Zhu, J.; Ozdemir, S.K.; Xiao, Y.F.; Li, L.; He, L.; Chen, D.R.; Yang, L. On-chip single nanoparticle detection and sizing by mode splitting in an ultrahigh-Q microresonator. Nat. Photonics 2010, 4, 46–49. [Google Scholar] [CrossRef]
- Lu, T.; Lee, H.; Chen, T.; Herchak, S.; Kim, J.H.; Fraser, S.E.; Flagan, R.C.; Vahala, K. High sensitivity nanoparticle detection using optical microcavities. Proc. Natl. Acad. Sci. USA 2011, 108, 5976–5979. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.P.; Wang, T.J.; Cao, C.; Wang, C. Gap induced mode evolution under the asymmetric structure in a plasmonic resonator system. Photonics Res. 2017, 5, 113–118. [Google Scholar] [CrossRef]
- Pang, T.T.; Gao, Y.P.; Xu, W.L.; Wang, C. Real-time sensing on the angular coordinates of nanoparticles using whispering-gallery mode optical microcavities. Europhys. Lett. 2021, 133, 14002. [Google Scholar] [CrossRef]
- Liao, J.; Yang, L. Optical whispering-gallery mode barcodes for high-precision and wide-range temperature measurements. Light Sci. Appl. 2021, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Li, B.B.; Bílek, J.; Hoff, U.B.; Madsen, L.S.; Forstner, S.; Prakash, V.; Schäfermeier, C.; Gehring, T.; Bowen, W.P.; Andersen, U.L. Quantum enhanced optomechanical magnetometry. Optica 2018, 5, 850–856. [Google Scholar] [CrossRef]
- Pang, T.T.; Gao, Y.P.; Xu, W.L.; Zheng, S.H.; Wang, C. Optical Magnetic Sensing Using Whispering- Gallery Mode Optomagnonical Cavity. IEEE Sens. J. 2021, 21, 2742–2748. [Google Scholar] [CrossRef]
- Wan, Y.; Fan, X.; Xu, B.; He, Z. Microwave frequency measurement with high accuracy and wide bandwidth based on whispering-gallery mode barcode. Opt. Lett. 2021, 46, 5008–5011. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, S.L.; Ling, T.; Guo, L.J. Imprinted Polymer Microrings as High-Performance Ultrasound Detectors in Photoacoustic Imaging. J. Lightware Technol. 2015, 33, 4318–4328. [Google Scholar] [CrossRef]
- Li, H.; Dong, B.; Zhang, X.; Shu, X.; Chen, X.; Hai, R.; Czaplewski, D.A.; Zhang, H.F.; Sun, C. Disposable ultrasound-sensing chronic cranial window by soft nanoimprinting lithography. Nat. Commun. 2019, 10, 4277. [Google Scholar] [CrossRef]
- Basiri-Esfahani, S.; Armin, A.; Forstner, S.; Bowen, W.P. Precision ultrasound sensing on a chip. Nat. Commun. 2019, 10, 132. [Google Scholar] [CrossRef]
- Westerveld, W.J.; Mahmud-Ul-Hasan, M.; Shnaiderman, R.; Ntziachristos, V.; Rottenberg, X.; Severi, S.; Rochus, V. Sensitive, small, broadband and scalable optomechanical ultrasound sensor in silicon photonics. Nat. Photonics 2021, 15, 341–345. [Google Scholar] [CrossRef]
- Kim, K.H.; Luo, W.; Zhang, C.; Tian, C.; Guo, L.J.; Wang, X.; Fan, X. Air-coupled ultrasound detection using capillary-based optical ring resonators. Sci. Rep. 2017, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Zhang, B.; Liu, Z.; Zhao, J.; Feng, Y.; Wan, L.; Li, Z. Microbubble resonators combined with a digital optical frequency comb for high-precision air-coupled ultrasound detectors. Photon. Res. 2020, 8, 303–310. [Google Scholar] [CrossRef]
- Yang, J.; Qin, T.; Zhang, F.; Chen, X.; Jiang, X.; Wan, W. Multiphysical sensing of light, sound and microwave in a microcavity Brillouin laser. Nanophotonics 2020, 9, 2915–2925. [Google Scholar] [CrossRef]
- Sun, J.; Meng, J.W.; Tang, S.J.; Li, C. An encapsulated optical microsphere sensor for ultrasound detection and photoacoustic imaging. Sci. China Phys. Mech. Astron. 2021, 65, 224211. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Tian, M.; Cheng, J.; Jiang, X.; Tan, Y. A Compact and Highly Sensitive Voice-Eavesdropping Microresonator. J. Lightware Technol. 2021, 39, 6327–6333. [Google Scholar] [CrossRef]
- Zhou, H.; Xiao, B.; Yang, N.; Yuan, S.; Zhu, S.; Duan, Y.; Shi, L.; Zhang, C.; Zhang, X. Real-time observation of the thermo-optical and heat dissipation processes in microsphere resonators. Opt. Express 2021, 29, 2402–2410. [Google Scholar] [CrossRef]
- Chen, Z.; Tu, X.; Dai, M.; Li, Q.; Fu, H.Y. Kerr Frequency Comb Generation in Microsphere Resonators With Normal Dispersion. J. Lightware Technol. 2022, 40, 1092–1097. [Google Scholar] [CrossRef]
- Monifi, F.; Özdemir, S.K.; Friedlein, J.; Yang, L. Encapsulation of a Fiber Taper Coupled Microtoroid Resonator in a Polymer Matrix. IEEE Photonics Technol. Lett. 2013, 25, 1458–1461. [Google Scholar] [CrossRef]
- Wang, P.; Ding, M.; Murugan, G.S.; Bo, L.; Guan, C.; Semenova, Y.; Wu, Q.; Farrell, G.; Brambilla, G. Packaged, high-Q, microsphere-resonator-based add-drop filter. Opt. Lett. 2014, 39, 5208–5211. [Google Scholar] [CrossRef]
- Zhao, G.; Özdemir, Ş.K.; Wang, T.; Xu, L.; King, E.; Long, G.L.; Yang, L. Raman lasing and Fano lineshapes in a packaged fiber-coupled whispering-gallery-mode microresonator. Sci. Bull. 2017, 62, 875–878. [Google Scholar] [CrossRef]
- Yang, D.; Duan, B.; Wang, A.; Pan, Y.; Wang, C.; Ji, Y.; Chen, J.h. Packaged Microbubble Resonator for Versatile Optical Sensing. J. Lightware Technol. 2020, 38, 4555–4559. [Google Scholar] [CrossRef]
- Carmon, T.; Yang, L.; Vahala, K.J. Dynamical thermal behavior and thermal self-stability of microcavities. Opt. Express 2004, 12, 4742–4750. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Modal coupling in traveling-wave resonators. Opt. Lett. 2002, 27, 1669–1671. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Zhao, G.; Savukov, I.; Yang, L. Polymer encapsulated microcavity optomechanical magnetometer. Sci. Rep. 2017, 7, 8896. [Google Scholar] [CrossRef]

| Reference | Diameter | Before Encapsulation | After Encapsulation |
|---|---|---|---|
| F. Monifi, et al. (2013) [29] | 120 m | ||
| Wang, et al. (2014) [30] | 153 m | − | |
| Zhao, et al. (2017) [31] | 80 m | − | |
| Yang, et al. (2020) [32] | 90 m | ||
| Sun, et al. (2021) [25] | 60 m | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Wang, H.; Wu, X.-Y.; Zhang, Y.; Yang, D.; Jiao, R.; Wang, C. Ultrasound Sensing Using Packaged Microsphere Cavity in the Underwater Environment. Sensors 2022, 22, 4190. https://doi.org/10.3390/s22114190
Wang K, Wang H, Wu X-Y, Zhang Y, Yang D, Jiao R, Wang C. Ultrasound Sensing Using Packaged Microsphere Cavity in the Underwater Environment. Sensors. 2022; 22(11):4190. https://doi.org/10.3390/s22114190
Chicago/Turabian StyleWang, Kai, Heng Wang, Xing-Yu Wu, Yong Zhang, Daquan Yang, Rongzhen Jiao, and Chuan Wang. 2022. "Ultrasound Sensing Using Packaged Microsphere Cavity in the Underwater Environment" Sensors 22, no. 11: 4190. https://doi.org/10.3390/s22114190
APA StyleWang, K., Wang, H., Wu, X.-Y., Zhang, Y., Yang, D., Jiao, R., & Wang, C. (2022). Ultrasound Sensing Using Packaged Microsphere Cavity in the Underwater Environment. Sensors, 22(11), 4190. https://doi.org/10.3390/s22114190







