Estimation Based on Chirp Modulation for Desired and Interference Power and Channel Occupancy Ratio in LoRa
Abstract
1. Introduction
- An estimation scheme of the desired signal power, CCI power, and COR based on the chirp modulation of LoRa is proposed.
- A packet selection based on the estimated CCI power is proposed to improve the estimation accuracy.
- A channel selection criterion for maximizing the PDR performance is constructed.
2. Related Works
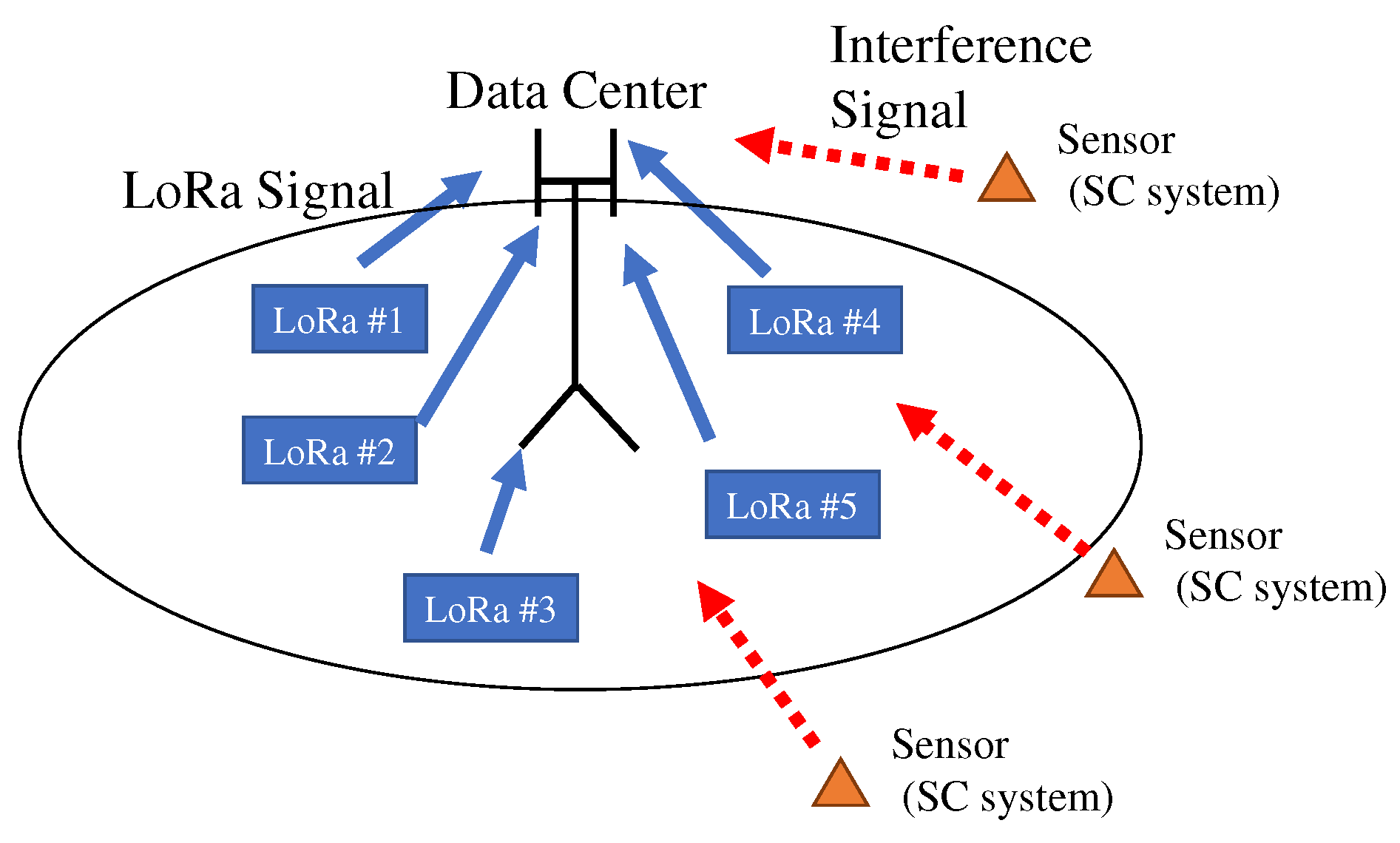
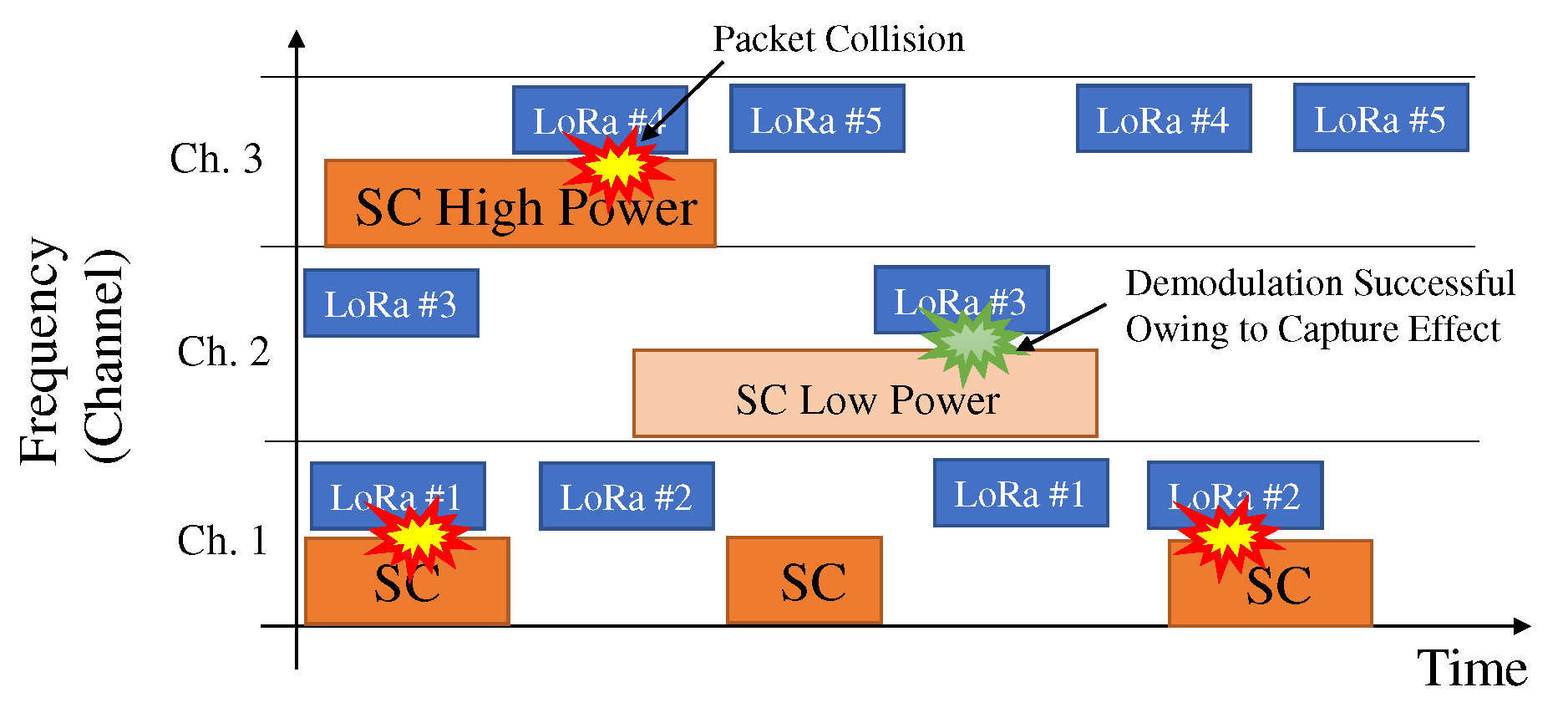
3. System Model
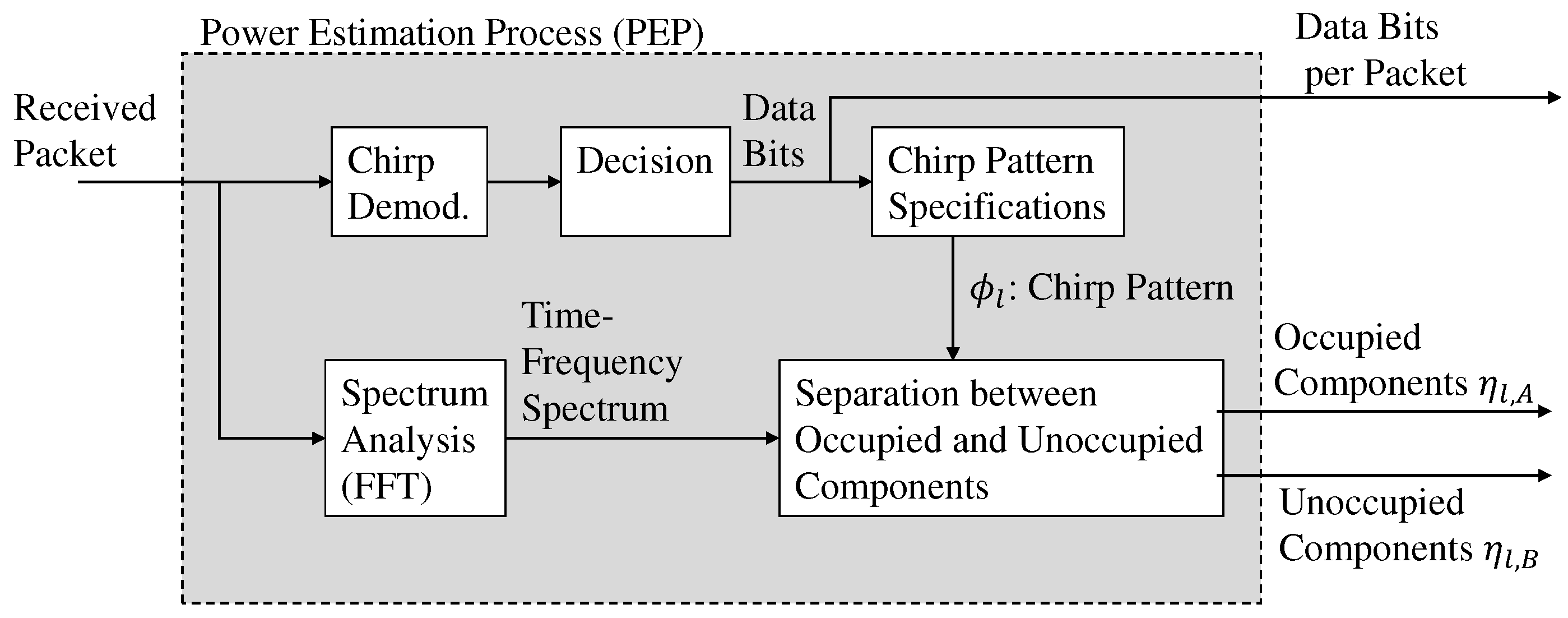
4. Proposed Estimation Scheme
4.1. Estimation of Desired Power, CCI Power, and COR
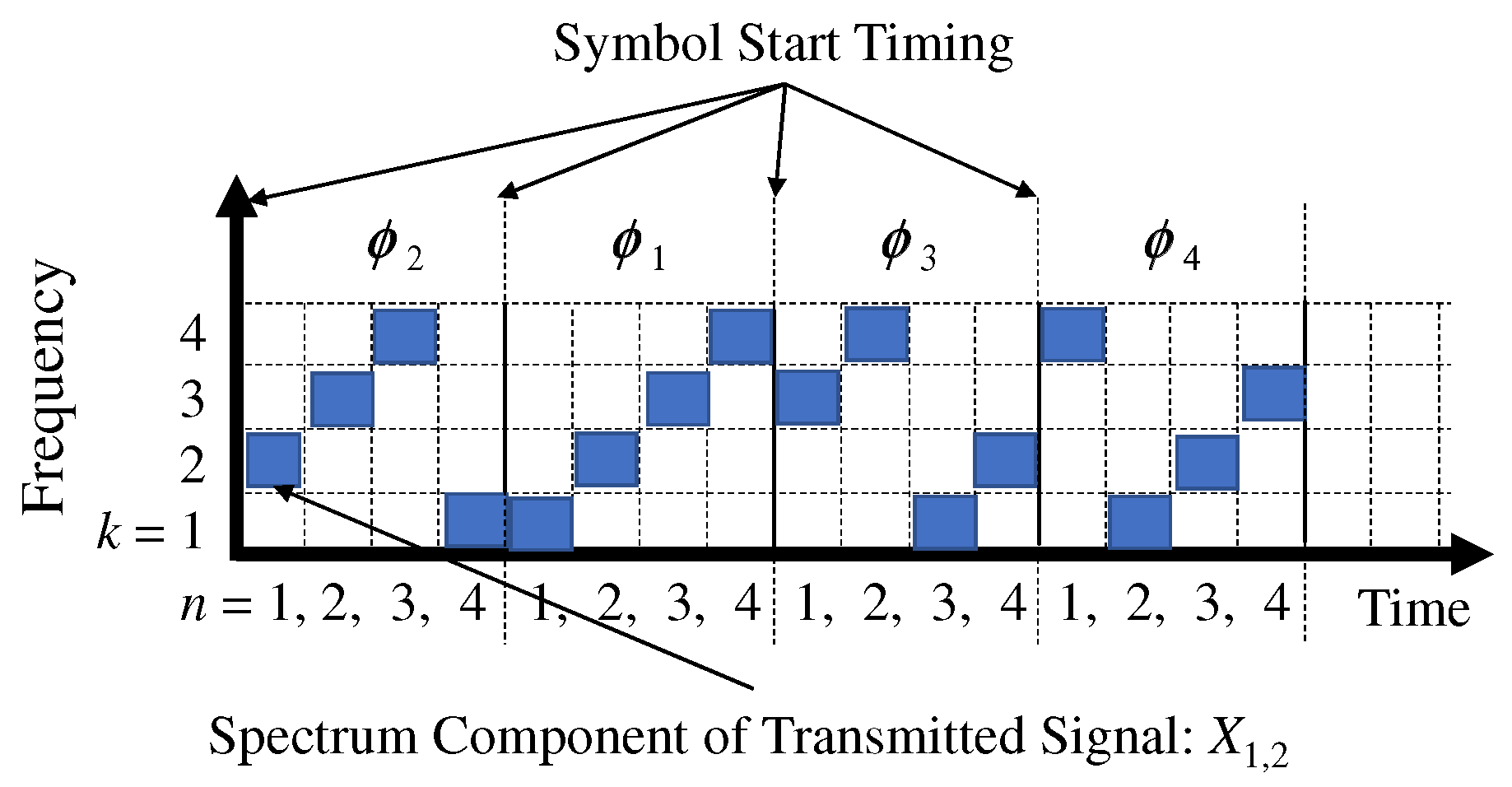
4.1.1. Signal Recovery
4.1.2. Estimation of Power
4.1.3. Estimation of Noise Power, CCI Power, and COR
4.2. Packet Selection
5. Channel Selection Scheme Based on Estimation of Power and COR
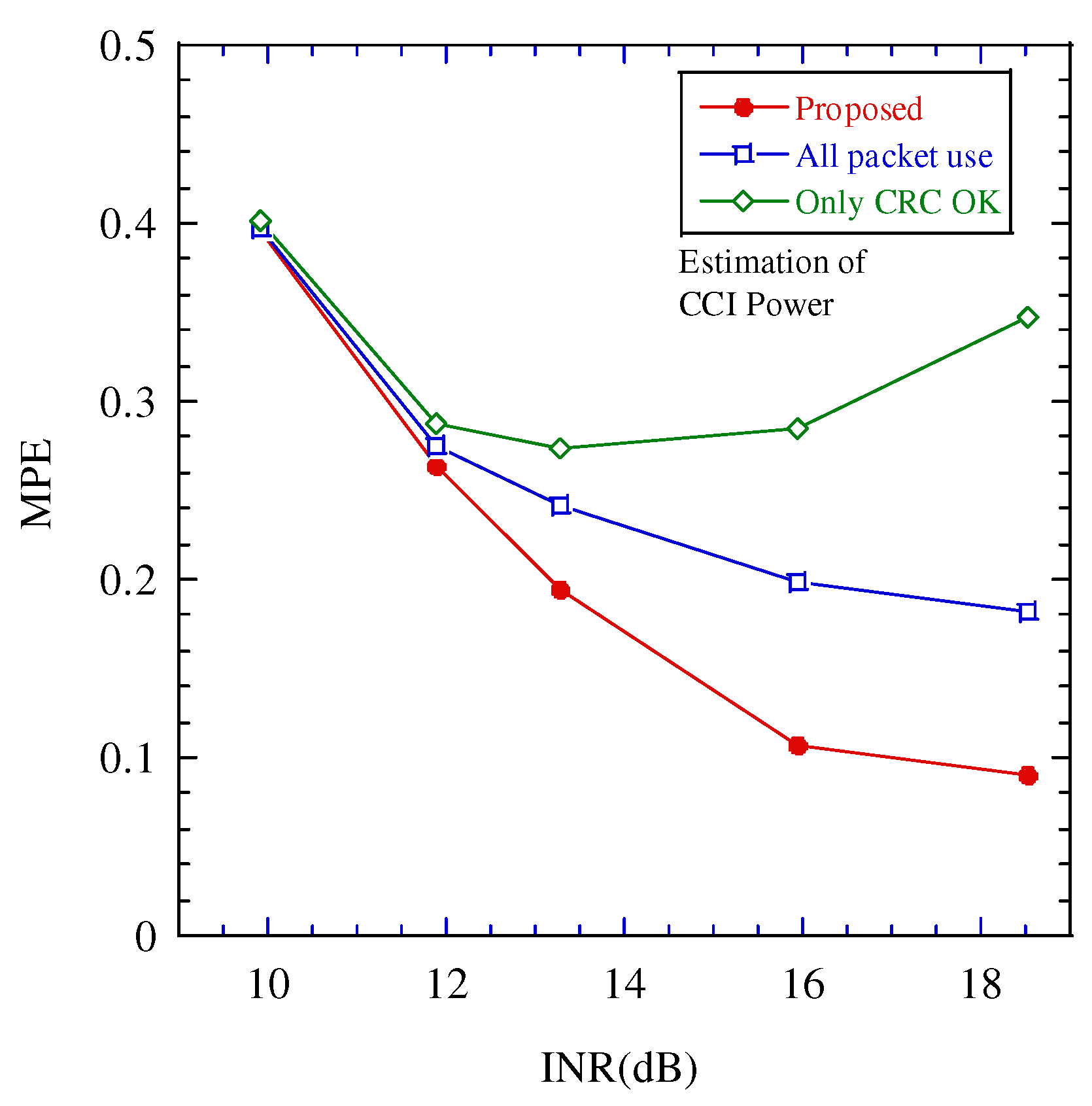
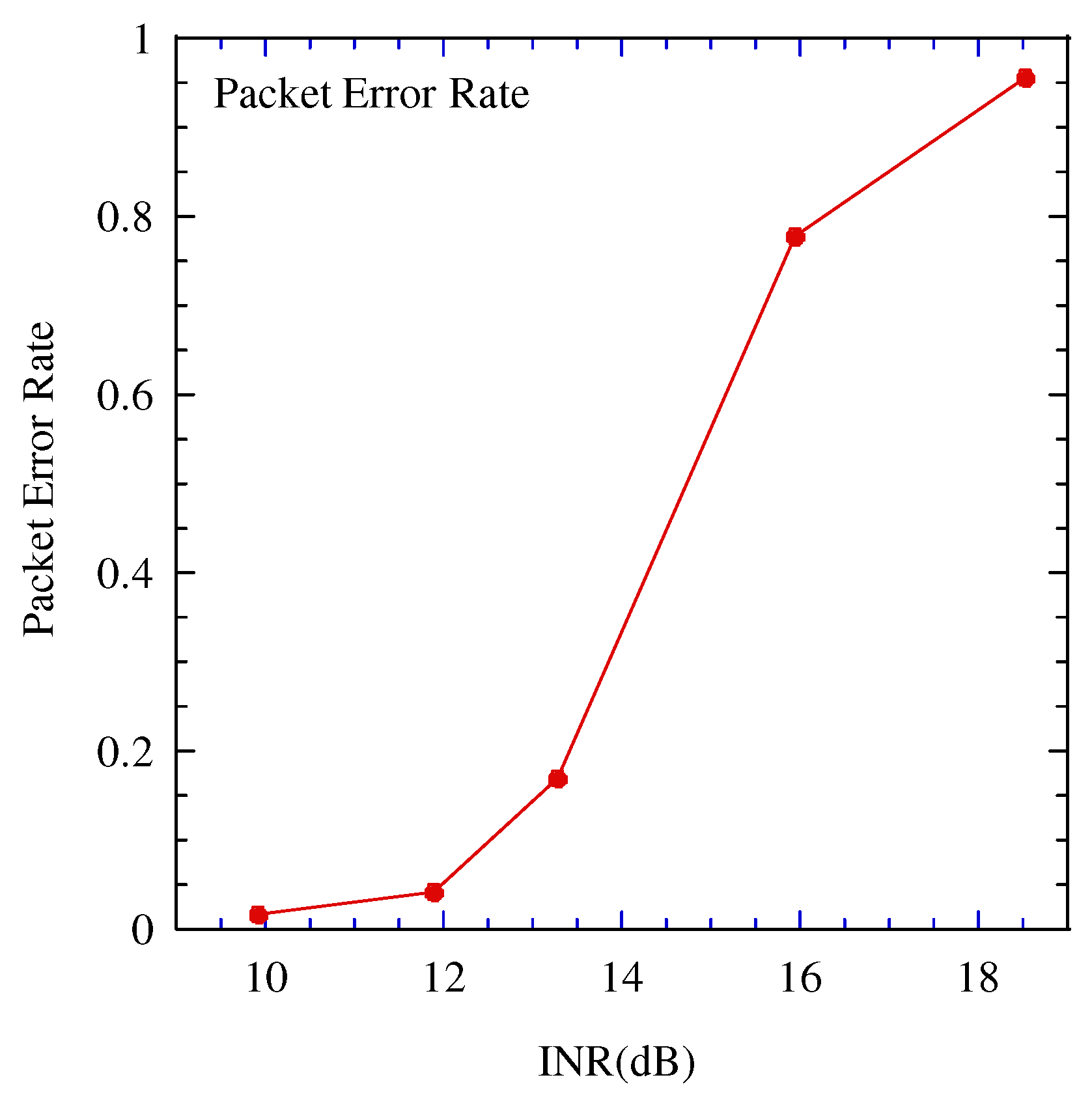
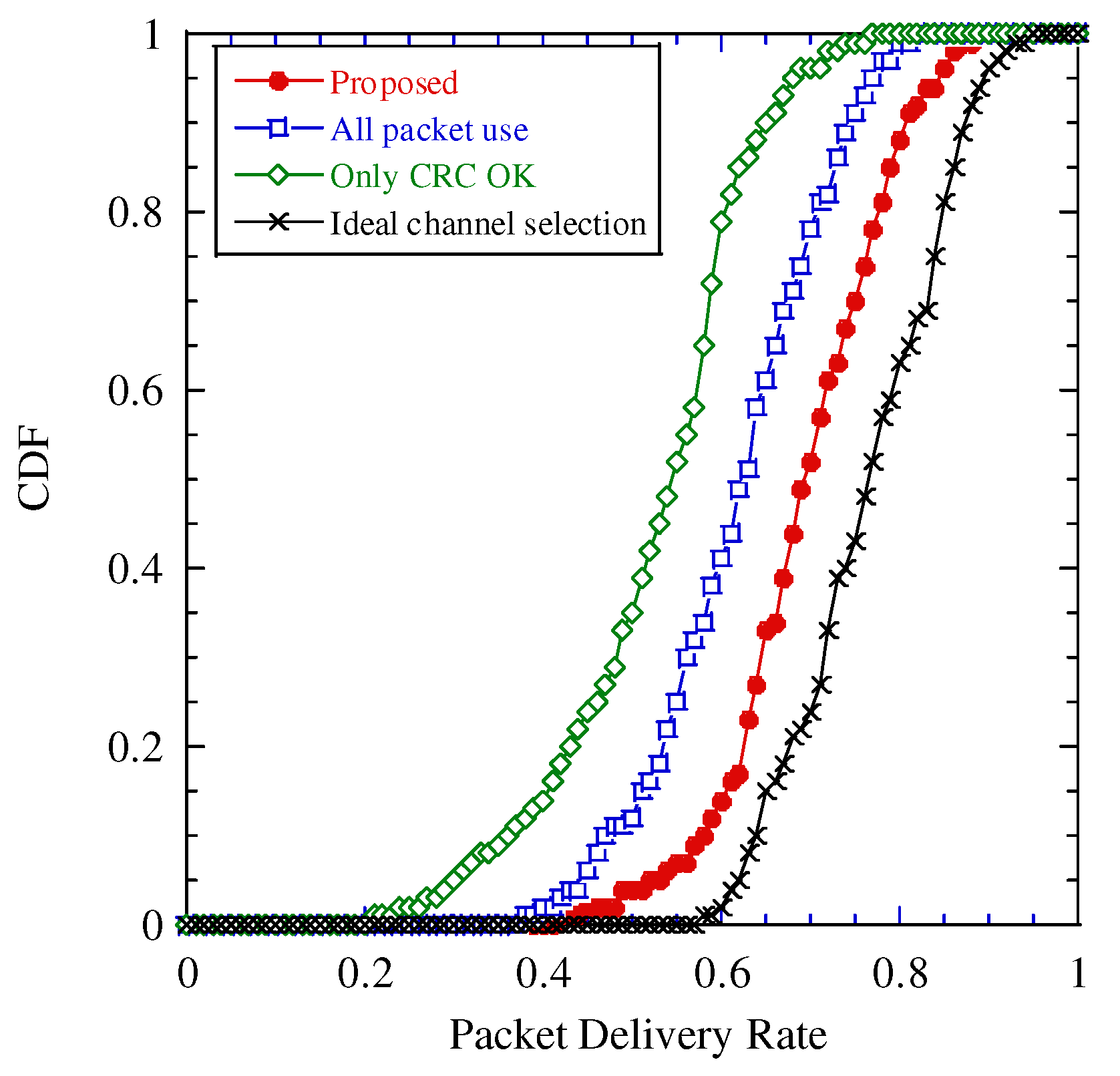
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qadir, Q.M.; Rashid, T.A.; Al-Salihi, N.K.; Ismael, B.; Kist, A.A.; Zhang, Z. Low Power Wide Area Networks: A Survey of Enabling Technologies, Applications and Interoperability Needs. IEEE Access 2018, 6, 77454–77473. [Google Scholar] [CrossRef]
- Wang, H.; Fapojuwo, A.O. A Survey of Enabling Technologies of Low Power and Long Range Machine-to-Machine Communications. IEEE Commun. Surv. Tutor. 2017, 19, 2621–2639. [Google Scholar] [CrossRef]
- Bockelmann, C.; Pratas, N.K.; Wunder, G.; Saur, S.; Navarro, M.; Gregoratti, D.; Vivier, G.; De Carvalho, E.; Ji, Y.; Stefanovic, C.; et al. Towards Massive Connectivity Support for Scalable mMTC Communications in 5G Networks. IEEE Access 2018, 6, 28969–28992. [Google Scholar] [CrossRef]
- Migabo, E.M.; Djouani, K.D.; Kurien, A.M. The Narrowband Internet of Things (NB-IoT) Resources Management Performance State of Art, Challenges, and Opportunities. IEEE Access 2020, 8, 97658–97675. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Fujii, T.; Takyu, O.; Ohta, M.; Adachi, K. Spectrum Sharing Exploiting Spectrum Database for LPWA. In Proceedings of the 2019 Eleventh International Conference on Ubiquitous and Future Networks (ICUFN), Zagreb, Croatia, 2–5 July 2019; pp. 60–65. [Google Scholar]
- Junjalearnvong, T.; Okumura, R.; Mizutani, K.; Harada, H. Performance Evaluation of Multi-hop Network Configuration for Wi-SUN FAN Systems. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–6. [Google Scholar]
- Hoeller, A.; Souza, R.D.; Alves, H.; Lopez, O.L.A.; Montejo-Sanchez, S.; Pellenz, M.E. Optimum LoRaWAN Configuration under Wi-SUN Interference. IEEE Access 2019, 7, 170936–170948. [Google Scholar] [CrossRef]
- Takyu, O.; Saiwai, T.; Fujii, T.; Umeda, Y. Performance for MAC Level Channel Capacity in Cognitive Radio with Carrier Sense Multiple Access and Transmitting Power Control. In Proceedings of the 2011 IEEE Vehicular Technology Conference (VTC Fall), San Francisco, CA, USA, 5–8 September 2011; pp. 1–5. [Google Scholar]
- Lehtomaki, J.J.; Lopez-Benitez, M.; Umebayashi, K.; Juntti, M. Improved Channel Occupancy Rate Estimation. IEEE Trans. Commun. 2015, 63, 643–654. [Google Scholar] [CrossRef][Green Version]
- Bennai, M.; Sydor, J.; Rahman, M. Automatic channel selection for cognitive radio systems. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 26–30 September 2010; pp. 1831–1835. [Google Scholar]
- Noreen, U.; Clavier, L.; Bounceur, A. LoRa-like CSS-based PHY layer, Capture Effect and Serial Interference Cancellation. In Proceedings of the European Wireless 2018, 24th European Wireless Conference, Catania, Italy, 2–4 May 2018; pp. 1–6. [Google Scholar]
- Vangelista, L. Frequency Shift Chirp Modulation: The LoRa Modulation. IEEE Signal Process. Lett. 2017, 24, 1818–1821. [Google Scholar] [CrossRef]
- Soya, H.; Takyu, O.; Shirai, K.; Ohta, M.; Fujii, T.; Sasamori, F.; Handa, S. Measurement Technique for Occupancy Ratio and Transition Ratio in Cognitive Radio System. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Kobayashi, G.; Takyu, O.; Adachi, K.; Ohta, M.; Fujii, T. Estimation of Desired power and Undesired power Using Chirp Demodulation and Evaluation of Accuracy. In Proceedings of the 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 1513–1518. [Google Scholar]
- Kobayashi, G.; Takyu, O.; Adachi, K.; Ohta, M.; Fujii, T. Proposal of interference power occupancy estimation method using chirp demodulation. In Proceedings of the 2021 Twelfth International Conference on Ubiquitous and Future Networks (ICUFN), Jeju Island, Korea, 17–20 August 2021; pp. 187–191. [Google Scholar]
- Kobayashi, G.; Takyu, O.; Adachi, K.; Ohta, M.; Fujii, T. Estimation Accuracy to Channel Occupancy Ratio and Signal Power under Co-Channel Interference in LoRa. IEICE Proc. Ser. 2021, 68. [Google Scholar] [CrossRef]
- Uy, C.H.; Bernier, C.; Charbonnier, S. Design of a Low Complexity Interference Detector for LPWA Networks. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Kyeremateng-Boateng, H.; Conn, M.; Josyula, D.; Mareboyana, M. Prediction of Radio Frequency Spectrum Occupancy. In Proceedings of the 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Guangzhou, China, 29 December 2020–1 January 2021; pp. 2028–2034. [Google Scholar]
- Toma, O.H.; Lopez-Benitez, M.; Patel, D.K.; Umebayashi, K. Primary Channel Duty Cycle Estimation under Imperfect Spectrum Sensing Based on Mean Channel Periods. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Sinkevich, E.V. Discrete Nonlinear Simulation of Radio Receivers for Electromagnetic Compatibility Analysis and Design: Estimation of the Signal-to-Interference Ratio. In Proceedings of the 2007 7th International Symposium on Electromagnetic Compatibility and Electromagnetic Ecology, St. Petersburg, Russia, 26–29 June 2007; pp. 166–169. [Google Scholar]
- Koshimizu, M.; Funada, R.; Harada, H.; Shirai, H. A new cochannel interference estimation method for the downlink frame of DPC-OF/TDMA. In Proceedings of the IEEE 60th Vehicular Technology Conference, VTC2004-Fall, Los Angeles, CA, USA, 26–29 September 2004; Volume 7, pp. 5096–5100. [Google Scholar]
- Kashyap, S.; Mehta, N.B. Power Gain Estimation and Its Impact on Binary Power Control in Underlay Cognitive Radio. IEEE Wirel. Commun. Lett. 2015, 4, 193–196. [Google Scholar] [CrossRef]
- Chen, G.; Dong, W.; Lv, J. LoFi: Enabling 2.4GHz LoRa and WiFi Coexistence by Detecting Extremely Weak Signals. In Proceedings of the IEEE INFOCOM 2021-IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar]
- Dykman, M.I.; Luchinsky, D.G.; Mannella, R.; McClintock, P.V.E.; Stein, N.D.; Stocks, N.G. Stochastic resonance in perspective. Il Nuovo Cim. D 1995, 17, 661–683. [Google Scholar] [CrossRef]
- Prokopenko, I.; Omelchuk, I.; Osipchuk, A.; Petrova, J. Robust Estimation of The Harmonic Signal Parameters In Non-Gaussian Interferences. In Proceedings of the 2019 International Conference on Information and Telecommunication Technologies and Radio Electronics (UkrMiCo), Odessa, Ukraine, 9–13 September 2019; pp. 1–6. [Google Scholar]
- Chen, F.; Ji, F.; Cao, T.; Xiong, S. Maximum Likelihood Based Measurement of Interference Level and Noise Power for Memoryless Gaussian Channel with Deterministic Interference. IEEE Trans. Commun. 2012, 60, 19–22. [Google Scholar] [CrossRef]
- Yamasuge, T.; Sasaki, S.; Kim, M. A study on low-level signal estimation in the spectrum sensing. IEICE Tech. Rep. 2016, 115, 121–127. [Google Scholar]
- Iwata, H.; Umebayashi, K.; Al-Tahmeesschi, A.; Lehtomaki, J. High-Efficiency FCME-Based Noise Power Estimation for Long-Term and Wide-Band Spectrum Measurements. IEEE Access 2021, 9, 149883–149893. [Google Scholar] [CrossRef]
- Gupta, H.; Rahman, M.S.; Curran, M. Shared Spectrum Allocation via Pathloss Estimation in Crowdsensed Shared Spectrum Systems. In Proceedings of the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Newark, NJ, USA, 11–14 November 2019; pp. 1–5. [Google Scholar]
- Kominami, D.; Hasegawa, Y.; Nogami, K.; Shimonishi, H.; Murata, M. Bayesian-based channel quality estimation method for LoRaWAN with unpredictable interference. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–7. [Google Scholar]
- Wigren, T. Low complexity Kalman filtering for Inter-Cell interference and power based load estimation in the WCDMA uplink. In Proceedings of the 2011 5th International Conference on Signal Processing and Communication Systems (ICSPCS), Honolulu, HI, USA, 12–14 December 2011; pp. 1–10. [Google Scholar]
- Morimoto, R.; Iwai, H.; Ibi, S.; Kurihara, T.; Shimizu, S.; Yano, K.; Suzuki, Y. Estimation of Total Interference Power by Clustering Multiple Wireless Nodes. In Proceedings of the 2020 International Symposium on Antennas and Propagation (ISAP), Osaka, Japan, 25–28 January 2021; pp. 537–538. [Google Scholar]
- Ghotbi, M.; Soleymani, M.R. Multistage parallel interference cancellation with power and phase estimation. In Proceedings of the IEEE 56th Vehicular Technology Conference, Vancouver, BC, Canada, 24–28 September 2002; Volume 3, pp. 1716–1719. [Google Scholar]
- Chi, Q.; Zhang, X.; Yang, D. Detection-assisted interference parameter estimation and interference cancellation for LTE-Advanced system. In Proceedings of the IEEE 2016 IEEE International Conference on Network Infrastructure and Digital Content (IC-NIDC), Beijing, China, 23–25 September 2016; pp. 229–233. [Google Scholar]
- Zheng, Z.; Yang, T.; Wang, W.; So, H.C. Robust Adaptive Beamforming via Simplified Interference Power Estimation. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3139–3152. [Google Scholar] [CrossRef]
- Baumgartner, S.; Hirtz, G. Narrowband interference estimation for OFDM based on power spectral density functions. In Proceedings of the IWSSIP 2014 Proceedings, Dubrovnik, Croatia, 12–15 May 2014; pp. 255–258. [Google Scholar]
- Shibata, Y.; Ohtsuki, T.; Mashinot, J. Undesired signal power estimation based on estimated superposed band for multicarrier transmission. In Proceedings of the 2015 21st Asia-Pacific Conference on Communications (APCC), Kyoto, Japan, 14–16 October 2015; pp. 642–646. [Google Scholar]
- Wulich, D.; Plotkin, E.I.; Swamy, M.N.S.; Tong, W. PLL based discrete time varying filter for estimation of parameters of a sine signal corrupted by a closely spaced FM interference. In Proceedings of the IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 1–3 May 1990; Volume 1, pp. 771–774. [Google Scholar]
- Hajizadeh, H.; Nabi, M.; Vermeulen, M.; Goossens, K. Coexistence Analysis of Co-Located BLE and IEEE 802.15.4 TSCH Networks. IEEE Sens. J. 2021, 21, 17360–17372. [Google Scholar] [CrossRef]
- Cerro, G.; Miele, G. A stand-alone sensor for spectrum occupancy monitoring in dynamic spectrum access framework. In Proceedings of the 2019 IEEE Sensors Applications Symposium (SAS), Sophia Antipolis, France, 11–13 March 2019; pp. 1–6. [Google Scholar]
- Iima, Y.; Kanzaki, A.; Hara, T.; Nishio, S. Overhearing-Based Data Transmission Reduction for Periodical Data Gathering in Wireless Sensor Networks. In Proceedings of the 2009 International Conference on Complex, Intelligent and Software Intensive Systems, Fukuoka, Japan, 16–19 March 2009; pp. 1048–1053. [Google Scholar]
- Asano, D.; Kuroyanagi, D.; Suzuki, H.; Motoyama, E.; Fuwa, Y. A Pseudo-TDMA MAC Protocol Using Randomly Determined Transmission Times for Landslide Prediction Wireless Sensor Networks. IEICE Trans. Commun. 2014, E97-B, 1449–1456. [Google Scholar] [CrossRef]
- RP2-1.0.1 LoRaWAN® Regional Parameters. Available online: https://lora-alliance.org/resource_hub/rp2-101-lorawan-regional-parameters-2/ (accessed on 18 May 2022).
- Jalloul, L.M.A.; Kohimann, M.; Medlock, J. SIR estimation and closed-loop power control for 3G. In Proceedings of the 2003 IEEE 58th Vehicular Technology Conference. VTC 2003-Fall (IEEE Cat. No.03CH37484), Orlando, FL, USA, 6–9 October 2003; Volume 2, pp. 831–835. [Google Scholar]
- Elshabrawy, T.; Robert, J. Closed-Form Approximation of LoRa Modulation BER Performance. IEEE Commun. Lett. 2018, 22, 1778–1781. [Google Scholar] [CrossRef]
- Aihara, N.; Adachi, K.; Takyu, O.; Ohta, M.; Fujii, T. Generalized Interference Detection Scheme in Heterogeneous Low Power Wide Area Networks. IEEE Sens Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Razavi, B. RF Microelectronics, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2012. [Google Scholar]




| Center frequency | 923 MHz |
| Spreading factor, | 7 |
| LoRa bandwidth | 250 kHz |
| SC Bandwidth | 200 kHz |
| LoRa and SC transmission power | 13 dBm |
| Number of packets for estimation | 1000 |
| Number of symbols per packet, | 200 |
| COR of SC | 0.7 |
| Distance between data centers and sensor in LoRa | 500 m |
| Distance between data centers of LoRa and SC transmitter | 500 m to 900 m |
| Propagation coefficient of the distance loss, a [47] | 4 |
| Propagation offset, b [47] | 9.5 |
| Propagation coefficient of the frequency loss, c [47] | 4.5 |
| Transmitted antenna gain | 0 dBi |
| Received antenna gain | 16 dBi |
| Shadowing deviation [47] | 3.48 dB |
| Shadowing coefficient | 0 |
| Noise power-spectrum density | −174 dBm/Hz |
| Amplification rate of the low-noise amplifier | 60 dB |
| Noise figure | 0 dB |
| Estimating Terms | Ideal | Proposed | All Packets Use | Only CRC OK |
|---|---|---|---|---|
| Noise + CCI power | −101 dBm | −100 dBm | −100 dBm | −103 dBm |
| Noise | −120 dBm | −120 dBm | −117 dBm | −120 dBm |
| COR | 0.70 | 0.70 | 0.96 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takyu, O.; Kobayashi, G.; Adachi, K.; Ohta, M.; Fujii, T. Estimation Based on Chirp Modulation for Desired and Interference Power and Channel Occupancy Ratio in LoRa. Sensors 2022, 22, 4140. https://doi.org/10.3390/s22114140
Takyu O, Kobayashi G, Adachi K, Ohta M, Fujii T. Estimation Based on Chirp Modulation for Desired and Interference Power and Channel Occupancy Ratio in LoRa. Sensors. 2022; 22(11):4140. https://doi.org/10.3390/s22114140
Chicago/Turabian StyleTakyu, Osamu, Gaku Kobayashi, Koichi Adachi, Mai Ohta, and Takeo Fujii. 2022. "Estimation Based on Chirp Modulation for Desired and Interference Power and Channel Occupancy Ratio in LoRa" Sensors 22, no. 11: 4140. https://doi.org/10.3390/s22114140
APA StyleTakyu, O., Kobayashi, G., Adachi, K., Ohta, M., & Fujii, T. (2022). Estimation Based on Chirp Modulation for Desired and Interference Power and Channel Occupancy Ratio in LoRa. Sensors, 22(11), 4140. https://doi.org/10.3390/s22114140







