A Spatial Autoregressive Quantile Regression to Examine Quantile Effects of Regional Factors on Crash Rates
Abstract
:1. Introduction
2. Literature Review
3. Data Description and Preparation
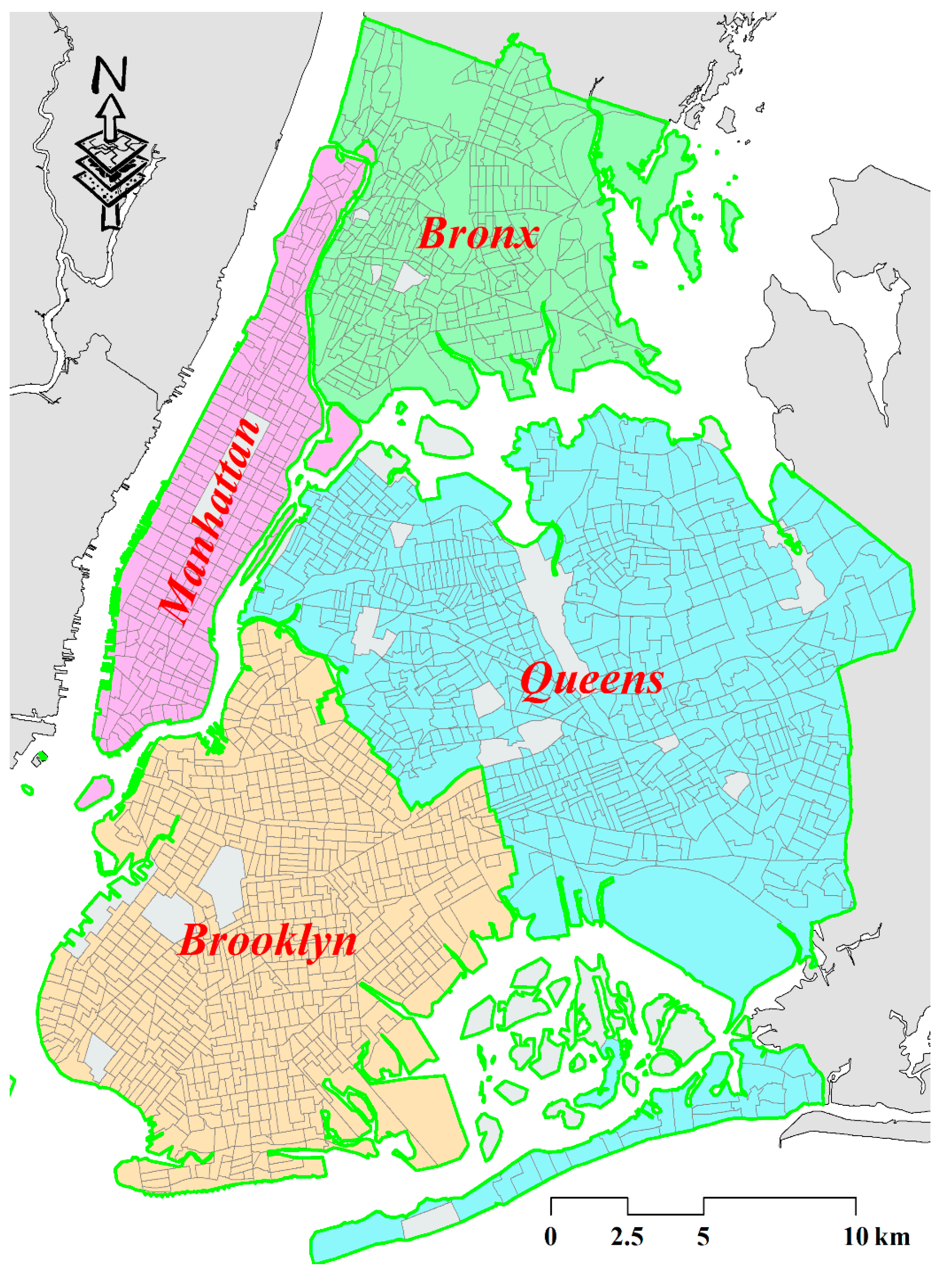
3.1. Study Area
3.2. Data Description and Preparation
3.3. Data Processing
4. Methods
4.1. Quantile Regression Model
4.2. Quantile Version for Spatial Autoagressive Model
5. Results and Discussion
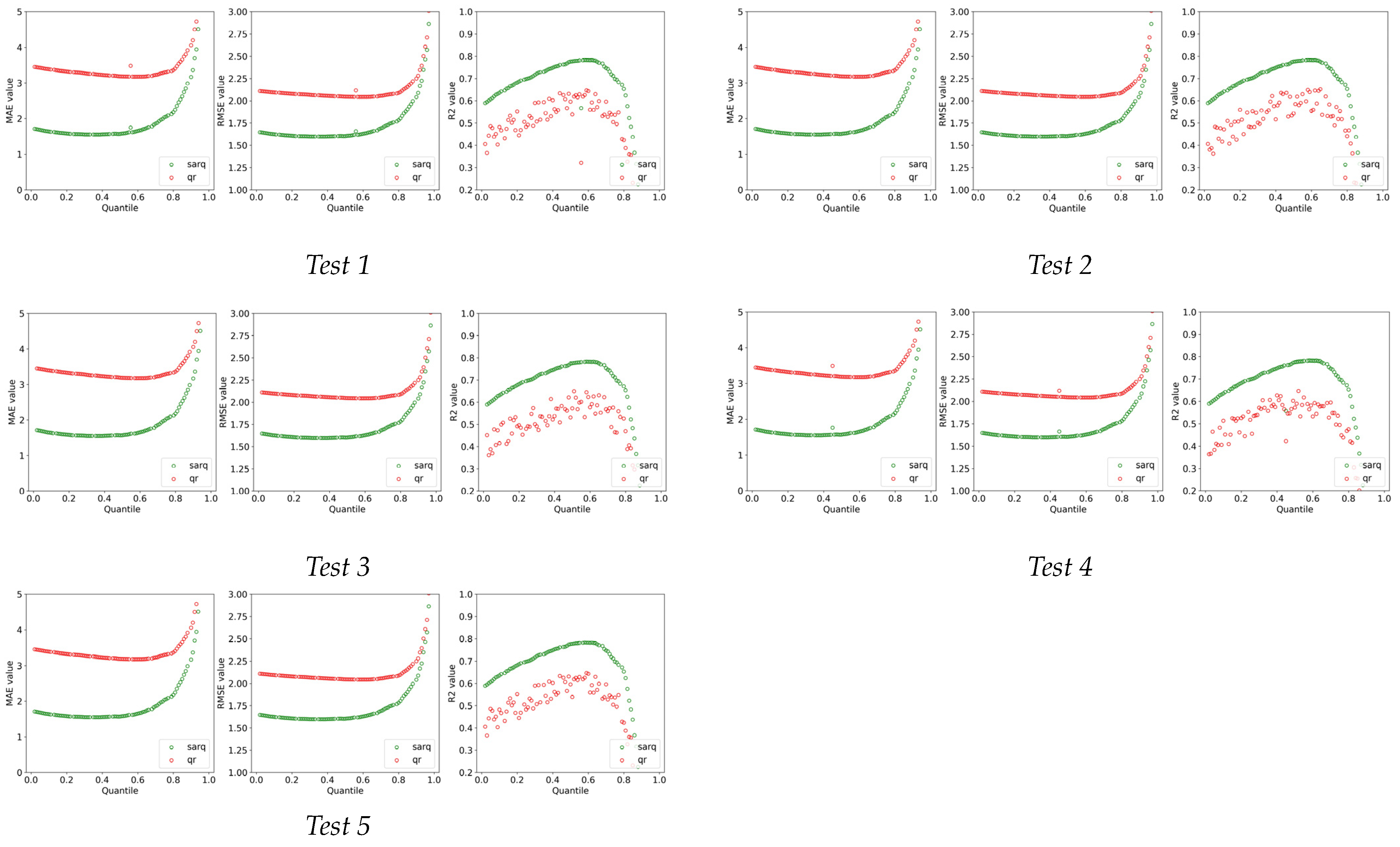
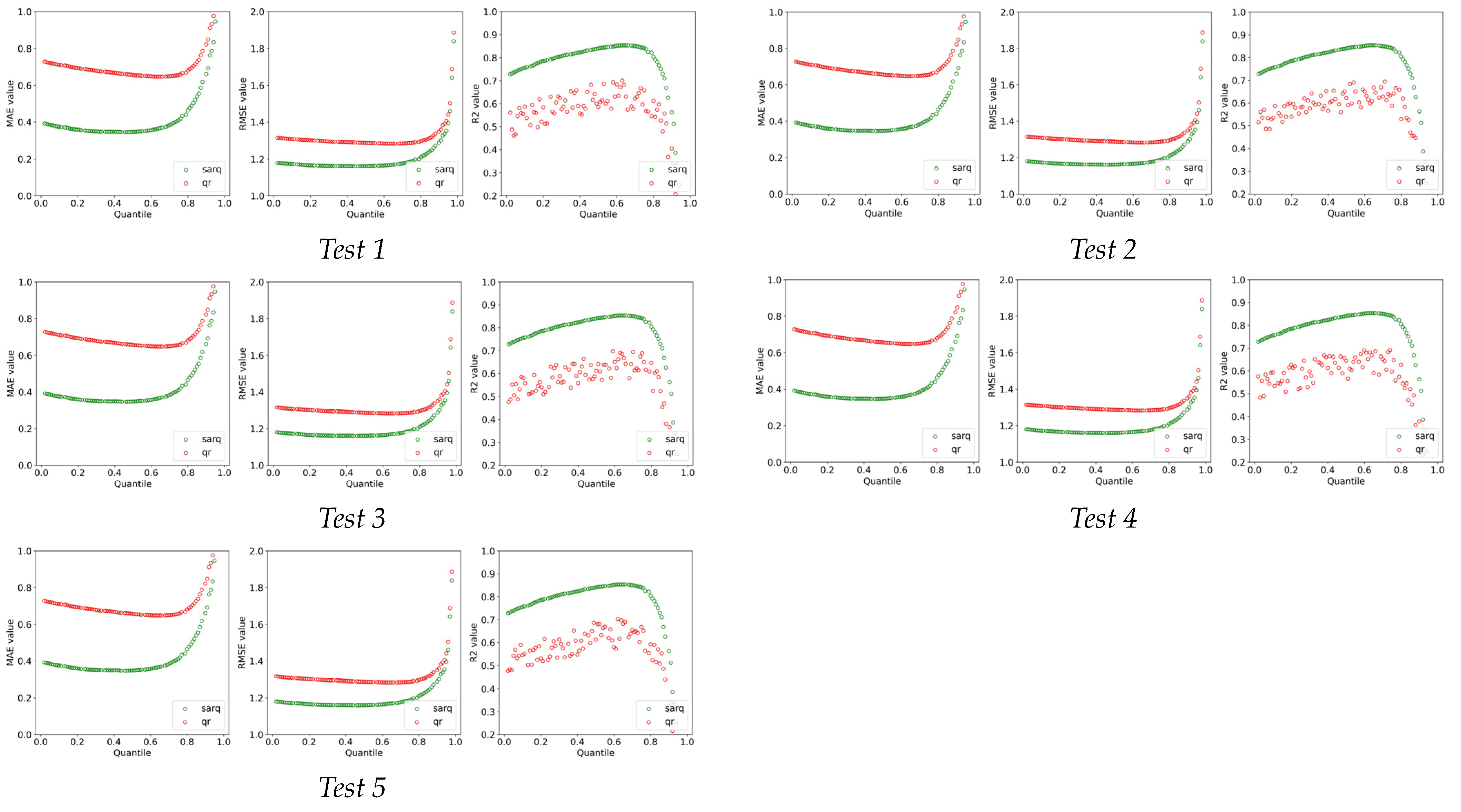
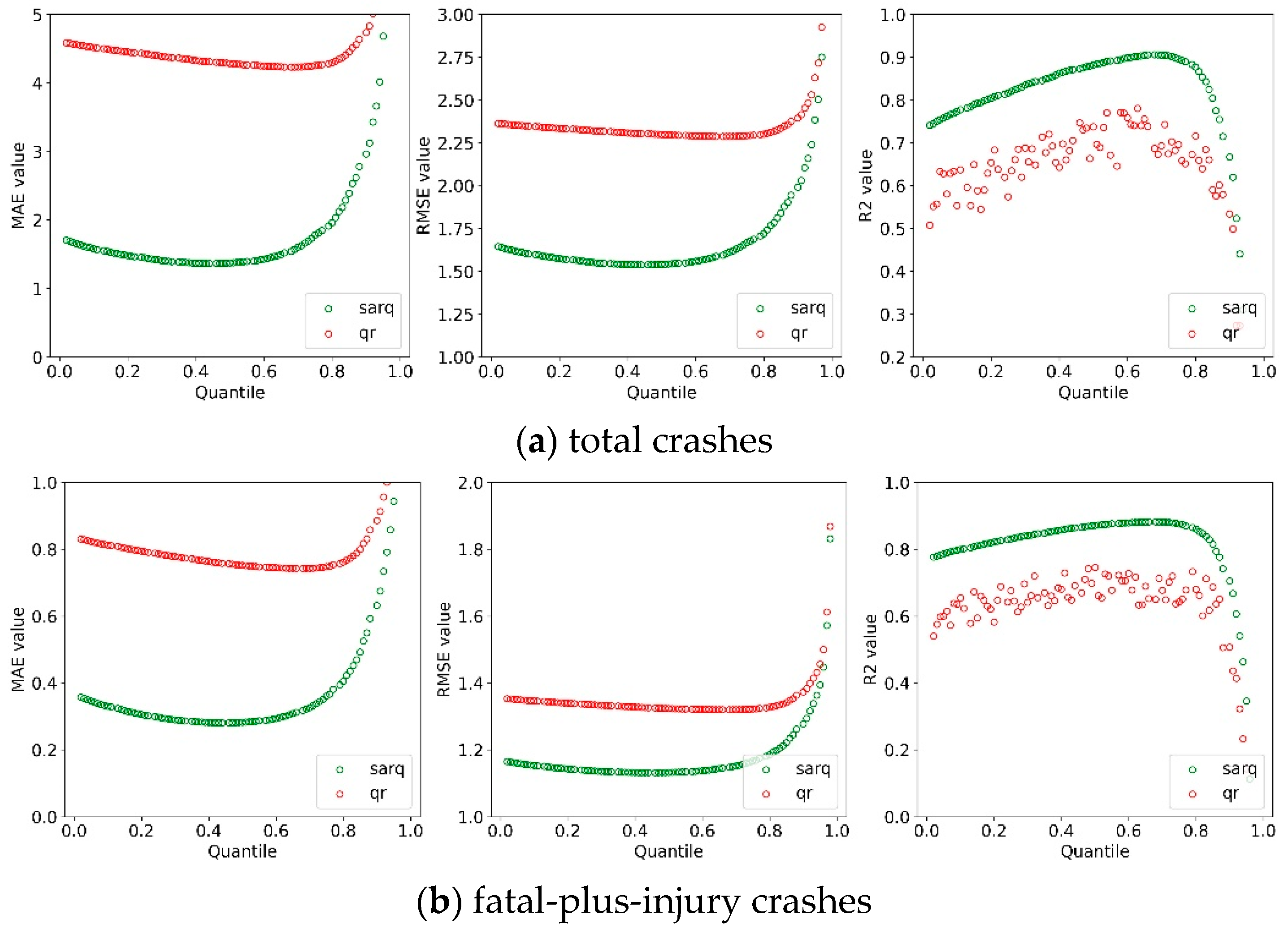
5.1. Model Comparison
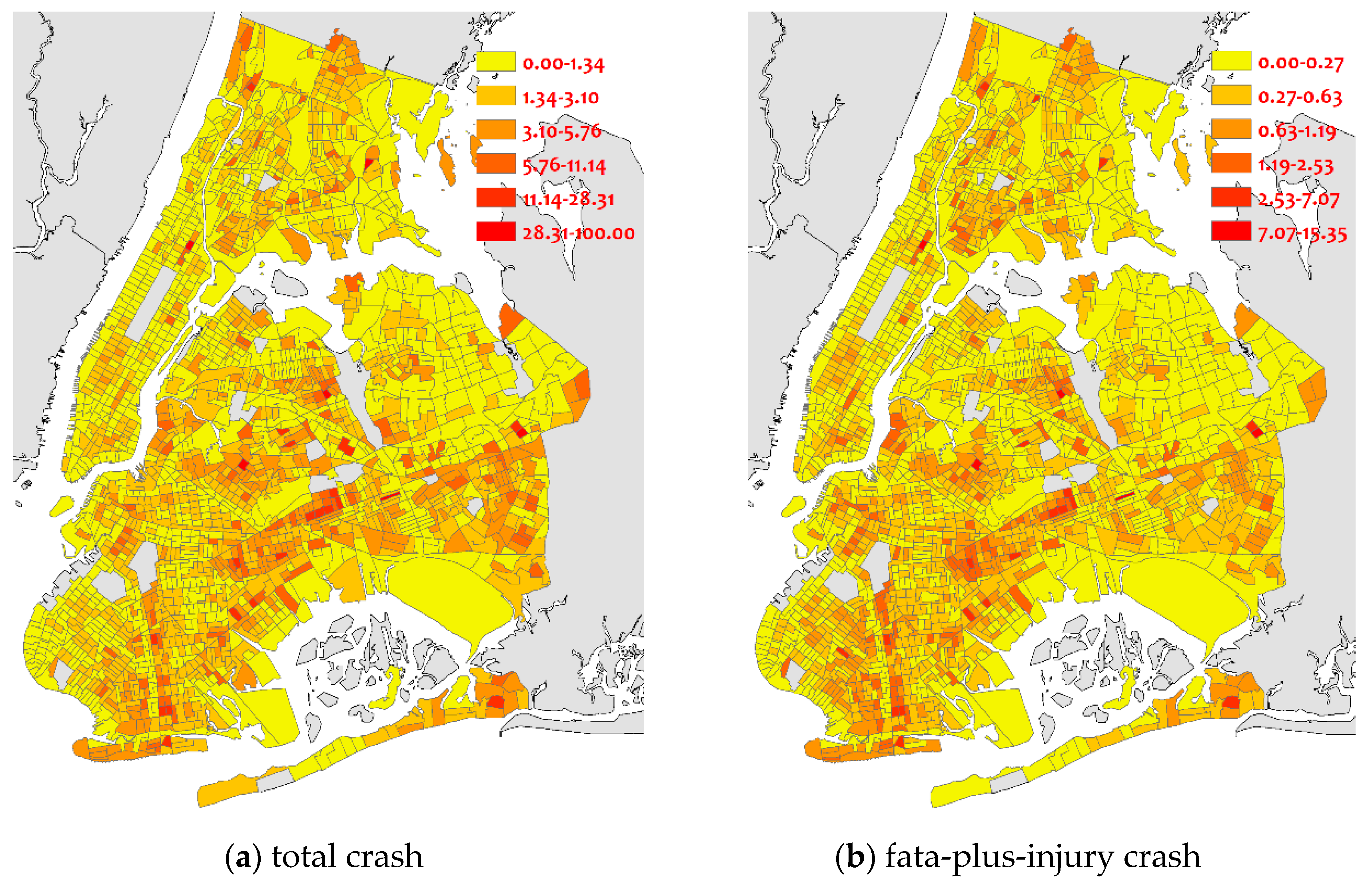
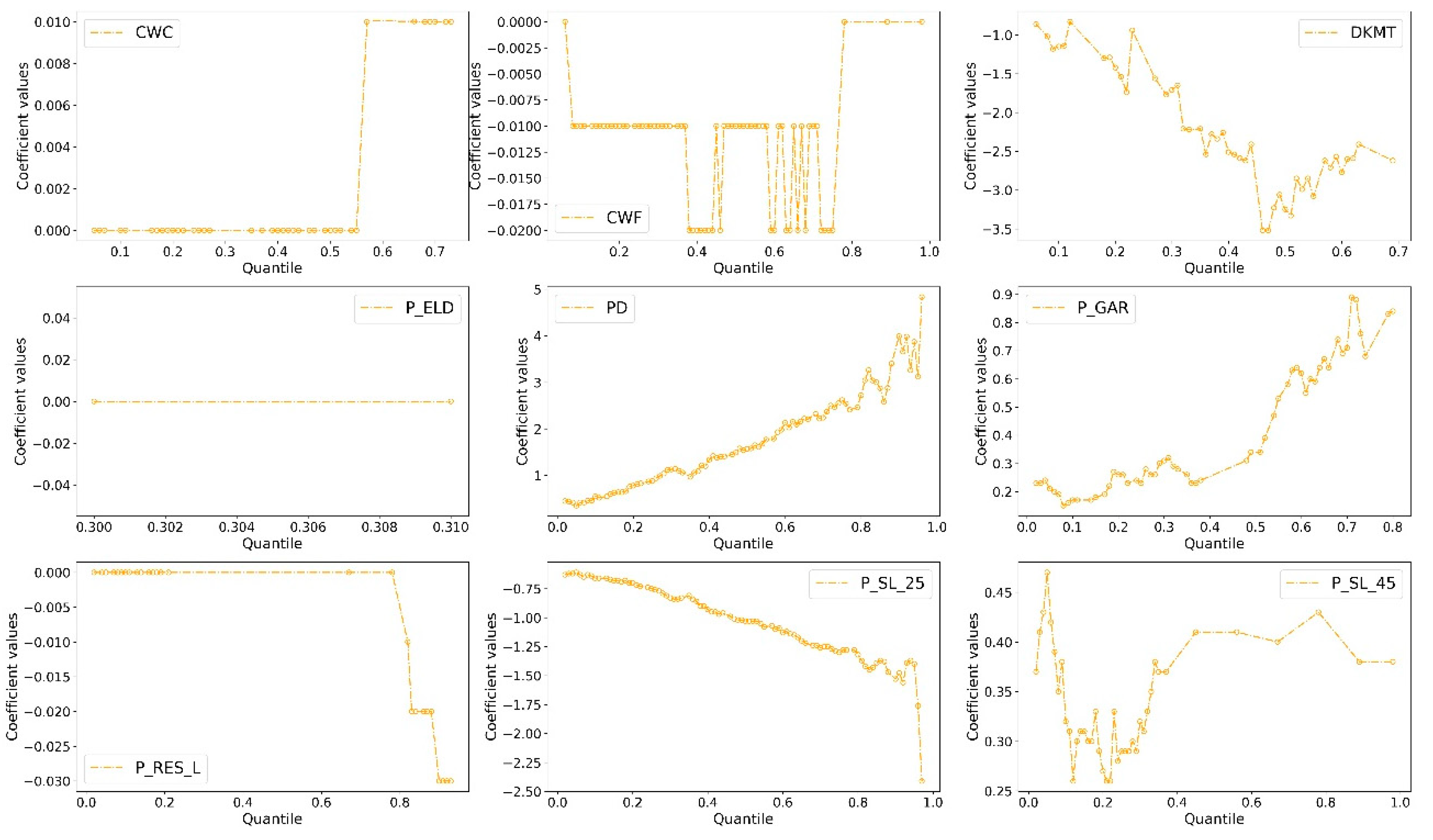
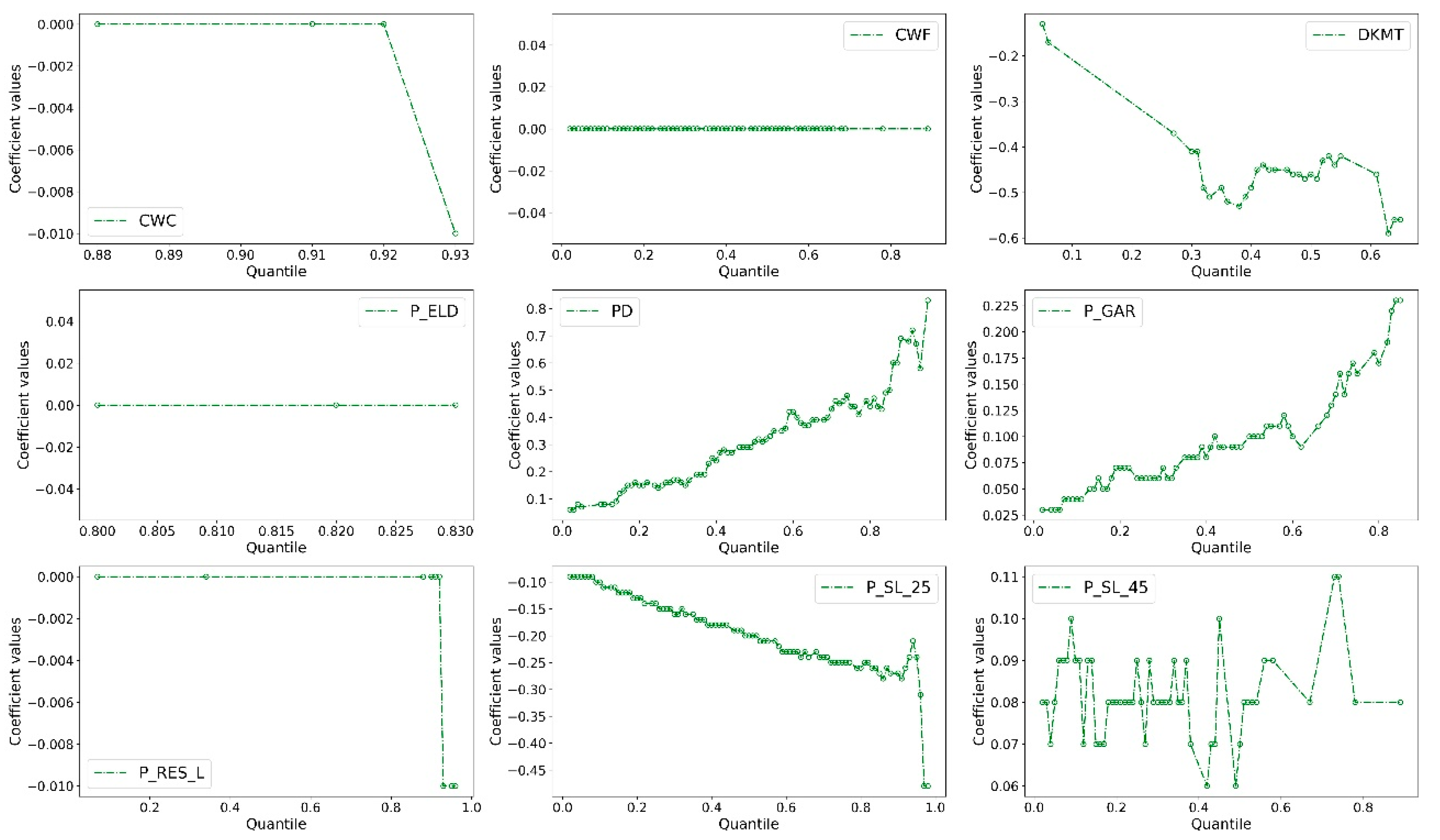
5.2. Parameter Estimation and Quantile Effects Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Cunto, F.J.C.; Saccomanno, F.F. Microlevel traffic simulation method for assessing crash potential at intersections. In Proceedings of the Transportation Research Board 86th Annual Meeting, Washington, DC, USA, 21–25 January 2007. [Google Scholar]
- Hezaveh, A.M.; Arvin, R.; Cherry, C.R. A geographically weighted regression to estimate the comprehensive cost of traffic crashes at a zonal level. Accid. Anal. Prev. 2019, 131, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Branion-Calles, M.; Götschi, T.; Nelsond, T.; Anaya-Boige, E.; Avila-Palencia, I. Cyclist crash rates and risk factors in a prospective cohort in seven European cities. Accid. Anal. Prev. 2020, 141, 105540. [Google Scholar] [CrossRef]
- Chand, S.; Dixit, V.V. Application of Fractal theory for crash rate prediction: Insights from random parameters and latent class tobit models. Accid. Anal. Prev. 2018, 112, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Ma, X.; Chen, S. Refined-scale panel data crash rate analysis using random-effects tobit model. Accid. Anal. Prev. 2014, 73, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Doecke, S.D.; Kloeden, C.N.; Dutschke, J.K.; Baldock, M.R.J. Safe speed limits for a safe system: The relationship between speed limit and fatal crash rate for different crash types. Traffic Inj. Prev. 2018, 19, 404–408. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Abdel-Aty, M.A.; Darwiche, A.L. County-Level Crash Risk Analysis in Florida: Bayesian Spatial Modeling. Transp. Res. Rec. J. Transp. Res. Board 2010, 2148, 27–37. [Google Scholar] [CrossRef]
- Zeng, Q.; Wen, H.; Huang, H.; Pei, X.; Wong, S.C. Incorporating temporal correlation into a multivariate random parameters Tobit model for modeling crash rate by injury severity. Transp. A Transp. Sci. 2017, 14, 177–191. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Z.; Liu, P.; Wu, Y. Modeling correlation and heterogeneity in crash rates by collision types using full bayesian random parameters multivariate Tobit model. Accid. Anal. Prev. 2019, 128, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Goldstick, J.E.; Carter, P.M.; Almani, F.; Brines, S.J.; Shope, J.T. Spatial variation in teens’ crash rate reduction following the implementation of a graduated driver licensing program in Michigan. Accid. Anal. Prev. 2019, 125, 20–28. [Google Scholar] [CrossRef]
- Xu, X.; Duan, L. Predicting Crash Rate Using Logistic Quantile Regression with Bounded Outcomes. IEEE Access 2017, 5, 27036–27042. [Google Scholar] [CrossRef]
- Tang, J.; Gao, F.; Liu, F.; Han, C.; Lee, J. Spatial heterogeneity analysis of macro-level crashes using geographically weighted Poisson quantile regression. Accid. Anal. Prev. 2020, 148, 105833. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, Y.; Li, L.; Liang, G. Self-reports of workloads and aberrant driving behaviors as predictors of crash rate among taxi drivers: A cross-sectional study in China. Traffic Inj. Prev. 2019, 20, 738–743. [Google Scholar] [CrossRef]
- Hao, L.; Naiman, D.Q.; Naiman, D.Q. Quantile Regression; Sage: Newcastle upon Tyne, UK; p. 207.
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Qin, X. Quantile Effects of Causal Factors on Crash Distributions. Transp. Res. Rec. J. Transp. Res. Board 2012, 2279, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Gao, L.; Zhang, Z. Analysis of Crash Data Using Quantile Regression for Counts. J. Transp. Eng. 2014, 140, 04013025. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Development of planning level transportation safety tools using Geographically Weighted Poisson Regression. Accid. Anal. Prev. 2010, 42, 676–688. [Google Scholar] [CrossRef]
- Xu, P.; Huang, H. Modeling crash spatial heterogeneity: Random parameter versus geographically weighting. Accid. Anal. Prev. 2015, 75, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Sze, N.; Chen, S.; Labi, S.; Zeng, Q. Analysing the main and interaction effects of commercial vehicle mix and roadway attributes on crash rates using a Bayesian random-parameter Tobit model. Accid. Anal. Prev. 2021, 154, 106089. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, T. Statistical Approaches to Crash Frequency Modelling: An overview of Poisson and Negative Binomial Models. J. Adv. Civ. Eng. Manag. 2019, 2. [Google Scholar] [CrossRef]
- Collins, F.S.; Varmus, H. A New Initiative on Precision Medicine. N. Engl. J. Med. 2015, 372, 793–795. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Zhang, H.; Chen, J.; He, M. Quantile Regression Models and Their Applications: A Review. J. Biom. Biostat. 2017, 8, 2155. [Google Scholar] [CrossRef] [Green Version]
- Teschke, K.; Harris, M.A.; Reynolds, C.C.O.; Shen, H.; Cripton, P.; Winters, M. Exposure-based Traffic Crash Injury Rates by Mode of Travel in British Columbia. Can. J. Public Health 2013, 104, e75–e79. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Moran, P.A. A test for the serial independence of residuals. Biometrika 1950, 37, 178–181. [Google Scholar] [CrossRef] [PubMed]
- McMillen, D. Conditionally parametric quantile regression for spatial data: An analysis of land values in early nineteenth century Chicago. Reg. Sci. Urban Econ. 2015, 55, 28–38. [Google Scholar] [CrossRef]
- Kim, T.; Muller, C. Two-stage quantile regression when the first stage is based on quantile regression. Econ. J. 2004, 7, 218–231. [Google Scholar] [CrossRef]
- McMillen, D.P. Quantile Regression for Spatial Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Huang, H.; Song, B.; Xu, P.; Zeng, Q.; Lee, J.; Abdel-Aty, M. Macro and micro models for zonal crash prediction with application in hot zones identification. J. Transp. Geogr. 2016, 54, 248–256. [Google Scholar] [CrossRef]
- Castillo-Manzano, J.I.; Castro-Nuño, M.; López-Valpuesta, L.; Vassallo, F.V. The complex relationship between increases to speed limits and traffic fatalities: Evidence from a meta-analysis. Saf. Sci. 2019, 111, 287–297. [Google Scholar] [CrossRef]
- Lee, C.; Abdel-Aty, M.; Park, J.; Wang, J.-H. Development of crash modification factors for changing lane width on roadway segments using generalized nonlinear models. Accid. Anal. Prev. 2015, 76, 83–91. [Google Scholar] [CrossRef]
- Vernon, D.D.; Cook, L.J.; Peterson, K.J.; Dean, J.M. Effect of repeal of the national maximum speed limit law on occurrence of crashes, injury crashes, and fatal crashes on Utah highways. Accid. Anal. Prev. 2004, 36, 223–229. [Google Scholar] [CrossRef]
- Asadi-Shekari, Z.; Moeinaddini, M.; Shah, M.Z. A pedestrian level of service method for evaluating and promoting walking facilities on campus streets. Land Use Policy 2014, 38, 175–193. [Google Scholar] [CrossRef]
- Moeinaddini, M.; Asadi-Shekari, Z.; Sultan, Z.; Shah, M.Z. Analyzing the relationships between the number of deaths in road accidents and the work travel mode choice at the city level. Saf. Sci. 2015, 72, 249–254. [Google Scholar] [CrossRef]
| Variables | Descriptions | Min | Average | Max | S.D. |
|---|---|---|---|---|---|
| Dependent Variables | |||||
| TCR | Total crash rate | 0.000 | 0.449 | 15.352 | 0.769 |
| I-F_CR | Injury and fatal crash rate | 0.000 | 2.231 | 100.001 | 4.353 |
| Independent Variables | |||||
| Education | Percent graduate high school or higher aged over 16 years old in each CT | 0.000 | 80.058 | 100.000 | 13.922 |
| PD | The number of people per km2 in each CT (in thousands) | 0.000 | 20.870 | 98.924 | 14.092 |
| P_YOU | Percent of youth (aged under 19) in each CT | 0.000 | 22.779 | 67.100 | 8.196 |
| P_ELD | Percent of elderly (aged over 60) in each CT | 0.000 | 19.139 | 100.000 | 8.444 |
| MHC | Median household incomes in each CT (in thousands / dollars) | 0.000 | 62.479 | 250.000 | 32.923 |
| N_VHU | The number of vacant housing units in each CT | 0.000 | 8.539 | 100.000 | 6.375 |
| CWC | Percent of people who commute to work by car in each CT | 0.000 | 27.976 | 100.000 | 17.969 |
| CWPT | Percent of people who commute to work by public transit in each CT | 0.000 | 55.601 | 100.000 | 16.317 |
| CWF | Percent of people who commute to work by foot in each CT | 0.000 | 9.157 | 100.000 | 9.563 |
| MCT | Mean commute time in each CTs (minutes) | 0.000 | 40.923 | 73.900 | 8.833 |
| P_COM | Percent of area used for commercial purpose in each CT | 0.000 | 0.234 | 1.000 | 0.202 |
| P_RES_L | Percent of area used for residential purpose in each CT | 0.000 | 0.726 | 1.000 | 0.204 |
| P_GAR | Percent of area used for garage purpose in each CT | 0.000 | 0.017 | 0.462 | 0.035 |
| P_IND | Percent of area used for industrial purpose in each CT | 0.000 | 0.017 | 0.856 | 0.057 |
| P_ENT_I | The entropy index used to measure the land use diversity in each CT | 0.000 | 0.547 | 1.234 | 0.240 |
| DKMT | Daily vehicle kilometer travelled in each CT (106 vehicle.km) | 0.000 | 0.411 | 5.489 | 0.580 |
| RD | The road length per km2 in each CT (km−1) | 2.435 | 96.239 | 319.955 | 29.254 |
| P_SL_20 | Percent of segment length posted speed 20 mph to total length in each CT | 0.000 | 0.032 | 1.000 | 0.136 |
| P_SL_25 | Percent of segment length posted speed 25 mph to total length in each CT | 0.000 | 0.904 | 1.000 | 0.185 |
| P_SL_30 | Percent of segment length with posted speed 30 mph to total length in each C | 0.000 | 0.012 | 0.508 | 0.042 |
| P_SL_35 | Percent of segment length with posted speed 35 mph to total length in each CT | 0.000 | 0.003 | 0.396 | 0.024 |
| P_SL_40 | Percent of segment length with posted speed 40 mph to total length in each CT | 0.000 | 0.005 | 0.530 | 0.037 |
| P_SL_45 | Percent of segment length with posted speed 45 mph to total length in each CT | 0.000 | 0.005 | 0.482 | 0.030 |
| P_SL_50 | Percent of segment length with posted speed 50 mph to total length in each CT | 0.000 | 0.023 | 0.527 | 0.064 |
| Variables | Total Crash Rate | Fatal-Plus-Injury Crash Rate | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| q = 0.1 | q = 0.3 | q = 0.5 | q = 0.7 | q = 0.9 | q = 0.1 | q = 0.3 | q = 0.5 | q = 0.7 | q = 0.9 | |
| PD | 0.554 ** (0.0014) | 1.131 *** (0.002) | 1.571 *** (0.0026) | 2.240 *** (0.004) | 3.390 ** (0.004) | 0.076 * (0.0003) | 0.174 ** (0.0004) | 0.312 *** (0.0006) | 0.431 *** (0.0009) | 0.680 * (0.003) |
| P_ELD | −0.001 (0.002) | −0.003 * (0.002) | −0.003 (0.0034) | −0.003 (0.006) | −0.006 (0.007) | 0.000 (0.0003) | 0.000 (0.0006) | −0.000 (0.008) | 0.001 (0.001) | 0.002 (0.002) |
| CWC | −0.007 ** (0.001) | −0.013 *** (0.0017) | −0.014 *** (0.0023) | −0.014 * (0.0034) | −0.004 (0.004) | −0.001 *** (0.0003) | −0.002 *** (0.0004) | −0.003 *** (0.0005) | −0.002 (0.0009) | −0.004 (0.002) |
| CWF | 0.002 * (0.002) | 0.003 (0.0018) | 0.004 ** (0.0033) | 0.007 ** (0.0044) | −0.001 (0.0048) | −0.000 (0.0004) | 0.000 (0.0004) | 0.000 (0.0008) | −0.000 (0.0012) | −0.004 (0.002) |
| P_RES_L | −0.003 ** (0.086) | 0.001 (0.108) | 0.000 (0.161) | −0.003 (0.272) | −0.03 ** (0.303) | 0.001 (0.016) | 0.000 (0.028) | 0.000 (0.0416) | −0.001 (0.069) | −0.004 ** (0.191) |
| P_GAR | 0.170 ** (0.608) | 0.314 ** (0.847) | 0.300 (0.992) | 0.712 ** (1.723) | 0.942 (1.615) | 0.040 ** (0.119) | 0.065 ** (0.249) | 0.100 ** (0.191) | 0.141 * (0.318) | 0.231 (1.095) |
| DVMT | −1.145 ** (0.058) | −1.712 * (0.065) | −3.252 *** (0.073) | −2.482 (0.086) | −2.756 (0.086) | −0.150 (0.011) | −0.413 * (0.014) | −0.458 ** (0.014) | −0.264 (0.019) | −0.789 (0.056) |
| P_SL_25 | −0.633 *** (0.105) | −0.834 *** (0.116) | −1.034 *** (0.214) | −1.323 *** (0.287) | −1.530 *** (0.271) | −0.102 *** (0.027) | −0.156 *** (0.035) | −0.199 *** (0.032) | −0.242 *** (0.056) | −0.274 *** (0.183) |
| P_S_45 | 0.321 ** (0.561) | 0.316 ** (0.474) | 0.178 (0.649) | 0.163 (0.779) | 0.532 (0.946) | 0.087 ** (0.098) | 0.081 ** (0.125) | 0.069 ** (0.113) | 0.008 (0.226) | 0.166 (0.754) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Gao, F.; Liu, X.; Tang, J. A Spatial Autoregressive Quantile Regression to Examine Quantile Effects of Regional Factors on Crash Rates. Sensors 2022, 22, 5. https://doi.org/10.3390/s22010005
Yu T, Gao F, Liu X, Tang J. A Spatial Autoregressive Quantile Regression to Examine Quantile Effects of Regional Factors on Crash Rates. Sensors. 2022; 22(1):5. https://doi.org/10.3390/s22010005
Chicago/Turabian StyleYu, Tianjian, Fan Gao, Xinyuan Liu, and Jinjun Tang. 2022. "A Spatial Autoregressive Quantile Regression to Examine Quantile Effects of Regional Factors on Crash Rates" Sensors 22, no. 1: 5. https://doi.org/10.3390/s22010005
APA StyleYu, T., Gao, F., Liu, X., & Tang, J. (2022). A Spatial Autoregressive Quantile Regression to Examine Quantile Effects of Regional Factors on Crash Rates. Sensors, 22(1), 5. https://doi.org/10.3390/s22010005






