Seismic Damage Identification Method for Curved Beam Bridges Based on Wavelet Packet Norm Entropy
Abstract
:1. Introduction
2. Basic Theory
2.1. Wavelet Packet Transform
2.2. Lp Norm
2.3. Information Entropy
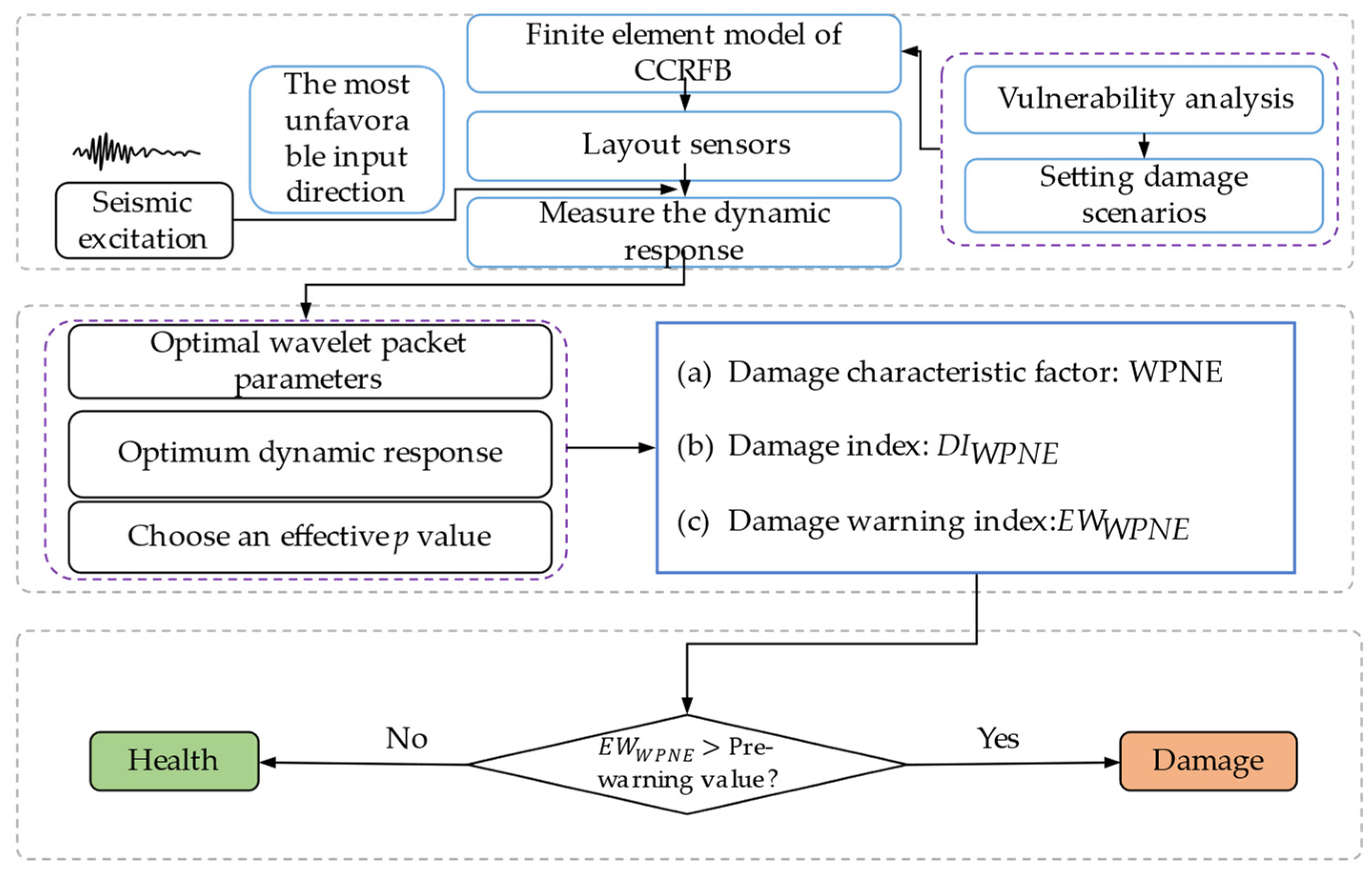
3. Damage Identification Method
3.1. Damage Identification Index
3.2. Damage Identification Steps
4. Dynamic Analysis of CCRFB
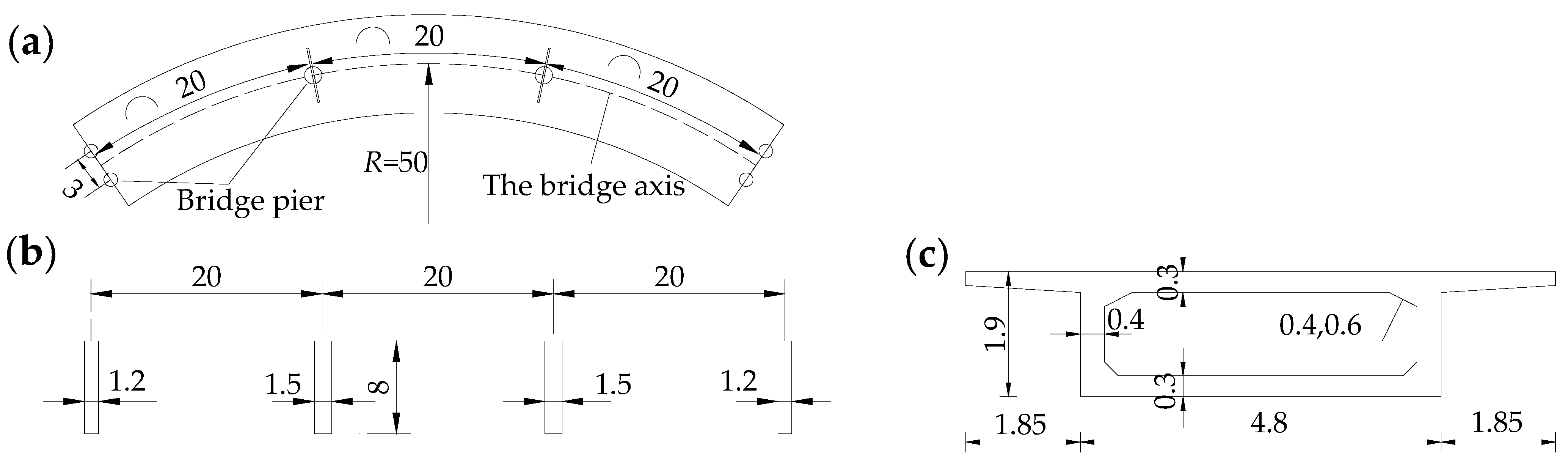
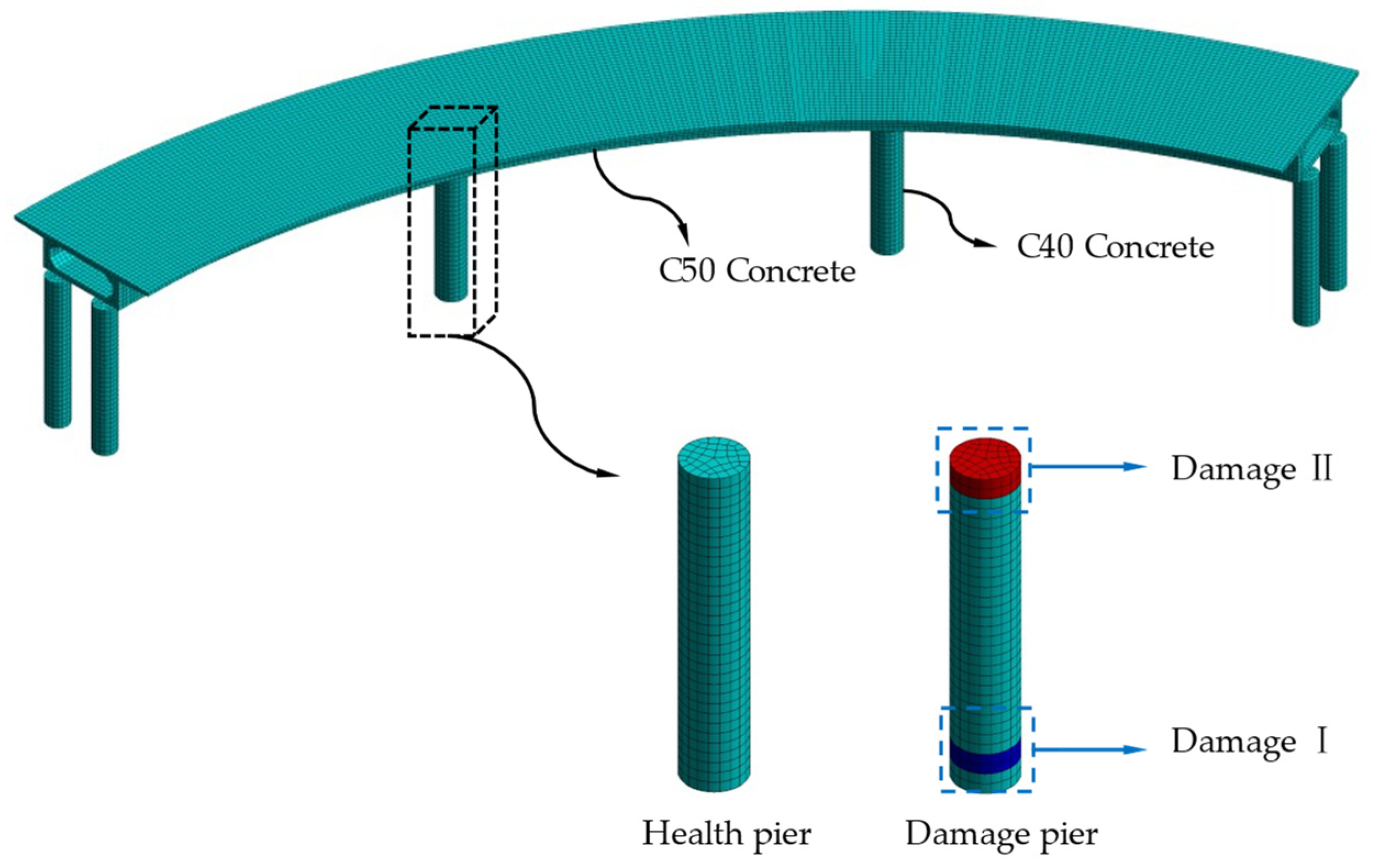
4.1. Establish a CCRFB Finite Element Model
4.2. Set Damage Scenarios
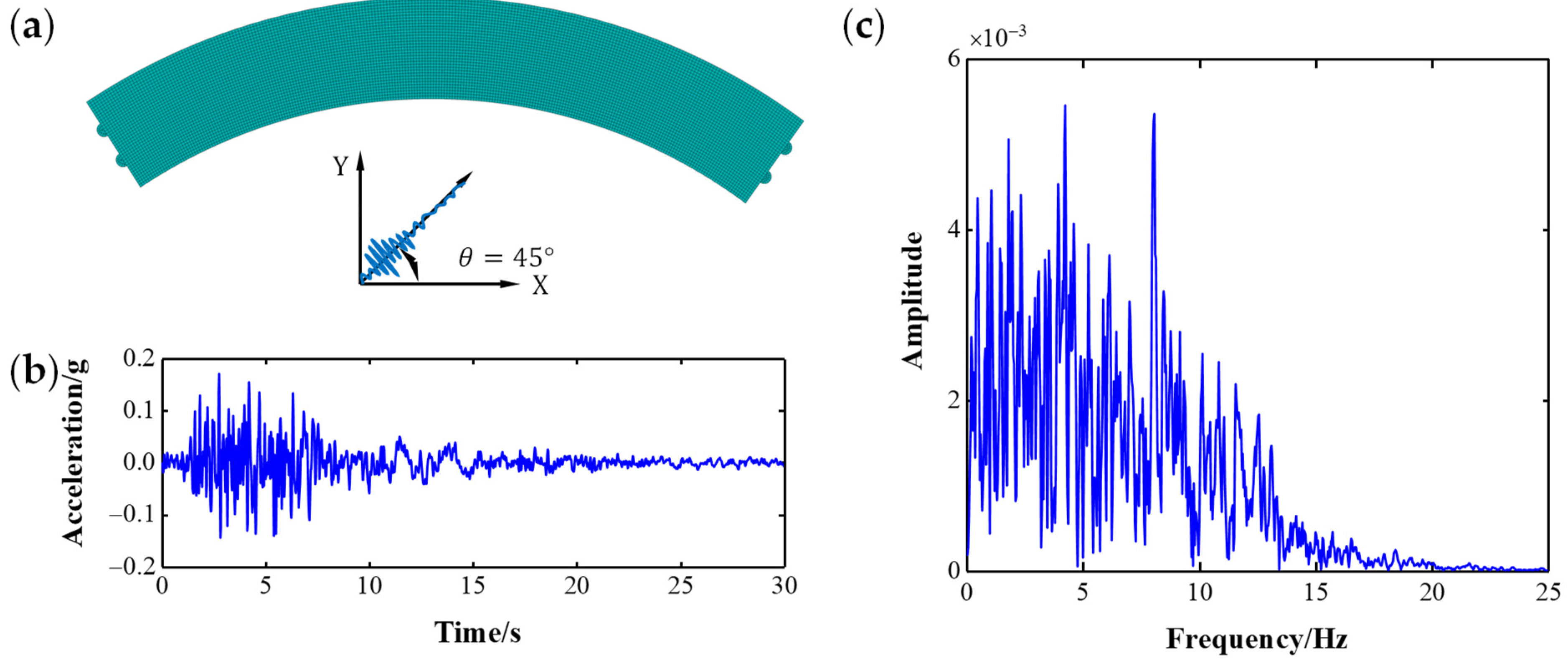
4.3. Enter Ground Motion Acceleration
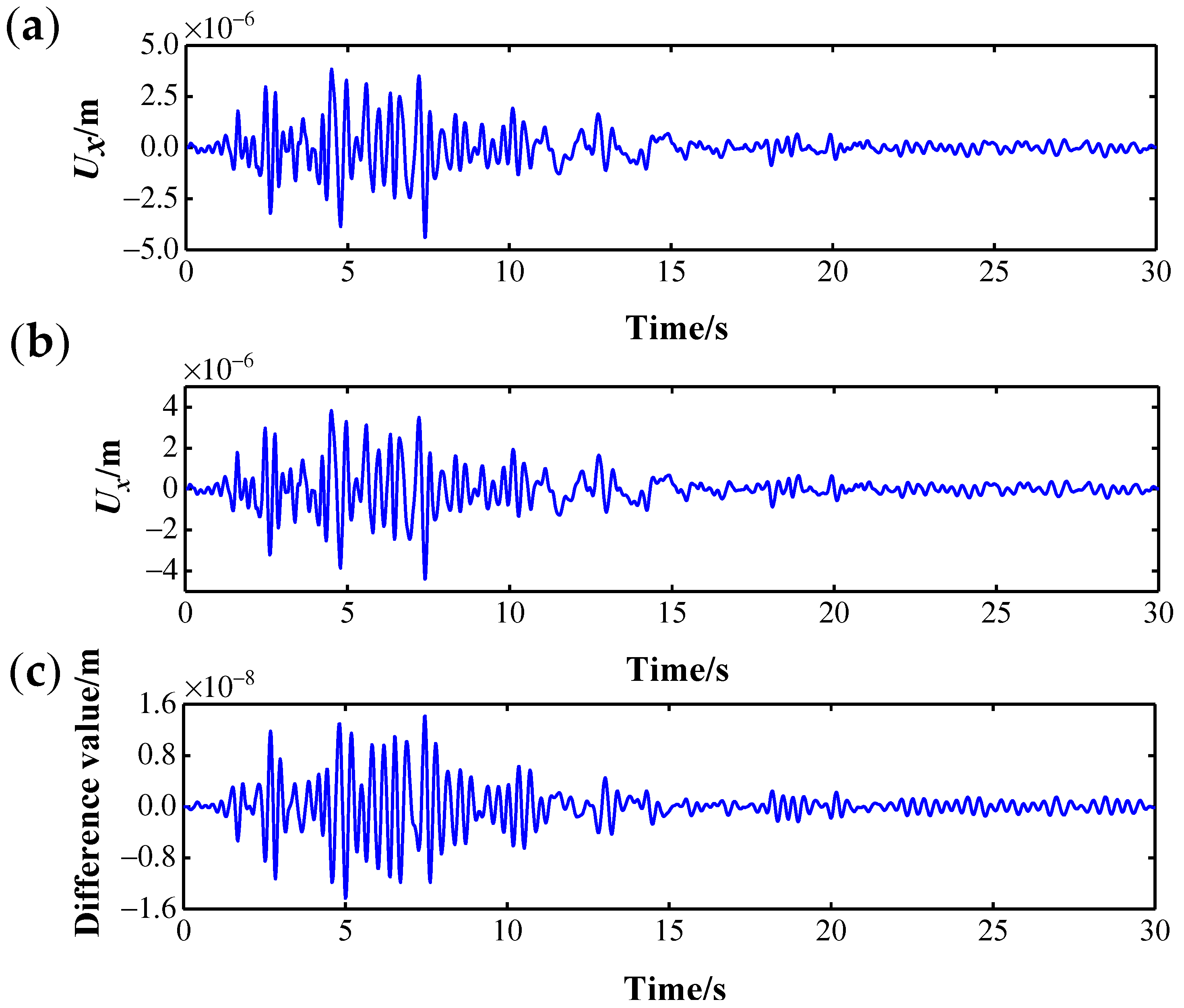
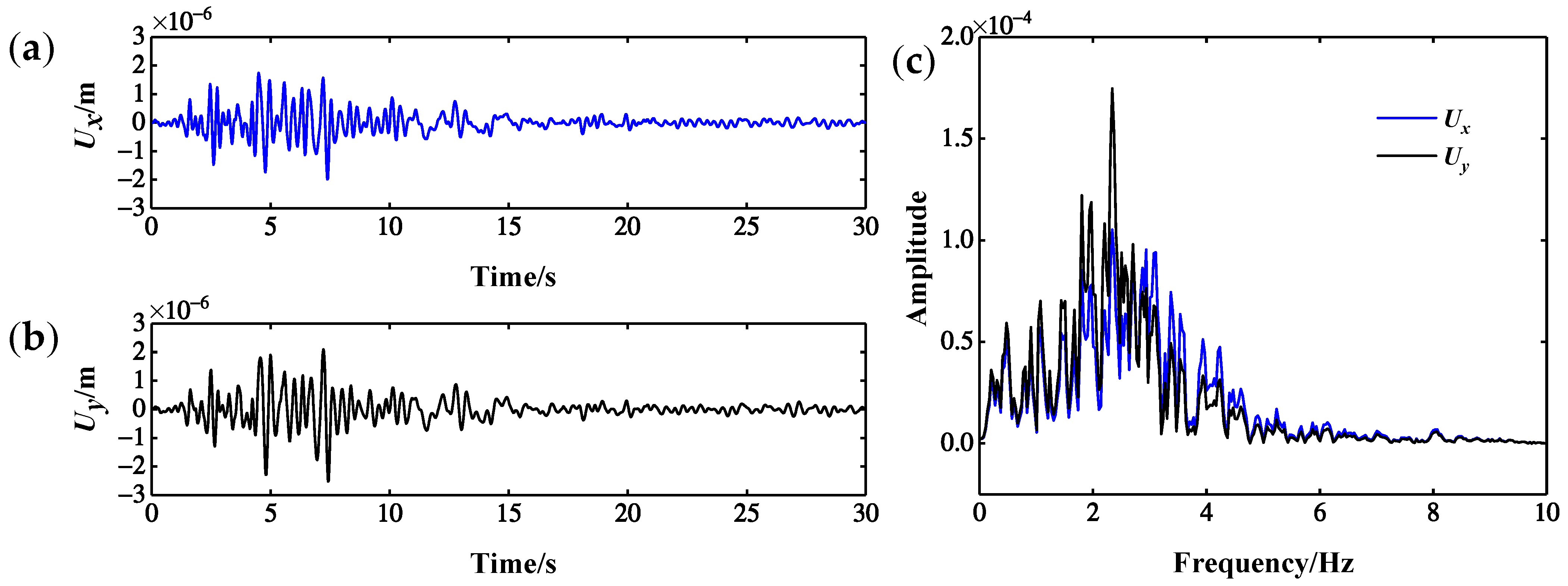
4.4. Measured Dynamic Response
5. Damage Identification for CCRFB
5.1. Choose Optimal Dynamic Response
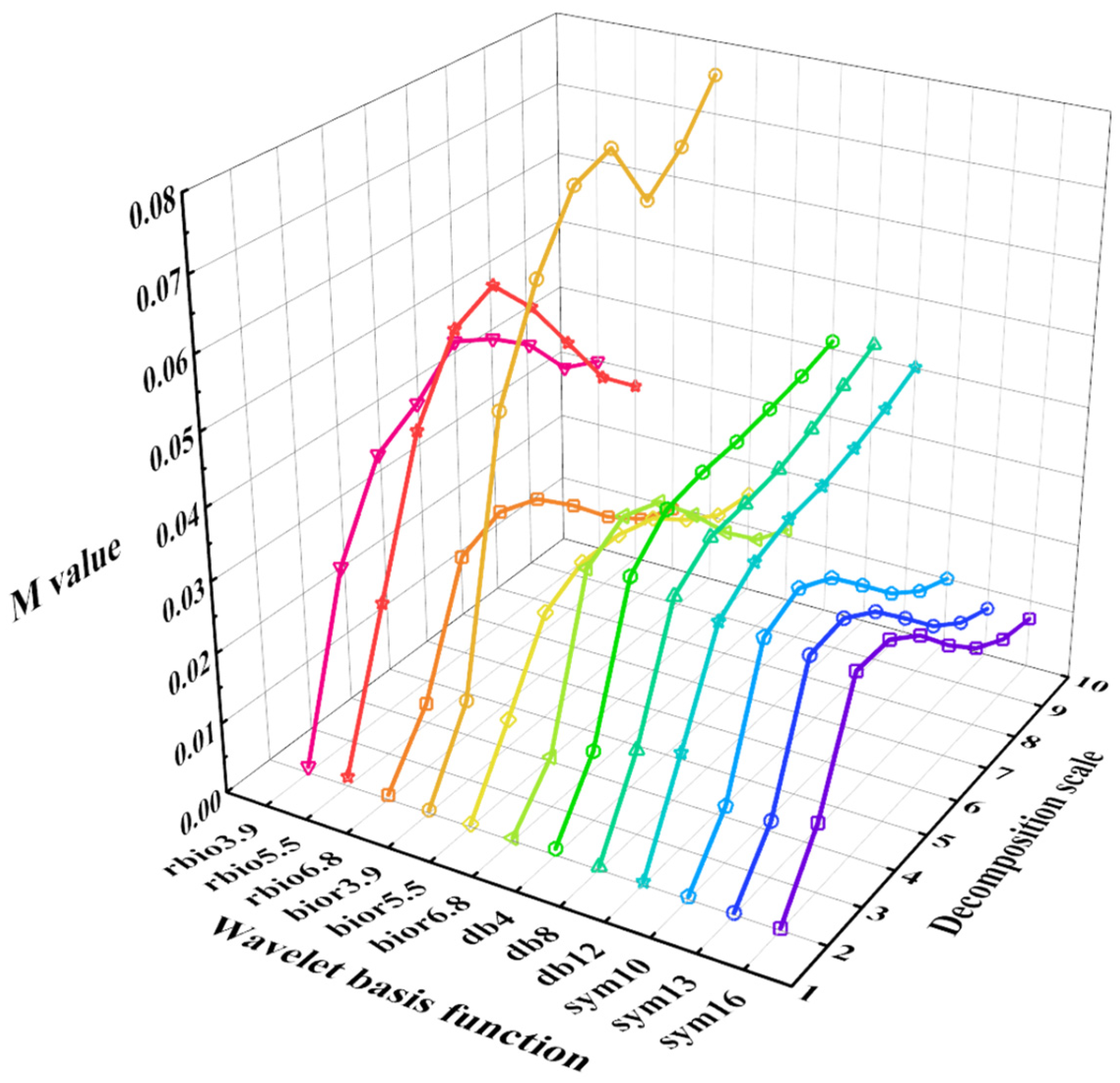
5.2. Select Optimal Wavelet Packet Parameters
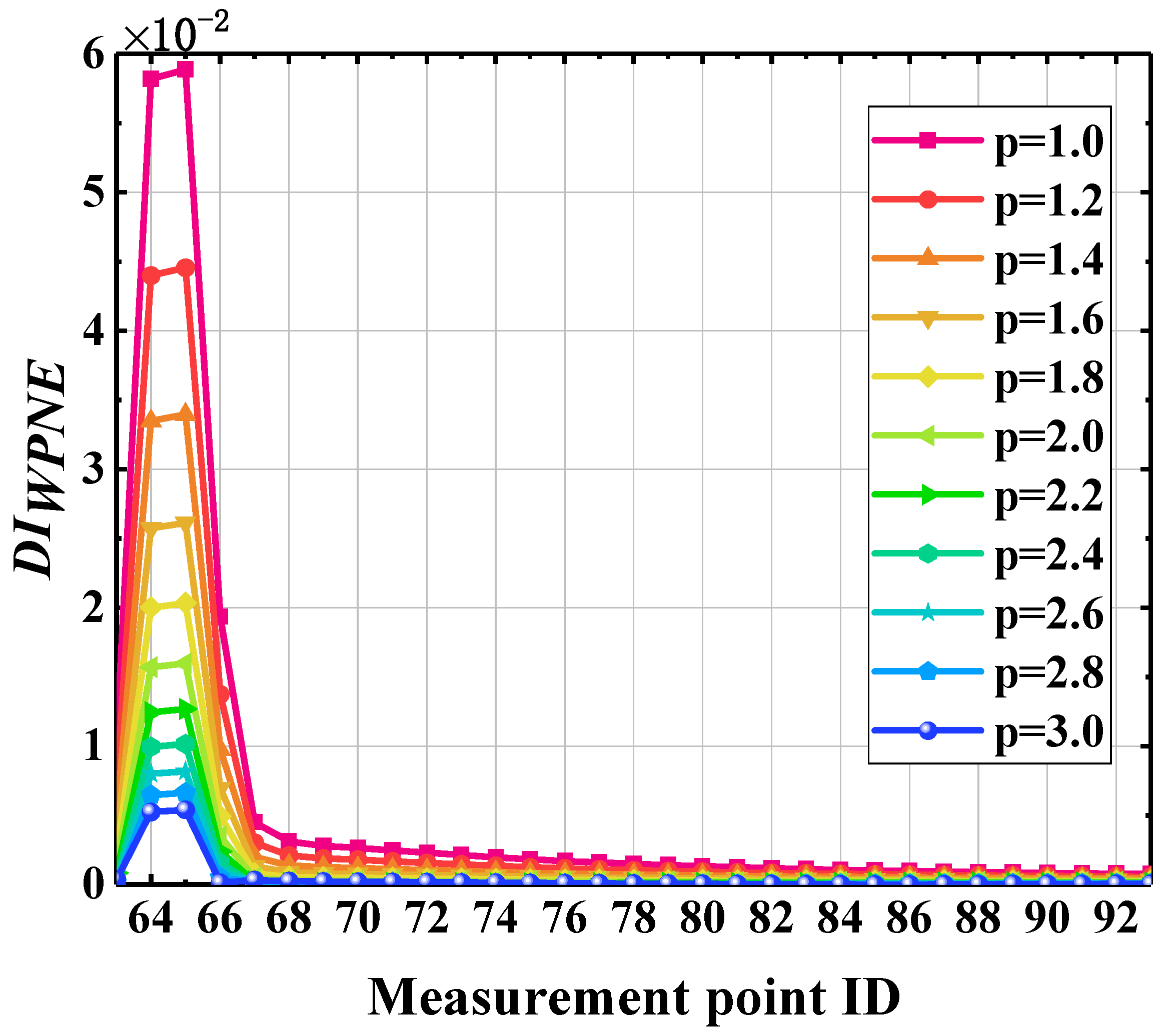
5.3. Select Valid p Values
5.4. Damage Identification Results
6. Discussion
6.1. Compare Identification Index Der
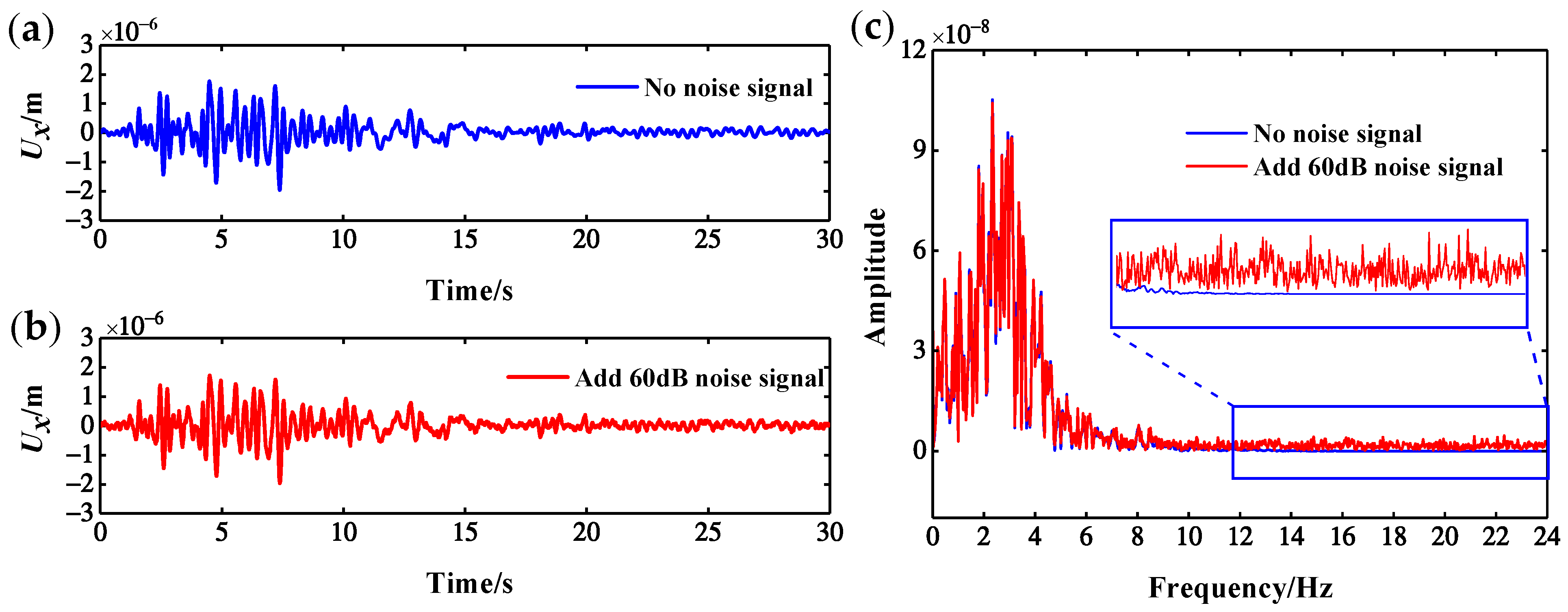
6.2. Noise Resistance Analysis
6.3. Effect of Seismic Excitation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiao, C.Y.; Liu, W.B.; Wu, S.W.; Gui, X.S.; Huang, J.F.; Long, P.H.; Li, W.F. Shake table experimental study of curved bridges with consideration of girder-to-girder collision. Eng. Struct. 2021, 237, 112216. [Google Scholar] [CrossRef]
- Ma, H.Y.; Sause, R.; Dong, J. Design of Horizontally Curved Steel Bridge Girders with Tubular Flanges. J. Bridge Eng. 2019, 24, 04019040. [Google Scholar] [CrossRef]
- Seo, J.; Linzell, D.G. Horizontally curved steel bridge seismic vulnerability assessment. Eng. Struct. 2012, 34, 21–32. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P.Z. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Liu, X.; Jin, B.Q.; Bai, Q.; Wang, Y.; Wang, D.; Wang, Y.C. Distributed Fiber-Optic Sensors for Vibration Detection. Sensors 2016, 16, 1164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, Z.R.; Zhou, J.X.; Wang, L.; Liu, J.K. Damage identification from static tests by eigenparameter decomposition and sparse regularization. Struct. Health Monit. 2020, 19, 1351–1374. [Google Scholar] [CrossRef]
- Vito, A. Experimental verification in static tests of a computational method for detecting the position of a defect. Eur. J. Environ. Civ. Eng. 2019, 15, 1–16. [Google Scholar] [CrossRef]
- Yazdanpanah, O.; Izadifard, R.A.; Dehestani, M. Static data based damage localization of beam-column structures considering axial load. Mech. Adv. Mater. Struc. 2020, 27, 1433–1450. [Google Scholar] [CrossRef]
- Guo, J.; Wang, L.; Takewaki, I. Static damage identification in beams by minimum constitutive relation error. Inverse Probl. Sci. Eng. 2019, 27, 1347–1371. [Google Scholar] [CrossRef]
- Miraglia, G.; Lenticchia, E.; Surace, C.; Ceravolo, R. Seismic damage identification by fitting the nonlinear and hysteretic dynamic response of monitored buildings. J. Civ. Struct. Health 2020, 10, 457–469. [Google Scholar] [CrossRef]
- Huang, T.X.; Schroder, K.U. Bayesian probabilistic damage characterization based on a perturbation model using responses at vibration nodes. Mech. Syst. Signal Process. 2020, 139, 106444. [Google Scholar] [CrossRef]
- Aras, F.; Akbas, T.; Eksi, H.; Ceribasi, S. Progressive Damage Analyses of Masonry Buildings by Dynamic Analyses. Int. J. Civ. Eng. 2020, 18, 903–917. [Google Scholar] [CrossRef]
- Mousavi, Z.; Varahram, S.; Ettefagh, M.M.; Sadeghi, M.H.; Razavi, S.N. Deep neural networks-based damage detection using vibration signals of finite element model and real intact state: An evaluation via a lab-scale offshore jacket structure. Struct. Health Monit. 2021, 20, 379–405. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Dai, X.X.; Chen, W.F. A piecewise constant level set method for damage identification of continuum structures based on natural frequencies. Struct. Multidiscip. Optim. 2019, 60, 2477–2491. [Google Scholar] [CrossRef]
- Gkoktsi, K.; Giaralis, A. A compressive MUSIC spectral approach for identification of closely-spaced structural natural frequencies and post-earthquake damage detection. Probabilist. Eng. Mech. 2020, 60, 103030. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Z.; Chen, J.L. Damage identification method based on continuous wavelet transform and mode shapes for composite laminates with cutouts. Compos. Struct. 2018, 191, 12–23. [Google Scholar] [CrossRef]
- Jahangiri, M.; Najafgholipour, M.A.; Dehghan, S.M.; Hadianfard, M.A. The efficiency of a novel identification method for structural damage assessment using the first vibration mode data. J. Sound Vib. 2019, 458, 1–16. [Google Scholar] [CrossRef]
- Ciambella, J.; Pau, A.; Vestroni, F. Modal curvature-based damage localization in weakly damaged continuous beams. Mech. Syst. Signal Process. 2019, 121, 171–182. [Google Scholar] [CrossRef]
- Yang, Z.B.; Radzienski, M.; Kudela, P.; Ostachowicz, W. Two-dimensional modal curvature estimation via Fourier spectral method for damage detection. Compos. Struct. 2016, 148, 155–167. [Google Scholar] [CrossRef]
- Dewangan, P.; Parey, A.; Hammami, A.; Chaari, F.; Haddar, M. Damage detection in wind turbine gearbox using modal strain energy. Eng. Fail. Anal. 2020, 107, 104228. [Google Scholar] [CrossRef]
- Yang, X.M.; Ouyang, H.J.; Guo, X.L.; Cao, S.C. Modal Strain Energy-Based Model Updating Method for Damage Identification on Beam-Like Structures. J. Struct. Eng. 2020, 146, 11. [Google Scholar] [CrossRef]
- Zhou, W.L.; Chelidze, D. Generalized eigenvalue decomposition in time domain modal parameter identification. J. Vib. Acoust. 2008, 130, 011001. [Google Scholar] [CrossRef]
- Mohammadi, N.; Nasirshoaibi, M. Modal parameter identification of a three-storey structure using frequency domain techniques FDD and EFDD and time domain technique SSI: Experimental studies and simulations. J. Vibroeng. 2017, 19, 2759–2776. [Google Scholar] [CrossRef]
- Song, Y.; Liang, L.; Du, Y.L.; Sun, B.C. Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration. Appl. Sci. 2020, 10, 1613. [Google Scholar] [CrossRef] [Green Version]
- Abdulkareem, M.; Bakhary, N.; Vafaei, M.; Noor, N.M.; Mohamed, R.N. Application of two-dimensional wavelet transform to detect damage in steel plate structures. Measurement 2019, 146, 912–923. [Google Scholar] [CrossRef]
- Xin, Y.; Hao, H.; Li, J. Operational modal identification of structures based on improved empirical wavelet transform. Struct. Control Health 2019, 26, 3. [Google Scholar] [CrossRef]
- Zhu, L.F.; Ke, L.L.; Zhu, X.Q.; Xiang, Y.; Wang, Y.S. Crack identification of functionally graded beams using continuous wavelet transform. Compos. Struct. 2019, 210, 473–485. [Google Scholar] [CrossRef]
- Guo, J.; Guan, D.Q.; Zhao, J.W. Structural Damage Identification Based on the Wavelet Transform and Improved Particle Swarm Optimization Algorithm. Adv. Civ. Eng. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, D.Y.; Tang, H.S.; Han, X. Experimental study of grout defect identification in precast column based on wavelet packet analysis. Int. J. Distrib. Sens. Netw. 2019, 15, 11. [Google Scholar] [CrossRef]
- Zhao, B.N.; Lei, D.; Fu, J.J.; Yang, L.Q.; Xu, W.X. Experimental study on micro-damage identification in reinforced concrete beam with wavelet packet and DIC method. Constr. Build. Mater. 2019, 210, 338–346. [Google Scholar] [CrossRef]
- Naderpour, H.; Fakharian, P. A synthesis of peak picking method and wavelet packet transform for structural modal identification. KSCE J. Civ. Eng. 2016, 20, 2859–2867. [Google Scholar] [CrossRef]
- Rajendran, P.; Srinivasan, S.M. Identification of Added Mass in the Composite Plate Structure Based on Wavelet Packet Transform. Strain 2016, 52, 14–25. [Google Scholar] [CrossRef]
- Chen, Y.J.; Xie, S.L.; Zhang, X.N. Damage identification based on wavelet packet analysis method. Int. J. Appl. Electromagn. 2016, 52, 407–414. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, R.W.; Zhou, Q.B. Damage Identification Using Wavelet Packet Transform and Neural Network Ensembles. Int. J. Struct. Stab. Dyn. 2018, 18, 1850148. [Google Scholar] [CrossRef]
- Wang, P.B.; Shi, Q.H. Damage Identification in Structures Based on Energy Curvature Difference of Wavelet Packet Transform. Shock Vib. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q.; Tian, Y.J.; Li, X.Y.; Wu, S.Q. Statistical damage classification method based on wavelet packet analysis. Struct. Eng. Mech. 2013, 46, 459–486. [Google Scholar] [CrossRef]
- Ren, W.X.; Sun, Z.S.; Xia, Y.; Hao, H.; Deeks, A.J. Damage identification of shear connectors with wavelet packet energy: Laboratory test study. J. Struct. Eng. ASCE 2008, 134, 832–841. [Google Scholar] [CrossRef]
- Ren, W.X.; Sun, Z.S. Structural damage identification by using wavelet entropy. Eng. Struct. 2008, 30, 2840–2849. [Google Scholar] [CrossRef]
- Diao, Y.S.; Zhang, X.C.; Sun, Z.F.; Guo, K.Z.; Wang, Y.M. Wavelet entropy based structural damage identification under seismic excitation. Smart Mater. Struct. 2018, 27, 105002. [Google Scholar] [CrossRef]
- Lee, S.G.; Yun, G.J.; Shang, S. Reference-free damage detection for truss bridge structures by continuous relative wavelet entropy method. Struct. Health Monit. 2014, 13, 307–320. [Google Scholar] [CrossRef]
- Li, S.C.; Zhang, L.; Tang, J.; Ling, D.J.; Wang, P.X. Damage Identification in Timber Structures Based on Wavelet Singular Spectrum Entropy. Math. Probl. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Li, D.Y.; Cao, M.S.; Deng, T.F.; Zhang, S.X. Wavelet Packet Singular Entropy-Based Method for Damage Identification in Curved Continuous Girder Bridges under Seismic Excitations. Sensors 2019, 19, 4272. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.S.; Ding, Y.J.; Ren, W.X.; Wang, Q.; Ragulskis, M.; Ding, Z.C. HierarchicalWavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions. Appl. Sci. 2017, 7, 391. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Liao, X.F.; He, X.; Tang, R.Q.; Deng, W.W. Smoothing inertial neurodynamic approach for sparse signal reconstruction via L-p-norm minimization. Neural Netw. 2021, 140, 100–112. [Google Scholar] [CrossRef]
- Li, H.; Bao, Y.Q.; Ou, J.P. Structural damage identification based on integration of information fusion and shannon entropy. Mech. Syst. Signal Process. 2008, 22, 1427–1440. [Google Scholar] [CrossRef]
- Sha, G.G.; Radzienski, M.; Cao, M.S.; Ostachowicz, W. A novel method for single and multiple damage detection in beams using relative natural frequency changes. Mech. Syst. Signal Process. 2019, 132, 335–352. [Google Scholar] [CrossRef]
- Zhu, J.S.; Sun, Y.D. Wavelet packet energy based damage detection index for bridge. J. Vib. Meas. Diagn. 2015, 35, 715–721, (In Chinese, This article was included in EI). [Google Scholar] [CrossRef]
- Cao, M.S.; Qiao, P.Z. Integrated wavelet transform and its application to vibration mode shapes for the damage detection of beam-type structures. Smart Mater. Struct. 2008, 17, 055014. [Google Scholar] [CrossRef]
- Yazdanpanah, O.; Mohebi, B.; Yakhchalian, M. Selection of optimal wavelet-based damage-sensitive feature for seismic damage diagnosis. Measurement 2020, 154, 1–21. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, J.Y.; Cao, M.S.; Damjanovic, D.; Ostachowicz, W. Identification of instantaneous tension of bridge cables from dynamic responses: STRICT algorithm and applications. Mech. Syst. Signal Process. 2020, 142, 106729. [Google Scholar] [CrossRef]
- Li, D.Y.; Xu, Z.M.; Ostachowicz, W.; Cao, M.S.; Liu, J.Q. Identification of multiple cracks in noisy conditions using scale-correlation-based multiscale product of SWPT with laser vibration measurement. Mech. Syst. Signal Process. 2020, 145, 106889. [Google Scholar] [CrossRef]
- Yan, W.J.; Zhao, M.Y.; Sun, Q.; Ren, W.X. Transmissibility-based system identification for structural health Monitoring: Fundamentals, approaches, and applications. Mech. Syst. Signal Process. 2019, 117, 453–482. [Google Scholar] [CrossRef]


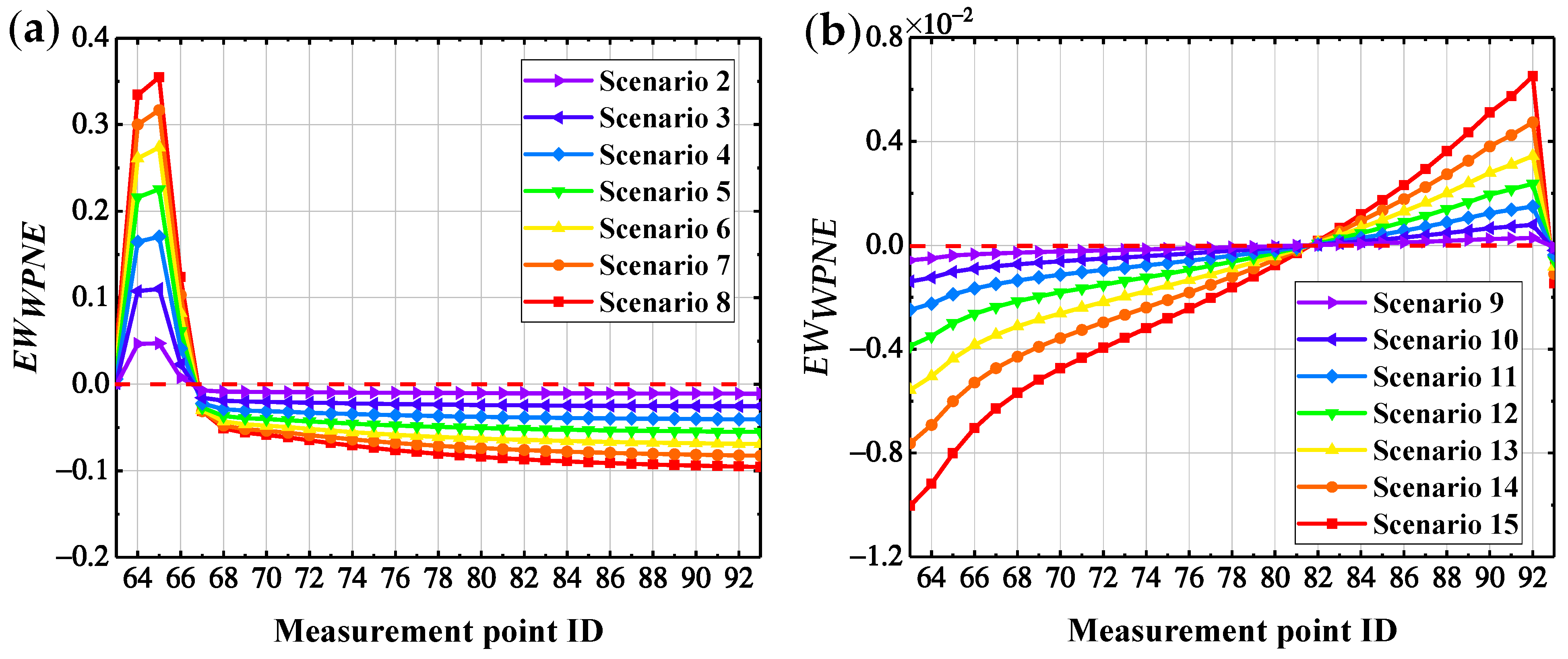
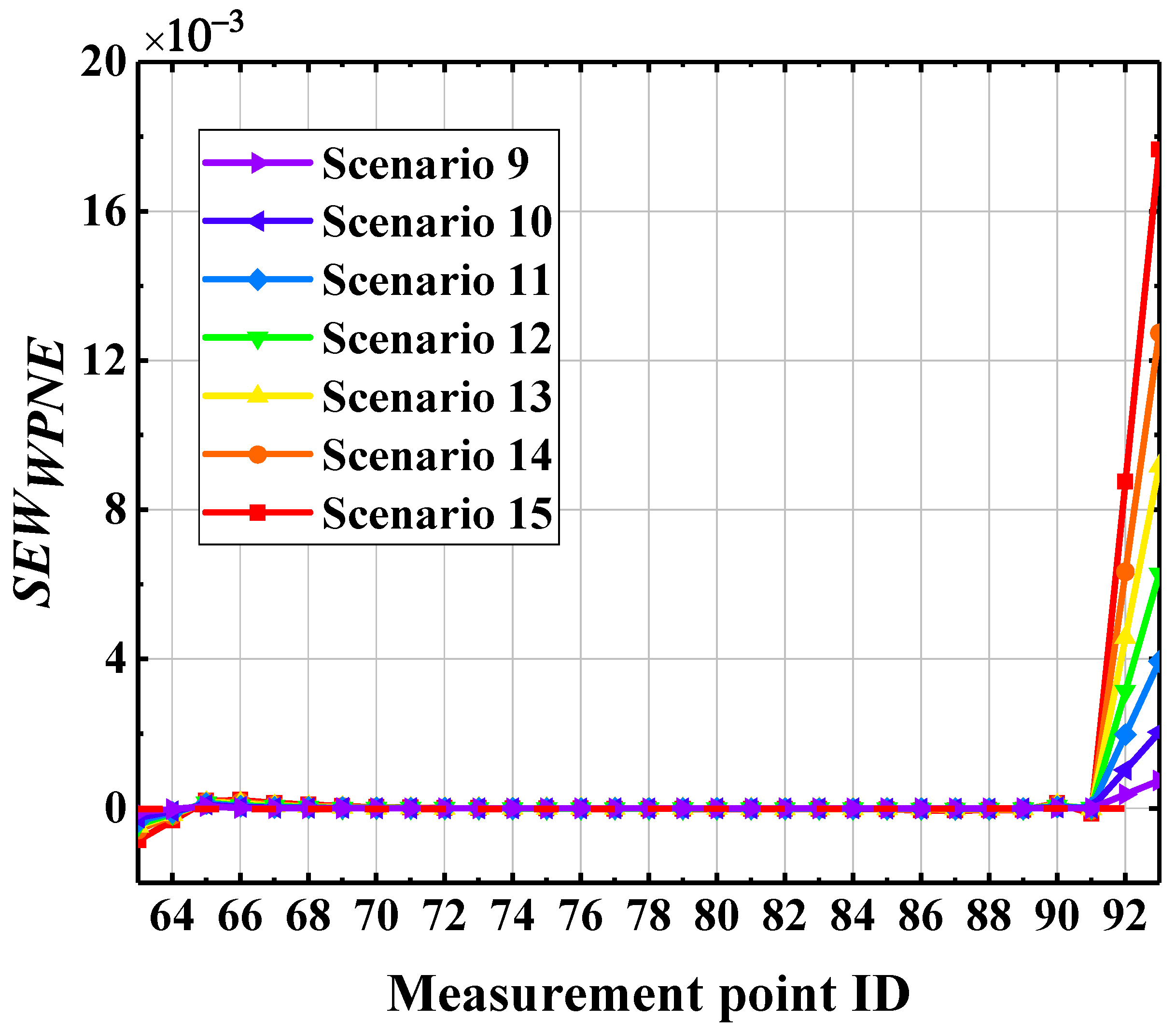
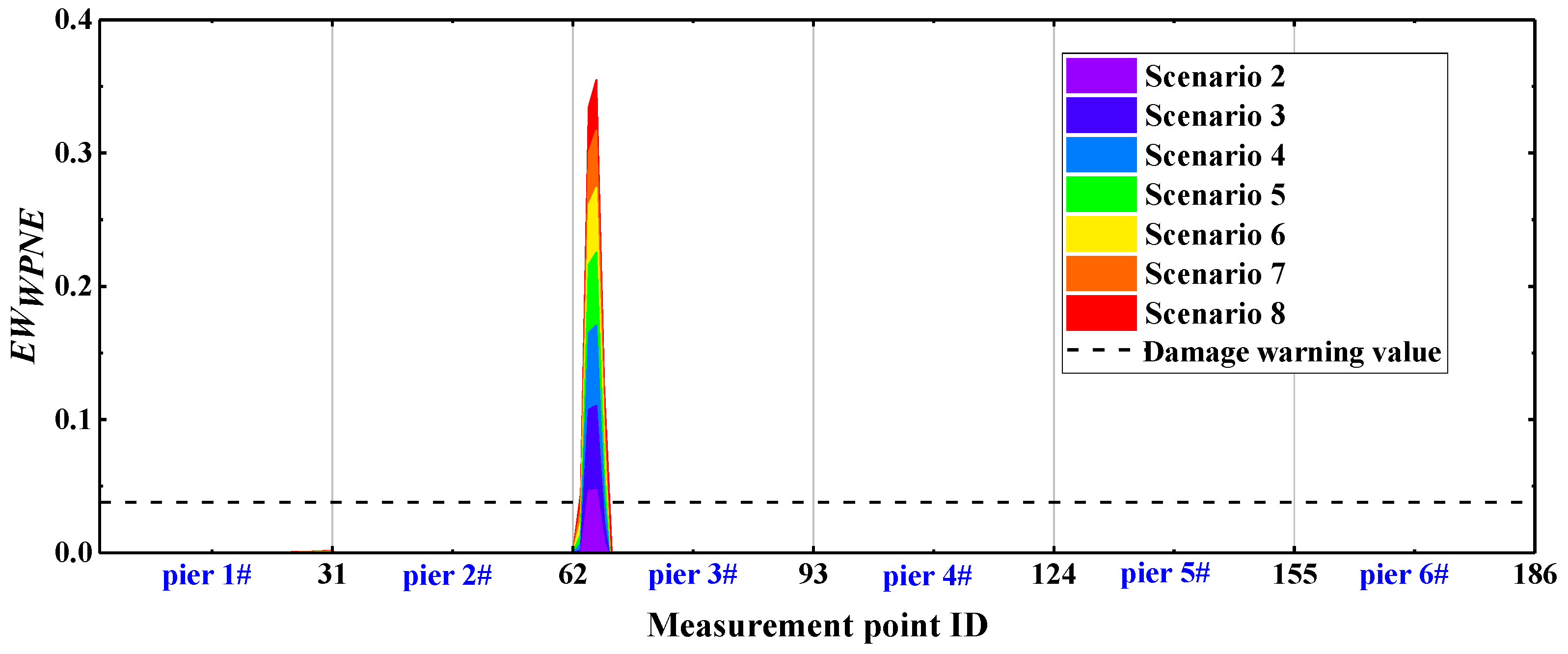
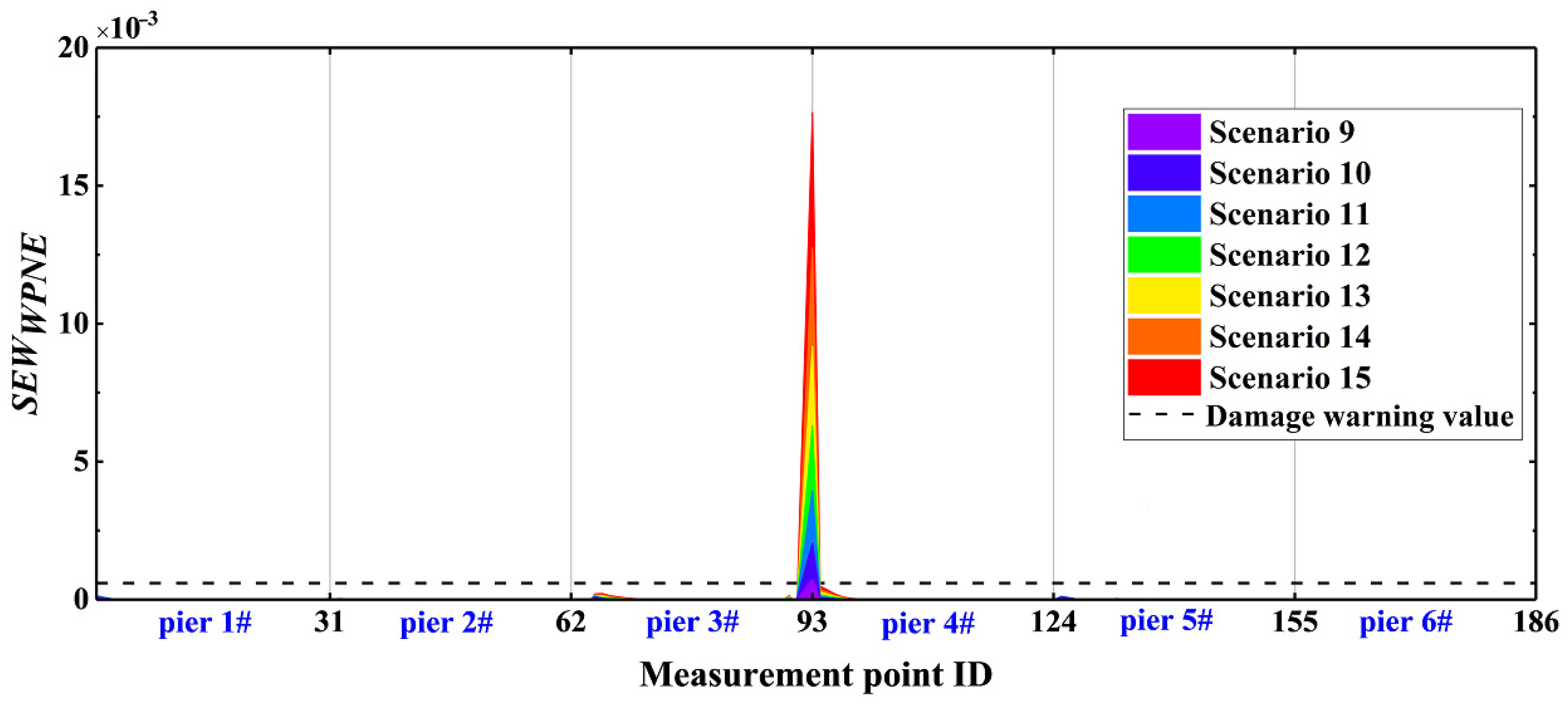
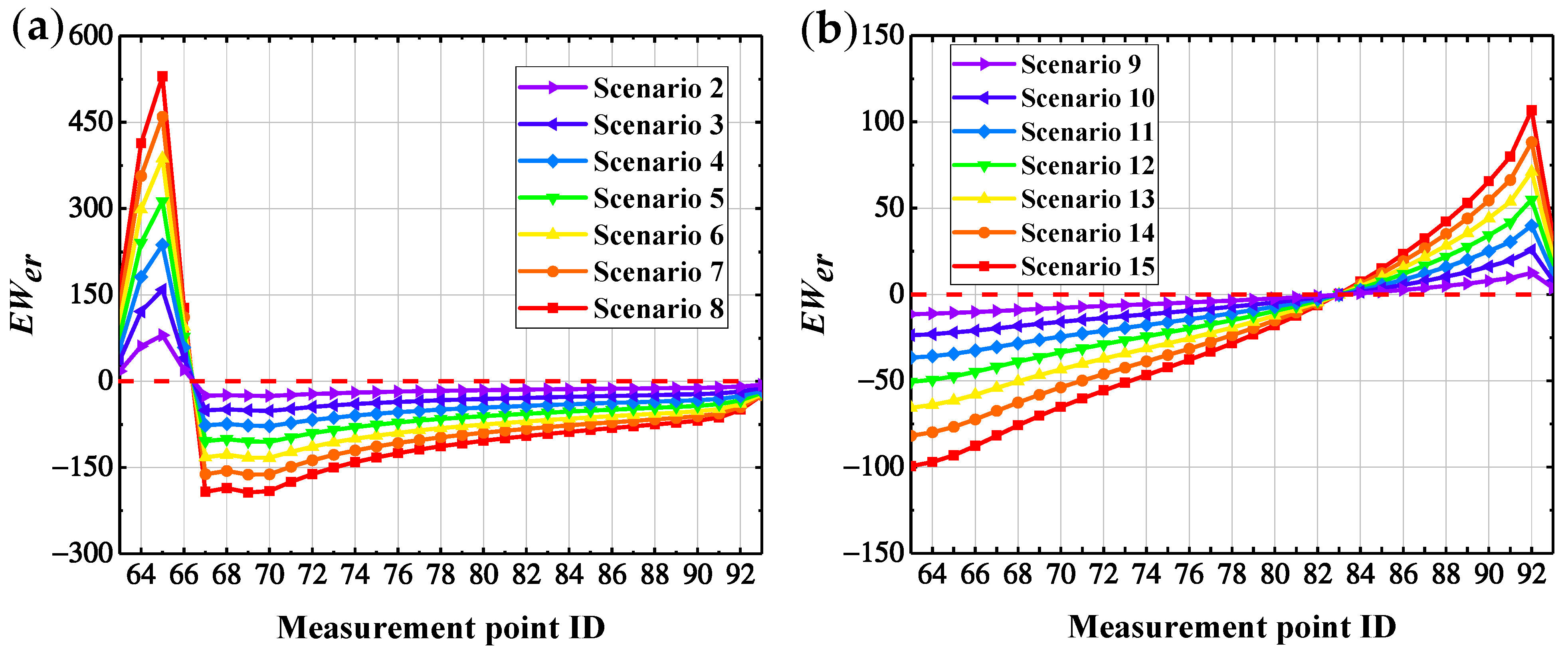
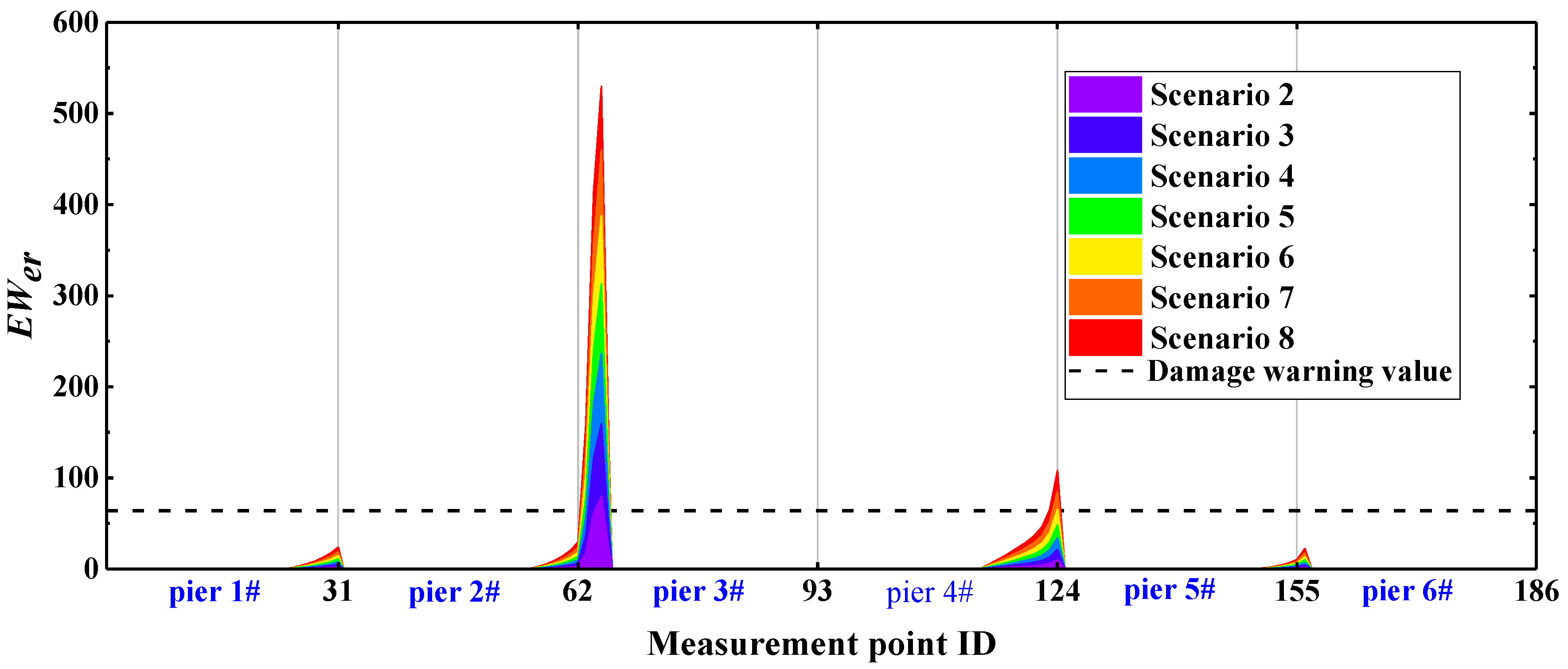
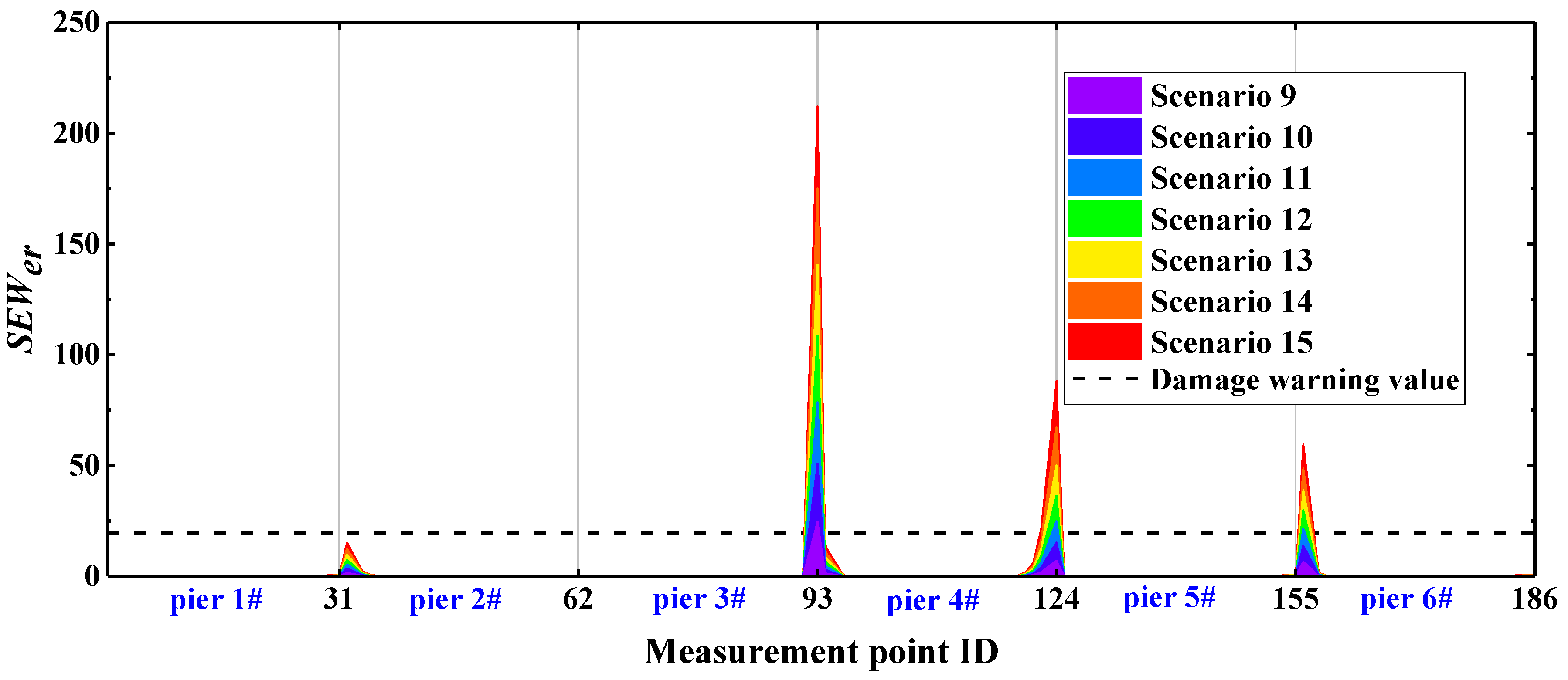
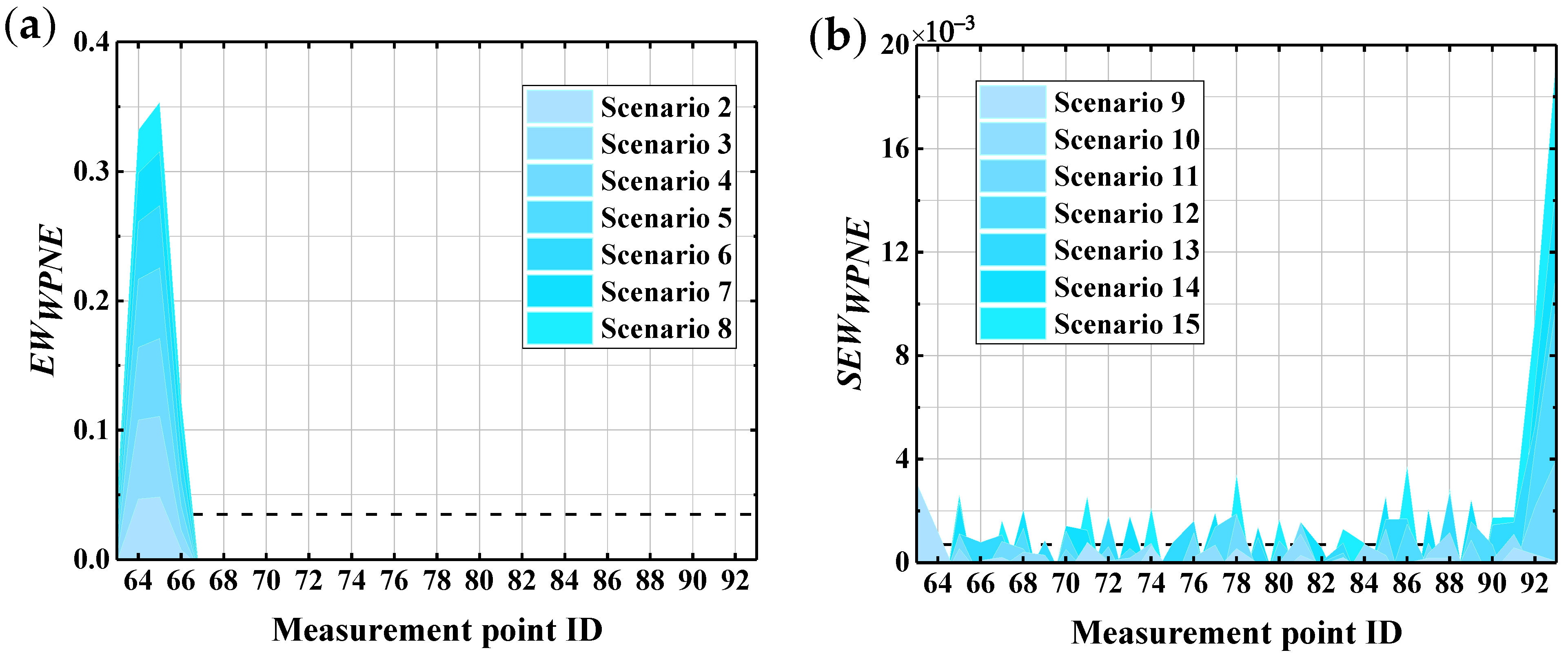

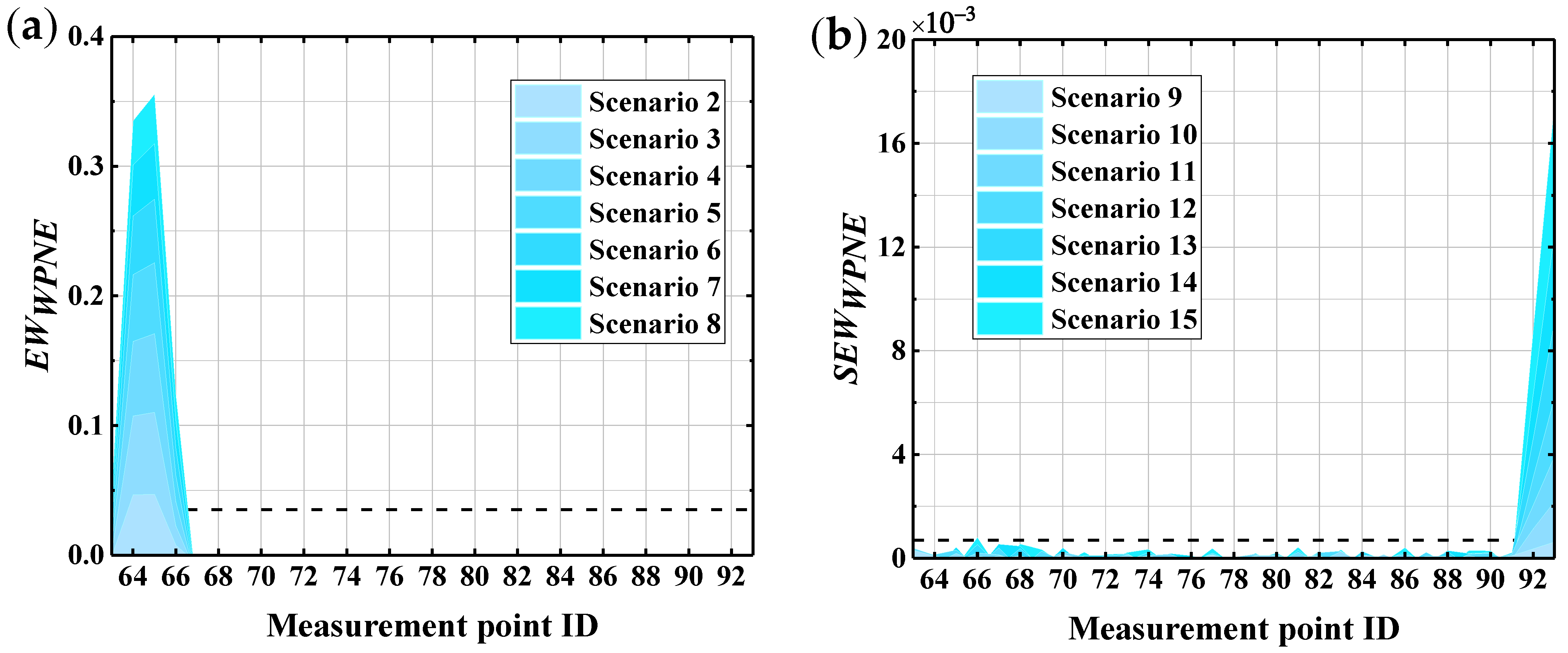
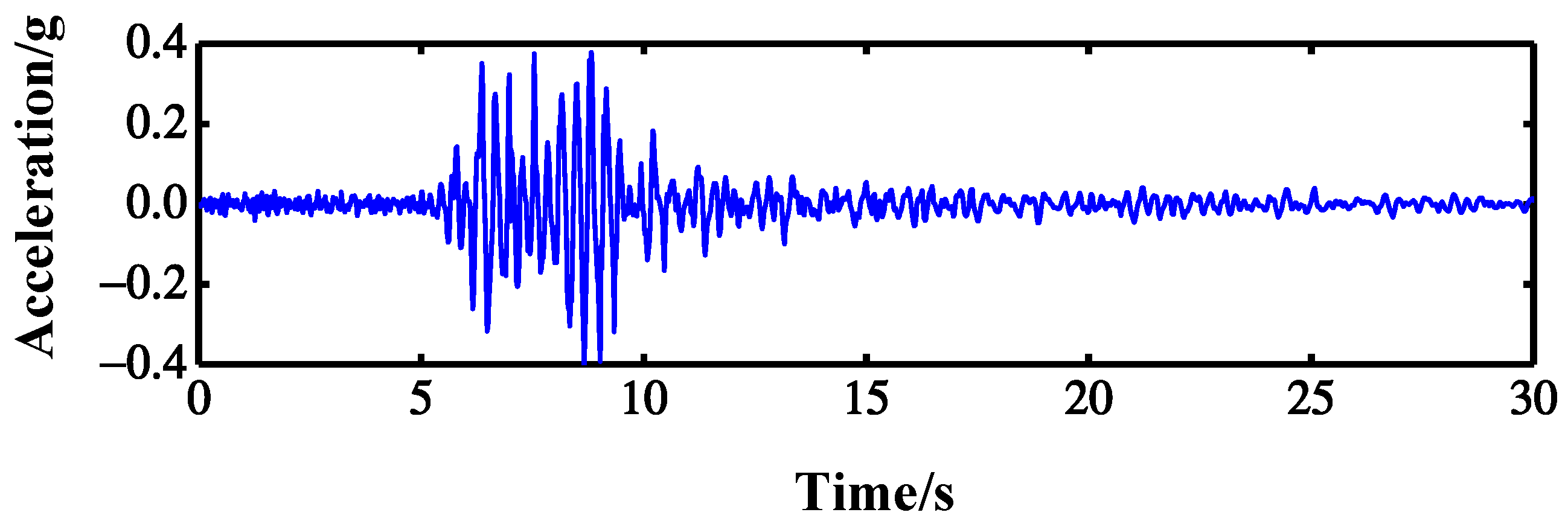
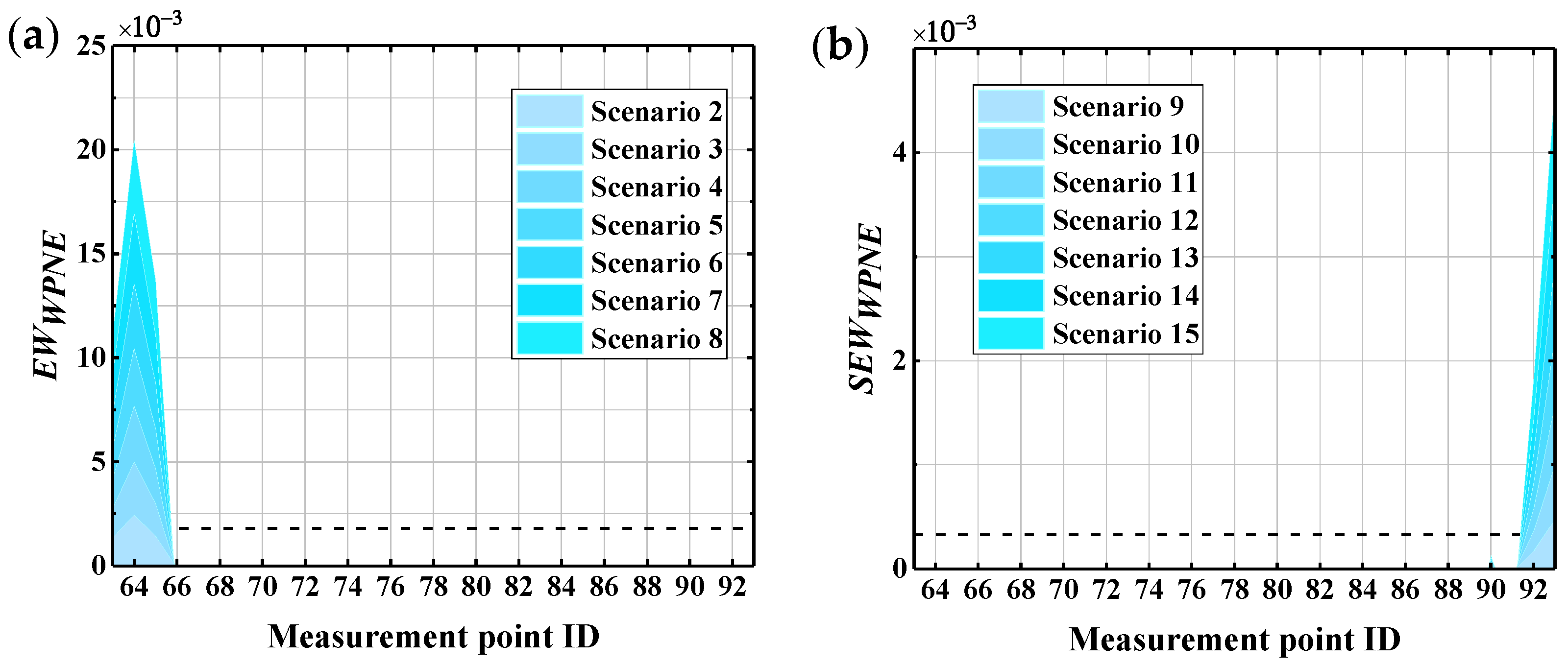
| Damage Location | Stiffness Reduction Rate | Damage Scenarios | Damage Location | Stiffness Reduction Rate | Damage Scenarios |
|---|---|---|---|---|---|
| I, II | 0% | 1 | |||
| I | 5% | 2 | II | 5% | 9 |
| I | 10% | 3 | II | 10% | 10 |
| I | 15% | 4 | II | 15% | 11 |
| I | 20% | 5 | II | 20% | 12 |
| I | 25% | 6 | II | 25% | 13 |
| I | 30% | 7 | II | 30% | 14 |
| I | 35% | 8 | II | 35% | 15 |
| Lower Damage I (EWWPNE) | Upper Damage II (SEWWPNE) | |
|---|---|---|
| Damage warning value | 3.8000 × 10−2 | 5.9645 × 10−4 |
| Scenario | MRR(%) | FRR(%) | NII(%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNR(dB) | SNR(dB) | SNR(dB) | ||||||||||
| 20 | 30 | 40 | 50 | 20 | 30 | 40 | 50 | 20 | 30 | 40 | 50 | |
| 2 | 8.92 | 2.03 | 0.00 | 0.00 | 14.42 | 7.76 | 2.56 | 0.00 | 77.95 | 90.37 | 97.44 | 100.00 |
| 3 | 5.21 | 1.70 | 0.00 | 0.00 | 10.27 | 5.47 | 0.80 | 0.00 | 85.06 | 92.92 | 99.20 | 100.00 |
| 4 | 1.09 | 0.04 | 0.00 | 0.00 | 8.71 | 3.28 | 0.10 | 0.00 | 90.29 | 96.68 | 99.90 | 100.00 |
| 5 | 0.02 | 0.00 | 0.00 | 0.00 | 3.55 | 1.29 | 0.00 | 0.00 | 96.43 | 98.71 | 100.00 | 100.00 |
| 6 | 0.00 | 0.00 | 0.00 | 0.00 | 1.08 | 1.06 | 0.00 | 0.00 | 98.92 | 98.94 | 100.00 | 100.00 |
| 7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.53 | 0.25 | 0.00 | 0.00 | 99.47 | 99.75 | 100.00 | 100.00 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.00 | 0.00 | 0.00 | 99.91 | 100.00 | 100.00 | 100.00 |
| Scenario | MRR(%) | FRR(%) | NII(%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNR(dB) | SNR(dB) | SNR(dB) | ||||||||||
| 40 | 50 | 60 | 70 | 40 | 50 | 60 | 70 | 40 | 50 | 60 | 70 | |
| 9 | 12.34 | 4.55 | 1.07 | 0.48 | 17.29 | 3.34 | 2.45 | 1.12 | 72.50 | 92.26 | 96.51 | 98.40 |
| 10 | 9.28 | 2.29 | 0.02 | 0.00 | 13.70 | 1.46 | 0.43 | 0.20 | 78.29 | 96.28 | 99.55 | 99.80 |
| 11 | 7.90 | 1.15 | 0.00 | 0.00 | 10.55 | 0.83 | 0.02 | 0.00 | 82.38 | 98.03 | 99.98 | 100.00 |
| 12 | 3.89 | 0.05 | 0.00 | 0.00 | 7.01 | 0.46 | 0.00 | 0.00 | 89.37 | 99.49 | 100.00 | 100.00 |
| 13 | 0.77 | 0.00 | 0.00 | 0.00 | 4.96 | 0.01 | 0.00 | 0.00 | 94.31 | 99.99 | 100.00 | 100.00 |
| 14 | 0.06 | 0.00 | 0.00 | 0.00 | 3.01 | 0.00 | 0.00 | 0.00 | 96.93 | 100.00 | 100.00 | 100.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 2.11 | 0.00 | 0.00 | 0.00 | 97.89 | 100.00 | 100.00 | 100.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, T.; Huang, J.; Cao, M.; Li, D.; Bayat, M. Seismic Damage Identification Method for Curved Beam Bridges Based on Wavelet Packet Norm Entropy. Sensors 2022, 22, 239. https://doi.org/10.3390/s22010239
Deng T, Huang J, Cao M, Li D, Bayat M. Seismic Damage Identification Method for Curved Beam Bridges Based on Wavelet Packet Norm Entropy. Sensors. 2022; 22(1):239. https://doi.org/10.3390/s22010239
Chicago/Turabian StyleDeng, Tongfa, Jinwen Huang, Maosen Cao, Dayang Li, and Mahmoud Bayat. 2022. "Seismic Damage Identification Method for Curved Beam Bridges Based on Wavelet Packet Norm Entropy" Sensors 22, no. 1: 239. https://doi.org/10.3390/s22010239
APA StyleDeng, T., Huang, J., Cao, M., Li, D., & Bayat, M. (2022). Seismic Damage Identification Method for Curved Beam Bridges Based on Wavelet Packet Norm Entropy. Sensors, 22(1), 239. https://doi.org/10.3390/s22010239







