Design and Measurement of a Dual FBG High-Precision Shape Sensor for Wing Shape Reconstruction
Abstract
:1. Introduction
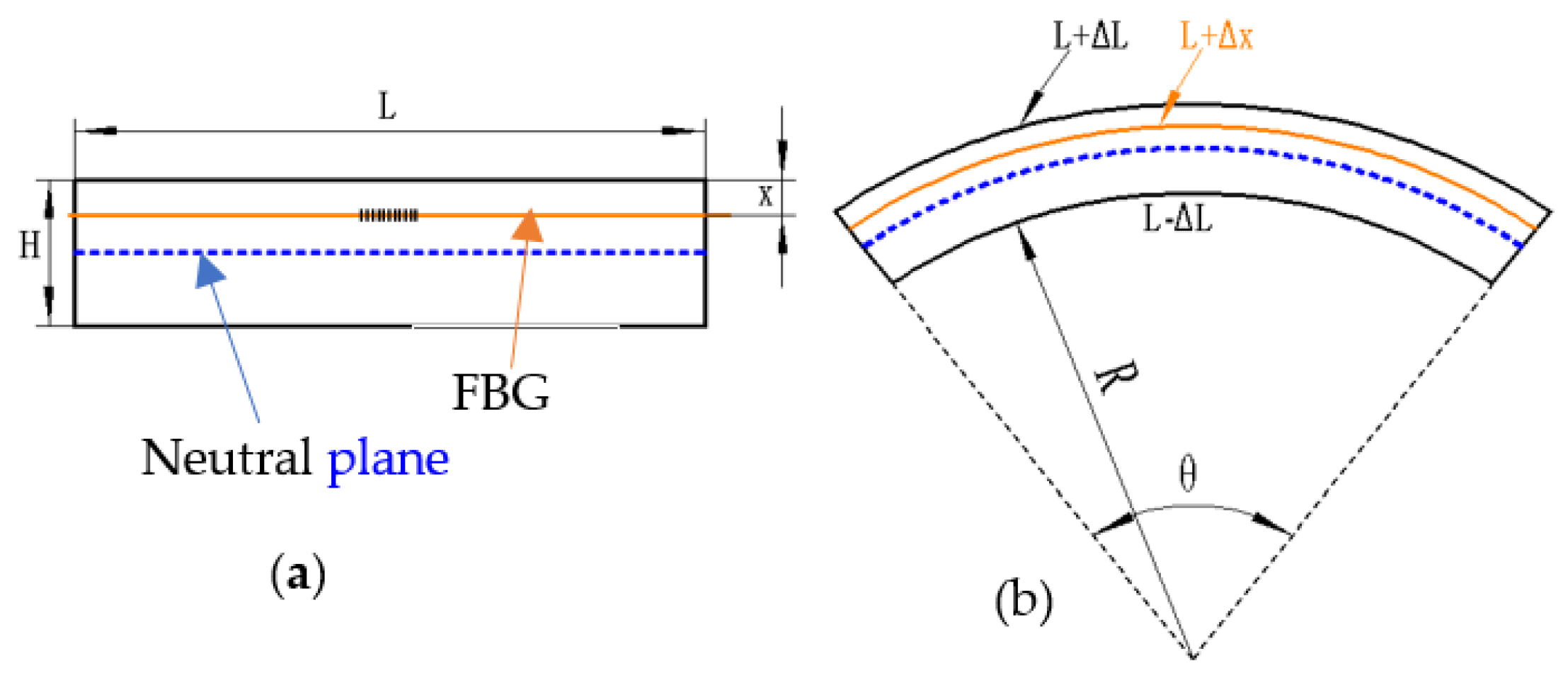
2. FBG Sensing Principle and Structure Analysis
2.1. Sensory Principle of FBG
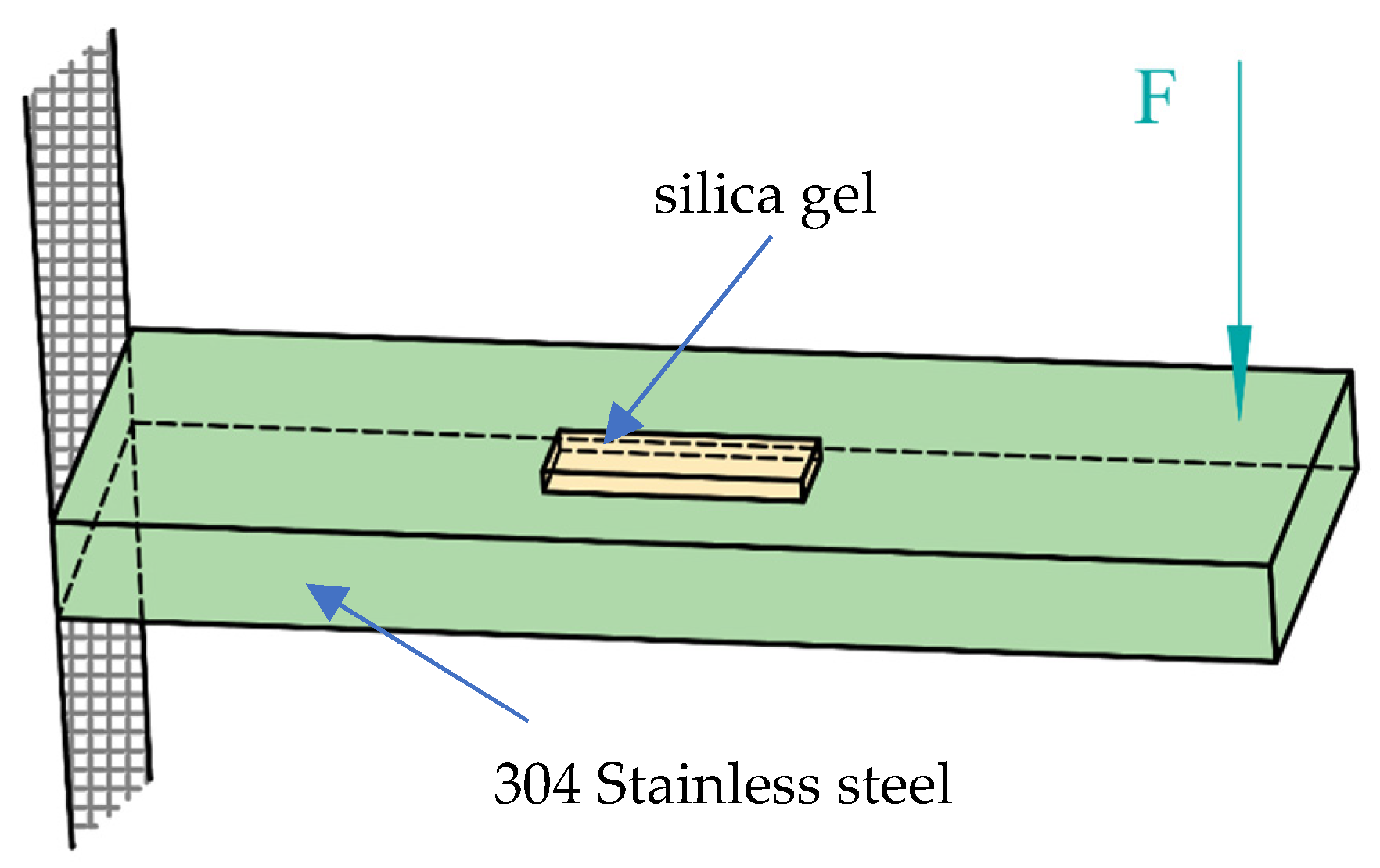
2.2. Effect of Soft Substrate Material Size on Shape Sensors
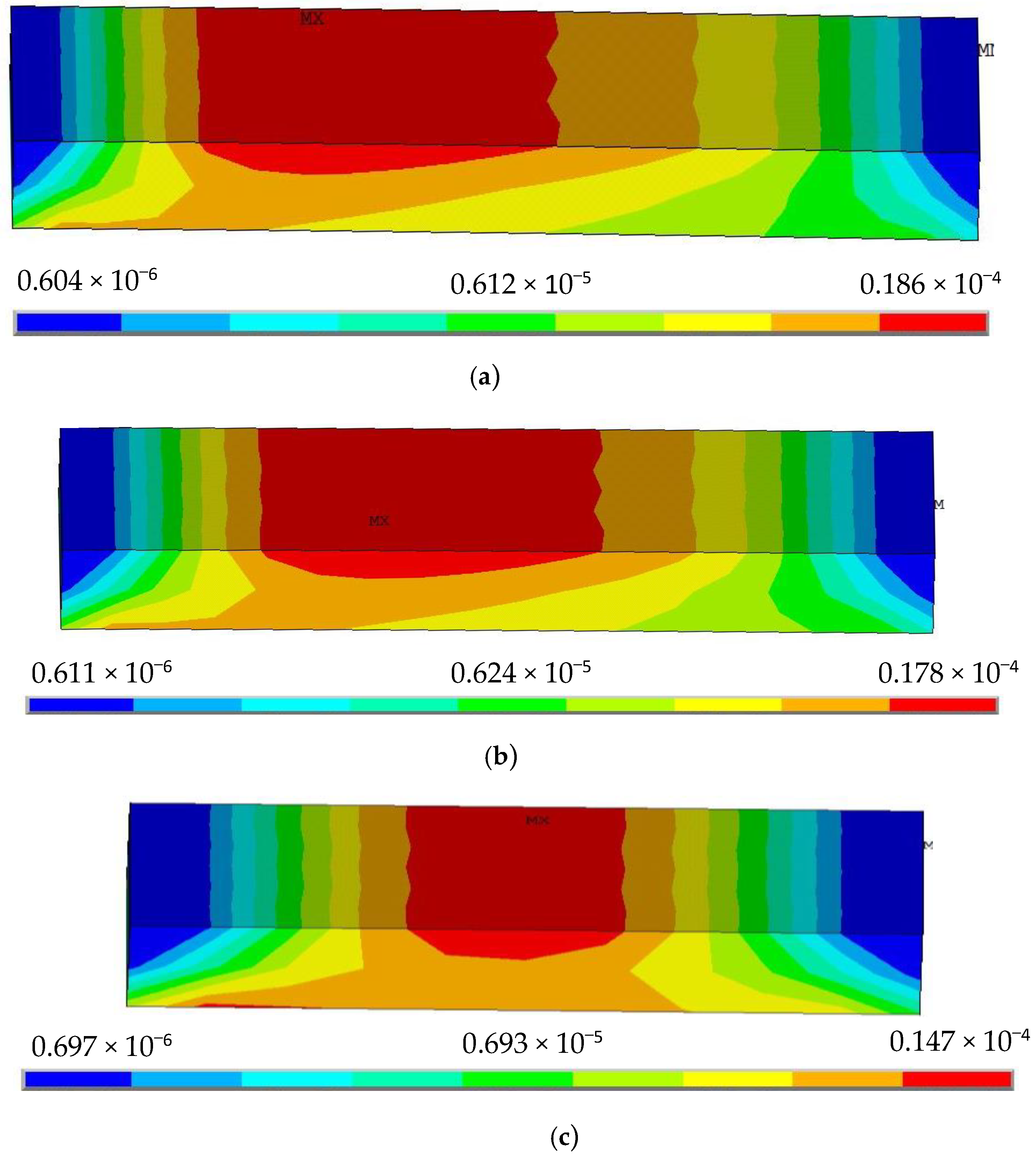
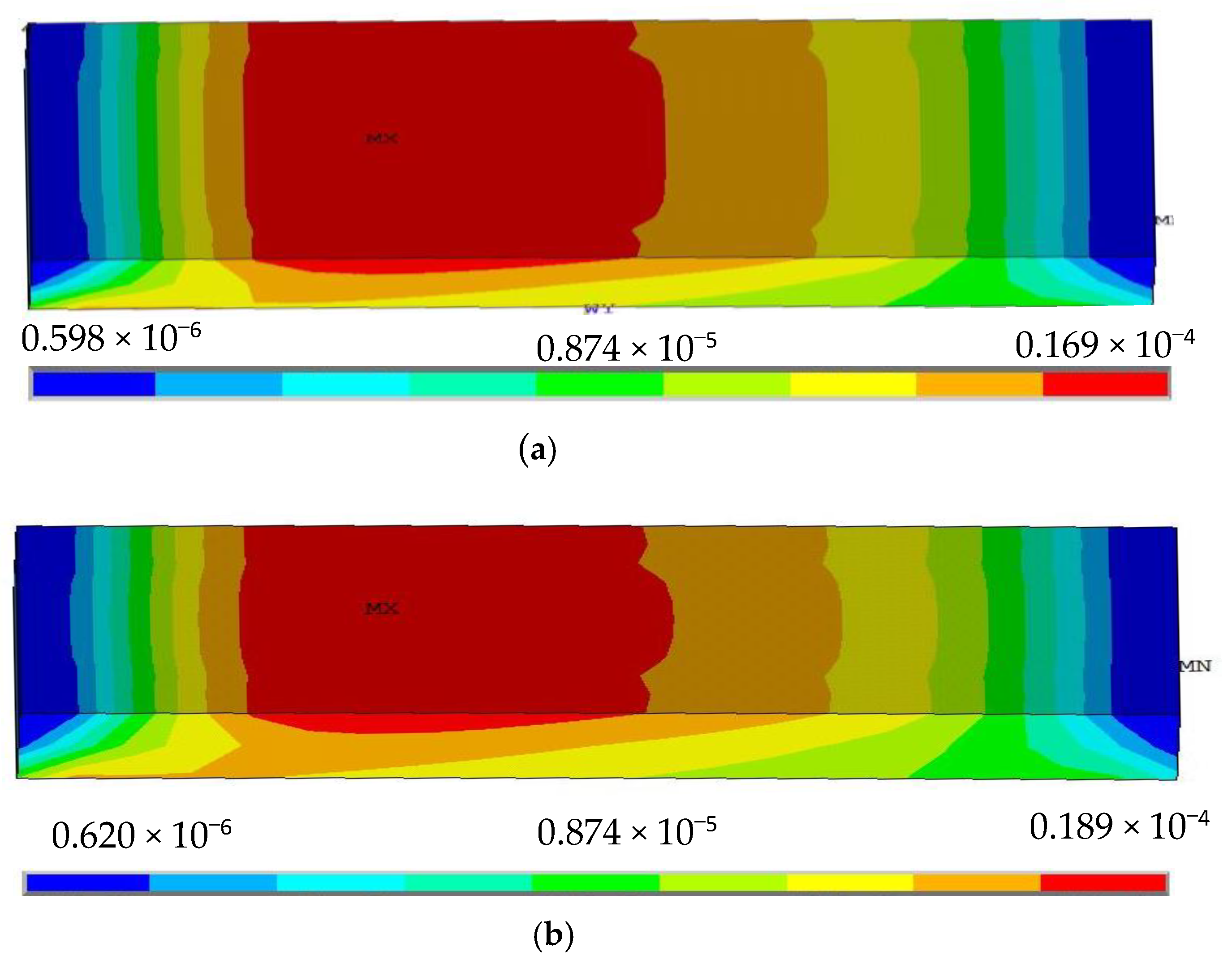
2.2.1. Variation of Silica Gel Length
- (1)
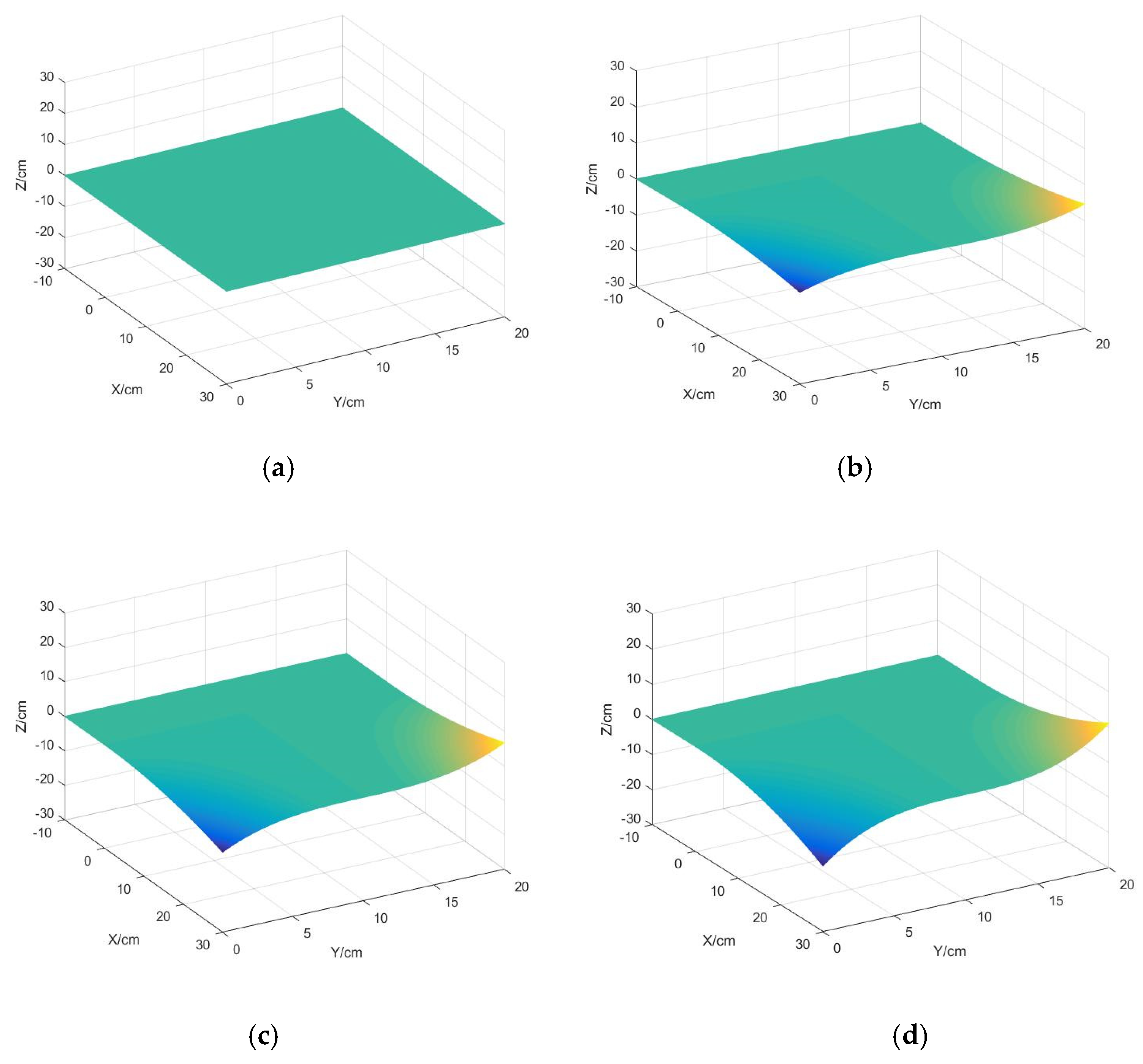
- If the length of the silica gel is longer, the stress area is larger and the maximum peak of the strain is greater, while the stress is concentrated in the upper layer of the neutral surface of the silica gel; if the length of the silica gel is smaller, the stress begins to shift from the upper layer to the lower layer of the neutral surface.
- (2)
- Regardless of the length of the silica gel, the stress distribution in the silica gel has left-right axis symmetry.
2.2.2. Variation of Silica Gel Width
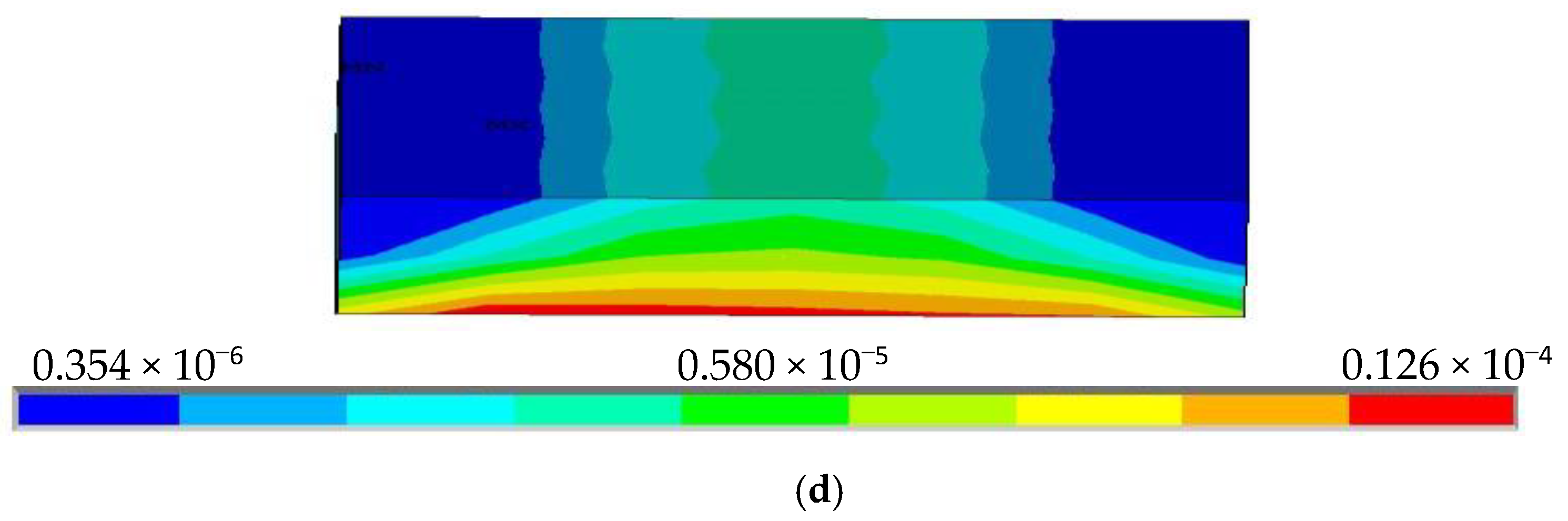
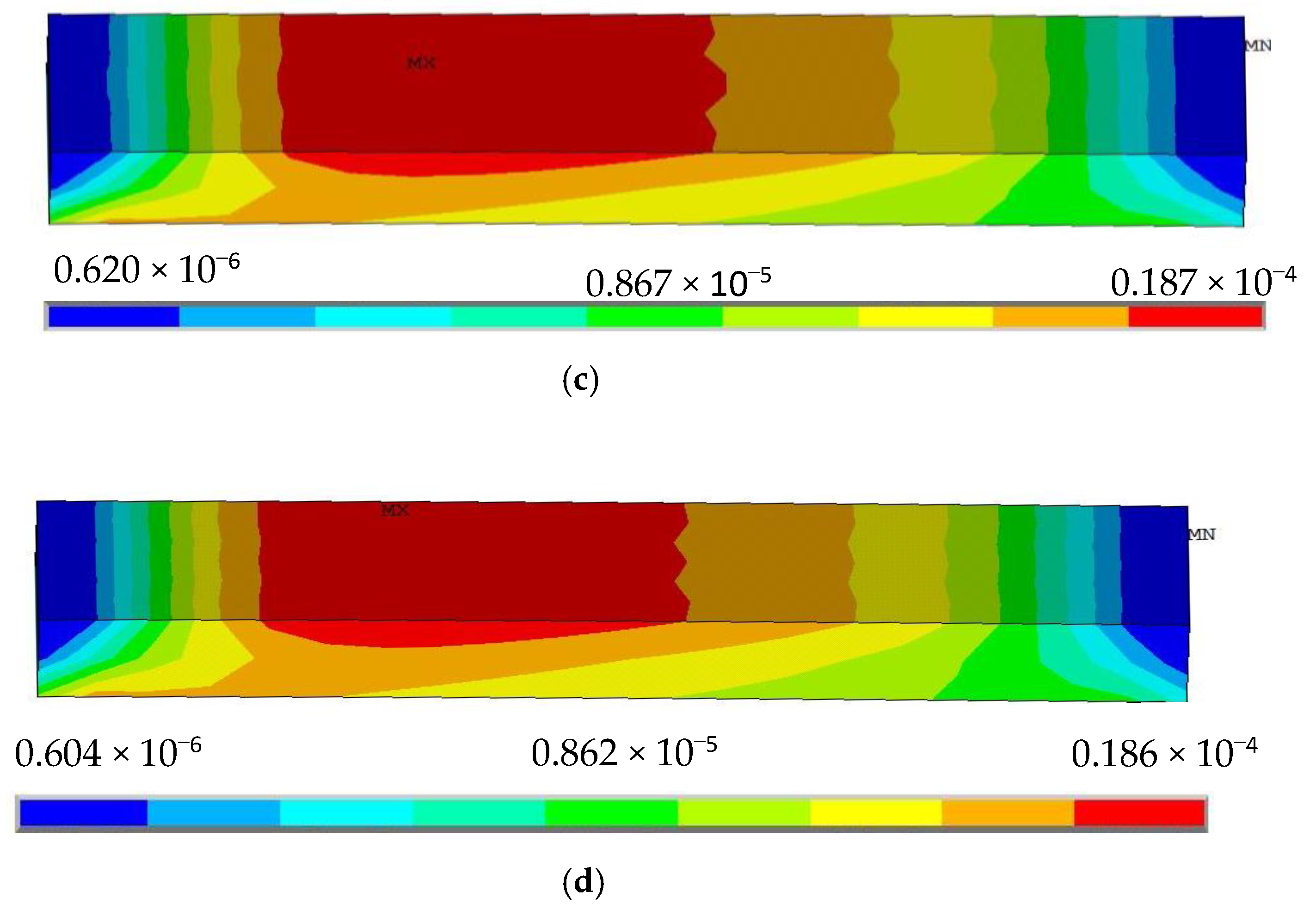
2.2.3. Variation of Silica Gel Thickness
- (1)
- When the silica gel thickness changes, the maximum stress position of silica gel will also change, the thickness of the silica gel gradually increases, the area of the stress maximum gradually decreases, its position moves closer to the center of the silica gel, the gel thickness tends to the thickness of the stainless steel and the stress distribution is likely to be transformed from the upper layer to both the upper and lower layers.
- (2)
- The stress of silica gel reaches the maximum when the thickness is 5 mm, and the maximum stress increases with increasing thickness when the thickness is below 5 mm. The maximum stress decreases with increasing thickness when the thickness is above 5 mm.
3. High-Precision FBG Shape Sensor Structure Design
3.1. The Stress Relevance between the Three Loading Methods
3.1.1. Constant Beam Size (Lb = 500 mm Hb = 4 mm)
3.1.2. Variable Beam Size
- (1)
- When the cantilever beam is subjected to a separate torque, the maximum equivalent stress at the FBG on the silica gel is ; when the cantilever beam is subjected to a separate force, the maximum equivalent stress at the FBG on the silica gel is ; and when the cantilever beam is subjected to a combination of torque and force, the maximum equivalent stress at the FBG on the silica gel is ; Equation (10) is always established, which is independent of the position of the loaded torque and independent of the size of the cantilever beam.
- (2)
- The value of the maximum equivalent stress at the FBG on the silica gel is affected by the size of the beam, the location of the loaded torque and other factors.
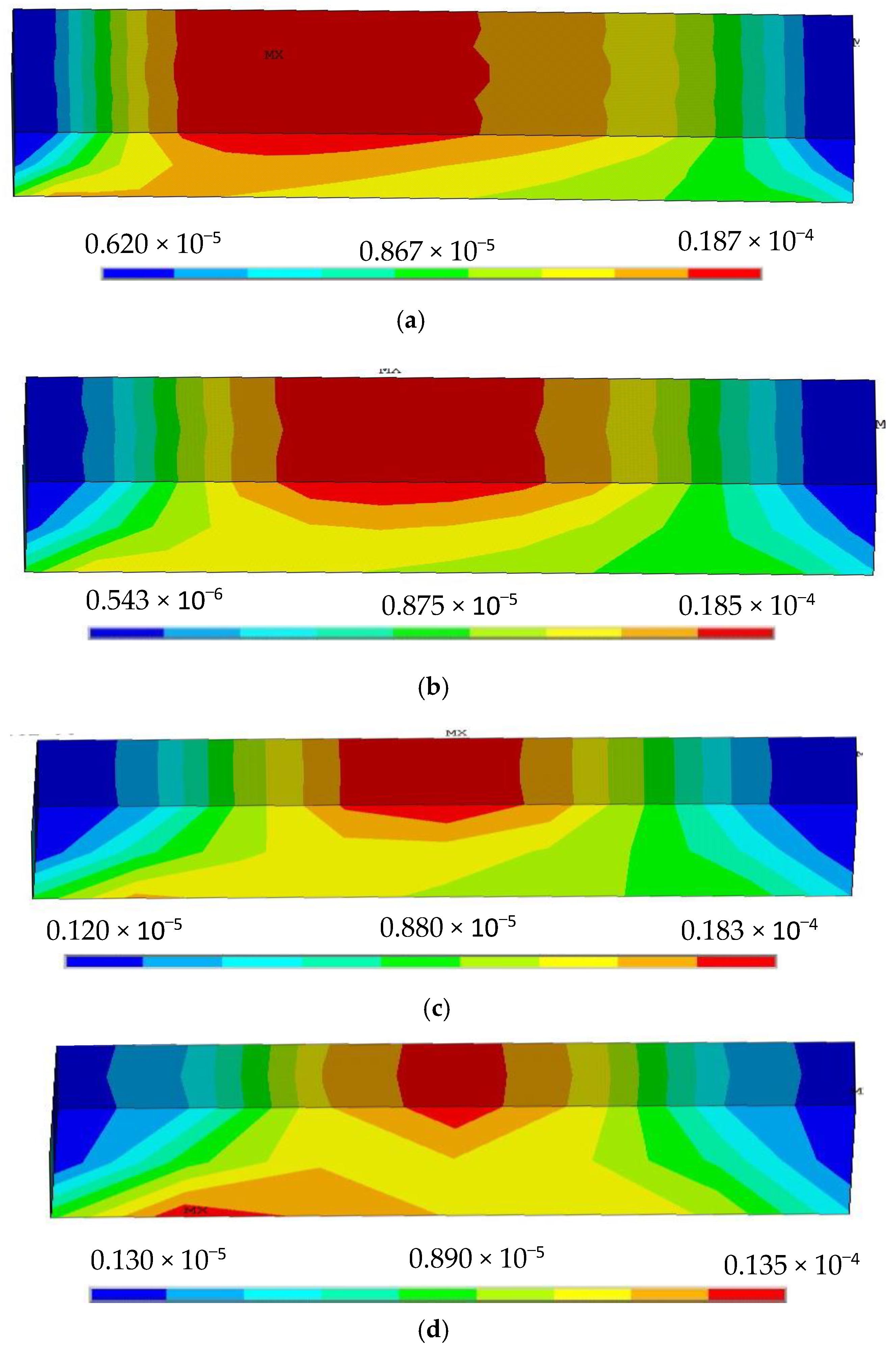
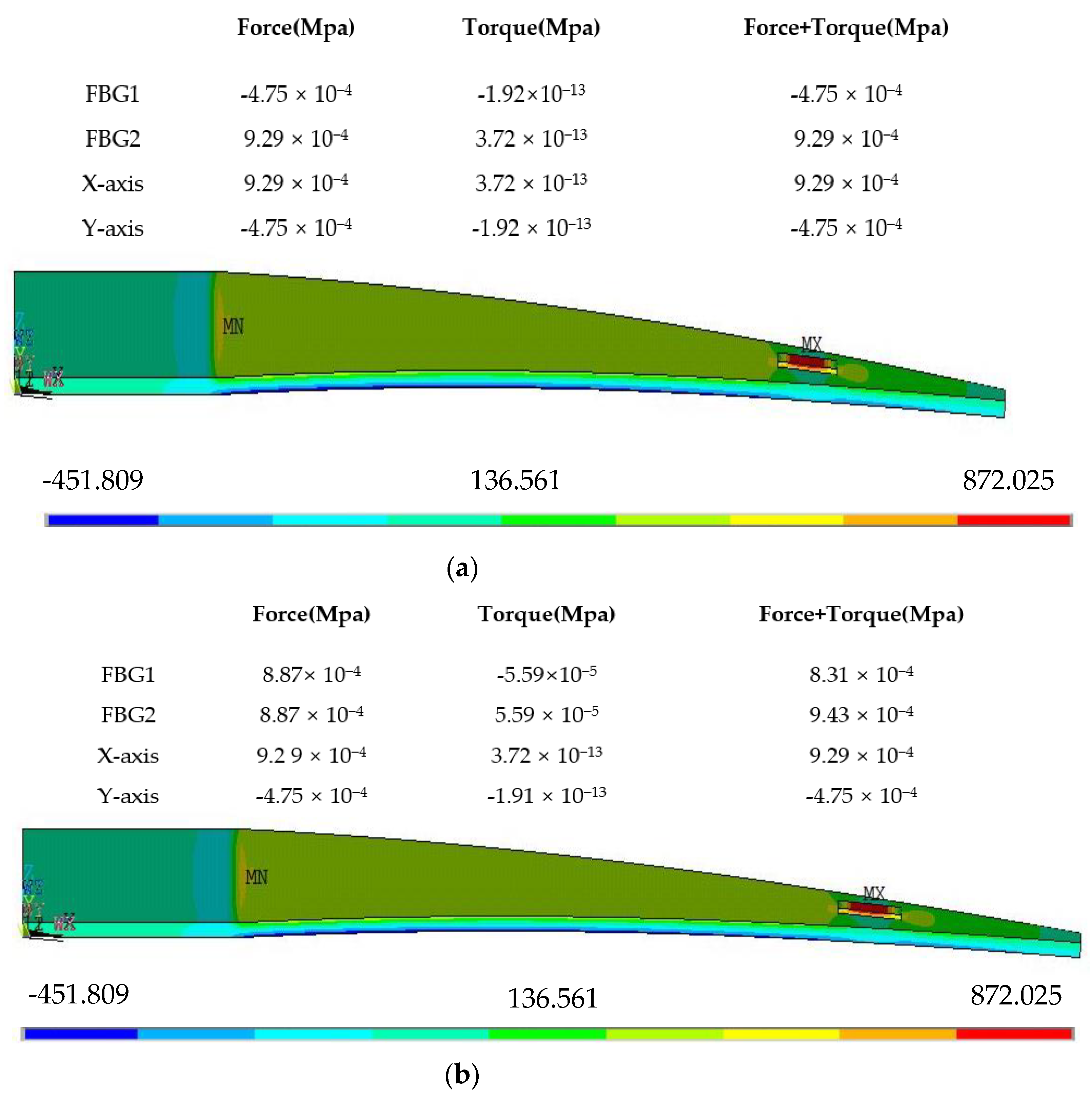
3.2. Influence of Angles and on Torque
- (1)
- The two FBGs correspond to the X-axis and Y-axis of the center of the silica gel, and the two maximum equivalent stress values at the positions of the two FBGs are 3.72 × 10−13 MPa and 1.92 × 10−13 MPa, respectively, which are generated by torque. These results show that the stress generated by torque is not sensitive to the X-axis and the Y-axis
- (2)
- : The maximum equivalent stress at the nodes where FBGs is located are shown in Table 7.
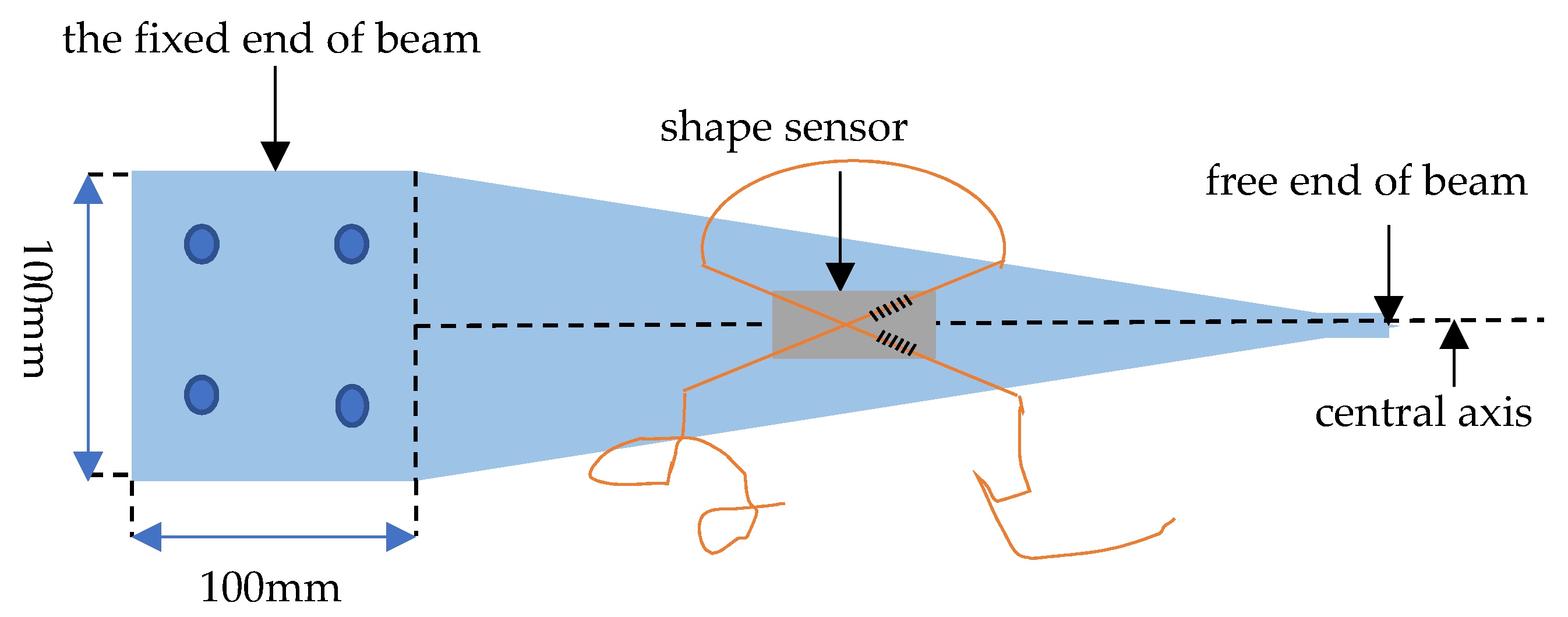
4. Sensor Performance Testing
4.1. Fabrication of the Dual FBG High-Precision Shape Sensor
4.2. FBG Shape Sensor Test Platform
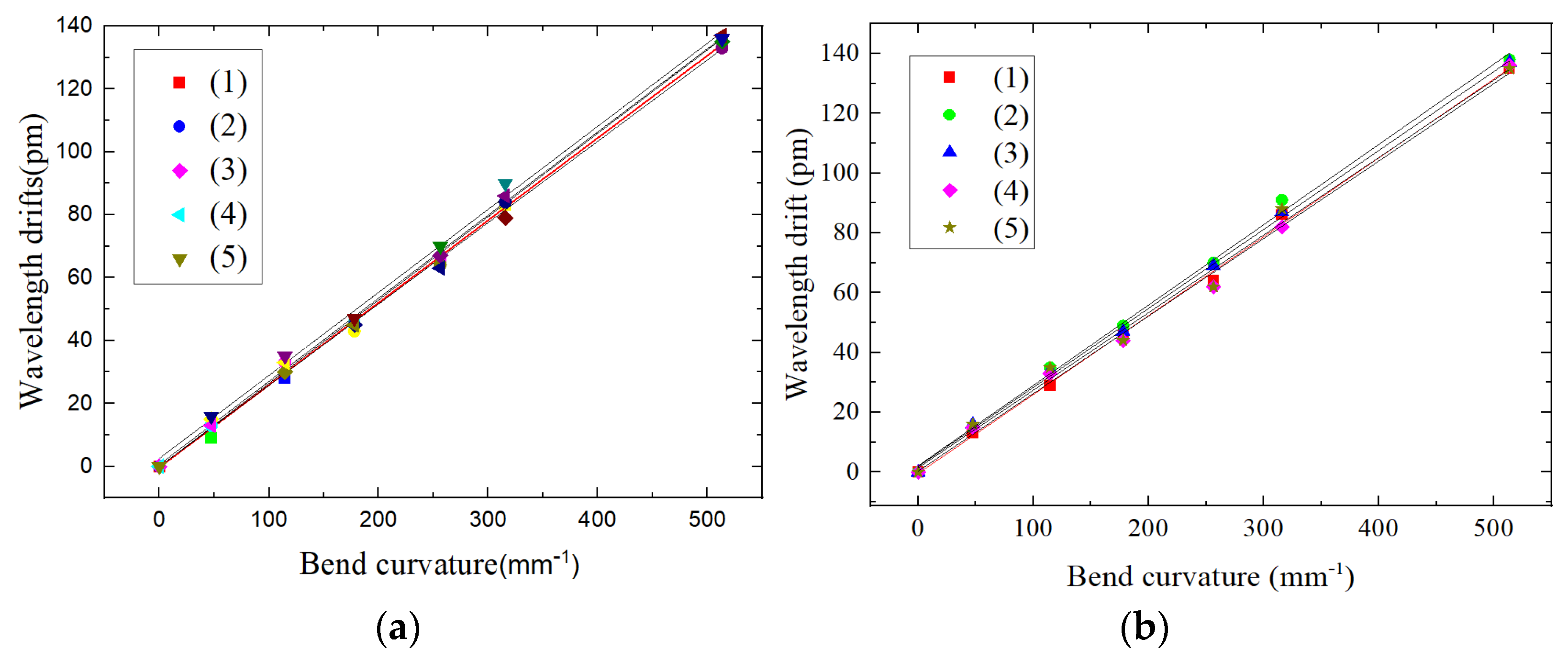
4.3. Sensor Parameter Calibration
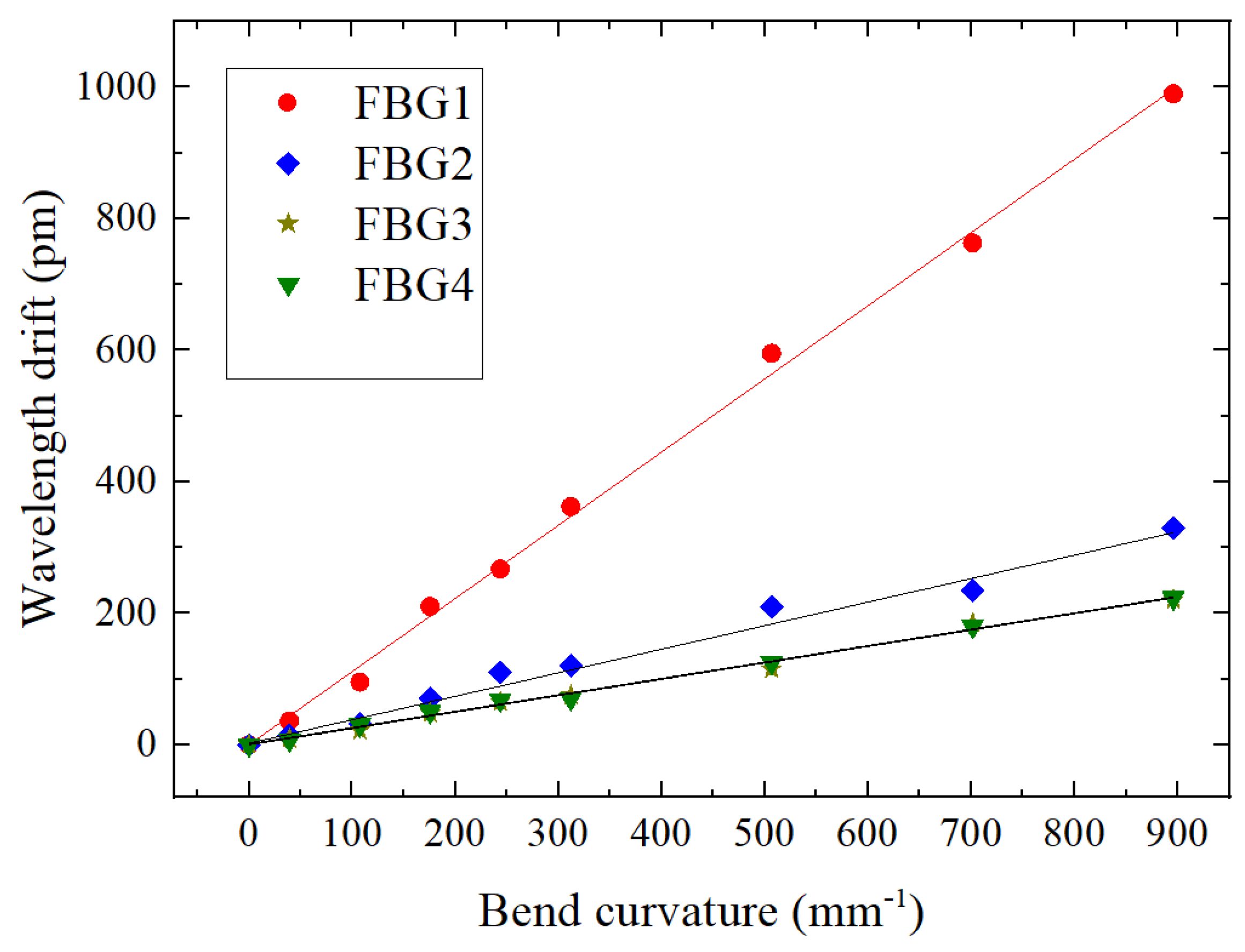
4.3.1. Curvature Calibration Loaded with Vertical Force
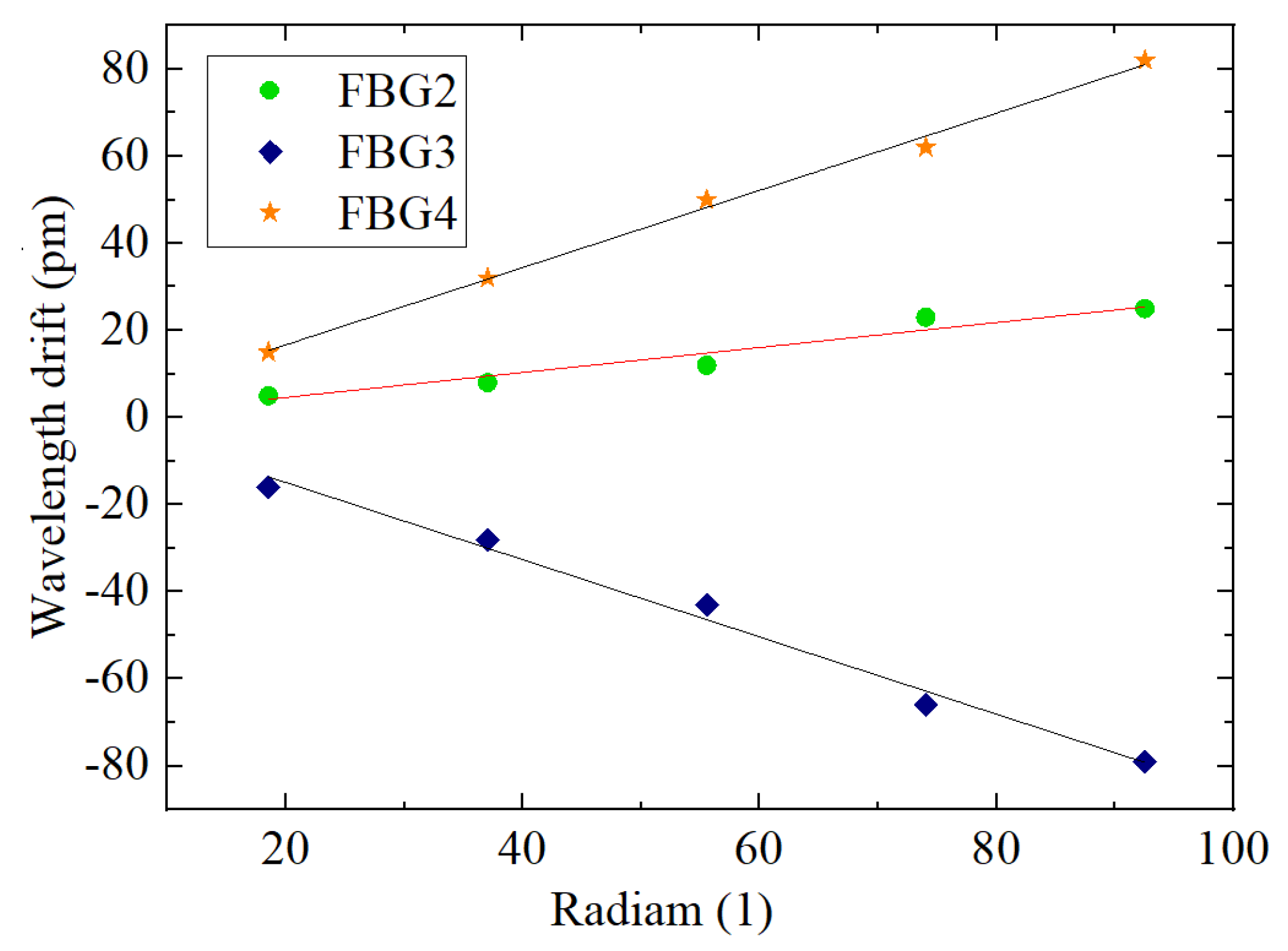
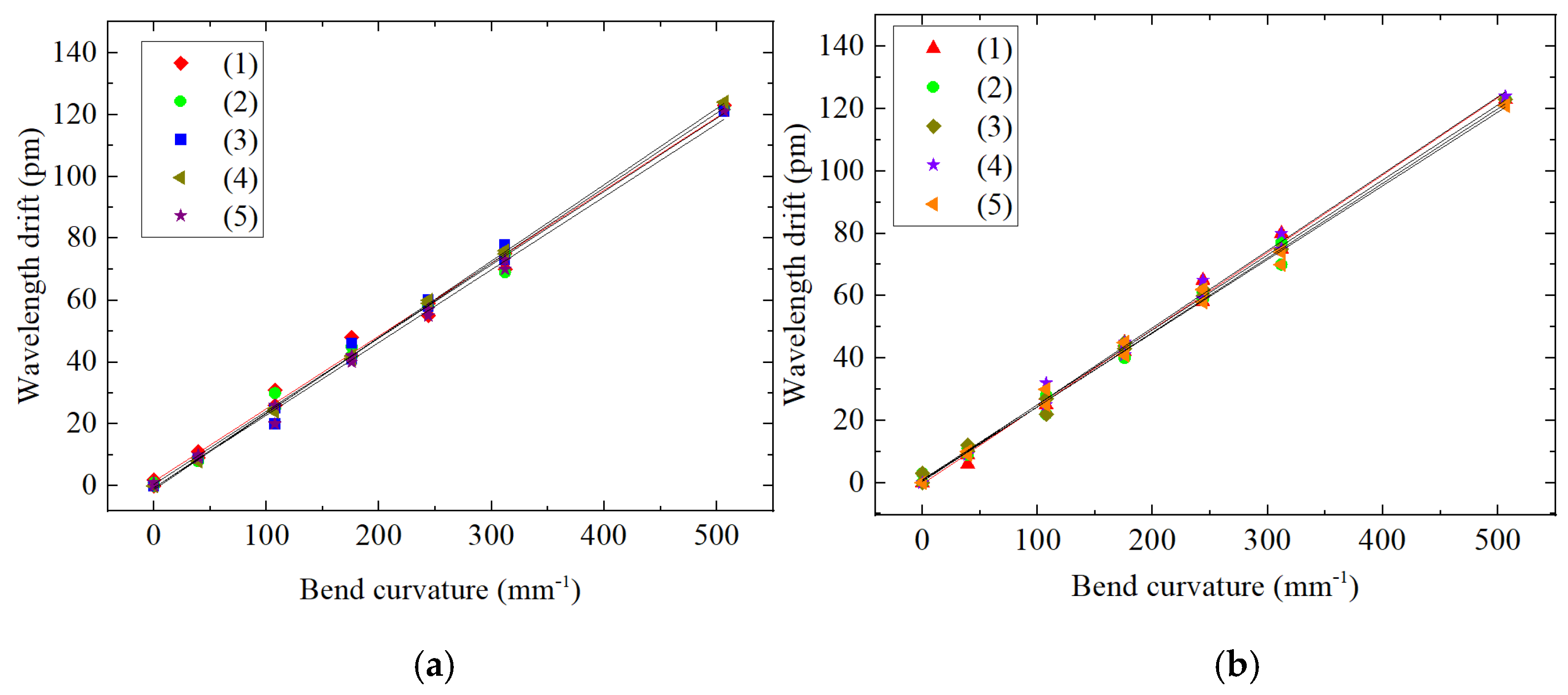
4.3.2. Calibration of the Rotation Radian Loaded with Torque
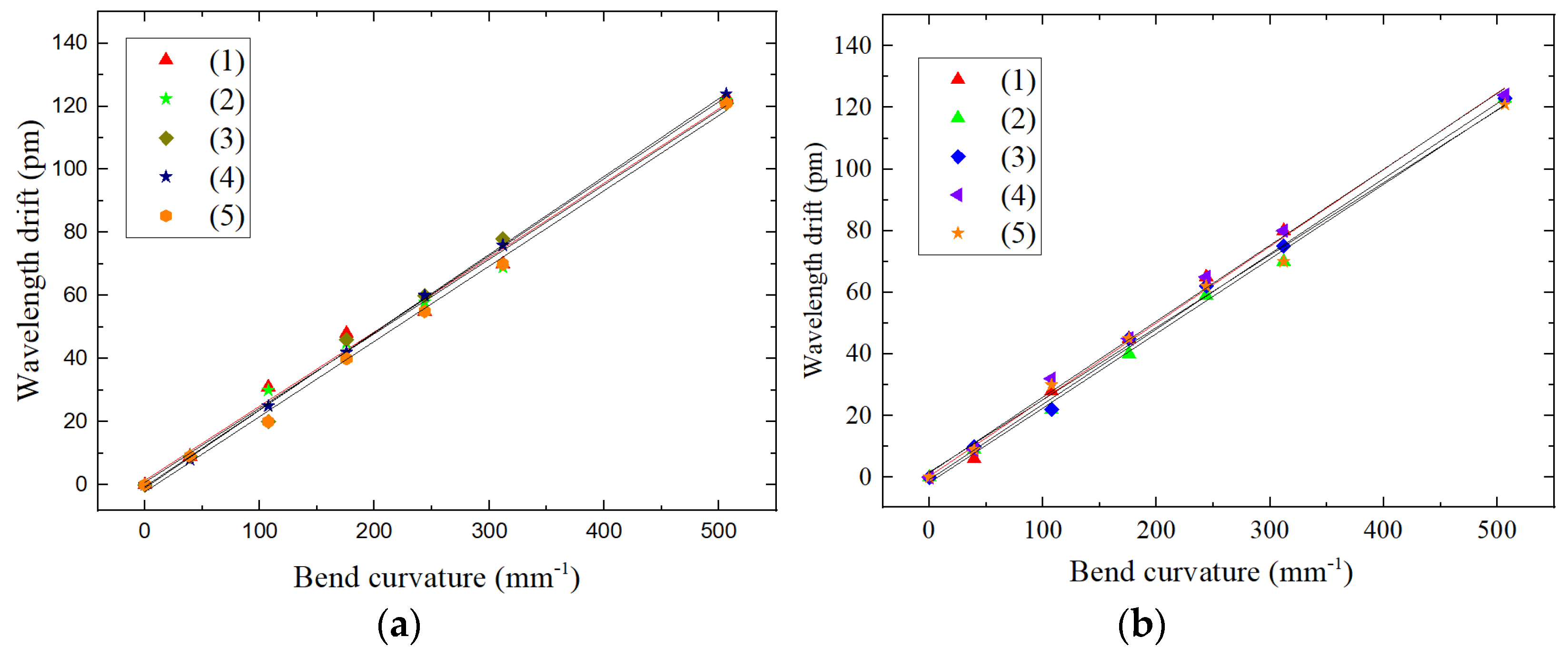
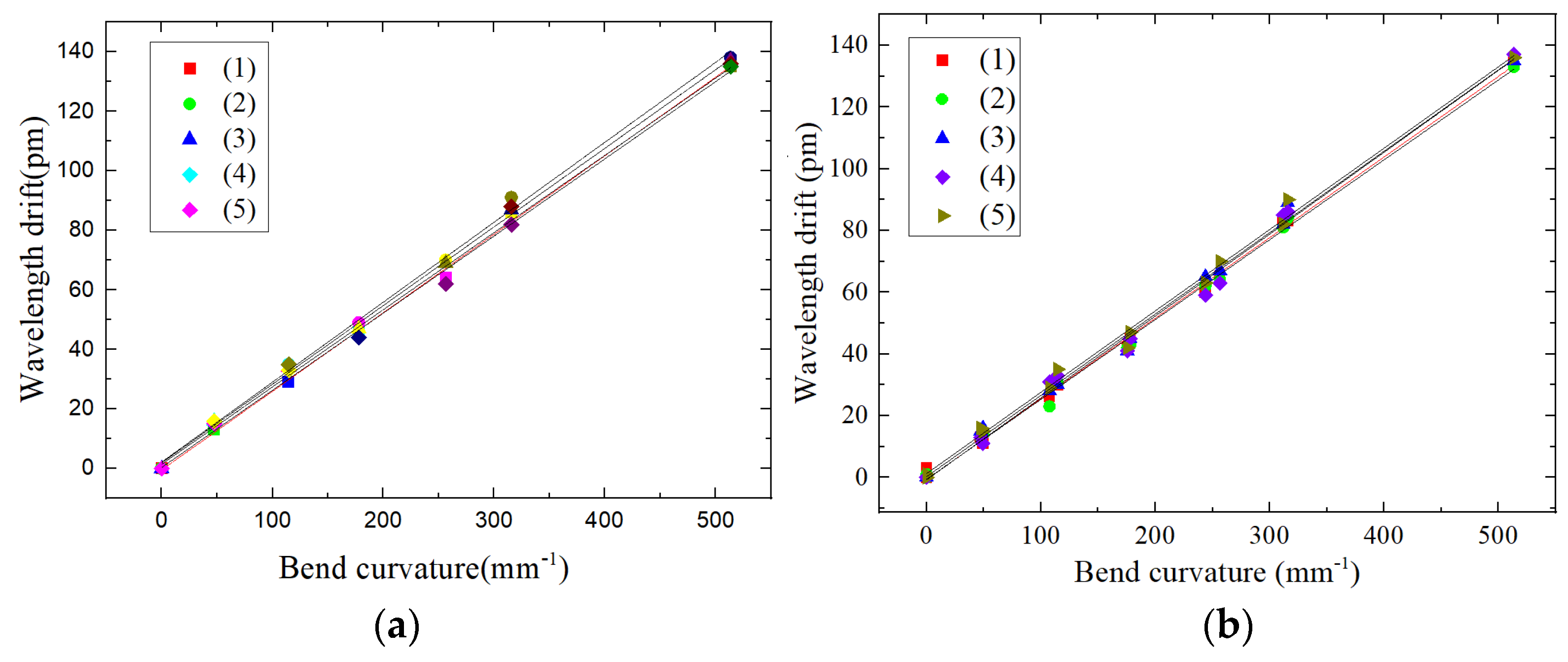
4.3.3. Calibration of the Dual FBG High-Precision Shape Sensor under a Combined Load
4.4. Error Analysis of Repeatability
4.5. Hysteresis Error Analysis
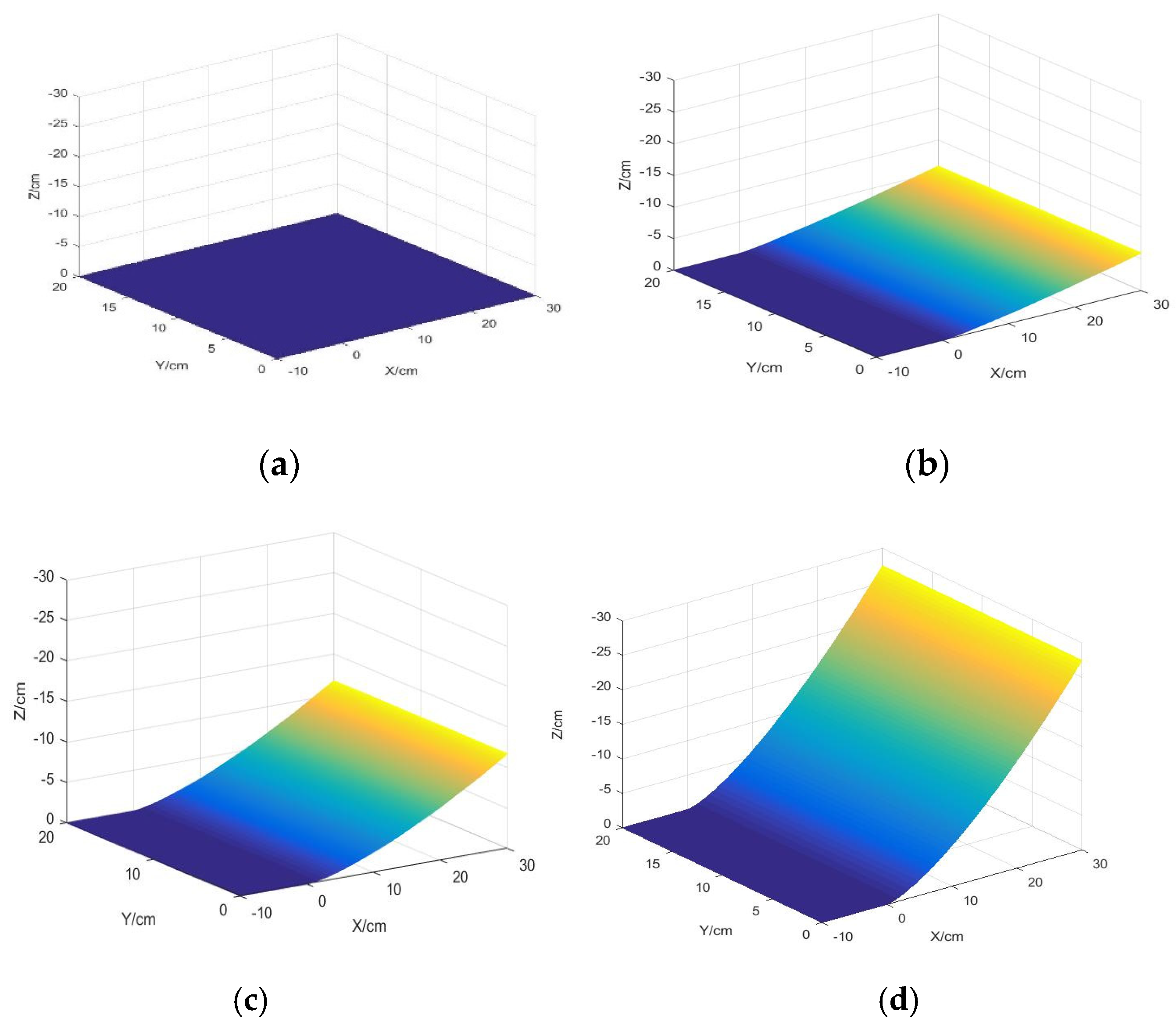
5. Shape Reconstruction Test of a Test Specimen
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.Y.; Cui, J.W.; Chen, M.M. Review on optical fiber shape sensing technology. Opt. Precis. Eng. 2020, 28, 10–29. [Google Scholar] [CrossRef]
- Waltermann, C.; Koch, J.; Angelmahr, M.; Burgmeier, J.; Schade, W. Fiber-optical 3d shape sensing. In Planar Waveguides and other Confined Geometries; Springer: New York, NY, USA, 2014; pp. 227–250. [Google Scholar]
- Shen, L.Y.; Xiao, H.; Qian, J.W.; Yang, L.J.; Zhang, Y.N. Shape reconstruction and visualization of endoscope. Chin. J. Sci. Instrum. 2014, 21, 2725–2730. [Google Scholar]
- Wei, W.; Zhou, Z.; Xiaoping, Z.; Rui, W. Explo-ring aeroelastic stability of very flexible solar powered UAV with geometrically large deformation. J. Northwestern Polytech. Univ. 2015, 33, 1–8. [Google Scholar]
- Pena, F.; Richards, L.; Parker, A.; Piazza, A.; Chan, P.; Hamory, P. Fiber Optic Sensing System (FOSS) Technology-A New Sensor Paradigm for Comprehensive Structural Monitoring and Model Validation Throughout the Vehicle Lifecycle. 2015. Available online: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20160001157.pdf.2015 (accessed on 3 August 2021).
- Ma, Z.; Chen, X. Fiber bragg gratings sensors for aircraft wing shape measurement: Recent applications and technical analysis. Sensors 2018, 19, 55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, G.K.; Qu, D.M.; Yan, G.; Song, Y.M.; Zhu, L.Q. Bending deformation of optical fiber sensing and shape reconstruction of soft pneumatic driver. J. Syst. Simul. 2019, 27, 1052–1059. [Google Scholar]
- Zhu, X.J.; Lu, M.Y.; Zhao, X.Y. 3D reconstruction algorithm and visualization analysis for space manipulator vibration shape. Opt. Precis. Eng. 2009, 21, 4706–4713. [Google Scholar]
- He, Y.L.; Zhang, X.; Sun, G.K.; Song, Y.M.; Zhu, L.Q. Flexible curvature sensor based on composite substrate. Opt. Precis. Eng. 2019, 27, 1270–1276. [Google Scholar]
- Davis, M.A.; Malinowski, E.; Chevalier, J.L.; Mcgregor, A.M.; Reaves, M. Body Shape, Position, and Posture Recognition Suit with Multi-Core Optical Shape Sensing Fiber. U.S. Patent US 9304019, 2016. [Google Scholar]
- Monsberger, C.M.; Lienhart, W. Distributed fiber optic shape sensing of concrete structures. Sensors 2021, 21, 6098. [Google Scholar] [CrossRef] [PubMed]
- Jang, M.; Kim, J.S.; Kang, K.; Kim, J.; Yang, S. Towards Finger Motion Capture System Using FBG Sensors. In Proceedings of the 2018 IEEE 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 3734–3737. [Google Scholar]
- Xu, C.; Khodaei, Z.S. Shape sensing with rayleigh backscattering fibre optic sensor. Sensors 2020, 20, 4040. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, Y.N.; Qian, J.W.; Shen, L.Y. Accuracy of position tracking and fabrication of thin diameter sensor. Meas. Sci. Technol. 2021, 32, 055202. [Google Scholar] [CrossRef]
- Zhao, Z.; Soto, M.A.; Ming, T.; Thévenaz, L. Distributed shape sensing using Brillouin scattering in multi-core fibers. Opt. Express 2016, 24, 25211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ba, D.X.; Chen, C.; Cheng, F.; Zhang, D.Y.; Lu, Z.W.; Fan, Z.G.; Dong, Y.K. A high-performance and temperature-insensitive shape sensor based on DPP-BOTDA. IEEE Photon. J. 2017, 10, 7100810. [Google Scholar] [CrossRef]
- Szostkiewicz, U.; Soto, M.A.; Yang, Z.; Dominguez-Lopez, A.; Thevenaz, L. High-resolution distributed shape sensing using phase-sensitive optical time-domain reflectometry and multicore fibers. Opt. Express 2019, 27, 20763. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Wang, Z.; Sui, Q.; Jing, W.; Dong, Y.; Li, Y. Design and optimization of fbg implantable flexible morphological sensor to realize the intellisense for displacement. Sensors 2018, 18, 2342. [Google Scholar] [CrossRef] [Green Version]
- Wang, C. 3D shapes detecting method of soft manipulator based on fiber Bragg grating sensor. Control Instrum. Chem. Ind. 2015, 42, 1130–1133. [Google Scholar]
- Zhi, G.H.; Di, H.T. Wind speed monitoring system based on optical fiber curvature sensor. Opt. Fiber Technol. 2021, 62, 102467. [Google Scholar] [CrossRef]
- Abro, A.Z.; Zhang, Y.F.; Hong, C.Y.; Ahmed, L.R.; Chen, N.L. Development of a smart garment for monitoring body postures based on fbg and flex sensing technologies. Sens. Actuators A Phys. 2018, 272, 153–160. [Google Scholar] [CrossRef]
- Abro, Z.A.; Hong, C.; Chen, N.; Zhang, Y.; Yasin, S. A fiber bragg grating-based smart wearable belt for monitoring knee joint postures. Text. Res. J. 2020, 90, 386–394. [Google Scholar] [CrossRef]
- He, Y.L.; Zhu, L.Q.; Sun, G.K.; Yu, M.X.; Dong, M.L. Design, Measurement and Shape Reconstruction of Soft Surgical Actuator Based on Fiber Bragg Gratings. Appl. Sci. 2018, 8, 1773. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Dong, M.; Sun, G.; Meng, F.; Song, Y.; Zhu, L. Shape monitoring of morphing wing using micro-optical sensors with different embedded depth. Opt. Fiber Technol. 2019, 48, 179–185. [Google Scholar] [CrossRef]
- Sun, G.; Wu, Y.; Li, H.; Zhu, L. 3D shape sensing of flexible morphing wing using fiber bragg grating sensing method. Opt. Int. J. Light Electron. Opt. 2018, 156, 83–92. [Google Scholar] [CrossRef]
- Wang, Q.L.; Zhou, X.H.; Jiang, H.J.; Sun, G.K.; Zhu, L.Q. Polyimide sensing layer for bending shape measurement in soft surgical manipulators. Optik 2019, 183, 179–188. [Google Scholar] [CrossRef]
- Leal Junior, A.G.; Theodosiou, A.; Diaz, C.; Marques, C.; Pontes, M.J.; Kalli, K. Simultaneous measurement of axial strain, bending and torsion with a single fiber bragg grating in CYTOP fiber. J. Lightwave Technol. 2018, 37, 971–980. [Google Scholar] [CrossRef]
- Henken, K.R.; Dankelman, J.; van den Dobbelsteen, J.J.; Cheng, L.K.; van der Heiden, M.S. Error analysis of fbg-based shape sensors for medical needle tracking. IEEE/ASME Trans. Mechatron. 2014, 19, 1523–1531. [Google Scholar]
- Sun, G.; Hu, Y.; Dong, M.; He, Y.; Yu, M.; Zhu, L. Flexible membrane curvature sensor based on multilayer polyimide substrate and optical fiber implantation. Optik 2018, 176, 559–566. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Qian, J.; Yi, X.; Shen, L. Analysis of strain transfer characteristics of no-substrate and thin diameter sensor-sciencedirect. Opt. Fiber Technol. 2020, 102, 2367. [Google Scholar]
- Othonos, A.; Kalli, K.; Kohnke, G.E. Fiber Bragg Gratings: Fundamentals and Applications in Telecommunications and Sensing; Physics Today: Boston, MA, USA, 2000. [Google Scholar]







| Size | a | b | c | d |
|---|---|---|---|---|
| length (mm) | 30 | 25 | 15 | 8 |
| width (mm) | 8 | 8 | 8 | 8 |
| thickness (mm) | 3 | 3 | 3 | 3 |
| Size | a | b | c | d |
|---|---|---|---|---|
| Length (mm) | 30 | 30 | 30 | 30 |
| Width (mm) | 25 | 15 | 10 | 8 |
| Thickness (mm) | 3 | 3 | 3 | 3 |
| Size | a | b | c | d |
|---|---|---|---|---|
| length (mm) | 30 | 30 | 30 | 30 |
| width (mm) | 10 | 10 | 10 | 10 |
| thickness (mm) | 2 | 5 | 8 | 10 |
| Parameter | Force | Torques | Force + Torques | |
|---|---|---|---|---|
| value | 800 N | 800 N·m | 800 N | 800 N·m |
| direction | vertical down | clockwise | vertical down | clockwise |
| loading point | End of beam (free end) | Any position of beam | End of beam (free end) | Any position of beam |
| Loaded | Force | Torque | Force + Torque | |||
|---|---|---|---|---|---|---|
| Point | FBG1 (MPa) | FBG2 (MPa) | FBG1 (MPa) | FBG1 (MPa) | FBG2 (MPa) | FBG1 (MPa) |
| 1/4 | 5.78 × 10−4 | 5.78 × 10−4 | −1.80 × 10−11 | 1.82 × 10−11 | 5.78 × 10−4 | 5.78 × 10−4 |
| 1/2 | 5.78 × 10−4 | 5.78 × 10−4 | −1.04 × 10−8 | 1.04 × 10−8 | 5.78 × 10−4 | 5.78 × 10−4 |
| 3/4 | 5.78 × 10−4 | 5.78 × 10−4 | −1.41 × 10−4 | 1.41 × 10−4 | 4.37 × 10−4 | 7.19 × 10−4 |
| Size/ | Force | Torque | Force +Torque | |||
|---|---|---|---|---|---|---|
| Loaded Point | FBG1(MPa) | FBG2 (MPa) | FBG1 (MPa) | FBG2 (MPa) | FBG1 (MPa) | FBG2 (MPa) |
| Lb = 300 mm, Hb = 4 mm,1/3 | 1.12 × 10−4 | 1.12 × 10−4 | −5.45 × 10−8 | 5.45 × 10−8 | 1.12 × 10−4 | 1.12 × 10−4 |
| Lb = 400 mm, Hb = 4 mm,1/3 | 1.86 × 10−4 | 1.86 × 10−4 | −3.62 × 10−10 | 3.62 × 10−10 | 1.86 × 10−4 | 1.86 × 10−4 |
| Lb = 500 mm, Hb = 5 mm,2/3 | 1.13 × 10−4 | 1.13 × 10−4 | −5.45 × 10−8 | 5.45 × 10−8 | 1.13 × 10−4 | 1.13 × 10−4 |
| Lb = 600 mm, Hb = 8 mm,2/3 | 2.49 × 10−4 | 2.49 × 10−4 | −3.57 × 10−7 | 3.57 × 10−7 | 2.49 × 10−4 | 2.49 × 10−4 |
(°) | Stress(torque) (MPa) | Stress(force) (MPa) | (°) | Stress(torque) (MPa) | Stress(force) (MPa) |
|---|---|---|---|---|---|
| = 0 = 90 | ---- | ---- | = 45 | 1.63 × 10−4 | 2.27 × 10−4 |
| = 10 | 5.59 × 10−5 | 8.87 × 10−4 | = 50 | 1.61 × 10−4 | 1.05 × 10−4 |
| = 20 | 1.05 × 10−4 | 7.65 × 10−4 | = 60 | 1.41 × 10−4 | 1.24 × 10−4 |
| = 30 | 1.41 × 10−4 | 5.78 × 10−4 | = 70 | 1.05 × 10−5 | 3.14 × 10−4 |
| = 40 | 1.61 × 10−4 | 3.49 × 10−4 | = 80 | 5.59 × 10−5 | 4.32 × 10−4 |
| Parameter | FBG1 | FBG2 | FBG4 | FBG3 |
|---|---|---|---|---|
| (Bare FBG) | (Single FBG Sensor) | (Dual FBG Shape Sensor) | ||
| Fiber type | single mode 1549.190 5 | single mode 1536.141 5 | single mode 1529.953 5 | single mode 1536.185 5 |
| Wavelength (nm) | ||||
| Grating length (mm) | ||||
| Peak reflectivity (%) | 75 | 75 | 75 | 75 |
| Parameters | FBG1 | FBG2 | FBG4 | FBG3 |
|---|---|---|---|---|
| (pm) | 217 | 70 | 49 | 48 |
| (m−1) | 0.896024 | 0.896024 | 0.896024 | 0.896024 |
| Sk (pm/m−1) | 242.18 | 78.12 | 54.69 | 53.57 |
| Parameters | FBG2 | FBG4 | FBG3 |
|---|---|---|---|
| (pm) | 25 | −80 | 83 |
| (1) | 0.09233 | 0.09233 | 0.09233 |
| Sr (pm/1) | 270.77 | −866.46 | 898.956 |
| Measured Points | Parameters | State I | State II | State III |
|---|---|---|---|---|
| point 1 | Reconstructed value(cm) | 1.582 | 2.497 | 5.868 |
| Measured value(cm) | 1.671 | 2.57 | 6.13 | |
| Error (%) | 5.33 | 2.84 | 4.27 | |
| point 2 | Reconstructed value(cm) | 4.65 | 8.566 | 19.52 |
| Measured value(cm) | 4.51 | 8.151 | 20.58 | |
| Error (%) | 3.1 | 5.09 | 5.15 |
| Measured Points | Parameters | State IV | State V | State VI | |||
|---|---|---|---|---|---|---|---|
| x-axi | z-axis | x-axi | z-axis | x-axi | z-axis | ||
| point 1 | Reconstructed values (cm) | 9.917 | 0.497 | 9.899 | 0.6798 | 9.891 | 1.254 |
| Measured values (cm) | 9.751 | 0.468 | 9.741 | 0.722 | 9.732 | 1.198 | |
| Error (%) | 1.7 | 6.13 | 1.62 | 5.84 | 1.63 | 4.67 | |
| point 2 | Reconstructed values (cm) | 24.51 | 2.848 | 23.99 | 4.48 | 23.08 | 7.074 |
| Measured values (cm) | 24.109 | 2.769 | 23.465 | 4.356 | 22.591 | 7.267 | |
| Error (%) | 1.66 | 2.85 | 2.24 | 2.85 | 2.16 | 2.66 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Liang, L.; Wang, H.; Dai, S.; Xu, Q.; Dong, R. Design and Measurement of a Dual FBG High-Precision Shape Sensor for Wing Shape Reconstruction. Sensors 2022, 22, 168. https://doi.org/10.3390/s22010168
Wu H, Liang L, Wang H, Dai S, Xu Q, Dong R. Design and Measurement of a Dual FBG High-Precision Shape Sensor for Wing Shape Reconstruction. Sensors. 2022; 22(1):168. https://doi.org/10.3390/s22010168
Chicago/Turabian StyleWu, Huifeng, Lei Liang, Hui Wang, Shu Dai, Qiwei Xu, and Rui Dong. 2022. "Design and Measurement of a Dual FBG High-Precision Shape Sensor for Wing Shape Reconstruction" Sensors 22, no. 1: 168. https://doi.org/10.3390/s22010168
APA StyleWu, H., Liang, L., Wang, H., Dai, S., Xu, Q., & Dong, R. (2022). Design and Measurement of a Dual FBG High-Precision Shape Sensor for Wing Shape Reconstruction. Sensors, 22(1), 168. https://doi.org/10.3390/s22010168





